(完整版)新人教版六年级下册圆柱与圆锥常见题型归纳整理
新人教版六年级下册圆柱与圆锥常见题型归纳整理

圆柱圆锥常见题型归纳一、公式转换1.基本公式:①圆柱的相关计算公式:底面积:S底=底面周长:C==。
圆柱侧面积=×(文字)S侧===。
(字母)逆推公式有:C=。
h=。
圆柱的表面积:S=2S底+S侧=。
圆柱的体积:V柱==逆推公式有:S=h=②圆锥的相关计算公式a.底面积:S底=πR2b.底面周长:C=πd=2πRc体积:V=1/3πR2h逆推公式有:S=h=③圆柱和圆锥的关系:1.等底等高的情况下,圆柱体积是圆锥体积的倍。
2.等底等高的情况下,圆锥体积是圆柱体积的。
3.等底等高的情况下,圆锥体积比圆柱体积少。
4.等底等高的情况下,圆柱体积比圆锥体积多倍。
5.圆柱与圆锥等底等体积,圆锥的高是圆柱的倍。
6.圆柱与圆锥等高等体积,圆锥的底面积是圆柱的倍。
2.题型总结①直接利用公式:分析清楚求的的是表面积,侧面积还是底面积以及体积。
半径变化导致底面周长,侧面积,底面积,体积的变化。
两个圆柱(或两个圆锥)半径,底面积,底面周长,侧面积,表面积,体积之比。
②圆柱与圆锥关系的转换:包括削成最大体积的问题(正方体,长方体与圆柱圆锥之间)③横截面的问题④浸水体积问题(水面上升部分的体积就是浸入水中物品的体积,等于盛水容积的底面积乘以上升的高度)容积是圆柱或长方体,正方体。
⑥不规则物体求体积(倒置、拼切)⑤等体积转换问题:一圆柱融化后做成圆锥,或圆柱中的溶液倒入圆锥,都是体积不变的问题,注意不要乘以1 3二、基本题型a求表面积:1,一个圆柱的侧面积是25.12平方厘米,底面半径是2厘米,求该圆柱的表面积是多少?求体积:2.一个圆柱型粮囤,底面半径是4米,高2米,若每立方米粮食重500千克,求该粮囤能装多少千克粮食?求侧面积3.一座大厦有四根同样的圆柱,已知圆柱的底面周长是15.7dm,高10m,如果4.要把圆柱的侧面都包裹上彩布,至少需彩布多少平方分米?4逆推求高一个圆柱,表面积是345.4平方厘米,底半径是5厘米,求它的高。
六年级下册)圆柱与圆锥常考题型分类与答案

六年级下册)圆柱与圆锥常考题型分类与答案六年级数学下册——圆柱与圆锥常考题型汇总与答案本文是一篇关于圆柱与圆锥的常考题型汇总与答案的文章。
其中包括了基本的公式直接求表面积的题型,以及横切、纵切、叠加、整体代换法、圆柱体转换成长方体、水中浸物、熔铸、旋转、扩大、圆柱圆锥比例等问题。
此外,还包括了压路机问题的相关内容。
横切问题:1、一根长2m的圆柱形木料被锯成三段,表面积增加了100.48cm3,求这段木料的体积。
纵切问题:2、一个底面直径是4cm,高是5cm的圆柱,沿着底面直径切开,表面积增加();沿着底面切开,表面积增加()。
叠加问题:3、将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体,求这个物体的表面积。
整体代换法:4、一个圆锥的高和底面半径都等于一个正方体的棱长,已知正方体的体积是90立方厘米,求这个圆锥的体积。
圆柱体转换成长方体:5、将一个高为8cm的圆柱沿着底面直径平均切成若干等份,拼成一个与它等底等高的长方体后,表面积增加了80cm2,求原来圆柱的体积。
水中浸物:6、一个圆柱水槽,底面半径是8厘米,水槽中完全浸没着一块铁,当铁块取出时,水面下降了5厘米。
这块铁的体积是多少?熔铸问题:7、把一块高12cm,横截面半径是3cm的圆柱形钢坯铸成一块底面半径是6cm的圆锥形钢坯,这个钢坯的高是多少?旋转问题:8、一个长4cm、宽3cm的长方体,以一条边为轴旋转一周,得到一个(),体积最大是();直角边分别为4cm与3cm的直角三角形,以一条直角边为轴旋转一周,得到一个(),体积最大是()。
扩大问题:9、一个圆柱的底面直径扩大2倍,高不变,它的底面积扩大(),侧面积扩大(),体积扩大()。
圆柱圆锥比例问题:10、一个圆锥与圆柱的体积比是3:2,底面积比是2:3,求圆柱与圆锥的高之比。
压路机问题:11、一台压路机的滚筒宽5m,直径为1.8m,如果它滚动了20周,压路的面积是多少平方米?12、一台压路机的滚筒长1.2m,底面直径为0.8m的圆柱,如果它分钟转5圈,那么它每分钟前进多少米?每分钟压过的面积是多少米?以上是本文介绍的圆柱与圆锥常考题型汇总与答案。
新版六年级数学下册《3.1.4 练习四》圆柱与圆锥知识点归纳与小结及习题(PPT版)

1.冬天护林工人给圆柱形的树干的下端涂防蛀涂料,
那么粉刷树干的面积是指树干下端的( B )。
A.底面积
B.侧面积
C.表面积
D.体积
2.把一个圆柱在平坦的桌面上滚动,那么滚动的路线 是( B )。A.圆弧源自B.长方形C.圆形
制作一根底面直径为12厘米、长为20厘米的圆柱形通风管, 至少要用多少平方厘米铁皮?
Thank you!
Good Bye!
15cm
10cm
6dm 5cm
6dm
12cm
15×10×4+10×10×2=800(cm2 )
6×6×6 =216(dm2 )
2×3.14×5×12=376.8(cm2) 3.14×5²×2=157(cm2) 376.8+157=533.8(cm2)
立体图形的表 面积都是指所 有表面的面积 之和
选一选。
通风管是两端都不封口的, 所以只需求侧面积。
侧面积=3.14×12×20=753.6(cm2) 需要铁皮=753.6(cm2) 答:至少要用754平方厘米铁皮。
注意:实际使用的铁皮要比计算的结果多
. 一些。省略尾数后,要向前位进1。这种
取近似值的方法叫做进一法。
30cm
林叔叔做了一个圆柱形的灯笼(如右图)。上下 底面的中间分别留出了78.5cm2,他用了多少彩纸?
截成4段,截了3次。
侧面积不变,1次增加两 个底面的面积,3次就增 加了6个地面的面积。
3.14×0.3²×6=1.6956(m2)
答:这些木料的表面积比原木料增加了 1.6956平方米。
一个圆柱的侧面展开图是一个正方形,求这个圆柱的底面
直径与高的比。
圆柱的高=正方形的 圆柱的底面周长=正方
2023年六年级下册数学第三单元圆柱与圆锥必考题型汇总

2023年六年级下册数学第三单元圆柱与圆锥必考题型汇总必考考点一 单位转换(1m 3=1000dm 3 1dm 3=1L 1cm 3=1mL 1m 2=100dm 2 )( )dm 38050 mL=( )L 2.7.45平方米=()平方分米 108平方分米=( )平方米4.06升=( )升( )毫升 5立方米20立方分米 =( )立方米必考考点二 圆柱体侧面展开(沿高展开得到长方形或正方形,一边是底面周长一边是高)1.边长是6 dm 的正方形纸围成一个圆柱形纸筒接头处不计),这个纸筒的高是( )dm,侧面积是()dm 2,体积是( )dm 3(得数保留一位小数)。
2. 一个圆柱底面直径是2分米,把它的侧面展开正好是一个正方形,这个圆柱的高是( )分米。
必考考点三 圆柱表面积、侧面积、体积(圆柱侧面积=底面周长×高 圆柱体积=底面积×高)3.学校大厅有4根圆柱形柱子,每根柱子的底面周长是25.12 dm ,高是5 m 。
如果每平方米需要油漆费0.5元,那么涂这4根柱子需要油漆费多少元?4圆柱的底面半径扩大2倍,高不变,它的体积就扩大( )。
A 、12B 、2倍C 、4倍D 、8倍5.圆锥的底面半径扩大为原来的2倍,高变为原来的21,那么体积变为原来的()。
6.一个圆柱形水池的底面直径是8米,池深2米,如果要在水池的底面和四周池壁抹上水泥,抹上水泥的面积是多少平方米?6.一种压路机滚筒,直径是1.2米,长3米,每分钟转10周,每分钟压路多少平方米?1. 3.6 m 3=7.做一对没有盖的铁皮水桶,它的底面周长是9.42分米,高4分米。
做20个这样的水桶需要铁皮多少平方分米?(得数保留整十平方分米)必考考点四 圆柱切开(切成两段增加2个底面积,切成三段增加4个底面积,切成4段增加6个底面积 )1.把一根长2米的圆木截成两段后,表面积增加了48平方厘米,这根圆木原来的体积是( )。
六下(人教版)第三圆柱与圆锥整理与复习 (附答案)
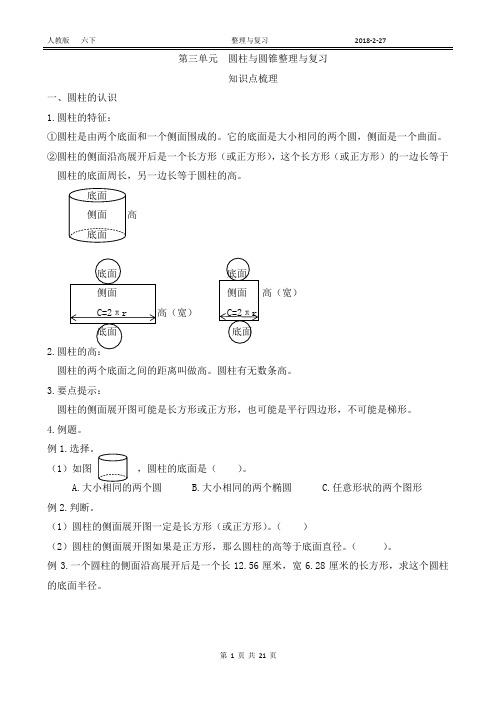
第三单元圆柱与圆锥整理与复习知识点梳理一、圆柱的认识1.圆柱的特征:①圆柱是由两个底面和一个侧面围成的。
它的底面是大小相同的两个圆,侧面是一个曲面。
②圆柱的侧面沿高展开后是一个长方形(或正方形),这个长方形(或正方形)的一边长等于圆柱的底面周长,另一边长等于圆柱的高。
高(宽)高(宽)2.圆柱的两个底面之间的距离叫做高。
圆柱有无数条高。
3.要点提示:圆柱的侧面展开图可能是长方形或正方形,也可能是平行四边形,不可能是梯形。
4.例题。
例1.(1)如图,圆柱的底面是()。
A. B.大小相同的两个椭圆 C.任意形状的两个图形例2.判断。
(1)圆柱的侧面展开图一定是长方形(或正方形)。
()(2)圆柱的侧面展开图如果是正方形,那么圆柱的高等于底面直径。
()。
例3.一个圆柱的侧面沿高展开后是一个长12.56厘米,宽6.28厘米的长方形,求这个圆柱的底面半径。
例1.(1)A例2.(1)×(2)×例3.12.56÷3.14÷2=2(厘米)或6.28÷3.14÷2=1(厘米)二、圆柱的表面积1.圆柱的侧面积:圆柱的侧面积=底面周长×高,用字母表示为s侧=ch,s侧=πdh,s侧=2πrh.2.圆柱的表面积:圆柱的表面积=侧面积+底面积×2.用字母表示为s表=2πrh+2πr2,s表=2πr(h+r)=c(h+r)3.要点提示:在解决实际问题是,并不是所有的圆柱形物体都有两个底面,有的只有一个底面,有的没有底面,要具体问题具体分析。
4.例题。
例1.选择。
(1)在手工课上,小明用纸板做了一个圆柱形笔筒,要求小明用了多少纸板,实际上就是求这个笔筒的()。
A.侧面积B.侧面积+2个底面积C.侧面积+1个底面积(2)一个圆柱形水桶的底面直径是8分米,高是2.5分米。
这个圆柱形水桶的占地面积是()平方分米。
A.25.12B.50.24C.62.8(3)用铁皮制作1节圆柱形的通风管,它的长是60厘米,底面直径是10厘米。
人教版六年级下册数学 最新圆柱和圆锥分类练习解析 38张幻灯片

• 解析: • 方法一:用6.28做底面周长,3.14做高。 • 体积: • 3.14×(6.28÷3.14÷2)2×3.14 • =9.8596立方分米 • 方法二:用3.14做底面周长,6.28做高。 • 体积: • 3.14×(3.14÷3.14÷2)2×6.28 • =4.9298立方分米
•
38、在一个底面直径是8厘米,高是10厘米的圆柱 形木头中间挖掉一个直径是6厘米的等高圆柱,剩
下物体的体积是(219.8 )立方厘米,表面积是 ( 483.56 )平方厘米。
• 解析: • 底面积: • 3.14×〖(8÷2)2-(6÷2)2〗 • =21.98平方厘米 • 体积:21.98×10=219.8立方厘米 • 内外侧面积: • 3.14×8×10+3.14×6×10=439.6平方厘米 • 表面积: • 439.6+21.98×2=483.56平方厘米
• 解析: • 圆柱的高: • 6.3÷7=0.9厘米
•
•
• 36、把一个底面积是6.28平方分米、高9 分米的圆柱体铁块熔铸成一个底面积是 12.56平方分米的圆锥体,圆锥体的高是 ( 13.5 )分米。
• 解析:
• 圆柱的体积:
• 6.28×9=56.52立方分米
• 圆锥的高:
• 56.52×3÷12.56=13.5分米
• 解析:
• 底面半径扩大2倍,底面积扩大4倍,高不 变,体积扩大4倍。
• 8、圆柱的高扩大2倍,底面半径缩小2倍, 它的体积( 缩小2倍 )。
• 解析:
• 底面半径缩小2倍,底面积缩小4倍,高扩 大2倍,体积缩小(4÷2=2)倍。
题型二、求圆柱侧面积类:
新人教版六年级下册圆柱与圆锥常见题型归纳整理

圆柱圆锥常见题型归纳一、公式转换1.基本公式:①圆柱的相关计算公式:底面积:S底=底面周长:C= = 。
圆柱侧面积= ×(文字)S侧= = = 。
(字母)逆推公式有:C= 。
h= 。
圆柱的表面积:S=2S底+S侧= 。
圆柱的体积:V柱= =逆推公式有:S= h=②圆锥的相关计算公式a.底面积:S底=πR2b.底面周长:C=πd=2πRc 体积:V= 1/3πR2 h逆推公式有:S= h=③圆柱和圆锥的关系:1. 等底等高的情况下,圆柱体积是圆锥体积的倍。
2. 等底等高的情况下,圆锥体积是圆柱体积的。
3. 等底等高的情况下,圆锥体积比圆柱体积少。
4. 等底等高的情况下,圆柱体积比圆锥体积多倍。
5. 圆柱与圆锥等底等体积,圆锥的高是圆柱的倍。
6. 圆柱与圆锥等高等体积,圆锥的底面积是圆柱的倍。
2.题型总结①直接利用公式:分析清楚求的的是表面积,侧面积还是底面积以及体积。
半径变化导致底面周长,侧面积,底面积,体积的变化。
两个圆柱(或两个圆锥)半径,底面积,底面周长,侧面积,表面积,体积之比。
②圆柱与圆锥关系的转换:包括削成最大体积的问题(正方体,长方体与圆柱圆锥之间)③横截面的问题④浸水体积问题(水面上升部分的体积就是浸入水中物品的体积,等于盛水容积的底面积乘以上升的高度)容积是圆柱或长方体,正方体。
⑥不规则物体求体积(倒置、拼切)⑤等体积转换问题:一圆柱融化后做成圆锥,或圆柱中的溶液倒入圆锥,都是体积不变1的问题,注意不要乘以3二、基本题型a求表面积:1,一个圆柱的侧面积是25.12平方厘米,底面半径是2厘米,求该圆柱的表面积是多少?求体积:2.一个圆柱型粮囤,底面半径是4米,高2米,若每立方米粮食重500千克,求该粮囤能装多少千克粮食?求侧面积3.一座大厦有四根同样的圆柱,已知圆柱的底面周长是15.7dm,高10m,如果要把圆柱的侧面都包裹上彩布,至少需彩布多少平方分米?4逆推求高一个圆柱,表面积是345.4平方厘米,底半径是5厘米,求它的高。
(六年级下册)圆柱与圆锥详细题型分类与答案 最终版

一、圆柱的表面积1.例题12.巩固3.拓展4.巩固圆柱与圆锥(一)本节课学习圆柱体表面积的一些运用.解决这些问题,有时需要结合实际,明确所求圆柱体的表面积有几个面;有时需要灵活地利用条件,间接得出所需要的数据进行计算;有时还需要观察图形,在观察与比较中搜索需要的信息.某化工厂有一个烟面,形状为圆柱形,底面半径是厘米,高是米,现在 要将烟囱增高到米.每增加平方米材料需要费用元,一共需要多少费用?808251120一个圆柱体的有盖油桶高分米,它的侧面展开后得到一个长分米的长方形.这个油桶共享了多少平方分米的铁皮?1025.12如图所示,有一块长方形铁皮,把其中的阴影部分剪下制成一个圆柱形油桶,求圆柱形油桶的表面积.如图所示,有一张长方体铁皮,剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱体的底面半径为厘米,那么原来长方形铁皮的面积是多少平方厘米(取).10π 3.142.巩固3.拓展4.巩固把一个正方体削成一个体积最大的圆柱,如果圆柱的侧面积是平方厘米.求正方体的表面积.314把一个横截面是正方形的长方体术料削剪成一个最大的圆柱体,圆柱体的表面积为平方厘米.底面直径与高的比是,原来长方体的表面积是多少?32.971:3已知一个圆柱的底面半径等于一个正方体棱长的一半,高等于这个正方体的棱长,这个正方体的底面积是平方分米.求这个圆柱的表面积.25五、“整体代换”法在求圆柱体表面积或体积时的应用在分数的计算和圆的面积计算中,我们曾经学过“整体代换”的方法,例如:计算一个圆的面积,将圆周率乘半径的平方即可,但是,有的时候我们不知道这个圆的半径是多少,只告诉你,这时就可以直接用乘求得圆的面积.今天,我们学习“整体代换”法在求圆柱体表面积或体积时的应用.=8r 2 3.148圆柱与圆锥(一)(课后作业)圆柱与圆锥(课后作业)1.六年级上学期其它圆柱与圆锥一个圆柱体高厘米,侧面积平方分米,它的底面积是多少平方厘米?8025.122.六年级上学期其它圆柱与圆锥一个圆柱体的侧面展开是一个正方形,圆柱的底面直径是厘米,这个 圆柱体的表面积是多少平方厘米?203.六年级上学期其它圆柱与圆锥一个圆柱体木块,底面直径是分米,高是米,现在将它截成两个圆柱体小木块,那么,表面积增加多少平方分米?107.54.六年级上学期其它圆柱与圆锥一个圆柱体木块,底面周长是厘米,高是厘米,现在将它截成四个圆柱体小木块.那么,这四个圆柱体小木块的表面积为多少平方厘米?25.1265.六年级上学期其它圆柱与圆锥一个圆柱体的表面积和一个长方形的面积相等,长方形的长等于圆柱体的底面周长,已知长方形的面积为平方厘米,圆柱体的高是厘米,圆柱体的底面半径是多少?131.884如图所示,有一个立体图形.下部是一个棱长为厘米的正方体,上部是一个半圆柱体.求这个立体图形的表面积.409.六年级上学期其它圆柱与圆锥将一个正方体木块切削成一个最大的圆柱体,这个圆柱体的体积是立方厘米,问:原来正方体的体积有多大?125610.六年级上学期其它圆柱与圆锥如图所示,一个圆柱体的侧面展开图为正方形,已知它的一个底面面积是平方厘米.求这个圆柱体的表面积.108.六年级上学期其它圆柱与圆锥14.六年级上学期其它圆柱与圆锥如图所示.这是一个底面半径为厘米,高为厘米的圆柱,在它的中间依次向下挖去半径分别为厘米、厘米、厘米,高分别为厘米、厘米、厘米的圆柱.最后得到的立体图形表面积是多少?44321210.515.六年级上学期其它圆柱与圆锥如图所示,在长为厘米的圆筒形管子的横截面上,量出的最长线段为厘米,管子的体积是多少?201013.六年级上学期其它圆柱与圆锥有大、小两种不带盖的圆柱形水桶,它们的表面积的和是平方分米,小桶和大桶的用料面积的比是,小桶的底面周长是分米,大桶的底面周长是分米.求大、小两个桶的侧面积各是多少?54331:262.894.2圆柱与圆锥(奥赛训练)11.六年级上学期其它圆柱与圆锥工人师傅将一张铁皮按图裁剪后,做成一个圆柱形铁皮罐,求这个铁皮罐的表面积(单位:分米).12.六年级上学期其它圆柱与圆锥圆柱形的售报亭的高和底面直径相等,如图所示,开一个边长等于底面半径的正方形售报窗口.窗口处挖去的圆柱部分的面积占圆柱形侧面积的几分之几?所示.表面积增加了多少平方厘米?厘米.那么,它的体积是多少平方二、圆柱的表面积和体积(二)1.例题22.巩固3.巩固4.拓展5.巩固根据圆柱体底面、侧面和表面积的特征,以及它们之间的关系可以解决一些求体积的趣题.下面,我们就开始学习这方面的知识.一个圆柱体的高是厘米,它的侧面展开是一个正方形,求这个圆柱体的体积是多少立方厘米?12.56一个圆柱体的高是厘米,它的侧面展开是一个正方形.求这个圆柱体的体积.31.4一个侧柱体,它的侧面展开是一个长方形(宽为圆柱体的高).已知展开后的长方形的长是宽的倍,且宽是厘米.求这个圆柱体的体积.215.7如图所示,一个圆柱形木块高厘米,若被锯掉厘米后,则表面积减少了平方厘米.求原来圆柱的体积.1208251.2一个圆柱体的高是厘米,若高减少厘米,则表面积比原来减少平方厘米.求原来圆柱体的体积.10394.2平方厘米;如果按如图所示切成24平方厘米;如果按如图所示切成43五、水中浸物1.例题52.巩固3.拓展4.巩固我们知道,酒瓶或饮料瓶的瓶颈处一般都不是规则的圆柱体,如果要求体积等问题,这时该怎么办呢?把一根圆柱体钢材等物体放入一个长方体或圆柱体的容器内,要求水面的高度,必须先判断物体是否全部浸没.通过今天的学习,大家就会明白了.如图所示,有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是毫升.现在瓶中装有一些饮料,正放时饮料高度为厘米,倒放时空余部分的高度为厘米.瓶内现有饮料多少毫升?1500205如图所示,某种酒瓶的瓶身呈圆柱形(不包括瓶颈),瓶身内直径为厘米.现在瓶中装有一些酒,正放时酒的高度是厘米,倒放时空余部分的高度是厘米.求这个酒瓶的容积.48123在一个底面积是平方厘米的玻璃杯中装入高厘米的水.现把一个底面半径是厘米、高厘米的圆柱形铁块垂直放入玻璃杯水中,问水面升高了多少厘米?(取)15315π3如图所示,有一个高厘米,容积是毫升的圆柱形容器,里面装满了水.现在把长厘米的圆柱垂直放入,使的底面与的底面接触,这时一部分水从容器中溢出.当把从中拿出来后,中的水高度为厘米.求圆柱的体积.5850A 16B B A B A A 6B 5.巩固一个盛有水的圆柱形容器,底面内半径为厘米,深厘米,水深厘米.现在将一个底面半径为厘米、高为厘米的铁圆柱垂直放入容器中,求这时容器的水深是多少厘米?520152176.小学高年级六年级下学期其它把一个高为分米的圆柱形木块沿底面直径竖直切成相同的两块,表面积增加了平方分米.求这个圆柱体的体积.7.5757.小学高年级六年级下学期其它一个底面半径为厘米的圆柱体容器,放入一个石块后,浸没在水中,水面上升了厘米.求这个石块的体积.528.小学高年级六年级下学期其它在一只底面半径为厘米的圆柱形水桶里有一个直径为厘米的圆柱形钢材浸没在水中,当钢材取出后,桶里的水面下降了厘米,这段钢材长多少厘米?151029.小学高年级六年级下学期其它某种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是升.现在瓶中有一些饮料,正放时饮料高度为厘米,倒放时空余部分的高度为厘米,如图所示,瓶内现在有饮料多少升?21052五、专题演练1.例题52.巩固3.巩固4.拓展已知一个圆锥的底面半径和高都等于一个正方体的棱长.这个正方体的体积是立方分米.求这个圆锥的体积.216一个圆柱体,底面积是平方分米,把它削成一个最大的圆锥,削去部分的体积是立方分米.求这个圆柱体的高.56两个正方体的体积之差是立方厘米,如果以每个正方体的一面为底,加工成最大的圆锥,加工成的两个圆锥的体积之差是多少立方厘米?1200一个边长是厘米的正方体玻璃缸中装着水,水中浸没了一个底面直径为厘米、高为厘米的铁质圆锥体和一个底面直径为厘米、高为厘米的铁质圆柱体.当圆锥体、圆柱体都从桶中取出后,桶内水将下降多少厘米?20125855.拓展圆柱与圆锥(三)(课后作业)1.小学高年级六年级下学期其它张大爷去年用长米、宽米的长方体苇席围成容积最大的圆柱形粮囤.今年改用长米、宽米的长方形苇席围成容积最大2132的圆柱形的粮囤.问今年粮囤的容积是去年粮囤容积的多少倍?2.小学高年级六年级下学期其它一个圆柱形的铁块厚厘米,如果把它锻造成底面直径相同的圆锥体,这个圆锥体的高是多少厘米?103.小学高年级六年级下学期其它优秀生培养教程12级第2讲圆柱与圆锥本讲巩固第4题这里有一个圆柱和一个圆锥(如图下图所示),它们的高和底面直径都标在图上,单位是厘米.请问:圆锥体积与圆柱体积的比是多少?4.小学高年级六年级下学期其它把一个长、宽、高分别是厘米、厘米、厘米的铁块和一个棱长为厘米的正方体铁块,熔铸成一个底面直径为厘米的973510圆锥形铁块.求这个圆锥的高是多少厘米?5.小学高年级六年级下学期其它一个立体图形由一个圆柱和一个圆锥组成,如图所示,它们的底面直径都是厘米,高都是厘米.这个立体图形的体积是612圆柱与圆锥(一)答案一、圆柱的表面积1、10248.96元2、351.68平方分米3、131.88平方分米4、828平方厘米二、圆柱的表面积(二)1、401.92平方厘米2、452.16平方厘米3、12.56平方厘米4、12.56平方厘米三、圆柱的表面积(三)1、18cm2、3.5cm3、166.42平方厘米4、124.03平方厘米四、圆柱的表面积(四)1、1331.36平方厘米2、7536平方厘米3、2081.4平方厘米4、385.4平方厘米五、四圆柱的表面积(四)1、8立方厘米2、600平方厘米3、18平方厘米4、117.75平方分米圆柱与圆锥(一)(课后作业)圆柱与圆锥(课后作业)1.【答案】平方厘米78.52.【答案】平方厘米4571.843.【答案】平方分米1574.【答案】平方厘米552.645.【答案】厘米36.【答案】平方厘米251.27.【答案】平方分米94.28.【答案】平方厘米117689.【答案】立方厘米160010.【答案】平方厘米145.614.【答案】平方厘米254.3415.【答案】平方厘米1570圆柱与圆锥(二)答案一、圆柱的表面积和体积(一)1、16平方厘米2、30平方厘米3、75.36平方分米4、62.8立方厘米5、21.98平方分米二、圆柱的表面积和体积(二)1、157.7536cm 32、246.49cm 33、1232.45cm 34、1570cm 35、7.85cm 3三、圆柱的表面积和体积(三)1、314cm 32、351.68cm 33、339.12cm 34、25.12cm 35、54cm 四、圆柱的表面积和体积(四)1、113.04cm 32、56.52cm 33、1413cm 34、32cm5、21.98cm 3五、水中浸物1、400ml2、753.6ml3、0.75cm4、25cm 35、17.72cm 圆柱与圆锥(二)(课后作业)1.【答案】52.【答案】立方厘米197.823.【答案】立方厘米19719.2 4.【答案】升37.68圆柱与圆锥(三)答案一、圆柱的表面积和体积(五)1、1.57m2、 2.5dm3、0.998m 34、339.12cm 3二、圆锥的表面积和体积(一)1、16cm 32、6cm3、64、35、(π≈3)108cm 3135cm 3三、圆锥的表面积和体积(二)1、2.52、72四、圆锥的表面积和体积(三)1、227cm2、4273、225cm4、2升5、32五、专题演练1、216π2、59dm 3、314cm 34、1.256cm 5、112cm 2圆柱与圆锥(三)(课后作业)1.【答案】922.【答案】303.【答案】1/244.【答案】125.【答案】452.166.【答案】平方厘米727.【答案】98.【答案】圆柱:,圆锥:40329.【答案】2410.【答案】3611.【答案】厘米7.2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱圆锥常见题型归纳
一、公式转换
1.基本公式:
①圆柱的相关计算公式:
底面积:S底=
底面周长:C= = 。
圆柱侧面积= ×(文字)
S侧= = = 。
(字母)
逆推公式有:C= 。
h= 。
圆柱的表面积:S=2S底+S侧= 。
圆柱的体积:V柱= =
逆推公式有:S= h=
②圆锥的相关计算公式a.底面积:S底=πR2
b.底面周长:C=πd=2πR
c 体积:V= 1/3πR2 h
逆推公式有:S= h=
③圆柱和圆锥的关系:
1. 等底等高的情况下,圆柱体积是圆锥体积的倍。
2. 等底等高的情况下,圆锥体积是圆柱体积的。
3. 等底等高的情况下,圆锥体积比圆柱体积少。
4. 等底等高的情况下,圆柱体积比圆锥体积多倍。
5. 圆柱与圆锥等底等体积,圆锥的高是圆柱的倍。
6. 圆柱与圆锥等高等体积,圆锥的底面积是圆柱的倍。
2.题型总结
①直接利用公式:分析清楚求的的是表面积,侧面积还是底面积以及体积。
半径变化导致底面周长,侧面积,底面积,体积的变化。
两个圆柱(或两个圆锥)半径,底面积,底面周长,侧面积,表面积,体积之比。
②圆柱与圆锥关系的转换:包括削成最大体积的问题(正方体,长方体与圆柱圆锥之间)
③横截面的问题
④浸水体积问题(水面上升部分的体积就是浸入水中物品的体积,等于盛水容积的底面积乘以上升的高度)容积是圆柱或长方体,正方体。
⑥不规则物体求体积(倒置、拼切)
⑤等体积转换问题:一圆柱融化后做成圆锥,或圆柱中的溶液倒入圆锥,都是体积不变
1
的问题,注意不要乘以
3
二、基本题型
a求表面积:
1,一个圆柱的侧面积是25.12平方厘米,底面半径是2厘米,求该圆柱的表面积是多少?
求体积:
2.一个圆柱型粮囤,底面半径是4米,高2米,若每立方米粮食重500千克,求该粮囤能装多少千克粮食?
求侧面积
3.一座大厦有四根同样的圆柱,已知圆柱的底面周长是15.7dm,高10m,如果要把圆柱的侧面都包裹上彩布,至少需彩布多少平方分米?
4逆推求高
一个圆柱,表面积是345.4平方厘米,底半径是5厘米,求它的高。
三、切割拼接问题,表面积增加或减少
1.基本公式:
a.横切:切面是圆,表面积增加2倍底面积,即S增=2πR2
b.竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4Rh
基本题型
1,把一长为1.6米的圆柱截成3段后,表面积增加了9.6平方米,求圆柱原来的体积?
2,把长为20分米的圆柱沿着底面直径劈开,表面积增加了80平方分米,求该圆柱原来的表面积是多少?
3.圆柱长2米,把它截成相等的4段后,表面积增加了18.84平方厘米,求每段的体积是多少?
4.把3个一样的圆柱,连成一个大圆柱,长9厘米,表面积减少12.56平方分米,求原来每个圆柱的体积是多少立方厘米?
5、把两个底面直径都是4厘米,长都是4分米圆柱形钢材焊接成一个长的圆柱形钢材,焊接成的圆柱形钢材的表面积比原来两个小圆柱形钢材的表面积之和减少了多少?
6、一根2米长的圆柱形木料, 横截面的半径是10厘米, 沿横截面的直径
垂直锯开, 分成相等的两块, 每块的体积和表面积各是多少?
四、放入或拿出物体,水面上升或下降。
①基本公式:水面上升(下降)的高度×容器的底面积=物体的体积
溢出的水的体积=物体的体积
②基本题型:
1.一个圆柱桶半径是5分米,把一铁块拿出后,水面下降3分米,求铁块体积?
2.一圆柱容器,半径20平方厘米,放入铁块后,水面上升2厘米,求铁块体积?
3.在直径为20厘米的圆柱容器中,放入半径为3厘米的圆锥,水面上升0.3厘米,求圆锥的高是多少?
4把高为3分米米的圆锥铁块放入装满水的容器中,溢出了3升水,求该圆锥的底面积是多少?
五、高增加或减少,侧面积增加或减少问题
1.关键点:A.画出展开图
B.圆柱底面周长=长方形的长圆柱高=长方形的宽
C.当圆柱底面周长=圆柱高时,圆柱展开是一个正方形
2.基本题型:
1.一圆柱的高减少2厘米,侧面积就减少50.24平方厘米,求圆柱体积减少多少?2一个圆柱展开是正方形,如果圆柱高增加2厘米,侧面积就增加1
2.56平方厘米,求圆柱原来的侧面积是多少?
3、一个圆柱的高增加3分米,侧面积就增加56.52平方分米,它的体积增加多少立方分米?
六、加工圆柱
1、关键点:找出加工后的圆柱的直径(或半径)
和高。
2基本题型:
1:把一个棱长是40厘米的正方体削成一个最大的圆柱体,
它的表面积和体积各是多少?
2、一个正方体棱长是4分米,把它削成一个最大的圆柱,削去的体积是多少?
3、一个长方体,长8分米,宽8分米,高12分米。
把它削成一个最大的圆柱,这个圆柱的体积为多少立方分米?
4.把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体,这个长方体的长是6.28厘米,高是5厘米,求它的体积。
5、把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体,这个长方体的宽是4厘米,高是5厘米,求它的体积。
6、把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体,这个长方体的底周长是41.4厘米,高是5厘米,求它的体积。
7、一个长方体木块,长10厘米宽8厘米高4厘米,把它削成一个圆柱,求削成圆柱体积最大是多少?
8、一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分
成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14
)
七、旋转成圆柱
1、关键点:找出旋转后的圆柱的直径(或半径)和高。
2基本题型:
1、用一张长8厘米,宽6厘米的长方形,旋转形成圆柱,求形成的圆柱的体积。
2、用一张长12.56厘米,宽6.28厘米的长方形卷形成圆柱,求卷成的圆柱的体积。
八、圆柱中的比
1、甲乙两个圆柱,底半径比是3:2,相等,它们的体积比是多少?
2、甲乙两个圆柱,底面积相等,高是比是4:5,它们的体积比是多少?
3、甲乙两个圆柱,底半径比是2:3,高的比是4:5,它们的体积比是多少?
九、抓住体积不变类题型(等积变形)
1.基本考点:用沙堆铺路,粮食的转换,钢铁铸造等
2.基本题型:
1.一个沙堆高2米,底面半径是10分米,用这堆沙铺宽1米,厚2厘米的路,可以铺多少米?
2.把一个半径为3cm ,高为10cm 的圆柱形铁块熔铸成底面半径为6平方厘米的圆锥型零件,求该零件高是多少?
九,圆锥圆柱的转换关系
1.基本关系:
等底等高:圆柱体积=3圆锥体积 (圆柱与圆锥等底等高,体积相差3
2Sh ) 等体积等底面积:圆锥高=3圆柱高
等体积等高:圆锥底面积=3圆柱底面积
1.圆柱圆锥等底等高,体积相差3厘米,求圆柱圆锥体积各是多少?
2.一个圆锥和一个圆柱,它们的体积相等,如果高也相等,当圆锥的底面积是3平方厘米,那么圆柱的底面积是( );如果它们的体积相等,底面积也相等,圆柱的高是3厘米,那么圆锥的高是( );等底等高的圆锥比圆柱的体积小( )。
