spss教程均值比较检验与方差分析
均值检验方差分析SPSS
一、实验目的及要求：1、目的用SPSS软件实现均值检验和方差分析。
2、内容及要求用SPSS对所要求数据进行相应的数据处理和分析：均值检验、方差分析。
二、仪器用具：三、实验方法与步骤:1.从网上下载到可用的数据2.将所需数据复制到SPSS中，并且把学校变量改为数值型变量，用1、2分别代替“A”和“B”。
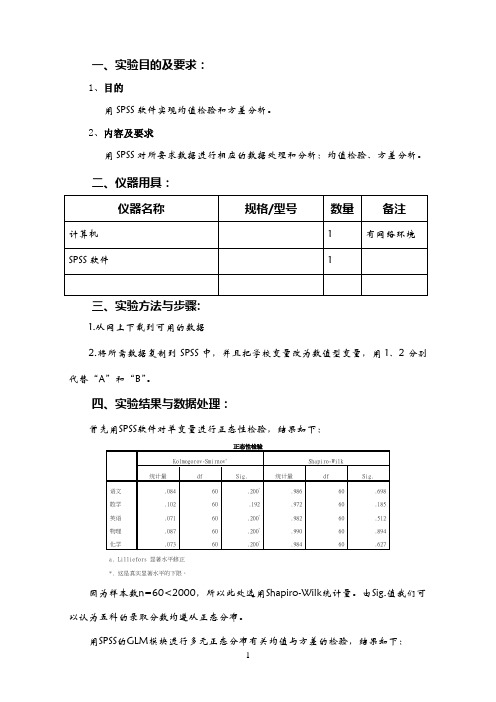
四、实验结果与数据处理：首先用SPSS软件对单变量进行正态性检验，结果如下：因为样本数n=60<2000，所以此处选用Shapiro-Wilk统计量。
由Sig.值我们可以认为五科的录取分数均遵从正态分布。
用SPSS的GLM模块进行多元正态分布有关均值与方差的检验，结果如下：第一张主体间因子表展示了样本数据分别来自两个学校的个数。
第二张多变量检验表给出了几个统计量，由Sig.值可以看出，无论从哪个统计量来看，两个学校的录取分数都是有显著差别的。
由于模型通过了显著性检验，意味着两所学校的录取分数线是不同的。
主体间因子N学校 A 30B 30由上面主体间效应的检验表可知五科分数的Sig.值均为0.000说明两个学校本科录取分数在五门课上都存在显著差别。
协方差矩阵等同性的 Box 检验aBox 的 M 14.729F .891df1 15df2 13544.526Sig. .575检验零假设，即观测到的因变量的协方差矩阵在所有组中均相等。
a. 设计 : 截距 + 学校该表为协方差阵相等的检验表，检验统计量为Box’s M，由Sig.值可以认为两个学校(总体)的协方差阵是相等的。
由误差方差等同性的Levene检验表，可以得知，在显著性水平为0.05水平下，五科分数的误差平方在两个学校间是没有显著差别。
下页成对比较表给出了不同学校五科录取分数的比较与检验及检验的可信性统计量。
综上：通过对两个学校的本科录取分数线的具体的比较分析，所得的数据表明，两个学校的本科录取分数线存在着明显的差异，并且在语文、数学、英语、物理和化学这五门课程的录取分数上均有显著的差异。
SPSS5—— 均值比较与检验
Total 203535.3 882
显著性水平sig.为0.000,小于0.05，说明各组均 值之间的差异显著，通过显著性检验。进而说 明两变量在总体中是相关的。
SPSS5—— 均值比较与检验
均值分析（MEANS）
什么时候会用这种方法： 举例： 1.不同受教育水平与收入之间是否相关。 2.不同年级与逃课次数是否相关。
SPSS5—— 均值比较与检验
按Analyze—Compare Means—Means顺序，打开 Means主对话框
分析变量（定距）
SPSS5—— 均值比较与检验 分组变量(定类）
SPSS5—— 均值比较与检验
均值分析（MEANS）
分析的对象：定类变量和定距变量总体中是 否存在相关关系。 分析的逻辑基础： 把所有的个案按照一定的分类变量分组以后， 使用均值（MEANS）过程分别计算各组的均 值，通过比较均值差异的大小来确定总体中 这两个变量是否相关。
分类变量和均值比较的变量
检验目的： 用于检验单个变量的均值与 假设检验值(给定的常数)之间是否存在 差异。
举例：以往的调查显示住房面积均值为 38平米，本研究就是探究住房面积均值 是否为38平米。
SPSS5—— 均值比较与检验
按Analyze—Compare Means—One-Sample T Test顺序，打开One-Sample T Test主对话框。
SPSS5—— 均值比较与检验
独立样本T检验主对话框
分组变量 （二分变量）
SPSS统计分析实用教程(第2版)
探索性分析
03
均值比较与t检验
总结词
单样本t检验用于检验单个样本的均值是否与已知的某个值或参考值存在显著差异。
详细描述
在单样本t检验中，我们将已知的某个值或参考值作为检验标准，然后比较单个样本的均值与此标准之间的差异。通过计算t统计量和对应的p值，我们可以判断样本均值与标准值是否存在显著差异。
单样本t检验
通过图形方式展示两个变量之间的关系，可以直观地观察到它们之间的模式和趋势。
相关分析
散点图
相关系数
预测模型
通过一个或多个自变量预测因变量的值，建立预测模型，并评估模型的拟合优度和预测能力。
回归系数
描述自变量对因变量的影响程度，通过回归系数可以了解各个自变量对因变量的贡献。
线性回归分析
非线性关系
协方差分析是在考虑一个或多个协变量的影响后，比较两个或多个分类变量对数值型变量的影响。通过控制协变量的影响，可以更准确地评估各组之间的差异，并确定分类变量对数值型变量的真实效应。
总结词
详细描述
协方差分析
05
非参数检验
适用范围
01
卡方检验主要用于比较实际观测频数与期望频数之间的差异。
计算方法
02
通过卡方统计量，即实际观测频数与期望频数的差的平方与期望频数的比值，来评估两者之间的差异程度。
聚类分析
聚类分析基于观测数据之间的相似性或距离将它们分组，使得同一聚类中的数据尽可能相似，不同聚类中的数据尽可能不同。
聚类分析在市场细分、生物信息学和社交网络等领域有广泛应用。
THANKS FOR
WATCHING
感谢您的观看
详细描述
探索性分析
总结词
探索性分析还可以用于预测和分类，例如决策树、逻辑回归等。
SPSS推断统计之均值比较与方差分析 PPT课件
提出原假设和备择假设
什么是备择假设？(alternative hypothesis) 1. 与原假设对立的假设，也称“研究假设” 2. 研究者想收集证据予以支持的假设总是有不
等号: , 或 3. 表示为 H1
H0值 临界值 计算出的样本统计量
利用 P 值进行检验 (决策准则)
1. 单侧检验
• 若p-值 ,不拒绝 H0 • 若p-值 < , 拒绝 H0
2. 双侧检验
• 若p-值 /2, 不拒绝 H0 • 若p-值 < /2, 拒绝 H0
假设检验中的两类错误
1. 第一类错误（弃真错误）
• 原假设为真时拒绝原假设 • 会产生一系列后果 • 第一类错误的概率为
✓ 配对样本t检验
•Paired-samples t-test •同一变量、同一组在不同的情况、均值差异
Independent-samples t-test
例子：sex differences in self-esteem scores (dataFile1.sav) • 研究问题
Is there a significant difference in the mean of self-esteem scores for males and females? • 分析单元：个人 (Individual) • 自变量：性别 (分类变量) •因变量：self-esteem score （等比变量） • 需满足的假定条件
被称为显著性水平
2. 第二类错误（取伪错误）
• 原假设为假时接受原假设 • 第二类错误的概率为(Beta)
假设检验的流程
《SPSS数据分析教程》方差分析
《SPSS数据分析教程》方差分析方差分析是一种常用的统计方法，用于比较三个或三个以上组之间的均值差异是否显著。
它用于探究不同组别的因素对所研究的因变量的影响是否具有统计显著性。
在SPSS数据分析教程中，方差分析是一个非常重要的分析方法。
本文将介绍方差分析的原理、SPSS中的操作步骤以及结果的解读。
方差分析的原理是基于三个或三个以上不同组别之间的方差之间的比较来判断均值之间的差异是否显著。
方差分析的核心思想是通过比较组内方差与组间方差的大小来判断均值的差异是否显著。
方差分析的原假设是所有组别的均值相等，而备择假设是至少存在一个组别的均值与其他组别的均值不相等。
在SPSS中进行方差分析的操作步骤如下：步骤1：打开SPSS软件，点击“变量视图”页面。
在第一栏输入不同组别的名称，例如“组别1”、“组别2”、“组别3”。
步骤2：在第二栏输入待分析的因变量名称，并设置其测量类型为“比例”。
步骤3：点击“数据视图”页面，输入各组别的数据。
确保每个组别的数据都在同一列中，并且分组的数据之间用“空格”或“逗号”隔开。
步骤4：点击菜单栏上的“分析，—比较手段，—单因素方差分析”。
步骤5：在方差分析的对话框中，将因变量移入因变量方框，将分组变量移入因子方框。
步骤6：点击“选项”按钮，出现选项对话框。
可以选择计算哪些统计量，如均值、标准差、总和平方和等。
步骤7：点击“确定”按钮，SPSS将得出方差分析的结果。
方差分析的结果包括了多个统计量，如SS（组间平方和）、SS（组内平方和）、MS（组内均方和）、MS（组间均方和）、F值和P值。
-SS（组间平方和）反映了组间差异的大小，SS（组内平方和）反映了组内差异的大小。
-MS（组间均方和）是SS（组间平方和）除以自由度（组间）得到的，反映了组间差异的平均大小。
-MS（组内均方和）是SS（组内平方和）除以自由度（组内）得到的，反映了组内差异的平均大小。
-F值是MS（组间均方和）除以MS（组内均方和）得到的，是判断组间差异是否显著的依据。
第5讲均值比较与方差分析
2019/12/7
5
体检资料包含的信息有编号、姓 名、文化程度、出生日期、体检日期、 身高、体重、疾病名称。
在 SPSS 中 ， 录 入 数 据 时 ， 首 先 要根据数据特征确定变量的名称、类 型(宽度，小数)、标签、值等。
本例中的变量特征如下：
2019/12/7
6
名称 编号 姓名 文化 出生日 体检日 身高 体重 疾病
且有如下规则：
F0 F0.01:高度显著 F0.05 F0 F0.01:显著 F0.1F0 F0.05:一般显著()
2019/12/7
40
2019/12/7
41
例4 对引例进行方差分析。 解 (1) 建立数据文件，格式为： 数据为2列，第1列为因子的水平，第 2列为对应的销售额。 (2) 分 析 -> 比 较 均 值 -> 单 因 素 ANOVA。 (3) 选销售额为因变量，竞争者 为因子。
在两因子分析中，不仅要通过试 验数据分析因子A的r水平及因子B的 s个水平对指标y是否有显著影响，有 时还要考虑两个因子联合起来对指标 y是否有显著影响，这种联合作用称 为因子的交互作用，记为A×B。
从平均销售额来看，好像竞争者
2019/12/7
33
个数对销售额有一定影响，但仔细分 析一下数据，问题就不那么简单。
可以看到，在竞争者个数相同的 条件下，不同超市的销售额也不完全 一样。由于试验时已考虑超市的其它 条件基本相同，产生这种差异的原因 主要是试验过程中各种偶然因素，称 之为试验误差。
2019/12/7
个具有配对关系的正态总体的样本均 值之间是否存在显著差异。
配对的两个样本值是一一对应的, 且容量相同。例如，一组病人治疗前 后身体的指标；一个年级学生的期中 和期末成绩。
SPSS数据的参数检验和方差分析
SPSS数据的参数检验和方差分析SPSS软件是一种用于统计和数据分析的工具，它可以进行各种参数检验和方差分析。
本文将重点介绍SPSS中的参数检验和方差分析，并提供一些建议和注意事项。
参数检验是一种统计方法，用于确定一个或多个总体参数的真实值。
在SPSS中，可以使用各种统计方法进行参数检验，例如t检验、方差分析（ANOVA）、卡方检验等。
t检验是用于比较两个样本均值是否显著不同的方法。
在SPSS中，可以通过选择“分析”->“比较均值”->“独立样本t检验”或“相关样本t检验”来执行t检验。
在进行t检验之前，需要确保数据符合正态分布和方差齐性的假设。
可以使用SPSS中的正态性检验和方差齐性检验来验证这些假设。
方差分析是用于比较三个或更多组之间差异的方法。
在SPSS中，可以通过选择“分析”->“方差”->“单因素方差分析”或“多因素方差分析”来执行方差分析。
在进行方差分析之前，同样需要检验正态性和方差齐性的假设。
在进行参数检验和方差分析时，还需确认是否使用方差分析的正确方法。
例如，如果有多个自变量，可能需要使用混合设计方差分析或多重方差分析等方法。
SPSS提供了多种不同的方差分析方法，可以根据具体研究设计选择适当的方法。
进行参数检验和方差分析时，还需要注意一些统计概念和报告结果的规范。
例如，结果中应包括样本均值、标准差、置信区间、显著性水平等信息。
此外，还应使用适当的图表和图形来展示数据和结果，以帮助读者更好地理解研究结果。
除了参数检验和方差分析，SPSS还可以进行其他类型的统计分析，例如相关分析、回归分析、因子分析等。
这些分析方法可以用来探索和描述数据之间的关系，以及预测和解释变量之间的关系。
在使用SPSS进行数据分析时，还需注意数据的质量和准确性。
确保数据输入正确、完整，处理缺失值和异常值等。
此外，也需要根据研究目的和问题选择合适的统计方法，并理解相关假设和前提条件。
总之，SPSS是一种功能强大的统计和数据分析工具，在参数检验和方差分析方面提供了丰富的方法和功能。
SPSS推断统计之均值比较与方差分析 PPT课件
自变量x 顺序变量 两个分类
数值变量
“回归分析和相关分析” （因变量用虚拟变量） Logistic回归 考上大学的概率
顺序变量 两个分类
ቤተ መጻሕፍቲ ባይዱ
两个顺序变量的 两个顺序
因
秩方法
变 量
数值变量
1.“回归分析和相关分析” 两个顺序 （自变量用虚拟变量）
“回归分析和相关分析” 气温与冰激凌销售量
男女教授工资间差异
所关心的参数主要有总体均值(μ)、标准差(σ)、总体比例 (π)等
总体参数通常用希腊字母表示
2. 统计量(statistic)
用来描述样本特征的概括性数字度量,它是根据样本数 据 计算出来的一些量,是样本的函数
所关心的样本统计量有样本均值、样本标准差(s) 、样本 比例(p)等
样本统计量通常用小写英文字母来表示
•样本很小的等距或等比变量的假设检验
假设检验
✓ 样本与总体之间、样本与样本之间在描述 统计量上是否存在显著差异
✓ 显著性检验 (Significant testing) ✓ 理论基础：样本分布理论 (Sampling
distribution)
提出原假设和备择假设
什么是原假设？(null hypothesis) 1. 待检验的假设，又称“0假设” 2. 研究者想收集证据予以反对的假设 3. 总是有等号 , 或 4. 表示为 H0
有了SPSS怎么作出统计决策？
使用P值（P-value） 1. 是一个概率值 2. 如果原假设为真，P-值是抽样分布中大于
或小于样本统计量的概率
• 左侧检验时，P-值为曲线下方小于等于检
验统计量部分的面积
• 右侧检验时，P-值为曲线下方大于等于检
均值检验、方差分析SPSS
均值检验、方差分析SPSS以下是为大家整理的均值检验、方差分析spss的相关范文，本文关键词为均值,检验,方差,分析,spss,实验,目的,要求,spss，您可以从右上方搜索框检索更多相关文章，如果您觉得有用，请继续关注我们并推荐给您的好友，您可以在综合文库中查看更多范文。
一、实验目的及要求：1、目的用spss软件实现均值检验和方差分析。
2、内容及要求用spss对所要求数据进行相应的数据处理和分析：均值检验、方差分析。
二、仪器用具：仪器名称计算机spss软件规格/型号数量11备注有网络环境三、实验方法与步骤:1.从网上下载到可用的数据2.将所需数据复制到spss中，并且把学校变量改为数值型变量，用1、2分别代替“A”和“b”。
四、实验结果与数据处理：首先用spss软件对单变量进行正态性检验，结果如下：正态性检验Kolmogorov-smirnova统计量语文数学英语物理化学.084.102.071.087.073df6060606060sig..200*.192.200.200*.200**sha piro-wilk统计量.986.972.982.990.984df6060606060sig..698.185.512.894.627a.Lilliefo rs显著水平修正*.这是真实显著水平的下限。
因为样本数n=60用spss的gLm模块进行多元正态分布有关均值与方差的检验，结果如下：1第一张主体间因子表展示了样本数据分别来自两个学校的个数。
第二张多变量检验表给出了几个统计量，由sig.值可以看出，无论从哪个统计量来看，两个学校的录取分数都是有显著差别的。
由于模型通过了显著性检验，意味着两所学校的录取分数线是不同的。
主体间因子学校Abn3030多变量检验b效应截距pillai的跟踪wilks的Lambdahotelling的跟踪Roy的最大根学校pillai的跟踪wilks的Lambdahotelling的跟踪Roy的最大根 a.精确统计量 b.设计:截距+学校值.999.0011554.6561554.656.851.1495.7105.710F16790.281a16790.28 1a16790.281a16790.281a61.672a61.672a61.672a61.672a假设df5.0005.0005.0005.0005.0005.0005.0005.000误差df54.00054.00054.00054.00054.00054.00054.00054.000sig..000.000.00 0.000.000.000.000.000主体间效应的检验源校正模型因变量语文数学英语物理化学截距语文数学英语物理化学学校语文数学英语物理III 型平方和1050.017a1470.150b1135.350c1859.267d1560.600e372408.817376833. 750388010.417389781.600383360.2671050.0171470.1501135.3501859. 267df11111111111111均方1050.0171470.1501135.3501859.2671560.600372408.817376833.75038 8010.417389781.600383360.2671050.0171470.1501135.3501859.267F4 8.25186.03439.83183.39241.65217113.20XX2052.62613612.47917482. 60010231.72248.25186.03439.83183.392sig..000.000.000.000.000.000.000.000.000.000.000.000.000.0002化学误差语文数学英语物理化学总计语文数学英语物理化学校正的总计语文数学英语物理化学a.R方=.454（调整R方=.445）b.R方=.597（调整R方=.590）c.R方=.407（调整R方=.397）d.R方=.590（调整R方=.583） e.R方=.418（调整R方=.408）1560.6001262.167991.1001653.2331293.1332173.133374721.00037929 5.000390799.000392934.000387094.0002312.1832461.2502788.583315 2.4003733.73315858585858606060606059595959591560.60021.76117. 08828.50422.29537.46841.652.000由上面主体间效应的检验表可知五科分数的sig.值均为0.000说明两个学校本科录取分数在五门课上都存在显著差别。
3_SPSS均值比较与检验-2
四、单因素方差分析
一、简介 单因素方差分析是检验由单一因素影响的多组 样本某因变量的均值是否有显著差异的问题。如果 各组之间有显著差异，说明这个因素（分类变量） 对因变量是有显著影响的，因素的不同水平会影响 到因变量的取值。 二、完全窗口分析 按AnalyzeCompared Means One-Way Anova顺序单击。打开 One-Way Anova主对话框， 如图
14
表6-5
单因素方差分析结果
表4-5是单因素方差分析结果。与表6-3比较， 增加3行：未加权项、加权线性项、与组间偏差 平方和的差。 表6-6 对比系数
表4-6列举了两组多项式的系数。
15
表4-8 LSD法和Tamhane’sT2法进行均值多重比较结果
16
表4-9 Duncan法进行均值多重比较结果
输入多项式各组均值的系数,输入一个系数单击Add按钮。系数 进入下面方框..依次输入各组均值的系数。 如果多项式中只包括第一与第四组的均值的系数,必须把第二、 第三个系数输入为0。 如果只包括第一与第二组的均值,则第三、第四个可不输入。 可同时建多个多项式，输入一组后按Next按钮；如果要修改则 按Previous按钮，修改后按Change按钮，删除按Remove按钮。
见图 4—2 多项式比较对话框
6
在此对话框中选择进行多重比较的方法 1.用t检验完成组间成对均值的比较，对多重比较错误率不 进行调整 2.同上，但通过设置每个检验的误差率来控制整个误差率 3.用t检验完成多重配对比较，为多重比较调整显著值，但 比2的界限要小 4.对所有可能的组合进行同步进入的均值配对比较 5.用F检验进行多重比较 6.在Studentized Range分布下进行多重比较 7.用Studentized Range分布进行所有各组均值间的配对比 较 8.用Studentized Range统计量进行所有组间均值的配对比 较, 用所有配对比较集合的误差率作为试验误差率 9.同8,但,其临界值是TUKEY和S-N-K的相应值的平均值 10.进行配对比较时,使用的逐步顺序与Student-NewmanKeuls检验的顺序一样,但并不是给每个检验设定一个误 差 率,而是给所有检验的误差率设定一个临界值 11.用Studentized最大系数进行比较检验和范围检验 12.用Studentized最大系数进行配对比较检验 13.用Studentized最大系数进行比较检验,使用贝叶斯逼近. 14.用t检验进行配对比较.
spss均值的比较与检验
21000.00,19000.00,33000.00,31500.00,18500.00,34000.00,29000.00
26000.00,25000.00,28000.00,30000.00,28500.00,27500.00,28000.0 0
26000.00
操作步骤：
1、
第十八页，共29页。
5.5.3 配对样本T检验
一、有关概念
进行配对样本T检验要求被比较的两个样本有配对关系，要求两个 样本均来自正态总体，而且均值是对于检验有意义的描述统计量。
设总体X~ N(μx,σx2), Y ~ N(μy,σy2), x1,x2,…xn和y1,y2,…yn分别是对应
的样本，分别取自X和Y的样本。Z＝X－Y， 和Sz2 分别是Z的样本均
若H0成立，则统计量T服从自由度为n-1的t分布。对于给定的α，由 t分布表可查得临界值t α/2(n-1), 使
P{|T|>t α/2(n-1)}= α 如果算得T的值t落入其拒绝域|t|>t α/2(n-1)内，则拒绝H0；否则不
能拒绝H0。
二、单样本T检验的功能与应用
执行单样本T检验过程，SPSS将显示：每个检验变量的统计量的均值、标准差和均
设总体X~ N(μx,σx2), Y ~ N(μy,σy2), X、Y独立。x1,x2,…xn和
y1,y2,…yn分别是取自X和Y的样本，
方差。
、X和YSx2、Sy2分别是样本均值和样本
检验的统计量其分布分两种情况：
（1）当σx= σy，即方差齐次性时
xy
t Sw
1 1 ~ t(nx ny 2) nx ny
第二页，共29页。
2、将要进行检验的变量放入右边的Test Variable(s)中
第5章SPSS均值比较T检验和方差分析
第5章SPSS均值比较T检验和方差分析第5章主要介绍了SPSS软件中进行均值比较的方法，包括t检验和方差分析。
本文将详细介绍SPSS中进行均值比较的步骤，以及如何解读结果。
5.1t检验t检验是一种用于比较两个样本均值差异的统计方法。
在SPSS中，进行t检验的步骤如下：1.打开SPSS软件，并导入需要进行t检验的数据集。
2.选择“分析”菜单，在下拉菜单中选择“比较均值”选项，再选择“独立样本t检验”选项。
3.在弹出的对话框中，将需要比较的变量移动到“因子”框中，将“分组变量”移动到“因子”框中，并选择需要进行的假设检验类型。
4.点击“确定”按钮，等待计算结果。
5.在输出窗口中，可以查看计算结果，包括均值、标准差、样本量、t值和p值等。
通常，我们关注的是p值，如果p值小于0.05，则认为差异显著。
例如，我们想比较男性和女性的体重是否有显著差异。
我们将体重作为因变量，性别作为自变量，进行t检验。
在计算结果中，如果p值小于0.05，则可以认为男女性别对体重有显著影响。
5.2方差分析方差分析是一种用于比较三个或更多个样本均值是否存在差异的统计方法。
在SPSS中，进行方差分析的步骤如下：1.打开SPSS软件，并导入需要进行方差分析的数据集。
2.选择“分析”菜单，在下拉菜单中选择“比较均值”选项，再选择“单因素方差分析”选项。
3.在弹出的对话框中，将需要比较的变量移动到“因子”框中，将“分组变量”移动到“因子”框中，并选择需要进行的假设检验类型。
4.点击“确定”按钮，等待计算结果。
5.在输出窗口中，可以查看计算结果，包括均值、标准差、样本量、F值和p值等。
通常，我们关注的是p值，如果p值小于0.05，则认为差异显著。
例如，我们想比较不同药物对治疗效果的影响。
我们将药物作为因变量，治疗效果作为自变量，进行方差分析。
在计算结果中，如果p值小于0.05，则可以认为不同药物对治疗效果有显著影响。
通过以上步骤，我们可以在SPSS中进行均值比较、t检验和方差分析。
《方差分析SPSS操作流程》
《方差分析SPSS操作流程》
方差分析是一种统计方法，用于分析两个或两个以上样本均值之间差异的显著性。
在SPSS软件中，进行方差分析的操作流程如下：
1.打开SPSS软件并导入数据：在SPSS软件中选择“文件”菜单，然后点击“打开”选项。
在弹出的对话框中选择数据文件并点击“打开”。
2.选择统计分析：在SPSS软件中选择“分析”菜单，然后点击“一元方差分析”选项。
3.选择变量：在弹出的对话框中，将待分析的变量从左侧的变量列表框拖动到右侧的因子列表框中。
4.设置参数：点击“选项”按钮，可以设置一些参数，如方差齐性检验、置信水平等。
根据实际需要进行设置后点击“确定”。
5.进行方差分析：点击“确定”按钮后，SPSS将执行方差分析并将结果呈现在输出窗口中。
6.解释结果：在输出窗口的方差分析结果表中，可以查看各项指标的统计值、F值、显著性水平等。
根据这些指标，可以判断不同样本均值之间的显著性差异。
需要注意的是，在进行方差分析之前需要满足一些前提条件，如样本间独立性、数据正态性、方差齐性等。
如果数据不满足这些前提条件，可能会影响方差分析的结果。
此外，还可以使用SPSS软件进行方差分析的更进一步的分析，如多元方差分析、协方差分析等。
这些更复杂的分析方法可以帮助研究人员更全面地了解样本均值之间的差异。
总之，方差分析是一种重要的统计方法，可以用于比较两个或两个以上样本均值之间的差异。
在SPSS软件中进行方差分析的操作流程相对简单，研究人员只需要按照上述步骤进行操作即可。
均值比较与方差分析
均值比较的上机实现Means过程单一样本T检验两独立样本T检验两配对样本T检验1 Means过程统计学上的定义和计算公式定义：Means过程是按照用户指定条件，对样本进行分组计算均数和标准差，如按性别计算各组的均数和标准差。
Means过程的计算公式为研究问题比较不同性别同学的数学成绩平均值和方差。
数据如表2-1所示。
实现步骤图2-1 在菜单中选择“Means”命令图2-2 Means对话框图2-3 “Means：Options”对话框结果和讨论2 单一样本T检验统计学上的定义和计算公式定义：SPSS单样本T检验是检验某个变量的总体均值和某指定值之间是否存在显著差异。
统计的前提样本总体服从正态分布。
也就是说单样本本身无法比较，进行的是其均数与已知总体均数间的比较。
计算公式如下。
单样本T检验的零假设为H0总体均值和指定检验值之间不存在显著差异。
采用T检验方法，按照下面公式计算T统计量：SPSS中实现过程研究问题分析某班级学生的高考数学成绩和全国的平均成绩70之间是否存在显著性差异。
数据如表2-1所示。
实现步骤图2-4 “One-Sample T Test”设置框图2-5 “One-Sample T Test：OPtions”对话框结果和讨论3 两独立样本T检验统计学上的定义和计算公式定义：所谓独立样本是指两个样本之间彼此独立没有任何关联，两个独立样本各自接受相同的测量，研究者的主要目的是了解两个样本之间是否有显著差异存在。
这个检验的前提如下。
∙两个样本应是互相独立的，即从一总体中抽取一批样本对从另一总体中抽取一批样本没有任何影响，两组样本个案数目可以不同，个案顺序可以随意调整。
∙样本来自的两个总体应该服从正态分布。
两独立样本T检验的零假设H0为两总体均值之间不存在显著差异。
在具体的计算中需要通过两步来完成：第一，利用F检验判断两总体的方差是否相同；第二，根据第一步的结果，决定T统计量和自由度计算公式，进而对T检验的结论作出判断。
spss教程均值比较检验与方差分析
第二章均值比较检验与方差分析在经济社会问题的研究过程中，常常需要比较现象之间的某些指标有无显著差异，特别当考察的样本容量n比较大时，由随机变量的中心极限定理知，样本均值近似地服从正态分布。
所以，均值的比较检验主要研究关于正态总体的均值有关的假设是否成立的问题。
◆本章主要内容：1、单个总体均值的 t 检验（One-Sample T Test）；2、两个独立总体样本均值的 t 检验（Independent-Sample T Test）；3、两个有联系总体均值均值的 t 检验（Paired-Sample T Test）；4、单因素方差分析（One-Way ANOVA）；5、双因素方差分析（General Linear Model Univariate）。
◆假设条件：研究的数据服从正态分布或近似地服从正态分布。
在Analyze菜单中，均值比较检验可以从菜单Compare Means，和General Linear Model得出。
如图2.1所示。
图2.1 均值的比较菜单选择项§2.1 单个总体的t 检验（One-Sample T Test）分析单个总体的 t 检验分析也称为单一样本的 t 检验分析，也就是检验单个变量的均值是否与假定的均数之间存在差异。
如将单个变量的样本均值与假定的常数相比较，通过检验得出预先的假设是否正确的结论。
例1：根据2002年我国不同行业的工资水平（数据库SY-2），检验国有企业的职工平均年工资收入是否等于10000元，假设数据近似地服从正态分布。
首先建立假设：H0：国有企业工资为10000元；H1：国有企业职工工资不等于10000元打开数据库SY-2，检验过程的操作按照下列步骤：1、单击Analyze →Compare Means →One-Sample T Test，打开One-Sample T Test 主对话框，如图2.2所示。
图2.2 一个样本的t检验的主对话框2、从左边框中选中需要检验的变量（国有单位）进入检验框中。
SPSS操作—方差分析
SPSS操作—方差分析
一、概念
方差分析（ANOVA）法是统计学中一种用于检验三个或以上水平的均数差异的统计方法。
方差分析从表面上看是利用方差的大小，在一定的概率和显著水平下，比较多组数据的均值差异，确定数据的显著性。
一般来说，它用来检验有多自变量时的均数差异，其中包括一个或多个因素，每个因素又有两个或者多个水平。
二、SPSS操作步骤
1、打开SPSS软件，点击“文件”，选择“新建”，在弹出的界面中选择“数据集”，点击“确定”，新建一个数据集。
2、将所要分析的数据输入到数据集中，在“变量视图”中定义响应变量和自变量，并设置其变量类型，完成数据的输入。
3、点击“分析”，选择“统计”，在弹出的界面中选择“参数检验”，点击“F检验”，然后在窗口中选择因变量和自变量，完成基本的参数设置，点击“确定”，弹出方差分析窗口，点击“确定”，即可开始运行方差分析。
4、方差分析运行完毕后，在输出窗口中可以看到结果，包括方差分析汇总表和方差分析的结果等信息。
5、方差分析的结果主要包括拟合度指数、F值、绝对值、样本量、概率值、单组比较、多组比较等内容，在这里。
知识4： 方差分析(多个总体均数比较)
方差分析/F检验（多个均数比较）前言：一、方差分析的基本思想方差是反映数据变异程度的统计指标。
利用方差的概念对变异度进行分解，所以方差分析亦称为变异度分析。
其基本思想是：根据研究目的和设计类型，将全部观察值的总变异分解为两个或多个部分，各部分的变异可由不同处理因素的影响效应或者误差的效应解释，将各影响因素产生的变异与随机误差变异进行比较，以推断该因素是否存在影响效应。
二、方差分析的应用条件独立性：各样本是相互独立的随机样本，个体观测值之间相互独立。
正态性：各样本均来自正态分布总体。
方差齐性：各样本所对应的总体方差相等。
三、常用的方差齐性检验方法F 检验：仅用于两总体方差相等Bartlett检验：通常要求数据满足正态性Levene检验(Levene‘s teste)：不依赖数据的分布类型，结果更稳健四、完全随机设计的方差分析完全随机设计(completely randomized design)的方差分析是指将研究对象通过完全随机化方法，分配至多个不同的处理组，比较多组的效应指标是否存在差别，亦称为单向方差分析(one-way ANOVA)/单因素方差分析。
注：完全随机设计的方差分析只涉及一个研究因素，因此，除了用于随机分组的试验性研究外，也常用于基于随机抽样的观察性研究多个均数的比较。
SPSS正文：一、单因素方差分析（单个因素作用，处理因素——独立正态方差齐）：SPSS操作：第一步：建立数据文件（变量：group 和观察值共2列；类似两组独立样本t检验的数据录入）；第二步：正态性检验（类似两组独立样本t检验的正态性检验）1、分割文件（data→split file→激活compare groups→调入group→OK）；自我经验，此处可有可无，分割和不分割的结果未变化。
2、正态性检验（analyze→nonparametrice tests→1-sample K-S→调入观察值，点击normal→OK）3、观察结果，若三组正态性检验P均＞0.05，则进行下一步。
第5讲均值比较与方差分析
F0 F0.01 : 高度显著 F0.05 F0 F0.01 : 显著 F0.1 F0 F0.05 : 一般显著()
2019/9/4
40
2019/9/4
41
例4 对引例进行方差分析。 解 (1) 建立数据文件，格式为： 数据为2列，第1列为因子的水平，第 2列为对应的销售额。 (2) 分 析 -> 比 较 均 值 -> 单 因 素 ANOVA。 (3) 选销售额为因变量，竞争者 为因子。
一变量的均值进行检验，用于检验样 本均值是否与给定的总体均值之间存 在显著差异。
例1 已知某年级15个学生身高数 据如下，检验其平均身高是否与全年 级平均身高165相同。
2019/9/4
18
解 分析->比较均值->单样本t检 验。
选身高入检验变量，检验值设为 165；选项中置信区间百分比默认为
0.95，即 0.05。
因子在试验中所取的不同状态称 为因子的水平，常用A1, A2, …, Ar表 示, r称为因子A的水平数。本例中显 然有4个水平。
从平均销售额来看，好像竞争者
2019/9/4
33
个数对销售额有一定影响，但仔细分 析一下数据，问题就不那么简单。
可以看到，在竞争者个数相同的 条件下，不同超市的销售额也不完全 一样。由于试验时已考虑超市的其它 条件基本相同，产生这种差异的原因 主要是试验过程中各种偶然因素，称 之为试验误差。
选择方差相等的结果。
t0 4.315 t 2 (n1 n2 2)
t0.005 (13) 3.01
2019/9/4
24
P t t0 0.001 0.01
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、两个独立总体样本均值的 t 检验（ Independent-Sample T Test ）；
3、两个有联系总体均值均值的 t 检验（ Paired-Sample T Test ）；
4、单因素方差分析（ One-Way ANOV）A；
5、双因素方差分析（ General Linear Model
Univariate ）。
1、单击 Analyze Compare Means Independent-sample T Test ，打开 Independent-sample T Test 主对话框如图 2.4 。
图 2.4 两个独立样本 t 检验的主对话框
2、选择要检验的变量“综合得分”进入检验框中。 3、选择分组变量“性别”进入分组框中，然后单击 Define Group 按纽，打 开分组对话框如 2.5 图所示，确定分组值后返回主对话框，如果没有分组，可以 选择 Cut point 单选项，并在激活的框内输入一个值作为分组界限值。 4、由 Option选择按纽确定置信度值和缺失值的处理方式。 5、点击 OK可得输出结果，见表 2.3统计分析检验结果。
首先建立假设： H0：国有企业工资为 10000元； H1：国有企业职工工资不等于 10000元
打开数据库 SY-2，检验过程的操作按照下列步骤： 1、单击 Analyze CompareMeans One-Sample T Test ，打开 One-Sample
T Test 主对话框，如图 2.2 所示。
95% Confidence Interval of the
Difference 置信区间
Lower
Upper
1795.5916 5324.2148
从上面检验结果表 2.1 （a）可以得出国有单位职工工资的平均值、标准差 和均值的标准误等反映数据特征的数据。从表 2.1 （ b）中可知检验的结果。即 相应的检验统计量 t 值为 4.229 ，自由度为 30，假设检验的 P 值（ sig ）小于 0.05 ， 故原假设不成立， 检验结论是拒绝原假设 H0，接受假设 H1。即认为国有企业职工 的平均工资与 10000 元的假设差异显著。
图 2.5 独立样本 t 检验 Define Groups 对话框
§2.2 两个总体的 t 检验
§2.2.1 两个独立样本的 t检验（ Independent-samples T Test ）
Independent-sample T Test 是检验两个没有联系的总体样本均值间是否存 在显著的差异， 两个没有联系的总体样本也称独立样本。 如两个无联系的企业生 产的同样产品之间的某项指标的均值的比较， 不同地区的儿童身高、 体重的比较 等，都可以通过抽取样本检验两个总体的均值是否存在显著的差异。
第二章 均值比较检验与方差分析
在经济社会问题的研究过程中， 常常需要比较现象之间的某些指标有无 显著差异，特别当考察的样本容量 n 比较大时，由随机变量的中心极限定理知， 样本均值近似地服从正态分布。 所以，均值的比较检验主要研究关于正态总体的 均值有关的假设是否成立的问题。
本章主要内容：
1、单个总体均值的 t 检验（ One-Sample T Test ）；
单个总体的 t 检验分析也称为单一样本的 t 检验分析，也就是检验单个变 量的均值是否与假定的均数之间存在差异。 如将单个变量的样本均值与假定的常 数相比较，通过检验得出预先的假设是否正确的结论。
例1：根据 2002年我国不同行业的工资水平（数据库 SY-2），检验国有企业 的职工平均年工资收入是否等于 10000元，假设数据近似地服从正态分布。
图 2.2 一个样本的 t 检验的主对话框
2、从左边框中选中需要检验的变量（国有单位）进入检验框中。 3、在 Test Value 框中键入原假设的均值数 10000。 4、单击 Options 按钮，得到 Options 对话框（如图 2.3 ），选项分别是置信 度（默认项是 95％）和缺失值的处理方式。选择后默认值后返回主对话框。
图 2.3 一个样本 t 检验的 Options 对话框
5、单击 OK，得输出结果。如表 2.1 所示。
表 2.1 （a） . 数据的基本统计描述
One-Sample Statistics
国有单位
N 样本容量
31
Mean 均值 13559.9032
Std. Deviation 标准差 4809.97099
例2．某医药研究所考察一种药品对男性和女性的治疗效果是否有显著差异， 调查了 10名男性服用者及 7名女性服用者，对他们服药后的各项指标进行综合评 分，服用的效果越好，分值就越高，每人所得的总分见表 2.2 ，试根据表中的数 据检验这种药品对男性和女性的治疗效果是否存在显著差异。
解：由于药品对男性或女性的影响是无联系的， 因此这两个样本是相互独立 的。可以应用两独立样本的假设检验。
Std. Error Mean 标准误 863.89629
表 2.1 (b). 一个样本均值 t 检验的检验结果
One-Sample Test
国有单位
t值 4.121
Test Value = 10000
df 自由度
30
Sig. (2-tailed) P值 .000
Mean Difference
均值差 3559.90323
首先，建立假设 H0：该药品对男性和女性的治疗效果没有显著差异； H1：该药品对男性和女性的治疗效果有显著差异。
表 2.2 男，女治疗效果的综合得分表
性
分
别
男
女
序
数 号
1
150
140
2
160
124
80
135
5
110
89
6
80
100
7
132
105
8
115
9
60
10
100
然后，根据表 1的数据建立数据文件 SY-4，并使用 SPSS进行假设检验，具体 操作步骤：
假设条件： 研究的数据服从正态分布或近似地服从正态分布。
在 Analyze 菜单中，均值比较检验可以从菜单 Compare Means，和 General Linear Model 得出。如图 2.1 所示。
图 2.1 均值的比较菜单选择项
§2.1 单个总体的 t 检验（ One-Sample T Test ）分析