西南交通大学峨眉校区材料力学B(全套课件203P)上
合集下载
西南交大材料力学
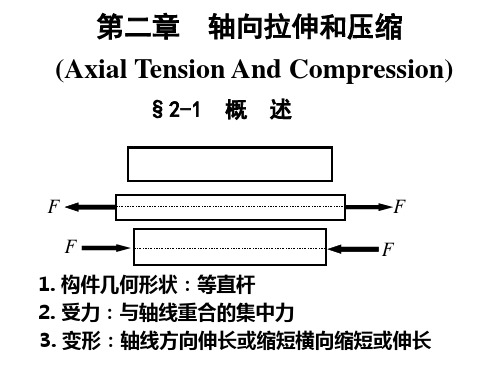
o F
x
A. 没有载荷作用的区段，轴力图为水平线； B. 在集中力作用截面上，轴力图发生突变， 突变的幅度为作用在该截面上的集中力的总和； C. 均布载荷作用的区段，轴力图为斜直线；
F
F
q=F/l
F
l
2l
l
D. 计算截面不应取在集中力作用截面上； E. 载荷不能平移。
F l F F q=F/l
重要推论 横截面上每根纵向纤维的变形相同， 横截面上每个点的受力相同，应力均匀分布。
s
F
}
FN
FN s= A n
FN= sA
单位： N/m2，帕（Pa），106Pa=1MPa， 9Pa=1GPa， 10 适用条件： ⑴ 上述公式对大多数横截面形状都适用； 但对于平截面假设不成立的某些特定截面, 上述公式不适用。
2l
l
§2-3 应力· 拉（压）杆内的应力
Ⅰ、应力的概念
F F
杆的强度
F
{ 横截面尺寸
s
轴力
}
FN
称为正应力（Normal Stress)
Ⅱ、拉（压）杆横截面上的应力
实验现象
F
a a' b' b c c' d' d
F
平面假设
原为平面的横截面在杆变形后仍为平面， 对于拉（压）杆且仍相互平行，仍垂直于轴线。
FN 2 q ( x l ) 2 F FR
F l (x l) F
x
F
未知内力方向按正向假设
4) 求第三段的内力
F F q=F/l F l 2l l
FN 3 F
5) 画轴力图
FN
F
西南交大材力期末试卷 材料力学B (A卷 终稿)(2010-2011第2学期)
正确答案为 _______。
6. 图示结构中，杆 AB 为刚性杆，设l1、l2、l3 分别表示杆 1、杆 2 及杆 3 的伸长，则当 分析各竖杆的内力时，相应的变形协调条件：
[A] l1=l2=l3 [C] 2l2= l1+l3
[B] l2= 2(l1+l3) [D] l3= l1-l2 正确答案为 _______。
(15 分)
四. 已知某点处的平面应力状态如图所示。试求： (1) 主应力的大小；(2) 最大切应力的大 小。 (15 分)
10MPa
50MPa
40MPa
第 4 页
( 共 6 页 )
五. 图示矩形截面杆件， 同时承受垂直于轴线的横向力 F 及平行于轴线的偏心压力 10F 作用， 已知 l=500mm，b=60mm，h=180mm，许用拉应力[σt]=30MPa，许用压应力[σc]=90MPa。 试确定 F 的许用值。
西南交通大学 2010－2011 学年第(二)学期试卷
课程代码 6322100 考试时间 120 分钟
密封装订线 题 号 得 分 一 二 三 四 五 六 七 总成绩
课程名称
材料力学B(A卷)阅卷教师签字： Nhomakorabea姓
名
一. 选择、填空题（每小题 3 分，共 30 分） 1. 图示杆的抗拉（压）刚度为 EA，杆长为 2l ，关于杆的总伸长量：
第 2 页
( 共 6 页 )
9. 一受扭圆轴的横截面如图所示，横截面上的最大切应力 max 40MPa ，则横截面上点 A 的切应力 A ____________。
10. 第三强度理论和第四强度理论的相当应力分别为 σr3 及 σr4，对于纯剪切应力状态，恒有 σr3/σr4= ______________。 二. 变截面杆受力如图，横截面面积分别为 A1=400mm2，A2=300mm2，A3=200mm2，各段长 度分别为 l1=300mm，l2=400mm，l3=400mm，材料的 E=200GPa。试求：(1) 绘出杆的轴 力图；(2) 计算杆内各段横截面上的正应力；(3) 计算 C 端的位移。 (15 分)
材料力学PPT课件
通常用
MPa＝N/mm2 ＝ 10 6 Pa
有些材料常数 GPa＝ kN/mm2 ＝ 10 9 Pa
工程上用 kg/cm2 ＝ 0.1 MPa
正应力s
剪应力
二、轴向拉压时横截面上应力
dA
dN dA •s
N
s dN
N dN s dA
A
A
求应力，先要找到应力在横截面上的分布情况。
应力是内力的集度，而内力与变形有关，所以
绘轴力图
（2）求应力 AB段：A1＝240240mm＝57600mm2
BC段：A2＝370370mm＝136900mm2
s1
N1 A1
50 103 57600
0.87 N
/ mm 2
0.87MPa
s2
N2 A2
150 103 136900
1.1N
/ mm 2
1.1MPa
应力为负号表示柱受压。正应力的正负号与轴力N相同。
Nl
A
l
————虎克定律（Hooke)
EA
l Pl
EA
计算中用得多
lE——N——弹性s横量（Mpa,
Gpa)
s
E
l EA E
实验中用得多
计算变形的两个实例：
1.一阶梯轴钢杆如图，AB段A1＝200mm2，BC和CD段截面积相同A2＝A3＝ 500mm2；l1= l2= l3=100mm。弹性模量E＝200GPa，荷载P1＝20kN，P2 ＝40kN 。试求：（1）各段的轴向变形；（2）全杆AD的总变形；
N1＝-20kN（压） N2＝-10kN（压） N3＝+30kN（拉）
§3 应力
一、应力：
内力在杆件截面上某一点的密集程度
11交大峨眉材料力学B
z
Fy
x
y
x
lx
Fz单独作用：
z
x
y
梁在竖直平面xy内发生平面 弯曲，z轴为中性轴 斜弯曲：两个互相垂直方向的平面 弯曲的组合
(2) 任意x截面上的弯矩 M z Fy (l x) F cos (l x) M cos 梁在水平平面xz内发生平面 M y Fz (l x) F sin (l x) M sin 弯曲，y轴为中性轴 其中：M F (l x) x截面上的总弯矩
b
a
a c c
d
M z ,max Wz M y ,max Wy
My
a
f
c
中性轴
（11-2）
M z ,max
e
d
d
a点: t ,max c点:
cos sin M max W Wy z
c,max
cos sin M max W Wy z
§11-2 非对称截面梁的平面弯曲
弯曲中心
一 非对称截面梁的平面弯曲
1. 对称截面梁的平面弯曲
Me
Me
M
z
x dA
C
z
Me
z
C
x y 挠曲线
y
y
y、z为形心主轴
z y
静力学条件 M y z dA E yzdA E I yz 0 A A
横截面不会绕y轴转动，只会绕z轴转动，梁变形后的轴线一定位 于xy平面内，与外力偶作用面共面，梁产生平面弯曲。
第十一章
弯曲问题的进一步研究 与组合变形
目
§11-1 §11-2 §11-3 §11-4 §11-5 概述
材料力学PPT课件
例：左图 左半部分： ∑Fx=0 FP=FN 右半部分：
,,
∑Fx=0 FP =FN
例13-1
已知小型压力机机架受力F的作用，如图，试求立柱截面 m-n上的内力
解： 1、假想从m-n面将机架截 开（如图）； 2、取上部，建立如图坐标 系，画出内力FN，MZ （方 向如图示）。
（水平部分/竖直部分的变形？）
3.当： 0≤x3≤a (起点在B点）
FQ3
内力图----弯矩图
❖ 当：0≤x1≤a 时， M11/6为直线
A点： x10M1A0； C点： x1aM1C56qa2
❖ 当：a≤x2≤2a 时，为二次曲线； M2=5qax2-q(x2-a)2/2
C点： x2 a,M2C65q.2a D点： x2 2a,M2D76q.2a
q(x)>0,抛物线，上凹 q(x)<0,抛物线，下凹 FQ =0,抛物线有极值
斜率由突变 图形成折线
有突变 突变量=M
❖ M=3kN.m,q=3kN/m,a=2m
解：求A、B处支反力
FAY=3.5kN;FBY 剪力图：如图，将梁分为三段
AC：q=0,FQC= FAY CB：q<0,FQB BD：q<0,FQB=6kN 弯矩图：
正应力、切应力
应力的概念
❖ 单位面积上内力的大小， 称为应力
❖ 平均应力Pm，如图所示
△F
Pm= △A
正应力σ
单位面积上轴力的大小，称为正应力；
切应力τ
单位面积上剪力的大小，称为切应力
应力单位为：1Pa=1N/m2 （帕或帕斯卡) 常用单位：MPa（兆帕），1MPa=106 Pa=1N/mm2
A—截面面积
❖ 当： 0≤x3≤a时（原点在B点，方 D点x： 3a,M3D7 6qa2M2D
,,
∑Fx=0 FP =FN
例13-1
已知小型压力机机架受力F的作用，如图，试求立柱截面 m-n上的内力
解： 1、假想从m-n面将机架截 开（如图）； 2、取上部，建立如图坐标 系，画出内力FN，MZ （方 向如图示）。
（水平部分/竖直部分的变形？）
3.当： 0≤x3≤a (起点在B点）
FQ3
内力图----弯矩图
❖ 当：0≤x1≤a 时， M11/6为直线
A点： x10M1A0； C点： x1aM1C56qa2
❖ 当：a≤x2≤2a 时，为二次曲线； M2=5qax2-q(x2-a)2/2
C点： x2 a,M2C65q.2a D点： x2 2a,M2D76q.2a
q(x)>0,抛物线，上凹 q(x)<0,抛物线，下凹 FQ =0,抛物线有极值
斜率由突变 图形成折线
有突变 突变量=M
❖ M=3kN.m,q=3kN/m,a=2m
解：求A、B处支反力
FAY=3.5kN;FBY 剪力图：如图，将梁分为三段
AC：q=0,FQC= FAY CB：q<0,FQB BD：q<0,FQB=6kN 弯矩图：
正应力、切应力
应力的概念
❖ 单位面积上内力的大小， 称为应力
❖ 平均应力Pm，如图所示
△F
Pm= △A
正应力σ
单位面积上轴力的大小，称为正应力；
切应力τ
单位面积上剪力的大小，称为切应力
应力单位为：1Pa=1N/m2 （帕或帕斯卡) 常用单位：MPa（兆帕），1MPa=106 Pa=1N/mm2
A—截面面积
❖ 当： 0≤x3≤a时（原点在B点，方 D点x： 3a,M3D7 6qa2M2D
(精品)材料力学(全套752页PPT课件)
Page46
§1-5 应变
构件受外力时单 元体(微体)会产 生变形
棱边长度改变
棱边夹角改变
b’ b
a
b b’
a
用正应变(normal strain)和切应变(shearing strain) 来描述微体的变形
Page47
棱边长度改变
ab ab ab ab线段的平均正应变
ab ab
lim ab a点沿ab方向的正应变
高压电线塔
毁坏的高压电线塔
Page14
码头吊塔
Page15
单梁式导弹翼面 1－辅助梁；2－翼肋；3－桁条；4－蒙皮；5－副翼；6－后墙； 7－翼梁；8－主接头；9－辅助接头
Page16
➢ 材料力学的基本假设 材料力学研究材料的宏观力学行为 材料力学主要研究钢材等金属材料
关于材料的基本假设： 连续性假设：认为材料无空隙地充满于整个构件。
ab0 ab
a
b b’
棱边夹角改变
c’ c
直角bac的改变量——直角bac的切应变
tan
a
b
Page48
§1-6 胡克定律
应力：正应力，切应力 应变：正应变，切应变
➢ 胡克定律(Hooke’s law) 单向受力
纯剪切
b’ b
切变模量
E
G
弹性(杨氏)模量 a
Page49
思考题：求a, b, c面上的切应力，并标明方向。 a b c
胡克的弹性实验装置
1678年：
发现“胡克定律”
雅各布.伯努利，马略特：
得出了有关梁、柱性能的 基础知识，并研究了材料的 强度性能与其它力学性能。
库伦：
修正了伽利略、马略特关 于梁理论中的错误，得到了 梁的弯曲正应力和圆杆扭转 切应力的正确结果
西南交大材料力学课件1
z y
My
My=FzF
Mz=FyF
FN=F
My=FzF
Mz=FyF
(y，z) z y F (yF，zF)
FN M y z M z y A I I z y
F FzF z FyF y A Iy Iz
令σ＝，
1 zF yF z y0 A Iy Iz
中性轴的位置与偏心距的关系：
M max 8kN m
t ,max
FN M max c,max A W
π 2 2 2 A ( D d ) 4080 mm 4 3 4 πD (1 ) W 124000 3 mm 32
二、偏心拉伸（压缩）
F z (yF，zF) y F
z
y
F
Mz My
1.2m
解：1)求反力
FB B
FA FB 5kN
2)求内力
A
1.6m 1.6m
m g
10kN C f
FN FAx 3kN
M ( x) FAy x 4x
B FB
A
FAx FAy
m
m-m 截面为危险截面
M max 4 2 8kN m
压缩+平面弯曲
3)求应力
FN 3kN
2 iy
i
2 y
zP
已知中性轴的截距求作用点:
d
1 O d d 8 8
iz2 yP ay
zP
az
d i y iz 4
ay d / 2
d yP 8
az
zP 0
矩形截面:
z 1 A
4
b
D
西南交通大学2013-2014学年第2学期材料力学B
西南交通大学2013－2014 学年第(2)学期考试试卷课程代码 6322100 课程名称 材料力学B 考试时间 120 分钟题号 一 二 三 四 五 六 七 总成绩 得分阅卷教师签字：一、选择题（每小题3分，共10小题）1.长度和横截面面积均相同的两杆，一为钢杆，一为铝杆，在相同的拉力用下（ ）. (A)铝杆的应力和钢杆相同，而变形大于钢杆 (B)铝杆的应力和钢杆相同，而变形小于钢杆 (C)铝杆的应力和变形都大于钢杆 (D)铝杆的应力和变形都小于钢杆2. 一直径为d 的实心圆轴受扭，横截面上的最大切应力为τ，若圆轴所受荷载不变，直径变为2d ，则横截面上的最大切应力为( )。
（A ）τ21 （B ）τ41 （C ）τ81 （D ）τ1613. 图示两端固定阶梯形钢杆，当温度升高时 ( ) 。
(A) AC 段应力较大，C 截面向左移； (B) AC 段应力较大，C 截面向右移； (C) CB 段应力较大。
C 截面向左移动； (D) CB 段应力较大，C 截面向右移动．4．不会引起静定结构产生内力的因素是（ ）(A) 集中力； (B) 集中力偶；(C) 分布力；(D) 温度变化。
5．低碳钢材料在拉伸实验过程中，不发生明显的塑性变形时，承受的最大应力应当小于 ( ) 的数值.（A ）比例极限；（B ）许用应力；（C ）强度极限；（D ）屈服极限。
班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6．低碳钢的应力-应变曲线如图所示，其上( )点的纵坐标值为该钢的强度极限b。
(A)e ； (B)f ； (C)g ； (D)h 。
7．图示应力状态，用第三强度理论校核时，其相当应力为( )。
(A)3r στ=； (B)3r στ=； (C)33r στ= ；(D)32r στ=。
8．某直梁横截面面积为常数横向力沿Y 方向作用，下图所示的四种截面形状中，抗弯能力最 强的截面形状为 （ ）。
(A)矩形 (B)工字形 (C)圆形 (D)正方形9．图示应力圆对应于应力状态（ ）。
材料力学绪论ppt课件
➢既安全又经济地设计构件
课程的研究方法：理论分析和实验手段相结合
• 一些理论以实验结果得出的某些假设为前提
• 材料的力学性能(材料在外力作用下的变形规律，以及 抵抗变形与破坏的能力)需要通过试验获得。
完整版PPT课件
19
材料的力学性能
不同材料制成的构件,其承载能力不一样。 构件的强度、刚度、稳定性与制作构件的 材料有关。 材料力学还要通过试验来研究材料的力学 性能,并在此基础上为构件选择合适的材料。
完整版PPT课件
28
2、小变形前提允许以变形前的受力分析代替变形后的受力分析
因构件在外力作用下发生的变形与原尺寸相比非常小， 在计算构件所受的力时，可按构件原始尺寸计算。
B
1 2 l
δ1
FN1
A
A
l
C
F
FN 2
F
δ2
A1
F
求FN1、 FN1 时，仍可 按构件原始尺寸计算。
完整版PPT课件
29
3、小变形前提保证叠加法成立 叠加法指构件在多个载荷作用下产生的变形——
课程特点
特点：“三多”——概念多、公式多、计算多
➢应注意在学习过程中及时归纳总结
完整版PPT课件
3
课程要求
上课适当作一些笔记，特别是一些补充例题 及其解题思路及方法；平时注意观察，对一般机 械结构有初步了解；学会处理力学问题的一般方 法。
➢由实际问题抽象出力学模型 ，对力学模型进行 分析，运用有关定理解决问题。
17
2000年10月25日上午10时许南京电视台演播厅工
程封顶，由于脚手架失稳，模板倒塌，造成6人死亡，
35人受伤，其中一名死者是南京电视台的摄象记者。
完整版PPT课件
课程的研究方法：理论分析和实验手段相结合
• 一些理论以实验结果得出的某些假设为前提
• 材料的力学性能(材料在外力作用下的变形规律，以及 抵抗变形与破坏的能力)需要通过试验获得。
完整版PPT课件
19
材料的力学性能
不同材料制成的构件,其承载能力不一样。 构件的强度、刚度、稳定性与制作构件的 材料有关。 材料力学还要通过试验来研究材料的力学 性能,并在此基础上为构件选择合适的材料。
完整版PPT课件
28
2、小变形前提允许以变形前的受力分析代替变形后的受力分析
因构件在外力作用下发生的变形与原尺寸相比非常小， 在计算构件所受的力时，可按构件原始尺寸计算。
B
1 2 l
δ1
FN1
A
A
l
C
F
FN 2
F
δ2
A1
F
求FN1、 FN1 时，仍可 按构件原始尺寸计算。
完整版PPT课件
29
3、小变形前提保证叠加法成立 叠加法指构件在多个载荷作用下产生的变形——
课程特点
特点：“三多”——概念多、公式多、计算多
➢应注意在学习过程中及时归纳总结
完整版PPT课件
3
课程要求
上课适当作一些笔记，特别是一些补充例题 及其解题思路及方法；平时注意观察，对一般机 械结构有初步了解；学会处理力学问题的一般方 法。
➢由实际问题抽象出力学模型 ，对力学模型进行 分析，运用有关定理解决问题。
17
2000年10月25日上午10时许南京电视台演播厅工
程封顶，由于脚手架失稳，模板倒塌，造成6人死亡，
35人受伤，其中一名死者是南京电视台的摄象记者。
完整版PPT课件
交大峨眉材料力学B幻灯片PPT
由于杆的两端可在任何方向自由转动， 所以当它失稳时必定在弯曲刚度最小的纵 向平面内发生弯曲，亦即绕惯性矩为最小
的形心主轴(通常称为弱轴)而弯曲。
w
设材料在线弹性范围内工作，就
可以应用挠曲线的近似微分方程
x
F
l
M (x)
E Izw M (x)
(6-1)
其中： M(x)Fw
y
F
式中的轴向压力F取为正值。这样，挠度w和弯 矩M(x)的符号就相一致。
x
F
w
x y
z y
E Izw M (x ) F w E Izw F w0
x
引入记号 k 2 F
F
EIz
则上式可以改写为二阶齐次线性微分方程
w k2w0 此微分方程的通解为
w A s i n k x B c o s k x
式中，A和B为积分常数
w
两端铰支压杆的位移边界条件
x
F
l
M (x)
l (a)
1
300
F
(b)
Байду номын сангаас4000N
但试验表明，当F=40N时，钢尺明
显变弯，此时已不能再承担更大的 压力。由此可见，钢尺的承载能力 并不取决于轴向压缩强度，而是与 钢尺受压时变弯有关。
压杆产生弯曲变形的原因：
(1)实际的压杆在制造时其轴线不可避免地会存在初曲率。(2) 作用在压杆上的外力的合力作用线也不可能毫无偏差地与杆的轴 线重合。（3）压杆的材料本身也不可避免地存在不均匀性。这些 因素都可能使压杆在外压力作用下除发生轴向压缩变形外，还发 生附加的弯曲变形。
l2
F
显然，能使压杆保持微弯平衡状态的最小轴向
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
m
F F
m
F
FN
x
F
x
0 FN
轴力图：为了清楚地看到轴力沿杆长的变化规律，可以用图线 的方式表示轴力的大小与横截面位置的关系。这样的图线称为 轴力图。
FN
o
例如前面例题的轴力图
F
x
x轴表示横截面位置，FN轴表示对应该位置的轴力大小。
F
FN F x
O
例 2-1 （书例2-1） 一等直杆受四个轴向外力作用，如图所示。试 作轴力图 1F2=25kN 2 F3=55kN F4=20kN F1=10kN
(a)
(b)
图1-4
( c)
2．构件正常工作的条件
一、构件应有足够的强度(strength) 要求：构件在外力作用下不发生断裂， 也不能产生显著的塑性变形（即撤除外 力后不能恢复的变形）。 二、构件应有足够的刚度(rigidity) 要求：构件在外力作用下其弹性变形 （即撤除外力后能恢复的变形）不超过 规定的限度 三、构件应有足够的稳定性(stability) 要求：压杆在一定的压力的作用下，能保 持其直线的平衡形式。 A C
A F1=10kN
1
B
FN 1
第二章 轴向拉伸和压缩
目
§2-1
§2-1 §2-3 §2-4 §2-5
录
概述
拉压杆的内力 横截面上的应力 斜截面的应力 拉压杆的变形和位移
§2-6
§2-7 §2-8 §2-9 §2-10 §2-11
应变能
材料在拉压时的力学性能 应力集中 强度计算 拉压超静定问题 装配应力和温度应力
§2-1
轴向拉伸与压缩的概念和实例
杆件：长度远大于横向尺寸的构件。 杆件分类：等截面直杆（图1-3a、d） 、 变截面直杆（图1-3c） ；等截面曲杆和 变截面曲杆如图1-3b。其中横截面是与 轴线垂直的截面；轴线是横截面形心的 连线。
板和壳：构件一个方向的尺寸（厚度）远小于其它两个方向的尺寸 ，如图1-4a和b所示。 块体：三个方向（长、 宽、高）的尺寸相差不 多的构件，如图1-4c所 示。
2.各向同性假设.
假设变形固体在各个方向具有相同的力学性能。这种材料称为 各向同性材料。如金属材料、搅拌均匀的混凝土。根据这一假 设，在研究了材料任一方向的力学性质后，就可以认为其结论 对其它方向也都适用。
3.小变形假设
即构件在外力作用下产生的变形与构件的原始尺寸相比很微 小的。根据这一假设，在列平衡方程时，可以不考虑外力作 用点处的微小位移，而按变形前的位置和尺寸进行计算。
第一章 绪 论
目
§1-1 §1-2 §1-3
录
材料力学的任务 变形固体的基本假设 杆件变形的基本形式
§1-1
材料力学的任务
1．几个术语
构件：组成各种 结构物的元件和 机械的零件，统 称为构件。 如图所示桥式起 重机的主梁、吊 钩、钢丝绳；如 图所示悬臂吊车 架的横梁AB，斜 杆CD都是构件。
构件根据几何形状的不同将构件分为： 杆件、板、壳和块体。
1. 内力的概念
F F
产生 外力 变形
迫使 晶粒距离改变
产生
附加内力
内力：指由外力作用所引起的、物体内相邻部 分之间分 布内力系的合力。（附加内力） 研究内力方法：截面法
2. 轴力和轴力图
取左： Fx 0
m
F
F
FN F 0
F
m
FN
得 FN F FN 称为轴力 取右： Fx 0 得
轴向拉压的受力特点 作用于杆件上的外力或外力合力的作用线与杆件轴线重合。 轴向拉压的变形特点 杆件产生沿轴线方向的伸长或缩短。
F
F
F
F
拉绳
P
课堂练习：图示各杆BC段为轴向拉伸（压缩）的是（ A ）
A
A B
C
F D
B
A B
C
F D
C
F A B
C
D
§2-2
拉(压)杆的内力
A 1
F1
C
2
30
B
B F 2
1
F2
30
B F
§1-3
杆件变形的基本形式
1.轴向拉伸或轴向压缩
当直杆受到一对大小相等、方向相反、作用线与杆件轴线重合 的外力作用时，其主要变形是长度的伸长或缩短。
F
F F
F
2.剪切
当直杆受到一对大小相等、方向相反、作 用线平行且相距很近的外力作用时，其主 要变形是相邻截面沿外力作用方向发生相 对错动。
§1-2 变形固体的基本假设 材料力学研究的对象是变形固体 1.连续均匀假设
认为在固体的整个体积内物质是连续分布的，各处的力学性能 是完全相同的。例如金属材料、搅拌均匀的混凝土构件均可看 成是连续体。总之，在宏观研究中，我们把变形固体抽象为连 续均匀的力学模型。这样构件内部的一些力学量（如变形、内 力等）可用坐标的连续函数表示。
x
F 0 FN
FN
F FN
F
x
轴力正负号规定：
F
FN FN
拉力
均为正 故FN 和FN
F
压力
上述求解拉（压）杆轴力的方法称为截面法，其基本步骤是：
① 截开：在需求内力的截面处，假想地用该截面将杆件一分为二。
②代替：任取一部分，另一部分对其作用以内力代替。(假设为正）
③平衡：建立该部分平衡方程，解出内力。
F F
3.扭转
当直杆受到一对大小相等、转向相反、作用面与杆轴线垂直的 力偶作用时，直杆的任意两个横截面将绕轴线发生相对转动。
4.弯曲
当直杆受到一对大小相等、转向相反、作用面与杆的纵向对称 平面重合的力偶作用时，直杆的任意两个横截面将绕垂直于纵 向对称面的轴作相对转到。
Me Me
实际受力杆件的变形多半为上述几种基本变形形式的组合，这种情 况称为组合变形。
力学教研室 CXS
内容
第一章 绪论
第二章 轴向拉伸和压缩 第三章 扭转 第四章 构件连接的实用计算 第五章 弯曲内力
第七章 梁的位移及简单超静定梁
第八章 应力状态分析 第九章 强度理论 第十章 组合变形 第十一章 压杆稳定
第六章 弯曲应力
附录Ⅰ 截面的几何性质
第十二章 能量方法
第十三章 动荷载 第十四章 交变应力
F
B
压杆
wB
ห้องสมุดไป่ตู้
D
FCD C
D
实验：研究构件的强度、刚度和稳定性的问题，都要涉及所用材 料的力学性能，而材料的力学性能是要由实验来测定。另外，实 际问题往往比较复杂，在进行理论分析时，有时要用实验来验证 。因此，实验在材料力学中占有很重要的地位。
3. 材料力学的任务
是研究构件（主要是杆件）的强度、刚度和稳定性的学科，为将 来合理地选择构件的材料，确定其截面尺寸和形状，提供必要的 理论基础与计算方法以及试验技术。
F F
m
F
FN
x
F
x
0 FN
轴力图：为了清楚地看到轴力沿杆长的变化规律，可以用图线 的方式表示轴力的大小与横截面位置的关系。这样的图线称为 轴力图。
FN
o
例如前面例题的轴力图
F
x
x轴表示横截面位置，FN轴表示对应该位置的轴力大小。
F
FN F x
O
例 2-1 （书例2-1） 一等直杆受四个轴向外力作用，如图所示。试 作轴力图 1F2=25kN 2 F3=55kN F4=20kN F1=10kN
(a)
(b)
图1-4
( c)
2．构件正常工作的条件
一、构件应有足够的强度(strength) 要求：构件在外力作用下不发生断裂， 也不能产生显著的塑性变形（即撤除外 力后不能恢复的变形）。 二、构件应有足够的刚度(rigidity) 要求：构件在外力作用下其弹性变形 （即撤除外力后能恢复的变形）不超过 规定的限度 三、构件应有足够的稳定性(stability) 要求：压杆在一定的压力的作用下，能保 持其直线的平衡形式。 A C
A F1=10kN
1
B
FN 1
第二章 轴向拉伸和压缩
目
§2-1
§2-1 §2-3 §2-4 §2-5
录
概述
拉压杆的内力 横截面上的应力 斜截面的应力 拉压杆的变形和位移
§2-6
§2-7 §2-8 §2-9 §2-10 §2-11
应变能
材料在拉压时的力学性能 应力集中 强度计算 拉压超静定问题 装配应力和温度应力
§2-1
轴向拉伸与压缩的概念和实例
杆件：长度远大于横向尺寸的构件。 杆件分类：等截面直杆（图1-3a、d） 、 变截面直杆（图1-3c） ；等截面曲杆和 变截面曲杆如图1-3b。其中横截面是与 轴线垂直的截面；轴线是横截面形心的 连线。
板和壳：构件一个方向的尺寸（厚度）远小于其它两个方向的尺寸 ，如图1-4a和b所示。 块体：三个方向（长、 宽、高）的尺寸相差不 多的构件，如图1-4c所 示。
2.各向同性假设.
假设变形固体在各个方向具有相同的力学性能。这种材料称为 各向同性材料。如金属材料、搅拌均匀的混凝土。根据这一假 设，在研究了材料任一方向的力学性质后，就可以认为其结论 对其它方向也都适用。
3.小变形假设
即构件在外力作用下产生的变形与构件的原始尺寸相比很微 小的。根据这一假设，在列平衡方程时，可以不考虑外力作 用点处的微小位移，而按变形前的位置和尺寸进行计算。
第一章 绪 论
目
§1-1 §1-2 §1-3
录
材料力学的任务 变形固体的基本假设 杆件变形的基本形式
§1-1
材料力学的任务
1．几个术语
构件：组成各种 结构物的元件和 机械的零件，统 称为构件。 如图所示桥式起 重机的主梁、吊 钩、钢丝绳；如 图所示悬臂吊车 架的横梁AB，斜 杆CD都是构件。
构件根据几何形状的不同将构件分为： 杆件、板、壳和块体。
1. 内力的概念
F F
产生 外力 变形
迫使 晶粒距离改变
产生
附加内力
内力：指由外力作用所引起的、物体内相邻部 分之间分 布内力系的合力。（附加内力） 研究内力方法：截面法
2. 轴力和轴力图
取左： Fx 0
m
F
F
FN F 0
F
m
FN
得 FN F FN 称为轴力 取右： Fx 0 得
轴向拉压的受力特点 作用于杆件上的外力或外力合力的作用线与杆件轴线重合。 轴向拉压的变形特点 杆件产生沿轴线方向的伸长或缩短。
F
F
F
F
拉绳
P
课堂练习：图示各杆BC段为轴向拉伸（压缩）的是（ A ）
A
A B
C
F D
B
A B
C
F D
C
F A B
C
D
§2-2
拉(压)杆的内力
A 1
F1
C
2
30
B
B F 2
1
F2
30
B F
§1-3
杆件变形的基本形式
1.轴向拉伸或轴向压缩
当直杆受到一对大小相等、方向相反、作用线与杆件轴线重合 的外力作用时，其主要变形是长度的伸长或缩短。
F
F F
F
2.剪切
当直杆受到一对大小相等、方向相反、作 用线平行且相距很近的外力作用时，其主 要变形是相邻截面沿外力作用方向发生相 对错动。
§1-2 变形固体的基本假设 材料力学研究的对象是变形固体 1.连续均匀假设
认为在固体的整个体积内物质是连续分布的，各处的力学性能 是完全相同的。例如金属材料、搅拌均匀的混凝土构件均可看 成是连续体。总之，在宏观研究中，我们把变形固体抽象为连 续均匀的力学模型。这样构件内部的一些力学量（如变形、内 力等）可用坐标的连续函数表示。
x
F 0 FN
FN
F FN
F
x
轴力正负号规定：
F
FN FN
拉力
均为正 故FN 和FN
F
压力
上述求解拉（压）杆轴力的方法称为截面法，其基本步骤是：
① 截开：在需求内力的截面处，假想地用该截面将杆件一分为二。
②代替：任取一部分，另一部分对其作用以内力代替。(假设为正）
③平衡：建立该部分平衡方程，解出内力。
F F
3.扭转
当直杆受到一对大小相等、转向相反、作用面与杆轴线垂直的 力偶作用时，直杆的任意两个横截面将绕轴线发生相对转动。
4.弯曲
当直杆受到一对大小相等、转向相反、作用面与杆的纵向对称 平面重合的力偶作用时，直杆的任意两个横截面将绕垂直于纵 向对称面的轴作相对转到。
Me Me
实际受力杆件的变形多半为上述几种基本变形形式的组合，这种情 况称为组合变形。
力学教研室 CXS
内容
第一章 绪论
第二章 轴向拉伸和压缩 第三章 扭转 第四章 构件连接的实用计算 第五章 弯曲内力
第七章 梁的位移及简单超静定梁
第八章 应力状态分析 第九章 强度理论 第十章 组合变形 第十一章 压杆稳定
第六章 弯曲应力
附录Ⅰ 截面的几何性质
第十二章 能量方法
第十三章 动荷载 第十四章 交变应力
F
B
压杆
wB
ห้องสมุดไป่ตู้
D
FCD C
D
实验：研究构件的强度、刚度和稳定性的问题，都要涉及所用材 料的力学性能，而材料的力学性能是要由实验来测定。另外，实 际问题往往比较复杂，在进行理论分析时，有时要用实验来验证 。因此，实验在材料力学中占有很重要的地位。
3. 材料力学的任务
是研究构件（主要是杆件）的强度、刚度和稳定性的学科，为将 来合理地选择构件的材料，确定其截面尺寸和形状，提供必要的 理论基础与计算方法以及试验技术。