正方形的外接圆和内切圆
外切球和内切球知识点总结

外切球和内切球知识点总结一、外切球和内切球的定义1. 外切球在几何学中,外切球是指一个球与另外一个几何体(通常是一个多边形或圆柱体)相切于凸多边形或凸多面体的每一侧面的情况。
外切球的直径等于两相切多边形(或多面体)的对边之和。
以正方形为例,外切球的定义如下:对于一个正方形,以正方形的每一条边为切点做球的切线,则球的外切球的半径等于正方形的边长的一半。
2. 内切球内切球是指一个球刚好被另外一个几何体(通常是一个多边形或圆柱体)所包围,并且与该几何体的每一边或面都相切的情况。
内切球的直径等于围绕这个球的多边形(或多面体)的对边之和。
以正方形为例,内切球的定义如下:对于一个正方形,用正方形的每个顶点作为球的切点,那么这个球就是正方形的内切球。
二、外切球和内切球的性质1. 外切球的性质外切球的性质主要有以下几点:(1)外切球的半径等于多边形(或多面体)的对角线的一半。
(2)对于任意多边形,外切球与多边形的外切圆心在一条直线上。
(3)外切球的切点在多边形(或多面体)的中点处。
(4)外切球的半径等于多边形(或多面体)的外接圆的半径。
2. 内切球的性质内切球的性质主要有以下几点:(1)内切球的半径等于多边形(或多面体)的内切圆的半径。
(2)对于任意多边形,内切球的内切圆心和多边形的顶点在一条直线上。
(3)内切球的切点在多边形(或多面体)的中点处。
(4)内切球的半径等于多边形(或多面体)的外接圆的半径减去多边形(或多面体)的半径。
三、外切球和内切球的应用外切球和内切球在数学、物理、工程等领域都有着重要的应用,下面将分别介绍它们在不同领域的具体应用。
1. 数学领域在数学领域,外切球和内切球主要应用于解决几何问题和优化问题。
例如,外切球和内切球可以用来求解多边形(或多面体)的面积、体积、周长等问题,同时也可以用来解决某些最优化问题,比如求解最大最小值等。
此外,外切球和内切球还可以应用于解决一些具体的数学难题,比如利用外切球和内切球的性质证明某些几何定理、求解某些不等式等。
内切圆公式大全

内切圆公式大全全文共四篇示例,供读者参考第一篇示例:内切圆是指一个圆完全嵌入在一个多边形内部,并且切正多边形的每一边。
内切圆在几何问题和工程设计中有着广泛的应用,因此了解内切圆的相关知识和公式是非常重要的。
在本文中,我们将分享一些关于内切圆的公式大全,希望能够帮助大家更好地理解和应用。
一、内切圆的半径计算公式1. 内切圆的半径公式:对于一个正五边形,其内切圆的半径r可以通过下面的公式来计算:r = a * sqrt(10 + 2 * sqrt(5))/10a代表正五边形的边长。
二、内切圆和外接圆的关系公式1. 内切圆和外接圆的半径关系:对于任意多边形,其内切圆的半径r和外接圆的半径R之间存在着以下关系:R = 2r三、内切圆和多边形边长的关系2. 内切圆和多边形内角的关系:对于一个正n边形,其内切圆和内角之间存在以下关系:角A = 180 - (n-2)*180/nA表示正n边形的内角。
四、常见多边形的内切圆公式总结第二篇示例:内切圆,俗称内切圆,是指一个圆与一个给定的多边形(三角形、四边形、正多边形)相切。
内切圆在数学中有着重要的应用,特别是在几何学和工程学中。
在实际生活和工程中,我们常常需要计算内切圆的半径、圆心和切点等信息。
内切圆的相关公式是很有必要了解和掌握的。
在几何中,内切圆与多边形的关系是一个经典问题,经常出现在数学竞赛和学习中。
内切圆的半径、圆心和切点等可以通过一些简单的公式来求解,下面我们就来介绍一下关于内切圆的一些常用公式。
我们来看一下内切圆的半径计算公式。
对于一个三角形ABC,假设其三边分别为a、b、c,内切圆的半径r可以用以下公式来表示:\[r = \frac{2S}{a+b+c}\]其中S表示三角形ABC的面积,可以通过海伦公式来计算。
海伦公式是用来计算三角形面积的公式,其表达式如下:\[S = \sqrt{p(p-a)(p-b)(p-c)}\]其中p是三角形ABC的半周长,即\(p = \frac{a+b+c}{2}\)。
多面体外接球半径内切球半径的常见几种求法

多面体外接球、内切球半径常见的5种求法如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.公式法例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为9,底面周长为3,则这个球的体积为8T 6x=3,T 1I ' I x =—解设正六棱柱的底面边长为x,咼为h,则有丿9 V3 2 2’_=6汉——xh, 石8 4 小一x/3•••正六棱柱的底面圆的半径r =-,球心到底面的距离d二上3.二外接球的半径2 2R=、r2d2「=1. . V球二—.3小结本题是运用公式R2-r2 d2求球的半径的,该公式是求球的半径的常用公式.多面体几何性质法例2已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是A. 16二B. 20 二C. 24 二D. 32 二解设正四棱柱的底面边长为x ,外接球的半径为R,则有4x2 = 16,解得x = 2.二2R = J22+22+42=2屈,二R = T6. •••这个球的表面积是4兀R2=24兀.选C.小结本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的.补形法例3若三棱锥的三个侧棱两两垂直,且侧棱长均为.3,则其外接球的表面积是.解据题意可知,该三棱锥的三条侧棱两两垂直,I把这个三棱锥可以补成一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球设其外接球的半径为R,则有(2R f =(応行(亦丫+(73$ =9.二R2=9.4故其外接球的表面积S =4二R2=9二.小结一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为 a b、c,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2R= a 2b 2c 2.寻求轴截面圆半径法例4正四棱锥S - ABCD 的底面边长和各侧棱长都为 V 2,点S 、A 、B 、C 、都在同 一球面上,则此球的体积为.解设正四棱锥的底面中心为O i ,外接球的球心为0, 所示.二由球的截面的性质,可得 00i _平面ABCD .又SO i _平面ABCD ,二球心0必在SO 所在的直线上.ASC 的外接圆就是外接球的一个轴截面圆,外接圆的 是外接球的半径.在 ASC 中,由 SA = SC = .2, AC =2,得 SA 2SC 2二 AC 2.••• AASC 是以AC 为斜边的Rt :.••• AC =1是外接圆的半径,也是外接球的半径.故V 球二—.23小结 根据题意,我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴 截面圆,于是该圆的半径就是所求的外接球的半径.本题提供的这种思路是探求正棱锥外 接球半径的通解通法,该方法的实质就是通过寻找外接球的一个轴截面圆,从而把立体几 何问题转化为平面几何问题来研究.这种等价转化的数学思想方法值得我们学习.确定球心位置法例5 在矩形ABCD 中,AB = 4,BC = 3,沿AC 将矩形ABCD 折成一个直二面角半径就如图3B - AC -D ,则四面体ABCD 的外接球的体积为A. 125 -- n 12B.空二C.D.125 3解 设矩形对角线的交点为0 ,则由矩形对角线互相平分,0A =0B =0C =0D . •••点0到四面体的四个顶点A 、B 、C 、D 的距离相等,即点0为四面体的外接球的球心,可知 如图2所示.二外接球的半径R = 0A =总.故2球='二R 3= 125二.选C.236出现多个垂直关系时建立空间直角坐标系,利用向量知识求解【例题】:已知在三棱锥 A - BCD 中,AD _面ABC ,. BAC =120,AB 二AD 二AC = 2, 求该棱锥的外接球半径 解:由已知建立空间直角坐标系 由平面知识得 5-1, 3,0)设球心坐标为x, y, z) 贝U A0 二 B0 二 CO 广 Dq 由.空间两.点 1间C 距离公式知解得 x = 1 y 3z = 13所以半径为R-12( 3)212=-21\ 33【结论】:空间两点间距离公式:P^ (x 1 -x 2)2(y 〔 - y 2)2 (乙-z 2)2四面体是正四面体外接球与内切球的圆心为正四面体高上的一个点,根据勾股定理知,假设正四面体的边长为 a 时,它的外接球半径为a 。
外接球和内切球问题总结归纳

外接球和内切球问题总结归纳外接球和内切球问题总结归纳在几何学中,外接球和内切球问题是一个重要的概念。
它们不仅在数学领域有着重要的应用,同时也被广泛运用在物理学、工程学以及计算机科学等领域。
本文将对外接球和内切球问题进行深入探讨,从基础概念到应用实例,帮助读者全面理解这一主题。
一、外接球和内切球的定义1. 外接球外接球是指一个球与给定的多边形的所有顶点相切于球面的情况。
在数学中,外接球常常与三角形、四边形等几何图形相关联,其特点是与多边形的各个顶点相切,并且球心通常位于多边形的某个重要位置。
2. 内切球内切球则是指一个球完全被给定的多边形所包围,且球与多边形的边界相切。
在实际应用中,内切球往往能够最大化地利用多边形所包围的空间,因此在工程设计和优化问题中具有重要意义。
二、外接球和内切球的性质1. 外接球的性质外接球的半径通常与多边形的边或者角有着特定的关系。
以三角形为例,外接圆的半径等于三角形三条边的乘积除以其周长的两倍。
这一性质在计算三角形的外接圆时具有重要意义,同时也为几何问题的解决提供了基础。
2. 内切球的性质内切球的半径与多边形的边界有着紧密的联系。
以正方形为例,内切圆的半径等于正方形的边长的一半。
这一性质在优化问题中有着重要的应用,能够帮助设计者最大化地利用空间,提高效率和节约成本。
三、外接球和内切球的应用1. 工程设计外接球和内切球在工程设计中有着广泛的应用。
例如在建筑设计中,内切球可以帮助设计者合理利用建筑空间,提高使用效率;在机械设计中,外接球则可以帮助设计者确定零部件的匹配度和适用性。
2. 计算机科学外接球和内切球也在计算机科学领域有着重要的应用。
例如在计算机图形学中,外接球和内切球经常被用来描述物体的外形和几何特征,同时也可以用于物体的碰撞检测和三维建模。
个人观点和总结外接球和内切球作为一个基础的数学概念,在几何学、工程学和计算机科学等领域有着重要的应用。
通过对外接球和内切球的定义、性质和应用进行深入探讨,我们可以更好地理解其在实际问题中的作用和意义,进一步拓展其在更多领域的应用。
几何形的内切圆和外接圆

几何形的内切圆和外接圆几何学中,内切圆和外接圆是与特定几何形状相关联的重要概念。
内切圆是指能够与给定的几何形状内切的圆,而外接圆则是能够与给定的几何形状外接的圆。
本文将首先介绍内切圆和外接圆的定义,并以具体的几何形状为例进行论述,以加深读者对这两个概念的理解。
一、内切圆内切圆,顾名思义,即与给定几何形状相切于内部的圆。
对于一个不规则的几何形状,能够存在唯一的内切圆。
我们以三角形为例来说明。
对于任意一个三角形,都可以找到唯一的内切圆,该圆的圆心与三角形的三条边相切,并且每条边都是圆的切线。
由于这个特点,我们可以得出内切圆的一个重要性质:内切圆的圆心是三角形三条角平分线的交点。
除了三角形,其他的几何形状也可以存在内切圆,比如正方形、圆形等。
不论几何形状如何,其内切圆的存在都与该几何形状的内部结构和性质有关。
二、外接圆外接圆是能够与给定几何形状相切于外部的圆。
与内切圆类似,我们以三角形为例进行论述。
对于任意一个三角形,都可以找到唯一的外接圆,该圆的圆心是三角形三个顶点的垂直平分线的交点,并且每条边的中垂线都是圆的切线。
外接圆的一个重要性质是:三角形的三个顶点都位于该圆上。
除了三角形,其他的几何形状也可以存在外接圆,比如正方形、圆形等。
外接圆的存在也与所给几何形状的外部结构和性质密切相关。
三、特殊情况在实际应用中,有些几何形状具有特殊的内切圆和外接圆。
1. 正方形对于正方形来说,其内切圆和外接圆是同一个圆。
正方形的内切圆和外接圆均以正方形的中心点为圆心。
2. 圆形对于圆形来说,其内切圆和外接圆也是同一个圆。
圆形的内切圆和外接圆以圆心为圆心。
在实际问题中,利用几何形的内切圆和外接圆,我们可以推导出一些重要的结论,解决一些实际应用问题。
例如,在建筑设计中,可以利用内切圆和外接圆来确定建筑物的布局和结构;在工程测量中,可以利用内切圆和外接圆来精确定位和校正测量数据。
结论几何形的内切圆和外接圆是几何学中重要的概念。
简单几何体的外接球和内切球的半径的求法
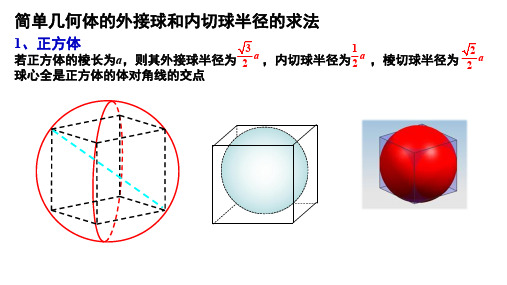
简单几何体的外接球和内切球半径的求法1、正方体若正方体的棱长为a ,则其外接球半径为 ,内切球半径为 ,棱切球半径为 球心全是正方体的体对角线的交点32a 12a 22a例:一个正方体的顶点都在球面上,它的棱长是a cm ,求球的体积.解:该球是正方体的外接球,球心到正方体各顶点的距离相等,因此球心是正方体的体对角线的交点,球的直径是正方体的体对角线长设球的半径为R ,a R a R 2332==得则)(23)23(34343333cm a a R πππ==∴球的体积为若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
外接球的球心到多面体各顶点的距离均相等。
例:将一个棱长为6cm 的正方体铁块磨制成一个球体零件,求可能制作的最大零件的体积。
解:这个最大的球体是正方体的内切球,球心到正方体各个面的距离相等,因此球心是正方体的体对角线的交点,球的直径是正方体的棱长设球的半径为R ,则2R =6,得R =3)(3633434333cm R πππ=⨯=∴最大零件的体积为若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
内切球的球心到多面体各面的距离均相等。
⑴正方体的内切球直径=⑵正方体的外接球直径=⑶与正方体所有棱相切的球直径=探究 若正方体的棱长为a ,则a3a2a右图,红色球是正方体的棱切球棱切球的球心到正方体各条棱的距离相等,因此球心是正方体的体对角线的交点,球的直径是正方体的面对角线的长2、长方体若长方体的长、宽、高分别为a、b、c,则其外接球半径为球心是长方体的体对角线的交点222 1+2a b c例:有一个球与长方体的面相切,这个球的最大直径是多少?长方体的长、宽、高中的最小者例:一个长方体的各顶点均在同一个球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为____________若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
27.4正方形与圆

A .O B E
D
C
6、⊙O是正五边形ABCDE的外接圆,弦AB的 弦心距OF叫正五边形ABCDE的 边心距 , 它是正五边形ABCDE的 内切 圆的半径。
中心 7、 ∠AOB叫做正五边形ABCDE的 角, 它的度数是 72度 D
E C
.O A F B
;
用48m长的篱笆在空地上围成一个
绿化场地,现有几种设计方案,正三角
中心 7、 ∠AOB叫做正五边形ABCDE的 角, 它的度数是 72度 D
E C
.O A F B
7、图中正六边形ABCDEF的中心角是 ∠AOB 60度 它的度数是
E
D .O
F
C B
A
如何画一个边长为2cm
的正六边形?
分 析
我们知道,把圆六等分,再依次连
接各等分点即可得到一个正六边形。但
半径为多少的圆,六等分后得到的正六
2
2
8 12
4
6 3
120°
60°
2
小结:
1、正多边形的判定方法: ①各边相等 ②各角相等 的多边形叫做正多边形。
2、正多边形的相关概念和计算: 中心、半径、中心角、边心距
五.拓展练习
• 1、两个正六边形的边长分别是3和4,这两 9:16 个正六边形的面积之比等于________ 2 • 2.圆内接正方形的半径与边长的比值是3 2 .圆内接正四边形的边长为4 cm,那么边 2 心距是________ • 4.已知圆内接正方形的边长为2,则该圆 的内接正六边形边长为__________ . 2 • 5. 圆内接正六边形的边长是8 cm用么该 8 正六边形的半径为________ ;边心距为 ________ 4 3 .
球的内切与外切

定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球大家知道,几何体的外接球和内切球问题是近几年的高考热点内容,尤其是几何体的外接球问题,基本上近几年的高考试题中都有出现。
归结起来这类问题主要包括两种类型:①已知几何体的顶点都在同一球面上,几何体满足一定的条件,求球的体积;②已知几何体的顶点都在同一球面上,几何体满足一定的条件,求球的表面积;解答这类问题的基本思路是根据问题给出的条件,求出球的半径,然后再运用球的体积(或表面积)公式进行计算得出结果。
从题型上看是5分小题,可能是选择题,也可能是填空题;从难易程度上看,属于中、低档难度的问题。
那么如何解答这类问题呢?下面通过例题的解析来回答这个问题。
【典例1】解答下列问题:1、已知三棱锥P—ABC的三个顶点在球O的球面上,PA=PB=PC,∆ABC是边长为2的正三角形,E,F分别是PA,AB 的中点,∠CEF=.90,则球O的体积为()(2019全国高考新课标I(理))A86πB46πC26πD6π2、《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”,现有一阳马,其正视图和侧1视图是如图所示的直角三角形,若该阳马的顶点都在同一个12球面上,则该球的体积为()(正视图)(侧视图)A 863πB86πC6πD24π的关键是求出外接球的半径;(2)解答已知几何体的顶点都在同一球面上,几何体满足一定的条件,求球的表面积的问题的基本方法是:①根据几何体底面的几何图形,确定底面多边形的外接圆的圆心1O ;②过底面外接圆的圆心作底面的垂线,在所作垂线上确定几何体外接球的球心O;③构造以外接球半径为斜边,O 1O 为一直角边的直角三角形;④在构造的直角三角形中求出外接球的半径R;⑤由公式:O S 球表=4π2R 求出外接球的表面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形的外接圆和内切圆
正方形的外接圆和内切圆是几何学中常见的概念,它们的性质与
应用在许多领域中都有着不可忽视的作用,尤其在工程设计和数学理
论方面更是如此。
首先,我们来了解一下什么是正方形、外接圆和内切圆。
正方形
是一种有着四个等长且相互垂直的边的四边形,它的特点是四个内角
都是直角,并且对边平行。
外接圆是指一个圆形恰好与正方形的四个
顶点相切,使得圆心位于正方形的外部,并且四条边都是圆的切线。
内切圆是一个圆形恰好位于正方形的内部,使得圆心位于正方形的中心,四条边都是圆的切线。
正方形的外接圆和内切圆有着很多有趣的性质。
首先,正方形的
外接圆和内切圆半径分别为正方形对角线的一半和正方形边长的一半。
其次,当正方形的对角线与一条边重合时,正方形的内切圆与这条边
重合,这意味着正方形的内切圆可以作为一个非常简单但灵活的标尺。
此外,正方形的外接圆和内切圆还可以用来计算正方形的面积、周长
以及各种角度。
在实际应用中,正方形的外接圆和内切圆广泛用于工程设计和数
学理论之中。
举例来说,在建筑设计中,正方形的外接圆可以用于绘
制建筑物的草图和布局,以确定建筑物的各种尺寸和比例。
在电子工
程中,内切圆可以用于计算电容器的最大容量和电感器的最大电感量。
在数学理论中,正方形的外接圆和内切圆又被广泛应用于圆锥曲线、椭圆曲线等知识的研究和证明中。
总之,正方形的外接圆和内切圆是一个有趣且实用的几何概念,它蕴藏着许多奥妙和应用。
在我们的日常工作和学习中,学会运用它们是非常重要的,相信在不久的将来它们会在更多的领域中发挥出不可替代的独特作用。
