江苏中考数学复习资料专题平行线与三角形.doc
中考数学专题复习全等三角形之辅助线做平行线

中考数学专题复习全等三角形(辅助线做平行线)学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.如图,△ABC是边长为4的等边三角形,点P在AB上,过点P作PE⊥AC,垂足为E,延长BC至点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.1B.1.8C.2D.2.52.如图,⊥ABC是边长为2的等边三角形,点P在AB上,过点P作PE⊥AC,垂足为E,延长BC到点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.0.5B.0.9C.1D.1.25评卷人得分二、填空题3.如图,四边形ABCD中,AC与BD相交于点O,且AC⊥BD,AC=BD=CD,点P 是⊥OCD角平分线的交点,点M是AB的中点,给出下列结论:⊥⊥CPD=135°;⊥BA=BP;⊥⊥P AC⊥⊥PDB;⊥S△ABP=S△DCP;⊥PM=12CD.其中正确的是___.(填序号)评卷人得分三、解答题4.如图,⊥ABC中,点D,E在边AB上,点F在边BC上,且AD=AC,EF=EC,⊥CEF=⊥A,连接DF.(1)在图1中找出与⊥ACE相等的角,并证明;(2)求证:⊥BDF=⊥EFC;(3)如图2,延长FD,CA交于点G,连接EG,若EG=AG,DE=kAE,求DG DF的值(用含k的代数式表示).5.如图所示:ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD CE=,连接DE交BC于点M.求让:MD ME=6.P为等边△ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.7.P为等边⊥ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC 边于D.(1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.8.如图,点P为等边⊥ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,(1)求证:DP=DQ;(2)过P作PE⊥AC于E,若BC=4,求DE的长.9.已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M.请探究:(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;(3)如图(3),当点E在CA的延长线上,点D在线段AB上(点D不与A,B重合),DE所在直线与直线BC交于点M,若CE=2BD,请直接写出线段MD与线段ME的数量关系.10.读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DB上,且⊥BAE=⊥CDE,求证:AB=CD分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明.图(1):延长DE到F使得EF=DE图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F图(3):过C点作CF⊥AB交DE的延长线于F.参考答案:1.C【解析】【分析】过P作BC的平行线交AC于F,通过AAS证明PFD⊥QCD,得FD CD=,再由APF 是等边三角形,即可得出12DE AC=.【详解】解:过P作BC的平行线交AC于F,Q FPD∴∠=∠,ABC是等边三角形,60APF B∴∠=∠=︒,60AFP ACB∠=∠=︒,APF∴△是等边三角形,AP PF∴=,⊥CQ=P A,⊥PF CQ=在PFD中和QCD中,FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,PFD∴⊥()QCD AAS,FD CD∴=,PE AC⊥于E,APF是等边三角形,AE EF∴=,=AE DC EF FD ED∴+=+,12DE AC∴=,4AC=,2DE∴=,故选:C.【点睛】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键.2.C【解析】【分析】过P作BC的平行线交AC于F,通过AAS证明PFD≌QCD,得FD CD=,再由APF 是等边三角形,即可得出12DE AC=.【详解】解:过P作BC的平行线交AC于F,Q FPD∴∠=∠,ABC是等边三角形,60APF B∴∠=∠=︒,60AFP ACB∠=∠=︒,APF∴是等边三角形,AP PF∴=,在PFD中和QCD中,FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,PFD∴≌()QCD AAS,FD CD∴=,PE AC⊥于E,APF是等边三角形,AE EF ∴=,AE DC EF FD ∴+=+,12DE AC ∴=, 2AC =, 1DE ∴=,故选:C . 【点睛】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键. 3.⊥⊥⊥⊥ 【解析】 【分析】由角平分线的定义,可得⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°,进而即可判断⊥;先证ACP DCP ≌,可得APD △是等腰直角三角形,进而得PAC PDB ≌,即可判断⊥;过点A 作AN ⊥BP 交PM 的延长线于点N ,可得AMN BMP ≌,再证明APN PDC ≌,从而得PM =12CD ,即可判断⊥;由ABP APM BMP APM AMN APN S S S S S S +=+==,即可判断⊥. 【详解】解:⊥AC ⊥BD ,点P 是⊥OCD 角平分线的交点,⊥⊥DOC =90°,⊥ODC +⊥OCD =90°,⊥CDP =12⊥CDO ,⊥DCP =12⊥DCO , ⊥⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°,⊥⊥CPD =180°-(⊥CDP +⊥DCP )=135°,故⊥正确; ⊥CP ,DP 分别平分⊥DCO ,⊥CDO , ⊥⊥DCP =⊥ACP ,⊥CDP =⊥BDP , ⊥AC =CD ,PC =PC , ⊥ACP DCP ≌,⊥AP =DP ,⊥CAP =⊥CDP =⊥BDP ,⊥APC =⊥DPC =135°, ⊥⊥DP A =360°-135°-135°=90°,⊥APD △是等腰直角三角形, 又⊥AC =BD ,⊥CAP =⊥BDP,AP =DP , ⊥PAC PDB ≌,故⊥正确; ⊥⊥DPB =⊥APC=135°,PB =PC , ⊥⊥BPC =360°-135°-135°=90°,⊥BPC △是等腰直角三角形,找不到证明BA =BP 的条件,故⊥错误; 过点A 作AN ⊥BP 交PM 的延长线于点N ,⊥⊥N =⊥BPM ,⊥P AN +⊥APB =180°, ⊥点M 是AB 的中点,即AM =BM , 又⊥⊥AMN =⊥BMP , ⊥AMN BMP ≌,⊥MN =PM =12PN ,AN =PB =PC ,AMNBMPSS=,⊥⊥DP A =⊥BPC =90°, ⊥⊥APB +⊥DPC =180°, 又⊥⊥P AN +⊥APB =180°, ⊥⊥P AN =⊥DPC , 又⊥AP =DP ,AN =PC , ⊥APN PDC ≌,⊥CD =PN =2PM ,即:PM =12CD ,故⊥正确; ⊥APNPDCSS=,AMNBMPSS=,⊥ABPAPMBMPAPMAMNAPNS SSSSS+=+==,⊥ABPDCPSS=,故⊥正确.故正确的是⊥⊥⊥⊥. 【点睛】本题主要考查全等三角形的判定和性质,平行线的性质,等腰直角三角形的判定和性质,熟练掌握中线倍长模型和旋转全等模型,是解题的关键. 4.(1)⊥DEF =⊥ACE ,证明见解析;(2)见解析;(3)k 【解析】 【分析】(1)由三角形外角的性质可得出答案;(2)连接CD ,过点E 作AC 的平行线与CD 交于点M ,证明⊥DEF ⊥⊥MEC (SAS ),由全等三角形的性质可得出⊥EDF =⊥EMC ,证出⊥EMD =⊥EFC ,则可得出结论;(3)连接CD ,过点E 作AC 的平行线与CD 交于点M ,证明⊥EFG ⊥⊥ECD (ASA ),由全等三角形的性质可得出GF =DC ,证出GD =DM ,则根据平行线分线段成比例即可得出答案. 【详解】解:(1)⊥DEF =⊥ACE . 证明:⊥⊥DEC 是⊥ACE 的外角, ⊥⊥DEC =⊥A +⊥ACE , ⊥⊥DEC =⊥DEF +⊥CEF , ⊥⊥DEC +⊥CEF =⊥A +⊥ACE , ⊥⊥CEF =⊥A , ⊥⊥DEF =⊥ACE ;(2)证明:连接CD ,过点E作AC 的平行线与CD 交于点M ,⊥AD =AC ,⊥⊥ADC=⊥ACD,⊥EM⊥AC,⊥⊥EMD=⊥ACD,⊥CEM=⊥ACE,⊥⊥EDM=⊥EMD,⊥DEF=⊥CEM,⊥ED=EM,又⊥EF=EC,⊥⊥DEF⊥⊥MEC(SAS),⊥⊥EDF=⊥EMC,⊥⊥BDF+⊥EDF=⊥EMD+⊥EMC=180°,⊥⊥BDF=⊥EMC,⊥EM⊥AC,⊥⊥DEM=⊥A,⊥⊥A=⊥CEF,⊥⊥DEM=⊥CEF,⊥⊥DEM中,⊥EMD=1802DEM︒-∠,⊥FEC中,⊥EFC=1802CEF︒-∠,⊥⊥EMD=⊥EFC,⊥⊥BDF=⊥EFC;(3)连接CD,过点E作AC的平行线与CD交于点M,⊥EG=AG,⊥⊥GAE=⊥GEA,⊥⊥DAC+⊥GAE=⊥GEA+⊥GED=180°,⊥⊥DAC=⊥GED,⊥⊥CEF=⊥DAC,⊥⊥DEG=⊥CEF,⊥⊥DEG+⊥DEF=⊥CEF+⊥DEF,即⊥GEF=⊥DEC,⊥⊥DEF⊥⊥MEC,⊥⊥EFG=⊥ECD,DF=MC,又⊥EF=EC,⊥⊥EFG⊥⊥ECD(ASA),⊥GF=DC,⊥DC﹣MC=GF﹣DF,即GD=DM,⊥EM⊥AC,⊥DM DEk MC AE==,⊥GD DMk DF MC==.【点睛】本题考查了全等三角形的性质与判定,平行线分线段成比例,三角形的内角和定理,三角形的外角性质,添加辅助线证明三角形全等是解题的关键.5.见详解【解析】【分析】过点D作DE⊥AC,交BC于点E,根据等边三角形和平行线的性质得⊥MDE=⊥MEC,DE=CE,从而证明∆EMD≅∆CME,进而即可得到结论.【详解】过点D作DE⊥AC,交BC于点E,⊥ABC是等边三角形,⊥⊥B=⊥ACB=60°,⊥DE⊥AC,⊥⊥DEB=⊥ACB=60°,⊥MDE=⊥MEC,⊥BDE是等边三角形,⊥BD=DE,⊥DE=CE,又⊥⊥EMD=⊥CME,⊥∆EMD≅∆CME,⊥MDME =.【点睛】本题主要考查等边三角形的性质和判定定理以及全等三角形的判定和性质定理,添加辅助线,构造等边三角形和全等三角形,是解题的关键.6.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF⊥BC交AC于点F;证出△APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明△PDF⊥⊥QDC,得出对应边相等即可;(2)过P作PF⊥BC交AC于F.同(1)由AAS证明△PFD⊥⊥QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF⊥BC交AC于点F.⊥⊥ABC是等边三角形,⊥⊥APF也是等边三角形,AP=PF=AF=CQ.⊥PF⊥BC,⊥⊥PFD=⊥DCQ.在△PDF和△QDC中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥PDF⊥⊥QDC(AAS),(2)如图2所示,过P作PF⊥BC交AC于F.⊥PF⊥BC,△ABC是等边三角形,⊥⊥PFD=⊥QCD,△APF是等边三角形,⊥AP=PF=AF.⊥PE⊥AC,⊥AE=EF.⊥AP=PF,AP=CQ,⊥PF=CQ.在△PFD和△QCD中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥PFD⊥⊥QCD(AAS),⊥FD=CD.⊥AE=EF,⊥EF+FD=AE+CD,⊥AE+CD=DE12=AC.⊥AC=6,⊥DE=3.【点睛】本题考查等边三角形的判定与性质、全等三角形的判定(AAS)与性质、平行线的性质,熟练掌握等边三角形的性质,解题的关键是掌握等边三角形的判定与性质、全等三角形的判定(AAS)与性质、平行线的性质,熟练掌握等边三角形的性质.7.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF⊥BC交AC于点F;证出⊥APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明⊥PDF⊥⊥QDC,得出对应边相等即可;(2)过P作PF⊥BC交AC于F.同(1)由AAS证明⊥PFD⊥⊥QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF⊥BC交AC于点F.⊥⊥ABC是等边三角形,⊥⊥APF也是等边三角形,AP=PF=AF=CQ.⊥PF⊥BC,⊥⊥PFD=⊥DCQ.在⊥PDF和⊥QDC中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,⊥⊥PDF⊥⊥QDC(AAS),⊥PD=DQ;(2)如图2所示,过P作PF⊥BC交AC于F.⊥PF⊥BC,⊥ABC是等边三角形,⊥⊥PFD=⊥QCD,⊥APF是等边三角形,⊥AP=PF=AF.⊥PE⊥AC,⊥AE=EF.⊥AP=PF,AP=CQ,⊥PF=CQ.在⊥PFD和⊥QCD中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,⊥⊥PFD⊥⊥QCD(AAS),⊥FD=CD.⊥AE=EF,⊥EF+FD=AE+CD,⊥AE+CD=DE12=AC.⊥AC=6,⊥DE=3.【点睛】本题考查了等边三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、平行线的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.8.(1)详见解析(2)ED=2【解析】【分析】(1)过P作PF⊥BQ,可得△APF为等边三角形,所以AP=PF,再证△DCQ⊥⊥DFP,即可得PD=DQ;(2)根据等腰三角形三线合一的性质可得AE=EF,根据全等三角形对应边相等可得FD =CD,然后求出2DE=AC,代入数据进行计算即可得解.(1)证明:如图,过点P作PF⊥BC,则⊥DPF=⊥Q,⊥⊥ABC为等边三角形,⊥⊥APF是等边三角形,⊥AP=PF,又⊥AP=CQ,⊥PF=CQ,在△DPF和△DQC中,DPF QPDF QDC PF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DPF⊥⊥DQC(AAS),⊥DP=DQ;(2)⊥⊥P AF为等边三角形,PE⊥AC,可得AE=EF,由(1)知,⊥DPF⊥⊥DQC⊥FD=CD,⊥AC=AE+EF+FD+CD,⊥AC=2EF+2FD=2(EF+FD)=2ED,⊥AC=BC=4,⊥2ED=4,⊥ED=2.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线构造出等边三角形和全等三角形是解题的关键,也是本题的难点.9.(1)DM=EM.理由见详解;(2)成立,理由见详解;(3)MD=12ME.【解析】【分析】(1)DM=EM;过点E作EF//AB交BC于点F,然后利用平行线的性质和已知条件可以证明△DBM⊥⊥EFM,接着利用全等三角形的性质即可证明题目的结论;(2)成立;过点E作EF//AB交CB的延长线于点F,然后利用平行线的性质与已知条件可以证明△DBM⊥⊥EFM,接着利用全等三角形的性质即可证明题目的结论;(3)MD=12ME.过点E作EF//AB交CB的延长线于点F,然后利用平行线的性质和已知条件得到△DBM⊥⊥EFM,接着利用相似三角形的性质即可得到结论;(1)解:DM=EM;证明:过点E作EF//AB交BC于点F,⊥AB=AC,⊥⊥ABC=⊥C;又⊥EF//AB,⊥⊥ABC=⊥EFC,⊥⊥EFC=⊥C,⊥EF=EC.又⊥BD=EC,⊥EF=BD.又⊥EF//AB,⊥⊥ADM=⊥MEF.在△DBM和△EFM中BDM FEMBMD FMEBD EF∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DBM⊥⊥EFM,⊥DM=EM.(2)解:成立;证明:过点E作EF//AB交CB的延长线于点F,⊥AB=AC,⊥⊥ABC=⊥C;又⊥EF//AB,⊥⊥ABC=⊥EFC,⊥⊥EFC=⊥C,⊥EF=EC.又⊥BD=EC,⊥EF=BD.又⊥EF//AB,⊥⊥ADM=⊥MEF.在△DBM和△EFM中BDE FEM BMD FME BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩⊥⊥DBM ⊥⊥EFM ;⊥DM =EM ;(3)解:过点E 作EF //AB 交CB 的延长线于点F ,⊥⊥DBM =⊥EFM ,⊥DMB =⊥EMF⊥⊥DBM ⊥⊥EFM ,⊥BD :EF =DM :ME ,⊥AB =AC ,⊥⊥ABC =⊥C ,⊥⊥F =⊥ABC ,⊥⊥F =⊥C ,⊥EF =EC ,⊥BD :EC =DM :ME =1:2,⊥MD =12ME . 【点睛】本题主要考查了三角形综合,涉及了等腰三角形性质和判定、全等三角形的判定与性质、相似三角形的判定和性质,利用平行构造全等三角形是解题关键.10.选择(1)(3)证明,证明见解析【解析】【分析】如图(1)延长DE 到F 使得EF=DE,证明△DCE⊥⊥FBE,得到⊥CDE=⊥F,BF=DC,结合题干条件即可得到结论;如图3,过C 点作CF⊥AB 交DE 的延长线于F,得到△ABE⊥⊥FCE,AB=FC,结合题干条件即可得到结论,【详解】如图(1)延长DE 到F 使得EF=DE在△DCE 和△FBE 中,EF DE DEC FEB BE EC =∠=∠=⎧⎪⎨⎪⎩⊥△DCE⊥⊥ FBE (SAS)⊥⊥CDE=⊥F,BF=DC⊥⊥BAE=⊥CDE⊥BF=AB⊥AB= CD如图3,过C 点作CF⊥AB 交DE 的延长线于F在△ABE 和△FCE 中B ECF BE ECBAE F ∠=∠=∠=∠⎧⎪⎨⎪⎩⊥△ABE⊥⊥ FCE(AAS),⊥AB=FC⊥⊥BAE=⊥CDE⊥⊥F=⊥CDE⊥CD=CF⊥AB=CD【点睛】此题考查全等三角形的判定与性质和等腰三角形的性质,解题关键在于利用三角形全等的性质证明。
初中数学平行线、三角形初步概念复习
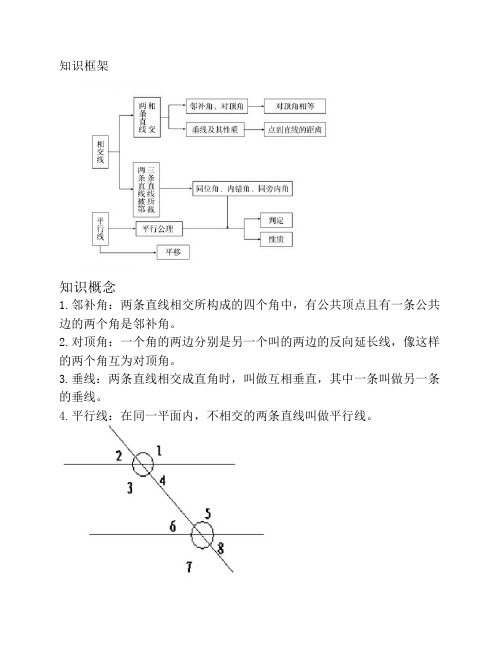
知识框架知识概念1.邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
2.对顶角:一个角的两边分别是另一个叫的两边的反向延长线,像这样的两个角互为对顶角。
3.垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线。
4.平行线:在同一平面内,不相交的两条直线叫做平行线。
5.同位角、内错角、同旁内角:同位角:∠1与∠5像这样具有相同位置关系的一对角叫做同位角。
内错角:∠2与∠6像这样的一对角叫做内错角。
同旁内角:∠2与∠5像这样的一对角叫做同旁内角。
6.命题:判断一件事情的语句叫命题。
7.定理与性质对顶角的性质:对顶角相等。
8垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
9.平行公理:经过直线外一点有且只有一条直线与已知直线平行。
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
10.平行线的性质:性质1:两直线平行,同位角相等。
性质2:两直线平行,内错角相等。
性质3:两直线平行,同旁内角互补。
11.平行线的判定:判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角相等,两直线平行。
12.平移:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移平移变换,简称平移。
平行线判定一、解答下列各题7.如图9,∠D =∠A,∠B =∠FCB,求证:ED∥CF.EBFDC图98.如图10,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由.132AECDBF图109.如图11,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。
求证:AB∥CD,MP∥NQ.F2ABCDE1PMN图11平行线性质1.如图1,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = .2.如图2,直线AB、CD被EF所截,若∠1 =∠2,则∠AEF +∠CFE = .图12431ABCDE12ABDCEF图22345ABCDFE图312ABCDEF图43.如图3所示(1)若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( ).(2)若∠2 =∠ ,则AE∥BF.(3)若∠A +∠ = 180°,则AE∥BF.4.如图4,AB∥CD,∠2 = 2∠1,则∠2 = .二、解答下列各题5.如图9,已知∠ABE +∠DEB = 180°,∠1 =∠2,求证:∠F =∠G.12ACBFGED6.如图10,DE∥BC,∠D∶∠DBC = 2∶1,∠1 =∠2,求∠DEB的度数.图1021BCED7.如图11,已知AB∥CD,试再添上一个条件,使∠1 =∠2成立.(要求给出两个以上答案,并选择其中一个加以证明)图1112ABEFDC8.如图12,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1 +∠2 = 90°.求证:(1)AB∥CD; (2)∠2 +∠3 = 90°.C图12123ABDF7.1与三角形有关的线段7.1.1三角形的边由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
江苏中考数学复习资料专题平行线与三角形

平行线与三角形复习材料一、相关知识点复习:(一)平行线1. 定义:在同一平面内,不相交的两条直线叫做平行线。
2. 判定:(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
(3)同旁内角相等,两直线平行。
(4)垂直于同一直线的两直线平行。
3•性质:(1) 经过直线外一点,有且只有一条直线与这条直线平行。
(2) 如果两条直线都与第三条直线平行,那么这两条直线平行(3) 两直线平行,同位角相等。
(4) 两直线平行,内错角相等。
(5) 两直线平行,同旁内角互补。
(二)三角形4. 一般三角形的性质(1) 角与角的关系:三个内角的和等于180°一个外角等于和它不相邻的两个内角之和,并且大于任何一个和它不相邻的内角。
(2) 边与边的关系:三角形中任两边之和大于第三边,任两边之差小于第三边。
(3) 边与角的大小对应关系:在一个三角形中,等边对等角;等角对等边。
(4) 三角形的主要线段的性质(见下表):5. 几种特殊三角形的特殊性质 (1) 等腰三角形的特殊性质:① 等腰三角形的两个底角相等;② 等腰三角形顶角的平分线、底边上的中线和底边上的高是同一条线段,这 条线段所在的直线是等腰三角形的对称轴。
(2) 等边三角形的特殊性质:① 等边三角形每个内角都等于60° ° ② 等边三角形外心、内心合一。
(3) 直角三角形的特殊性质:① 直角三角形的两个锐角互为余角; ② 直角三角形斜边上的中线等于斜边的一半;③ 勾股定理:直角三角形斜边的平方等于两直角边的平方和(其逆命题也成立);④ 直角三角形中,30°的角所对的直角边等于斜边的一半;⑤ 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
1S △ = a h ( h 是a 边上的咼)2 1 1 S △ = a b = c h(a 、b 是直角边, 2 2a 是边长)(4) 等底等高的三角形面积相等;等底的三角形面积的比等于它们的相应的高的 比;等高的三角形的面积的比等于它们的相应的底的比。
苏州市初三数学中考复习专题五三角形及其全等相似

五、三角形及其全等、相似徐国红吴中区木渎实验中学【近三年江苏省十三大市中考三角形及其全等、相似的分值与比率】(仅供参考)【课标要求】1.三角形的有关概念:(1)了解三角形有关的概念,掌握三角形的三边关系;(2)理解三角形内角和定理及推论;(3)理解三角形的角平分线、中线、高的概念及画法和性质.2.特殊三角形的性质和判定:(1)了解等腰三角形及等边三角形的有关概念,掌握其性质及判定;(2)掌握线段中垂线和角平分线的性质及判定;(3)了解直角三角形的有关概念,掌握其性质与判定;(4)掌握勾股定理与逆定理,并能用来解决有关问题.3.全等三角形:(1)理解全等三角形的定义和性质;(2)掌握三角形全等的性质与判定,熟练掌握三角形全等的证明;4.相似三角形:(1)比例线段:了解比例线段的有关概念及其性质,并会用比例的性质解决简单的问题.(2)相似图形:了解相似多边形,相似三角形的概念,掌握其性质和判定并会运用;(3)相似三角形:①了解两个三角形相似的概念,探索两个三角形相似的条件;②能利用图形的相似解决一些实际问题;③通过实例了解中心投影和平行投影,了解视点、视线及盲区的涵义;(4)位似了解位似变换和位似图形的概念,掌握并运用其性质.【课时分布】).【知识回顾】(1)三角形的概念及性质三角形的概念:由三条线段首尾顺次相接组成的图形,叫做三角形.三角形的性质:①三角形的内角和是180°;②三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于与它不相邻的任何一个内角;③三角形的任意两边之和大于第三边;三角形任意两边之差小于第三边.(2)三角形中的重要线段三角形的角平分线:三角形一个角的平分线和这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称高.三角形的中线在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.三角形的中位线①连接三角形两边中点的线段叫做三角形的中位线.②定理:三角形的中位线平行于第三边,且等于它的一半.(3)三角形的外心、内心①三角形三边的垂直平分线交于一点,这个点叫做三角形的外心,三角形的外心到三角形各顶点的距离相等.②三角形的三条角平分线交于一点,这个点叫做三角形的内心,三角形的内心到三角形三边的距离相等.(4)等腰三角形等腰三角形的有关概念及分类:①有两边相等的三角形叫等腰三角形,三边相等的三角形叫做等边三角形,也叫正三角形;②等腰三角形分为腰和底不相等的等腰三角形和腰和底相等的等腰三角形;等腰三角形的性质:①等腰三角形的两个底角相等(简称为“等边对等角”);②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”);③等腰三角形是轴对称图形.等腰三角形的判定:①有两边相等的三角形是等腰三角形;②如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”).(5)等边三角形的性质与判定等边三角形的性质:①等边三角形的内角相等,且都等于60°;②等边三角形的三条边都相等;等边三角形的判定:①三条边相等的三角形是等边三角形;②三个角相等的三角形是等边三角形;③有一个角为60°的等腰三角形是等边三角形.(6)线段的垂直平分线线段的垂直平分线概念:经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线. 线段的垂直平分线性质:线段垂直平分线上的点到这条线段两个端点的距离相等.线段的垂直平分线判定:到一条线段的两个端点距离相等的点在线段的垂直平分线上,线段的垂直平分线可以看作是到线段两端点距离相等的点的集合.(7)角平分线的性质及判定角平分线的性质:角平分线上的点到角的两边的距离相等.角平分线的判定:角的内部到角的两边距离相等的点在角的平分线上,角的平分线可以看作是到角两边距离相等的点的集合.直角三角形的性质:①直角三角形的两锐角互余; ②直角三角形中,30°角所对的边等于斜边的一半; ③直角三角形斜边上的中线等于斜边的一半;④勾股定理:直角三角形两直角边的平方和等于斜边的平方. 直角三角形的判定: ①有一个角等于90°的三角形是直角三角形; ②有两角互余的三角形是直角三角形;③如果三角形一边上的中线等于这边的一半,则该三角形是直角三角形; ④勾股定理的逆定理:如果三角形一条边的平方等于另外两条边的平方和,那么这个三角形是直角三角形.(8)全等三角形的性质与判定 全等三角形的概念:能够完全重合的两个三角形叫做全等三角形. 全等三角形的性质:全等三角形的对应边、对应角分别相等. 全等三角形的判定:①有三边对应相等的两个三角形全等,简记为(SSS);②有两边和它们的夹角对应相等的两个三角形全等,简记为(SAS); ③有两角和它们的夹边对应相等的两个三角形全等,简记为(ASA); ④有两角和其中一角的对边对应相等的两个三角形全等,简记为(AAS); ⑤有斜边和一条直角边对应相等的两个直角三角形全等,简记为(HL). (9)比例线段比例线段的概念:在四条线段a ,b ,c ,d 中,如果其中两条线段的比等于另外两条线段的比,即dc b a = (或a ∶b =c ∶d ),那么这四条线段a ,b ,c ,d 叫做成比例线段,简称比例线段. 比例线段的性质: ①基本性质:a b =cdad =bc ; ②合比性质:a b =cdddc b b a +=+; ③等比性质:若a b =c d =···=mn (b +d +···+n ≠0),那么ba n db mc a =+⋅⋅⋅+++⋅⋅⋅++.黄金分割的概念:点C 把线段AB 分成两条线段AC 和BC ,如果AC AB =BCAC ,则线段AB 被点C 黄金分割,点C 叫线段AB 的黄金分割点,AC 与AB 的比叫做黄金比. (10)相似多边形相似多边形的概念:对应角相等、对应边成比例的两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比,相似比为1的两个多边形全等. 相似多边形的性质:①相似多边形的对应角相等,对应边成比例;②相似多边形周长的比等于相似比;③相似多边形面积的比等于相似比的平方. (11)相似三角形 相似三角形概念各角对应相等,各边对应成比例的两个三角形叫做相似三角形. 相似三角形判定:① 平行于三角形一边的直线和其他两边(或两边延长线)相交,所构成的三角形与原三角形相似;②两角对应相等,两三角形相似;③两边对应成比例且夹角相等,两三角形相似; ④三边对应成比例,两三角形相似. 相似三角形性质:①相似三角形的对应角相等,对应边成比例;②相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比; ③相似三角形周长的比等于相似比;④相似三角形面积的比等于相似比的平方. (12)图形的位似 图形位似的概念:如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点,那么这两个图形叫位似图形.这个点叫做位似中心,这时的相似比称为位似比. 图形的位似性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比.3.能力要求例1 如图5-1-1,在△ABC 中,AB=AC ,点D 是BC 的中点,点E 在AD 上.(1)求证:BE=CE ;(2)如图5-1-2,若BE 的延长线交AC 于点F ,且BF ⊥AC ,垂足为F ,∠BAC =45°,原题设其它条件不变.求证:△AEF ≌△BCF . 【分析】(1)根据等腰三角形三线合一的性质可得AD 是BC 边上的垂直平分线,然后利用线段垂直平分线的性质定理,可直接证明BE=CE ;(2)先判定△ABF 为等腰直角三角形,再根据等腰直角三角形的两直角边相等可得AF=BF ,再根据同角的余角相等求出∠EAF =∠CBF ,然后利用“角边角”证明△AEF 和BCF 全等即可.【解】(1)∵AB=AC ,D 是BC 的中点,∴AD ⊥BC . ∴BE=CE .(2)∵∠BAC =45°,BF ⊥AF ,∴△ABF 为等腰直角三角形. ∴AF=BF .∵AB=AC ,点D 是BC 的中点,∴AD ⊥BC .∴∠EAF +∠C =90°. ∵BF ⊥AC ,∴∠CBF +∠C =90°.∴∠EAF =∠CBF .在△AEF 和△BCF 中,90EAF CBFAF BF AFE BFC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴△AEF ≌△BCF (ASA ).【说明】本题考查了全等三角形的判定与性质,等腰三角形三线合一的性质,线段垂直平分线的性质定理,等腰直角三角形的判定与性质,同角的余角相等的性质,是基础题,熟记和灵活运用三角形全等的判定方法与各性质是解题的关键.例2 如图5-2,四边形ABCD 中,AC 平分∠DAB ,∠ADC =∠ACB =90°,E 为AB 的中点.(1)求证:2AC =AB ·AD ;(2)求证:CE ∥AD ;(3)若AD =4,AB =6,求AC AF的值.【分析】(1)由AC 平分∠DAB ,∠ADC =∠ACB =90°,可证得△ADC ∽△ACB ,然后由相似三角形的对应边成比 例,证得2AC =AB ·AD ;(2)由E 为AB 的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE =BE =AE ,继而可证得∠DAC =∠ECA ,得到CE ∥AD ; (3)易证得△AFD ∽△CFE ,然后由相似三角形的对应边成比例,求得ACAF的值. 【解】(1)∵AC 平分∠DAB ,∴∠DAC =∠CAB . ∵∠ADC =∠ACB =90°,∴△ADC ∽△ACB . ∴AD :AC =AC :AB .∴AC 2=AB ·AD .(2)∵E 为AB 的中点,∠ACB=90°∴CE =12AB =AE .∴∠EAC =∠ECA . ∵∠DAC =∠CAB ,∴∠DAC =∠ECA .∴CE ∥AD . (3)∵CE ∥AD ,∴△AFD ∽△CFE .∴AD :CE =AF :CF . ∵CE =12AB ,∴CE =12×6=3. ∵AD =4,∴43AF CF =.∴74AC AF =. 【说明】此题考查了相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质.相似三角形相似的判定方法有:(1)平行于三角形的一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.其基本图形可分别记为“A ”型和“X ”型,在应用时要善于从复杂的图形中抽象出这些基本图形;(2) 两角对应相等,两三角形相似,此种判定方法最为常用,应熟练掌握; (3) 两边对应成比例且夹角相等,两三角形相似; (4) 三边对应成比例,两三角形相似.例3 如图5-3,在Rt △ABC 中,∠C =90°,点P 为AC 边上的一点,将线段AP 绕点A 顺时针方向旋转(点P 对应点P ′),当AP 旋转至AP ′⊥AB 时,点B ,P ,P ′恰好在同一直线上,此时作P ′E ⊥AC 于点E .(1)求证:∠CBP =∠ABP ;(2)求证:AE =CP ; (3)当32CP PE =,BP ′=AB 的长【分析】(1)根据旋转的性质可得AP=AP′,根据等边对等角的性质可得∠APP′=∠AP′P ,再根据等角的余角相等证明即可;(2)过点P 作PD ⊥AB 于D ,根据角平分线上的点到角的两边的距离相等可得CP=DP ,然后求出∠P AD=∠AP′E ,从而证明△APD 和△P′AE 全等,根据全等三角形对应边相等可得AE=DP ,从而得证; (3)设CP=3k ,PE=2k ,表示出AE=CP=3k ,AP ′=AP=5k ,然后利用勾股定理列式求出P ′E=4k ,再证明△ABP ′和△EPP ′相似,根据相似三角形对应边成比例列式求出P ′A=12AB ,然后在Rt △ABP ′中,利用勾股定理列式求解即可. 【解】(1)∵AP′是AP 旋转得到,∴AP=AP ′. ∴∠APP′=∠AP′P . ∵∠C =90°,AP′⊥AB , ∴∠CBP +∠BPC =90°,∠ABP +∠AP′P 又∵∠BPC =∠APP′,∴∠CBP =∠ABP . (2)如图5-3-1,过点P 作PD ⊥AB 于D . ∵∠CBP =∠ABP ,∠C =90°,∴CP=DP , ∵P′E ⊥AC ,∴∠EAP′+∠AP′E =90°. 又∵∠P AD +∠EAP′=90°,∴∠P AD =∠在△APD 和△P′AE 中,'''PAD AP EADP P EA AP AP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△APD ≌△P′AE (AAS ). ∴AE=DP . ∴AE=CP . (3)∵32CP PE =,∴设CP =3k ,PE =2k ,则AE=CP =3k ,AP ′=AP =3k +2k =5k . 在Rt △AEP′中,P′E 4k =,∵∠C =90°,P′E ⊥AC ,∴∠CBP +∠BPC =90°,∠EP′P +∠P′PE =90°, ∵∠BPC =∠EPP′(对顶角相等), ∴∠CBP =∠PP′E .∵∠CBP =∠ABP ,∴∠ABP =∠PP′E . 又∵∠BAP′=∠P′EP =90°,∴△ABP′∽△EPP′. ∴''AB P A P E PE =,即'42AB P A k k =,解得P′A =12AB . 在Rt △ABP′中,AB 2+P′A 2=BP′2,即AB 2+14AB 2=(2,解得AB =10. 【说明】本题考查了全等三角形的判定与性质,旋转的性质,角平分线的性质定理,勾股定理,相似三角形的判定与性质,在解题中可以发现,图形的全等或相似往往不是解决问题的最终目的,而是一种手段和途径,体现了图形的全等和相似的“工具性”.类似于本题这种“一题多问”的出题形式,应注意上下题之间的内在联系,把握住这种联系,就容易找到解题的突破口.如本题中较难的第(3)小题,利用(2)中的结论能很快的表示出AP′的长度,结合已知条件BP′=55,就容易想到用k 来表示出AB 的长度,最后利用勾股定理得出关于k 的方程,从而解决问题.例4 如图5-4,已知AB ⊥BD ,CD ⊥BD .(1)若AB =9,CD =4,BD =15,请问在BD 上是否存在P 点,使以P ,A ,B 三点为顶点的三角形与以P ,C ,D 三点为顶点的三角形相似?若存在,则有多少个这样的P 点,并求BP 的长;若不存在,请说明理由;(2) 若AB =m ,CD =n ,BD = l ,请问在m ,n ,l 满足什么关系时,存在以P ,A ,B 三点为顶点的三角形与以P ,C ,D 三点为顶点的三角形相似的一个P 点?【分析】 由于问题中没有明确两个直角三角形的对应关系,因此每 小问应按两种对应关系来说明.【解】(1)设BP =x ,则DP =15−x . 若△ABP ∽△CDP ,则AB BP CD DP =,即9415x x=-,解得13513x =. 若△ABP ∽△PDC ,则AB BP PD CD =,即9154x x =-,得方程:212360x x -+=.解得x =3或12. 所以BP =13513,3或12. (2)设BP =x ,则DP =l −x . 若△ABP ∽△CDP ,则AB BPCD DP =,即m n x l x =-,解得ml x m n =+. 若△ABP ∽△PDC ,则AB BP PD CD =,即m xl x n=-.得方程:20x lx mn -+=,24l mn ∆=-.当240l mn ∆=-<时,存在以P 、A 、B 三点为顶点的三角形与以P 、C 、D 三点为顶点的三角形相似的一个P 点;当240l mn ∆=-=时,存在以P 、A 、B 三点为顶点的三角形与以P 、C 、D 三点为顶点的三角形相似的两个P 点;当240l mn ∆=->时,存在以P 、A 、B 三点为顶点的三角形与以P 、C 、D 三点为顶点的三角形相似的三个P 点. 【说明】三角形相似如果没有明确对应关系,需要分情形来讨论,这个知识点也是相似问题中常考内容之一,要会利用图形中的已知条件来排除不必要的分类情况.由于本题是两个直角三角形,所以对应关系有两种.由于数量关系的制约,本题有一种对应关系是始终存在的,另一种对应关系则需要通过一元二次方程的判别式来进行讨论.解题时注意数形结合、分类讨论、方程思想的应用.例5 如图5-5-1,矩形ABCD 中,∠ACB =30°,将一块直角三角板的直角顶点P 放在两对角线AC ,BD 的交点处,以点P 为旋转中心转动三角板,并保证三角板的两直角边分别于边AB ,BC 所在的直线相交,交点分别为E ,F .(1)当PE ⊥AB ,PF ⊥BC 时,如图5-5-1,则PEPF的值为 ; (2)现将三角板绕点P 逆时针旋转α(0°<α<60°)角,如图5-5-2,求PEPF的值; (3)在(2)的基础上继续旋转,当60°<α<90°,且使AP :PC =1:2时,如图5-5-3,PEPF的值是否变化?证明你的结论.(1)证明△APE ≌△PCF ,得PE=CF ;在Rt △PCF 中,解直角三角形求得PF的值; (2)如图5-5-4所示,作辅助线,构造直角三角形,证明△PME ∽△PNF ,并利用(1)的结论,求得PEPF的值; (3)如图5-5-5所示,作辅助线,构造直角三角形,首先证明△APM ∽△PCN ,求得PMPN的值;然后证明△PME ∽△PNF ,从而由PE PM PF PN =求得PE PF 的值.与(1)、(2)问相比较,PEPF的值发生了变化. 【解】(1)∵矩形ABCD ,∴AB ⊥BC ,P A=PC .∵PE ⊥AB ,BC ⊥AB ,∴PE ∥BC .∴∠APE =∠PCF .∵PF ⊥BC ,AB ⊥BC ,∴PF ∥AB . ∴∠P AE =∠CPF . ∵在△APE 与△PCF 中,PAE CPF PA PC APE PCF ∠=∠⎧⎪=⎨⎪∠=∠⎩.∴△APE ≌△PCF (ASA ),∴PE=CF .在Rt △PCF 中,PF PF CF PE ==t a n 30°,∴PEPF(2)如图5-5-4,过点P 作PM ⊥AB 于点M ,PN ⊥BC 于点N ,则PM ⊥PN . ∵PM ⊥PN ,PE ⊥PF ,∴∠EPM=∠FPN .又∵∠PME =∠PNF =90°,∴△PME ∽△PNF .∴PE PM PF PN=. 由(1)知,PM PN∴PEPF(3)答:变化.如图5-5-5,过点P 作PM ⊥AB 于点M ,PN ⊥BC 于点N ,则PM ⊥PN ,PM ∥BC ,PN ∥AB . ∵PM ∥BC ,PN ∥AB ,∴∠APM =∠PCN ,∠P AM=∠CPN . ∴△APM ∽△PCN . ∴21==PC AP CN PM ,得CN =2PM . 在Rt △PCN 中,2PN PN CN PM ==t a n 30°,∴PMPN. ∵PM ⊥PN ,PE ⊥PF , ∴∠EPM =∠FPN . 又∵∠PME =∠PNF =90°,∴△PME ∽△PNF .∴PE PM PF PN ==. ∴PEPF 的值发生变化. 【说明】本题考查了相似三角形的判定与性质、矩形的性质、全等三角形的判定与性质、解直角三角形等知识点.本题三问的解题思路是一致的:都是通过直接作辅助线构造直角三角形,通过相似三角形或全等三角形转化为题(1)或类似于题(1)的问题,从而解决.对于此类从特殊到一般的思路设置问题情境的综合题,解题的思路往往是将一般情况转化为特殊情况来解决.因此,在分析和解决此类问题的过程中要善于从特殊情况中总结和归纳出解题的基本思路和方法,并应用于一般情形.要特别注意从特殊到一般和化归思想的应用.例6 如图5-6,在△ABC 中,∠B =45°,BC =5,高AD =4,矩形EFPQ 的一边QP 在BC 边上,E 、F 分别在AB 、AC 上,AD 交EF 于点H .(1)求证:AH EFAD BC=; (2)设EF=x ,当x 为何值时,矩形EFPQ 的面积最大?并求出最大面积;(3)当矩形EFPQ 的面积最大时,该矩形EFPQ 以每秒1个单位的速度沿射线DA 匀速向上运动(当矩形的边PQ 到达A 点时停止运动),设运动时间为t 秒,矩形EFPQ 与△ABC 重叠部分的面积为S ,求S 与t 的函数关系式,并写出t 的取值范围. 【分析】(1)由相似三角形,列出比例关系式,即可证明,或利用相似三角形对应高的比等于相似比也可解决;(2)首先求出矩形EFPQ 面积的表达式,然后利用二次函数求其最大面积; (3)本问是运动型问题,要点是弄清矩形EFPQ 的运动过程:(I)当0≤t ≤2时,如图5-7-1所示,此时重叠部分是一个矩形和一个梯形; (II)当2<t ≤4时,如图5-7-2所示,此时重叠部分是一个三角形. 【解】(1)∵矩形EFPQ ,∴EF ∥B C ,∴△AHF ∽△ADC . ∴AH AFAD AC=. ∵EF ∥BC ,∴△AEF ∽△ABC . ∴EF AF BC AC=. ∴AH EFAD BC =. (2)∵∠B =45°,∴BD=AD =4. ∴CD =BC −BD =5−4=1. ∵EF ∥BC ,∴△AEH ∽△ABD . ∴AH EHAD BD=. ∵EF ∥BC ,∴△AFH ∽△ACD . ∴AH HFAD CD=. ∴EH HF BD CD =,即41EH HF=. ∴EH=4HF . 已知EF=x ,则EH=45x . ∵∠B =45︒,∴EQ=BQ=BD −QD =BD −EH =4−45x . ∴S 矩形EFPQ =EF ·EQ =x ·(4−45x )=−45x 2+4x =−45(x −52)2+5. ∴当x=52时,矩形EFPQ 的面积最大,最大面积为5. (3)解:由(2)可知,当矩形EFPQ 的面积最大时,矩形的长为52,宽为4−45×52=2. (I)当0≤t ≤2时,如图5-5-1所示.设矩形与AB 、AC 分别交于点K 、N ,与AD 分别交于点H 1,D 1. 此时DD 1=t ,H 1D 1=2,∴HD 1=HD -DD 1=2-t ,HH 1=H 1D 1-HD 1=t ,AH 1=∵KN ∥EF ,∴1AH KN EF AH =,即2522KN t -=,得KN =54S =S 梯形KNFE +S 矩形EFP 1Q 1=12(KN +EF )·HH 1+E F ·EQ 1=12 [54(2−t )+52]×t +52(2−t )=258t -+5. 图5-6-1(II)当2<t ≤4时,如图5-5-2所示.设矩形与AB 、AC 分别交于点K 、N ,与AD 交于点D此时DD 2=t ,AD 2=AD -DD 2=4-t , ∵KN ∥EF ,∴2AD KN EF AH =,即4522KN t -=,得KN =5S =S △AKN =12K N ·AD 2 =12 (5-54t )(4-t )=58t 2-5t +10.综上所述,S 与t 的函数关系式为:S =2255(085510(24)8t t t t t ⎧-+≤⎪⎪⎨⎪-+<≤⎪⎩.【说明】本题是相似三角形的判定和性质与二次函数的最值相结合的综合题.本题的(1)、(2)两小题改编自教材中的习题,因此在复习过程中,要注意教材中典型问题和基本图形的复习、归纳和延伸.第(3)小题这类题要注意自变量的取值范围.对于图形运动的问题,往往需要将图形的运动转换到图形的线段长度上,实现这一转换的主要途径常是通过图形的相似来实现.【复习建议】 1.三角形的全等、相似是平面几何中的重要的内容,在中考中不论是基础题还是压轴题往往都要涉及到全等或相似的有关知识.事实上,许多中考题在教材中都能找到它的“源头”,有鉴于此,在进行复习时,应以教材为“纲”,紧扣教材.重视双基训练.要掌握典型的例题、习题,能对典型试题进行拆分和组合,引导学生学会从多角度、多侧面来分析解决典型试题,从中抽离出基本图形和基本规律方法;要结合三角形全等和相似的特点进行专项有针对性的训练,加大知识的横向与纵向联系,提高答题速度和质量,提高应变能力.要指导学生掌握解题方法,对例题、习题能举一反三,达到触类旁通; 2.复习时要注意总结和归纳例题、习题中所体现的数学思想和方法,重视解题方法和解题策略的教学.涉及三角形全等、相似的问题中常用到的数学思想方法有:化归思想、函数与方程思想、数形结合思想、分类讨论思想等,这些思想方法在中考试题中都有体现.要注重培养学生用数学思想方法解决问题的意识,引导学生审题时要透过现象看本质,注意隐含条件的挖掘,学会将实际问题转化为数学问题,建立数学模型,从而解决问题; 3.复习中要重视数学逻辑推理能力的训练和书写规范的训练,要及时纠正学生在解题时,出现的答题不规范,抓不住得分要点,思维不严谨等问题.避免学生出现题题会做,题题被扣分的现象.。
2022年中考数学真题-专题11 平行线与三角形(1)(全国通用解析版)

专题11 平行线与三角形一.选择题(2022·湖北宜昌·中考真题)1. 如图,在ABC 中,分别以点B 和点C 为圆心,大于12BC 长为半径画弧,两弧相交于点M ,N .作直线MN ,交AC 于点D ,交BC 于点E ,连接BD .若7AB =,12AC =,6BC =,则ABD △的周长为( )A. 25B. 22C. 19D. 18【答案】C【解析】 【分析】由垂直平分线的性质可得BD =CD ,由△ABD 的周长=AB +AD +BD =AB +AD +CD =AB +AC 得到答案.【详解】解:由作图的过程可知,DE 是BC 的垂直平分线,∴BD =CD ,∵7AB =,12AC =,∴ △ABD 的周长=AB +AD +BD=AB +AD +CD=AB +AC=19.故选:C【点睛】此题考查了线段垂直平分线的作图、线段垂直平分线的性质、三角形的周长等知识,熟练掌握线段垂直平分线的性质是解题的关键.(2022·浙江台州·中考真题)2. 如图,点D 在ABC 的边BC 上,点P 在射线AD 上(不与点A ,D 重合),连接PB ,PC .下列命题中,假命题是( )A. 若AB AC =,AD BC ⊥,则PB PC =B. 若PB PC =,AD BC ⊥,则AB AC =C. 若AB AC =,12∠=∠,则PB PC =D. 若PB PC =,12∠=∠,则AB AC =【答案】D【解析】【分析】根据等腰三角形三线合一的性质证明PD 是否是BC 的垂直平分线,判断即可.【详解】因为AB=AC ,且AD ⊥BC ,得AP 是BC 的垂直平分线,所以PB=PC ,则A 是真命题;因为PB=PC ,且AD ⊥BC ,得AP 是BC 的垂直平分线,所以AB=AC ,则B 是真命题;因为AB=AC ,且∠1=∠2,得AP 是BC 的垂直平分线,所以PB=PC ,则C 是真命题;因为PB=PC ,△BCP 是等腰三角形,∠1=∠2,不能判断AP 是BC 的垂直平分线,所以AB 和AC 不一定相等,则D 是假命题.故选:D .【点睛】本题主要考查了等腰三角形的性质和判定,掌握性质定理是解题的关键. (2022·江苏宿迁·中考真题)3. 若等腰三角形的两边长分别是3cm 和5cm ,则这个等腰三角形的周长是( )A. 8cmB. 13cmC. 8cm 或13cmD. 11cm 或13cm 【答案】D【解析】【分析】题目给出等腰三角形有两条边长为3和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【详解】解:当3是腰时,∵3+3>5,∴3,3,5能组成三角形,此时等腰三角形的周长为3+3+5=11(cm),当5是腰时,∵3+5>5,5,5,3能够组成三角形,此时等腰三角形的周长为5+5+3=13(cm),则三角形的周长为11cm或13cm.故选:D【点睛】本题考查等腰三角形的性质及三角形三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.(2022·浙江杭州·中考真题)4. 如图,CD⊥AB于点D,已知∠ABC是钝角,则()A. 线段CD是ABC的AC边上的高线B. 线段CD是ABC的AB边上的高线C. 线段AD是ABC的BC边上的高线D. 线段AD是ABC的AC边上的高线【答案】B【解析】【分析】根据高线的定义注意判断即可.【详解】∵线段CD是ABC的AB边上的高线,∴A错误,不符合题意;∵线段CD是ABC的AB边上的高线,∴B正确,符合题意;∵线段AD是ACD的CD边上的高线,∴C错误,不符合题意;∵线段AD是ACD的CD边上的高线,∴D错误,不符合题意;故选B.【点睛】本题考查了三角形高线的理解,熟练掌握三角形高线的相关知识是解题的关键.(2022·湖南邵阳·中考真题)5. 下列长度的三条线段能首尾相接构成三角形的是()A. 1cm,2cm,3cmB. 3cm,4cm,5cmC. 4cm,5cm,10cmD. 6cm,9cm,2cm【答案】B【解析】【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【详解】解:根据三角形的三边关系,知A、1+2=3,不能组成三角形,故选项错误,不符合题意;B、3+4>5,能够组成三角形,故选项正确,符合题意;C、5+4<10,不能组成三角形,故选项错误,不符合题意;D、2+6<9,不能组成三角形,故选项错误,不符合题意;故选:B.【点睛】此题考查了三角形的三边关系.解题的关键是看较小的两个数的和是否大于第三个数.(2022·云南·中考真题)6. 如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF若添加下列条件中的某一个.就能使DOE FOE,你认为要添加的那个条件是()A. OD =OEB. OE =OFC. ∠ODE =∠OEDD. ∠ODE =∠OFE【答案】D【解析】【分析】根据OB 平分∠AOC 得∠AOB =∠BOC ,又因为OE 是公共边,根据全等三角形的判断即可得出结果.【详解】解:∵OB 平分∠AOC∴∠AOB =∠BOC当△DOE ≌△FOE 时,可得以下结论:OD =OF ,DE =EF ,∠ODE =∠OFE ,∠OED =∠OEF .A 答案中OD 与OE 不是△DOE ≌△FOE 的对应边,A 不正确;B 答案中OE 与OF 不是△DOE ≌△FOE 的对应边,B 不正确;C 答案中,∠ODE 与∠OED 不是△DOE ≌△FOE 的对应角,C 不正确; D 答案中,若∠ODE =∠OFE ,在△DOE 和△FOE 中, DOE FOE OE OEODE OFE =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△DOE ≌△FOE (AAS )∴D 答案正确.故选:D .【点睛】本题考查三角形全等的判断,理解全等图形中边和角的对应关系是解题的关键.(2022·浙江湖州·中考真题)7. 如图,已知在锐角△ABC 中,AB =AC ,AD 是△ABC 的角平分线,E 是AD 上一点,连结EB ,E C .若∠EBC =45°,BC =6,则△EBC 的面积是( )A. 12B. 9C. 6D. 【答案】B【解析】【分析】根据三线合一可得ED BC ⊥,根据垂直平分线的性质可得EB EC =,进而根据∠EBC =45°,可得BEC △为等腰直角三角形,根据斜边上的中线等于斜边的一半可得132DE BC ==,然后根据三角形面积公式即可求解. 【详解】解: AB =AC ,AD 是△ABC 的角平分线,,AD BD BD DC ∴⊥=,EB EC ∴=,∠EBC =45°,45ECB EBC ∠=∠=︒,∴BEC △为等腰直角三角形,6BC =, ∴132DE BC ==, 则△EBC 的面积是13692⨯⨯=.故选B .【点睛】本题考查了等腰三角形的性质与判定,垂直平分线的性质,直角三角形中斜边上的中线等于斜边的一半,掌握等腰三角形的性质与判定是解题的关键. (2022·江苏扬州·中考真题)8. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为ABC ∆,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )A. ,,AB BC CAB. ,,AB BC B ∠C. ,,AB AC B ∠D. ,,∠∠A B BC【答案】C【解析】 【分析】根据SSS ,SAS ,ASA 逐一判定,其中SSA 不一定符合要求.【详解】A. ,,AB BC CA .根据SSS 一定符合要求;B. ,,AB BC B ∠.根据SAS 一定符合要求;C. ,,AB AC B ∠.不一定符合要求;D. ,,∠∠A B BC .根据ASA 一定符合要求.故选:C .【点睛】本题考查了三角形全等的判定,解决问题的关键是熟练掌握判定三角形全等的SSS ,SAS ,ASA 三个判定定理.(2022·山东泰安·中考真题)9. 如图,30AOB ∠=︒,点M 、N 分别在边OA OB 、上,且3,5OM ON ==,点P 、Q 分别在边OB OA 、上,则MP PQ QN ++的最小值是( )A. 2- 2-【答案】A【解析】 【分析】作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,连接M ′N ′,即为MP +PQ +QN 的最小值;证出△ONN ′为等边三角形,△OMM ′为等边三角形,得出∠N ′OM ′=90°,由勾股定理求出M ′N ′即可.【详解】解:作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,如图所示:连接M ′N ′,即为MP +PQ +QN 的最小值.根据轴对称的定义可知:5ON ON '==,3OM OM '==,∠N ′OQ =∠M ′OB =30°, ∴∠NON ′=60°,'60MOM ∠=︒,∴△ONN ′为等边三角形,△OMM ′为等边三角形,∴∠N ′OM ′=90°,∴在Rt △M ′ON ′中,M ′N=故选:A .【点睛】本题考查了轴对称--最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.(2022·浙江金华·中考真题)10. 如图,AC 与BD 相交于点O ,,OA OD OB OC ==,不添加辅助线,判定ABO DCO △≌△的依据是( )A. SSSB. SASC. AASD. HL【答案】B【解析】 【分析】根据OA OD =,OB OC =,AOB COD ∠=∠正好是两边一夹角,即可得出答案.【详解】解:∵在△ABO 和△DCO 中,OA OD AOB COD OB OC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABO DCO ≌△△,故B 正确. 故选:B .【点睛】本题主要考查了全等三角形的判定,熟练掌握两边对应相等,且其夹角也对应相等的两个三角形全等,是解题的关键.(2022·浙江金华·中考真题)11. 已知三角形的两边长分别为5cm 和8cm ,则第三边的长可以是( )A. 2cmB. 3cmC. 6cmD. 13cm【答案】C【解析】【分析】先确定第三边的取值范围,后根据选项计算选择.【详解】设第三边的长为x ,∵ 角形的两边长分别为5cm 和8cm ,∴3cm <x <13cm ,故选C .【点睛】本题考查了三角形三边关系定理,熟练确定第三边的范围是解题的关键. (2022·安徽·中考真题) 12. 已知点O 是边长为6的等边△ABC 的中心,点P 在△ABC 外,△ABC ,△P AB ,△PBC ,△PCA 的面积分别记为0S ,1S ,2S ,3S .若12302S S S S ++=,则线段OP 长的最小值是( )A. 2C.【答案】B【解析】【分析】根据12302S S S S ++=,可得1012S S =,根据等边三角形的性质可求得△ABC 中AB 边上的高1h 和△P AB 中AB 边上的高2h 的值,当P 在CO 的延长线时,OP 取得最小值,OP =CP -OC ,过O 作OE ⊥BC ,求得OC =【详解】解:如图,2PDB BDC S S S ,3PDA ADC S S S , ∴1231()()PDB BDC PDA ADC S S S S SS S S ++=++++ =1()()PDB PDA BDC ADC S SS S S ++++ =1PAB ABC S S S ++=110S S S ++=102S S +=02S , ∴1012S S =, 设△ABC 中AB 边上的高为1h ,△P AB 中AB 边上的高为2h , 则0111116322S AB h h h ,1222116322S AB h h h , ∴211332h h ,∴122h h =,∵△ABC 是等边三角形, ∴22166()332h , 2113322h h ,∴点P 在平行于AB ,且到AB ∴当点P 在CO 的延长线上时,OP 取得最小值,过O 作OE ⊥BC 于E , ∴12932CP h h , ∵O 是等边△ABC 的中心,OE ⊥BC ∴∠OCE =30°,CE =132BC = ∴OC =2OE∵222OE CE OC +=,∴2223(2)OE OE ,解得OE∴OC =∴OP =CP -OC 52332. 故选B .【点睛】本题考查了等边三角形的性质,勾股定理,三角形的面积等知识,弄清题意,找到P 点的位置是解题的关键.(2022·四川南充·中考真题) 13. 如图,在Rt ABC 中,90,C BAC ∠=︒∠的平分线交BC 于点D ,DE //AB ,交AC 于点E ,DF AB ⊥于点F ,5,3DE DF ==,则下列结论错误的是( )A. 1BF =B. 3DC =C. 5AE =D. 9AC =【答案】A【解析】 【分析】根据角平分线的性质得到CD =DF =3,故B 正确;根据平行线的性质及角平分线得到AE =DE =5,故C 正确;由此判断D 正确;再证明△BDF ≌△DEC ,求出BF =CD =3,故A 错误.【详解】解:在Rt ABC 中,90,C BAC ∠=︒∠的平分线交BC 于点D ,DF AB ⊥,∴CD =DF =3,故B 正确;∵DE =5,△CE =4,∵DE //AB ,∴∠ADE =∠DAF ,∵∠CAD =∠BAD ,∴∠CAD =∠ADE ,∴AE =DE =5,故C 正确;∴AC =AE +CE =9,故D 正确;∵∠B =∠CDE ,∠BFD =∠C =90°,CD =DF ,∴△BDF ≌△DEC ,∴BF =CD =3,故A 错误;故选:A .【点睛】此题考查了角平分线的性质定理,平行线的性质,等边对等角证明角相等,全等三角形的判定及性质,熟记各知识点并综合应用是解题的关键. (2022·四川德阳·中考真题)14. 八一中学校九年级2班学生杨冲家和李锐家到学校的直线距离分别是5km 和3km .那么杨冲,李锐两家的直线距离不可能...是( ) A. 1kmB. 2kmC. 3kmD. 8km【答案】A【解析】【分析】利用构成三角形的条件即可进行解答.【详解】以杨冲家、李锐家以及学校这三点来构造三角形,设杨冲家与李锐家的直线距离为a ,则根据题意有:5-353a +<<,即28a <<,当杨冲家、李锐家以及学校这三点共线时,538a =+=或者532a =-=, 综上a 的取值范围为:28a ≤≤,据此可知杨冲家、李锐家的距离不可能是1km ,故选:A .【点睛】本题考查了构成三角形的条件的知识,构成三角的条件:三角形中任意的两边之和大于第三边,任意的两边之差小于第三边.(2022·山东泰安·中考真题) 15. 如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =( )A. 40°B. 45°C. 50°D. 60°【答案】C【解析】 【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠F AP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC =∠ACD ﹣∠ABC =2x °﹣(x °﹣40°)﹣(x °﹣40°)=80°,∴∠CAF =100°,在Rt △PF A 和Rt △PMA 中,{PA PAPM PF ==,∴Rt △PF A ≌Rt △PMA (HL ),∴∠F AP =∠P AC =50°.故选C .【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM =PN =PF 是解题的关键.(2022·浙江绍兴·中考真题)16. 如图,把一块三角板ABC 的直角顶点B 放在直线EF 上,30C ∠=︒,AC ∥EF ,则1∠=( )A. 30°B. 45°C. 60°D. 75°【答案】C【解析】【分析】根据三角板的角度,可得60A ∠=︒,根据平行线的性质即可求解. 【详解】解:30C ∠=︒,9060A C ∴∠=︒-∠=︒AC ∥EF ,160A ∴∠=∠=︒故选C【点睛】本题考查了平行线的性质,掌握平行线的性质是解题的关键. (2022·安徽·中考真题)17. 两个矩形的位置如图所示,若1∠=α,则2∠=( )A. 90α-︒B. 45α-︒C. 180α︒-D. 270α︒-【答案】C【解析】 【分析】用三角形外角性质得到∠3=∠1-90°=α-90°,用余角的定义得到∠2=90°-∠3=180°-α.【详解】解:如图,∠3=∠1-90°=α-90°,∠2=90°-∠3=180°-α.故选:C .【点睛】 本题主要考查了矩形,三角形外角,余角,解决问题的关键是熟练掌握矩形的角的性质,三角形的外角性质,互为余角的定义.(2022·浙江杭州·中考真题)18. 如图,已知AB CD ∥,点E 在线段AD 上(不与点A ,点D 重合),连接CE .若∠C =20°,∠AEC =50°,则∠A =( )A. 10°B. 20°C. 30°D. 40°【答案】C【解析】 【分析】根据三角形外角的性质、平行线的性质进行求解即可;【详解】解:∵∠C +∠D =∠AEC ,∴∠D =∠AEC -∠C =50°-20°=30°,∵AB CD ∥,∴∠A =∠D=30°,故选:C .【点睛】本题主要考查三角形外角的性质、平行线的性质,掌握相关性质并灵活应用是解题的关键.(2022·湖南娄底·中考真题)19. 一条古称在称物时的状态如图所示,已知180∠=︒,则2∠=( )A. 20︒B. 80︒C. 100︒D. 120︒【答案】C【解析】【分析】如图,由平行线的性质可得80,BCD ∠=︒ 从而可得答案.【详解】解:如图,由题意可得:,AB CD ∥ 180∠=︒,180,BCD218080100,故选C 【点睛】本题考查的是平行线的性质,邻补角的含义,掌握“两直线平行,内错角相等”是解本题的关键.(2022·江苏苏州·中考真题)20. 如图,直线AB 与CD 相交于点O ,75AOC ∠=︒,125∠=︒,则2∠的度数是( )A. 25°B. 30°C. 40°D. 50°【答案】D【解析】【分析】根据对顶角相等可得75BOD ∠=︒,之后根据125∠=︒,即可求出2∠.【详解】解:由题可知75BOD AOC ∠=∠=︒,125∠=︒∵,217525BOD ∴∠=∠-∠=︒-︒=50︒.故选:D .【点睛】本题主要考查对顶角和角的和与差,掌握对顶角相等是解决问题的关键.二.填空题(2022·湖南株洲·中考真题)21. 如图所示,点O 在一块直角三角板ABC 上(其中30ABC ∠=︒),OM AB ⊥于点M ,ON BC ⊥于点N ,若OM ON =,则ABO ∠=_________度.【答案】15【解析】【分析】根据ON BC ⊥,OM AB ⊥,OM ON =判断OB 是ABC ∠的角平分线,即可求解.【详解】解:由题意,ON BC ⊥,OM AB ⊥,OM ON =,即点O 到BC 、AB 的距离相等,△ OB 是ABC ∠的角平分线,△ 30ABC ∠=︒, △1152ABO ABC ∠=∠=︒. 故答案为:15.【点睛】本题考查角平分线的定义及判定,熟练掌握“到一个角的两边距离相等的点在这个角的平分线上”是解题的关键.(2022·浙江嘉兴·中考真题)22. 小曹同学复习时将几种三角形的关系整理如图,请帮他在横线上____填上一个适当的条件.【答案】60A ∠=︒(答案不唯一)【解析】【分析】利用等边三角形的判定定理即可求解.【详解】解:添加60A ∠=︒,理由如下: ABC 为等腰三角形,180602A B C ︒-∠∴∠=∠==︒, ABC ∴为等边三角形,故答案为:60A ∠=︒(答案不唯一).【点睛】本题考查了等边三角形的判断,解题的关键是掌握三角形的判断定理. (2022·浙江绍兴·中考真题)23. 如图,在ABC 中,40ABC ∠=︒,80BAC ∠=︒,以点A 为圆心,AC 长为半径作弧,交射线BA 于点D ,连接CD ,则BCD ∠的度数是______.【答案】10°或100°【解析】【分析】分两种情况画图,由作图可知得AC AD =,根据等腰三角形的性质和三角形内角和定理解答即可.【详解】解:如图,点D 即为所求;在ABC ∆中,40ABC ∠=︒,80BAC ∠=︒,180408060ACB ∴∠=︒-︒-︒=︒,由作图可知:AC AD =,1(18080)502ACD ADC ∴∠=∠=︒-︒=︒, 605010BCD ACB ACD ∴∠=∠-∠=︒-︒=︒;由作图可知:AC AD =',ACD AD C ∴∠'=∠',80ACD AD C BAC ∠'+∠'=∠=︒,40AD C ∴∠'=︒,1801804040100BCD ABC AD C ∴∠'=︒-∠-∠'=︒-︒-︒=︒.综上所述:BCD ∠的度数是10︒或100︒.故答案为:10︒或100︒.【点睛】本题考查了作图-复杂作图,三角形内角和定理,等腰三角形的判定与性质,解题的关键是掌握基本作图方法.(2022·云南·中考真题)24. 已知△ABC 是等腰三角形.若∠A =40°,则△ABC 的顶角度数是____.【答案】40°或100°【解析】【分析】分∠A 为三角形顶角或底角两种情况讨论,即可求解.【详解】解:当∠A 为三角形顶角时,则△ABC 的顶角度数是40°;当∠A 为三角形底角时,则△ABC 的顶角度数是180°-40°-40°=100°;故答案为:40°或100°.【点睛】本题考查了等腰三角形的性质,此类题目,难点在于要分情况讨论. (2022·山东滨州·中考真题)25. 如图,屋顶钢架外框是等腰三角形,其中AB AC =,立柱AD BC ⊥,且顶角120BAC ∠=︒,则C ∠的大小为_______.【答案】30°##30度【解析】【分析】先由等边对等角得到B C ∠=∠,再根据三角形的内角和进行求解即可.【详解】AB AC =,B C ∴∠=∠,120BAC ∠=︒,180BAC B C ∠+∠+∠=︒,180120302C ︒-︒∴∠==︒, 故答案为:30°.【点睛】本题考查了等腰三角形的性质及三角形的内角和定理,熟练掌握知识点是解题的关键.(2022·山东泰安·中考真题)26. 如图,△ ABC 中,∠BAC =90°,AB =3,AC =4,点 D 是 BC 的中点,将△ ABD 沿 AD 翻折得到△ AED ,连 CE ,则线段 CE 的长等于_____【答案】75【解析】【详解】如图,过点A 作AH △BC 于点H ,连接BE 交AD 于点O △△△ABC 中,△BAC =90°△AB =3△AC =4,点D 是BC 的中点,△BC 5=△AD =BD =2.5△ △12BC ·AH =12AC ·AB △即2.5AH =6△△AH =2.4△由折叠的性质可知,AE =AB △DE =DB =DC △△AD 是BE 的垂直平分线,△BCE 是直角三角形,△S △ADB =12AD ·OB =12BD ·AH △△OB =AH =2.4△△BE =4.8△△CE 75=. 故答案为△75. 【点睛】本题的解题要点有△△1△读懂题意,画出符合要求的图形;(2)作AH △BC 于点H ,连接BE 交AD 于点O ,利用面积法求出AH 和OB 的长;(3)一个三角形中,若一边上的中线等于这边的一半,则这边所对的角是直角. (2022·湖北武汉·中考真题)27. 如图,沿AB 方向架桥修路,为加快施工进度,在直线AB 上湖的另一边的D 处同时施工.取150ABC ∠=︒,1600m BC =,105BCD ∠=︒,则C ,D 两点的距离是_________m .【答案】【解析】【分析】如图所示:过点C 作CE BD ⊥于点E ,先求出800m CE =,再根据勾股定理即可求出CD 的长.【详解】如图所示:过点C 作CE BD ⊥于点E ,则∠BEC =∠DEC =90°, 150ABC ∠=︒,30CBD ∴∠=︒,∴∠BCE =90°-30°=60°,又105BCD ∠=︒,45CDB ∴∠=︒,∴∠ECD =45°=∠D ,∴CE DE =,1600m BC =,111600800m 22CE BC ∴==⨯=,22222CD CE DE CE ∴=+=,即CD ==.故答案为:【点睛】本题考查三角形内角和定理、等腰三角形的判定与性质、直角三角形的性质及勾股定理,解题的关键是熟练掌握相关内容并能灵活运用.(2022·湖北黄冈·中考真题)28. 勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m (m ≥3,m 为正整数),则其弦是________(结果用含m 的式子表示).【答案】m 2+1【解析】【分析】2m 为偶数,设其股是a ,则弦为a +2,根据勾股定理列方程即可得到结论.【详解】∵2m 为偶数,∴设其股是a ,则弦为a +2,根据勾股定理得,(2m )2+a 2=(a +2)2,解得a =m 2-1,∴弦长为m 2+1,故答案为:m 2+1.【点睛】本题考查了勾股数,勾股定理,熟练掌握勾股定理是解题的关键. (2022·江苏苏州·中考真题)29. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC 是“倍长三角形”,底边BC 的长为3,则腰AB 的长为______.【答案】6【解析】【分析】分类讨论:AB =AC =2BC 或BC =2AB =2AC ,然后根据三角形三边关系即可得出结果.【详解】解:∵△ABC 是等腰三角形,底边BC =3∴AB =AC当AB =AC =2BC 时,△ABC 是“倍长三角形”;当BC =2AB =2AC 时,AB +AC =BC ,根据三角形三边关系,此时A 、B 、C 不构成三角形,不符合题意;所以当等腰△ABC 是“倍长三角形”,底边BC 的长为3,则腰AB 的长为6. 故答案为6.【点睛】本题考查等腰三角形,三角形的三边关系,涉及分类讨论思想,结合三角形三边关系,灵活运用分类讨论思想是解题的关键.(2022·江苏扬州·中考真题)30. 将一副直角三角板如图放置,已知60E ∠=︒,45C ∠=︒,EF BC ∥,则BND ∠=________°.【答案】105【解析】【分析】根据平行线的性质可得45FAN B ∠=∠=︒,根据三角形内角和定理以及对顶角相等即可求解.【详解】45B C ∠︒∠==,EF BC ∥,∴45FAN B ∠=∠=︒,△△E =60°△△△F =30°△180105BND ANF F BAF ∴∠=∠=︒-∠-∠=︒故答案为:105【点睛】本题考查了平行线的性质,三角形内角和定理,掌握平行线的性质是解题的关键.(2022·湖北黄冈·中考真题)31. 如图,直线a ∥b ,直线c 与直线a ,b 相交,若∠1=54°,则∠3=________度.【答案】54【解析】【分析】根据对顶角相等和平行线的性质“两直线平行同位角相等”,通过等量代换求解.【详解】因为a△b ,所以23∠=∠,因为12∠∠,是对顶角,所以12∠=∠,所以31∠=∠,因为154∠=︒,所以354∠=︒,故答案为:54.【点睛】本题考查了平行线的性质和对顶角的性质,熟练掌握对顶角相等,两直线平行同位角相等、内错角相等,加以灵活运用求解相关角的度数是解题关键. (2022·四川达州·中考真题)32. 如图,在Rt ABC 中,90C ∠=︒,20B ∠=︒,分别以点A ,B 为圆心,大于12AB 的长为半径作弧,两弧分别相交于点M ,N ,作直线MN ,交BC 于点D ,连接AD ,则CAD ∠的度数为_____.【答案】50︒##50度【解析】【分析】根据作图可知DA DB =,20DAB B ∠=∠=︒,根据直角三角形两个锐角互余,可得70CAB ∠=︒,根据CAD CAB DAB ∠=∠-∠即可求解.【详解】解:∵在Rt ABC 中,90C ∠=︒,20B ∠=︒,∴70CAB ∠=︒,由作图可知MN 是AB 的垂直平分线,DA DB ∴=,∴20DAB B ∠=∠=︒,∴CAD CAB DAB∠=∠-∠702050︒-︒=︒,故答案为:50︒.【点睛】本题考查了基本作图,垂直平分线的性质,等边对等角,直角三角形的两锐角互余,根据题意分析得出MN是AB的垂直平分线,是解题的关键.(2022·湖北黄冈·中考真题)33. 如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件_____,使△ABC≌△DEF.【答案】∠A=∠D或BC=EF或BE=CF或∠ACB=∠F【解析】【分析】判定一般三角形全等一共有四种方法,根据这四种方法一一选择即可.【详解】解:添加BE=CF∵BE=CF,∴BC=EF,∵AB∥DE,∴∠B=∠DEF,∵AB=DE,∴△ABC≌△DEF(SAS).故答案为:AB=DE(答案不唯一).视频【点睛】本题考查的是三角形全等的判定,根据判定的方法选择合适的方法,关键是要能熟练运用三角形的判定方法.三.解答题(2022·浙江温州·中考真题)∥,交AB于点E.34. 如图,BD是ABC的角平分线,DE BC(1)求证:EBD EDB ∠=∠.(2)当AB AC =时,请判断CD 与ED 的大小关系,并说明理由.【答案】(1)见解析 (2)相等,见解析【解析】【分析】(1)利用角平分线的定义和平行线的性质可得结论;(2)利用平行线的性质可得ADE AED ∠=∠, 则AD= AE ,从而有CD = BE ,由(1) 得,EBD EDB ∠=∠,可知BE = DE ,等量代换即可.【小问1详解】证明:△BD 是ABC 的角平分线,△CBD EBD ∠=∠.△DE BC ∥,△CBD EDB ∠=∠,△EBD EDB ∠=∠.【小问2详解】CD ED =.理由如下:△AB AC =,△C ABC ∠=∠.△DE BC ∥,△,ADE C AED ABC ∠=∠∠=∠,△ADE AED ∠=∠,△AD AE =,△AC AD AB AE -=-,即CD BE =.由(1)得EBD EDB ∠=∠,△BE ED =,△CD ED =.【点睛】本题主要考查了平行线的性质,等腰三角形的判定与性质,角平分线的定义等知识,熟练掌握平行与角平分线可推出等腰三角形是解题的关键. (2022·四川乐山·中考真题)35. 如图,B 是线段AC 的中点,,AD BE BD CE ∥∥,求证:ABD BCE △≌△.【答案】证明过程见详解【解析】【分析】运行平行线的性质可证△A =△EBC ,△DBA =△C ,结论即可得证.【详解】证明△B 是AC 中点,△AB =BC ,△AD BE ∥,△△A =△EBC ,△BD EC ∥,△△DBA =△C ,在△ABD 和△BCE 中,A EBC AB BC DBA C ∠=∠⎧⎪=⎨⎪∠=∠⎩,△△ABD ≌△BCE (ASA).【点睛】本题考查了全等三角形的判定、平行线的性质,掌握两直线平行同位角相等的知识是解答本题的关键.(2022·浙江杭州·中考真题)36. 如图,在Rt △ACB 中,∠ACB =90°,点M 为边AB 的中点,点E 在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.(1)求证:CE=CM.(2)若AB=4,求线段FC的长.【答案】(1)见解析(2【解析】【分析】(1)根据直角三角形的性质可得MC=MA=MB,根据外角的性质可得∠MEC=∠A+∠ACE,∠EMC=∠B+∠MCB,根据等角对等边即可得证;(2)根据CE=CM先求出CE的长,再解直角三角形即可求出FC的长.【小问1详解】证明:∵∠ACB=90°,点M为边AB的中点,∴MC=MA=MB,∴∠MCA=∠A,∠MCB=∠B,∵∠A=50°,∴∠MCA=50°,∠MCB=∠B=40°,∴∠EMC=∠MCB+∠B=80°,∵∠ACE=30°,∴∠MEC=∠A+∠ACE=50°,∴∠MEC=∠EMC,∴CE=CM;【小问2详解】解:∵AB=4,∴CE=CM=12AB=2,∵EF⊥AC,∠ACE=30°,∴FC=CE•cos30°=【点睛】本题考查了直角三角形的性质,涉及三角形外角的性质,解直角三角形等,熟练掌握并灵活运用直角三角形的性质是解题的关键.(2022·陕西·中考真题)37. 如图,在△ABC 中,点D 在边BC 上,CD =AB ,DE ∥AB ,∠DCE =∠A .求证:DE =BC .【答案】证明见解析【解析】【分析】利用角边角证明△CDE ≌△ABC ,即可证明DE =BC .【详解】证明:∵DE ∥AB ,∴∠EDC =∠B .又∵CD =AB ,∠DCE =∠A ,∴△CDE ≌△ABC (ASA).∴DE =BC .【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定是本题的关键.(2022·湖南衡阳·中考真题)38. 如图,在ABC 中,AB AC =,D 、E 是BC 边上的点,且BD CE =,求证:AD AE =.【答案】见解析【解析】【分析】利用等腰三角形的性质可得B C ∠=∠,再由SAS 证明ABD ACE △≌△,从而得AD AE =.【详解】证明:∵AB AC =,∴B C ∠=∠,在ABD △和ACE 中,AB AC B C BD CE =⎧⎪∠=∠⎨⎪=⎩,∴()ABD ACE SAS △≌△,∴AD AE =.【点睛】本题考查等腰三角形的性质,全等三角形的性质与判定,熟练掌握相关性质定理是解题的关键.(2022·湖南怀化·中考真题)39. 如图,在等边三角形ABC 中,点M 为AB 边上任意一点,延长BC 至点N ,使CN =AM ,连接MN 交AC 于点P ,MH ⊥AC 于点H .(1)求证:MP =NP ;(2)若AB =a ,求线段PH 的长(结果用含a 的代数式表示).【答案】(1)见详解;(2)0.5a .【解析】【分析】(1)过点M 作MQ ∥CN ,证明MQP NCP ≅△△即可;(2)利用等边三角形的性质推出AH =HQ ,则PH =HQ +PQ =0.5(AQ +CQ ).【小问1详解】如下图所示,过点M 作MQ ∥CN ,△ABC 为等边三角形,MQ ∥CN , △1AM AB AQ AC==, 则AM =AQ ,且△A =60°,△AMQ △为等边三角形,则MQ =AM =CN ,又△MQ ∥CN ,△△QMP =△CNP ,在MQP NCP △与△中,MPQ NPC QMP CNP QM CN ∠=∠⎧⎪∠=∠⎨⎪=⎩△MQP NCP ≅△△,则MP =NP ;【小问2详解】△AMQ △为等边三角形,且MH △AC ,△AH =HQ ,又由(1)得,MQP NCP ≅△△,则PQ =PC ,△PH =HQ +PQ =0.5(AQ +CQ )=0.5AC =0.5a .【点睛】本题考查了等边三角形的性质与判定、三角形全等的判定,正确作出辅助线是解题的关键.(2022·浙江丽水·中考真题)40. 如图,将矩形纸片ABCD 折叠,使点B 与点D 重合,点A 落在点P 处,折痕为EF .(1)求证:PDE CDF △≌△;(2)若4cm,5cm CD EF ==,求BC 的长.【答案】(1)证明见解析(2)163cm 【解析】【分析】(1)利用ASA 证明即可;(2)过点E 作EG ⊥BC 交于点G ,求出FG 的长,设AE =x ,用x 表示出DE 的长,在Rt △PED 中,由勾股定理求得答案.【小问1详解】∵四边形ABCD 是矩形,∴AB =CD ,∠A =∠B =∠ADC =∠C =90°,由折叠知,AB =PD ,∠A =∠P ,∠B =∠PDF =90°,∴PD =CD ,∠P =∠C ,∠PDF =∠ADC ,∴∠PDF -∠EDF =∠ADC -∠EDF ,∴∠PDE =∠CDF ,在△PDE 和△CDF 中,P C PD CDPDE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴PDE CDF △≌△(ASA );【小问2详解】如图,过点E 作EG ⊥BC 交于点G ,∵四边形ABCD 是矩形,∴AB =CD =EG =4cm ,又∵EF =5cm ,∴3GF ==,设AE =x ,∴EP =x ,由PDE CDF △≌△知,EP =CF =x ,∴DE =GC =GF +FC =3+x ,在Rt △PED 中,222PE PD DE +=,即()22243x x +=+, 解得,76x =, ∴BC =BG +GC =77163663++=cm . 【点睛】本题考查了翻折变换,矩形的性质,勾股定理,全等三角形的判定和性质,根据翻折变换的性质将问题转化到直角三角形中利用勾股定理是解题的关键. (2022·四川自贡·中考真题)41. 如图,△ABC 是等边三角形,,D E 在直线BC 上,DB EC =.求证:D E ∠=∠ .【答案】详见解析【解析】【分析】由等边三角形的性质以及题设条件,可证△ADB ≌△AEC ,由全等三角形的性质可得D E ∠=∠.【详解】证明:△△ABC 是等边三角形,∴AB=AC ,∠ABC =∠ACB ,∴∠ABD =∠ACE ,在△ADB 和△AEC 中,AB AC ABD ACE DB EC =⎧⎪=⎨⎪=⎩∠∠∴△ADB ≌△AEC (SAS ),∴D E ∠=∠.【点睛】本题考查等边三角形的性质、补角的性质、全等三角形的判定和性质,综合性强,但是整体难度不大.(2022·重庆·中考真题)42. 我们知道,矩形的面积等于这个矩形的长乘宽,小明想用其验证一个底为a ,高为h 的三角形的面积公式为12S ah =.想法是:以BC 为边作矩形BCFE ,点A 在边FE 上,再过点A 作BC 的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:证明:用直尺和圆规过点A 作BC 的垂线AD 交BC 于点D .(只保留作图痕迹)在ADC 和CFA △中,∵AD BC ⊥,∴90ADC ∠=︒.∵90F ∠=︒,。
【2014中考复习方案】(苏科版)中考数学复习权威课件:17几何初步及平行线、相交线

2.角的有关性质及计算.
例1.[2012•北京] 如图17-1,直线 AB、CD交于点O,射线OM平分 ∠AOC,若∠BOD=76°,则 ∠BOM等于( C ) A.38° B.104° C.142° D.144°
考点聚焦 归类探究 回归教材
图17-1
第17课时┃归类探究
(1)度量法;(2)叠合法
1°=60′,1′=60″ 从一个角的顶点引出的一条射线,把这个角分成两个 相等的角,这条线叫做这个角的平分线
考点聚焦 归类探究 回归教材
第17课时┃考点聚焦
考点3
1
几何计数
过任意三个不在同一直线上的n个点中的两个点
n( n-1 ) 可以画____________ 条 2
第17课时 几何初步及平行线、相交线 第18课时 多边形与三角形 第19课时 全等三角形 第20课时 等腰三角形 第21课时 直角三角形与勾股定理 第22课时 相似三角形及其应用 第23课时 锐角三角函数
第24课时 解直角三角形的应用
第17课时 几何初步及平行 线、相交线
第17课时┃考点聚焦
考 点 聚 焦
两直线平行,同位角相等
两直线平行,内错角相等 两直线平行,同旁内角互补
考点聚焦 归类探究 回归教材
第17课时┃考点聚焦
考点8
垂直
如果两条直线相交成________ 直角 ,那么这两条直线互相垂直, 其中一条叫做另一条的垂线,互相垂直的两条直线的交点 垂足 叫做________
垂直 垂直的 性质
一条 直线与已知直线 在同一平面内,过一点有且只有________ 垂直
互为补 角
性质 拓展
相等 同角(或等角)的补角________
专题10 平行线与三角形-2022年中考数学真题分项汇编(第2期)试题及答案

专题10 平行线与三角形一.选择题1.(2022·内蒙古通辽)如图,一束光线AB 先后经平面镜OM ,ON 反射后,反射光线CD 与AB 平行,当35ABM ∠=︒时,DCN ∠的度数为( )A .55︒B .70︒C .60︒D .35︒ 2.(2022·河北)要得知作业纸上两相交直线AB ,CD 所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):对于方案Ⅰ、Ⅰ,说法正确的是( )A .Ⅰ可行、Ⅰ不可行B .Ⅰ不可行、Ⅰ可行C .Ⅰ、Ⅰ都可行D .Ⅰ、Ⅰ都不可行 3.(2022·河南)如图,直线AB ,CD 相交于点O ,EO ⅠCD ,垂足为O .若Ⅰ1=54°,则Ⅰ2的度数为( )A .26°B .36°C .44°D .54°4.(2022·湖北鄂州)如图,直线l 1∥l 2,点C 、A 分别在l 1、l 2上,以点C 为圆心,CA 长为半径画弧,交l 1于点B ,连接AB .若ⅠBCA =150°,则Ⅰ1的度数为( )A .10°B .15°C .20°D .30°5.(2022·湖南郴州)如图,直线a b ∥,且直线a ,b 被直线c ,d 所截,则下列条件不能..判定直线c d ∥的是( )A .34∠=∠B .15180∠+∠=︒C .12∠=∠D .14∠=∠ 6.(2022·山东潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB 与CD 平行,入射光线l 与出射光线m 平行.若入射光线l 与镜面AB 的夹角14010'∠=︒,则6∠的度数为( )A .10040'︒B .9980'︒C .9940'︒D .9920'︒7.(2022·北京)如图,利用工具测量角,则1∠的大小为( )A .30°B .60°C .120°D .150°8.(2022·黑龙江)如图,ABC 中,AB AC =,AD 平分BAC ∠与BC 相交于点D ,点E 是AB 的中点,点F 是DC 的中点,连接EF 交AD 于点P .若ABC 的面积是24, 1.5PD =,则PE 的长是( )A .2.5B .2C .3.5D .39.(2022·贵州遵义)如图1是第七届国际数学教育大会(ICME )会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若1AB BC ==,30AOB ∠=︒,则点B 到OC 的距离为( )A B C .1 D .210.(2022·广西)活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如己知ⅠABC 中,ⅠA =30°, AC =3,ⅠA形有两个(我们发现其中如图的ⅠABC 是一个直角三角形),则满足已知条件的三角形的第三边长为()B.3C.D.3A.11.(2022·山东烟台)如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是()A.北偏东70°B.北偏东75°C.南偏西70°D.南偏西20°12.(2022·河北)如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC 的()A.中线B.中位线C.高线D.角平分线13.(2022·广西贺州)如图,在Rt△ABC中,ⅠC=90°,ⅠB=56°,则ⅠA的度数为()A .34︒B .44︒C .124︒D .134︒14.(2022·湖南永州)如图,在Rt ABC △中,90ABC ∠=︒,60C ∠=°,点D 为边AC 的中点,2BD =,则BC 的长为( )AB .C .2D .415.(2022·湖南永州)下列多边形具有稳定性的是( )A .B .C .D .16.(2022·广西玉林)请你量一量如图ABC 中BC 边上的高的长度,下列最接近的是( )A .0.5cmB .0.7cmC .1.5cmD .2cm17.(2022·黑龙江大庆)下列说法不正确...的是( ) A .有两个角是锐角的三角形是直角或钝角三角形B .有两条边上的高相等的三角形是等腰三角形C .有两个角互余的三角形是直角三角形D .底和腰相等的等腰三角形是等边三角形18.(2022·广西梧州)如图,在ABC 中,,AB AC AD =是ABC 的角平分线,过点D 分别作,DE AB DF AC ,垂足分别是点E ,F ,则下列结论错误..的是( )A .90ADC ∠=B .DE DF =C .AD BC = D .BD CD =19.(2022·四川乐山)如图,等腰△ABC 的面积为AB =AC ,BC =2.作AE ∥BC 且AE =12BC .点P 是线段AB 上一动点,连接PE ,过点E 作PE 的垂线交BC 的延长线于点F ,M 是线段EF 的中点.那么,当点P 从A 点运动到B 点时,点M 的运动路径长为( )AB .3C .D .420.(2022·四川凉山)下列长度的三条线段能组成三角形的是( )A .3,4,8B .5,6,11C .5,6,10D .5,5,1021.(2022·四川成都)如图,在ABC 和DEF 中,点A ,E ,B ,D 在同一直线上,AC DF ∥,AC DF =,只添加一个条件,能判定ABC DEF △≌△的是( )A .BC DE =B .AE DB =C .A DEF ∠=∠D .ABC D ∠=∠22.(2022·山东聊城)如图,ABC 中,若80BAC ∠=︒,70ACB ∠=︒,根据图中尺规作图的痕迹推断,以下结论错误的是( )A .40BAQ ∠=︒B .12DE BD = C .AF AC = D .25EQF ∠=︒ 23.(2022·海南)如图,直线m n ∥,ABC 是等边三角形,顶点B 在直线n 上,直线m 交AB 于点E ,交AC 于点F ,若1140∠=︒,则2∠的度数是( )A .80︒B .100︒C .120︒D .140︒24.(2022·黑龙江齐齐哈尔)如图所示,直线a Ⅰb ,点A 在直线a 上,点B 在直线b 上,AC =BC ,ⅠC =120°,Ⅰ1=43°,则Ⅰ2的度数为( )A .57°B .63°C .67°D .73°25.(2022·湖北恩施)已知直线12l l ∥,将含30°角的直角三角板按图所示摆放.若1120∠=︒,则2∠=( )A .120°B .130°C .140°D .150°二.填空题 26.(2022·辽宁锦州)如图,在ABC 中,,30AB AC ABC =∠=︒,点D 为BC 的中点,将ABC 绕点D 逆时针旋转得到A B C ''',当点A 的对应点A '落在边AB 上时,点C '在BA 的延长线上,连接BB ',若1AA '=,则BB D '△的面积是____________.27.(2022·湖南郴州)如图.在ABC 中,90C ∠=︒,AC BC =.以点A 为圆心,以任意长为半径作弧交AB ,AC 于D ,E 两点;分别以点D ,E 为圆心,以大于12DE 长为半径作弧,在BAC ∠内两弧相交于点P ;作射线AP 交BC 于点F ,过点F 作FG AB ⊥,垂足用G .若8cm AB =,则BFG 的周长等于________cm .28.(2022·江苏常州)如图,在ABC 中,E 是中线AD 的中点.若AEC △的面积是1,则ABD △的面积是______.29.(2022·黑龙江哈尔滨)在ABC 中,AD 为边BC 上的高,30ABC ∠=︒,20CAD ∠=︒,则BAC ∠是___________度.30.(2022·四川成都)如图,在ABC 中,按以下步骤作图:①分别以点B 和C 为圆心,以大于12BC 的长为半径作弧,两弧相交于点M 和N ;②作直线MN 交边AB 于点E .若5AC =,4BE =,45B ∠=︒,则AB 的长为_________.31.(2022·内蒙古通辽)在Rt ABC 中,90C ∠=︒,有一个锐角为60︒,6AB =,若点P 在直线..AB 上(不与点A ,B 重合),且30PCB ∠=︒,则AP 的长为_______. 32.(2022·湖南岳阳)如图,在ABC 中,AB AC =,AD BC ⊥于点D ,若6BC =,则CD =______.33.(2022·江苏无锡)△ABC 是边长为5的等边三角形,△DCE 是边长为3的等边三角形,直线BD 与直线AE 交于点F .如图,若点D 在△ABC 内,ⅠDBC =20°,则ⅠBAF =________°;现将△DCE 绕点C 旋转1周,在这个旋转过程中,线段AF 长度的最小值是________.34.(2022·湖南永州)我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,则AE =______.35.(2022·黑龙江齐齐哈尔)在ⅠABC 中,AB =6AC =,45B ∠=,则BC =______________.36.(2022·贵州遵义)如图,在等腰直角三角形ABC 中,90BAC ∠=︒,点M ,N 分别为BC ,AC 上的动点,且AN CM =,AB =.当AM BN +的值最小时,CM 的长为__________.37.(2022·广西)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么ⅠBAC 的大小为______38.(2022·广西桂林)如图,点C 是线段AB 的中点,若AC =2cm ,则AB =_____cm .39.(2022·贵州遵义)数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.小组成员查阅相关资料,得到如下信息:信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;信息二:如图2,赤道半径OA 约为6400千米,弦BC OA ∥,以BC 为直径的圆的周长就是北纬28°纬线的长度;(参考数据:π3≈,sin 280.47︒≈,cos280.88︒≈,tan 280.53︒≈) 根据以上信息,北纬28°纬线的长度约为__________千米.三.解答题40.(2022·广东)如图,已知AOC BOC ∠=∠,点P 在OC 上,PD OA ⊥,PE OB ⊥,垂足分别为D ,E .求证:OPD OPE ≌.41.(2022·广西)校园内有一块四边形的草坪造型,课外活动小组实地测量,并记录数据,根据造型画如图的四边形ABCD ,其中 AB =CD =2米,AD =BC =3米,ⅠB =30(1)求证:ⅠABC ⅠⅠCDA ;(2)求草坪造型的面积.42.(2022·贵州铜仁)如图,点C 在BD 上,,,,⊥⊥⊥=AB BD ED BD AC CE AB CD .求证:ABC CDE △≌△.43.(2022·四川宜宾)已知:如图,点A 、D 、C 、F 在同一直线上,AB DE ∥,B E ∠=∠,BC EF =.求证:AD CF =.44.(2022·北京)下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.三角形内角和定理:三角形三个内角和等于180°,已知:如图,ABC ∆, 求证:180.A B C ∠+∠+∠=方法一证明:如图,过点A 作.DE BC ∥方法二证明:如图,过点C 作.CD AB ∥45.(2022·湖南长沙)如图,AC 平分BAD CB AB CD AD ∠⊥⊥,,,垂足分别为B ,D .(1)求证:ABC ADC △△≌;(2)若43AB CD ==,,求四边形ABCD 的面积.46.(2022·湖南湘潭)在ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,过点B 、C 分别作l 的垂线,垂足分别为点D 、E .(1)特例体验:如图①,若直线l BC ∥,AB AC ==分别求出线段BD 、CE 和DE 的长;(2)规律探究:①如图②,若直线l 从图①状态开始绕点A 旋转()045αα<<︒,请探究线段BD 、CE 和DE 的数量关系并说明理由;②如图③,若直线l 从图①状态开始绕点A 顺时针旋转()4590αα︒<<︒,与线段BC 相交于点H ,请再探线段BD 、CE 和DE 的数量关系并说明理由;(3)尝试应用:在图③中,延长线段BD 交线段AC 于点F ,若3CE =,1DE =,求BFC S △.47.(2022·江苏常州)在四边形ABCD 中,O 是边BC 上的一点.若OAB OCD ≌,则点O 叫做该四边形的“等形点”.(1)正方形_______“等形点”(填“存在”或“不存在”);(2)如图,在四边形ABCD 中,边BC 上的点O 是四边形ABCD 的“等形点”.已知CD =5OA =,12BC =,连接AC ,求AC 的长;(3)在四边形EFGH 中,EH //FG .若边FG 上的点O 是四边形EFGH 的“等形点”,求OF OG的值.48.(2022·北京)在ABC 中,90ACB ∠=,D 为ABC 内一点,连接BD ,DC ,延长DC 到点E ,使得.CE DC =(1)如图1,延长BC 到点F ,使得CF BC =,连接AF ,EF ,若AF EF ⊥,求证:BD AF ⊥;(2)连接AE ,交BD 的延长线于点H ,连接CH ,依题意补全图2,若222AB AE BD =+,用等式表示线段CD 与CH 的数量关系,并证明.49.(2022·湖北武汉)如图,在四边形ABCD 中,AD BC ∥,80B ∠=︒.(1)求BAD ∠的度数;(2)AE 平分BAD ∠交BC 于点E ,50BCD ∠=︒.求证:AE DC ∥.50.(2022·福建)如图,点B ,F ,C ,E 在同一条直线上,BF =EC ,AB =DE ,ⅠB =ⅠE .求证:ⅠA =ⅠD .51.(2022·四川广安)如图,点D 是ⅠABC 外一点,连接BD 、 AD ,AD 与BC 交于点O .下列三个等式:①BC =AD ;②ⅠABC =ⅠBAD ;③AC = BD .请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明.已知: ,求证:专题10 平行线与三角形一.选择题1.(2022·内蒙古通辽)如图,一束光线AB 先后经平面镜OM ,ON 反射后,反射光线CD 与AB 平行,当35ABM ∠=︒时,DCN ∠的度数为( )A .55︒B .70︒C .60︒D .35︒【答案】A 【分析】根据题意得:ⅠABM =ⅠOBC , ⅠBCO =ⅠDCN ,然后平行线的性质可得ⅠBCD =70°,即可求解.【详解】解:根据题意得:ⅠABM =ⅠOBC , ⅠBCO =ⅠDCN ,ⅠⅠABM =35°,ⅠⅠOBC =35°,ⅠⅠABC =180°-ⅠABM -ⅠOBC =180°-35°-35°=110°,ⅠCD ⅠAB ,ⅠⅠABC +ⅠBCD =180°,ⅠⅠBCD =180°-ⅠABC =70°,ⅠⅠBCO +ⅠBCD +ⅠDCN =180°, ⅠBCO =ⅠDCN , Ⅰ1(180)552DCN BCD ︒︒-∠=∠=.故选:A 【点睛】本题主要考查了平行线的性质,熟练掌握两直线平行,同旁内角互补是解题的关键. 2.(2022·河北)要得知作业纸上两相交直线AB ,CD 所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):对于方案Ⅰ、Ⅰ,说法正确的是( )A .Ⅰ可行、Ⅰ不可行B .Ⅰ不可行、Ⅰ可行C .Ⅰ、Ⅰ都可行D .Ⅰ、Ⅰ都不可行【答案】C 【分析】用夹角可以划出来的两条线,证明方案Ⅰ和Ⅰ的结果是否等于夹角,即可判断正误【详解】方案Ⅰ:如下图,BPD ∠即为所要测量的角ⅠHEN CFG ∠=∠ⅠMN PD ∥ⅠAEM BPD ∠=∠故方案Ⅰ可行方案Ⅰ:如下图,BPD ∠即为所要测量的角在EPF 中:180BPD PEF PFE ∠+∠+∠=︒则:180BPD AEH CFG ∠=︒-∠-∠故方案Ⅰ可行故选:C【点睛】本题考查平行线的性质和判定,三角形的内角和;本题的突破点是用可画出夹角的情况进行证明3.(2022·河南)如图,直线AB ,CD 相交于点O ,EO ⅠCD ,垂足为O .若Ⅰ1=54°,则Ⅰ2的度数为( )A .26°B .36°C .44°D .54°【答案】B 【分析】根据垂直的定义可得90COE ∠=︒,根据平角的定义即可求解.【详解】解: EO ⅠCD ,90COE ∴∠=︒,12180COE ∠+∠+∠=︒,2180905436∴∠=︒-︒-︒=︒.故选:B .【点睛】本题考查了垂线的定义,平角的定义,数形结合是解题的关键.4.(2022·湖北鄂州)如图,直线l 1∥l 2,点C 、A 分别在l 1、l 2上,以点C 为圆心,CA 长为半径画弧,交l 1于点B ,连接AB .若ⅠBCA =150°,则Ⅰ1的度数为( )A .10°B .15°C .20°D .30°【答案】B 【分析】由作图得ABC ∆为等腰三角形,可求出15ABC ∠=︒,由l 1∥l 2得1ABC ∠=∠,从而可得结论.【详解】解:由作图得,CA CB =,ⅠABC ∆为等腰三角形,ⅠABC CAB ∠=∠ⅠⅠBCA =150°,Ⅰ11(180)(180150)1522ABC ACB ∠=︒-∠=︒-︒=︒ Ⅰl 1∥l 2Ⅰ115ABC ∠=∠=︒故选B【点睛】本题主要考查了等腰三角形的判定与性质,平行线的性质等知识,求出15ABC ∠=︒是解答本题的关键.5.(2022·湖南郴州)如图,直线a b ∥,且直线a ,b 被直线c ,d 所截,则下列条件不能..判定直线c d ∥的是( )A .34∠=∠B .15180∠+∠=︒C .12∠=∠D .14∠=∠【答案】C 【分析】利用平行线的判定条件进行分析即可得出结果.【详解】解:A 、当34∠=∠时,c d ∥;故A 不符合题意;B 、当15180∠+∠=︒时,c d ∥;故B 不符合题意;C 、当12∠=∠时,a b ∥;故C 符合题意;D 、Ⅰa b ∥,则12∠=∠,Ⅰ14∠=∠,则24∠∠=,Ⅰc d ∥;故D 不符合题意;故选:C【点睛】本题主要考查平行线的判定,解答的关键是熟记平行线的判定条件并灵活运用. 6.(2022·山东潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB 与CD 平行,入射光线l 与出射光线m 平行.若入射光线l 与镜面AB 的夹角14010'∠=︒,则6∠的度数为( )A .10040'︒B .9980'︒C .9940'︒D .9920'︒【答案】C 【分析】由入射光线与镜面的夹角等于反射光线与镜面的夹角,可得Ⅰ1=Ⅰ2,可求出Ⅰ5,由l //m 可得Ⅰ6=Ⅰ5【详解】解:由入射光线与镜面的夹角等于反射光线与镜面的夹角,可得Ⅰ1=Ⅰ2, Ⅰ14010'∠=︒Ⅰ24010'∠=︒Ⅰ518012180401040109940'''∠=︒-∠-∠=︒-︒-︒=︒Ⅰl //m Ⅰ659940'∠=∠=︒ 故选:C【点睛】本题主要考查了平行线的性质,熟记两直线平行,内错角相等是解答本题的关键.7.(2022·北京)如图,利用工具测量角,则1∠的大小为( )A .30°B .60°C .120°D .150°【答案】A【分析】利用对顶角相等求解.【详解】解:量角器测量的度数为30°,由对顶角相等可得,130∠=︒.故选A .【点睛】本题考查量角器的使用和对顶角的性质,掌握对顶角相等是解题的关键. 8.(2022·黑龙江)如图,ABC 中,AB AC =,AD 平分BAC ∠与BC 相交于点D ,点E 是AB 的中点,点F 是DC 的中点,连接EF 交AD 于点P .若ABC 的面积是24, 1.5PD =,则PE 的长是( )A .2.5B .2C .3.5D .3【答案】A 【分析】连接DE ,取AD 的中点G ,连接EG ,先由等腰三角形“三线合一“性质,证得AD ⅠBC ,BD =CD ,再由E 是AB 的中点,G 是AD 的中点,求出S △EGD =3,然后证△EGP Ⅰ△FDP (AAS ),得GP =CP =1.5,从而得DG =3,即可由三角形面积公式求出EG 长,由勾股定理即可求出PE 长.【详解】解:如图,连接DE ,取AD 的中点G ,连接EG ,ⅠAB =AC ,AD 平分BAC ∠与BC 相交于点D ,ⅠAD ⅠBC ,BD =CD ,ⅠS △ABD =112422ABC S =⨯=12, ⅠE 是AB 的中点, ⅠS △AED =111222ABD S =⨯=6, ⅠG 是AD 的中点, ⅠS △EGD =11622AED S =⨯=3, ⅠE 是AB 的中点,G 是AD 的中点, ⅠEG ∥BC ,EG =12BD =12CD ,ⅠⅠEGP =ⅠFDP =90°,ⅠF 是CD 的中点,ⅠDF =12CD ,ⅠEG =DF ,ⅠⅠEPG =ⅠFPD ,ⅠⅠEGP ⅠⅠFDP (AAS ),ⅠGP =PD =1.5,ⅠGD =3,ⅠS △EGD =12GD EG ⋅=3,即1332EG ⨯=, ⅠEG =2,在Rt ⅠEGP 中,由勾股定理,得PE =,故选:A .【点睛】本题考查等腰三角形的性质,三角形面积,全等三角形判定与性质,勾股定理,熟练掌握三角形中线分三角形两部分的面积相等是解题的关键.9.(2022·贵州遵义)如图1是第七届国际数学教育大会(ICME )会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若1AB BC ==,30AOB ∠=︒,则点B 到OC 的距离为( )A B C .1 D .2【答案】B【分析】根据题意求得2OB =,进而求得=OC【详解】解:在Rt ,Rt ABO BOC 中,30AOB ∠=︒,1AB BC ==,2OB ∴=,OC ∴设B 到OC 的距离为h ,1122OC h BC BO ∴⋅=⋅,h ∴==, 故选B .【点睛】本题考查了勾股定理,含30度角的直角三角形的性质,掌握以上知识是解题的关键.10.(2022·广西)活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如己知ⅠABC 中,ⅠA =30°, AC =3,ⅠA 形有两个(我们发现其中如图的ⅠABC 是一个直角三角形),则满足已知条件的三角形的第三边长为( )A.B .3 C .D .3【答案】C 【分析】分情况讨论,当ⅠABC 是一个直角三角形时,当ⅠAB 1C 是一个钝角三角形时,根据含30°的直角三角形的性质及勾股定理求解即可.【详解】如图,当ⅠABC 是一个直角三角形时,即90C ∠=︒,30,A BC ∠=︒=2∴==AB BC如图,当ⅠAB 1C 是一个钝角三角形时,过点C 作CD ⅠAB 1,90CDA CDB ∴∠=︒=∠,1CB CB =,1BD B D ∴=,30,3A AC ∠=︒=,1322CD AC ∴==, 3BC =1B D BD ∴===,1BB ∴11AB AB BB ∴=-综上,满足已知条件的三角形的第三边长为故选:C .【点睛】本题考查了根据已知条件作三角形,涉及含30°的直角三角形的性质及勾股定理,熟练掌握知识点是解题的关键.11.(2022·山东烟台)如图,某海域中有A ,B ,C 三个小岛,其中A 在B 的南偏西40°方向,C 在B 的南偏东35°方向,且B ,C 到A 的距离相等,则小岛C 相对于小岛A 的方向是( )A .北偏东70°B .北偏东75°C .南偏西70°D .南偏西20° 【答案】A【分析】根据题意可得ⅠABC=75°,ADⅠBE,AB=AC,再根据等腰三角形的性质可得ⅠABC =ⅠC=75°,从而求出ⅠBAC的度数,然后利用平行线的性质可得ⅠDAB=ⅠABE=40°,从而求出ⅠDAC的度数,即可解答.【详解】解:如图:由题意得:ⅠABC=ⅠABE+ⅠCBE=40°+35°=75°,ADⅠBE,AB=AC,ⅠⅠABC=ⅠC=75°,ⅠⅠBAC=180°﹣ⅠABC﹣ⅠC=30°,ⅠADⅠBE,ⅠⅠDAB=ⅠABE=40°,ⅠⅠDAC=ⅠDAB+ⅠBAC=40°+30°=70°,Ⅰ小岛C相对于小岛A的方向是北偏东70°,故选:A..【点睛】本题考查了方向角,等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.12.(2022·河北)如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC 的()A.中线B.中位线C.高线D.角平分线【答案】D∠=∠,作出选择即可.【分析】根据折叠的性质可得CAD BAD【详解】解:如图,Ⅰ由折叠的性质可知CAD BAD ∠=∠,ⅠAD 是BAC ∠的角平分线,故选:D .【点睛】本题考查折叠的性质和角平分线的定义,理解角平分线的定义是解答本题的关键.13.(2022·广西贺州)如图,在Rt △ABC 中,ⅠC =90°,ⅠB =56°,则ⅠA 的度数为( )A .34︒B .44︒C .124︒D .134︒【答案】A【分析】根据直角三角形的两个锐角互余,即可得出ⅠA 的度数.【详解】解:ⅠRt △ABC 中,ⅠC =90°,ⅠB =56°,ⅠⅠA =90°-ⅠB =90°-56°=34°;故选:A .【点睛】本题考查了直角三角形的性质:直角三角形的两个锐角互余;熟练掌握直角三角形的性质,并能进行推理计算是解决问题的关键.14.(2022·湖南永州)如图,在Rt ABC △中,90ABC ∠=︒,60C ∠=°,点D 为边AC 的中点,2BD =,则BC 的长为( )AB .C .2D .4【分析】根据三角形内角和定理可得ⅠA=30°,由直角三角形斜边上的中线的性质得出AC=2BD=4,再利用含30度角的直角三角形的性质求解即可.【详解】解:ⅠⅠABC=90°,ⅠC=60°,ⅠⅠA=30°,Ⅰ点D为边AC的中点,BD=2ⅠAC=2BD=4,ⅠBC=122AC ,故选:C.【点睛】题目主要考查三角形内角和定理及直角三角形斜边上中线的性质,含30度角的直角三角形的性质等,理解题意,综合运用这些知识点是解题关键.15.(2022·湖南永州)下列多边形具有稳定性的是()A.B.C.D.【答案】D【分析】利用三角形具有稳定性直接得出答案.【详解】解:三角形具有稳定性,四边形、五边形、六边形都具有不稳定性,故选D.【点睛】本题考查三角形的特性,牢记三角形具有稳定性是解题的关键.16.(2022·广西玉林)请你量一量如图ABC中BC边上的高的长度,下列最接近的是()A.0.5cm B.0.7cm C.1.5cm D.2cm【分析】作出三角形的高,然后利用刻度尺量取即可.【详解】解:如图所示,过点A 作AO ⅠBC ,用刻度尺直接量得AO 更接近2cm ,故选:D .【点睛】题目主要考查利用刻度尺量取三角形高的长度,作出三角形的高是解题关键. 17.(2022·黑龙江大庆)下列说法不正确...的是( ) A .有两个角是锐角的三角形是直角或钝角三角形B .有两条边上的高相等的三角形是等腰三角形C .有两个角互余的三角形是直角三角形D .底和腰相等的等腰三角形是等边三角形【答案】A【分析】利用等腰三角形的性质与判定、等边三角形的性质与判定、直角三角形的判定,对各选项逐项分析可得出正确答案.【详解】解:A 、设Ⅰ1、Ⅰ2为锐角,因为:Ⅰ1+Ⅰ2+Ⅰ3=180°,所以:Ⅰ3可以为锐角、直角、钝角,所以该三角形可以是锐角三角形,也可以是直角或钝角三角形,故A 选项不正确,符合题意;B 、如图,在△ABC 中,BE ⅠAC ,CD ⅠAB ,且BE =CD .ⅠBE ⅠAC ,CD ⅠAB ,ⅠⅠCDB =ⅠBEC =90°,在Rt △BCD 与Rt △CBE 中,CD BE BC CB=⎧⎨=⎩,ⅠRt △BCD ⅠRt △CBE (HL ),ⅠⅠABC =ⅠACB ,ⅠAB =AC ,即△ABC 是等腰三角形.,故B 选项正确,不符合题意;C 、根据直角三角形的判定:有两个角互余的三角形是直角三角形,,故C 选项正确,不符合题意;D 、底和腰相等的等腰三角形是等边三角形,故D 选项正确,不符合题意;故选:A .【点睛】本题综合考查了等腰三角形的性质与判定、等边三角形的性质与判定、直角三角形的判定,要求学生在学习过程中掌握三角形的各种性质及推论,不断提升数学学习的能力.18.(2022·广西梧州)如图,在ABC 中,,AB AC AD =是ABC 的角平分线,过点D 分别作,DE AB DF AC ,垂足分别是点E ,F ,则下列结论错误..的是( )A .90ADC ∠=B .DE DF =C .AD BC = D .BD CD = 【答案】C【分析】根据等腰三角形底边上的高线、顶角的角平分线、底边上的中线这三线合一及角平分线的性质即可判断求解.【详解】解:Ⅰ,AB AC AD =是ABC 的角平分线,Ⅰ,AD BC BD CD ,Ⅰ90ADC ∠=,故选项A 、D 结论正确,不符合题意;又AD 是BAC ∠的角平分线,,DE AB DF AC ,ⅠDE DF =,故选项B 结论正确,不符合题意;由已知条件推不出AD BC =,故选项C 结论错误,符合题意;故选:C .【点睛】本题考察了等腰三角形的性质及角平分线的性质,属于基础题,熟练掌握其性质即可.19.(2022·四川乐山)如图,等腰△ABC 的面积为AB =AC ,BC =2.作AE ∥BC 且AE =12BC .点P 是线段AB 上一动点,连接PE ,过点E 作PE 的垂线交BC 的延长线于点F ,M 是线段EF 的中点.那么,当点P 从A 点运动到B 点时,点M 的运动路径长为( )AB .3C .D .4 【答案】D【分析】当P 与A 重合时,点F 与C 重合,此时点M 在N 处,当点P 与B 重合时,如图,点M 的运动轨迹是线段MN .求出CF 的长即可解决问题.【详解】解:过点A 作AD ⊥BC 于点D ,连接CE ,∵AB =AC ,∴BD =DC =12BC =1, ∵AE =12BC , ∴AE =DC =1,∵AE ∥BC ,∴四边形AECD 是矩形,∴S △ABC =12BC ×AD =12×2×AD∴AD CE =AD当P 与A 重合时,点F 与C 重合,此时点M 在CE 的中点N 处,当点P 与B 重合时,如图,点M 的运动轨迹是线段MN .∵BC =2,CE由勾股定理得BE =4,cos ∠EBC =BC BE BE BF =,即244BF=, ∴BF =8,∵点N 是CE 的中点,点M 是EF 的中点,∴MN =12BF =4, ∴点M 的运动路径长为4,故选:D .【点睛】本题考查点的轨迹、矩形的判定和性质、解直角三角形、勾股定理等知识,解题的关键是正确寻找点M 的运动轨迹,学会利用起始位置和终止位置寻找轨迹,属于中考填空题中的压轴题.20.(2022·四川凉山)下列长度的三条线段能组成三角形的是( )A .3,4,8B .5,6,11C .5,6,10D .5,5,10【答案】C【分析】根据三角形的三边关系定理(任意两边之和大于第三边)逐项判断即可得.【详解】解:A 、3478+=<,不能组成三角形,此项不符题意;B 、5611+=,不能组成三角形,此项不符题意;C 、561110+=>,能组成三角形,此项符合题意;D 、5510+=,不能组成三角形,此项不符题意;故选:C .【点睛】本题考查了三角形的三边关系定理,熟练掌握三角形的三边关系定理是解题关键.21.(2022·四川成都)如图,在ABC 和DEF 中,点A ,E ,B ,D 在同一直线上,AC DF ∥,AC DF =,只添加一个条件,能判定ABC DEF △≌△的是( )A .BC DE =B .AE DB =C .A DEF ∠=∠D .ABC D ∠=∠【答案】B 【分析】根据三角形全等的判定做出选择即可.【详解】A 、BC DE =,不能判断ABC DEF △≌△,选项不符合题意;B 、AE DB =,利用SAS 定理可以判断ABC DEF △≌△,选项符合题意;C 、A DEF ∠=∠,不能判断ABC DEF △≌△,选项不符合题意;D 、ABC D ∠=∠,不能判断ABC DEF △≌△,选项不符合题意;故选:B .【点睛】本题考查三角形全等的判定,根据SSS 、SAS 、ASA 、AAS 判断三角形全等,找出三角形全等的条件是解答本题的关键.22.(2022·山东聊城)如图,ABC 中,若80BAC ∠=︒,70ACB ∠=︒,根据图中尺规作图的痕迹推断,以下结论错误的是( )A .40BAQ ∠=︒B .12DE BD =C .AF AC =D .25EQF ∠=︒ 【答案】D 【分析】根据线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质判断即可.【详解】Ⅰ80BAC ∠=︒,70ACB ∠=︒,ⅠⅠB =180°-ⅠBAC -ⅠACB =30°,A .由作图可知,AQ 平分BAC ∠,Ⅰ1402BAP CAP BAC ∠=∠=∠=︒, 故选项A 正确,不符合题意;B .由作图可知,MQ 是BC 的垂直平分线,Ⅰ90DEB ∠=︒,Ⅰ30B ∠=︒,Ⅰ12DE BD =,故选项B 正确,不符合题意; C .Ⅰ30B ∠=︒,40BAP ∠=︒,Ⅰ70AFC ∠=︒,Ⅰ70C ∠=︒,ⅠAF AC =,故选项C 正确,不符合题意;D .Ⅰ70EFQ AFC ∠=∠=︒,90QEF ∠=︒,Ⅰ20EQF ∠=︒;故选项D 错误,符合题意.故选:D .【点睛】本题考查了线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质等知识,解题的关键是读懂图象信息.23.(2022·海南)如图,直线m n ∥,ABC 是等边三角形,顶点B 在直线n 上,直线m 交AB 于点E ,交AC 于点F ,若1140∠=︒,则2∠的度数是( )A .80︒B .100︒C .120︒D .140︒【答案】B 【分析】根据等边三角形的性质可得ⅠA =60°,再由三角形外角的性质可得ⅠAEF =Ⅰ1-ⅠA =80°,从而得到ⅠBEF =100°,然后根据平行线的性质,即可求解.【详解】解:ⅠABC 是等边三角形,ⅠⅠA =60°,ⅠⅠ1=140°,ⅠⅠAEF =Ⅰ1-ⅠA =80°,ⅠⅠBEF =180°-ⅠAEF =100°,Ⅰm n ∥,ⅠⅠ2=ⅠBEF =100°.故选:B【点睛】本题主要考查了等边三角形的性质,三角形外角的性质,平行线的性质,熟练掌握等边三角形的性质,三角形外角的性质,平行线的性质是解题的关键.24.(2022·黑龙江齐齐哈尔)如图所示,直线a Ⅰb ,点A 在直线a 上,点B 在直线b 上,AC =BC ,ⅠC =120°,Ⅰ1=43°,则Ⅰ2的度数为( )A .57°B .63°C .67°D .73°【答案】D【分析】根据等腰三角形的性质可求出30ABC ∠=︒,可得出+173ABC ∠∠=︒,再根据平行线的性质可得结论.【详解】解:ⅠAC =BC ,ⅠABC ∆是等腰三角形,Ⅰ=120C ∠︒ Ⅰ11(180)(180120)3022ABC C ∠=︒-∠=︒-︒=︒ Ⅰ1304373ABC ∠+∠=︒+︒=︒Ⅰa Ⅰb ,Ⅰ2173ABC ∠=∠+∠=︒ 故选:D【点睛】本题主要考查了等腰三角形的判定与性质,以及平行线的性质,求出173ABC ∠+∠=︒是解答本题的关键.25.(2022·湖北恩施)已知直线12l l ∥,将含30°角的直角三角板按图所示摆放.若1120∠=︒,则2∠=( )A .120°B .130°C .140°D .150°【答案】D【分析】根据平行线的性质可得Ⅰ3=Ⅰ1=120°,再由对顶角相等可得Ⅰ4=Ⅰ3=120°,然后根据三角形外角的性质,即可求解.【详解】解:如图,根据题意得:Ⅰ5=30°,Ⅰ12l l ∥,ⅠⅠ3=Ⅰ1=120°,ⅠⅠ4=Ⅰ3=120°,ⅠⅠ2=Ⅰ4+Ⅰ5,ⅠⅠ2=120°+30°=150°.故选:D【点睛】本题主要考查了平行线的性质,对顶角相等,三角形外角的性质,熟练掌握平行线的性质,对顶角相等,三角形外角的性质是解题的关键.二.填空题26.(2022·辽宁锦州)如图,在ABC 中,,30AB AC ABC =∠=︒,点D 为BC 的中点,将ABC 绕点D 逆时针旋转得到A B C ''',当点A 的对应点A '落在边AB 上时,点C '在BA 的延长线上,连接BB ',若1AA '=,则BB D '△的面积是____________.【分析】先证明A AD ' 是等边三角形,再证明AO BC '⊥,再利用直角三角形30角对应的边是斜边的一般分别求出A B ''和A O ',再利用勾股定理求出OD ,从而求得BB D '△的面积.【详解】解:如下图所示,设A B ''与BD 交于点O ,连接A D '和AD ,Ⅰ点D 为BC 的中点,,30AB AC ABC =∠=︒,ⅠAD BC ⊥,A D B C '''⊥,A D '是B A C '''∠的角平分线,AD 是BAC ∠,Ⅰ120B A C ︒'''∠=,120BAC ︒∠=Ⅰ60BAD B A D ︒'∠'=∠=ⅠA D AD '=,ⅠA AD ' 是等边三角形,Ⅰ1A A AD A D ''===,Ⅰ18060BA B B A C ︒︒'''''∠=-∠=,ⅠBA B A AD '''∠=∠,Ⅰ//A B AD '',ⅠAO BC '⊥, Ⅰ1122A O A D ''==,ⅠOD ==Ⅰ22A B A D '''==Ⅰ30A BD A DO ︒''∠=∠=,ⅠBO OD =Ⅰ13222OB '=-=,2BD OD ==Ⅰ113222BB DS BD B O ''=⨯⨯==. 【点睛】本题考查等腰三角形、等边三角形和直角三角形的性质,证明A AD ' 是等边三角形是解本题的关键.27.(2022·湖南郴州)如图.在ABC 中,90C ∠=︒,AC BC =.以点A 为圆心,以任意长为半径作弧交AB ,AC 于D ,E 两点;分别以点D ,E 为圆心,以大于12DE 长为半径作弧,在BAC ∠内两弧相交于点P ;作射线AP 交BC 于点F ,过点F 作FG AB ⊥,垂足用G .若8cm AB =,则BFG 的周长等于________cm .【答案】8【分析】由角平分线的性质,得到CF GF =,然后求出BFG 的周长即可.【详解】解:根据题意,在ABC 中,90C ∠=︒,AC BC =,由角平分线的性质,得CF GF =,ⅠBFG 的周长为:()8BG BF FG AB AG BC AB AC BC AB ++=-+=-+==;故答案为:8【点睛】本题考查了角平分线的性质,解题的关键是掌握角平分线的性质.28.(2022·江苏常州)如图,在ABC 中,E 是中线AD 的中点.若AEC △的面积是1,则ABD △的面积是______.【答案】2【分析】根据ACE ∆的面积DCE =∆的面积,ABD ∆的面积ACD =∆的面积计算出各部分三角形的面积.【详解】解:AD 是BC 边上的中线,E 为AD 的中点,根据等底同高可知,ACE ∆的面积DCE =∆的面积1=,ABD ∆的面积ACD =∆的面积2AEC =∆的面积2=,故答案为:2.【点睛】本题考查了三角形的面积,解题的关键是利用三角形的中线平分三角形面积进行计算.29.(2022·黑龙江哈尔滨)在ABC 中,AD 为边BC 上的高,30ABC ∠=︒,20CAD ∠=︒,则BAC ∠是___________度.【答案】40或80##80或40【分析】根据题意,由于ABC 类型不确定,需分三种情况:高在三角形内部、高在三角形边上和高在三角形外部讨论求解.【详解】解:根据题意,分三种情况讨论:①高在三角形内部,如图所示:在ABD ∆中,AD 为边BC 上的高,30ABC ∠=︒,90903060BAD ABC ∴∠=︒-∠=︒-︒=︒,20CAD ∠=︒,602080BAC BAD CAD ∴∠=∠+∠=︒+︒=︒;②高在三角形边上,如图所示:。
七年级相交线与平行线、全等三角形复习整理资料

相交线与平行线复习一、对顶角、邻补角、邻余角、互补、互余、垂线1. 相关概念(1) 对顶角:公共顶点+反向边,对顶角相等。
(2) 邻补角:公共边+两侧边反向,邻补角和为180° (3) 邻余角:公共边+两侧边互相垂直。
(4) 互补与邻补的区别、互余和邻余的区别。
(5) 平面内的直线位置关系有:重合、相交(垂直、斜交)、平行 (6) 两条直线相交所成的角的角度x 取值范围(0< x <180°)两直线的夹角的角度y 的取值范围 (0< y ≤90°) ,当y=90°时,两直线垂直(7) 平面内,过任意一点有且只有一条直线与已知直线垂直(作图)平面内,过已知直线外...一点有且只有一条直线与已知直线平行(作图) (8) 点到直线的距离——直线外一点到这条直线的垂线段...的长度..(作图) 对顶角、邻补角的区分:下面四个图形中,∠1与∠2是对顶角的图形的个数是( )12121212例题:如果两个角的两条分别互相平行,则这两个角的数量关系是_________________ 如果两个角的两条边分别互相垂直,则这两个角的数量关系是_______________ 若两条直线相交所成的四个角中,其中一个比另一个的2倍少20度,则这两直线的夹角是______ 2. 几个基本图形中的角的关系 (图1)可得OE ⊥OD ,从而可得互余关系的角__________________________ 可得互补关系的角__________________ (图2)已知OA ⊥OB ,OC ⊥OD可得相等的角_______________________________ 可得∠BOC 与 ∠____________互补 (图3)OE ⊥AB ,OB 平分∠DOF ,若∠EOC =115°,则∠BOF = ,∠COF = 。
(图1) (图2)二、同位角、内错角、同旁内角1. 相关概念: “三线八角”图2. 能利用概念找清角的关系 以下概念必须具有公共边(截线): (1)描出要判定的两个角,看清公共边(截线)同位角F 、内错角Z 、同旁内角C(2三、平行线的判定与性质1.判定与性质、相关结论(1).⎫−−−→⎪⎬←−−−⎪⎭判定性质同位角相等内错角相等(两直线平行)同旁内角互补(数量关系与位置关系的转化)(2).平行线的传递性——同平行于一条直线的两直线平行(性质)(3).平面内同垂直于一直线的两直线平行(不可直接利用,可由同位角等证明)(4).平行线间的距离处处相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习好资料欢迎下载平行线与三角形复习材料一、相关知识点复习:(一)平行线1.定义:在同一平面内,不相交的两条直线叫做平行线。
2.判定:(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
(3)同旁内角相等,两直线平行。
(4)垂直于同一直线的两直线平行。
3.性质:(1)经过直线外一点,有且只有一条直线与这条直线平行。
(2)如果两条直线都与第三条直线平行,那么这两条直线平行。
(3)两直线平行,同位角相等。
(4)两直线平行,内错角相等。
(5)两直线平行,同旁内角互补。
(二)三角形4.一般三角形的性质(1) 角与角的关系:三个内角的和等于 180°;一个外角等于和它不相邻的两个内角之和,并且大于任何—个和它不相邻的内角。
(2)边与边的关系:三角形中任两边之和大于第三边,任两边之差小于第三边。
(3)边与角的大小对应关系:在一个三角形中,等边对等角;等角对等边。
(4)三角形的主要线段的性质 (见下表 ):名称角平分线基本性质①三角形三条内角平分线相交于一点(内心);内心到三角形三边距离相等;②角平分线上任一点到角的两边距离相等。
中线三角形的三条中线相交于一点。
高三角形的三条高相交于一点。
边的垂直平三角形的三边的垂直平分线相交于一点(外心);分线外心到三角形三个顶点的距离相等。
中位线三角形的中位线平行于第三边且等于第三边的一半。
5.几种特殊三角形的特殊性质(1)等腰三角形的特殊性质:①等腰三角形的两个底角相等;②等腰三角形顶角的平分线、底边上的中线和底边上的高是同一条线段,这条线段所在的直线是等腰三角形的对称轴。
(2)等边三角形的特殊性质:①等边三角形每个内角都等于60°;②等边三角形外心、内心合一。
(3)直角三角形的特殊性质:①直角三角形的两个锐角互为余角;②直角三角形斜边上的中线等于斜边的一半;③勾股定理:直角三角形斜边的平方等于两直角边的平方和(其逆命题也成立);④直角三角形中, 30°的角所对的直角边等于斜边的一半;⑤直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
6.三角形的面积(1) 一般三角形: S △ = 1a h( h 是 a 边上的高)2(2) 直角三角形: S △ = 1a b =1c h( a、b 是直角边, c 是斜边, h 是斜边上的2 2高)(3) 等边三角形: S △ = 3 a2( a 是边长)4(4)等底等高的三角形面积相等;等底的三角形面积的比等于它们的相应的高的比;等高的三角形的面积的比等于它们的相应的底的比。
7.相似三角形(1)相似三角形的判别方法:① 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似;② 如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似;③ 如果一个三角形的三边和另一个三角形的三边对应成比例,那么这两个三角形相似。
(2)相似三角形的性质:① 相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比;② 相似三角形的周长比等于相似比;③ 相似三角形的面积比等于相似比的平方。
8.全等三角形两个能够完全重合的三角形叫全等三角形,全等三角形的对应角相等,对应边相等,其他的对应线段也相等。
判定两个三角形全等的公理或定理:①一般三角形有SAS、 ASA 、AAS 、SSS;②直角三角形还有 HL二、巩固练习:一、选择题:1. 如图,若A . 20o2.如图,∠AB ∥CD ,∠ C = 60o ,则∠ A +∠ E =(B . 30oC .40oD .60o1=∠2,则下列结论一定成立的是())A .AB ∥CD B .AD ∥BC C .∠ B=∠D 3. 如图, AD ⊥ BC , DE ∥AB ,则∠ B 和∠ 1 的关系是(D .∠ 3=∠4)A. 相等B. 互补C. 互余D. 不能确定4.如图,下列判断正确的是()A .∠ 1 和∠ 5 是同位角;B .∠ 2 和∠ 6 是同位角;C .∠ 3 和∠ 5 是内错角;D .∠ 3 和∠ 6 是内错角.5. 下列命题正确的是()A .两直线与第三条直线相交,同位角相等;B .两直线与第三条直线相交,内错角相等;C .两直线平行,内错角相等;D .两直线平行,同旁内角相等。
6.如图,若 AB ∥CD ,则()A .∠1 = ∠4B .∠3 = ∠5C .∠4 = ∠5D .∠3 = ∠4.如图,l 1∥l 2,则 α= ()7A .50°B .80°C .85°D .95°8.下列长度的三条线段能组成三角形的是()A.3cm ,4cm ,8cmB.5cm ,6cm , 11cm学习好资料欢迎下载C.5cm,6cm,10cmD.3cm,8cm, 12cm9.等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为(A.150 °B.80 °C.50 °或 80°D.70 °10.如图,点 D、E、F 是线段 BC 的四等分点,点 A 在 BC 外,连接 AB 、AD 、 AE、 AF、 AC,若 AB = AC ,则图中的全等三角形共有()对A.2B.3C.4D.511.三角形的三边分别为a、 b、c,下列哪个三角形是直角三角形?(A. a = 3,b = 2,c = 4B. a = 15, b = 12,c = 9C. a = 9,b = 8,c = 11D. a = 7,b = 7,c = 412.如图,△AED ∽ △ABC ,AD = 4cm ,AE = 3cm,AAC = 8cm,那么这两个三角形的相似比是() EA.3B.1C.3 DD. 2B 4 2 813.下列结论中,不正确的是()A.有一个锐角相等的两个直角三角形相似;B.有一个锐角相等的两个等腰三角形相似;C.各有一个角等于120°的两个等腰三角形相似;D.各有一个角等于60°的两个等腰三角形相似。
二、填空题:14.如图,直线 a∥b,若∠ 1 = 50 ,°则∠2= 。
15.如图, AB ∥CD,∠ 1 = 40 ,°则∠2= 。
16.如图, DE∥BC,BE 平分∠ ABC ,若∠ ADE = 80°,则∠ 1 = . ))C17.如图,l1∥l2,∠ 1 = 105 °∠, 2 = 140 °,则∠α = .18.△ ABC 中, BC = 12cm, BC 边上的高AD = 6cm,则△ABC 的面积为。
19.如果一个三角形的三边长分别为x, 2, 3,那么 x 的取值范围是。
20.在△ABC 中,AB = AC ,∠ A = 80 ,°则∠ B = ,∠C = 。
21.在△ABC 中,∠ C = 90 ,°∠ A = 30 ,°BC = 4cm,则 AB = 。
22.已知直角三角形两直角边分别为 6 和 8,则斜边上的中线长是。
23.等腰直角三角形的斜边为2,则它的面积是。
24.在 Rt△ABC 中,其中两条边的长分别是 3 和 4,则这个三角形的面积等于。
25.已知等腰三角形的一边长为6,另一边长为 10,则它的周长为。
26.等腰三角形底边上的高等于腰长的一半,则它的顶角度数为。
27.如图, A、B 两点位于一个池塘的两端,冬冬想用绳子测量 A、B 两点间的距离,但绳子不够长,一位同学帮他想了一个办法:先在地上取一个可以直接到达 A、B 的点 C,找到 AC,BC 的中点 D、 E,并且测得 DE 的长为 15m,则 A 、 B 两点间的距离为 __________.28.如图,在△ ABC 和△DEF 中, AB=DE ,∠ B=∠E.要使△ ABC ≌△ DEF,需要补充的是一个条件:。
..29.太阳光下,某建筑物在地面上的影长为36m,同时量得高为 1.2m 的测杆影长为 2m,那么该建筑物的高为。
三、解答题:30.如图,已知△ABC 中, AB = AC ,AE = AF ,D 是 BC 的中点求证:∠1 =∠231.如图,已知 D 是 BC 的中点, BE⊥AE 于 E,CF⊥AE 于 F求证: BE = CF32.如图, CE 平分∠ ACB 且 CE⊥ BD ,∠DAB = ∠DBA ,AC = 18,△CDB 的周长是 28。
求 BD 的长。
33.已知:如图,点D、E 在△ABC 的边 BC 上, AD=AE,BD=EC,求证: AB =ACAB D EC 34. * 一条河的两岸有一段是平行的,在河的这一岸每隔5m 有一棵树,在河的对岸每隔 50m 有一根电线杆,在此岸离岸边25m 处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且这两棵树之间还有三棵树。
(1)根据题意,画出示意图;(2)求河宽。
练习答案:一、选择题1、D2、B3、C4、A5、C6、C7、C8、C9、C10、C11、B12、B13、B二、填空题214、130°15、140°16、 40°17、65° 18、36cm19、1<x<5 20、50°、 50°21、8cm 22、523、124、6或3 725、22 或 2626、 120°27、30m228、BC=EF 或∠ A=∠D 或∠ C=∠ F 29、21.6m三、证明题30、BE=CF 、∠ B=∠C 、BD=DC →△ BED ≌△ CFD →∠ 1=∠231、△ BED ≌△ CFD →BE=CF32、∠ A=∠DBA →AD=BD → CD+BD=AC=18、△ CDB 的周长是 28→BC=1033、AD=AE →∠ ADE=∠ AED →∠ ADB=∠AEC →△ ABD ≌△ AEC → AB=ACC34、A解:如图,根据题意,有 AB ∥ CD ,PM ⊥CD 于 N 点,交 AB 于 M 点,且 AB=20m ,PNCD=50m , PM=25m ,MAB ∥ CD →△ PAB ∽△ PCD →PM ABPN =CDBD25 20→→ PN=62.5→MN=37.5PN=50。
