初三圆的证明专题训练包括答案.docx

合集下载

中考数学总复习《圆综合解答题》专题训练-附答案

中考数学总复习《圆综合解答题》专题训练-附答案学校：___________班级：___________姓名：___________考号：___________ 1．如图△ABC内接于⊙O AB、CD是⊙O的直径E是DA长线上一点且∠CED=∠CAB．(1)求证：CE是⊙O的切线；求线段CE的长．(2)若DE=3√5tanB=122．如图在△ABC中AB=AC以AB为直径作⊙O交BC于点D．过点D作DE⊥AC 垂足为E延长CA交⊙O于点F．(1)求证：DE是⊙O的切线；⊙O的半径为5 求线段CF的长．(2)若tanB=123．如图△ABC内接于⊙O直径DE⊙AB于点F交BC于点M DE的延长线与AC的延长线交于点N连接AM．（1）求证：AM＝BM；（2）若AM⊙BM DE＝8 ⊙N＝15° 求BC的长．4．如图△ABC内接于⊙O AB是⊙O的直径D是⊙O上的一点CO平分∠BCD CE⊥AD垂足为E AB与CD相交于点F．(1)求证：CE是⊙O的切线；时求CE的长．(2)当⊙O的半径为5sinB=355．如图1 锐角△ABC内接于⊙O⊙BAC=60°若⊙O的半径为2√3．(1)求BC的长度；(2)如图2 过点A作AH⊙BC于点H若AB+AC=12 求AH的长度．6．如图AB是⊙O的直径M是OA的中点弦CD⊥AB于点M过点D作DE⊥CA交CA的延长线于点E．(1)连接AD则∠AOD=_______；(2)求证：DE 与⊙O 相切；(3)点F 在BC ⏜上 ∠CDF =45° DF 交AB 于点N ．若DE =6 求FN 的长．7．如图 AB 是⊙O 的直径点C 为⊙O 上一点 OF ⊥BC 垂足为F 交⊙O 于点E AE 与BC 交于点H 点D 为OE 的延长线上一点且∠ODB =∠AEC ．(1)求证：BD 是⊙O 的切线(2)求证：CE 2=EH ⋅EA(3)若⊙O 的半径为52 sinA =35 求BH 和DF 的长． 8．如图在⊙ABC 中 ⊙C=90° 点O 在AC 上以OA 为半径的⊙O 交AB 于点D BD 的垂直平分线交BC 于点E 交BD 于点F 连接DE ．（1）求证：直线DE 是⊙O 的切线（2）若AB=5 BC=4 OA=1 求线段DE 的长．9．如图 AB 是⊙O 的直径弦CD 与AB 交于点E 过点B 的切线BP 与CD 的延长线交于点P 连接OC CB ．(1)求证：AE ·EB =CE ·ED(2)若⊙O 的半径为 3 OE =2BE CE DE =95 求tan∠OBC 的值及DP 的长．10．如图菱形ABCD中AB=4以AB为直径作⊙O交AC于点E过点E作EF⊥AD于点F．(1)求证：EF是⊙O的切线(2)连接OF若∠BAD=60°求OF的长．(3)在（2）的条件下若点G是⊙O上的一个动点则线段CG的取值范围是什么？11．如图点C在以AB为直径的半圆O上（点C不与A B两点重合）点D是弧AC的中点DE⊥AB于点E连接AC交DE于点F连接OF过点D作半圆O的切线DP 交BA的延长线于点P．(1)求证：AC∥DP(2)求证：AC=2DE的值．(3)连接CE CP若AE⊙EO=1⊙2求CECP12．如图1 AB为⊙O直径CB与⊙O相切于点B D为⊙O上一点连接AD OC若AD//OC．（1）求证：CD为⊙O的切线（2）如图2 过点A作AE⊥AB交CD延长线于点E连接BD交OC于点F若AB=3AE=12求BF的长．13．已知：如图在⊙O中∠PAD=∠AEP AF=CF AB是⊙O的直径CD⊥AB于点G．(1)求证：AP是⊙O的切线．(2)若AG=4tan∠DAG=2求△ADE的面积．(3)在（2）的条件下求DQ的长．14．如图已知AB是⊙O的直径点E是⊙O上异于A B的点点F是弧EB的中点连接AE AF BF过点F作FC⊙AE交AE的延长线于点C交AB的延长线于点D⊙ADC的平分线DG交AF于点G交FB于点H．(1)求证：CD是⊙O的切线(2)求sin⊙FHG的值(3)若GH＝4√2HB＝2 求⊙O的直径．15．如图⊙O的两条弦AB、CD互相垂直垂足为E且AB=CD．(1)求证：AC=BD．(2)若OF⊥CD于F OG⊥AB于G问四边形OFEG是何特殊四边形？并说明理由．(3)若CE=1，DE=3求⊙O的半径．16．【问题提出】如图1 △ABC为⊙O内接三角形已知BC=a圆的半径为R 探究a R sin∠A之间的关系．【解决问题】如图2 若∠A为锐角连接BO并延长交⊙O于点D连接DC则∠A=∠D在△DBC中BD为⊙O的直径BC=a所以BD=2R,∠BCD=90°．所以在Rt△DBC中建立a R sin∠D的关系为________________．所以在⊙O内接三角形△ABC中a R sin∠A之间的关系为________________．类比锐角求法当∠A为直角和钝角时都有此结论．【结论应用】已知三角形△ABC中∠B=60°,AC=4则△ABC外接圆的面积为________．17．已知AB为⊙O的直径PA PC是⊙O的的切线切点分别为A C过点C作CD//AB交⊙O于D．（1）如图当P D O共线时若半径为r求证CD=r（2）如图当P D O不共线时若DE=2CE=8求tan∠POA．18．如图1 已知矩形ABCD中AB=2√3AD=3 点E为射线BC上一点连接DE以DE为直径作⊙O（1）如图2 当BE=1时求证：AB是⊙O的切线（2）如图3 当点E为BC的中点时连接AE交⊙O于点F连接CF求证：CF=CD （3）当点E在射线BC上运动时整个运动过程中CF长度是否存在最小值？若存在请直接写出CF长度的最小值若不存在请说明理由．19．已知四边形ABCD为⊙O的内接四边形直径AC与对角线BD相交于点E作CH⊥BD于H CH与过A点的直线相交于点F∠FAD=∠ABD.（1）求证：AF为⊙O的切线（2）若BD平分∠ABC求证：DA=DC（3）在（2）的条件下N为AF的中点连接EN若∠AED+∠AEN=135°⊙O 的半径为2√2求EN的长.20．如图1 直线l1⊥l2于点M以l1上的点O为圆心画圆交l1于点A B交l2于点C D OM＝4 CD＝6 点E为弧AD上的动点CE交AB于点F AG⊙CE 于点G连接DG AC AD．（1）求⊙O的半径长（2）若⊙CAD＝40° 求劣弧弧AD的长（3）如图2 连接DE是否存在常数k使CE−DE=k·EG成立？若存在请求出k的值若不存在请说明理由（4）若DG⊙AB则DG的长为（5）当点G在AD的右侧时请直接写出⊙ADG面积的最大值．参考答案1．（1）证明：⊙AB是⊙O的直径⊙∠ACB=90°⊙∠CAB+∠B=90°⊙∠CED=∠CAB∠B=∠D⊙∠CED+∠D=90°⊙∠DCE=∠ACB=90°⊙CD⊥CE⊙CD是⊙O的直径即OC是⊙O半径⊙CE是⊙O的切线（2）由（1）知CD⊥CE在Rt△ABC和Rt△DEC中⊙∠B=∠D tanB=12⊙tan∠B=tan∠D=CECD =12⊙CD=2CE在Rt△CDE中CD2+CE2=DE2DE=3√5⊙(2CE)2+CE2=(3√5)2解得CE=3（负值舍去）即线段CE的长为3．2．解：（1）⊙OB=OD⊙∠ABC=∠ODB⊙AB=AC⊙∠ABC=∠ACB⊙∠ODB=∠ACB⊙OD∥AC⊙DE⊥AC OD是半径⊙DE⊥OD⊙DE是⊙O的切线．（2）连接BF AD⊙⊙O的半径为5 AB为直径⊙AB=10∠ADB=90°∠BFC=90°⊙tanB=1设AD=x则BD=2x2在Rt△ABD中由勾股定理得：AD2+BD2=AB2即x2+(2x)2=102解得：x=2√5或x=−2√5（舍去）⊙BD=2x=4√5⊙AB=AC∠ADB=90°⊙BD=CD⊙BC=2BD=8√5由（1）知OD∥AC⊙∠ODB=∠C⊙OB=OD⊙∠B=∠ODB=∠C⊙tanC=tanB=1即CF=2BF2在Rt△BCF中BF2+CF2=BC2即BF2+(2BF)2=(8√5)2解得BF=8或BF=−8（舍去）⊙CF=2BF=16．3．（1）证明：⊙直径DE⊙AB于点F⊙AF＝BF⊙AM＝BM（2）连接AO BO如图由（1）可得AM＝BM⊙AM⊙BM⊙⊙MAF＝⊙MBF＝45°⊙⊙CMN＝⊙BMF＝45°⊙AO＝BO DE⊙AB∠AOB⊙⊙AOF＝⊙BOF＝12⊙⊙N＝15°⊙⊙ACM＝⊙CMN+⊙N＝60° 即⊙ACB＝60°∠AOB．⊙⊙ACB＝12⊙⊙AOF＝⊙ACB＝60°．⊙DE＝8⊙AO＝4．得AF＝2√3在Rt⊙AOF中由sin∠AOF=AFAO在Rt⊙AMF中AM＝√2AF＝2√6．得BM= AM＝2√6得CM＝2√2在Rt⊙ACM中由tan∠ACM=AMCM⊙BC＝CM+BM＝2√2+2√6．4．（1）证明：⊙弧AC=弧AC⊙∠ADC=∠B．⊙OB=OC⊙∠B=∠OCB．⊙CO平分∠BCD⊙∠OCB=∠OCD⊙∠ADC=∠OCD．⊙CE⊥AD⊙∠ADC+∠ECD=90°⊙∠OCD+∠ECD=90°即CE⊥OC．⊙OC为⊙O的半径⊙CE是⊙O的切线．（2）连接OD得OD=OC⊙∠ODC=∠OCD．⊙∠OCD=∠OCB=∠B⊙∠ODC=∠B⊙CO=CO⊙△OCD≌△OCB⊙CD=CB．⊙AB是⊙O的直径⊙∠ACB=90°⊙AC=AB⋅sinB=10×35=6⊙CB=√AB2−AC2=√102−62=8⊙CD=8⊙CE=CD⋅sin∠ADC=CD⋅sinB=8×35=245．5．解：（1）连接OB OC过点O作OD⊙BC于点D⊙BD =CD =12BC⊙⊙A =60°⊙⊙BOC =2⊙A =120°⊙OB =OC⊙⊙OBC =⊙OCB =180°−∠BOC2=30°⊙OB =2√3⊙BD =OB •cos30°=2√3×√32=3⊙BC =2BD =6．（2）设点G 为此三角形ABC 内切圆的圆心（角平分线的交点）过G 分别向ABAC BC 作垂线GM GN GQ⊙GM =GN =GQ CQ =CN BQ =BM AM =AN⊙AM +AN =AB +AC -BC =6⊙AM =AN =3．在Rt △AGM 中⊙⊙GAM =30°⊙GM =√3⊙S △ABC =12BC •AH =S △ABG +S △BCG +S △ACG=12AB •GM +12BC •GQ +12AC •GN=12GM（AB+AC+CB）=9√3∵BC=6, S△ABC=12BC•AH⊙AH=3√3．6．（1）解：如图1 连接OD AD⊙AB是⊙O的直径CD⊥AB⊙AB垂直平分CD⊙M是OA的中点⊙OM=12OA=12OD⊙cos∠DOM=OMOD =12⊙∠DOM=60°即∠AOD=60°故答案为：60°（2）解：⊙CD⊥AB AB是⊙O的直径⊙CM=MD⊙M是OA的中点⊙AM=MO又⊙∠AMC=∠DMO⊙△AMC≌△OMD⊙∠ACM=∠ODM⊙CA∥OD⊙DE⊥CA⊙∠E=90°⊙∠ODE=180°−∠E=90°⊙DE⊥OD⊙DE与⊙O相切（3）如图2 连接CF CN⊙OA⊥CD于M⊙M是CD中点⊙NC=ND⊙∠CDF=45°⊙∠NCD=∠NDC=45°⊙∠CND=90°⊙∠CNF=90°由（1）可知∠AOD=60°∠AOD=30°⊙∠ACD=12在Rt△CDE中∠E=90°∠ECD=30°DE=6=12⊙CD=DEsin30°在Rt△CND中∠CND=90°∠CDN=45°CD=12⊙CN=CD•sin45°=6√2⊙∠AOD=60°，OA=OD⊙△OAD是等边三角形⊙∠OAD=60°∠CAD=2∠OAD=120°⊙∠CFD=180°−∠CAD=60°在Rt△CNF中∠CNF=90°∠CFN=60°CN=6√2 =2√6．⊙FN=CNtan60°7．（1）证明：如图1所示⊙∠ODB=∠AEC∠AEC=∠ABC⊙∠ODB=∠ABC⊙OF⊥BC⊙∠BFD=90°⊙∠ODB+∠DBF=90°⊙∠ABC+∠DBF=90°即∠OBD=90°⊙BD⊥OB⊙AB是⊙O的直径⊙BD是⊙O的切线（2）证明：连接AC如图2所示⊙OF⊥BC⊙弧BE=弧CE⊙∠CAE=∠ECB⊙∠CEA=∠HEC⊙△AEC ∽△CEH⊙CE EH =EACE⊙CE 2=EH ⋅EA（3）解：连接BE 如图3所示⊙AB 是⊙O 的直径⊙∠AEB =90°⊙⊙O 的半径为52 sin∠BAE =35 ⊙AB =5 BE =AB ⋅sin∠BAE =5×35=3 ⊙EA =√AB 2−BE 2=4⊙弧BE =弧CE⊙BE =CE =3⊙CE 2=EH ⋅EA⊙EH =94⊙在Rt △BEH 中 BH =√BE 2+EH 2=√32+(94)2=154 ⊙∠A =∠C⊙sinC =sinA⊙OF ⊥BC 垂足为F⊙在Rt △CFE 中 FE =CE ⋅sinC =3×35=95 ⊙CF =√CE 2−EF 2=√32−(95)2=125 ⊙BF =CF =125⊙OF =√BO 2−BF 2=√(52)2−(125)2=710 ⊙∠ODB =∠ABC⊙tan∠ODB =tan∠ABC⊙BFDF =OFBF⊙BF 2=OF ⋅DF⊙(125)2=710DF ⊙DF =28835．8．解：（1）连接OD 如图⊙EF 垂直平分BD⊙ED=EB⊙⊙EDB=⊙B⊙OA=OD⊙⊙A=⊙ODA⊙⊙A+⊙B=90°⊙⊙ODA+⊙EDB=90°⊙⊙ODE=90°⊙OD⊙DE⊙直线DE 是⊙O 的切线（2）作OH⊙AD 于H 如图则AH=DH 在Rt △OAB 中 sinA=BC AB =45在Rt △OAH 中 sinA=OH OA =45⊙OH=45⊙AH=√12−(45)2=35⊙AD=2AH=65 ⊙BD=5﹣65=195⊙BF=12BD=1910在Rt⊙ABC 中 cosB=45 在Rt⊙BEF 中 cosB=BF BE =45⊙BE=54×1910=198 ⊙线段DE 的长为198．9．(（1）证明：连接AD∵∠A =∠BCD ∠AED =∠CEB ∴ΔAED ∽ΔCEB∴ AECE =EDEB∴AE ·EB =CE ·ED（2）解：∵⊙O 的半径为 3 ∴OA =OB =OC =3∵OE =2BE∴OE =2 BE =1 AE =5 ∵ CEDE =95 ∴设CE =9x DE =5x∵AE ·EB =CE ·ED∴5×1=9x ·5x解得：x 1=13 x 2=−13（不合题意舍去） ∴CE =9x =3 DE =5x =53 过点C 作CF ⊥AB 于F∵OC =CE =3∴OF =EF =12OE =1∴BF =2在RtΔOCF中∵∠CFO=90°∴CF2+OF2=OC2∴CF=2√2在RtΔCFB中∵∠CFB=90°∴tan∠OBC=CFBF =2√22=√2∵CF⊥AB于F∴∠CFB=90°∵BP是⊙O的切线AB是⊙O的直径∴∠EBP=90°∴∠CFB=∠EBP在ΔCFE和ΔPBE中{∠CFB=∠PBE EF=BE ∠FEC=∠BEP∴ΔCFE≅ΔPBE(ASA)∴EP=CE=3∴DP=EP−ED=3−53=43．10．:解：（1）证明：如图连接OE．⊙四边形ABCD是菱形∴∠CAD=∠CAB∵OA=OE∴∠CAB=∠OEA∴∠CAD=∠OEA∴OE∥AD∵EF⊥AD∴OE⊥EF又⊙OE是⊙O的半径⊙EF是⊙O的切线．（2）解：如图连接BE．⊙AB是⊙O的直径∴∠AEB=90°∵∠BAD=60°∴∠CAD=∠CAB=30°在Rt△ABE中AE=AB·cos30°=2√3在Rt△AEF中EF=AE·sin30°=√3AB=2在Rt△OEF中OE=12⊙OF=√OE2+EF2=√4+3=√7．（3）解：如图过点C作CM垂直AB交AB延长线于点M由（2）知∠BAD=60°∴∠ACB=∠CAB=30°，∠CBM=60°∴AB=BC=4，BM=2，CM=2√3∴AM=6，OM=6−2=4．⊙OC=√OM2+CM2=√42+(2√3)2=2√7⊙CG近=2√7−2CE远=2√7+2⊙线段CG的取值范围是：2√7−2≤CG≤2√7+211．（1）证明：连接OD∵D为弧AC的中点∴OD⊥AC又∵DP为⊙O的切线∴OD⊥DP∴AC∥DP（2）证明：∵DE⊥AB∴∠DEO=90°由（1）可知OD⊥AC设垂足为点M∴∠OMA=90°∴∠DEO=∠OMA AC=2AM又∵∠DOE=∠AOM OD=OA∴△ODE≌△OAM(AAS)∴DE=AM∴AC=2AM=2DE（3）解：连接OD OC CE CP∵∠ODP=∠OED=90°∠DOE=∠DOP ∴△DOE∽△POD∴ODOP =OEOD∴OD2=OE⋅OP ∵OC=OD∴OC2=OE⋅OP∴OCOE =OPOC又∵∠COE=∠POC ∴△COE∽△POC∴CECP =OEOC∵AE:EO=1:2∴OEOA =23∴OEOC =23∴CECP =23．12．解：（1）连接OD⊙CB与⊙O相切于点B⊙OB⊥BC⊙AD//OC⊙∠A=∠COB,∠ADO=∠DOC⊙OA=OD⊙∠A=∠ADO=∠COB=∠DOC⊙△DOC≌△BOC(SAS)⊙∠ODC=∠OBC=90°⊙OD⊥DC又OD为⊙O半径⊙CD为⊙O的切线（2）解：设CB=x⊙AE⊥EB⊙AE为⊙O的切线⊙CD CB为⊙O的切线⊙ED=AE=4,CD=CB=x,∠DOC=∠BCO⊙BD⊥OC过点E作EM⊥BC于M则EM=12,CM=x−4⊙(4+x)2=122+(x−4)2解得x=9⊙CB=9⊙OC=√62+92=3√13⊙AB是直径且AD⊙OC⊙⊙OFB=⊙ADB=⊙OBC=90°又⊙⊙COB=⊙BOF⊙⊙OBF⊙⊙OCB⊙OB BF =OCBC⊙BF=OB⋅BCOC =6×93√13=1813√1313．（1）证明：如图所示连接AC ⊙AB是⊙O的直径CD⊥AB⊙弧AD=弧AC⊙∠AEP=∠ADC⊙∠PAD=∠AEP⊙∠PAD=∠ADC⊙AP∥CD⊙AP⊥AB⊙AB是⊙O的直径⊙AP是⊙O的切线（2）解：如图所示连接BD⊙AF=CF⊙∠FAC=∠FCA⊙弧CE=弧AD⊙弧AD=弧AC⊙弧AD=弧AC=弧CE⊙∠ADG=∠QDG⊙AB⊥CD⊙∠AGD=∠QGD=90°又⊙OG=OG⊙△AGD≌△OGD(ASA)⊙QG=AG=4∠DQG=∠DAG=2在Rt△ADG中tan∠DAG=DGAG⊙DG=2AG=8⊙QD=√DG2+QG2=4√5连接OD过点E作EH⊥AB于H设圆O的半径为r则OG=r−4在Rt△ODG中由勾股定理得OD2=OG2+DG2⊙r2=(r−4)2+82解得r=10⊙AB=20⊙BQ=12⊙∠AEQ=∠DBQ，∠EAQ=∠BDQ⊙△AQE∽△DQB⊙QE BQ =AQDQ即QE12=84√5⊙QE=12√55⊙∠EQH=∠DQG=∠DAG⊙在Rt△EQH中tan∠EQH=EHQH=2⊙EH=2QH⊙EH2+QH2=QE2⊙4QH2+QH2=1445⊙QH=125⊙EH=245⊙S△ADE=S△ADQ+S△AEQ=12AQ⋅DG+12AQ⋅EH=12×8×8+12×8×245=70.4．（3）解：由（2）得DQ=4√5．14．（1）证明：连接OF．⊙OA＝OF⊙⊙OAF＝⊙OF A⊙EF̂=FB̂,⊙⊙CAF＝⊙F AB⊙⊙CAF＝⊙AFO⊙OF∥AC⊙AC⊙CD⊙OF⊙CD⊙OF是半径⊙CD是⊙O的切线．（2）⊙AB是直径⊙⊙AFB＝90°⊙OF⊙CD⊙⊙OFD＝⊙AFB＝90°⊙⊙AFO＝⊙DFB⊙⊙OAF＝⊙OF A⊙⊙DFB＝⊙OAF⊙GD平分⊙ADF⊙⊙ADG＝⊙FDG⊙⊙FGH＝⊙OAF+⊙ADG⊙FHG＝⊙DFB+⊙FDG⊙⊙FGH＝⊙FHG＝45°⊙sin⊙FHG=sin45°=√22（3）解：过点H作HM⊙DF于点M HN⊙AD于点N．⊙HD平分⊙ADF⊙HM＝HNS△DHF⊙S△DHB= FH⊙HB=DF ⊙DB⊙⊙FGH是等腰直角三角形GH＝4√2⊙FH＝FG＝4⊙DF DB =42=2设DB＝k DF＝2k⊙⊙FDB＝⊙ADF⊙DFB＝⊙DAF ⊙⊙DFB⊙⊙DAF⊙DF2＝DB•DA⊙AD＝4k⊙GD平分⊙ADF⊙FG AG =DFAD=12⊙AG＝8⊙⊙AFB＝90° AF＝12 FB＝6∴AB=√AF2+BF2=√122+622=6√5⊙⊙O的直径为6√515．（1）证明：⊙AB=CD⊙弧AB=弧CD⊙弧AB−弧BC=弧CD−弧BC即弧AC=弧BD⊙AC=BD（2）解：四边形OFEG是正方形.理由如下：⊙AB⊥CD OF⊥CD OG⊥AB⊙∠AED=∠OGE=∠OFE=90°⊙四边形OFEG是矩形．如图连接OA OD．⊙OF⊥CD OG⊥AB⊙CF=DF AG=BG．⊙CD=AB⊙AG=DF．⊙OG=√OA2−AG2OF=√OD2−DF2OA=OD⊙OG=OF⊙四边形OFEG是正方形（3）解：⊙CE=1 DE=3⊙CD=4⊙CF=DF=2⊙EF=CF-CE=2-1=1．⊙四边形OFEG是正方形⊙OF=EF=1．在Rt△OED中OD=√OF2+DF2=√5⊙⊙O的半径为√5．16．:解：【解决问题】如图连接BO并延长交⊙O于点D连接DC则∠A=∠D 在△DBC中⊙BD为⊙O的直径BC=a⊙BD=2R,∠BCD=90°⊙sinD=BCBD =a2R⊙sinA=a2R故答案为：sinD=a2R sinA=a2R【结论应用】解：设△ABC外接圆的半径为R ⊙∠B=60°,AC=4⊙sinB=AC2R⊙√3 2=42R解得：R=43√3⊙△ABC外接圆的面积为π×(43√3)2=163π．故答案为：163π17．（1）证明：连接OC⊙PA PC是⊙O的切线切点分别为A C ⊙PA=PC∠PAO=∠PCO=90°在RtΔPAO和RtΔPCO中{PA=PCPO=PO⊙RtΔPAO≌RtΔPCO(HL)⊙∠POA=∠POC⊙CD//AB⊙∠CDO=∠DOA⊙∠CDO=∠COD⊙CD=OC=r（2）解：设OP交CD于E连接OC过O作OH⊥CD于点H由（1）可知RtΔPAO≌RtΔPCO⊙∠POA=∠POC⊙CD//AB⊙∠CEO=∠EOA⊙∠CEO=∠COE⊙CE=CO=8⊙CD=CE+ED=10⊙OH⊥CD⊙CH=DH=5⊙EH=DH−DE=3在RtΔCHO中⊙OH=√OC2−CH2=√82−52=√39在RtΔOHE中⊙tan∠POA=tan∠HEO=OHEH =√393⊙tan∠POA=√393．18．解：（1）如图过点O作OM⊥AB且OM的反向延长线交CD于点N．由题意可知四边形BCNM为矩形⊙MN=AD=3⊙O为圆心即O为DE中点⊙N为DC中点即线段ON为△DEC中位线又⊙CE=BC−BE=3−1=2⊙ON=12CE=1⊙OM=MN -ON=3-1=2．在Rt △DEC 中 DE =√CD 2+CE 2=√(2√3)2+22=4． ⊙OD=DE=OM=2．即AB 为⊙O 的切线．（2）设⊙O 与AD 交于点G 连接CG EG DF FG ⊙DE 为直径⊙∠EGD =∠EFD =90°．⊙∠GEC =90°⊙CG 为直径．⊙∠CFG =∠CDG =90°⊙E 为BC 中点⊙G 为AD 中点在Rt △AFD 中 FG 为中线⊙AG=DG=FG在Rt △CFG 和Rt △CDG 中 {FG =DG CG =CG⊙△CFG ≅△CDG(HL)．⊙CF=CD ．（3）如图取AD 中点H 连接CH FH FD ．由（2）可知FH =12AD =32 在Rt △CDH 中 CH =√CD 2+HD 2=√(2√3)2+(32)2=√572 ⊙CF ≥CH −FH =√572−32． ⊙当F 点在CH 上时CF 长有最小值最小值为√572−32．19．解：（1）⊙AC 为⊙O 的直径⊙⊙ADC =90°⊙⊙DAC +⊙DCA =90°．⊙弧AD =弧AD⊙⊙ABD =⊙DCA ．⊙⊙F AD =⊙ABD⊙⊙F AD =⊙DCA⊙⊙F AD +⊙DAC =90°⊙CA ⊙AF⊙AF 为⊙O 的切线．（2）连接OD ．⊙弧AD =弧AD⊙⊙ABD=1⊙AOD．2⊙弧DC=弧DC⊙DOC．⊙⊙DBC=12⊙BD平分⊙ABC⊙⊙ABD=⊙DBC⊙⊙DOA=⊙DOC⊙DA=DC．（3）连接OD交CF于M作EP⊙AD于P．⊙AC为⊙O的直径⊙⊙ADC=90°．⊙DA=DC⊙DO⊙AC⊙⊙F AC=⊙DOC=90° AD=DC=√(2√2)2+(2√2)2=4 ⊙⊙DAC=⊙DCA=45° AF⊙OM．⊙AO=OCAF．⊙OM=12⊙⊙ODE+⊙DEO=90° ⊙OCM+⊙DEO=90°⊙⊙ODE=⊙OCM．⊙⊙DOE=⊙COM OD=OC⊙⊙ODE⊙⊙OCM⊙OE=OM．设OM=m⊙OE =m AE =2√2−m AP =PE =2−√22m⊙DP =2+√22m ． ⊙⊙AED +⊙AEN =135° ⊙AED +⊙ADE =135°⊙⊙AEN =⊙ADE ．⊙⊙EAN =⊙DPE⊙⊙EAN ⊙⊙DPE⊙AE DP =AN PE ⊙2√2−m 2+√22m =m2−√22m⊙m =2√23⊙AN =2√23 AE =4√23由勾股定理得：NE =2√103．20．解：（1）连接OD⊙AB 是⊙O 的直径 l 1⊥l 2 CD ＝6⊙CM =DM =12CD =3在Rt △DOM 中 OM ＝4⊙OD=√OM2+CM2=5即⊙O的半径长为5（2）⊙AB是⊙O的直径l1⊥l2⊙弧BC=弧BD⊙∠BAD=∠BAC=12∠CAD=20°⊙∠BOD=2∠BAD=40°⊙∠AOD=180°−∠BOD=140°⊙劣弧弧AD的长为140×π×5180=35π9（3）存在常数k=2理由如下：如图在CG上截取CH=DE连接AH AE⊙AB垂直平分CD⊙AC=AD又⊙⊙ACH=⊙ADE⊙⊙ACH⊙⊙ADE（SAS）⊙AH=AE⊙ AG⊙HE⊙HG=EG⊙CE-DE=2EG⊙k=2（4）⊙DG⊙AB⊙⊙CFM⊙⊙CGD⊙FM DG =CFCG=CMCD=12⊙CF=FG DG=2FM⊙⊙CMF=⊙AGF⊙CFM=⊙AFG ⊙⊙CFM⊙⊙AFG⊙CF AF =FMFG⊙FM×AF=CF×FG=CF2设FM=x则AF=9-x⊙x(9−x)=32+x2解得：x=32或3⊙DG=3或6（5）如图取AC的中点P当PG⊙AD时⊙ADG的面积最大在Rt△AMC中⊙CMA=90° CM=3 AM=OA+OM=5+4=9⊙AD=AC=√CM2+AM2=√32+92=3√10在Rt△AGC中⊙CGA=90° 点P为AC的中点⊙PG=12AC=3√102过点C作CN⊙AD于点N在Rt⊙CDN和Rt⊙ADM中⊙⊙CND=⊙AMD=90° ⊙CDN=⊙ADM ⊙Rt⊙CDN~Rt⊙ADM⊙CN AM =CDAD⊙CN=AM⋅CDAD =9×63√10=9√105设PG交AD于点K ⊙PK⊙AD CN⊙AD ⊙PK⊙CN⊙⊙APK⊙⊙CAN⊙PK CN =APAC=12⊙PK=12CN=9√1010⊙GK=PG−PK=3√102−9√1010=3√105⊙⊙ADG面积的最大值为12AD⋅GK=12×3√10×3√105=9．。

九年级上册圆的证明题及答案

DOBC A EPEECOB P D AOBACDBACDO1．如图，已知直线PA 交⊙O 于A 、B 两点，AE 是⊙O 的直径，C 为⊙O 上一点，且AC 平分∠PAE ，过点C 作CD ⊥PA 于D ．（1）求证：CD 是⊙O 的切线；（2）若AD ：DC =1：3，AB =8，求⊙O 的半径．（1）证明：连结OC ．∵ OC =OA ，∴ ∠OAC = ∠OCA∵ AC 平分∠PAE ，∴ ∠DAC = ∠OAC ，∴ ∠DAC = ∠OCA ， ∴ AD ∥OC ．∵ CD ⊥PA ，∴ ∠ADC = ∠OCD =90°，即 CD ⊥OC ，点C 在⊙O 上，∴ CD 是⊙O 的切线．（2）解：过O 作OE ⊥AB 于E ．∴ ∠OEA =90°∵ AB =8， ∴ AE =4．在Rt △AEO 中，∠AEO =90°，∴ AO 2=42+OE 2． ∵ ∠EDC = ∠OEA =∠DCO =90°，∴ 四边形DEOC 是矩形， ∴ OC =DE ，OE =CD ．∵ AD:DC =1:3，∴ 设AD =x ，则DC =OE =3x ，OA =OC =DE =DA +AE =x +4， ∴ (x +4)2=42+(3x )2，解得 x 1=0(不合题意，舍去)，x 2=1．则 OA =5．∴ ⊙O 的半径是5． 2.如图1和图2，MN 是⊙O 的直径，弦AB 、CD•相交于MN•上的一点P ，•∠APM=∠CPM ．（1）由以上条件，你认为AB 和CD 大小关系是什么，请说明理由．（2）若交点P 在⊙O 的外部，上述结论是否成立若成立，加以证明；若不成立，请说明理由．BA CE DP ONM FB A CE DPNM F解：（1）AB=CD 理由：过O 作OE 、OF 分别垂直于AB 、CD ，垂足分别为E 、F∵∠APM=∠CPM ∴∠1=∠2 OE=OF 连结OD 、OB 且OB=OD ∴Rt △OFD ≌Rt △OEB ∴DF=BE 根据垂径定理可得：AB=CD（2）作OE ⊥AB ，OF ⊥CD ，垂足为E 、F ∵∠APM=∠CPN 且OP=OP ，∠PEO=∠PFO=90° ∴Rt △OPE ≌Rt △OPF ∴OE=OF 连接OA 、OB 、OC 、OD易证Rt △OBE ≌Rt △ODF ，Rt △OAE ≌Rt △OCF ∴∠1+∠2=∠3+∠4 ∴AB=CD3．如图，AB 是⊙O 的直径，BD 是⊙O 的弦，延长BD 到C ，使AC=AB ，BD 与CD 的大小有什么关系为什么解：BD=CD 理由是：如图，连接AD ∵AB 是⊙O 的直径 ∴∠ADB=90°即AD ⊥BC 又∵AC=AB ∴BD=CD4. 如图，点O 是△ABC 的内切圆的圆心，若∠BAC=80°，则∠BOC=（） A ．130° B ．100° C ．50° D ．65° 答案A5．如图，AB 为⊙O 的直径，C 是⊙O 上一点，D 在AB 的延长线上，且∠DCB=•∠A ．（1）CD 与⊙O 相切吗如果相切，请你加以证明，如果不相切，请说明理由．（2）若CD 与⊙O 相切，且∠D=30°，BD=10，求⊙O 的半径．解：（1）CD 与⊙O 相切 ∵AB 是直径 ∴∠ACB=90°，即∠ACO+∠OCB=90°∵∠A=∠OCA 且∠DCB=∠A ∴∠OCA=∠DCB ∴∠OCD=90° 综上：CD 是⊙O 的切线．（2）在Rt △OCD 中，∠D=30° ∴∠COD=60° ∴∠A=30° ∴∠BCD=30° ∴BC=BD=10 ∴AB=20，∴r=10 答：（1）CD 是⊙O 的切线，（2）⊙O 的半径是10．6．如图，已知正六边形ABCDEF ，其外接圆的半径是a ，•求正六边形的周长和面积．解：如图所示，由于ABCDEF 是正六边形，所以它的中心角等于3606︒=60°，•△OBC 是等边三角形，从而正六边形的边长等于它的半径．因此，所求的正六边形的周长为6a 在Rt △OAM 中，OA=a ，AM=12AB=12a 利用勾股定理，可得边心距OM=221()2a a -=123a∴所求正六边形的面积=6×12×AB×OM=6×12×a×32a=323a 27．已知扇形的圆心角为120°，面积为300πcm 2．（1）求扇形的弧长；（2）若将此扇形卷成一个圆锥，则这个圆锥的轴截面面积为多少解：（1）如图所示： ∵300π=2120360R π ∴R=30∴弧长L=12030180π⨯⨯=20π（cm ）（2）如图所示： ∵20π=20πr ∴r=10，R=30 AD=900100-=202 ∴S 轴截面=12×BC×AD =12×2×10×202=2002（cm 2）因此，扇形的弧长是20πcm 卷成圆锥的轴截面是2002cm 2． 8.如图，AB 是⊙O 的直径，BC 是弦，OD ⊥BC 于E ，交⋂BC 于D ． (1)请写出五个不同类型的正确结论； (2)若BC =8，ED ＝2，求⊙O 的半径．解：(1)不同类型的正确结论有：①BE =CE ;②弧BD=弧CD ③∠BED =90°④∠BOD =∠A ;⑤AC ∥OD ，⑥AC ⊥BC ; ⑦OE 2+BE 2=OB 2;⑧S △ABC ＝BC ·OE ;⑨△BOD 是等腰三角形，⑩△BOE ∽△BAC ; (2)∵OD ⊥BC ， ∴BE ＝CE =12BC =4．设⊙O 的半径为R ，则OE =OD －DE=R －2．在Rt △OEB 中，由勾股定理得 OE 2＋BE 2=OB 2，即(R －2)2＋42=R 2．解得R ＝5． ∴ ⊙ O 的半径为59.已知：如图等边ABC △内接于⊙O ，点P 是劣弧PC 上的一点（端点除外），延长BP 至D ，使BD AP =，连FDECBAOM结CD ．（1）若AP 过圆心O ，如图①，请你判断PDC △是什么三角形并说明理由．（2）若AP 不过圆心O ，如图②，PDC △又是什么三角形为什么解：（1）PDC △为等边三角形．理由：ABC ∵△为等边三角形AC BC =∴，又∵在⊙O 中PAC DBC ∠=∠又AP BD =∵ APC BDC ∴△≌△． PC DC =∴ 又AP ∵过圆心O ，AB AC =，60BAC ∠=°1302BAP PAC BAC ∠=∠=∠=∴° 30BAP BCP ∠=∠=∴°，30PBC PAC ∠=∠=°303060CPD PBC BCP ∠=∠+∠=+=∴°°° PDC ∴△为等边三角形．（2）PDC △仍为等边三角形理由：先证APC BDC △≌△（过程同上） PC DC =∴ 60BAP PAC ∠+∠=∵° 又BAP BCP ∠=∠∵，PAC PBC ∠=∠60CPD BCP PBC BAP PAC ∠=∠+∠=∠+∠=∴° 又PC DC =∵ PDC ∴△为等边三角形．10.(1)如图OA 、OB 是⊙O 的两条半径，且OA ⊥OB ，点C 是OB 延长线上任意一点：过点C 作CD 切⊙O 于点D ，连结AD 交DC 于点E ．求证：CD=CE(2)若将图中的半径OB 所在直线向上平行移动交OA 于F ，交⊙O 于B ，其他条件不变，那么上述结论CD=CE 还成立吗为什么(3)若将图中的半径OB 所在直线向上平行移动到⊙O 外的CF ，点E 是DA 的延长线与CF 的交点，其他条件不变，那么上述结论CD=CE 还成立吗为什么解：(1)证明：连结OD 则OD ⊥CD ，∴∠CDE+∠ODA=90° 在Rt △AOE 中，∠AEO+∠A=90°在⊙O 中，OA=OD ∴∠A=∠ODA ， ∴∠CDE=∠AEO 又∵∠AEO=∠CED ，∠CDE=∠CED ∴CD=CE (2)CE=CD 仍然成立． ∵原来的半径OB 所在直线向上平行移动∴CF ⊥AO 于F ，在Rt △AFE 中，∠A+∠AEF=90°．连结OD ，有∠ODA+∠CDE=90°，且OA=OD ．∠A=∠ODA ∴∠AEF=∠CDE 又∠AEF=∠CED ∴∠CED=∠CDE ∴CD=CE(3)CE=CD 仍然成立．∵原来的半径OB 所在直线向上平行移动．AO ⊥CF 延长OA 交CF 于G ，在Rt △AEG 中，∠AEG+∠GAE=90° 连结OD ，有∠CDA+∠ODA=90°，且OA=OD ∴∠ADO=∠OAD=∠GAE ∴∠CDE=∠CED ∴CD=CEAOCPB图①AOCPB图②11.AB 是⊙O 的直径，PA 切⊙O 于A ，OP 交⊙O 于C ，连BC ．若30P ∠=o，求B ∠的度数．解： PA Q 切⊙O 于A AB ，是⊙O 的直径， ∴90PAO ∠=o．30P ∠=o Q ，∴60AOP ∠=o ．∴1302B AOP ∠=∠=o12.如图，四边形ABCD 内接于⊙O ，BD 是⊙O 的直径，AE CD ⊥，垂足为E ，DA 平分BDE ∠．（1）求证：AE 是⊙O 的切线；（2）若301cm DBC DE ∠==o，，求BD 的长．（1）证明：连接OA ，DA Q 平分BDE ∠，BDA EDA ∴∠=∠．OA OD ODA OAD =∴∠=∠Q ，．OAD EDA ∴∠=∠．OA CE ∴∥． AE DE ⊥Q ，9090AED OAE DEA ∴∠=∠=∠=o o ，．AE OA ∴⊥．AE ∴是⊙O 的切线．（2）BD Q 是直径，90BCD BAD ∴∠=∠=o．3060DBC BDC ∠=∠=o o Q ，，120BDE ∴∠=o ．DA Q 平分BDE ∠，60BDA EDA ∴∠=∠=o ．30ABD EAD ∴∠=∠=o ．在Rt AED △中，90302AED EAD AD DE ∠=∠=∴=oo，，．在Rt ABD △中，903024BAD ABD BD AD DE ∠=∠=∴==oo，，． DE Q 的长是1cm ，BD ∴的长是4cm ．13.如图，已知在⊙O 中，AB=34，AC 是⊙O 的直径，AC ⊥BD 于F ，∠A=30°.(1)求图中阴影部分的面积；(2)若用阴影扇形OBD 围成一个圆锥侧面，请求出这个圆锥的底面圆的半径. 解：连结AD ．∵AC ⊥BD ，AC 是直径，∴AC 垂直平分BD 。

中考数学专题复习《圆的证明与计算》检测题(含答案)

专题二圆的证明与计算类型一圆基本性质的证明与计算1.如图，⊙O 的半径为5，点P 在⊙O 外，PB 交⊙O 于A 、B 两点，PC 交⊙O 于D 、C 两点． (1)求证：P A ·PB ＝PD ·PC ；(2)若P A ＝454，AB ＝194，PD ＝DC ＋2，求点O 到PC 的距离．第1题图2. 如图，△ABC 是⊙O 的内接三角形，AB ＝AC ，点P 是AB ︵的中点，连接P A ，PB ，PC .(1)如图①，若∠BPC ＝60°，求证：AC ＝3AP ； (2)如图②，若sin ∠BPC ＝2425，求tan ∠P AB 的值．第2题图3. 已知⊙O 中弦AB ⊥弦CD 于E ，tan ∠ACD ＝32. (1)如图①，若AB 为⊙O 的直径，BE ＝8，求AC 的长；(2)如图②，若AB 不为⊙O 的直径，BE ＝4，F 为BC ︵上一点，BF ︵＝BD ︵，且CF ＝7，求AC 的长．第3题图4.如图，△ABC 中，AB ＝AC ，以AB 为直径作⊙O ，交BC 于点D ，交CA 的延长线于点E ，连接AD 、DE .(1)求证：D 是BC 的中点；(2)若 DE ＝3，BD －AD ＝2，求⊙O 的半径； (3)在(2)的条件下，求弦AE 的长．第4题图5.如图，⊙O 的半径为1，A ，P ，B ，C 是⊙O 上的四个点， ∠APC ＝∠CPB ＝60°.(1)判断△ABC 的形状：________；(2)试探究线段P A ，PB ，PC 之间的数量关系，并证明你的结论； (3)当点P 位于AB ︵的什么位置时，四边形APBC 的面积最大？求出最大面积．第5题图备用图类型二与切线有关的证明与计算(一、与三角函数结合1.已知：如图，在△ABC中，AB＝BC，D是AC中点，BE平分∠ABD 交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F.(1)求证：AC与⊙O相切；(2)当BD＝6，sin C＝35时，求⊙O的半径．第1题图2.如图，AB为⊙O的直径，P是BA延长线上一点，PC切⊙O于点C，CG是⊙O的弦，CG⊥AB，垂足为D.(1)求证：∠PCA＝∠ABC；(2)过点A作AE∥PC，交⊙O于点E，交CD于点F，连接BE.若sin ∠P ＝35，CF ＝5，求BE 的长．第2题图3. 如图①，在⊙O 中，直径AB ⊥CD 于点E ，点P 在BA 的延长线上，且满足∠PDA ＝∠ADC .(1)判断直线PD 与⊙O 的位置关系，并说明理由；(2)延长DO 交⊙O 于M (如图②)，当M 恰为BC ︵的中点时，试求DE BE 的值；(3)若P A ＝2，tan ∠PDA ＝12，求⊙O 的半径．第3题图二、与相似三角形结合1.如图，在Rt △ABC 中，∠ACB ＝90°，E 是BC 的中点，以AC 为直径的⊙O 与AB 边交于点D ，连接DE . (1)求证：△ABC ∽△CBD ； (2)求证：直线DE 是⊙O 的切线．第1题图2. 如图，⊙O 的圆心在Rt △ABC 的直角边AC 上，⊙O 经过C 、D 两点，与斜边AB 交于点E ，连接BO 、ED ，有BO ∥ED ，作弦EF ⊥AC 于G ，连接DF .(1)求证：CO ·CD ＝DE ·BO ；(2)若⊙O 的半径为5，sin ∠DFE ＝35，求EF 的长．第2题图3. 如图，在△ABC 中，AB ＝AC ，以AB 为直径作半圆⊙O ，交BC 于点D ，连接AD ，过点D 作DE ⊥AC ，垂足为点E ，交AB 的延长线于点F .(1)求证：EF 是⊙O 的切线；(2)若⊙O 的半径为5，sin ∠ADE ＝45，求BF 的长．第3题图4.如图，在△ABC中，∠C＝90°，以AB上一点O为圆心，OA长为半径的圆恰好与BC相切于点D，分别交AC、AB于点E、F.(1)若∠B＝30°，求证：以A、O、D、E为顶点的四边形是菱形；(2)若AC＝6，AB＝10，连接AD，求⊙O的半径和AD的长．第4题图5.已知Rt△ABC中，AB是⊙O的弦，斜边AC交⊙O于点D，且AD ＝DC，延长CB交⊙O于点E.(1)图①的A、B、C、D、E五个点中，是否存在某两点间的距离等于线段CE的长？请说明理由；(2)如图②，过点E作⊙O的切线，交AC的延长线于点F.①若CF＝CD时，求sin∠CAB的值；②若CF＝aCD(a>0)时，试猜想sin∠CAB的值．(用含a的代数式表示，直接写出结果)第5题图6.已知：如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，OF延长线交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB＝∠AEC.(1)求证：BD是⊙O的切线；(2)求证：CE2＝EH·EA；(3)若⊙O 的半径为5，sin A ＝35，求BH 的长．第6题图7.如图①，△ABC 内接于⊙O ，∠BAC 的平分线交⊙O 于点D ，交BC 于点E (BE ＞EC )，且BD ＝2 3.过点D 作DF ∥BC ，交AB 的延长线于点F .(1)求证：DF 为⊙O 的切线；(2)若∠BAC ＝60°，DE ＝7，求图中阴影部分的面积；(3)若AB AC ＝43，DF ＋BF ＝8，如图②，求BF 的长．第7题图三、与全等三角形结合1.如图，已知PC 平分∠MPN ，点O 是PC 上任意一点，PM 与⊙O 相切于点E ，交PC 于A 、B 两点． (1)求证：PN 与⊙O 相切；(2)如果∠MPC ＝30°，PE ＝23，求劣弧BE ︵的长．第1题图2.如图，已知BC是⊙O的弦，A是⊙O外一点，△ABC为正三角形，D为BC的中点，M是⊙O上一点，并且∠BMC ＝60°.(1)求证：AB是⊙O的切线；(2)若E、F分别是边AB、AC上的两个动点，且∠EDF＝120°，⊙O 的半径为2.试问BE＋CF的值是否为定值，若是，求出这个定值；若不是，请说明理由．第2题图3. 已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥AC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接AE.(1)求证：AE与⊙O相切；(2)连接BD，若ED∶DO＝3∶1，OA＝9，求AE的长和tan B的值．第3题图4. 如图，PB为⊙O的切线，B为切点，直线PO交⊙O于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O 交于点C，连接BC，AF.(1)求证：直线P A为⊙O的切线；(2)试探究线段EF、OD、OP之间的等量关系，并加以证明；(3)若BC＝6，tan∠F＝12，求cos∠ACB的值和线段PE的长．第4题图5. 如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，∠ACB 的平分线CD 交⊙O 于点D ，过点D 作⊙O 的切线PD ，交CA 的延长线于点P ，过点A 作AE ⊥CD 于点E ，过点B 作BF ⊥CD 于点F . (1)求证：PD ∥AB ； (2)求证：DE ＝BF ；(3)若AC ＝6，tan ∠CAB ＝43，求线段PC 的长．第5题图6.如图，点P 是⊙O 外一点，P A 切⊙O 于点A ，AB 是⊙O 的直径，连接OP ，过点B 作BC ∥OP 交⊙O 于点C ，连接AC 交OP 于点D . (1)求证：PC 是⊙O 的切线；(2)若PD ＝163，AC ＝8，求图中阴影部分的面积；(3)在(2)的条件下，若点E 是AB ︵的中点，连接CE ，求CE 的长．第6题图7. 如图①，AB是⊙O的直径，OC⊥AB，弦CD与半径OB相交于点F，连接BD，过圆心O作OG∥BD，过点A作⊙O的切线，与OG 相交于点G，连接GD，并延长与AB的延长线交于点E.(1)求证：GD＝GA；(2)求证：△DEF是等腰三角形；(3)如图②，连接BC，过点B作BH⊥GE，垂足为点H，若BH＝9，⊙O的直径是25，求△CBF的周长．第7题图专题二圆的证明与计算类型一圆基本性质的证明与计算1. (1)证明：如解图，连接AD，BC，∵四边形ABCD内接于⊙O，∴∠P AD＝∠PCB，∠PDA＝∠PBC，∴△P AD ∽△PCB ， ∴P A PD ＝PC PB ， ∴P A ·PB ＝PD ·PC ；(2)解：如解图，连接OD ，过O 点作OE ⊥DC 于点E ， ∵P A ＝454，AB ＝194，PD ＝DC ＋2，∴PB ＝P A ＋AB ＝16，PC ＝PD ＋DC ＝2DC ＋2， ∵P A ·PB ＝PD ·PC ，∴454×16＝(DC ＋2)(2DC ＋2)，解得DC ＝8或DC ＝－11(舍去)， ∴DE ＝12DC ＝4， ∵OD ＝5，∴在Rt △ODE 中，OE ＝OD 2－DE 2＝3，即点O 到PC 的距离为3.2. (1)证明：∵∠BAC 与∠BPC 是同弧所对的圆周角， ∴∠BAC ＝∠BPC ＝60°，又∵AB ＝AC ，∴△ABC 为等边三角形， ∴∠ACB ＝60°， ∵点P 是AB ︵的中点， ∴P A ︵＝PB ︵，∴∠ACP ＝∠BCP ＝12∠ACB ＝30°，而∠APC ＝∠ABC ＝60°， ∴△APC 为直角三角形， ∴tan ∠APC ＝AC AP ， ∴AC ＝AP tan60°＝3AP ；(2)解：连接AO 并延长交PC 于点E ，交BC 于点F ，过点E 作EG ⊥AC 于点G ，连接OC ，BO ，如解图，∵AB ＝AC ， ∴AF ⊥BC ， ∴BF ＝CF ， ∵点P 是AB ︵中点， ∴∠ACP ＝∠PCB ， ∴EG ＝EF .∵∠BPC ＝∠BAC ＝12∠BOC ＝∠FOC ， ∴sin ∠FOC ＝sin ∠BPC ＝2425，设FC ＝24a ，则OC ＝OA ＝25a ，∴OF ＝OC 2－FC 2＝7a ，AF ＝25a ＋7a ＝32a ，在Rt △AFC 中，∵AC 2＝AF 2＋FC 2， ∴AC ＝（32a ）2＋（24a ）2＝40a ， ∵∠EAG ＝∠CAF ， ∴△AEG ∽△ACF ， ∴EG CF ＝AE AC ，又∵EG ＝EF ，AE ＝AF －EF ，第2题解图∴EG 24a ＝32a －EG 40a ，解得EG ＝12a ，在Rt △CEF 中，tan ∠ECF ＝EF FC ＝12a 24a ＝12， ∵∠P AB ＝∠PCB ，∴tan ∠P AB ＝tan ∠PCB ＝tan ∠ECF ＝12. 3. 解：(1)如解图①，连接BD ， ∵直径AB ⊥弦CD 于点E ， ∴CE ＝DE ，∵∠ACD 与∠ABD 是同弧所对的圆周角， ∴∠ACD ＝∠ABD ， ∴tan ∠ABD ＝tan ∠ACD ＝32， ∴ED EB ＝AE CE ＝32，即ED 8＝32， ∴ED ＝12， ∴CE ＝ED ＝12，又∵AE ＝32CE ＝18， ∴AC ＝AE 2＋CE 2＝613；(2)连接CB ，过B 作BG ⊥CF 于G ，如解图②， ∵BF ︵＝BD ︵， ∴∠BCE ＝∠BCG ，在△CEB 和△CGB 中第3题解图①⎩⎪⎨⎪⎧∠BCE ＝∠BCG ∠BEC ＝∠BGC BC ＝BC， ∴△CEB ≌△CGB (AAS)， ∴BE ＝BG ＝4，∵四边形ACFB 内接于⊙O ， ∴∠A ＋∠CFB ＝180°，又∵∠CFB ＋∠BFG ＝180°， ∴∠BFG ＝∠A ， ∵∠FGB ＝∠AEC ＝90°， ∴△BFG ∽△CAE ， ∴FG BG ＝AE CE ＝32， ∴FG ＝32BG ＝6， ∴CE ＝CG ＝13， ∴AE ＝32CE ＝392，∴AC ＝AE 2＋CE 2＝13213. 4. (1)证明：∵AB 是⊙O 的直径， ∴∠ADB ＝90°，即AD ⊥BC ， ∵AB ＝AC ，∴等腰△ABC ，AD 为BC 边上的垂线， ∴BD ＝DC ， ∴D 是BC 的中点； (2)解：∵AB ＝AC ，∴∠ABC ＝∠C ，∵∠ABC 和∠AED 是同弧所对的圆周角， ∴∠ABC ＝∠AED ， ∴∠AED ＝∠C ， ∴CD ＝DE ＝3， ∴BD ＝CD ＝3， ∵BD －AD ＝2， ∴AD ＝1，在Rt △ABD 中，由勾股定理得AB 2＝BD 2＋AD 2＝32＋12＝10， ∴AB ＝10，∴⊙O 的半径＝12AB ＝102； (3)解：如解图，连接BE ， ∵AB ＝10， ∴AC ＝10，∵∠ADC ＝∠BEA ＝90°，∠C ＝∠C ， ∴△CDA ∽△CEB ， ∴AC BC ＝CD CE ，由(2)知BC ＝2BD ＝6，CD ＝3， ∴106＝3CE ， ∴CE ＝9510，∴AE ＝CE －AC ＝9510－10＝4510. 5. 解：(1)等边三角形．第4题解图【解法提示】∵∠APC ＝∠CPB ＝60°，又∵∠BAC 和∠CPB 是同弧所对的圆周角，∠ABC 和∠APC 是同弧所对的圆周角，∴∠BAC ＝∠CPB ＝60°，∠ABC ＝∠APC ＝60°， ∴∠BAC ＝∠ABC ＝60°， ∴AC ＝BC ，又∵有一个角是60°的等腰三角形是等边三角形， ∴△ABC 是等边三角形． (2)P A ＋PB ＝PC .证明如下：如解图①，在PC 上截取PD ＝P A ，连接AD ， ∵∠APC ＝60°， ∴△P AD 是等边三角形， ∴P A ＝AD ＝PD ，∠P AD ＝60°，又∵∠BAC ＝60°， ∴∠P AB ＝∠DAC ，在△P AB 和△DAC 中， ∵⎩⎪⎨⎪⎧AP ＝AD ∠P AB ＝∠DAC ，AB ＝AC ∴△P AB ≌△DAC (SAS)， ∴PB ＝DC ， ∵PD ＋DC ＝PC ， ∴P A ＋PB ＝PC ，(3)当点P 为AB ︵的中点时，四边形APBC 的面积最大．理由如下：如解图②，过点P 作PE ⊥AB ，垂足为E ，第5题解图①第5题解图②过点C 作CF ⊥AB ，垂足为F ， ∵S △P AB ＝12AB ·PE ，S △ABC ＝12AB ·CF ， ∴S 四边形APBC ＝12AB ·(PE ＋CF )．当点P 为AB ︵的中点时，PE ＋CF ＝PC ，PC 为⊙O 的直径，此时四边形APBC 的面积最大，又∵⊙O 的半径为1，∴其内接正三角形的边长AB ＝ 3 ， ∴四边形APBC 的最大面积为12×2×3＝ 3 . 类型二与切线有关的证明与计算一、与三角函数结合针对演练1. (1)证明：连接OE ，如解图， ∵AB ＝BC 且D 是AC 中点， ∴BD ⊥AC ， ∵BE 平分∠ABD ， ∴∠ABE ＝∠DBE ， ∵OB ＝OE ， ∴∠OBE ＝∠OEB ， ∴∠OEB ＝∠DBE ， ∴OE ∥BD ，第1题解图∵BD ⊥AC ， ∴OE ⊥AC ， ∵OE 为⊙O 半径， ∴AC 与⊙O 相切；(2)解：∵BD ＝6，sin C ＝35，BD ⊥AC ， ∴BC ＝BDsin C ＝10， ∴AB ＝BC ＝10.设⊙O 的半径为r ，则AO ＝10－r ， ∵AB ＝BC ， ∴∠C ＝∠A ， ∴sin A ＝sin C ＝35， ∵AC 与⊙O 相切于点E ， ∴OE ⊥AC ，∴sin A ＝OE OA ＝r 10－r ＝35，∴r ＝154，即⊙O 的半径是154.2. (1)证明：连接OC ，如解图， ∵PC 切⊙O 于点C ， ∴OC ⊥PC ， ∴∠PCO ＝90°， ∴∠PCA ＋∠OCA ＝90°， ∵AB 为⊙O 的直径，第2题解图∴∠ACB ＝90°， ∴∠ABC ＋∠OAC ＝90°， ∵OC ＝OA ， ∴∠OCA ＝∠OAC ， ∴∠PCA ＝∠ABC ； (2)解：∵AE ∥PC ， ∴∠PCA ＝∠CAF ， ∵AB ⊥CG ， ∴AC ︵＝AG ︵， ∴∠ACF ＝∠ABC ， ∵∠PCA ＝∠ABC ， ∴∠ACF ＝∠CAF ， ∴CF ＝AF ， ∵CF ＝5， ∴AF ＝5， ∵AE ∥PC ， ∴∠F AD ＝∠P ， ∵sin ∠P ＝35， ∴sin ∠F AD ＝35，在Rt △AFD 中，AF ＝5，sin ∠F AD ＝35， ∴FD ＝3，AD ＝4， ∴CD ＝CF ＋FD ＝8，在Rt △OCD 中，设OC ＝r ， ∴r 2＝(r －4)2＋82，∴r ＝10， ∴AB ＝2r ＝20， ∵AB 为⊙O 的直径， ∴∠AEB ＝90°，在Rt △ABE 中，sin ∠EAD ＝35， ∴BE AB ＝35， ∵AB ＝20， ∴BE ＝12.3. 解：(1)直线PD 与⊙O 相切，理由如下：如解图①，连接DO ，CO ， ∵∠PDA ＝∠ADC ， ∴∠PDC ＝2∠ADC ， ∵∠AOC ＝2∠ADC ， ∴∠PDC ＝∠AOC ， ∵直径AB ⊥CD 于点E ， ∴∠AOD ＝∠AOC ， ∴∠PDC ＝∠AOD ， ∵∠AOD ＋∠ODE ＝90°， ∴∠PDC ＋∠ODE ＝90°， ∴OD ⊥PD ， ∵OD 是⊙O 的半径， ∴直线PD 与⊙O 相切； (2)如解图②，连接BD ， ∵M 恰为BC ︵的中点，第3题解图①∴∠CDM ＝∠BDM ， ∵OD ＝OB ， ∴∠BDM ＝∠DBA ， ∴∠CDM ＝∠DBA ， ∵直线PD 与⊙O 相切， ∴∠PDA ＋∠ADO ＝90°，又∵AB 是⊙O 的直径，∴∠ADB ＝90°，即∠ADO ＋∠BDM ＝90°， ∴∠PDA ＝∠BDM ， ∴∠PDA ＝∠DBA ＝∠CDM ，又∵∠PDA ＝∠ADC ， ∴∠PDM ＝3∠CDM ＝90°， ∴∠CDM ＝30°， ∴∠DBA ＝30°， ∴DE BE ＝tan30°＝33； (3)如解图③，∵tan ∠PDA ＝12，∠PDA ＝∠ADC ， ∴AE DE ＝12，即DE ＝2AE ，在Rt △DEO 中，设⊙O 的半径为r ， DE 2＋EO 2＝DO 2， ∴(2AE )2＋(r －AE )2＝r 2，解得r ＝52AE ，在Rt △PDE 中，DE 2＋PE 2＝PD 2，第3题解图②第3题解图③∴(2AE )2＋(2＋AE )2＝PD 2， ∵直线PD 与⊙O 相切，连接BD ，由(2)知∠PDA ＝∠DBA ，∠P ＝∠P ， ∴△P AD ∽△PDB ， ∴PD PB ＝P A PD ，∴PD 2＝P A ·PB ，即PD 2＝2×(2＋2r )， ∴(2AE )2＋(2＋AE )2＝2×(2＋2r )，化简得5AE 2＋4AE ＝4r ， ∵r ＝52AE ，解得r ＝3. 即⊙O 的半径为3. 二、与相似三角形结合针对演练1. 证明：(1)∵AC 为⊙O 的直径， ∴∠ADC ＝90°， ∴∠CDB ＝90°，又∵∠ACB ＝90°， ∴∠ACB ＝∠CDB ，又∵∠B ＝∠B ， ∴△ABC ∽△CBD ； (2)连接DO ，如解图，∵∠BDC ＝90°，E 为BC 的中点， ∴DE ＝CE ＝BE ， ∴∠EDC ＝∠ECD ，第1题解图又∵OD ＝OC ， ∴∠ODC ＝∠OCD ，而∠OCD ＋∠DCE ＝∠ACB ＝90°， ∴∠EDC ＋∠ODC ＝90°，即∠EDO ＝90°， ∴DE ⊥OD ， ∵OD 为⊙O 的半径， ∴DE 与⊙O 相切．2. (1)证明：连接CE ，如解图， ∵CD 为⊙O 的直径， ∴∠CED ＝90°， ∵∠BCA ＝90°， ∴∠CED ＝∠BCO ， ∵BO ∥DE ， ∴∠BOC ＝∠CDE ， ∴△CBO ∽△ECD ， ∴CO DE ＝BO CD ， ∴CO ·CD ＝DE ·BO ；(2)解：∵∠DFE ＝∠ECO ，CD ＝2·OC ＝10，∴在Rt △CDE 中，ED ＝CD ·sin ∠ECO ＝CD ·sin ∠DFE ＝ 10×35＝6，∴CE ＝CD 2－ED 2＝102－62＝8，在Rt △CEG 中，EG CE ＝sin ∠ECG ＝35， ∴EG ＝35×8＝245，第2题解图根据垂径定理得：EF ＝2EG ＝485. 3. (1)证明：如解图，连接OD ， ∵AB 是⊙O 的直径， ∴∠ADB ＝90°， ∵AB ＝AC ，∴AD 垂直平分BC ，即DC ＝DB ， ∴OD 为△BAC 的中位线， ∴OD ∥AC . 而DE ⊥AC ， ∴OD ⊥DE ， ∵OD 是⊙O 的半径， ∴EF 是⊙O 的切线；(2)解：∵∠DAC ＝∠DAB ，且∠AED ＝∠ADB ＝90°， ∴∠ADE ＝∠ABD ，在Rt △ADB 中，sin ∠ADE ＝sin ∠ABD ＝AD AB ＝45，而AB ＝10， ∴AD ＝8，在Rt △ADE 中，sin ∠ADE ＝AE AD ＝45， ∴AE ＝325， ∵OD ∥AE ， ∴△FDO ∽△FEA ，∴OD AE ＝FO F A ，即5325＝BF ＋5BF ＋10，第3题解图∴BF ＝907.4. (1)证明：如解图①，连接OD 、OE 、ED . ∵BC 与⊙O 相切于点D ， ∴OD ⊥BC ，∴∠ODB ＝90°＝∠C ， ∴OD ∥AC ， ∵∠B ＝30°， ∴∠A ＝60°， ∵OA ＝OE ，∴△AOE 是等边三角形， ∴AE ＝AO ＝OD ，∴四边形AODE 是平行四边行， ∵OA ＝OD ，∴平行四边形AODE 是菱形； (2)解：设⊙O 的半径为r . ∵OD ∥AC ， ∴△OBD ∽△ABC ，∴OD AC ＝OBAB ，即10r ＝6(10－r )．解得r ＝154， ∴⊙O 的半径为154.如解图②，连接OD 、DF 、AD . ∵OD ∥AC ， ∴∠DAC ＝∠ADO ，第4题解图①∵OA ＝OD ， ∴∠ADO ＝∠DAO ， ∴∠DAC ＝∠DAO ， ∵AF 是⊙O 的直径， ∴∠ADF ＝90°＝∠C ， ∴△ADC ∽△AFD ， ∴AD AC ＝AF AD ， ∴AD 2＝AC ·AF ，∵AC ＝6，AF ＝154×2＝152， ∴AD 2＝152×6＝45，∴AD ＝45＝3 5.(9分) 5. 解：(1)存在，AE ＝CE . 理由如下：如解图①，连接AE ，ED ， ∵AC 是△ABC 的斜边， ∴∠ABC ＝90°， ∴AE 为⊙O 的直径， ∴∠ADE ＝90°，又∵D 是AC 的中点， ∴ED 为AC 的中垂线， ∴AE ＝CE ；(2)①如解图②，∵EF 是⊙O 的切线， ∴∠AEF ＝90°.第5题解图①由(1)可知∠ADE＝90°，∴∠AED＋∠EAD＝90°，∵∠AED＋∠DEF＝90°，∴∠EAD＝∠DEF.又∵∠ADE＝∠EDF＝90°∴△AED∽△EFD，∴ADED＝EDFD，∴ED2＝AD·FD.又∵AD＝DC＝CF，∴ED2＝2AD·AD＝2AD2，在Rt△AED中，∵AE2＝AD2＋ED2＝3AD2，由(1)知∠AED＝∠CED，又∵∠CED＝∠CAB，∴∠AED＝∠CAB，∴sin∠CAB＝sin∠AED＝ADAE＝13＝33.②sin∠CAB＝a＋2 a＋2.【解法提示】由(2)中的①知ED2＝AD·FD，∵CF＝aCD(a＞0)，∴CF＝aCD＝aAD，∴ED2＝AD·DF＝AD(CD＋CF)＝AD(AD＋aAD)＝(a＋1)AD2，在Rt△AED中，AE2＝AD2＋ED2＝(a＋2)AD2，∴sin ∠CAB ＝sin ∠AED ＝ADAE ＝1a ＋2＝a ＋2a ＋2. 6. (1)证明：∵∠ODB ＝∠AEC ，∠AEC ＝∠ABC ， ∴∠ODB ＝∠ABC ， ∵OF ⊥BC ， ∴∠BFD ＝90°，∴∠ODB ＋∠DBF ＝90°， ∴∠ABC ＋∠DBF ＝90°，即∠OBD ＝90°， ∴BD ⊥OB ， ∵OB 为⊙O 的半径， ∴BD 是⊙O 的切线；(2)证明：连接AC ，如解图①所示： ∵OF ⊥BC ， ∴BE ︵＝CE ︵， ∴∠ECH ＝∠CAE ， ∵∠HEC ＝∠CEA ， ∴△CEH ∽△AEC ， ∴CE EH ＝EA CE ， ∴CE 2＝EH ·EA ；(3)解：连接BE ，如解图②所示： ∵AB 是⊙O 的直径， ∴∠AEB ＝90°，∵⊙O 的半径为5，sin ∠BAE ＝35，第6题解图①第6题解图②∴AB ＝10，BE ＝AB ·sin ∠BAE ＝10×35＝6，在Rt △AEB 中，EA ＝AB 2－BE 2＝102－62＝8， ∵BE ︵＝CE ︵， ∴BE ＝CE ＝6， ∵CE 2＝EH ·EA ， ∴EH ＝CE 2EA ＝628＝92，在Rt △BEH 中，BH ＝BE 2＋EH 2＝62＋（92）2＝152.7. (1)证明：连接OD ，如解图①， ∵AD 平分∠BAC 交⊙O 于D ， ∴∠BAD ＝∠CAD ， ∴BD ︵＝CD ︵， ∴OD ⊥BC ， ∵BC ∥DF ， ∴OD ⊥DF ， ∴DF 为⊙O 的切线；(2)解：连接OB ，连接OD 交BC 于P ，作BH ⊥DF 于H ，如解图①，∵∠BAC ＝60°，AD 平分∠BAC ， ∴∠BAD ＝30°，∴∠BOD ＝2∠BAD ＝60°，又∵OB ＝OD ，∴△OBD 为等边三角形， ∴∠ODB ＝60°，OB ＝BD ＝23，第7题解图①∴∠BDF ＝30°， ∵BC ∥DF ， ∴∠DBP ＝30°，在Rt △DBP 中，PD ＝12BD ＝3，PB ＝3PD ＝3，在Rt △DEP 中， ∵PD ＝3，DE ＝7，∴PE ＝（7）2－（3）2＝2， ∵OP ⊥BC ， ∴BP ＝CP ＝3，∴CE ＝CP －PE ＝3－2＝1，易证得△BDE ∽△ACE ， ∴BE AE ＝DE CE ，即5AE ＝71， ∴AE ＝577. ∵BE ∥DF ， ∴△ABE ∽△AFD ，∴BE DF ＝AE AD ，即5DF ＝5771277，解得DF ＝12，在Rt △BDH 中，BH ＝12BD ＝3， ∴S 阴影＝S △BDF －S 弓形BD ＝S △BDF －(S 扇形BOD －S △BOD )＝12·12·3－60·π·（23）2360＋34·(23)2＝93－2π；(7分)(3)解：连接CD ，如解图②，由AB AC ＝43可设AB ＝4x ，AC ＝3x ，BF ＝y ， ∵BD ︵＝CD ︵， ∴CD ＝BD ＝23， ∵DF ∥BC ，∴∠F ＝∠ABC ＝∠ADC ， ∴∠FDB ＝∠DBC ＝∠DAC ， ∴△BFD ∽△CDA ， ∴BD AC ＝BF CD ，即233x ＝y 23，∴xy ＝4，∵∠FDB ＝∠DBC ＝∠DAC ＝∠F AD ，而∠DFB ＝∠AFD ， ∴△FDB ∽△F AD ， ∴DF AF ＝BF DF ， ∵DF ＋BF ＝8， ∴DF ＝8－BF ＝8－y ， ∴8－y y ＋4x ＝y 8－y ，整理得：16－4y ＝xy ， ∴16－4y ＝4，解得y ＝3，即BF 的长为3.(10分) 三、与全等三角形结合第7题解图②针对演练1. (1)证明：连接OE ，过点O 作OF ⊥PN ，如解图所示， ∵PM 与⊙O 相切， ∴OE ⊥PM ，∴∠OEP ＝∠OFP ＝90°， ∵PC 平分∠MPN ， ∴∠EPO ＝∠FPO ，在△PEO 和△PFO 中， ⎩⎪⎨⎪⎧∠EPO ＝∠FPO ∠OEP ＝∠OFP OP ＝OP， ∴△PEO ≌△PFO (AAS)， ∴OF ＝OE ，∴OF 为圆O 的半径且OF ⊥PN, 则PN 与⊙O 相切；(2)解：在Rt △EPO 中，∠MPC ＝30°，PE ＝23， ∴∠EOP ＝60°，OE ＝PE ·tan30°＝2， ∴∠EOB ＝120°，则劣弧BE ︵的长为120π×2180＝4π3.2. (1)证明：如解图①，连接BO 并延长交⊙O 于点N ，连接CN ， ∵∠BMC ＝60°， ∴∠BNC ＝60°， ∵∠BNC ＋∠NBC ＝90°， ∴∠NBC ＝30°，又∵△ABC 为等边三角形，第1题解图∴∠BAC ＝∠ABC ＝∠ACB ＝60°， ∴∠ABN ＝30°＋60°＝90°， ∴AB ⊥BO ，即AB 为⊙O 的切线．(2)解：BE ＋CF ＝3，是定值．理由如下：如解图②，连接D 与AC 的中点P ， ∵D 为BC 中点， ∴AD ⊥BC ， ∴PD ＝PC ＝12AC ，又∵∠ACB ＝60°，∴PD ＝PC ＝CD ＝BD ＝12AC ， ∴∠DPF ＝∠PDC ＝60°， ∴∠PDF ＋∠FDC ＝60°，又∵∠EDF ＝120°， ∴∠BDE ＋∠FDC ＝60°， ∴∠PDF ＝∠BDE ，在△BDE 和△PDF 中， ⎩⎪⎨⎪⎧∠EBD ＝∠DPF BD ＝PD∠BDE ＝∠PDF， ∴△BDE ≌△PDF (ASA)， ∴BE ＝PF ，∴BE ＋CF ＝PF ＋CF ＝CP ＝BD ， ∵OB ⊥AB ，∠ABC ＝60°，第2题解图②∴∠OBC ＝30°，又∵OB ＝2，∴BD ＝OB ·cos30°＝2×32＝3，即BE ＋CF ＝ 3.3. (1)证明：连接OC ，如解图①， ∵OD ⊥AC ，OC ＝OA ， ∴∠AOD ＝∠COD . 在△AOE 和△COE 中， ⎩⎪⎨⎪⎧OA ＝OC ∠AOE ＝∠COE OE ＝OE， ∴△AOE ≌△COE (SAS)， ∴∠EAO ＝∠ECO . 又∵EC 是⊙O 的切线， ∴∠ECO ＝90°， ∴∠EAO ＝90°. ∴AE 与⊙O 相切；(2)解：设DO ＝t ，则DE ＝3t ，EO ＝4t ，在△EAO 和△ADO 中，⎩⎪⎨⎪⎧∠EOA ＝∠AOD ∠EAO ＝∠ADO， ∴△EAO ∽△ADO ， ∴AO DO ＝EO AO ，即9t ＝4t 9， ∴t ＝92，即EO ＝18.第3题解图①∴AE ＝EO 2－AO 2＝182－92＝93；延长BD 交AE 于点F ，过O 作OG ∥AE 交BD 于点G ，如解图②， ∵OG ∥AE ， ∴∠FED ＝∠GOD 又∵∠EDF ＝∠ODG ， ∴△EFD ∽△OGD ， ∴EF OG ＝ED OD ＝31，即EF ＝3GO . 又∵O 是AB 的中点， ∴AF ＝2GO ，∴AE ＝AF ＋FE ＝5GO ， ∴5GO ＝93， ∴GO ＝935， ∴AF ＝1835， ∴tan B ＝AF AB ＝35.4. (1)证明：如解图，连接OB ， ∵PB 是⊙O 的切线， ∴∠PBO ＝90°，∵OA ＝OB ，BA ⊥PO 于点D ， ∴AD ＝BD ，∠POA ＝∠POB ，又∵PO ＝PO ，∴△P AO ≌△PBO (SAS)， ∴∠P AO ＝∠PBO ＝90°，第3题解图②第4题解图∴OA ⊥P A ，∴直线P A 为⊙O 的切线；(2)解：线段EF 、OD 、OP 之间的等量关系为EF 2＝4OD ·OP . 证明：∵∠P AO ＝∠PDA ＝90°，∴∠OAD ＋∠AOD ＝90°，∠OP A ＋∠AOP ＝90°，∴∠OAD ＝∠OP A ，∴△OAD ∽△OP A ，∴ OD OA ＝OA OP ，即OA 2＝OD ·OP ，又∵EF ＝2OA ，∴EF 2＝4OD ·OP ；(3)解：∵OA ＝OC ，AD ＝BD ，BC ＝6，∴OD ＝12BC ＝3，设AD ＝x ，∵tan ∠F ＝12，∴FD ＝2x ，OA ＝OF ＝FD －OD ＝2x －3，在Rt △AOD 中，由勾股定理，得(2x －3)2＝x 2＋32，解之得，x 1＝4，x 2＝0(不合题意，舍去)，∴AD ＝4，OA ＝2x －3＝5，∵AC 是⊙O 直径，∴∠ABC ＝90°，又∵AC ＝2OA ＝10，BC ＝6，∴ cos ∠ACB ＝610＝35.∵OA 2＝OD ·OP ，∴3(PE ＋5)＝25，∴PE ＝103.5. (1)证明：连接OD ，如解图，∵AB 为⊙O 的直径，∴∠ACB ＝90°，∵∠ACB 的平分线交⊙O 于点D ，∴∠ACD ＝∠BCD ＝45°，∴∠DAB ＝∠ABD ＝45°，∴△DAB 为等腰直角三角形，∴DO ⊥AB ，∵PD 为⊙O 的切线，∴OD ⊥PD ，∴PD ∥AB ；(2)证明：∵AE ⊥CD 于点E ，BF ⊥CD 于点F ，∴AE ∥BF ，∴∠FBO ＝∠EAO ，∵△DAB 为等腰直角三角形，∴∠EDA ＋∠FDB ＝90°，∵∠FBD ＋∠FDB ＝90°，∴∠FBD ＝∠EDA ，在△FBD 和△EDA 中，⎩⎪⎨⎪⎧∠BFD ＝∠DEA ∠FBD ＝∠EDA BD ＝DA， ∴△FBD ≌△EDA (AAS)，∴DE ＝BF ；第5题解图(3)解：在Rt △ACB 中，∵AC ＝6，tan ∠CAB ＝43，∴BC ＝6×43＝8，∴AB ＝AC 2＋BC 2＝62＋82＝10，∵△DAB 为等腰直角三角形，∴AD ＝AB 2＝52， ∵AE ⊥CD ，∴△ACE 为等腰直角三角形，∴AE ＝CE ＝AC 2＝62＝32，在Rt △AED 中，DE ＝AD 2－AE 2＝（52）2－（32）2＝42，∴CD ＝CE ＋DE ＝32＋42＝72，∵AB ∥PD ，∴∠PDA ＝∠DAB ＝45°，∴∠PDA ＝∠PCD ，又∵∠DP A ＝∠CPD ，∴△PDA ∽△PCD ，∴PD PC ＝P A PD ＝AD DC ＝5272＝57， ∴P A ＝57PD ，PC ＝75PD ，又∵PC ＝P A ＋AC ，∴57PD ＋6＝75PD ，解得PD ＝354，∴PC ＝57PD ＋6＝57×354＋6＝254＋6＝494.6. (1)证明：如解图①，连接OC ，∵P A 切⊙O 于点A ，∴∠P AO ＝90°，∵BC ∥OP ，∴∠AOP ＝∠OBC ，∠COP ＝∠OCB ，∵OC ＝OB ，∴∠OBC ＝∠OCB ，∴∠AOP ＝∠COP ，在△P AO 和△PCO 中，⎩⎪⎨⎪⎧OA ＝OC ∠AOP ＝∠COP OP ＝OP， ∴△P AO ≌△PCO (SAS)，∴∠PCO ＝∠P AO ＝90°，∴OC ⊥PC ，∵OC 为⊙O 的半径，∴PC 是⊙O 的切线；(2)解：由(1)得P A ，PC 都为圆的切线，∴P A ＝PC ，OP 平分∠APC ，∠ADO ＝∠P AO ＝90°， ∴∠P AD ＋∠DAO ＝∠DAO ＋∠AOD ，又∵∠ADP ＝∠ADO ，∴∠P AD ＝∠AOD ，∴△ADP ∽△ODA ，∴AD PD ＝DO AD ，第6题解图①∴AD 2＝PD ·DO ，∵AC ＝8，PD ＝163， ∴AD ＝12AC ＝4，OD ＝3，在Rt △ADO 中，AO ＝AD 2＋OD 2＝5，由题意知OD 为△ABC 的中位线，∴BC ＝6，AB ＝BC 2＋AC 2＝10.∴S 阴影＝12S ⊙O －S △ABC ＝12·π·52－12×6×8＝25π2－24；(3)解：如解图②，连接AE 、BE ，作BM ⊥CE 于点M ， ∴∠CMB ＝∠EMB ＝∠AEB ＝90°，∵点E 是AB ︵的中点，∴AE ＝BE ，∠EAB ＝∠EBA ＝45°，∴∠ECB ＝∠CBM ＝∠ABE ＝45°，CM ＝MB ＝BC ·sin45°＝32，BE ＝AB ·cos45°＝52，∴EM ＝BE 2－BM 2＝42，则CE ＝CM ＋EM ＝7 2.7. (1)证明：连接OD ，如解图①所示，∵OB ＝OD ，∴∠ODB ＝∠OBD .∵OG ∥BD ，∴∠AOG ＝∠OBD ，∠GOD ＝∠ODB ，∴∠DOG ＝∠AOG ，在△DOG 和△AOG 中，第6题解图②第7题解图①⎩⎪⎨⎪⎧OD ＝OA ∠DOG ＝∠AOG OG ＝OG， ∴△DOG ≌△AOG (SAS)，∴GD ＝GA ；(2)证明：∵AG 切⊙O 于点A ，∴AG ⊥OA ，∴∠OAG ＝90°，∵△DOG ≌△AOG ，∴∠OAG ＝∠ODG ＝90°，∴∠ODE ＝180°－∠ODG ＝90°，∴∠ODC ＋∠FDE ＝90°，∵OC ⊥AB ，∴∠COB ＝90°，∴∠OCD ＋∠OFC ＝90°，∵OC ＝OD ，∴∠ODC ＝∠OCD ，∴∠FDE ＝∠OFC ，∵∠OFC ＝∠EFD ，∴∠EFD ＝∠EDF ，∴EF ＝ED ，∴△DEF 是等腰三角形；(3)解：过点B 作BK ⊥OD 于点K ，如解图②所示：则∠OKB ＝∠BKD ＝∠ODE ＝90°，∴BK ∥DE ，∴∠OBK ＝∠E ，∵BH ⊥GE ，∴∠BHD ＝∠BHE ＝90°， ∴四边形KDHB 为矩形， ∴KD ＝BH ＝9，∴OK ＝OD －KD ＝72，在Rt △OKB 中，∵OK 2＋KB 2＝OB 2，OB ＝252， ∴KB ＝12，∴tan ∠E ＝tan ∠OBK ＝OK KB ＝724，sin ∠E ＝sin ∠OBK ＝OK OB ＝725，∵tan ∠E ＝OD DE ＝724，∴DE ＝3007，∴EF ＝3007，∵sin ∠E ＝BH BE ＝725，∴BE ＝2257，∴BF ＝EF －BE ＝757，∴OF ＝OB －BF ＝2514，在Rt △COF 中，∠COB ＝90°， ∴OC 2＋OF 2＝FC 2，∴FC ＝125214，在Rt △COB 中，∵OC 2＋OB 2＝BC 2，OC ＝OB ＝252， ∴BC ＝2522，∴BC ＋CF ＋BF ＝1502＋757， ∴△CBF 的周长＝1502＋757.。

河南中考数学题型四与圆有关的证明与计算及答案.docx

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】题型四与圆有关的证明与计算(近6年连续考查)【题型解读】近6年连续在解答题中考查，考查的类型有两种：①在2017年中考查与切线性质有关的证明与计算，设问有：证明线段的相等和利用勾股定理求线段长；②其余5年考查的是特殊四边形的动态探究，考查该类型的时候，第二问往往是以两个填空题的形式出现，主要考查内容是菱形、正方形的判定，其中菱形的判定是必考内容.类型一与切线判定有关的证明与计算1.如图，D是⊙O上的一点，C是直径AB延长线上一点，连接BD，CD，且∠A＝∠BD C.(1)求证：CD是⊙O的切线；(2)若CM平分∠ACD，且分别交AD，BD于点M，N，当DM＝2时，求MN的长.第1题图2.如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP＝A C.(1)求证：P A是⊙O的切线；(2)若AB＝3，BC＝2，求⊙O的半径.第2题图3.(2019南充)如图，在△ABC中，以AC为直径的⊙O交AB于点D，连接CD，∠BCD＝∠A.(1)求证：BC是⊙O的切线；(2)若BC＝5，BD＝3，求点O到CD的距离.第3题图4.(2019济宁)如图，AB 是⊙O 的直径，C 是⊙O 上一点，D 是AC ︵的中点，E 为OD 延长线上一点，且∠CAE ＝2∠C ，AC 与BD 交于点H ，与OE 交于点F .(1)求证：AE 是⊙O 的切线；(2)若DH ＝9，tan C ＝34，求直径AB 的长.第4题图类型二与切线性质有关的证明与计算(2017.18)1.(2019河南定心卷)如图，⊙O为△ABC的外接圆，AB＝AC，直线MN与⊙O相切于点C，弦BD∥MN，AC与BD相交于点E，连接AD，C D.(1)求证：△ABE≌△ACD；(2)若AB＝5，BC＝3，求AE的长.第1题图2.如图，在△ABC中，∠C＝90°，D是AB边上一点，以BD为直径的⊙O与边AC相切于点E，与边BC交于点F，过点E作EH⊥AB于点H，连接BE.(1)求证：BC＝BH；(2)若AB＝5，AC＝4，求CE的长.第2题图3.如图，半圆O的直径为AB，D是半圆上的一个动点(不与点A，B重合)，连接BD并延长至点C，使CD＝BD，过点D作半圆O的切线交AC于点E.(1)求证：DE⊥AC；(2)若BD＝2，且AB＝3BD，求DE的长.第3题图4.(2019桂林改编)如图，BM是以AB为直径的⊙O的切线，B为切点，BC平分∠ABM，弦CD交AB 于点E，DE＝OE.(1)求证：∠CAE＝∠CBA；(2)求证：OA2＝OE·DC；(3)求tan∠ACD的值.第4题图类型三特殊四边形的动态探究题(2019、2015、2014.17；2018.19；2016.18)1.如图所示，AD∥BC，∠BAD＝90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过点C作CF⊥BE于点F.(1)线段BF与图中哪条线段相等？写出来并加以证明；(2)若AB＝12，BC＝13，P从E出发沿ED方向运动，Q从C出发向B运动，两点同时出发且速度均为每秒1个单位.填空：①当运动时间为秒时，四边形EPCQ是矩形；②当运动时间为秒时，四边形EPCQ是菱形.第1题图2.如图，已知BC是⊙O的直径，AD与⊙O相切于点A，CD∥OA交⊙O于另一点E.(1)求证：△ACD∽△BCA；(2)若A是⊙O上一动点，则①当∠B＝时，以A，O，C，D为顶点的四边形是正方形；②当∠B＝时，以A，O，C，E为顶点的四边形是菱形.第2题图3.如图，在Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O，交AC于点D，过点D作⊙O的切线，交BC于点E.(1)求证：EB＝EC；(2)填空：①当∠BAC＝时，△CDE为等边三角形；②连接OD，当∠BAC＝时，四边形OBED是菱形.第3题图4.如图，四边形ABCD内接于⊙O，对角线AC为⊙O的直径，过点C作AC的垂线交AD的延长线于点E，过点D作⊙O的切线，交EC于点F.(1)求证：EF＝FC；(2)填空：①当∠ACD的度数为时，四边形ODFC为正方形；②若AD＝4，DC＝2，则四边形ABCD的最大面积是.第4题图5.(2019许昌模拟)如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC，分别交AC，AB的延长线于点E，F.(1)求证：EF是⊙O的切线；(2)填空：①当∠BAC的度数为时，四边形ACDO为菱形；②若⊙O的半径为5，AC＝3CE，则BC的长为.第5题图6.如图，已知AB是⊙O的直径，PC与⊙O相切于点P，过点A作直线AC⊥PC交⊙O于另一点D，连接P A，PB，PO.(1)求证：AP平分∠CAB；(2)若P是直径AB上方半圆弧上一动点，⊙O的半径为2，则①当弦AP＝时，以A，O，P，C为顶点的四边形是正方形；②当弧AP＝时，以A，D，O，P为顶点的四边形是菱形.第6题图7.(2019新乡模拟)如图，在⊙O中，AB为直径，点P为⊙O外一点，且P A＝AB，P A，PB交⊙O于D，E两点，∠P AB为锐角，连接DE，OD，OE.(1)求证：∠EDO＝∠EBO；(2)填空：若AB＝8，①△AOD的最大面积为；②当DE＝时，四边形OBED为菱形.第7题图8. 如图，点A ，C ，B 是⊙O 上三点，且C 是劣弧AB ︵的中点，点E ，F 是弦AB 上两点，且AF ＝BE . (1)求证：OE ＝OF ；(2)填空：若⊙O 的半径为2，①当∠AOB ＝时，四边形AOBC 是菱形； ②当∠AOB ＝90°时，四边形AOBC 的面积是 .第8题图9.(2019开封模拟)如图，在▱ABCD 中，⊙O 是△ABC 的外接圆，CD 与⊙O 相切于点C ，点P 是劣弧BC ︵上的一个动点(点P 不与点B ，C 重合)，连接P A ，PB ，P C.(1)求证：CA ＝CB ；(2)当AP ＝AC 时，试判断△APC 与△CBA 是否全等，请说明理由； (3)填空：当∠D ＝时，四边形ABCD 是菱形.第9题图10.如图，以△ABC一边AB为直径作⊙O，与另外两边分别交于点D、E，且点D为BC的中点，连接DE.(1)证明：△ABC是等腰三角形；(2)填空：①当∠B＝时，四边形BDEO是菱形；②当∠B＝时，△AOE是直角三角形.第10题图11.如图，△ABC内接于⊙O，AB＝AC，连接AO并延长交⊙O于点D，交BC于点E，BF平分∠ABC，交AD于点F，连接BD，C D.(1)求证：△BDE≌△CDE；(2)填空：①连接CF，当∠BAC＝时，四边形BDCF是菱形；②当∠FBD＝时，四边形ABDC是正方形.第11题图12.如图，已知△ABC内接于⊙O，AB是⊙O的直径，OD∥AC，AD＝O C.(1)求证：四边形OCAD是平行四边形；(2)探究：①当∠B＝时，四边形OCAD是菱形；②当∠B满足什么条件时，AD与⊙O相切？请说明理由.第12题图参考答案类型一与切线判定有关的证明与计算1.(1)证明：如解图，连接OD.∵AB为⊙O的直径，∴∠ADB＝90°，即∠A＋∠ABD＝90°，又∵OD＝OB，∴∠ABD＝∠ODB，∵∠A＝∠BDC，∴∠BDC＋∠ODB＝90°，即∠ODC＝90°.∵OD是⊙O的半径，∴CD是⊙O的切线；第1题解图(2)解：∵CM平分∠ACD，∴∠DCM＝∠ACM，又∵∠A＝∠BDC，∴∠A＋∠ACM＝∠BDC＋∠DCM，即∠DMN＝∠DNM，∵∠ADB＝90°，DM＝2，∴DN＝DM＝2，∴在Rt△NDM中，由勾股定理得，MN＝DM2＋DN2＝2 2.2.(1)证明：如解图，连接OA，∵∠B＝60°，∴∠AOC＝2∠B＝120°，又∵OA＝OC，∴∠OAC＝∠OCA＝30°，又∵AP＝AC，∴∠P＝∠ACO＝30°，∴∠OAP＝∠AOC－∠P＝90°，∴OA⊥P A，∵OA为⊙O的半径，∴P A是⊙O的切线；第2题解图(2)解：如解图，过点C 作CE ⊥AB 于点E . 在Rt △BCE 中，∠B ＝60°，BC ＝2， ∴BE ＝BC ·cos B ＝1，CE ＝3， ∵AB ＝3，∴AE ＝AB －BE ＝2，∴在Rt △ACE 中，AC ＝AE 2＋CE 2＝7， ∴AP ＝AC ＝7.∴在Rt △P AO 中，OA ＝tan30°·7＝33×7＝213， ∴⊙O 的半径为213. 3. (1)证明：∵AC 是⊙O 的直径， ∴∠ADC ＝90°. ∴∠A ＋∠ACD ＝90°， ∵∠BCD ＝∠A ，∴∠BCD ＋∠ACD ＝∠ACB ＝90°， ∴OC ⊥BC .又∵OC 为⊙O 的半径， ∴BC 是⊙O 的切线；(2)解：如解图，过点O 作OE ⊥CD 于点E . 在Rt △BCD 中，∵BC ＝5，BD ＝3， ∴CD ＝4.∵∠ADC ＝∠CDB ＝90°，∠BCD ＝∠A ， ∴Rt △BDC ∽Rt △CDA . ∴CD AD ＝BD CD ＝34， ∴AD ＝163.∵OE ⊥CD ， ∴E 为CD 的中点．又∵点O 是AC 的中点， ∴OE ＝12AD ＝83.∴点O 到CD 的距离为83.第3题解图4. (1)证明：∵D 是AC ︵的中点， ∴OD ⊥AC ，即∠AFO ＝90°， ∴∠CAB ＋∠AOF ＝90°.又∵∠CAE ＝2∠C ＝2∠B ＝∠AOF ，∴∠CAE ＋∠CAB ＝∠AOF ＋∠CAB ＝90°＝∠EAO ， ∴EA ⊥AB .又∵AB 为⊙O 的直径， ∴AE 是⊙O 的切线； (2)解：如解图，连接AD ，∵∠C ＝∠B ＝∠HDF ，D 是AC ︵的中点， ∴∠C ＝∠DAH ＝∠B ， ∵AB 是⊙O 的直径， ∴∠ADB ＝90°， ∴Rt △ADH ∽Rt △BDA ， ∵tan C ＝34，∴AD BD ＝DH DA ＝34， ∵DH ＝9，∴AD ＝12，BD ＝16，在Rt △DAB 中，AB ＝AD 2＋BD 2＝20.第4题解图类型二与切线性质有关的证明与计算1. (1)证明：如解图，连接OC ， ∵直线MN 与⊙O 相切于点C ， ∴OC ⊥MN . ∵BD ∥MN ， ∴OC ⊥BD . ∴BC ︵＝CD ︵. ∴∠BAE ＝∠CAD . 在△ABE 和△ACD 中，⎩⎪⎨⎪⎧∠ABE ＝∠ACD AB ＝AC ∠BAE ＝∠CAD， ∴△ABE ≌△ACD (ASA)；第1题解图(2)解：由(1)知∠BAC ＝∠CAD ＝∠CBD ， ∴△BCE ∽△ACB . ∴BC AC ＝CECB. ∵AC ＝AB ＝5，BC ＝3， ∴CE ＝95.∴AE ＝AC －CE ＝165.2. (1)证明：如解图，连接OE ， ∵AC 与⊙O 相切于点E ， ∴OE ⊥AC . ∵∠C ＝90°， ∴BC ⊥AC . ∴OE ∥BC . ∴∠CBE ＝∠OEB . ∵OE ＝OB ， ∴∠EBO ＝∠OEB . ∴∠CBE ＝∠EBO ， ∵CE ⊥BC ，EH ⊥AB ， ∴CE ＝EH .在Rt △EBC 和Rt △EBH 中，∵⎩⎪⎨⎪⎧CE ＝HE ，BE ＝BE ， ∴Rt △EBC ≌Rt △EBH (HL)． ∴BC ＝BH ；第2题解图(2)解：∵AB ＝5，AC ＝4，∴在Rt △ABC 中，根据勾股定理可得BC ＝AB 2－AC 2＝3. ∵BC ＝BH ， ∴BH ＝3.∴AH ＝AB －BH ＝5－3＝2. 设CE ＝EH ＝x ，则AE ＝4－x ，在Rt △AEH 中，根据勾股定理可得AH 2＋EH 2＝AE 2，即22＋x 2＝(4－x )2，解得x ＝32，∴CE ＝32.3. (1)证明：如解图，连接OD . ∵DE 是半圆O 的切线，切点为D ， ∴OD ⊥DE ，∵BD ＝CD ，OA ＝OB ， ∴OD 是△ABC 的中位线， ∴OD ∥AC . ∴DE ⊥AC ；第3题解图(2)解：如解图，连接AD ， ∵AB 是半圆O 的直径， ∴∠ADB ＝90°，即AD ⊥BC ，又∵DC ＝BD ＝2，∴AD 是BC 的垂直平分线， ∴AB ＝AC ， ∴∠ABD ＝∠ACD . 又∵DE ⊥AC ， ∴∠CED ＝90°， ∴∠ADB ＝∠DEC ， ∴△ABD ∽△DCE . ∴DE AD ＝DCAB ，即DE ＝AD ·DC AB，在Rt △ABD 中，BD ＝2，AB ＝3BD ＝6， ∴AD ＝62－22＝42，∴DE ＝42×26＝423.4. (1)证明：∵BM 是⊙O 的切线， ∴∠ABM ＝90°. ∵BC 平分∠ABM ， ∴∠ABC ＝12∠ABM ＝45°.∵AB 为⊙O 的直径， ∴∠ACB ＝90°， ∴∠BAC ＝45°， ∴∠CAE ＝∠CBA ；(2)证明：如解图，连接OC 和OD . ∵OC ＝DO ，DE ＝OE ， ∴∠OCD ＝∠ODC ＝∠DOE . ∴△OCD ∽△EDO ， ∴DO OE ＝DCOD，即DO 2＝OE ·DC . 又∵OA ＝DO ， ∴OA 2＝OE ·DC ；第4题解图(3)解：由(1)知，△ACB 为等腰直角三角形， ∴C 为AB ︵的中点，CO ⊥AB ，如解图，过点E 作EF ⊥AC 于点F ，设圆的半径为r ，∠DCO ＝θ，则有∠EOD ＝∠CDO ＝θ，∠CEO ＝∠EOD ＋∠CDO ＝2θ，由θ＋2θ＝90°，得θ＝30°，在Rt △COE 中，OE ＝33r ，则AE ＝r －33r ＝3－33r ，AC ＝2r . 在Rt △AEF 中，AF ＝EF ＝22×3－33r ＝32－66r ， ∴CF ＝AC －AF ＝2r －32－66r ＝32＋66r ，∴tan ∠ACD ＝EFCF ＝32－66r 32＋66r ＝2－ 3.类型三特殊四边形的动态探究题1.解：(1)BF ＝AE . 证明如下：由题意可知∠A ＝∠BFC ＝90°，BC ＝BE . ∵AD ∥BC ， ∴∠AEB ＝∠FBC ，在△ABE 与△FCB 中， ⎩⎪⎨⎪⎧∠EAB ＝∠BFC ∠AEB ＝∠FBC BE ＝CB， ∴△ABE ≌△FCB (AAS)． ∴AE ＝BF ； (2)①8；【解法提示】设运动时间为t 秒，∵四边形EPCQ 是矩形，∴∠APC ＝90°，∴四边形ABCP 是矩形，∴AP ＝BC .由勾股定理知AE ＝5，∴EP ＝13－5＝8，∴t ＝8.②13.【解法提示】∵四边形EPCQ 是菱形，∴QE ＝QC ，∴点Q 与点B 重合，∴CQ ＝CB ＝13，∴t ＝13. 2. (1)证明：∵AD 与⊙O 相切于点 A ， ∴OA ⊥AD ， ∵CD ∥OA ， ∴∠ADC ＝90°， ∵BC 是⊙O 的直径， ∴∠BAC ＝90°， ∴∠BAC ＝∠ADC ，又∵CD ∥OA ， ∴∠ACD ＝∠CAO ， ∵OA ＝OC ， ∴∠ACO ＝∠CAO ， ∴∠ACD ＝∠ACO ， ∴△ACD ∽△BCA ； (2)解：① 45°；【解法提示】∵四边形AOCD 为正方形，∴∠AOC ＝90°，∵OA ＝OC ，∴∠OCA ＝∠OAC ＝45°，∵∠BAC ＝90°，OA ＝OB ，∴∠B ＝∠OAB ＝90°－45°＝45°.② 60°.【解法提示】如解图，连接AE ，∵AD 为切线，∴∠DAE ＝∠ECA ，∠OAD ＝90°.∵四边形AOCE 为菱形，∴∠OAC ＝∠EAC ，∴∠DAE ＝∠ECA ＝∠OAC ＝30°，∴∠ACO ＝30°，∴∠AOB ＝∠ACO ＋∠OAC ＝30°＋30°＝60°，∵OA＝OB，∴∠B＝60°.第2题解图3. (1)证明：如解图，连接OD，BD，∵∠ABC＝90°，AB是⊙O的直径，∴BC是⊙O的切线．∵DE是⊙O的切线，∴BE＝DE.∴∠EBD＝∠EDB.∵AB是⊙O的直径，∴∠ADB＝90°.∴∠EBD＋∠C＝90°，∠EDB＋∠CDE＝90°.∴∠C＝∠EDC.∴DE＝CE.∴EB＝EC；第3题解图(2)解：① 30°；【解法提示】当△CDE为等边三角形时，则∠CDE＝∠C＝60°，∵∠ABC＝90°，∴∠BAC＝90°－60°＝30°.②45°.【解法提示】当四边形OBED是菱形时，BO＝DE，DE∥OB，BE＝OD，BE∥OD，∵∠ABC＝90°，∴∠BOD＝90°，∵OD＝OA，∴∠BAC＝45°.4. (1)证明：∵AC是⊙O的直径，CE⊥AC，∴CE是⊙O的切线．又∵DF是⊙O的切线，且交CE于点F，∴DF＝CF，∴∠CDF＝∠DCF，∵AC是⊙O的直径，∴∠ADC＝90°，∴∠DCF＋∠E＝90°，∠CDF＋∠EDF＝90°，∴∠E＝∠EDF，∴DF＝EF，∴EF＝FC；(2)解：① 45°；【解法提示】如解图，连接OD ，∵四边形ODFC 是正方形，∴∠DOC ＝90°，又∵OD ＝OC ，∴∠OCD ＝∠ODC ＝45°，∴∠ACD ＝∠OCD ＝45°.第4题解图② 9.【解法提示】∵AC 为⊙O 的直径，∴∠ADC ＝∠ABC ＝90°，∵AD ＝4，DC ＝2，∴AC ＝AD 2＋CD 2＝25，∴要使四边形ABCD 的面积最大，则△ABC 的面积最大，∴当△ABC 是等腰直角三角形时，△ABC 的面积最大，∴四边形ABCD 的最大面积＝12×4×2＋12×25×5＝9.5. (1)证明：如解图，连接OD ， ∵OA ＝OD ， ∴∠OAD ＝∠ODA ， ∵AD 平分∠EAF ， ∴∠DAE ＝∠DAO ， ∴∠DAE ＝∠ADO ， ∴OD ∥AE ， ∵AE ⊥EF ， ∴OD ⊥EF ，又∵OD 为⊙O 的半径， ∴EF 是⊙O 的切线；第5题解图(2)解：① 60°；【解法提示】如解图，连接CD ，当四边形ACDO 为菱形时，AO ∥CD ，AC ∥OD ，已知AD 为∠BAC 的平分线，∴∠OAD ＝∠ODA ＝∠ADC ＝∠CAD ，又∵∠CDA ＝∠CBA ，∠ACB ＝90°，∴∠ABC ＝30°，∠BAC ＝60°.②8.【解法提示】如解图，设OD 与BC 交于点G ，∵AB 为直径，∴∠ACB ＝90°，∵DE ⊥AC ，∴四边形CEDG 是矩形，∴DG ＝CE ，∵AC ＝3CE ，∴OG ＝12AC ＝32CE ，∴OD ＝52CE ＝5，∴CE ＝2，∴AC ＝6，∵AB ＝2×5＝10，∴BC ＝AB 2－AC 2＝8.6. (1)证明：如解图，∵PC 与⊙O 相切于点P ， ∴OP ⊥PC . ∵AC ⊥PC ，∴AC ∥OP . ∴∠1＝∠3. ∵OP ＝OA ， ∴∠2＝∠3， ∴∠1＝∠2， ∴AP 平分∠CAB ；第6题解图(2)解：① 22；【解法提示】∵AOPC 为正方形，∴OP ＝OA ＝2，∠POA ＝90°，∴AP ＝OP 2＋OA 2＝2 2. ②23π或43π. 【解法提示】当AD ＝AP ＝OP ＝OD 时，∵四边形ADOP 为菱形，∴△AOP 和△AOD 为等边三角形，则∠AOP ＝60°，lAP ︵＝60×2π180＝23π；当AD ＝DP ＝PO ＝OA 时，∵四边形ADPO 为菱形，∴△AOD 和△DOP为等边三角形，则∠AOP ＝120°，lAP ︵＝120×2π180＝43π.综上所述，当弧AP 为23π或43π时，以A ，D ，O ，P为顶点的四边形是菱形．7. (1)证明：如解图，连接AE ,第7题解图∵AB 为⊙O 的直径， ∴∠AEB ＝90°， ∵P A ＝AB ， ∴E 为PB 的中点， ∵AO ＝OB ， ∴OE ∥P A ，∴∠ADO ＝∠DOE ，∠A ＝∠EOB ， ∵OD ＝OA ， ∴∠A ＝∠ADO ， ∴∠EOB ＝∠DOE ， ∵OD ＝OE ＝OB ， ∴∠EDO ＝∠EBO ； (2)解：① 8；【解法提示】∵AB ＝8，∴OA ＝4，当OA 边上的高最大时，△AOD 的面积最大，此时点D 是AB ︵的中点，∴OD ⊥AB ，∴S △AOD ＝12×4×4＝8. ② 4.【解法提示】当四边形OBED 为菱形时，OD ＝OB ＝BE ＝DE ＝12AB ，∴DE ＝4. 8. (1)证明：∵OA ＝OB ，∴∠OAB ＝∠OBA ，∵AF ＝BE ，∴AE ＝BF ，在△OAE 和△OBF 中，⎩⎪⎨⎪⎧OA ＝OB ∠OAB ＝∠OBA AE ＝BF，∴△OAE ≌△OBF (SAS)，∴OE ＝OF ；(2)解：①120°；② 2.【解法提示】①如解图，连接OC ，∵四边形AOBC 是菱形，∴OA ＝AC ＝BC ＝OB ，∵OA ＝OC ，∴OA ＝AC ＝BC ＝OB ＝OC ，∴△AOC 和△BOC 都是等边三角形，∴∠AOC ＝∠BOC ＝60°，∴∠AOB ＝∠AOC＋∠BOC ＝60°＋60°＝120°；②如解图，设OC 与AB 交于点D ，∵点C 是劣弧AB ︵的中点，∴OC ⊥AB ，∵OA ＝OB ，∴AD ＝BD ，∠AOC ＝∠BOC ＝45°，∴OD ＝BD ，∵OB ＝2，∴BD ＝OD ＝1，∴AB ＝2，∴S 四边形AOBC ＝S △AOB ＋S △ACB ＝12AB ·OD ＋12AB ·CD ＝12AB ·OC ＝12×2×2＝ 2.第8题解图9. (1)证明：如解图，连接CO 并延长交AB 于点E ，∵CD 与⊙O 相切于点C ，∴CE ⊥CD ，∵四边形ABCD 为平行四边形，∴AB ∥CD ，∴CE ⊥AB ，∴AE ＝BE ，∴CA ＝CB ；第9题解图(2)解：当AC ＝AP 时，△APC ≌△CBA .理由如下：∵CA ＝CB ，AC ＝AP ，∴∠ABC ＝∠BAC ，∠APC ＝∠ACP ，∵∠ABC ＝∠APC ，∴∠BAC ＝∠ACP ，在△APC 与△CBA 中，⎩⎪⎨⎪⎧∠APC ＝∠CBA ∠ACP ＝∠CAB AC ＝CA，∴△APC ≌△CBA (AAS)；(3)解：60°.【解法提示】∵ABCD 是菱形，∴∠B ＝∠D ，AB ＝BC ＝CD ＝DA ，由(1)可知，CA ＝CB ，∴△ABC 是等边三角形，∴∠D ＝∠B ＝60°.10. (1)证明：如解图，连接AD ，∵AB 是⊙O 的直径，∴∠BDA ＝90°.∵D 为BC 的中点，∴BD ＝DC ，∴AB ＝AC ，∴△ABC 是等腰三角形；(2)解：① 60°；② 67.5°.【解法提示】①当∠B ＝60°时，四边形BDEO 是菱形．如解图，连接OD ，∵∠B ＝60°，∴△ABC 是等边三角形，△OBD 是等边三角形，∴△AOE 是等边三角形，△DOE 是等边三角形，∴OB ＝BD ＝DE ＝EO , ∴四边形BDEO 是菱形；②若△AOE 是直角三角形，只有一种情况，即∠AOE ＝90°，∵OA ＝OE ，∴∠OAE ＝∠AEO ＝45°，由(1)知 △ABC 是等腰三角形，∴∠B ＝∠C ＝180°－45°2＝67.5°.第10题解图11. (1)证明：∵AD 是⊙O 的直径，∴∠ABD ＝∠ACD ＝90°.在Rt △ABD 和Rt △ACD 中，∵⎩⎪⎨⎪⎧AB ＝AC AD ＝AD ， ∴Rt △ABD ≌Rt △ACD (HL)，∴∠ADB ＝∠ADC ，BD ＝CD ，在△BDE 和△CDE 中，⎩⎪⎨⎪⎧BD ＝CD ∠ADB ＝∠ADC DE ＝DE，∴△BDE ≌△CDE (SAS)；(2)解：① 60°；② 67.5°.【解法提示】①∵四边形BDCF 是菱形，∴∠FBC ＝∠DBC ，∵BF 平分∠ABC ，∴∠ABF ＝∠FBC ＝∠DBC ，又∵∠ABD ＝90°，∴∠ABF ＝∠FBC ＝30°，∴∠ABC ＝60°，又∵AB ＝AC ，∴△ABC 为等边三角形，∴∠BAC ＝60°；②∵四边形ABDC 是正方形，∴∠ABC ＝∠DBC ＝45°，∵BF 平分∠ABC ，∴∠ABF ＝∠FBC ＝22.5°，∴∠FBD ＝∠FBC ＋∠DBC ＝22.5°＋45°＝67.5°.12. (1)证明：∵OA ＝OC ，AD ＝OC ，∴OA ＝AD ，∠OAC ＝∠OCA ，∴∠AOD ＝∠ADO ，∵OD ∥AC ，∴∠OAC ＝∠AOD ，∴∠OAC ＝∠OCA ＝∠AOD ＝∠ADO ，∴∠AOC ＝∠OAD ，∴OC ∥AD ，∵OC ＝AD ，∴四边形OCAD 是平行四边形；(2)解：①30°；【解法提示】∵四边形OCAD 是菱形，∴OC ＝AC ，又∵OC ＝OA ，∴OC ＝OA ＝AC ，∴∠AOC ＝60°，∴∠B ＝12∠AOC ＝30°. ②当∠B ＝45°时，AD 与⊙O 相切．理由如下：∵AD 与⊙O 相切，∴∠OAD ＝90°，∵AD ∥OC ，∴∠AOC ＝90°，∴∠B ＝12∠AOC ＝45°.。

2023年中考数学专题训练——圆的计算和证明(附答案)

2023年中考专题训练——圆的计算和证明1．AB为⊙O直径，BC为⊙O切线，切点为B，CO平行于弦AD，作直线DC．(1)求证：DC为⊙O切线；(2) 若AD·OC=8，求⊙O半径．2．如图，四边形ABCD内接于⊙O，∠BAD =90°，AC是对角线．点E在BC的延长线上，且∠CED =∠BAC．（1）判断DE与⊙O的位置关系，并说明理由；（2）BA与CD的延长线交于点F，若DE∥AC，AB=4，AD =2，求AF的长．3．如图，已知在⊙O中，AB是⊙O的直径，AC＝8，BC＝6．（1）求⊙O的面积；（2）若D为⊙O上一点，且△ABD为等腰三角形，直接写出CD的长为．4．如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D＝60°，且AB＝6，过O点作OE⊥AC，垂足为E．（1）求OE的长；（2）若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积．（结果精确到0．01）5．如图，△AB ．C 内接于⊙0，点D 在半径OB 的延长线上，∠BCD=∠A=30°．（1）判断直线CD 与⊙0的位置关系，并说明理由（2）若⊙0的半径为1，求阴影部分面积．6．如图，已知Rt ABC ∆中，90ACB ∠=︒，E 为AB 上一点，以AE 为直径作O 与BC 相切于点D ，连接ED 并延长交AC 的延长线于点F ．（1）求证：AE AF =；（2）若5,4AE AC ==，求BE 的长．7．如图，AB 是⊙O 的直径，BD 是⊙O 的弦，延长BD 到点C ，使DC =BD ，连结AC 交⊙O 于点F ．（1）AB 与AC 的大小有什么关系？请说明理由；（2）若AB =8，∠BAC =45°，求：图中阴影部分的面积．8．如图，在△ABC 中，BA ＝BC ，以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，BC 的延长线于⊙O 的切线AF 交于点F ．（1）求证：∠ABC ＝2∠CAF ；（2）若AC ＝10，CE ：EB ＝1：4，求CE 的长．9．如图，在⊙O 中，半径OA 与弦BD 垂直，点C 在⊙O 上，∠AOB ＝80°(1) 若点C 在优弧BD 上，求∠ACD 的大小(2) 若点C 在劣弧BD 上，直接写出∠ACD 的大小10．如图，在等腰ABC 中，120BAC ∠=︒，AD 是BAC ∠的角平分线，且6AD =，以点A 为圆心，AD 长为半径画弧EF ，交AB 于点E ，交AC 于点F ，（1）求由弧EF 及线段FC 、CB 、BE 围成图形（图中阴影部分）的面积；（2）将阴影部分剪掉，余下扇形AEF ，将扇形AEF 围成一个圆锥的侧面，AE 与AF 正好重合，圆锥侧面无重叠，求这个圆锥的高h ．11．如图，四边形是平行四边形，以AB 为直径的O 经过点D, E 是O 上一点,且45AED ∠=︒．(1)判断CD与O的位置关系，并说明理由;(2) 若BC=2 .求阴影部分的面积.(结果保留π 的形式)．12．如图，AB是⊙O的直径，点D是⊙O外一点，AB＝AD，BD交⊙O于点C，AD交⊙O于点E，点P是AC的延长线上一点，连接PB、PD，且PD⊥AD(1)判断PB与⊙O的位置关系，并说明理由；(2)连接CE，若CE＝3，AE＝7，求⊙O的半径．13．如图，AB是⊙O的弦，半径OE⊥AB，P为AB的延长线上一点，PC与⊙O相切于点C，CE与AB交于点F．（1）求证：PC＝PF；（2）连接OB，BC，若OB∥PC，BC＝tan P＝34，求FB的长．14．已知，P A、PB是⊙O的切线，切点分别为A、B，AC是⊙O的直径．（1）如图1，若∠BAC＝25°，求∠P的度数；（2）如图2，延长PB、AC相交于点D．若AP＝AC，求cos D的值．15．如图，AB为⊙O的直径，C为⊙O上一点，∠ABC的平分线交⊙O于点D，DE⊥BC于点E．（1）试判断DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为3，BC＝4，求CE的长．16．如图，已知直线MN与以AB为直径的半圆相切于点C，∠A＝28°．(1)求∠ACM的度数；(2)在MN上是否存在一点D，使AB•CD＝AC•BC，为什么？17．如图，在⊙O上依次有A、B、C三点，BO的延长线交⊙O于E，AE CE，过点C作CD∥AB 交BE的延长线于D，AD交⊙O于点F．（1）求证：四边形ABCD是菱形；（2）连接OA、OF，若∠AOF＝3∠FOE且AF＝3，求CF的长．18．如图，△ABC内接于⊙O，且AB＝AC，D是AC上一点，AD与BC交于E，AF⊥DB，垂足为F．（1）求证：∠ADB＝∠CDE；（2）若AF＝DC＝6，AB＝10，求△DBC的面积．19．如图，AB是半圆O的直径，C是AB延长线上一点，CD与半圆O相切于点D，连接AD，BD．（1）求证：∠BAD＝∠BDC；（2）若sin∠BDC，BC＝2，求⊙O的半径．20．同学们都学习过《几何》课本第三册第199页的第11题，它是这样的：如图，A为⊙O 的直径EF上的一点，OB是和这条直径垂直的半径，BA和⊙O相交于另一点C，过点C的切线和EF的延长线相交于点D，求证：DA＝DC．（1）现将图1中的直径EF所在直线进行平行移动到图2所示的位置，此时OB与EF垂直相交于H，其它条件不变．①求证：DA＝DC；②当DF：EF＝1：8，且DF AB•AC的值．（2）将图2中的EF所在直线继续向上平行移动到图3所示的位置，使EF与OB的延长线垂直相交于H，A为EF上异于H的一点，且AH小于⊙O的切线交EF于D，试猜想：DA＝DC是否仍然成立？证明你的结论．参考答案：1．（1证明见解析；（2）2.【分析】（1）连接OD ，要证明DC 是 O 的切线，只要证明∠ODC=90°即可．根据题意，可证△OCD ≌△OCB ，即可得∠CDO=∠CBO=90°，由此可证DC 是 O 的切线；（2）连接BD ，OD ．先根据两角对应相等的两三角形相似证明△ADB ∽△ODC ，再根据相似三角形对应边成比例即可得到r 的值．【解析】解：（1）证明：连接OD.∵OA=OD ，∴∠A=∠ADO.∵AD ∥OC ，∴∠A=∠BOC ，∠ADO=∠COD ，∴∠BOC=∠COD.∵在△OBC 与△ODC 中，{OB ODBOC DOC OC OC=∠=∠=，∴△OBC ≌△ODC(SAS)，∴∠OBC=∠ODC ，又∵BC 是O 的切线，∴∠OBC=90°，∴∠ODC=90°，∴DC 是O 的切线；（2）连接BD.∵在△ADB 与△ODC 中,{90A COD ADB ODC ∠=∠∠=∠=︒∴△ADB ∽△ODC ，∴AD:OD=AB:OC ，∴AD ⋅OC=OD ⋅AB=r ⋅2r=2r²,即2r²=8，故r=2．2．（1）DE与⊙O相切，证明见解析；（2）83 AF .【分析】（1）连接BD，先根据圆周角定理证明BD是⊙O的直径，证明∠BDC+∠CDE=90°，即BD⊥DE，即可得出DE与⊙O相切；（2）先根据平行线的性质得∠BHC=∠BDE=90°，由垂径定理得AH=CH，由垂直平分线的性质得BC=AB=4，CD=AD=2，证明△FAD∽△FCB，列比例式得CF=2AF，设 AF=x，则DF=CF-CD=2x-2，根据勾股定理列方程可解答．【解析】解：（1）DE与⊙O相切，理由是：连接BD，如下图，∵四边形ABCD内接于⊙O，∠BAD=90°，∴BD是⊙O的直径，即点O在BD上，∴∠BCD=90°，∴∠CED+∠CDE=90°．∵∠CED=∠BAC，又∵∠BAC=∠BDC，∴∠CED=∠BDC，∴∠BDC+∠CDE=90°，即∠BDE=90°，∴DE⊥BD于点D，∴DE与⊙O相切．（2）如下图，BD与AC交于点H，∵DE ∥AC ，∴∠BHC=∠BDE=90°．∴BD ⊥AC ．∴AH=CH ．∴BC=AB=4，CD=AD=2．∵∠FAD=∠FCB=90°，∠F=∠F ，∴△FAD ∽△FCB ，2=4AF AD CF CB ∴=， ∴CF=2AF ，设 AF=x ，则DF=CF-CD=2x-2．在Rt △ADF 中，DF 2=AD 2+AF 2，∴（2x-2）2=22+x 2．解得： 128,03x x ==（舍去）， 83AF ∴=．【点评】本题考查圆周角定理，垂径定理，垂直平分线的性质定理，相似三角形的性质和判定，切线的判定，勾股定理．（1）证明切线最常用的办法，即如果直线与圆有交点，则连接交点与圆心的半径，只有证明这条半径与该直线垂直即可，此问中能依据90°圆周角所对的弦是直径证明BD 是⊙O 的直径是解题关键；（2）中能通过证明△FAD ∽△FCB ，得出CF=2AF 是解题关键．3．（1）25π；（2272【分析】（1）先利用圆周角定理得到90ACB ∠=︒．再利用勾股定理计算出AB ，然后利用圆的面积公式计算；（2）作直径DD AB '⊥，BH CD ⊥于H ，如图，利用垂径定理得到AD BD =，再证明ADB ∆为等腰直角三角形得到252DB AB =，利用BCH ∆为等腰直角三角形得到232CH BH ==42DH =72CD =股定理计算CD '即可．【解析】解：（1）AB 是O 的直径，90ACB ∴∠=︒．8AC ∴=，6BC =，10AB ∴=．O ∴的面积2525ππ=⨯=；（2）作直径DD AB '⊥，BH CD ⊥于H ，如图，则AD BD =，AD BD ∴=，45ACD BCD ∠=∠=︒， AB 是O 的直径，90ADB ∴∠=︒，ADB ∴∆为等腰直角三角形，DB AB ∴== 又∵45BCD BAD ∠=∠=︒，∴BCH ∆为等腰直角三角形，CH BH ∴===在Rt BDH ∆中，DHCD CH DH ∴=+=DD '是O 的直径，90DCD ∴∠'=︒，CD ∴'=综上所述，CD【点评】本题考查了与圆有关的计算，涉及了圆周角定理、垂径定理和勾股定理．解题关键是正确画出图形得出ADB ∆为等腰直角三角形，并用勾股定理求解．4．（1）OE=32；（2）32π．【分析】（1）根据∠D=60°，可得出∠B=60°，继而求出BC ，判断出OE 是△ABC 的中位线，就可得出OE 的长；（2）连接OC ，将阴影部分的面积转化为扇形FOC 的面积．【解析】解：（1）∵∠D=60°，∴∠B=60°（圆周角定理），又∵AB=6，∴BC=3，∵AB 是⊙O 的直径，∴∠ACB=90°，∵OE ⊥AC ，∴OE ∥BC ，又∵点O 是AB 中点，∴OE 是△ABC 的中位线，∴OE=1232BC =；（2）连接OC ，则易得△COE ≌△AFE ，故阴影部分的面积=扇形FOC 的面积，S 扇形FOC =260333260π⨯=π．即可得阴影部分的面积为32π．【点评】此题考查扇形的面积，含30°角的直角三角形的计算及圆周角定理等，解题关键在于将不规则图形转化为规则图形进行求解．5．（1）相切，理由见解析；（236π 【分析】（1）根据“同弧所对的圆周角等于圆心角的一半”求出∠O 的度数，再根据半径相等求出△OCB 为等边三角形，即可得出答案；（2）根据∠O 的度数和半径求出CD 的长度，进而求出△COD 的面积，利用扇形面积公式求出扇形OCB 的面积，三角形的面积减去扇形的面积即可得出答案.【解析】解：（1）∵∠A=30°∴∠O=2∠A=60°又OB=OC∴△OBC 为等边三角形，∠OCB=60°又∠BCD=30°∴∠OCD=∠OCB+∠BCD=90°∴CD 与⊙O 相切（2）由（1）可知△OCD 为直角三角形，∠O=60°又半径为1，即OC=1∴CD OC tan O ∠==∴12OCD S CO CD =⨯⨯=2OCB 601S 3606ππ⨯⨯==扇形∴OCB S S 6OCD S π=-=阴影扇形【点评】本题考查的是圆的综合，难度适中，牢记圆中的相关定理和性质是解决本题的关键. 6．（1）见解析；（2）53BE =. 【分析】（1）连接OD ，根据切线的性质得到OD ⊥BC ，根据平行线的判定定理得到OD ∥AC ，求得∠ODE=∠F ，根据等腰三角形的性质得到∠OED=∠ODE ，等量代换得到∠OED=∠F ，于是得到结论；（2）根据平行得出BOD BAC ∆∆∽，再由BO OD AB AC=可得到关于BE 的方程，从而得出结论．【解析】（1）证明：连接OD ，∵BC 切O 于点D ，∴OD BC ⊥．∴90ODC ︒∠=．又90ACB ︒∠=，∴//OD AC ，∴ODE F ∠=∠．∵OE OD ，∴OED ODE ∠=∠，∴OED F ∠=∠．∴AE AF =．（2）解：∵//OD AC ，∴BOD BAC ∆∆∽，∴BO OD AB AC=． ∵5,4AE AC ==，∴ 2.5OE OD ==， ∴ 2.5 2.554BE BE +=+， ∴53BE =．【点评】本题考查了切线的性质，平行线的性质，相似三角形的判定和性质，等腰三角形的判定与性质等知识，正确的作出辅助线是解题的关键．7．（1）AB =AC ；（2）242π-【分析】（1）连接AD ，根据圆周角定理可以证得AD 垂直且平分BC ，然后根据垂直平分线的性质证得AB ＝AC ；（2）连接OD 、过D 作DH ⊥AB ，根据扇形的面积公式解答即可．【解析】（1）AB =AC ．理由是：连接AD ．∵AB 是⊙O 的直径，∴∠ADB =90°，即AD ⊥BC ，又∵DC =BD ，∴AB =AC ；（2）连接OD 、过D 作DH ⊥AB ．∵AB =8，∠BAC =45°，∴∠BOD =45°，OB =OD =4，∴DH 2∴△OBD 的面积=1422422⨯⨯扇形OBD 的面积=24542360ππ⋅⋅=，阴影部分面积=242π-【点评】本题考查了圆周角定理以及等腰三角形的性质定理，理解弧的度数和对应圆心角的度数的关系是关键．8．（1）见解析；（2）CE ＝2．【分析】（1）首先连接BD ，由AB 为直径，可得∠ADB=90°，又由AF 是⊙O 的切线，易证得∠CAF=∠ABD．然后由BA=BC，证得：∠ABC=2∠CAF；（2）首先连接AE，设CE=x，由勾股定理可得方程：（）2=x2+（3x）2求得答案．【解析】（1）证明：如图，连接BD．∵AB为⊙O的直径，∴∠ADB＝90°，∴∠DAB+∠ABD＝90°．∵AF是⊙O的切线，∴∠F AB＝90°，即∠DAB+∠CAF＝90°．∴∠CAF＝∠ABD．∵BA＝BC，∠ADB＝90°，∴∠ABC＝2∠ABD．∴∠ABC＝2∠CAF．（2）解：如图，连接AE，∴∠AEB＝90°，设CE＝x，∵CE：EB＝1：4，∴EB＝4x，BA＝BC＝5x，AE＝3x，在Rt△ACE中，AC2＝CE2+AE2，即（2＝x2+（3x）2，∴x＝2．∴CE＝2．【点评】此题考查了切线的性质，三角函数以及勾股定理，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用是解题关键．9．（1）∠ACD=40°；（2）∠ACD=40°或140°．【分析】（1）由AO⊥BD，根据垂径定理可得AD AB，再利用等弧对等角，以及圆周角定理即可求出结果；（2）如图所示，点C 有两个位置，分别利用圆周角定理的推论和圆周角定理求出即可.【解析】解：（1）∵AO ⊥BD ，∴AD AB =，∴∠AOB =2∠ACD ，∵∠AOB =80°，∴∠ACD =40°；（2）如图，①当点C 1在AB 上时，∠AC 1D =∠ACD =40°；②当点C 2在AD 上时，∵∠AC 2D +∠ACD =180°，∴∠AC 2D =140°. 综上所述，∠ACD =40°或140°．【点评】本题考查了圆周角定理及其推论和垂径定理等知识，熟练掌握上述知识、正确分类是解本题的关键.10．（1）312π；（2）42h =【分析】（1）利用等腰三角形的性质得到AD BC ⊥，BD CD =，则可计算出BD 63=后利用扇形的面积公式，利用由弧EF 及线段FC 、CB 、BE 围成图形（图中阴影部分）的面积ABC EAF =S S -扇形进行计算；（2）设圆锥的底面圆的半径为r ，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到120π62πr 180⋅⋅=，解得r 2=，然后利用勾股定理计算这个圆锥的高h ．【解析】∵在等腰ABC 中，BAC 120∠=︒，∴B 30∠=︒，∵AD 是BAC ∠的角平分线，∴AD BC ⊥，BD CD =， ∴BD 3AD 63== ∴BC 2BD 3==∴由弧EF 及线段FC 、CB 、BE 围成图形（图中阴影部分）的面积2ABC EAF 1120π6=S S 6123312π2360⋅⋅-=⨯⨯=扇形. （2）设圆锥的底面圆的半径为r ，根据题意得120π62πr180⋅⋅=，解得r2=，这个圆锥的高h【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了等腰三角形的性质和扇形的面积公式．11．（1）相切，证明见解析（2）3-23π.【分析】(1)连接BD，OD求出∠ABD=∠AED=45°，根据DC∥AB推出∠CDB=45°求出∠ODC=90°根据切线的判定推出即可(2)求出∠AOD=∠BOD=90°，求出AO，OD分别求出△AOD扇形DOB，平行四边形ABCD 的面积相减即可求出答案【解析】(1)解CD与⊙O的位置关系是相切理由是连接BD，OD∵∠AED=45°∴∠ABD=∠AED=45°∵四边形ABCD是平行四边形，∴DC∥AB,∴∠CDB=45°∵OD=OB,∴∠ODB=∠OBD=45°∴∠ODC=45°+45°=90°∵OD为半径,∴CD与⊙O的位置关系是相切;(2)解AB∥CD,∠ODC=90°∴∠DOB=90°=∠DOA,∵四边形ABCD是平行四边形,∴AD=BC=2,在△AOD中由勾股定理得:2AO2=222∴S △AOD=12 OA×OD=12×2×2S 扇形BOD=26022=3603⨯ππ S 平行四边形ABCD=AB×2×2∴阴影部分的面积是:4-1-23π=3-23π.【点评】此题考查切线的判定，勾股定理，扇形面积，平行四边形的性质，解题关键在于作辅助线12．(1)PB 与⊙O 相切，理由见解析；(2)⊙O 的半径为4.5．【分析】（1）根据线段垂直平分线的性质可得PB =PD ，通过证明△ABP 与△ADP 全等，根据全等三角形对应角相等可得∠ABP =∠ADP =90°，再根据切线的判定定理即可得证；（2）根据全等三角形的性质得∠BAC =∠DAC ，得到BC =CE =3，然后证明△DCE 与△DAB 相似，然后根据相似三角形的对应边成比可推导得出DC •DB ＝DE •DA ，代入相关数据即可求得答案．【解析】(1)PB 与⊙O 相切，理由如下：∵AB 是⊙O 的直径，∴AC ⊥BD ，又AB ＝AD ，∴AP 是线段BD 的垂直平分线，∴PB ＝PD ，在△ABP 和△ADP 中， AB AD PB PD AP AP =⎧⎪=⎨⎪=⎩，∴△ABP ≌△ADP (SSS)，∴∠ABP ＝∠ADP ＝90°，∴PB 与⊙O 相切；(2)连接CE ，∵△ABP≌△ADP，∴∠BAC＝∠DAC，∴BC CE=，∴BC＝CE＝3，∵AB＝AD，AC⊥BD，∴BC＝CD＝3，∵四边形ABCE是⊙O的内接四边形，∴∠DBA+∠CEA=180°，∵∠DEC+∠CEA=180°，∴∠DBA=∠DEC，又∵∠CDE=∠ADB，∴△DCE∽△DAB，∴DC：DA=DE：DB，∴DC•DB＝DE•DA，即3×6＝DE×(DE+7)，解得，DE＝2，∴DA＝2+7＝9，∴AB＝AD＝9，∴⊙O的半径为4.5．【点评】本题考查了切线的判定，圆内接四边形的性质，相似三角形的判定与性质，熟练掌握相关的性质定理与判定定理是解题的关键．13．（1）证明见解析；（2）FB＝2【分析】（1）连接OC，根据切线的性质以及OE⊥AB，可知∠E+∠EF A＝∠OCE+∠FCP＝90°，从而可得∠EF A＝∠FCP，继而可推得∠CFP＝∠FCP，再根据等角对等边即可证得；（2）过点B作BG⊥PC于点G，由OB∥PC，OB＝OC，BC＝，从而求得OB＝3，继而证得四边形OBGC是正方形，从而有OB＝CG＝BG＝3，从而有34BGPG=，求得PG＝4，再利用勾股定理可求得PB长，继而可求出FB长．【解析】解：（1）连接OC，∵PC是⊙O的切线，∴∠OCP＝90°，∵OE＝OC，∴∠E＝∠OCE，∵OE⊥AB，∴∠E+∠EF A＝∠OCE+∠FCP＝90°，∴∠EF A＝∠FCP，∵∠EF A＝∠CFP，∴∠CFP＝∠FCP，∴PC＝PF；（2）过点B作BG⊥PC于点G，∵OB∥PC，∴∠COB＝90°，∵OB＝OC，BC＝2∴OB＝3，∵BG⊥PC，∴四边形OBGC是正方形，∴OB＝CG＝BG＝3，∵tan P＝34，∴34 BGPG，∴PG＝4，∴由勾股定理可知：PB＝5，∵PF＝PC＝7，∴FB＝PF﹣PB＝7﹣5＝2．【点评】本题考查了切线的性质，勾股定理，等腰三角形的判定，正方形的判定，锐角三角函数的定义等，解题的关键是正确添加辅助线，灵活运用相关知识求解．14．（1）50°；（2）cosD＝45．【分析】（1）连接OB．根据平行的想得到PA⊥AO，PB⊥OB，根据四边形的内角和即可得到结论；（2）连结OP交AB于点E，再连OB、BC，根据切线的性质得到∠PAC=∠PBO=90°，推出OP是AB的垂直平分线，根据相似三角形的性质即可得到结论．【解析】（1）证明：如图1，连接OB．∵PA、PB分别切⊙O于A、B两点，∴PA⊥AO，PB⊥OB，∴∠PAO＝∠PBO＝90°．∵∠BAC＝25°，OB＝OA，∴∠BOA＝180°﹣25°﹣25°＝130°，∴∠P＝360°﹣90°﹣90°﹣130°＝50°；（2）解：如图2，连结OP交AB于点E，再连OB、BC，∵PA、PB是⊙O的切线，∴∠PAC＝∠PBO＝90°，∵AP＝AC，AC是⊙O的直径，∴12OAPA=，∵PB＝PA，OB＝OA，∴OP是AB的垂直平分线，∵∠OAP＝90°，AE⊥OP，∴△OEA∽△AEP∽△OAP，∴OA OE OP OA=，设OE＝a，可得AE＝BE＝BC＝2a，PE＝4a，∴OP＝5a，∴OA，PA＝PB＝，∵∠ABC＝∠AEO＝90°，∴OP∥BC，∴△DBC∽△DPO，∴CDOD＝BDOD＝BCOP＝25．∴BD 45，OD＝535，∴cos D＝BDOD＝45．【点评】本题考查了切线的性质，四边形的内角和，相似三角形的判定和性质，平行线的判定，正确的作出辅助线是解题的关键．15．（1）DE与⊙O相切，证明详见解析；（2）EC＝1.【分析】（1）连接OD，由题意可得∠CBD=∠ODB=∠DBO，可得OD∥BE，可证DE⊥OD，即可证DE与⊙O相切；（2）过点D作DF⊥AB于点F，连接DC，由题意可证Rt△DF A≌Rt△DEC，Rt△DBF≌Rt△DBE，可得AF=EC，BF=BE，即可求EC的长．【解析】解：（1）DE与⊙O相切理由如下：连接OD∵OB＝OD∴∠OBD＝∠ODB∵∠ABC的平分线交⊙O于点D，∴∠ABD＝∠CBD∴∠CBD＝∠ODB∴OD∥BE∵DE⊥BC于点E．∴DE⊥OD∴DE与⊙O相切（2）过点D作DF⊥AB于点F，连接DC，∵∠ABD＝∠CBD，DE⊥BE，DF⊥AB∴DF＝DE，AD DC=∴AD＝CD∵AD＝CD，DF＝DE∴Rt△DF A≌Rt△DEC（HL）∴AF＝EC∵DF＝DE，DB＝DB∴Rt△DBF≌Rt△DBE（HL）∴BF＝BE∵BA＝BF+AF＝BE+AF＝BC+EC+CE＝6∴4+2CE＝6∴EC＝1【点评】本题考查了直线与圆的位置关系，圆周角定理，全等三角形判定和性质，添加恰当辅助线构造全等三角形是本题的关键．16．(1)∠ACM＝62°；(2)存在符合条件的点D，使AB•CD＝AC•BC，理由见解析.【分析】(1)求∠ACM的度数,需求出∠B的度数;在Rt ABC∆中,已知∠A的度数,即可求出∠B、∠ACM的度数;(2)乘积的形式通常可以转化为比例的形式:①AB BCAC CD=,此时需证Rt ABC Rt CBD∆~∆,那么过B作MN的垂线,那么垂足即为符合条件的D点;②AB ACBC CD=,此时需证Rt ABC Rt ACD∆~∆,则过A作MN的垂线,垂足也符合D点的条件.两者的证明过程一致,都是通过弦切角得出一组对应角相等,再加上一组直角得出三角形相似.【解析】(1)∵AB是半圆的直径，∴∠ACB＝90°，∴∠B＝90°﹣∠A＝62°，∵直线MN与以AB为直径的半圆相切于点C，∴∠ACM＝∠B＝62°；(2)存在符合条件的点D，使AB•CD＝AC•BC，①过A作AD⊥MN于D，则AB•CD＝AC•BC，证明：∵MN是半圆的切线，且切点为C，∴∠ACD＝∠B，∵∠ADC＝∠ACB＝90°，∴△ABC∽△ACD，∴AB AC BC CD=，即AB•CD＝AC•BC；②过B作BD⊥MN于D，则AB•CD＝AC•BC，证明过程同①，因此MN上存在至少一点D，使AB•CD＝AC•B C．【点评】本题考查了弦切角定理及相似三角形的判定和性质,要求学生能够熟练掌握相似的判断和性质并应用.17．（1）证明见解析；（2）53π【分析】（1）先根据圆的性质得：∠CBD=∠ABD，由平行线的性质得：∠ABD=∠CDB，根据直径和等式的性质得：，AB BC=，由一组对边平行且相等可得四边形ABCD是平行四边形，由AB=BC可得结论；（2）先设∠FOE=x，则∠AOF=3x，根据∠ABC+∠BAD=180°，列方程得：4x+2x+12（180-3x）=180，求出x的值，接着求CF所对的圆心角和半径的长，根据弧长公式可得结论．【解析】（1）证明：∵AE CE=，∴∠CBD＝∠ABD，∵CD∥AB，∴∠ABD＝∠CDB，∴∠CBD＝∠CDB，∴CB＝CD，∵BE是⊙O的直径，∴AB BC=，∴AB＝BC＝CD，∵CD∥AB，∴四边形ABCD是菱形；（2）∵∠AOF＝3∠FOE，设∠FOE＝x，则∠AOF＝3x，∠AOD＝∠FOE+∠AOF＝4x，∵OA＝OF，∴∠OAF＝∠OF A＝12（180﹣3x）°，∵OA＝OB，∴∠OAB＝∠OBA＝2x，∴∠ABC＝4x，∵BC∥AD，∴∠ABC+∠BAD＝180°，∴4x+2x+12（180﹣3x）＝180，x＝20°，∴∠AOF＝3x＝60°，∠AOE＝80°，∴∠COF＝80°×2﹣60°＝100°，∵OA＝OF，∴△AOF是等边三角形，∴OF＝AF＝3，∴CF的长＝1003180π⨯＝53π．【点评】本题考查平行四边形和菱形的判定和性质、等边三角形的判定和性质、弧长公式，平行线的性质等知识，解题的关键是学会设未知数，列方程求角的度数，证明三角形是等边三角形是解题的突破点，属于中考常考题型．18．（1）证明见解析（2）18【分析】（1）根据AB=AC，可得出∠ABC=∠BCA，再根据圆内接四边形的性质可得出∠CDE=∠ABC，从而得出答案；（2）作AM⊥CD于点M，根据题意可得出BF，还可证明△ACM≌△ABF，从而可得出△DBC 的面积．【解析】（1）证明：∵AB＝AC，∴∠ABC＝∠BCA＝∠ADB，∵四边形ABCD是圆内接四边形，∴∠CDE＝∠ABC，∴∠ADB＝∠CDE；（2）解：作AM⊥CD于点M，∵AB＝10，AF＝6，∴BF＝8，∵AD平分∠BDM，AM＝AF＝6，∴△ACM≌△ABF，∴CM＝BF＝8，∴DF＝DM＝CM﹣CD＝2．∴BD＝BF+DF＝10＝AB．∴∠BAD＝∠ADB＝∠ADM，∴AB∥CD，∴S△DBC＝S△ADC＝12CD×AM＝18．【点评】本题考查了等腰三角形的性质、全等三角形的判定和性质以及圆周角定理，熟练掌握这些性质是解题的关键.19．（1）证明见解析（2）3【分析】（1）连接OD，如图，先由切线的性质得∠ODB+∠BDC=90°，再由圆周角定理得到∠ODB+∠ODA=90°，则∠BDC=∠ODA，加上∠ODA=∠BAD，然后等量代换即可得到结论；（2）利用正弦定义得sin∠A=sin∠BDC=5BDAB设5，AB=5x，则5，然后证明△CBD∽△CDA，则利用相似比可计算出CD和AB，从而得到圆的半径．【解析】（1）证明：连接OD，如图，∵CD与半圆O相切于点D，∴OD⊥CD，∴∠ODC＝90°，即∠ODB+∠BDC＝90°，∵AB是半圆O的直径，∴∠BDA＝90°，即∠ODB+∠ODA＝90°，∴∠BDC＝∠ODA，∵OD ＝OA ，∴∠ODA ＝∠BAD ，∴∠BAD ＝∠BDC ；（2）解：∵sin ∠A ＝sin ∠BDC∴BD AB =设BD ，AB ＝5x ，则AD ，∵∠BAD ＝∠BDC ，∠BCD ＝∠DCA ，∴△CBD ∽△CDA ，∴12BC CD BD CD AC AD ====，而BC ＝2，∴CD ＝4，AC ＝8，∴AB ＝AC ﹣BC ＝6，∴⊙O 的半径位3．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．解决（2）小题的关键是构建△CBD 与△CDA 相似．20．（1）①见解析②24（2）结论DA ＝DC 仍然成立【分析】（1）①连接OC ，利用切线的性质则可得到OC ⊥DC ，然后得到∠DCA=90°-∠ACO=90°-∠B=∠DAC ，利用等角对等边得到DA=DC 即可；②利用DF ：EF=1：8，然后利用切线长定理求得DC 的长，进而得到DC 、AD 的长，然后利用切线长定理得：AB•AC=AE•AF=24；（2）结论仍然成立，延长BO 交⊙O 于K ，连CK ，利用切线的性质可以得到∠DCA=∠CKB=90°-∠CBK ，从而得到∠DCA=∠BAH ，问题得证.【解析】（1）①证明：连OC ，则OC ⊥DC ，∴∠DCA＝90°﹣∠ACO＝90°﹣∠B，又∠DAC＝∠BAE＝90°﹣∠B，∴∠DAC＝∠DCA∴DA＝DC，②∵DF：EF＝1：8，DF2∴EF＝8DF＝2，又DC为切线，∴DC2＝DF•DE22＝18，∴DC＝2∴AD＝DC＝2∴AF＝AD﹣DF＝2∴AE＝EF﹣AF＝2，∴AB•AC＝AE•AF＝24；（2）结论DA＝DC仍然成立，理由如下：延长BO交⊙O于K，连CK，则∠KCB＝90°，又DC为⊙O的切线，∴∠DCA＝∠CKB＝90°﹣∠CBK，又∠BAH＝90°﹣∠HBA，而∠CBK＝∠HBA，∴∠DCA＝∠BAH，∴DA＝DC．【点评】本题考查了切线的性质、垂径定理及切割线定理的内容，是一道比较复杂的切线的性质的综合题，难度较大．。

中考数学《圆的综合》专题训练(含有答案)

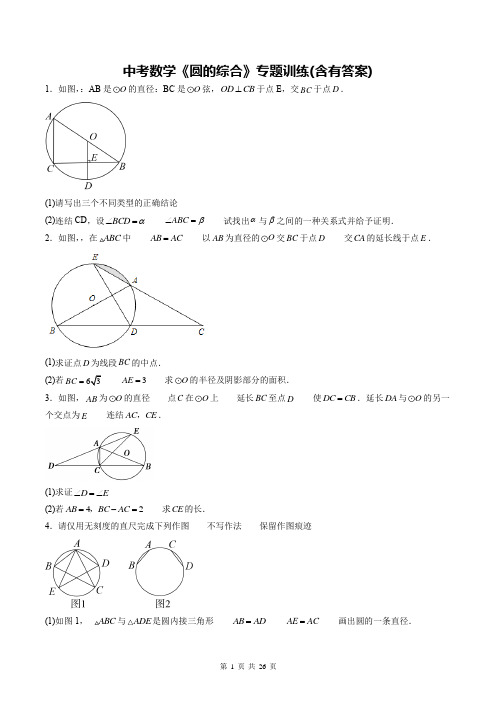
中考数学《圆的综合》专题训练(含有答案)1．如图，：AB 是O 的直径：BC 是O 弦，OD CB ⊥于点E ，交BC 于点D ．(1)请写出三个不同类型的正确结论(2)连结CD ，设BCD α∠= ABC β∠= 试找出α与β之间的一种关系式并给予证明．2．如图，，在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D 交CA 的延长线于点E ．(1)求证点D 为线段BC 的中点．(2)若63BC = 3AE = 求O 的半径及阴影部分的面积．3．如图，AB 为O 的直径点C 在O 上延长BC 至点D 使DC CB =．延长DA 与O 的另一个交点为E 连结AC CE ，．(1)求证D E ∠=∠(2)若42AB BC AC =-=，求CE 的长．4．请仅用无刻度的直尺完成下列作图不写作法保留作图痕迹(1)如图1， ABC 与ADE 是圆内接三角形 AB AD = AE AC = 画出圆的一条直径．(2)如图2 ， AB CD 是圆的两条弦 AB CD =且不相互平行画出圆的一条直径． 5．如图，AB 是O 的直径点D 在AB 的延长线上点C 在O 上 ,30CA CD CDA =∠=︒．(1)求证CD 是O 的切线(2)若O 的半径为6 求点A 到CD 所在直线的距离．6．如图，点C 在以AB 为直径的O 上过C 作O 的切线交AB 的延长线于E AD CE ⊥于D 连接AC ．(1)求证ACD ABC ∠=∠(2)若3tan 4CAD ∠= 8AD = 求O 直径AB 的长．7．如图，已知以Rt ABC 的直角边AC 为直径作O 交斜边AB 于点E 连接EO 并延长交BC 的延长线于点D 连接AD 点F 为BC 的中点连接EF ．(1)求证EF 是O 的切线(2)若O 的半径为6 8CD = 求AB 的长．8．如图， AB 是半圆O 的直径 D 为半圆O 上的点(不与A B 重合) 连接AD 点C 为BD 的中点过点C 作CF AD ⊥ 交AD 的延长线于点F 连接BF AC 交于点E ．(1)求证FC 是半圆O 的切线(2)若3AF = 23AC = 求半圆O 的半径及AE 的长．9．如图， AB 为O 的直径 C 为BA 延长线上一点 CD 是O 的切线 D 为切点 OF AD ⊥于点E 交CD 于点F ．(1)求证ADC AOF ∠=∠ (2)若53OC OB = 24BD = 求EF 的长． 10．如图，所示 AB 是O 的直径点D 在AB 上点C 在O 上 AD AC =CD 的延长线交O 于点E ．(1)在CD 的延长线上取一点F 使BF BC = 求证BF 是O 的切线 (2)若2AB = 2CE 求图中阴影部分的面积．11．如图， ABC 内接于O AB 为O 的直径 D 为BA 延长线上一点连接CD 过O 作OF BC ∥交AC 于点E 交CD 于点F ACD AOF ∠=∠．(1)求证CD 为圆O 的切线 (2)若1sin 4D =10BC = 求EF 的长． 12．如图，四边形ABCD 是O 的内接四边形 AD CD = 70BAC ∠=︒ 50∠=°ACB ．(1)求ABD ∠的度数 (2)求BAD ∠的度数．13．如图，四边形ABCD 是O 的内接四边形且对角线BD 为O 的直径过点A 作AE CD ⊥ 与CD 的延长线交于点E 且DA 平分BDE ∠．(1)求证AE 是O 的切线(2)若O 的半径为5 6CD = 求DA 的长．14．如图，在正方形ABCD 中有一点P 连接AP BP 旋转APB △到CEB 的位置．(1)若正方形的边长是8 4BP =．求阴影部分面积 (2)若4BP = 7AP = 135APB ∠=︒ 求PC 的长．15．如图， AB 是O 的直径 OD 垂直于弦AC 于点E 且交O 于点D F 是BA 延长线上一点若CDB BFD ∠=∠．(1)求证 FD 是O 的一条切线(2)若15AB = 9BC = 求DF 的长． 16．如图，O 是ABC ∆的外接圆 AE 切O 于点A AE 与直径BD 的延长线相交于点E ．(1)如图，① 若70C ∠=︒ 求E ∠的大小 (2)如图，① 若AE AB = 求E ∠的大小．17．已知如图，直线MN 交O 于A B 两点 AC 是直径 AD 平分CAM ∠交O 于D 过D 作DE MN ⊥于E ．(1)求证DE 是O 的切线(2)若8cm DE = 4cm AE = 求O 的半径．18．已知四边形ABCD 内接于O C 是DBA 的中点 FC AC ⊥于C 与O 及AD 的延长线分别交于点,E F 且DE BC =．(1)求证~CBA FDC(2)如果9,4AC AB == 求tan ACB ∠的值．参考答案与解析1．(1)见解析(2)关系式为2=90αβ+︒ 证明见解析【分析】（1）AB 是O 的直径 BC 是弦 OD BC ⊥于E 本题满足垂径定理．（2）连接,CD DB 根据四边形ACDB 为圆内接四边形可以得到290αβ+=︒．【解析】（1）解不同类型的正确结论有 ①BE CE = ①BD CD = ①90BED ∠=︒ ①BOD A ∠=∠ ①AC OD ∥ ①AC BC ⊥ ①222OE BE OB += ①ABC S BC OE =⋅△ ①BOD 是等腰三角形 ①BOE BAC △∽△等等．（2）如图，连接,CD DBα与β之间的关系式为290αβ+=︒证明AB 为圆O 的直径90A ABC ∴∠+∠=︒①又四边形ACDB 为圆内接四边形180A CDB ∠∠∴+=︒①∴①-①得90CDB ABC ∠∠-=︒①18021802CDB BCD α∠=︒-∠=︒- 即180290αβ︒--=︒ ①2=90αβ+︒．【点评】本题考查了圆的一些基本性质且有一定的开放性垂径定理圆内接四边形的性质掌握圆的相关知识． 2．(1)见解析 (2)半径为3 39π324S =阴【分析】（1）连结AD 可得90ADB ∠=︒ 已知AB AC = 根据等腰三角形三线合一的性质即可得证点D 为线段BC 的中点（2）根据已知条件可证ABC DEC ∽△△ 得到ED ECAB BC= 22BD AB EC =⋅ 且EDC △是等腰三角形进而得到ED DC BD == 设AB x = 则(()22333x x =+ 解方程即可求得O 的半径连接OE 可证AOE △是等边三角形再根据AOEAOE S S S =-阴扇形即可求出阴影部分的面积【解析】（1）连结AD①AB 为O 的直径 ①90ADB ∠=︒ ①AB AC = ①BD CD =即点D 为线段BC 的中点．（2）①B E ∠=∠ C C ∠=∠ ①ABC DEC ∽△△ ①ED ECAB BC= ①AB AC = ①B C ∠=∠ ①C E ∠=∠ ①ED DC BD == ①22BD AB EC =⋅ 设AB x = 则 (()22333x x =+解得19x =-（舍去） 26x = ①O 的半径为3 连接OE ①60AOE =︒∠ ①AOE △是等边三角形 ①AE 33①AOEAOE S S S=-阴扇形260313333602π⨯⨯=-⨯ 39π324=【点评】本题主要考查等腰三角形的性质相似三角形的判定和性质不规则图形面积的计算熟练掌握相关知识点是解题的关键． 3．(1)见解析 (2)CE 的长为17【分析】（1）由AB 为O 的直径得90ACB ∠=︒ 通过证明()ACD ACB ≌SAS 得到D B ∠=∠ 又由B E ∠=∠ 从而得到D E ∠=∠（2）设BC x = 则2AC x =- 在Rt ABC 中由勾股定理可得222AC BC AB += 即()22224x x -+= 解一元二次方程得到BC 的长由（1）知D E ∠=∠ 从而得到CD CE = 又由DC CB = 得到17CE CB ==【解析】（1）证明AB 为O 的直径90ACB ∴∠=︒180ACD ACB ∠+∠=︒90ACD ∴∠=︒在ACD 和ACB △中AC AC ACD ACB DC BC =⎧⎪∠=∠⎨⎪=⎩()ACD ACB ∴≌SASD B ∴∠=∠ BE ∠=∠D E ∴∠=∠（2）解设BC x =2BC AC -=∴2AC x =-在Rt ABC 中由勾股定理可得222AC BC AB += 即()22224x x -+=解得117x = 217x = 17BC ∴=由（1）得D E ∠=∠ CD CE ∴= DC CB =17CE CB ∴==∴ CE 的长为17【点评】本题主要考查了圆周角定理三角形全等的判定与性质等腰三角形的性质勾股定理解直角三角形熟练掌握圆周角定理三角形全等的判定与性质等腰三角形的性质是解题的关键． 4．(1)见解析 (2)见解析【分析】（1）设BC DE 交于点G 连接AG 交圆于点F 即可作答（2）连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N 即可作答．【解析】（1）如图，设BC DE 交于点G 连接AG 并延长交圆于点F线段AF 即为所求证明如图， BC AE 交于点Q DE AC 交于点P 连接DB 交AF 于点H①AB AD = AE AC = ①C E ∠=∠ ADE ABC =∠∠ ①DAE BAC ∠=∠①DAE BAC ≌ ①BC DE = ①DAE BAC ∠=∠ ①BAE DAC ∠=∠①AB AD = ADE ABC =∠∠ ①DAP BAQ ≌ ①AQ AP = ①AE AC = ①QE PC =①QGE PGC ∠=∠ C E ∠=∠ ①QGE PGC ≌ ①QG PG =①AG AG = AQ AP = ①QAG PAG ≌ ①QAG PAG ∠=∠ ①BAE DAC ∠=∠ ①BAG DAG ∠=∠ ①AH AH = AB AD = ①BAH DAH ≌①BH DH = 90AHB AHD ∠=∠=° ①AF 垂直平分弦DB ①AF 是圆的直径（2）如图，连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N线段MN 即为所求．证明方法同（1）．【点评】本题主要考查了垂径定理圆周角定理以及全等三角形的判定与性质等知识掌握圆周角定理以及垂径定理是解答本题的关键． 5．(1)见解析 (2)9【分析】（1）已知点C 在O 上先连接OC 由已知CA CD = 30CDA ∠=︒ 得30CAO ∠=︒ 30ACO ∠=︒ 所以得到60COD ∠=︒ 根据三角形内角和定理得90DCO ∠=︒ 即能判断直线CD 与O 的位置关系．（2）要求点A 到CD 所在直线的距离先作AE CD ⊥ 垂足为E 由30CDA ∠=︒ 得12AE AD = 在Rt OCD △中半径6OD = 所以212OD OC == 18AD OA OD =+= 从而求出AE ．【解析】（1）①ACD 是等腰三角形 30D ∠=︒①30CAD CDA ∠=∠=︒．连接OC①AO CO =①AOC 是等腰三角形①30CAO ACO ∠=∠=︒①60COD ∠=︒在COD △中又①30CDO ∠=︒①90DCO ∠=︒①CD 是O 的切线即直线CD 与O 相切．（2）过点A 作AE CD ⊥ 垂足为E ．在Rt OCD △中 ①30CDO ∠=︒①212OD OC ==61218AD AO OD =+=+=在Rt ADE △中①30EDA ∠=︒①点A 到CD 边的距离为92AD AE ==．【点评】此题考查的知识点是切线的判定与性质解题的关键是运用直角三角形的性质及30°角所对直角边的性质．6．(1)见解析 (2)252AB =．【分析】（1）连接OC 由DE 为O 的切线得到OC DE ⊥ 再由AD CE ⊥ 得到AD OC ∥ 得到OCA CAD ∠=∠ 根据OA OC = 利用等边对等角得到OCA CAB ∠=∠ 等量代换得到CAD CAB ∠=∠ 由AB 为O 的直径可知90ACB ∠=︒ 最后根据等角的余角相等可得结论（2）在Rt CAD △中利用锐角三角函数定义求出CD 的长根据勾股定理求出AD 的长由（1）易证ADC ACB 得到AD AC AC AB= 即可求出AB 的长．【解析】（1）解连接OC由题意可知DE 与O 的相切于COC DE ∴⊥AD CE ⊥AD OC ∴∥OCA CAD ∴∠=∠OA OC =OCA CAB ∴∠=∠CAD CAB ∴∠=∠ AB 为O 的直径90ACB ∴∠=︒90CAD ACD CAB ABC ∴∠+∠=∠+∠=︒ACD ABC ∴∠=∠（2）在Rt CAD △中3tan 4CDCAD AD ∠== 8AD =364CD AD ∴==22226810AC CD AD ∴+=+=由（1）可知CAD CAB ∠=∠90D ACB ∠=∠=︒ADC ACB ∴ADACAC AB ∴=81010AB∴= 252AB ∴=【点评】此题考查了切线的性质以及解直角三角形熟练掌握切线的判定与性质是解本题的关键． 7．(1)证明见解析 (2)125AB =【分析】（1）连接FO 可根据三角形中位线的性质可判断OF AB ∥ 然后根据直径所对的圆周角是直角可得CE AE ⊥ 进而知OF CE ⊥ 然后根据垂径定理可得FEC FCE ∠=∠OEC OCE ∠=∠ 再通过Rt ABC 可知90OEC FEC ∠+∠=︒ 因此可证EF 为O 的切线（2）根据题意可先在Rt OCD △中求出OD 然后在Rt EFD 中求出FC 最终在Rt ABC 中求解AB 即可．【解析】（1）证连接FO 则由题意OF 为Rt ABC 的中位线①OF AB ∥①AC 是O 的直径①CE AE ⊥①OF AB ∥①OF CE ⊥①由垂径定理知 OF 所在直线垂直平分CE①FC FE = OE OC =①FEC FCE ∠=∠ OEC OCE ∠=∠①90ACB ∠=︒即90OCE FCE ∠+∠=︒①90OEC FEC ∠+∠=︒即90FEO ∠=︒①EF 是O 的切线（2）解①O 的半径为6 8CD = 90ACB ∠=︒①OCD 为直角三角形 6OC OE == 8CD = ①2210OD OC CD += 10616ED OD OE =+=+=由（1）知 EFD △为直角三角形且FC FE =①设FC FE x == 则8FD FC CD x =+=+①由勾股定理 222EF ED FD +=即()222168x x +=+ 解得12x =即12FC FE ==①点F 为BC 的中点①224BC FC ==①212AC OC ==①在Rt ABC 中 22125AB BC AC +①125AB =【点评】本题考查切线的证明圆的基本性质以及勾股定理解三角形等掌握切线的证明方法熟练运用圆中的基本性质是解题关键．8．(1)见解析(2)半径为2 123AE =【分析】（1）根据点C 为弧BD 的中点得出FAC CAB ∠∠= 然后得出FAC ACO ∠∠= 根据平行线的性质得出CF OC ⊥ 进而即可求解（2）连接BC 设OC 与BF 相交于点P 证明AFC ACB ∽ 得出4AB = 证明BOP BAF ∽得出1322OP AF == 进而证明ECP EAF ∽ 根据相似三角形的性质列出比例式进而即可求解．【解析】（1）证明连接OC 如图，点C 为弧BD 的中点∴CD CB =FAC CAB ∠∠∴=又OA OC =CAB ACO ∠∠∴=FAC ACO ∠∠∴=∴OC AF ∥又CF AD ⊥CF OC ∴⊥FC ∴是半圆O 的切线．（2）解连接BC 如图，AB 是半圆O 的直径90ACB ∠∴=︒90AFC ACB ∠∠∴==︒又FAC CAB ∠∠=AFC ACB ∴∽ ∴AFACAC AB = 23234AB ∴=∴半圆O 的半径为2．设OC 与BF 相交于点POC AF ∥BOP BAF ∴∽ ∴12OPOB AF AB == ∴1322OP AF == ∴12PC OC OP =-=OC AF ∥ECP EAF ∴∽ ∴EC PCAE AF = 即123AC AEAE -= 2316AE-=∴123AE = 【点评】本题考查了切线的性质与判定相似三角形的性质与判定掌握切线的判定以及相似三角形的性质与判定是解题的关键．9．(1)见解析(2)3【分析】（1）连接DO 根据CD 是O 的切线 OF AD ⊥ 证明ADC DOF ∠∠= 利用等腰三角形三线合一性质证明ADC AOF ∠∠=．（2）利用平行线分线段成比例定理计算OE 证明CFO CDB △∽△ 计算OF两线段作差即可求解．【解析】（1）如图，连接DO CD 是O 的切线OD DF ∴⊥90ADC ADO ∠∠∴+=︒OF AD ⊥ OA OD =90DOF ADO ∠∠∴+=︒ DOF AOF ∠∠=ADC DOF ∠∠∴=ADC AOF ∠∠∴=．（2）如图，连接DO CD 是O 的切线OD DF ∴⊥90CDO ∠∴=︒53OC OB =设5(0)CO k k => 则3DO OB AO k ===4CD k ∴=538CB CO OB k k k ∴=+=+= AB 是O 的直径 24BD =AD DB ∴⊥OF AD ⊥∴OF BD ∥ ∴AO AE OB ED = CFO CDB △∽△ ∴OF CO BD CB= AE ED ∴=5524538OF k k k ==+ ∴1122OE BD == 15OF = 3EF OF OE ∴=-=．【点评】本题考查了切线的性质等腰三角形的三线合一性质平行线分线段成比例定理相似三角形的性质与判定熟练掌握切线的性质相似三角形的性质与判定是解题的关键．10．(1)证明过程见解析 (2)142π-【分析】（1）AB 是O 的直径 AC AD = BF BC = 可求出90FBD ∠=︒ AB BF ⊥ 由此即可求证（2）如图，所示（见解析）连接,CO EO 可得1OC OE == 可证222CO O CE += 90COE ∠=︒ 根据扇形面积的计算方法即可求解．【解析】（1）证明①AB 是O 的直径①90ACB ∠=︒①90ACD BCD ∠+∠=︒①AC AD =①ACD ADC ∠=∠①ADC BDF ∠=∠①ACD BDF ∠=∠①BC BF =①BCD F ∠=∠①90BDF F ∠+∠=︒①180()90FBD FDB F ∠=︒-∠+∠=︒①AB BF ⊥ 且OB 是O 的半径①BF 是O 的切线．（2）解如图，所示连接,CO EO①2AB =①1OC OE == ①2CE ①222CO EO += 2222CE == ①222CO O CE +=①90COE ∠=︒ ①29011111360242ππS ⨯=-⨯⨯=-阴影 ①图中阴影部分的面积为142π-．【点评】本题主要考查圆的基础知识掌握圆的切线的证明方法扇形面积的计算方法是解题的关键．11．(1)见解析(2)3【分析】（1）连接CO 根据OF BC ∥可得B AOF ∠=∠ 根据直径所对的圆周角为直角可得90B CAB ∠+∠=︒ 再根据AO CO =得出CAB ACO ∠=∠ 最后证明90ACD ACO ∠+∠=︒即可（2）根据中位线定理得出152OE BC == 证明DBC DOF ∽ 根据相似三角形对应边成比例即可求解．【解析】（1）证明连接CO①OF BC ∥①B AOF ∠=∠①AB 为O 的直径①90ACB ∠=︒ 则90B CAB ∠+∠=︒①90AOF CAB ∠+∠=︒①AO CO =①CAB ACO ∠=∠①ACD AOF ∠=∠①90ACD ACO ∠+∠=︒ 即OC CD ⊥①CD 为圆O 的切线（2）①AB 为O 的直径①点O 为AB 中点①OF BC ∥①OE 为ABC 中位线 ①152OE BC == ①1sin 4D = OC CD ⊥ ①4OD OC = 则5BD OD OB OC =+=①OF BC ∥①DBC DOF ∽ ①OF OF BC BD = 即4510OC OF OC = 解得8OF =①853EF OF OE =-=-=．【点评】本题主要考查了切线的判定和性质圆周角定理相似三角形的判定和性质以及解直角三角形解题的关键是掌握切线的判定和性质以及相似三角形的判定和性质．12．(1)30︒(2)100︒【分析】（1）根据三角形内角和定理可得60ABC ∠=︒ 再由AD CD = 可得ABD CBD ∠=∠ 即可求解（2）根据圆周角定理可得30ABD ACD ∠∠==︒ 从而得到80BCD ∠=︒ 再由圆内接四边形的性质即可求解．【解析】（1）解①70,50BAC ACB ∠=︒∠=︒①18060ABC BAC ACB ∠=︒-∠-∠=︒①AD CD = ①1302ABD CBD ABC ∠=∠=∠=︒ （2）解由圆周角定理得30ABD ACD ∠∠==︒①80BCD ACB ACD ∠=∠+∠=︒①四边形ABCD 是O 的内接四边形①180100BAD BCD ∠=︒-∠=︒．【点评】本题主要考查了圆内接四边形的性质圆周角定理等知识熟练掌握圆内接四边形的性质圆周角定理是解题的关键．13．(1)见解析(2)AD 的长是25【分析】（1）连接OA 根据已知条件证明OA AE ⊥即可解决问题（2）作OF CD ⊥ 则四边形OAEF 是矩形且132DF CD ==由此可求得DE 的长在Rt OFD △中勾股定理求出OF 即AE 的长在Rt AED △中利用勾股定理求DA ．【解析】（1）证明如图，连接OA①AE CD ⊥①90DAE ADE ∠+∠=︒．①DA 平分BDE ∠①ADE ADO ∠=∠又①OA OD =①OAD ADO ∠=∠①90DAE OAD ∠+∠=︒①OA AE ⊥①AE 是O 的切线（2）解过点O 作OF CD ⊥于F ．①90OAE AEF OFE ∠︒=∠=∠=①四边形OAEF 是矩形①5EF OA AE OF ===，．①OF CD ⊥ ①132DF FC CD ===①532DE EF DF =-=-=在Rt OFD △中 2222534OF OD DF --=①4AE OF ==在Rt AED △中 22224225AD AE DE ++=①AD 的长是25【点评】本题考查了切线的判定与性质垂径定理圆周角定理勾股定理解决本题的关键是掌握切线的判定与性质．14．(1)12π(2)9【分析】(1) 根据题意 CEB APB ABC PBE S S S S S =+--阴影扇形扇形根据公式计算即可．(2) 连接PE 根据题意 45,135,90PEB CEP PEC ∠=︒∠=︒∠=︒ 根据勾股定理计算即可．【解析】（1）如图， ①正方形ABCD 旋转APB △到CEB 的位置①APB CEB ≌ 90ABC PBE ∠=∠=︒ =CEB APB S S ①CEB APB ABC PBE S S S S S =+--阴影扇形扇形①ABC PBE S S S =-阴影扇形扇形①48BP AB ==， ①9064901612360360S πππ︒⨯⨯︒⨯⨯=-=︒︒阴影．（2）连接PE根据题意 45,135PEB APB CEP ∠=︒∠=∠=︒ AP CE =①90PEC ∠=︒①4BP = 7AP =①2227,4432CE PE ==+=①222273281PC CE PE =+=+=解得9PC =．【点评】本题考查了正方形的性质旋转的性质阴影面积的计算扇形面积公式勾股定理熟练掌握旋转的性质阴影面积的计算扇形面积公式勾股定理是解题的关键．15．(1)证明见解析(2)10DF =【分析】（1）因为CDB CAB ∠=∠ CDB BFD ∠=∠ 所以CAB BFD ∠=∠ 即可得出FD ①AC 可得得出OD FD ⊥ 进而得出结论（2）利用勾股定理先求解AC 再利用垂径定理得出AE 的长可得OE 的长证明AEO FDO ∽ 再利用相似三角形的判定与性质得出DF 的长．【解析】（1）①CDB CAB ∠=∠ CDB BFD ∠=∠①CAB BFD ∠=∠①FD AC ∥①OD 垂直于弦AC 于点E①OD FD ⊥①FD 是O 的一条切线（2）①AB 为O 的直径①90ACB ∠=︒①15AB = 9BC = ①2215912AC -= 7.5AO OB OD ===①DO AC ⊥①6AE CE == ①227.56 4.5OE -①AC FD ∥①AEO FDO ∽ ①AE EO FD DO = ①4.567.5FD= 解得10DF =．经检验符合题意.【点评】本题主要考查了相似三角形的判定与性质垂径定理圆周角定理切线的判定以及平行线的判定掌握相似三角形的判定与性质垂径定理圆周角定理以及平行线的判定是解题的关键．16．(1)50︒(2)30︒【分析】（1）连接OA 先由切线的性质得OAE ∠的度数求出2142AOB C ∠=∠=︒ 进而得AOE ∠ 则可求出答案（2）连接OA 根据等腰三角形的性质及切线的性质列方程求解即可．【解析】（1）连接OA ．如图，①AE 切O 于点AOA AE ∴⊥90OAE ∴∠=︒70C ∠=︒2270140AOB C ∴∠=∠=⨯︒=︒又180AOB AOE ∠+∠=︒40AOE ∴∠=︒90AOE E ∠+∠=︒904050E ∴∠=︒-︒=︒．（2）连接OA 如图，①设E x ∠=．AB AE =ABE E x ∴∠=∠=OA OB =OAB ABO x ∴∠=∠=2AOE ABO BAO x ∴∠=∠+∠=． AE 是O 的切线OA AE ∴⊥ 即90OAE ∠=︒在OAE ∆中 90AOE E ∠+∠=︒即290x x +=︒解得30x =︒30E ∴∠=︒．【点评】本题主要考查了切线的性质等腰三角形的性质圆周角的性质三角形内角和的性质用方程思想解决几何问题关键是熟悉掌握这些性质．17．(1)见解析(2)10cm【分析】(1)连接OD 根据平行线的判定与性质可得90ODE DEM ∠=∠=︒ 又点D 在O 上即可证得DE 是O 的切线(2)首先根据勾股定理可得AD 的长再由ACD ADE ∽ 根据相似三角形的性质列出比例式代入数据即可求得圆的半径．【解析】（1）证明如图，连接ODOA OD =OAD ODA ∠=∠∴ AD 平分CAM ∠OAD DAE ∴∠=∠ODA DAE ∴∠=∠DO MN ∴∥DE MN ⊥90ODE DEM ∴∠=∠=︒ 即OD DE ⊥ 又点D 在O 上 OD 为O 的半径DE ∴是O 的切线（2）解90AED ∠=︒ 8cm DE = 4cm AE =22228445AD DE AE ∴++如图，连接CDAC 是直径90ADC AED ∴∠=∠=︒CAD DAE ∠=∠ACD ADE ∴△∽△AD AC AE AD ∴= 4545=解得20AC =O ∴的半径为10cm ．【点评】本题考查圆了切线的判定；等边对等角平行线的判定与性质圆周角定理勾股定理相似三角形的判定和性质等知识在圆中学会正确添加辅助线是解决问题的关键．18．(1)见解析 (2)49【分析】（1）欲证~CBA FDC ，只要证明两个角对应相等就可以．可以转化为证明DE BC =就可以（2）由~CBA FDC 可得814CF = ACB F ∠=∠ 进而即可得到答案．【解析】（1）证明①四边形ABCD 内接于O①CBA CDF ∠=∠．①DE BC =①BCA DCE ∠=∠．①~CBA FDC（2）解①C 是DBA 的中点①9CD AC ==①~CBA FDC 4AB = ①AB AC CD CF = 即499CF= ①814CF = ①~CBA FDC ①94tan tan 8194AC ACB F CF ∠=∠===．【点评】本题考查的是圆的综合题；涉及弧、弦的关系；等腰三角形的性质；相似三角形的判定与性质；锐角三角函数；掌握相似三角形的判定和性质是解答此题的关键．。

中考数学专题训练圆的证明与计算(含答案)

圆的证明与计算1.如图，已知八ABC内接于AO, P是圆外一点，PA为40的切线, = PB,连接0P ,线段AB与线段0P相交于点D.(1)求证：PB为40的切线；- 4⑵ 若PA=4P0, z\0的半径为10,求线段PD的长.5(1)证明：△△△△△0Az\0Bz\ZSPA/SPBA0AA0BA0PA0PA△ 3APz\8BP(SSS) △A210APA210BPA/SPAA210AAAAA210APA90 △A210BPA90 △A0BA210AAAA/SPBA210AAAA_ _ 4_ _ ............(2)解：APA/VP0A210AAAA 10A PA第1题图第1题解图△ △ Rt AOP A Z1OA A A J P O22\21|P O^ A10A人人八人50人A/POA V A3AO OD△ cos AOP/^O P A A O AAODA6A人_ _____ 32APD APOAODA-y.32.AAAAABCA/iAB^CA/lDABCAAAAADADCA/lAAB/SDAAAzOA AEA21OAAAAADE.A 1AAAACA/1OAAAAA2AA C OSA32^C A 24 A A A AE A A.第2题图(1)证明：AABAACAAD ADC △Az^CAz^BAz^DACA^CA△RAC△2△AAZEA21BA△RAC△任△Z^EA/IOAAAAA21ADEA90 △△任△21EAD"0° △A/DACA21EADA90 △△任AC490° △AOAA21OAAAAAACAODAAAA(2)解：AAAAADA DF 丛C△任△第2题解图DAADCCA…1… 人△CF A2ACA12ACF 3ARtzCDFAAA G(C/\C D A5A△DC A 20 △AAD A 20 △ARtzCDFAAAAAAA DF ,CD2-CF216 △A21ADEA21DFCA90 AEA21CAA21ADEA21DFCA噬噜△AE 20A— A20 AA Z^EA25A20 16A21OAA/AEA 25.3.如图，在AABC中，AB=BC,以AB为直径作AO,交BC于点D,交AC 于点E,过点E作AO的切线EF,交BC于点F.(1)求证：EFABC;(2)若 CD=2, tan C=2,求 AO 的半径.第3题图(1)证明：如解图，连接BE, OE.第3题解图AAB为AO的直径，△MEB=90 .AAB=BC,△点E是AC的中点，△点O是AB的中点，AOEABC,△EF是AO的切线，△EF4E.△EFABC;(2)解：如解图，连接AD,八AB为AO的直径，△ AADB=90 ,△CD=2, tan C=AD 2CDAAD=4.设 AB=x,贝U BD=x-2.在 RtAABD 中, 由勾股定理得AB2=AD2+BD2,即 x2=42+ (x— 2) 2, 解得x=5,即AB=5,△ 8的半径为5 .24.AAAAZOWZ1ABAAAAABCAAADA21BCAAAAAE.A 1AAA/SDACA21DCEA..................1人人人人A2A ABA 2A siD △不△ AAE4/X.第4题图(1)证明：Z^DA/IOAAAA△PAB A90 .Z^BA/IOAAAAA21ACBA90 .A/DACA21CABA90 2ICABA/^ABCA 90 △A/DACA/^BC.AOCAOBAA.BCBCOCOCBAAAZDCEAz^OCBAA21DACA21DCEA(2)解：AABA2 △AAOA1.△sinD A ODAODA3ZDC A2 △ARtzDAOAA△△△△△AD △ OD2AOA2A2 2 △A21DACA21DCEA21DA/1DAA21DECA21DCAA A DC A DE A DA A DC 人2人DEA2 ,2 A2△RE △ ,2 △AAEAAD ADE △ 2.5.AAABA21OAAZDAA/DAAAAAADACDAOAA21ABA21EAA/OA1AAACEACBAA2AAAFABFAA/ABFAAAA人人-人人人 DE人5人人…人人人A3A/CDA 15ABE4 1OZ A E A13AAZ O AA A-(:第5题图(1)证明：△△△△△OB4A第5题解图BBCAOJAAAAAOBABCA AzOBCA 90 △A21OBAA21CBEA90 △AOAAOBAA21OABA21OBAAA21OAB+ACBEA 90 △A21CDAOAAA21OABA21DEAA90 △AA/CEBA21DEAAA21CBEA21CEBAACEACBA(2)解：△△△△△/△ADA ADO ACD AOAA AAF AOF △Az^OAAOFAA21AOFAAAAAAA/AOF=60O△」_1 _____ ____ _A21ABFA2^AOFA30 △(3)解：△△△△△C\CG》B△工△△CD AOAAA21ADEA21CGEA900△AA/AEDA21CEGAA21ADEA21CGEA人DE人EG人5人A AE A CE A13AACEABCAACEA13A人 (26)△DE -旌.-------- 24△ △•■△△△△△△" ..AE DE△石△486.AAAA/lABCDAAAzO^BA/lOAAAADADCAAAABAACDAAA EA/®FAECA21ECAAAAA/W\AZBD.△ 1 △△△ ABFC△2DAAA2AAE/^OAA cosADEAA3AAA 2AAAA/BCA6AzBFAA.第6题图(1)证明：Z^BA/IOAAAAA21BDAA90 .ABF /SECAA21BFCA90 △AAAABCDA/1OAAAAAAAA21BCFA21BADAA21BFCA21BDAA(2)解：△△△△△OD3C4A21BFCA21BDAABF BC△BD'^A B'AODA/lOAAAzADACDA AODAAAACAZ^BA/IOAAAA△ AACB=90 △AODABCA △任OD△心X OE ODA BE A BC AZ^E^OA21OEA2OB/SBEA3OBAOD OE 2△■占M—— -ABC BE 3ABC Z^ODA3瑞瑞舄△:△△ 21ADB A 90 △A21ADEA21BDFA90 △A21BDFA21DBFA90 △A21ADEA21DBFAR第6题解图/SRt/SBDFAA cosDBF 混率△ cos ADE2^A4(3)解：ABCz^ODABCA6AAODA4A /^EA4ZBEA12 △ △任OD△心CA 人DE人OD人A CE A BC A…人3 人ACEA2DEA △ △/EDA△八EBC△任△小£△A21AEDA21CEBA 人AE人DE人A C E A BE AADE CEAAE BEAADE 3D E A4X 12 △ /SDEA4V2( AAAA )△ACDA2V2A/^DA2V2AA21BFCA21BDAA 人CF 人AD 人A CF A2_J A△BC△母△造△ 8 △… 3 2ACF A^AARtzBCFAAAAAAAAAABFA . BC2A CF2Z^3~214.7.AAABAA OAAA/ICD^BAAAzHAAAAC△△知作EG3C交CD的延长线于点 G,连接AE交CD于点F,且EG=FG,连接CE.(1)求证：z\ECF△&CE;(2)求证：EG是AO的切线；(3)延长AB交GE的延长线于点 M ,若tan工=3 ,AH=3,4求EM的值.第7题图(1)证明：3cAEG,△8=3CG,「AB是AO的直径，ABACD,△A D = A C ,△3EF=AACD,△8=MEF,△任CF=4ECG,△任CF△&CE;(2)证明：如解图，连接OE,第7题解图△GF=GE,△&FE=^GEF=AAFH,△OA=OE,△3AE=4OEA,△AAFH+^FAH=90 ,△&EF+AAEO=90 ,△&EO=90 ,AGEAOE,VOEMAO的半径，△EG是AO的切线；(3)解：如解图，连接OC,设AO的半径为r.在 Rt「AHC 中，一一AH 3tan zACH=tan 应=空=± , HC 4AAH=3,AHC=4.在 Rt^HOC 中，△OC=r, OH=r—3, HC=4, △ (r —3) 2+42=r2,解得r= 25 ,6△GM AAC,△ 3AH=2\M,△ 3EM=AAHC=90 △ AAHC/XNEO,AH HCEM OE ，即高8.如图，AB 为AO 的直径，C 、G 是AO 上两点，过点 C 的直线CD^BG 交BG 的延长线于点D,交BA 的延长线于点E,连接BC,交OD 于点F, 且BC 平分4ABD.(1)求证：CD 是AO 的切线；⑵若OF 2,求4E 的度数； FD 3⑶连接AD,在(2)的条件下，若CD=2V3,求AD 的长.H第8题图(1)证明：如解图，连接OC,△ EM 25 8△OC=OB, BC 平分 AABD, △3CB=z\OBC, AOBC=ADBC,AzX)BC=AOCB,AOC ABD,Az^BDC=AECO,△CD ABD,△ z!BDC=90 ,△任CO=90 ,△OC 是AO 的半径，△CD 是AO 的切线；(2)解：由(1)知，OC^BD, △8CF=4DBF, △COFMBDF,A21OCFA21DBF, △.史FD△器AOC ABD, △任OC △任BD,△如 FD3,设 OE=2a,则 EB=3a,△OB=a,△OC=a,△3CE=90 , OC=1OE, 2△任=30 ;(3)解：△任=30 , ABDE=90 ,△任BD=60 ,VBC 平分 ADBE,/. AOBC=ADBC=1 EBD=30 , 2△CD=2 .3 ,ABC=4 3, BD=6,△空2 , DB 3△OC=4,如解图，过点D作DM3B于点M ,△RMB=90 ,ABD=6, ADBM=60 ,ABM=3, DM=3 3 ,△OC=4,△AB=8,AAM=AB—BM=5,△ RMA=90 , DM=3J3,AAD= VDM 2 AM 2 2V13 .9.如图，在3BC中，八ACB=90°,。

最新整理中考热点7与圆有关的证明问题含答案.doc

热点17 与圆有关的证明问题（时间：100分钟总分：100分）一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是符合题目要求的）1．已知AB、CD是⊙O的两条直径，则四边形ADBC一定是（）A．等腰梯形 B．正方形 C．菱形 D．矩形2．如图1，DE是⊙O的直径，弦AB⊥ED于C，连结AE、BE、AO、BO，则图中全等三角形有（）A．3对 B．2对 C．1对 D．0对（1） (2) (3) (4)3．垂径定理及推论中的四条性质：①经过圆心；②垂直于弦；③平分弦；④平分弦所对的弧．由上述四条性质组成的命题中，假命题是（）A．①②⇒③④ B．①③⇒②④C．①④⇒②③ D．②③⇒①④4．Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，给出下列三个结论：①以点C为圆心，•2.3cm 长为半径的圆与AB相离；②以点C为圆心，2.4cm长为半径的圆与AB相切；•③以点C 为圆心，2.5cm长为半径的圆与AB相交，则上述结论正确的有（）A．0个 B．1个 C．2个 D．3个5．在⊙O中，C是AB的中点，D是AC上的任意一点（与A、C不重合），则（）A．AC+CB=AD+DB B．AC+CB<AD+DBC．AC+CB>AD+DB D．AC+CB与AD+DB的大小关系不确定6．如图2，梯形ABCD内接于⊙O，AD∥BC，EF切⊙O于点C，则图中与∠ACB相等的角（不包括∠ACB）共有（）．A．1个 B．2个 C．3个 D．4个7．如图3，在△ABC中，AD是高，AE是直径，AE交BC于G，有下列四个结论：•①A D2=BD·CD；②BE2=EG·AE；③AE·AD=AB·AC；④AG·EG=BG·CG．其中正确结论的有（）A．1个 B．2个 C．3个 D．4个8．如图4，AB是⊙O的直径，CD为弦，AE⊥CD于E，BF⊥CD于F，交⊙O于G．•下面的结论：①EC=DF；②AE+BF=AB；③AE=GF；④FG·FB=EC·ED．其中正确的有（）A．①②③ B．①③④ C．②③④ D．①②④9．如图5，圆内接△ABC的外角∠ACH的平分线与圆交于D点，DP⊥AC，•垂足是P，DH⊥BH，=；③AP=BH；④DH为圆的切线，其中一定成垂足是H，下列结论：①CH=CP；②AD BD立的是（）A．①②④ B．①③④ C．②③④ D．①②③(5) (6) (7) (8)10．如图6，在⊙O中，AB=2CD，那么（）A．2AB CD>; B．2AB CD<;C．2AB CD=; D．AD与2CD的大小关系可能不确定二、填空题（本大题共8小题，每小题3分，共24分）11．在⊙O中，若AB⊥MN于C，AB为直径，MN•为弦，•试写出一个你认为正确的结论：_________．12．已知⊙O1和⊙O2的半径分别为10cm，6cm，OO的长为3cm，则⊙O1与⊙O2的位置关系是_________．13．如图7，C是⊙O的直径AB延长线上一点，过点C作⊙O的切线CD，D为切点，连结AD、OD、BD，请你根据图中所给的条件（不再标字母或添辅助线），写出一个你认为正确的结论____________．14．已知⊙O的直径为10，P为直线L上一点，OP=5，那么直线L与⊙O•的位置关系是_______．15．在△ABC中，∠C=90°，AC=3，BC=4，点O是△ABC的外心，现以O为圆心，•分别以2，2．5，3为半径作⊙O，则点C与⊙O的位置关系分别是________．16．以等腰△ABC的一腰AB为直径作圆，交底边BC于D，则∠BAD与∠CAD•的大小关系是∠BAD________∠CAD．17．在△ABC中，AB=5，AC=4，BC=3，以C为圆心，以AB•的位置关系是____________．18．如图8所示，A、B、C是⊙O上的三点，当BC平分∠ABO时得结论_________．三、解答题（本大题共46分，19～23题每题6分，24题、25题每题8分，解答题应写出文字说明、证明过程或演算步骤）19．如图，AB是⊙O的弦（非直径），C、D是AB上两点，并且OC=OD，求证：AC=BD．20．已知：如图，在△ABC中，AB=AC，以AB为直径的⊙O与BC交于点D，与AC•交于点E，求证：△DEC为等腰三角形．21．如图，AB是⊙O的直径，弦AC与AB成30°角，CD与⊙O切于C，交AB•的延长线于D，求证：AC=CD．，BF和AD交于E，22．如图20-12，BC为⊙O的直径，AD⊥BC，垂足为D，AB AF求证：AE=BE．23．如图，AB是⊙O的直径，以OA为直径的⊙O1与⊙O2的弦相交于D，DE⊥OC，垂足为E．（1）求证：AD=DC．（2）求证：DE是⊙O1的切线．24．如图，已知直线MN与以AB为直径的半圆相切于点C，∠A=28°．（1）求∠ACM的度数．（2）在MN上是否存在一点D，使AB·CD=AC·BC，说明理由．25．如图，在Rt △ABC 中，∠C=90°，AC=5，BC=12，⊙O 的半径为3．（1）若圆心O 与C 重合时，⊙O 与AB 有怎样的位置关系？（2）若点O 沿CA 移动，当OC 等于多少时，⊙O 与AB 相切？答案：一、选择题1．D 2．A 3．B 4．D 5．C 6．D 7．B 8．B 9．D 10．A 二、填空题11．BM=BN 等 12．内含 13．∠ADO=∠BDC 等 14．相交或相切 15．在圆外、•在圆上、在圆内 16．= 17．相交 18．OC ∥AB 等三、解答题19．证明：过点O 作OE ∥AB 于E ，则AE=BE ．在△OCD 中，OE ⊥CD ，OC=OD ，∴CE=•DE ．•∴AC=BD ．20．证明：∵四边形ABDE 是圆内接四边形，∴∠DEC=∠B ．又∵AB=AC ，∴∠B=∠C ，∴∠DEC=∠C ，∴DE=CD ． ∴△DEC 为等腰三角形．21．证明：连结BC ，由AB 是直径可知，9030ACB A ∠=︒⎫⎬∠=︒⎭⇒∠ABC=60°．CD 是切线⇒∠BCD=∠A=30°⇒∠D=30°=∠A ⇒AC=CD ． 22．证明：连结AB ，AC ，90909090BC BAC ABC ACB AD BC ADB ABC BAD ⇒∠=︒⇒∠+∠=︒⎫⎬⊥⇒∠=︒⇒∠+∠=︒⎭是直径ACB BADAB AF ACB ABF ⇒∠=∠⎫⎪⎬=⇒∠=∠⎪⎭⇒∠BAD=∠ABF ⇒AE=BE ．23．证明：（1）连结OD ，AO 是直径90ADO AO CO ⇒∠=︒⎫⇒⎬=⎭AD=DC ．（2）连结O 1D ，111O D O A A ADO OA OC A C =⇒∠=∠⎫⎬=⇒∠=∠⎭190C ADO DE CE C CDE ⇒∠=∠⎫⎬⊥⇒∠+∠=︒⎭1119090ADO CDE O DE D O ⇒∠+∠=︒⇒∠=︒⎫⎬⎭在上⇒DE 是切线．24．解：（1）连结BC ，9028AB ACB A ⇒∠=︒⎫⎬∠=︒⎭是直径⇒∠B=62°．MN 是切线⇒∠ACM=∠B=62°．（2）过点B 作BD ⊥MN ，则190BDC ACBMN BCN A ∠=︒=∠⎫⎬⇒∠=∠⎭是切线⇒△ACB ∽△ B⇒1AC ABCD BC=⇒AB ·CD 1=AC ·BC ．过点A 作AD 2⊥MN ，则190AD C ACBMN MCA CBA ∠=︒=∠⎫⎬⇒∠=∠⎭是切线⇒△ABC ∽△ACD 2⇒2CD AC AB CB=⇒CD 2·AB=AC ·CB 25．解：（1）过点C 作CH ⊥AB 于H ，由三角形的面积公式得AB ·CH=AC ·BC ，∴CH=AC BC AB =6013，即圆心到直线的距离d=6013． ∵d=6013>3，∴⊙O 与AB 相离．（2）过点O 作OE ⊥AB 于E ，则OE=3．∵∠AEO=∠C=90°，∠A=∠A ，∴△AOE ∽△ABC ， ∵OA=OE AB BC =31313124⨯=∴OC=AC-OA=5-134=74．∴当OC=74时，⊙O与AB相切．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

下载试卷文档前说明文档：1.试题左侧二维码为该题目对应解析；2.请同学们独立解答题目，无法完成题目或者对题目有困惑的，扫描二维码查看解析，杜绝抄袭；3.只有老师通过组卷方式生成的二维码试卷，扫描出的解析页面才有“求老师讲解”按钮，菁优网原有的真题试卷、电子书（习题集）上的二维码试卷扫出的页面无此按钮。

学生点击该按钮以后，下载试卷教师可查看被点击的相关统计数据。

4. 自主组卷的教师使用该二维码试卷后，可在“菁优网->我的空间->我的收藏-> 我的下载”处点击图标查看学生扫描的二维码统计图表，以便确定讲解重点。

5.在使用中有任何问题，欢迎在“意见反馈”提出意见和建议，感谢您对菁优网的支持。

2015 年 04 月 19 日九年级数学组的初中数学组卷(扫描二维码可查看试题解析)一．解答题（共 17 小题）1 ．（2014?辽阳）如图，在△ ABC，AB=AC ，以 AB 为直径的⊙O分别交 AC、 BC 于点 D、 E，点 F 在 AC 的延长线上，且∠CBF= ∠CAB．（1）求证：直线 BF 是⊙O 的切线；（2）若 AB=5 ， sin ∠ CBF=，求 BC 和 BF 的长．2 ．（2014?吉林）如图，四边形 OABC 是平行四边形，以 O 为圆心， OA 为半径的圆交 AB 于点 D，延长 AO 交⊙O于点 E，连接 CD，CE，若 CE 是⊙O的切线，解答下列问题：（1）求证： CD 是⊙O的切线；（2）若 BC=3 ， CD=4 ，求平行四边形 OABC 的面积．3 ．（2014?天水）如图，点 D 为⊙O上一点，点 C 在直径 BA 的延长线上，且∠CDA= ∠ CBD．（1）判断直线 CD 和⊙O的位置关系，并说明理由．（2）过点 B 作⊙O的切线 BE 交直线 CD 于点 E，若 AC=2 ，⊙O 的半径是 3，求 BE的长．4 ．（2013?德州）如图，已知⊙O的半径为 1 ， DE 是⊙O的直径，过点 D 作⊙O的切线 AD ， C 是 AD 的中点， AE 交⊙O于 B 点，四边形 BCOE 是平行四边形．（1）求 AD 的长；（2） BC 是⊙O的切线吗？若是，给出证明；若不是，说明理由．5 ．（2013?菏泽）如图，BC 是⊙O的直径， A 是⊙O 上一点，过点 C 作⊙O的切线，交 BA 的延长线于点D，取 CD 的中点 E， AE 的延长线与BC 的延长线交于点P．（1）求证： AP 是⊙O的切线；（2） OC=CP ， AB=6 ，求 CD 的长．6 ．（2013?聊城）如图，AB 是⊙O的直径， AF 是⊙O 切线， CD 是垂直于AB 的弦，垂足为 E，过点 C 作 DA 的平行线与AF 相交于点 F， CD=，BE=2．求证：（1）四边形 FADC 是菱形；（2） FC 是⊙O 的切线．7 ．（2012?北京）已知：如图， AB 是⊙O 的直径， C 是⊙O上一点， OD⊥ BC于点D，过点 C 作⊙O的切线，交 OD 的延长线于点E，连接 BE．（1 ）求证： BE 与⊙O相切；（2 ）连接 AD 并延长交BE 于点 F，若 OB=9 ， sin∠ ABC=，求BF的长．8 ．（2012?济宁）如图，AB 是⊙O的直径， AC 是弦， OD⊥ AC于点 D，过点 A 作⊙O的切线 AP， AP 与 OD 的延长线交于点P，连接 PC、 BC．......（1）猜想：线段 OD 与 BC 有何数量和位置关系，并证明你的结论．（2）求证： PC 是⊙O的切线．9 ．（2012?德阳）如图，已知点 C 是以 AB 为直径的⊙O上一点， CH⊥ AB于点 H，过点 B 作⊙O的切线交直线AC 于点 D，点 E 为 CH 的中点，连接 AE 并延长交BD 于点 F，直线 CF 交 AB 的延长线于G．（1）求证： AE?FD=AF?EC ；（2）求证： FC=FB；（3）若 FB=FE=2 ，求⊙O的半径 r 的长．10 ．（2012?黔南州）已知：如图，点 C 在以 AB 为直径的⊙O上，点 D 在 AB 的延长线上，∠ BCD=∠A．（1 ）求证： CD 为⊙O的切线；（2 ）过点 C 作 CE⊥ AB于 E．若 CE=2 ，cosD=，求AD的长．11 ．（ 2012?广安）如图，在 △ ABC 中，∠ ABC= ∠ ACB 以，AC 为直径的 ⊙O 分别交AB 、 BC 于点 M 、 N ，点 P 在 AB 的延长线上，且 ∠ CAB=2 ∠ BCP ．（ 1 ）求证：直线 CP 是⊙O 的切线．（ 2 ）若 BC=2， sin ∠ BCP= ，求点 B 到 AC 的距离．（ 3 ）在第（ 2）的条件下，求 △ ACP 的周长．12 ．（ 2012?黄冈）如图，在 △ ABC 中， BA=BC ，以 AB 为直径作半圆⊙ O ，交 AC于点 D ，过点 D 作 DE ⊥BC ，垂足为点E ．（ 1 ）求证： DE 为 ⊙O 的切线；（ 2 ）求证： BD 2=AB?BE ．13 ．（2011?芜湖）如图，已知直线 PA 交⊙O于 A、 B 两点， AE 是⊙O 的直径，点C 为⊙O 上一点，且 AC 平分∠ PAE ，过 C 作 CD 丄 PA，垂足为 D ．（1）求证： CD 为⊙O的切线；（2）若 DC+DA=6 ，⊙O 的直径为 10 ，求 AB 的长度．14 ．（2011?凉山州）如图，已知△点 F，点 E 为的中点，连接BE交AC于点ABC，以 BC 为直径，O 为圆心的半圆交AC 于M ， AD 为△ABC 的角平分线，且 AD⊥BE，垂足为点 H．（1）求证： AB 是半圆 O 的切线；（2）若 AB=3 ， BC=4 ，求 BE 的长．15 ．（2011?乐山）如图， D 为⊙O上一点，点 C 在直径 BA 的延长线上，且∠CDA= ∠ CBD．（1）求证： CD 是⊙O的切线；（2）过点 B 作⊙O的切线交 CD 的延长线于点 E，若 BC=6 ， tan ∠ CDA=，求 BE 的长．16 ．（2011?广安）如图所示， P 是⊙O 外一点， PA 是⊙O 的切线，A 是切点， B 是⊙O 上一点，且 PA=PB ，连接 AO 、 BO、 AB，并延长 BO 与切线 PA 相交于点 Q．（1 ）求证： PB 是⊙O的切线；（2）求证： AQ?PQ=OQ?BQ ；（3 ）设∠ AOQ=α，若，OQ=15，求AB的长．17 ．（2012?达州）如图， C是以 AB 为直径的⊙O上一点，过 O 作 OE⊥ AC于点 E，过点 A 作⊙O的切线交OE 的延长线于点F，连接 CF 并延长交BA 的延长线于点P．（1 ）求证： PC 是⊙O的切线．（2 ）若 AF=1 ， OA=，求PC的长．......2015 年 04 月 19 日九年级数学组的初中数学组卷参考答案与试题解析一．解答题（共 17 小题）1．（2014?辽阳）如图，在△ ABC，AB=AC ，以 AB 为直径的⊙O分别交 AC、 BC 于点 D、E，点 F 在 AC 的延长线上，且∠ CBF= ∠ CAB．（1）求证：直线 BF 是⊙O 的切线；（2）若 AB=5 ， sin ∠ CBF=，求 BC 和 BF 的长．考切线的判定与性质；勾股定理；圆周角定理；相似三角形的判定与性质；解直角三点：角形．专几何综合题．题：分（ 1）连接 AE，利用直径所对的圆周角是直角，从而判定直角三角形，利用直角三析：角形两锐角相等得到直角，从而证明∠ABF=90°．（ 2）利用已知条件证得△ AGC∽△ ABF利，用比例式求得线段的长即可．解（ 1）证明：连接 AE，答：∵ AB是⊙O 的直径，......∴∠AEB=90 °，∴∠1+ ∠ 2=90 °．∵AB=AC ，∴∠ 1=∠ CAB．∵∠ CBF=∠ CAB，∴∠1= ∠ CBF∴∠CBF+ ∠ 2=90 °即∠ABF=90°∵AB是⊙O的直径，∴直线 BF 是⊙O的切线．（2）解：过点 C 作 CG⊥ AB于 G．∵ sin ∠ CBF=，∠ 1= ∠ CBF ，∴ sin ∠ 1=，∵在 Rt △ AEB中，∠AEB=90 °AB=5，，∴BE=AB?sin ∠ 1=，∵AB=AC ，∠ AEB=90 °，∴ BC=2BE=2，在 Rt△ABE 中，由勾股定理得AE==2，∴ sin∠ 2===，cos∠ 2= ==，在Rt△CBG 中，可求得 GC=4 ，GB=2 ，∴ AG=3 ，∵GC∥ BF ，∴△AGC∽△ABF ，∴∴ BF==点本题考查常见的几何题型，包括切线的判定，角的大小及线段长度的求法，要求学评：生掌握常见的解题方法，并能结合图形选择简单的方法解题．2．（2014?吉林）如图，四边形 OABC 是平行四边形，以O为圆心，OA为半径的圆交AB 于点 D，延长 AO 交⊙O于点 E，连接 CD， CE，若 CE 是⊙O的切线，解答下列问题：（1）求证： CD 是⊙O的切线；（2）若 BC=3 ， CD=4 ，求平行四边形 OABC 的面积．考切线的判定与性质；全等三角形的判定与性质；平行四边形的性质．点：专证明题．题：分（ 1）连接 OD ，求出∠ EOC=∠ DOC，根据 SAS 推出△ EOC≌△ DOC，推出析：∠ ODC=∠ OEC=90°根，据切线的判定推出即可；（ 2）根据全等三角形的性质求出CE=CD=4 ，根据平行四边形性质求出OA=3 ，根据平行四边形的面积公式求出即可．解（ 1）证明：连接 OD ，答：∵ OD=OA，∴∠ODA=∠ A，∵四边形 OABC 是平行四边形，∴OC∥ AB，∴∠EOC=∠ A，∠COD=∠ ODA，∴∠EOC=∠ DOC，在△EOC 和△DOC 中∴△EOC≌△ DOC（SAS），∴∠ODC=∠ OEC=90 °，即OD⊥DC，∴ CD是⊙O的切线；（2）解：∵△ EOC≌△ DOC，∴ CE=CD=4 ，∵四边形 OABC 是平行四边形，∴OA=BC=3 ，∴平行四边形OABC 的面积 S=OA × CE=3 × 4=12 ．点本题考查了全等三角形的性质和判定，切线的判定，平行四边形的性质的应用，解评：此题的关键是推出△EOC≌△DOC．3．（2014?天水）如图，点 D 为⊙O 上一点，点 C 在直径 BA 的延长线上，且∠CDA= ∠ CBD．（1）判断直线 CD 和⊙O的位置关系，并说明理由．（2）过点 B 作⊙O的切线 BE 交直线 CD 于点 E，若 AC=2 ，⊙O 的半径是 3，求 BE的长．考切线的判定与性质．点：专几何图形问题．题：分（ 1）连接 OD ，根据圆周角定理求出∠ DAB+∠ DBA=90°求，出∠ CDA+∠ ADO=90°，析：根据切线的判定推出即可；（ 2）根据勾股定理求出 DC，根据切线长定理求出 DE=EB ，根据勾股定理得出方程，求出方程的解即可．解解：（ 1）直线 CD 和⊙O 的位置关系是相切，答：理由是：连接OD，∵AB是⊙O的直径，∴∠ ADB=90 °，∴∠ DAB+ ∠ DBA=90 °，∵∠ CDA= ∠ CBD，∴∠ DAB+ ∠ CDA=90 °，∵OD=OA，∴∠DAB= ∠ ADO，∴∠CDA+ ∠ ADO=90 °，即OD⊥CE，∴直线 CD 是⊙O 的切线，即直线 CD 和⊙O 的位置关系是相切；（ 2）∵AC=2 ，⊙O的半径是 3，∴OC=2+3=5 ，OD=3 ，在Rt△CDO 中，由勾股定理得： CD=4 ，∵ CE切⊙O于 D ，EB 切⊙O于 B，∴ DE=EB ，∠ CBE=90 °，设 DE=EB=x ，在 Rt △CBE 中，由勾股定理得： CE 2 =BE 2+BC 2，则（ 4+x ） 2=x 2+ （ 5+3 ） 2，解得： x=6 ，即 BE=6 ．点本题考查了切线的性质和判定，勾股定理，切线长定理，圆周角定理，等腰三角形评：的性质和判定的应用，题目比较典型，综合性比较强，难度适中．4．（ 2013?德州）如图，已知 ⊙O 的半径为 1， DE 是 ⊙O 的直径，过点 D 作⊙O 的切线 AD ， C 是 AD 的中点，AE 交 ⊙O 于 B 点，四边形 BCOE 是平行四边形．（ 1 ）求 AD 的长；（ 2 ） BC 是 ⊙O 的切线吗？若是，给出证明；若不是，说明理由．考切线的判定与性质；直角三角形斜边上的中线；平行四边形的性质．点：专计算题．题：分（ 1）连接 BD，由 ED 为圆 O 的直径，利用直径所对的圆周角为直角得到∠ DBE为直析：角，由 BCOE 为平行四边形，得到 BC 与 OE 平行，且 BC=OE=1 ，在直角三角形 ABD 中， C 为 AD 的中点，利用斜边上的中线等于斜边的一半求出AD 的长即可；（ 2）连接 OB，由 BC 与 OD 平行， BC=OD ，得到四边形 BCDO 为平行四边形，由AD 为圆的切线，利用切线的性质得到 OD 垂直于 AD ，可得出四边形 BCDO 为矩形，利用矩形的性质得到 OB 垂直于 BC，即可得出 BC 为圆 O 的切线．解解：（ 1）连接 BD，∵ DE是直径∴∠ DBE=90°，答：∵四边形 BCOE 为平行四边形，∴BC∥ OEBC=OE=1，，在Rt△ABD 中， C 为 AD 的中点，∴ BC= AD=1 ，则 AD=2 ；（ 2）是，理由如下：如图，连接 OB．∵ BC∥OD， BC=OD ，∴四边形 BCDO 为平行四边形，∵AD为圆O 的切线，∴ OD⊥ AD，∴四边形 BCDO 为矩形，∴OB⊥ BC，则 BC 为圆 O 的切线．点此题考查了切线的判定与性质，直角三角形斜边上的中线性质，以及平行四边形的评：判定与性质，熟练掌握切线的判定与性质是解本题的关键．5．（2013?菏泽）如图， BC 是⊙O 的直径，A 是⊙O 上一点，过点 C 作⊙O的切线，交 BA 的延长线于点D，取 CD 的中点 E， AE 的延长线与BC 的延长线交于点P．（1）求证： AP 是⊙O的切线；（2） OC=CP ， AB=6 ，求 CD 的长．考切线的判定与性质；解直角三角形．点：分（ 1）连接 AO ， AC（如图）．欲证 AP 是⊙O 的切线，只需证明OA⊥ AP 即可；析：（2）利用（1）中切线的性质在Rt △ OAP中利用边角关系求得∠ ACO=60°然．后在Rt △ BAC、 Rt △ ACD中利用余弦三角函数的定义知AC=2，CD=4．解（ 1）证明：连接 AO ，AC（如图）．答：∵ BC是⊙O 的直径，∴∠BAC= ∠ CAD=90 °．∵E是 CD 的中点，∴CE=DE=AE ．∴∠ ECA= ∠ EAC．∵ OA=OC，∴∠ OAC=∠ OCA．∵ CD是⊙O的切线，∴CD⊥ OC．∴∠ECA+ ∠ OCA=90 °．∴∠EAC+ ∠ OAC=90 °．∴OA⊥ AP．∵A是⊙O 上一点，∴AP是⊙O的切线；（ 2）解：由（ 1）知 OA⊥ AP．在Rt△OAP 中，∵∠ OAP=90°，OC=CP=OA ，即 OP=2OA ，∴ sinP= = ，∴∠P=30 °．∴∠AOP=60 °．∵OC=OA，∴∠ACO=60 °．在Rt△BAC 中，∵∠ BAC=90°，AB=6 ，∠ ACO=60°，∴ AC==2，又∵在 Rt△ACD 中，∠ CAD=90°，∠ ACD=90° ﹣∠ACO=30°，∴ CD===4 ．点本题考查了切线的判定与性质、解直角三角形．注意，切线的定义的运用，解题的评：关键是熟记特殊角的锐角三角函数值．6．（2013?聊城）如图， AB 是⊙O的直径， AF 是⊙O切线， CD 是垂直于 AB 的弦，垂足为 E，过点 C 作 DA 的平行线与AF 相交于点F， CD=，BE=2．求证：（1）四边形 FADC 是菱形；（2） FC 是⊙O 的切线．考切线的判定与性质；菱形的判定．.. . . ..点：专压轴题．题：分（ 1）首先连接 OC ，由垂径定理，可求得 CE 的长，又由勾股定理，可求得半径OC析：的长，然后由勾股定理求得AD 的长，即可得 AD=CD ，易证得四边形FADC 是平行四边形，继而证得四边形FADC 是菱形；（ 2）首先连接 OF ，易证得 △ AFO ≌△ CFO ，继而可证得 FC 是 ⊙O 的切线．解证明：（ 1 ）连接 OC ，答： ∵ AB 是 ⊙O 的直径， CD ⊥ AB ，∴ CE=DE= CD=×4 =2 ，设 OC=x ，∵ BE=2 ，∴ OE=x ﹣2 ，在 Rt △OCE 中， OC 2=OE 2+CE 2，22 + （ 2 2，∴x = （ x ﹣ 2））解得： x=4 ，∴ OA=OC=4 ，OE=2 ，∴ AE=6 ，在 Rt △AED 中， AD==4，∴ AD=CD ，∵ AF 是 ⊙O 切线， ∴ AF ⊥ AB ，......∵CD⊥ AB，∴ AF ∥ CD，∵CF∥ AD，∴四边形 FADC 是平行四边形，∵AD=CD ，∴平行四边形FADC 是菱形；（2）连接 OF， AC，∵四边形 FADC 是菱形，∴ FA=FC ，∴∠ FAC= ∠ FCA ，∵ AO=CO，∴∠ OAC=∠ OCA，∴∠FAC+ ∠ OAC=∠ FCA+ ∠ OCA，即∠OCF=∠OAF=90°，即OC⊥FC，∵点 C 在⊙O 上，∴ FC是⊙O 的切线．......点此题考查了切线的判定与性质、菱形的判定与性质、垂径定理、勾股定理以及全等评：三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．7．（2012?北京）已知：如图， AB 是⊙O 的直径， C 是⊙O上一点， OD⊥ BC于点 D，过点 C 作⊙O的切线，交 OD 的延长线于点E，连接 BE．（1）求证： BE 与⊙O相切；（2）连接 AD 并延长交 BE 于点 F，若 OB=9 ， sin ∠ ABC=，求 BF 的长．考切线的判定与性质；相似三角形的判定与性质；解直角三角形．点：专几何综合题．题：分（ 1）连接 OC，先证明△OCE≌△OBE，得出 EB⊥OB，从而可证得结论．析：解答：（2）过点 D 作 DH⊥ AB，根据 sin ∠ ABC=，可求出 OD=6 ， OH=4 ， HB=5 ，然后由△ADH∽△ AFB，利用相似三角形的性质得出比例式即可解出BF 的长．证明：（ 1 ）连接 OC，∵OD⊥ BC，∴∠COE=∠ BOE，在△OCE 和△OBE 中，∵，∴△OCE≌△ OBE，∴∠OBE= ∠ OCE=90 即°，OB⊥ BE，∵OB 是⊙O半径，∴ BE与⊙O相切．（ 2）过点 D 作 DH⊥ AB，连接 AD 并延长交BE 于点 F，∵∠DOH=∠ BOD，∠DHO=∠ BDO=90 °，∴△ODH∽△OBD，∴==又∵sin ∠ABC= ， OB=9 ，∴ OD=6 ，易得∠ABC=∠ODH，∴ sin∠ ODH=，即=，∴ OH=4 ，∴ DH==2，又∵△ ADH∽△ AFB，∴=，=，∴ FB=．点此题考查了切线的判定与性质、相似三角形的判定与性质，解答本题的关键是掌握评：切线的判定定理，在第二问的求解中，一定要注意相似三角形的性质的运用．8．（2012?济宁）如图， AB 是⊙O的直径， AC 是弦， OD⊥ AC于点 D ，过点 A 作⊙O的切线 AP， AP 与 OD 的延长线交于点P，连接 PC、 BC．（1）猜想：线段 OD 与 BC 有何数量和位置关系，并证明你的结论．（2）求证： PC 是⊙O的切线．考点：分析：切的判定与性；全等三角形的判定与性；三角形中位定理；周角定理．（1）根据垂径定理可以得到 D 是 AC 的中点， OD 是△ ABC的中位，根据三角形的中位定理可以得到 OD∥BC， CD= BC；（2）接 OC， OP 与⊙O 交于点 E，可以得△ OAP≌△ OCP，利用全等三角形的角相等，以及切的性定理可以得到：∠ OCP=90°，即OC⊥PC，即可等．解答：（ 1）猜想： OD∥ BC，OD= BC．明：∵ OD⊥AC，∴AD=DC∵AB是⊙O的直径，∴ OA=OB⋯2分∴OD是△ ABC的中位，∴OD∥ BC，OD= BC（2）明：接 OC， OP 与⊙O交于点 E．∵ OD⊥ AC，OD 心 O，∴，即∠ AOE=∠ COE在△OAP 和△OCP 中，，∴△OAP≌△O CP，∴∠OCP=∠ OAP∵PA是⊙O的切线，∴∠ OAP=90 °．∴∠ OCP=90 °即，OC⊥ PC∴ PC是⊙O 的切线．点本题考查了切线的性质定理以及判定定理，三角形的中位线定理，证明圆的切线的评：问题常用的思路是根据切线的判定定理转化成证明垂直的问题．9．（2012?德阳）如图，已知点 C 是以 AB 为直径的⊙O上一点， CH⊥ AB于点 H ，过点 B 作⊙O 的切线交直线AC 于点 D，点 E 为 CH 的中点，连接 AE 并延长交 BD 于点 F，直线CF 交 AB 的延长线于G．（1）求证： AE?FD=AF?EC ；（2）求证： FC=FB；（3）若 FB=FE=2 ，求⊙O的半径 r 的长．......考切线的判定与性质；等腰三角形的性质；等腰三角形的判定；直角三角形斜边上的点：中线；勾股定理；圆周角定理；相似三角形的判定与性质．专证明题；几何综合题；压轴题．题：分（ 1）由 BD 是⊙O的切线得出∠ DBA=90 °推，出 CH∥ BD，证△ AEC∽△ AFD得，出比析：例式即可；（ 2）连接 OC， BC，证△ AEC∽△ AFD ，△ AHE∽△ ABF推出，BF=DF ，根据直角三角形斜边上中线性质得出 CF=DF=BF即可；（ 3）求出 EF=FC，求出∠ G=∠ FAG推，出 AF=FG ，求出 AB=BG ，求出∠ FCB= ∠ CAB 推出 CG 是⊙O切线，由切割线定理得出（2+FG）2=BG× AG=2BG2，在Rt△ BFG解答：中，由勾股定理得出BG2=FG2﹣ BF2，推出 FG2﹣ 4FG﹣ 12=0 ，求出 FG 即可．（1）证明：∵BD是⊙O的切线，∴∠ DBA=90 °，∵ CH⊥ AB，∴ CH∥ BD，∴△AEC∽△AFD ，∴=，∴AE?FD=AF?EC ．（2）证明：连接 OC， BC，∵ CH∥ BD，∴△ AEC∽△ AFD ，△ AHE∽△ ABF ，∴=，=，∴==，∵CE=EH （E 为 CH 中点），∴BF=DF ，∵ AB为⊙O的直径，∴∠ACB= ∠ DCB=90 °，∵BF=DF ，∴ CF=DF=BF （直角三角形斜边上的中线等于斜边的一半），即CF=BF．（3）解：∵ BF=CF=DF 已（证）， EF=BF=2 ，∴ EF=FC ，∴∠ FCE= ∠ FEC ，∵∠AHE= ∠ CHG=90 °，∴∠FAH+ ∠ AEH=90 °，∠G+∠ GCH=90 °，∵∠AEH= ∠ CEF ，∴∠G=∠ FAG，∴AF=FG ，∵ FB ⊥ AG，∴AB=BG ，∵BF切⊙O于 B，∴∠ FBC= ∠ CAB，∵ OC=OA ，CF=BF ，∴∠ FCB= ∠ FBC ，∠ OCA=∠ OAC ，∴∠ FCB= ∠ CAB ，∵∠ ACB=90 °，∴∠ ACO+∠ BCO=90 °，∴∠ FCB+ ∠ BCO=90 °，即 OC ⊥CG ，∴ CG 是 ⊙O 切线，∵ GBA 是 ⊙O 割线， AB=BG （已证），FB=FE=2 ，∴由切割线定理得：（ 2+FG ） 2=BG × AG=2BG 2，在 Rt △BFG 中，由勾股定理得： BG 2=FG 2﹣ BF 2，2，∴ FG ﹣ 4FG ﹣ 12=0 解得： FG=6 ， FG= ﹣ 2（舍去），由勾股定理得：AB=BG==4， ∴⊙O 的半径是 2．点本题考查了切线的性质和判定，相似三角形的性质和判定，等腰三角形的性质和判......评：定，直角三角形斜边上中线的性质，圆周角定理，勾股定理等知识点的综合运用，题目综合性比较强，有一定的难度．10 ．（2012?黔南州）已知：如图，点 C在以 AB 为直径的⊙O上，点 D 在 AB 的延长线上，∠ BCD= ∠ A．（1 ）求证： CD 为⊙O的切线；（2 ）过点 C 作 CE⊥ AB于 E．若 CE=2 ，cosD=，求AD的长．考切线的判定与性质；圆周角定理；解直角三角形．点：分（ 1）先连接 CO，根据 AB 是⊙O直径，得出∠ 1+ ∠ OCB=90 °再，根据 AO=CO ，得析：出∠1=∠A，最后根据∠4=∠A，证出OC⊥CD，即可得出CD 为⊙O的切线；（ 2）根据 OC⊥ CD，得出∠ 3+ ∠ D=90 °再，根据 CE⊥ AB，得出∠ 3+ ∠ 2=90 °从，而得出 cos∠2=cosD，再在△OCD 中根据余弦定理得出CO 的值，最后根据⊙O的半径为，即可得出AD 的长．解证明：（ 1 ）连接 CO，答：∵ AB是⊙O 直径∴∠1+ ∠ OCB=90 °，∵AO=CO，......∴∠1= ∠ A．∵∠4= ∠ A，∴∠4+ ∠ OCB=90 °．即∠OCD=90°．∴OC⊥ CD．又∵OC是⊙O 半径，∴ CD为⊙O的切线．（2）∵ OC⊥ CD于 C，∴∠3+ ∠ D=90 °．∵CE⊥ AB于 E，∴∠3+ ∠ 2=90 °．∴∠2= ∠ D．∴cos ∠ 2=cosD ，在△OCD 中，∠ OCD=90°，∴cos ∠ 2=，∵cosD= ， CE=2 ，∴=，tanD==，∴CO= ，∴⊙O的半径为．......∴ OD== =，AD=．点本题考查了切线的判定与性质，要证某线是圆的切线，已知此线过圆上某点，连接评：圆心与这点（即为半径），再证垂直即可，同时考查了三角函数的知识．11 ．（2012?广安）如图，在△ ABC中，∠ABC= ∠ ACB以，AC 为直径的⊙O分别交 AB、 BC于点 M 、N ，点 P 在 AB 的延长线上，且∠CAB=2∠BCP．（1）求证：直线 CP 是⊙O 的切线．（2）若 BC=2，sin∠ BCP=，求点B到AC的距离．（3）在第（ 2）的条件下，求△ ACP的周长．考切线的判定与性质；等腰三角形的性质；勾股定理；相似三角形的判定与性质；解点：直角三角形．专几何综合题；压轴题．......题：分（ 1）根据∠ ABC= ∠ ACB且∠析：得到2∠BCP+2∠BCA=180°，CAB=2 ∠ BCP在，△ ABC中∠ ABC+ ∠ BAC+ ∠ BCA=180 °，从而得到∠BCP+∠BCA=90°，证得直线 CP 是⊙O的切线．（ 2）作 BD⊥ AC于点 D ，得到 BD∥ PC，从而利用sin∠ BCP=sin∠ DBC==，求得DC=2，再根据勾股定理求得点 B 到 AC 的距离为 4．（ 3）先求出 AC 的长度，然后利用BD∥ PC的比例线段关系求得CP 的长度，再由勾股定理求出AP 的长度，从而求得△ACP 的周长．解解：（ 1）∵∠ ABC=∠ACB 且∠CAB=2∠BCP，在△ABC中，答：∠ ABC+∠ BAC+∠ BCA=180°∴2 ∠ BCP+2 ∠ BCA=180 °，∴∠ BCP+ ∠ BCA=90 °，又 C 点在直径上，∴直线 CP 是⊙O的切线．（2）如右图，作 BD⊥ AC 于点 D，∵ PC⊥ AC∴BD∥ PC∴∠PCB= ∠ DBC∵BC=2 ， sin ∠ BCP= ，∴ sin∠ BCP=sin∠ DBC==，解得： DC=2 ，∴由勾股定理得： BD=4 ，∴点 B 到 AC 的距离为4．（3）如右图，连接 AN ，∵ AC为直径，∴∠ ANC=90 °，∴ Rt △ ACN中，AC==5 ，又CD=2 ，∴AD=AC﹣CD=5 ﹣2=3 ．∵BD∥ CP，∴，∴CP= ．在 Rt△ACP 中， AP==，AC+CP+AP=5++ =20 ，∴△ACP的周长为20．点本题考查了切线的判定与性质等知识，考查的知识点比较多，难度较大．评：12 ．（2012?黄冈）如图，在 △ ABC 中， BA=BC ，以 AB 为直径作半圆 ⊙ O ，交 AC 于点 D ，过点 D 作 DE ⊥BC ，垂足为点 E ．（ 1 ）求证： DE 为 ⊙O 的切线；（ 2 ）求证： BD 2=AB?BE ．考切线的判定与性质；圆周角定理；相似三角形的判定与性质．点：专证明题．题：分（ 1）连接 OD 、 BD ，根据圆周角定理可得 ∠ ADB=90 °继，而得出点 D 是 AC 中点，析：判断出 OD 是三角形 ABC 的中位线，利用中位线的性质得出∠ODE=90°，这样可判断出结论．（ 2）根据题意可判断 △ BED ∽△ BDC 从，而可得 BD 2=BC?BE ，将 BC 替换成 AB 即可得出结论．解证明：（ 1 ）连接 OD 、 BD ，则∠ADB=90°（圆周角定理），答： ∵ BA=BC ，∴ CD=AD （三线合一），又 ∵AO=OB ，∴ OD 是 △ ABC 的中位线，∴ OD ∥ BC ，∵∠ DEB=90 °，∴∠ ODE=90 °即，OD ⊥ DE ，故可得 DE 为 ⊙O 的切线；（ 2）∵∠ EBD= ∠ DBC ，∠ DEB= ∠ CDB ，∴△ BED ∽△ BDC ，∴= ，又 ∵AB=BC ，∴= ，故 BD 2=AB?BE ．点此题考查了切线的判定及性质、三角形的中位线的判定与性质等腰三角形的性质，评：解答本题的关键是得出点D 是 AC 中点，求出 ∠ODE 是直角，有一定难度．13 ．（ 2011?芜湖）如图，已知直线上一点，且 AC 平分 ∠PAE ，过 C 作 PA 交 ⊙O 于 A 、 B 两点，AE 是 ⊙O 的直径，点 C 为⊙O CD 丄 PA ，垂足为 D ．（1）求证： CD 为⊙O的切线；（2）若 DC+DA=6 ，⊙O 的直径为 10 ，求 AB 的长度．考切线的判定与性质；勾股定理；矩形的判定与性质；垂径定理．点：专几何综合题．题：分（ 1）连接 OC，根据题意可证得∠ CAD+∠ DCA=90°再，根据角平分线的性质，得析：∠ DCO=90°，则CD为⊙O 的切线；（ 2）过 O 作 OF⊥ AB，则∠ OCD=∠ CDA= ∠ OFD=90 °得，四边形OCDF 为矩形，设AD=x ，在 Rt △ AOF中，由勾股定理得（ 5﹣ x）2+ （ 6﹣ x）2=25 ，从而求得 x 的值，由勾股定理得出AB 的长．解（ 1）证明：连接 OC，答：∵ OA=OC，∴∠OCA=∠ OAC，∵ AC平分∠ PAE ，∴∠DAC= ∠ CAO，∴∠DAC= ∠ OCA，∴ PB ∥ OC ， ∵ CD ⊥ PA ，∴ CD ⊥ OC ，CO 为 ⊙O 半径，∴ CD 为 ⊙O 的切线；（ 2）解：过 O 作 OF ⊥ AB ，垂足为 F ，∴∠ OCD=∠ CDA= ∠ OFD=90 °，∴四边形 DCOF 为矩形，∴ OC=FD ，OF=CD ． ∵DC+DA=6 ，设 AD=x ，则 OF=CD=6 ﹣x ， ∵⊙O 的直径为 10 ， ∴ DF=OC=5 ，∴ AF=5﹣ x ，在 Rt △AOF 中，由勾股定理得AF 2 +OF 2=OA 2 ．即（ 5﹣ x ）2 + （ 6﹣x ）2=25 ，化简得 x 2﹣11x+18=0 ，解得 x 1=2 ， x 2=9 ．∵ CD=6﹣ x 大于 0，故 x=9 舍去， ∴ x=2 ，从而 AD=2 ， AF=5 ﹣ 2=3 ，∵ OF ⊥ AB ，由垂径定理知，F 为 AB 的中点，∴AB=2AF=6 ．点本题考查了切线的判定和性质、勾股定理、矩形的判定和性质以及垂径定理，是基评：础知识要熟练掌握．14 ．（2011?凉山州）如图，已知△ ABC，以 BC 为直径， O 为圆心的半圆交AC 于点 F，点E 为的中点，连接BE交AC于点M，AD为△ ABC的角平分线，且AD⊥ BE，垂足为点H．（1）求证： AB 是半圆 O 的切线；（2）若 AB=3 ， BC=4 ，求 BE 的长．考切线的判定与性质；勾股定理；圆周角定理；相似三角形的判定与性质．点：专几何综合题；压轴题．题：分（ 1）连接 EC， AD 为△ABC 的角平分线，得∠1=∠2，又 AD⊥BE，可证∠3=∠4，由.. . . ..析：对顶角相等得 ∠4=∠5，即 ∠3=∠5，由 E 为的中点，得 ∠6=∠7，由 BC 为直径得∠ E=90 °即，∠ 5+ ∠ 6=90 °由，AD ∥ CE 可证 ∠ 2= ∠ 6从，而有 ∠ 3+ ∠ 7=90 °证，明结论；（ 2）在 Rt △ ABC 中，由勾股定理可求 AC=5 ，由 ∠ 3= ∠4得 AM=AB=3 ，则 CM=AC﹣ AM=2 ，由（ 1 ）可证 △CME ∽△ BCE ，利用相似比可得 EB=2EC ，在 Rt △BCE 中，根据 BE 2 +CE 2=BC 2，得 BE 2+ （） 2=4 2，可求 BE ．解（ 1）证明：连接 EC ，答： ∵ AD ⊥ BE 于 H ，∠ 1= ∠ 2 ，∴∠ 3= ∠ 14 （分）∵∠ 4= ∠ 5 ，∴∠ 4= ∠ 5= ∠ 32，分（）又 ∵E 为的中点，∴ =，∴∠ 6= ∠ 7 ，3（分），∵ BC 是直径， ∴∠ E=90 °，∴∠ 5+ ∠ 6=90 °，又 ∵∠ AHM=∠E=90°，∴ AD ∥ CE ，∴∠ 2= ∠ 6= ∠ 1 ，∴∠ 3+ ∠ 7=90 °，又 ∵BC 是直径，.学习帮手... . . ..（ 2）解：∵ AB=3 ，BC=4 ，由（ 1）知，∠ ABC=90°，∴ AC===5 （ 5 分）在 △ABM 中，AD ⊥BM 于 H ，AD 平分 ∠BAC ，∴ AM=AB=3 ，∴ CM=2 （6 分）∵∠ 6= ∠ 7 ，为∠E 公共角，∴△ CME ∽△ BCE 得，= = = ，（ 7 分）∴ EB=2EC ，在 Rt △ BCE 中， BE 2+CE 2=BC 2，即 BE 2+ （） 2 =4 2 ，解得 BE=．（ 8 分）点本题考查了切线的判定与性质，相似三角形的判定与性质，圆周角定理，勾股定理评：的运用．关键是由已知条件推出相等角，构造互余关系的角推出切线，利用相等角推出相似三角形，由相似比得出边长的关系，由勾股定理求解．15 ．（ 2011?乐山）如图， D 为⊙O 上一点，点 C 在直径 BA 的延长线上，且 ∠ CDA= ∠ CBD ．（1 ）求证： CD 是 ⊙O 的切线；（2 ）过点 B 作⊙O的切线交CD 的延长线于点E，若 BC=6 ， tan ∠ CDA=，求 BE 的长．考切线的判定与性质；圆周角定理；相似三角形的判定与性质．点：专几何综合题；压轴题．题：分（ 1）连 OD ，OE，根据圆周角定理得到∠ ADO+∠ 1=90°而，∠ CDA=∠ CBD，析：∠ CBD=∠ 1于，是∠ CDA+∠ ADO=90°；（ 2）根据切线的性质得到ED=EB， OE⊥ BD，则∠ ABD= ∠ OEB，到得tan ∠ CDA=tan∠ OEB=，易证Rt△ CDO∽ Rt△ CBE得，到===，求得CD ，然后在 Rt △ CBE中，运用勾股定理可计算出BE 的长．解（ 1）证明：连 OD ， OE，如图，答：∵ AB为直径，∴∠ADB=90 °即，∠ ADO+∠ 1=90 °，又∵∠ CDA=∠CBD，而∠CBD=∠1，∴∠1= ∠ CDA，∴∠CDA+ ∠ ADO=90 °即，∠ CDO=90 °，∴ CD 是 ⊙O 的切线；（ 2）解：∵ EB 为⊙O 的切线， ∴ ED=EB ， OE ⊥ DB ，∴∠ ABD+ ∠ DBE=90 °，∠ OEB+ ∠ DBE=90 °， ∴∠ ABD= ∠ OEB ，∴∠ CDA= ∠ OEB ．而 tan ∠CDA= ，∴ tan ∠ OEB== ，∵ Rt △ CDO ∽ Rt △ CBE ，∴= = = ，∴ CD= × 6=4 ，在 Rt △CBE 中，设 BE=x ，∴（x+4 ）2 =x 2 +6 2，解得 x=．即 BE 的长为．点本题考查了切线的判定与性质：过半径的外端点与半径垂直的直线是圆的切线；也评：考查了圆周角定理的推论以及三角形相似的判定与性质．16 ．（2011?广安）如图所示， P 是⊙O外一点， PA 是⊙O的切线，A 是切点， B 是⊙ O 上一点，且 PA=PB ，连接 AO 、 BO、 AB，并延长 BO 与切线 PA 相交于点Q ．（1）求证： PB 是⊙O的切线；（2）求证： AQ?PQ=OQ?BQ ；（3 ）设∠ AOQ=α，若，OQ=15，求AB的长．考切线的判定与性质；全等三角形的判定与性质；勾股定理；相似三角形的判定与性点：质；解直角三角形．专几何综合题；压轴题．题：分（ 1）连接 OP，与 AB 交于点 C．欲证明 PB 是⊙O 的切线，只需证明∠ OBP=90 即°析：可；（ 2）根据相似三角形的判定定理AA 证明△ QAO∽△ QBP，然后由相似三角形的对应边成比例求得= ，即 AQ?PQ=OQ?BQ；（ 3）在 Rt △O AQ 中根据勾股定理和三角函数的余弦值的定义解得QB=27 ，利用（ 1）的结论求得 PQ=45 ，即 PA=36 ，又由勾股定理知 OP=12；然后由切线的性质求 AB 的长．解（ 1）证明：连接 OP，与 AB 交于点 C．答：∵PA=PB，OA=OB，OP=OP，∴△OAP≌△ OBP（SSS），∴∠OBP= ∠ OAP，∵PA是⊙O的切线， A 是切点，∴∠ OAP=90 °，∴∠ OBP=90 °即，PB 是⊙O 的切线；（2）证明：∵∠ Q=∠ Q，∠ OAQ=∠ QBP=90 °，∴△QAO∽△QBP，∴= ，即 AQ?PQ=OQ?BQ ；（ 3）连 OP 并交 AB 于点 C，在Rt△OAQ 中，∵ OQ=15，cosα=，∴OA=12 ，AQ=9 ，∴QB=27 ；∵=，∴PQ=45 ，即 PA=36 ，∴OP=12；∵∠APO= ∠ APO，∠PAO= ∠ PCA=90 °∴△PAC∽△POA，∴=，∴ PA?OA=OP?AC ，即 36 × 12=12?AC ，∴ AC=，故AB=．点本题综合考查了切线的判定与性质、相似三角形与全等三角形的判定与性质、解直评：角三角形以及勾股定理．图形中的线段的求法，可以通过特殊角的三角函数值、切线的有关知识及勾股定理求解．17 ．（2012?达州）如图， C 是以 AB 为直径的⊙O上一点，过 O 作 OE⊥ AC于点 E，过点A 作⊙O的切线交OE 的延长线于点F，连接 CF 并延长交BA 的延长线于点P．（1 ）求证： PC 是⊙O的切线．（2 ）若 AF=1 ， OA=，求PC的长．考切线的判定与性质；勾股定理；圆周角定理；相似三角形的判定与性质．点：专几何综合题；压轴题．题：分（ 1）连接 OC，根据垂径定理，利用等角代换可证明∠ FAC= ∠ FCA然，后根据切线的析：性质得出∠FAO=90°，然后即可证明结论．（ 2）先证明△ PAF ∽△ PCO利，用相似三角形的性质得出PC 与 PA 的关系，在Rt △ PCO中，利用勾股定理可得出 x 的值，继而也可得出PC 得长．解（ 1）证明：连接 OC，答：∵ OE⊥ AC，∴AE=CE ，FA=FC，∴∠ FAC= ∠ FCA ，∵ OA=OC（圆的半径相等），∴∠ OAC=∠ OCA，∴∠ OAC+∠ FAC= ∠ OCA+∠ FCA即∠，FAO= ∠ FCO，∵ FA与⊙O相切，且 AB 是⊙O的直径，∴FA ⊥ AB，∴∠FCO= ∠ FAO=90 °，∵ CO是半径，∴ PC是⊙O 的切线；（ 2）解：∵PC是⊙O的切线，∴∠PCO=90 °，又∵∠ FPA=∠OPC，∠ PAF=90°，∴△PAF ∽△PCO，∴∵ CO=OA=，AF=1，∴ PC=PA，设 PA=x ，则 PC=．在 Rt△PCO 中，由勾股定理得：，解得：，∴ PC=2×=．点此题考查了切线的性质、勾股定理、圆周角定理、相似三角形的判定与性质，涉及评：知识点较多，解答本题要求熟练掌握切线的判定定理及性质，有一定难度．。