浙江省黄岩中学高一数学暑假作业(九)
浙江省黄岩中学高一数学暑假作业及答案

浙江省2019年黄岩中学高一数学暑假作业及答案知识只有反复练习,才能记得牢靠。
精品小编准备了高一数学暑假作业及答案,具体请看以下内容。
一、选择题1、下列各组角中,终边相同的是( )(A)390°与690°(B)-330°与750°(C)480°与-420°(D)300°与-840°解析:B2、若为第一象限的角,则sin2,,,中能确定为正值的个数是( )(A)0个(B)1个(C)2个(D)2个以上解析:C3、扇形的半径为r,面积为,则这个扇形的中心角的弧度数是( )(A) (B) (C)2 (D)解析:D4、已知α+β=3π,则下列等式中一定成立的是( )(A)sinα= sinβ(B)cosα= cosβ(C)tanα=tanβ(D)cotα= cotβ解析:A5、若角的终边落在直线x+y=0上,则=( )(A)-2 (B)2 (C)-2或2 (D)0解析:D6、下列函数式能同时成立的是( )(A)sin=,cos= (B)sin=0.35,cos=0.65(C)sin=,cos=- (D)tan=1,cot=-1解析:C7、下列四个数中与sin相等的是①sin(nπ+) ②sin(2nπ±)③sin[(2n+1)π-] ④sin[nπ+(-1)n](nZ) ( )(A)①③(B)②③(C) ②④(D)③④解析:D8、已知tanα=m,<α<,则sinα= ( )与当今“教师”一称最接近的“老师”概念,最早也要追溯至宋元时期。
金代元好问《示侄孙伯安》诗云:“伯安入小学,颖悟非凡貌,属句有夙性,说字惊老师。
”于是看,宋元时期小学教师被称为“老师”有案可稽。
清代称主考官也为“老师”,而一般学堂里的先生则称为“教师”或“教习”。
可见,“教师”一说是比较晚的事了。
如今体会,“教师”的含义比之“老师”一说,具有资历和学识程度上较低一些的差别。
浙江省黄岩中学高一数学暑假作业(十)

高一数学暑假作业(十)一、 选择题:1、设b r 是a r的相反向量,则下列说法中错误的是 ( )(A )a r 和b r 的长度一定相等 (B )a r 和b r是平行向量(C )a r 和b r 一定不相等 (D )a r 是b r的相反向量2、1e u r 和2e u u r是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基 底的是 ( )(A )1e u r + 2e u u r 和1e u r -2e u u r (B )31e u r -22e u u r 和42e u u r -61e u r(C )1e u r + 22e u u r 和2e u u r +21e u r (D )2e u u r 和 2e u u r +1e u r3、已知△ABC 的顶点A (2,3),B (8,-4),和重心G (2,-1),则点C 的坐标是 (A )(4,-3) (B )(1,4) (C )(-4,-2) (D )(-2,-2) ( )4、下列命题中:①若b r ≠0r ,且a r ·b r =c r ·b r ,则a r =c r ;②若a r =b r ,则3a r <4b r;③(a r ·b r ) ·c r =a r ·(b r ·c r ), 对任意向量a r ,b r ,c r 都成立;④a r 2·b r 2=(a r ·b r )2;正确命题的个数为 ( ) (A )0 (B )1 (C )2 (D )35、已知A 、B 、C 三点共线,且A 、B 、C 三点的纵坐标分别为2,5,10,则A 点分BC 所得的比为 ( ) (A )83 (B )38 (C )-83 (D )-38 6、已知O 为原点,点A 、B 的坐标分别为(a, 0)、(0,a )a 是正常数,点P 在线段AB 上,且AP =t AB (0≤t ≤1),则OA ·OP 的最大值 ( ) (A )a (B )2a (C )3a (D )a 2二、填空题:7、已知同一直线上的三点顺次为A (-y ,6),B (-2,y ),C (x ,-6),若12=u u u r u u u r BC AB ,则x=___________,y=_____________。
(新课标)高一数学暑假作业(九)
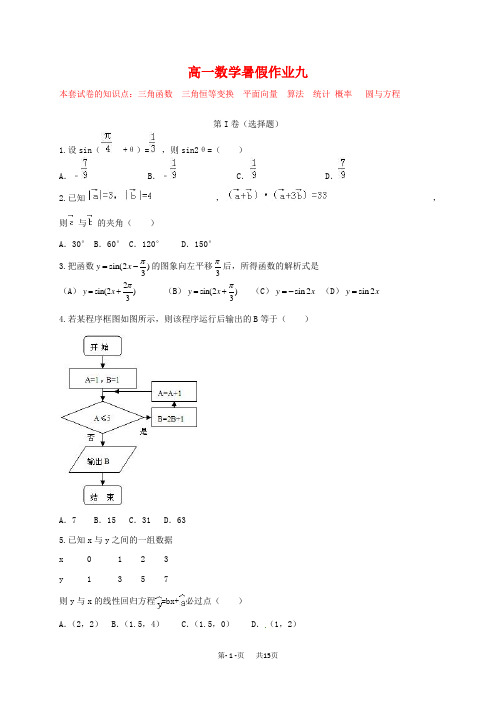
高一数学暑假作业九本套试卷的知识点:三角函数 三角恒等变换 平面向量 算法 统计 概率 圆与方程第I 卷(选择题)1.设sin (+θ)=,则sin2θ=( )A .﹣B .﹣C .D .2.已知,,则与的夹角( )A .30°B .60°C .120°D .150°3.把函数sin(2)3y x π=-的图象向左平移3π后,所得函数的解析式是(A )2sin(2)3y x π=+ (B )sin(2)3y x π=+ (C )sin 2y x =- (D )sin 2y x =4.若某程序框图如图所示,则该程序运行后输出的B 等于( )A .7B .15C .31D .635.已知x 与y 之间的一组数据则y 与x 的线性回归方程=bx+必过点( ) A .(2,2) B .(1.5,4)C .(1.5,0)D .(1,2)6. (2016新课标高考题)已知θ是第四象限角,且sin(θ+π4)=35,则tan(θ–π4)= .sin(﹣600°)的值是()A.B.﹣C.D.﹣7.某时段内共有100辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h 的汽车数量为()A.38辆B.28辆C.10辆D.5辆8.方程x2+y2+2ax﹣4y+(a2+a)=0表示一个圆,则a的取值范围是()A.[4,+∞)B.(4,+∞)C.(﹣∞,4] D.(﹣∞,4)9.在一次模拟考试后,从高三某班随机抽取了20位学生的数学成绩,其分布如下:分数在130分(包括130分)以上者为优秀,据此估计该班的优秀率约为()A.10% B.20% C.30% D.40%10.要完成下列3项抽样调查:①从某班10名班干部中随机抽取3人进行一项问卷调查.②科技报告厅的座位有60排,每排有50个,某次报告会恰好坐满听众,报告会结束后,为了解听众意见,需要随机抽取30名听众进行座谈.③某高中共有160名教职工,其中教师120名,行政人员16名,后勤人员24名.为了解教职工的文化水平,拟随机抽取一个容量为40的样本.较为合理的抽样方法是()A.①简单随机抽样,②分层抽样,③系统抽样B.①简单随机抽样,②系统抽样,③分层抽样C.①系统抽样,②简单随机抽样,③分层抽样D.①分层抽样,②系统抽样,③简单随机抽样第II卷(非选择题)11.若cosα=,tanα<0,则sinα= .12.已知函数f(x)=,有下列四个结论:①函数f(x)在区间[﹣,]上是增函数:②点(,0)是函数f(x)图象的一个对称中心;③函数f(x)的图象可以由函数y=sin2x的图象向左平移得到;④若x∈[0,],则函数f(x)的值域为[0,].则所有正确结论的序号是.13.已知||=||=||=1,且⊥,则(+﹣)•的最大值是.14.已知sinα=﹣,α为第三象限角,则等于.15.为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:(Ⅰ)求出表中字母m,n所对应的数值;(Ⅱ)在图中补全频率分布直方图;(Ⅲ)根据频率分布直方图估计该校高一女生身高的中位数(保留两位小数)16.已知函数f(x)=2cosx(sinx+cosx),x∈R.(1)求的值;(2)求函数f(x)的单调递增区间;(3)求函数f(x)在区间上的最大值和最小值.17.已知=(cos,sin),,且(I)求的最值;(II)是否存在k的值使?2015-2016下学期高一数学暑假作业九试卷答案1.A【考点】二倍角的余弦;三角函数的恒等变换及化简求值.【专题】计算题.【分析】根据两角和的正弦函数公式和特殊角的三角函数值化简已知条件,然后两边平方利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,即可sin2θ的值.【解答】解:由sin(+θ)=sin cosθ+cos sinθ=(sinθ+cosθ)=,两边平方得:1+2sinθcosθ=,即2sinθcosθ=﹣,则sin2θ=2sinθcosθ=﹣.故选A【点评】此题考查学生灵活运用二倍角的正弦函数公式、两角和与差的正弦函数公式及特殊角的三角函数值化简求值,是一道基础题.2.C【考点】数量积表示两个向量的夹角.【专题】常规题型.【分析】利用向量的多项式乘法展开,利用向量模的平方等于向量的平方及向量的数量积公式,求出向量夹角的余弦,利用向量夹角的范围,求出向量的夹角.【解答】解:设两个向量的夹角为θ∵∴∴9+16×3+12×4cosθ=33∴∵θ∈[0,π]∴θ=120°故选C.【点评】求向量的夹角问题一般应该先求出向量的数量积,再利用向量的数量积公式求出向量夹角的余弦,注意夹角的范围,求出夹角.3.B【知识点】三角函数图像变换【试题解析】把函数的图象向左平移个单位得到:故答案为:B4.D【考点】程序框图;设计程序框图解决实际问题.【专题】图表型.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算B值并输出,模拟程序的运行过程,即可得到答案.【解答】解:程序在运行过程中各变量的值如下表示:A B 是否继续循环循环前 1 1/第一圈 2 3 是第二圈 3 7 是第三圈 4 15 是第三圈 5 31 是第四圈 6 63 否则输出的结果为63.故选D.【点评】本题考查的知识点是程序框图,在写程序的运行结果时,模拟程序的运行过程是解答此类问题最常用的办法.5.B【考点】线性回归方程.【专题】计算题;概率与统计.【分析】先分别计算平均数,可得样本中心点,利用线性回归方程必过样本中心点,即可得到结论.【解答】解:由题意, =(0+1+2+3)=1.5, =(1+3+5+7)=4∴x 与y 组成的线性回归方程必过点(1.5,4) 故选:B .【点评】本题考查线性回归方程,解题的关键是利用线性回归方程必过样本中心点. 6. 【答案】43- 【解析】试题分析:由题意,π3π4sin(),cos(),4545θθ+=+=ππ3sin sin cos cos ,445ππ4cos cos sin sin ,445θθθθ⎧+=⎪⎪∴⎨⎪-=⎪⎩解得sin cos θθ⎧=⎪⎪⎨⎪=⎪⎩所以1tan 7θ=-,1π1tan tan π474tan().π1431tan tan 1147θθθ----===-+-⨯ 考点:三角变换【点评】此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键. 7.A【考点】用样本的频率分布估计总体分布. 【专题】计算题.【分析】根据频率分步直方图看出时速超过60km/h 的汽车的频率比组距的值,用这个值乘以组距,得到这个范围中的频率,用频率当概率,乘以100,得到时速超过60km/h 的汽车数量. 【解答】解:根据频率分步直方图可知时速超过60km/h 的概率是10×(0.01+0.028)=0.38, ∵共有100辆车,∴时速超过60km/h 的汽车数量为0.38×100=38(辆) 故选A .【点评】本题考查用样本的频率估计总体分布,频数、频率和样本容量三者之间的关系是知二求一,这种问题会出现在选择和填空中,有的省份也会以大题的形式出现,把它融于统计问题中. 8.D【考点】二元二次方程表示圆的条件.【专题】计算题;方程思想;综合法;直线与圆. 【分析】根据二元二次方程表示圆的条件进行求解即可.【解答】解:方程x2+y2+2ax﹣4y+(a2+a)=0表示一个圆,则4a2+16﹣4(a2+a)>0,解得a<4,故选:D.【点评】本题主要考查圆的一般方程的应用,根据二元二次方程表示圆的条件是解决本题的关键.9.B【考点】频率分布表.【专题】计算题;整体思想;定义法;概率与统计.【分析】根据统计表和样本来估计总体的概念即可求出.【解答】解:由表可知,优秀的人数为3+1=4,故分数在130分(包括130分)以上者为优秀,则优秀率为=20%,故据此估计该班的优秀率约20%,故选:B.【点评】本题考查了频率分布表的应用和用样本来估计总体,属于基础题.10.B【考点】简单随机抽样.【专题】计算题;整体思想;定义法;概率与统计.【分析】观察所给的四组数据,根据四组数据的特点,把所用的抽样选出来①简单随机抽样,②系统抽样,③分层抽样.【解答】解:观察所给的四组数据,①个体没有差异且总数不多可用随机抽样法,简单随机抽样,②将总体分成均衡的若干部分指的是将总体分段,在第1段内采用简单随机抽样确定一个起始编号,在此编号的基础上加上分段间隔的整倍数即为抽样编号,系统抽样,③个体有了明显了差异,所以选用分层抽样法,分层抽样,故选: B.【点评】简单随机抽样是一种最简单、最基本的抽样方法.常用的简单随机抽样方法有抽签法和随机数法.简单随机抽样和系统抽样过程中,每个个体被抽取的可能性是相等的.11.﹣【考点】同角三角函数基本关系的运用.【专题】转化思想;综合法;三角函数的求值.【分析】由条件利用同角三角函数的基本关系求得sinα的值.【解答】解:∵cosα=,tanα<0,则sinα<0,且sinα=﹣=﹣,故答案为:﹣.【点评】本题主要考查同角三角函数的基本关系,属于基础题.12.①②【考点】正弦函数的图象.【专题】三角函数的图像与性质.【分析】画出函数的图象,①根据函数的单调性即可求出单调增区间;②根据函数的对称中心即可求出函数f(x)的对称中心;③根据函数图象的平移即可得到结论;④根据函数单调性和定义域即可求出值域,进而得到正确结论的个数【解答】解:∵f(x)=,画出函数的图象如图所示∴函数f(x)的增区间为{x|﹣+2kπ≤2x+≤+2kπ,k∈z}即{x|﹣π+kπ≤x≤+kπ,k∈z},∴区间[﹣,]是函数f(x)一个增函数:故①正确,∴函数f(x)图象的对称中心为2x+=kπ,即x=kπ﹣,当k=1时,x=,∴点(,0)是函数f(x)图象的一个对称中心,故②正确,对于③函数f(x)的图象可以由函数y=sin2x的图象向左平移得到,故③错误;对于④x∈[0,],则函数f(x)的值域为[﹣1,],故④错误.故答案为:①②【点评】本题考查了正弦函数的单调性及对称性,同时要求学生掌握三角函数的有关性质(单调性,周期性,奇偶性,对称性等).13.﹣1【考点】平面向量数量积的运算.【专题】计算题;转化思想;三角函数的求值;平面向量及应用.【分析】||=||=||=1,且⊥,不妨设=(1,0),=(0,1),=(cosθ,sinθ)(θ∈[0,2π)),代入化简利用三角函数的单调性最值即可得出.【解答】解:∵||=||=||=1,且⊥,不妨设=(1,0),=(0,1),=(cosθ,sinθ)(θ∈[0,2π))则(+﹣)•=(1﹣cosθ)•cosθ+(1﹣sinθ)•sinθ=sinθ+cosθ﹣1=﹣1﹣1,∴(+﹣)•的最大值是﹣1.故答案为:﹣1.【点评】本题考查了三角函数的单调性最值、向量的坐标运算数量积运算性质,考查了推理能力与计算能力,属于中档题.14.﹣【考点】同角三角函数基本关系的运用.【专题】计算题;三角函数的求值.【分析】由已知及同角三角函数基本关系的运用可求cosα,将所求化简可得,代入即可求值.【解答】解:∵sinα=﹣,α为第三象限角,∴cosα=﹣=﹣∴====﹣.故答案为:﹣.【点评】本题主要考查了同角三角函数基本关系的运用,二倍角公式的应用,属于基本知识的考查.15.【考点】频率分布直方图;众数、中位数、平均数.【专题】计算题;整体思想;定义法;概率与统计.【分析】(Ⅰ)频率分布直方图中,小矩形的高等于每一组的,它们与频数成正比,小矩形的面积等于这一组的频率,则组距等于频率除以高,建立关系即可解得.(Ⅱ)画出即可,(Ⅲ)设中位数为x,则154<x<158,利用定义即可求出.【解答】解:(Ⅰ)由题意M==50,落在区间.【考点】根的存在性及根的个数判断.【专题】数形结合;转化法;函数的性质及应用.【分析】(Ⅰ)若方程f(x)=kx有三个解,利用函数与方程之间的关系转化为两个函数的交点个数问题,利用数形结合即可试求实数k的取值范围;(Ⅱ)作出函数f(x)的图象,利用数形结合以及函数定义域和值域之间的关系进行求解即可.【解答】解:(Ⅰ)若方程f(x)=kx有三个解,当x=0时,方程x2﹣2|x|=kx,成立,即当x=0是方程的一个根,当x≠0时,等价为方程x2﹣2|x|=kx有两个不同的根,即k=x﹣,设g(x)=x﹣,则g(x)=,作出函数g(x)的图象如图:则当﹣2<k<2时,k=x﹣有两个不同的交点,即此时k=x﹣有两个非零的根,f(x)=kx有三个解,综上﹣2<k<2.(Ⅱ)作出函数f(x)的图象如图:则函数f(x)的值域为.则m≥﹣1,若m=﹣1,则f(﹣1)=﹣1,由f(x)=﹣1,得x=﹣1或x=1,即当m=﹣1,n=0时,即定义域为,此时函数的值域为,满足条件.【点评】本题主要考查根的个数的判断,利用函数与方程之间的关系进行转化,利用数形结合是解决本题的关键.16.【考点】三角函数中的恒等变换应用;正弦函数的图象;三角函数的最值.【专题】数形结合;转化思想;三角函数的求值;三角函数的图像与性质.【分析】(1)由函数f (x )=2cosx (sinx+cosx ),x ∈R ,=﹣=﹣,=﹣=﹣.代入计算即可得出.(2)利用倍角公式、和差公式即可化为:f (x )=.(3)当时,可得,利用正弦函数的单调性最值即可得出.【解答】解:(1)∵函数f (x )=2cosx (sinx+cosx ),x ∈R , =﹣=﹣,=﹣=﹣.∴===2.(2)f (x )=2cosx (sinx+cosx )=2sinxcosx+2cos 2x=sin2x+cos2x+1=,由≤≤2k π+,(k ∈Z ),解得≤x≤k π+,∴函数f (x )的单调递增区间为(k ∈Z ).(3)当时,,∴当,即时,函数f (x )取得最大值,当,即时,函数f (x )取得最小值0.【点评】本题考查了三角函数的图象与性质、倍角公式、和差公式,考查了推理能力与计算能力,属于中档题.17.【考点】平面向量数量积的运算;两角和与差的余弦函数. 【专题】平面向量及应用.【分析】(I )由数量积的定义可得=cos θ﹣,下面换元后由函数的最值可得;(II)假设存在k的值满足题设,即,然后由三角函数的值域解关于k的不等式组可得k的范围.【解答】解:(I)由已知得:∴==2cosθ∴==cosθ﹣令∴cosθ﹣=t﹣,(t﹣)′=1+>0∴t﹣为增函数,其最大值为,最小值为﹣∴的最大值为,最小值为﹣(II)假设存在k的值满足题设,即∵,∴cos2θ=∵,∴≤cos2θ≤1∴﹣∴2﹣<k≤2+或k=﹣1故存在k的值使【点评】本题为向量的综合应用,涉及向量的模长和导数法求最值,属中档题.。
高中暑假作业:高一数学暑假作业参考答案

高中暑假作业:高一数学暑假作业参考答案高中暑假作业:高一数学暑假作业参考答案高中暑假作业:高一数学暑假作业参考答案【】高中暑假作业:高一数学暑假作业参考答案是查字典数学网为您整理的最新学习资料,请您详细阅读!一、选择题(本大题共12小题,每小题4分,共48分)题号 1 2 3 4 5 6 7 8 9 10 11 12答案 B A A B D B A D C A B B二、填空题(本大题共4小题,每小题4分,共16分)13. ; 14. ; 15. ; 16.三.解答题(本大题共4大题,共36分,解答应写出文字说明、证明过程或演算步骤)17. (本小题8分)已知 , 且 , ,求 .解∵ ,cos =- ,sin = . (2)分又∵0 , , ,又sin( + )= ,,cos( + )=-=- =- , ...............................4分sin =sin[( + )- ]=sin( + )cos -cos( + )sin= - = . ...............................8分又∵ = - =ma+nb- a=(m- )a+nb.= - =b- a=- a+b.又∵C、M、B三点共线,与共线.存在实数t1,使得 =t1 ,(m- )a+nb=t1(- a+b)消去t1得,4m+n=1 ②...............................6分由①②得m= ,n= ,= a+ b. ...............................8分注:本题解法较多,只要正确合理均可酌情给分.查字典数学网的编辑为大家带来的高中暑假作业:高一数学暑假作业参考答案,希望能为大家提供帮助。
高一数学暑假作业及答案

2021年高一数学暑假作业及答案2021年高一数学暑假作业及答案【】复习的重点一是要掌握所有的知识点,二就是要大量的做题,查字典数学网的编辑就为各位考生带来了2021年高一数学暑假作业及答案一、选择题1.T1=,T2=,T3=,那么以下关系式正确的选项是()A.T1,即T2bdB.dcaC. dbaD.bda【解析】由幂函数的图象及性质可知a0,b1,0ca.应选D. 【答案】 D3.设{-1,1,,3},那么使函数y=x的定义域为R且为奇函数的所有的值为()A.1,3B.-1,1C.-1,3D.-1,1,3【解析】 y=x-1=的定义域不是R;y=x=的定义域不是R;y=x 与y=x3的定义域都是R,且它们都是奇函数.应选A.【答案】 A4.幂函数y=f(x)的图象经过点,那么f(4)的值为()A.16B.2C. D.【解析】设f (x)=x,那么2==2-,所以=-,f(x)=x-,f(4)=4-=.应选C.【答案】 C二、填空题5.n{-2,-1,0,1,2,3},假设nn,那么n=________. 【解析】∵--,且nn,y=xn在(-,0)上为减函数.又n{-2,-1,0,1,2,3},n=-1或n=2.【答案】 -1或26.设f(x)=(m-1)xm2-2,假如f(x)是正比例函数,那么m=________,假如f(x)是反比例函数,那么m=________,假如f(x)是幂函数,那么m=________.【解析】 f(x)=(m-1)xm2-2,假设f(x)是正比例函数,那么m=假设f(x)是反比例函数,那么即m=-1;假设f(x)是幂函数,那么m-1=1,m=2.【答案】-1 2三、解答题7.f(x)=,(1)判断f(x)在(0,+)上的单调性并证明;(2)当x[1,+)时,求f(x)的最大值.【解析】函数f(x)在(0,+)上是减函数.证明如下:任取x1、x2(0,+),且x10,x2-x10,x12x220.f(x1)-f(x2)0,即f(x1)f(x2).函数f(x)在(0,+)上是减函数.(2)由(1)知,f(x)的单调减区间为(0,+),函数f(x)在[1,+)上是减函数,函数f(x)在[1,+)上的最大值为f(1)=2.8.幂函数y=xp-3(pN*)的图象关于y轴对称,且在(0,+)上是减函数,求满足(a-1)(3+2a)的a的取值范围. 【解析】∵函数y=xp-3在(0,+)上是减函数,p-30,即p3,又∵pN*,p=1,或p=2.∵函数y=xp-3的图象关于y轴对称,p-3是偶数,取p=1,即y=x-2,(a-1)(3+2a)∵函数y=x在(-,+)上是增函数,由(a-1)(3+2a),得a-13+2a,即a-4.所求a的取值范围是(-4,+).以上就是查字典数学网高中频道为您整理的2021年高一数学暑假作业及答案,欢送大家进入高考频道理解2021年最新的信息,帮助同学们学业有成!。
浙江省黄岩中学高一数学暑假作业(十七)

高一数学暑假作业(十七) 一、选择题: 1、点P 在直线MN 上,且12MP PN =u u u r u u u r ,则点P 分MN u u u u r 所成的比为( ) (A )21 (B )31 (C )±21 (D )2或21 2、已知P 1(-1,2),P 2(2,-3),点P(x ,1)分12P P u u u u r 所成的比为λ,则x 的值为( )(A )4 (B )41 (C )-52 (D )不能确定 3、在△ABC 中,已知A (2,3),B (8,-4),G (2,-1)是中线AD 上一点,且2AG GD =u u u r u u u r 则点C坐标为( )(A )(-4,2) (B )(―4,―2) (C )(4,-2) (D )(4,2) 4、下列命题:①|a ϖ·b v |=|a ϖ|·|b ϖ| ②|a ϖ2|=aϖ2 ③(a v ·b v )·c v =a ϖ·(b ϖ·c ϖ) ④(a ϖλ)·(b ϖλ)=λ(a v ·b v )其中正确的命题个数为( )(A )1 (B )2 (C )3 (D )4 5、非零向量a ϖ,b ϖ,满足|a ϖ|=|b ϖ|,且a ϖ与b ϖ不平行,则向量a ϖ+b ϖ与a ϖ-b ϖ的位置关系是( )(A )平行 (B )垂直 (C )共线且同向 (D )共线且反向6、下列命题中正确的是( ) (A )若a ϖ·b v =0,则a ϖ=0ϖ或b ϖ=0ϖ (B )若a ϖ·b v =0,则a ϖ//b ϖ (C )若a ϖ⊥b ϖ,则a ϖ·b v =(a ϖ·b v )2 (D )若a ϖ,b ϖ共线,则a ϖ·b v =|a ϖ|·|b ϖ|7、已知a ϖ=(3,-4),b ϖ=(-2,3),则a ϖ·(a ϖ+b ϖ)=( )(A )-13 (B )7 (C )6 (D )268、已知a ϖ=(1,3),b ϖ=(-3,3),则a ϖ与b ϖ的夹角为( )(A )6π (B )3π (C )2π (D )32π 9、已知P(cos α,sin α),Q(cos β,sin β),则|PQ|的最大值为( )(A )2 (B )2 (C )4 (D )2210、)32()(j j j j i i ϖϖϖϖϖϖ-⋅++⋅的值为( )(A )0 (B )1 (C )2 (D )-211、已知a ϖ=(2,0),b ϖ=(-1,y),且a ϖ与b ϖ的夹角为32π,则y 值为( ) (A )3 (B )33 (C )±3 (D )±33 12、“a ϖ与b ϖ为共线向量”是“a ϖ与b ϖ方向相同”的( )(A )充分非必要条件 (B )必要非充分条件(C )充要条件 (D )既非充分又非必要条件13、向量a ϖ=(k ,2),b ϖ=(2,2),且a ϖ⊥b ϖ,则k 的值为( )(A )2 (B )2 (C )-2 (D )-214、一个平行四边形的三个顶点的坐标分别是(5,7),(-3,5),(3,4),则第四个顶点的坐标不可能是( )(A )(-1,8) (B )(-5,2) (C )(11,6) (D )(5,2)二、填空题:15、设A(x ,0),B(0,y),若A ,B 关于点P(-1,2)对称,则x+y= 。
【高一】高一数学(文)暑假作业及答案

【高一】高一数学(文)暑假作业及答案【导语】学习是一个坚持不懈的过程,走走停停便难有成就。
比如烧开水,在烧到80度是停下来,等水冷了又烧,没烧开又停,如此周而复始,又费精力又费电,很难喝到水。
学习也是一样,学任何一门功课,都不能只有三分钟热度,而要一鼓作气,天天坚持,久而久之,不论是状元还是伊人,都会向你招手。
逍遥右脑为正在努力学习的你整理了《高一数学(文)暑假作业及答案》,希望对你有帮助!【一】一、选择题(在每小题给出的四个选项中只有一项是符合题目要求的)1.下列函数中,满足“对任意,时,都有”的是()A.B.C.D.2.如果函数在区间上是减函数,在区间上是增函数,那么a的取值范围是()A.B.C.D.3.奇函数f(x)的定义域为R.若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=() A.-2B.-1C.0D.14.下列函数中,在其定义域内既是奇函数又是减函数的是()A.B.C.D.5.如果奇函数在时,,那么使成立的的取值范围是()A.B.C.D.6.设偶函数在上为减函数,则的解集为()A.B.C.D.7.定义在R上的偶函数满足,设的大小关系是()A.c8.定义在R上的奇函数满足,且在区间上是增函数,则()A.B.C.D.二、填空题9.函数在上为减函数,则的取值范围是10.已知与都是定义在R上的奇函数,=+2,且,则=.11.设f(x)是定义在R上的周期为2的函数,当x∈[-1,1)时,,则=________.12.下列四个结论:①偶函数的图象一定与直角坐标系的纵轴相交;②奇函数的图象一定通过直角坐标系的原点;③既是奇函数,又是偶函数的函数一定是=0();④偶函数f(x)在上单调递减,则f(x)在上单调递增.其中正确的命题的序号是三、解答题(应写出文字说明、证明过程或演算步骤)13.设函数=是奇函数,其中,,(1)求的值;(2)判断并证明在上的单调性.14.已知函数对任意的x,y总有,且当x时,,(1)求证在R上是奇函数;(2)求证在R上是减函数;(3)求在[-3,3]上的最值. 15.函数是定义在R上的奇函数,当时,.(1)求时,的解析式;(2)是否存在这样的正数a,b,当时,的值域为?若存在,求出所有的a,b的值;若不存在,请说明理由。
高一数学暑假作业(附解析)

2019 高一数学暑假作业精选(附解析)2019 高一数学暑假作业精选下面查字典数学网为大家整理了高一数学暑假作业精选,希望大家在空余时间进行复习练习和学习,供参考。
大家暑期快乐哦。
一、选择题1. 已知函数f(x)=lg ,若f(a)= ,则f(-a) 等于()A. B.-C.2D.-2[ 答案] B[ 解析] f(a)=lg= ,f(-a)=lg()-1=-lg=-.2. 函数y=ln(1-x) 的图象大致为()[ 答案] C[解析]要使函数y=ln(1-x)有意义,应满足1-x0 , x1,排除A、B;又当x0 时,-x0,1-x1 ,y=ln(1-x)0 ,排除D,故选C.3. (2019 北京理,2) 下列函数中,在区间(0 ,+)上为增函数的是()A.y=B.y=(x-1)2C.y=2-xD.y=log0.5(x+1)[ 答案] A[ 解析] y= 在[-1 ,+) 上是增函数,y=在(0 , +)上为增函数.4. 设函数f(x)= ,若f(3)=2 ,f(-2)=0 ,则b=()A.0B.-1C.1D.2[ 答案] A[ 解析] f(3)=loga4=2 ,a=2. f(-2)=4-2a+b=4-4+b=0 ,b=0.5. (2019〜2019学年度山东潍坊二中高一月考)已知函数y=log2(1-x) 的值域为(- ,0) ,则其定义域是()A.(- ,1)B.(0 ,)C.(0,1)D.(1 ,+)[ 答案] C[解析] 函数y=log2(1-x) 的值域为(- ,0),log2(1-x)0 ,01 ,00,x2-2x0 ,即0log54log530 ,1log54log53(log53)20 ,而log451 ,cb.3. 已知函数f(x)= ,若f(x0)3 ,则x0 的取值范围是()A.x08B.x00 或x08C.03,xO+11,即xOO,无解;当x02 时,log2x03 ,x023 ,即x08,x08.4. 函数f(x)=ax+loga(2x+1)(a0 且a1) 在[0,2] 上的最大值与最小值之和为a2,则a的值为()A. B.5 C. D.4[ 答案] A[ 解析] 当a1 时,ax 随x 的增大而增大,loga(2x+1) 随x 的增大而增大,函数f(x) 在[0,2] 上为增函数,f(x)max=a2+loga5 ,f(x)min=1 ,a2+loga5+1=a2 ,loga5+1=0 ,loga5=-1 ,a=( 不合题意舍去).当0f(x)max=1 ,f(x)min=a2+loga5 ,1+a2+loga5=a2 ,loga5=-1 ,a=.二、填空题5. (2019〜2019学年度江西南昌市联考)定义在R上的偶函数f(x) 在[0 ,+) 上单调递减,且f()=0 ,则满足f(x)0 的集合为.[ 答案] (0 ,)(2 ,+) [ 解析] 本题主要考查函数的奇偶性、单调性的应用和对数不等式的解法.因为定义在R上的偶函数f(x)在[0 , +)上单调递减,所以在(- ,0] 上单调递增. 又f()=0 ,所以f(-)=0 ,由f(x)0 可得x- ,或x,解得x(0 ,)(2 ,+).6. (2019 福建文,15)函数f(x)=的零点个数是_________ .[ 答案] 2[解析]当x2,令x2-2=0 ,得x=-;当x0 时,令2x-6+lnx=0 ,即lnx=6-2x ,在同一坐标系中,画出函数y=6-2x 与y=lnx 的图象如图所示.由图象可知,当x0 时,函数y=6-2x 与y=lnx 的图象只有一个交点,即函数f(x) 有一个零点.综上可知,函数f(x) 有 2 个零点.三、解答题7. 已知函数f(x)=lg(4-x2).(1) 求函数f(x) 的定义域;(2) 判断函数f(x) 的奇偶性,并证明.[ 解析] (1) 要使函数f(x) 有意义,应满足4-x20 ,x24,-20 ,且a1) 的图象关于原点对称.(1) 求m的值;(2) 判断函数f(x) 在(1 ,+) 上的单调性.[ 解析] (1)f(x)=loga(a0 ,且a1) 的图象关于原点对称,f(x) 为奇函数.f(-x)=-f(x).loga=-loga=loga ,1-m2x2=1-x2 ,m2=1,m=1 或m=-1.当m=1 时,不满足题意,舍去,故m=-1.(2)f(x)=loga=loga.设x1,x2(1 ,+) ,且x10,x1x2-x1+x2-1x1x2-x2+x1-1 ,又x1,x2(1 ,+) ,(x1+1)(x2-1)=x1x2-x1+x2-10 ,(x2+1)(x1-1)=x1x2-x2+x1-10 ,1.当01 时,loga0 ,即f(x1)f(x2) ,故函数f(x) 在(1 ,+)上是减函数.综上可知,当a1 时,f(x) 在(1 ,+)上为减函数;当0f(1)=-2 ,即x1 时,f(x) 的值域是(-2 ,+).当x1 时,f(x)=logx 是减函数,所以f(x)f(1)=0 ,即x1, f(x) 的值域是(- ,0].于是函数f(x) 的值域是(- ,0](-2 ,+)=R.(2) 若函数f(x) 是(- ,+) 上的减函数,则下列三个条件同时成立:当x1 时,f(x)=x2-(4a+1)x-8a+4 是减函数,于是1,则a当x1 时,f(x)=logax 是减函数,则0 以上就是高一数学暑假作业精选,希望能帮助到大家。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学暑假作业(九)
一、选择题:
1、下列各式中,正确的是( )
(A )|b ||a ||b a | ⋅=⋅ (B )222)(b a b a
⋅=⋅
(C )若⊥a (c b -),则b a ⋅=c a ⋅ (D )b a ⋅=c a ⋅,则b =c
2、已知|a |=|b |=1,a 与b 的夹角为90°,且c =2a +3b ,d =k a -4b ,c ⊥d ,则
k 的值为( )
(A )-6 (B )6 (C )3 (D )-3
3、已知a =(1,2),b =(x ,1),且a +2b 与2a -b 平行,则x=( ) (A )1 (B )2 (C )31
(D )2
1 4、已知向量10e ≠,λ∈R ,a =1e +λ2e ,b =21e ,若向量a 与b 共线,则下列关系
一定成立的是( )
(A )λ=0 (B )20e = (C )1e //2e (D )1e //2e 或λ=0
5、已知(4,3),(5,6)a b =-=,则34a a b -⋅的值是( )
(A )63 (B )83 (C )23 (D )57
6、已知AB =3(1e +2e ),CB =2e -1e ,CD =21e +2e ,则下列关系一定成立的是( )
(A )A 、B 、C 三点共线 (B )A 、B 、D 三点共线
(C )A 、C 、D 三点共线 (D )B 、C 、D 三点共线
7、已知平面内三个点A (0,3),B (3,3),C (x ,-1),且AB BC ⊥,则x 的值
为( )
(A )5 (B )3 (C )-1 (D )-5
8、已知P 1(2,-1),P 2(0,5),且点P 在线段P 1P 2的延长线上,使|P 1P|=2|PP 2|,则P
点的坐标是( )
(A )(-2,11) (B )(34,1) (C )(32,3) (D )(2,-7) 9、将函数y=l og 2(2x)的图象F 按a =(2,-1)平移到F ',则F '的解析式为( )
(A )y=l og 2[2(x -2)]-1 (B )y=l og 2[2(x+2)]-1
(C )y=l og 2[2(x+2)]+1 (C )y=l og 2[2(x -2)]+1
二、填空题:
10、已知(1,2),(1,4)a b =-=-,则a b -在a b +上的投影等于_____________。
11、若|a |=3,|b |=4,且(a +b )·(a +3b )=33,则a 与b 的夹角为 。
12、一树干被台风吹断折成60°角,树干底部与树尖着地处相距20米,树干原来的高度
是 。
13、若将函数y=2x 的图象按a 平移后,得到函数y=2x+6的图象,则符合条件的a 是 。
14、给出以下命题
①点C 在线段AB 上,且|AC|=
32|AB|,则2AC BC = ②在△ABC 中,有0AB BC CA ++= ③数量积不满足结合律,即)()(c b a c b a
⋅⋅≠⋅⋅
④若0=⋅b a ,则a 、b 中至少有一个为0 ⑤若|a |>|b |,则a >b
⑥一个人向西行走100m ,然后改变方向向南行走100m ,则此人两次位移的和为向西南行走1002m 。
其中正确的命题序号为 (要求:把你认为正确的命题序号都填上)。
三、解答题
15、平面内有三个已知点A (1,-2),B (7,0),C (-5,6),求,,AB AC AB AC +,AB AC -。
16、已知两点A (-2,4),B (6,0)在直线AB 上求点C ,使12AC AB =。
17、用向量法证明梯形两腰中点连线平行于上下两底且等于它们长度和的一半。
18、已知O 为原点,A 、B 、C 为平面内三点,求证:A 、B 、C 三点在一条直线上的充要条件是
OC OA OB αβ=+,且α,β∈R ,α+β=1。
19、如图,在△ABC 中,D 为边BC 上的点,且BD k DC =,E 为DA 上一点,且DE lEA =,延长BE 交AC 于F ,求F 分有向线段CA 的比λ。
20、平面内有向量OA =(1,7),OB =(5,1),OP =(2,1),点X 为直线OP 上的一个动点。
(1)当XA ·XB 取最小值时,求OX 的坐标;
(2)当点X 满足(1)的条件和结论时,求cos ∠AXB 的值。
A B C
D E F
高一暑假作业答案(九)
1、C
2、B
3、D
4、D
5、B
6、C
7、D
8、B
9、A
10、-6 11、120° 12、203米 13、(-3,0) 14、③⑥
15、AB =(6,2) AC =(-6,8) AB AC + =(0,10) AB AC -=(12,-6)
16、C 1(2,2),C 2(-6,6) 17、略 18、略 19、k k )1(+=
λ 20、(1)OX =(4,2)(2)cos ∠AXB=17174-。
