主成分分析和聚类分析
数学建模各种分析方法

现代统计学1.因子分析(Factor Analysis)因子分析的基本目的就是用少数几个因子去描述许多指标或因素之间的联系,即将相关比较密切的几个变量归在同一类中,每一类变量就成为一个因子(之所以称其为因子,是因为它是不可观测的,即不是具体的变量),以较少的几个因子反映原资料的大部分信息.运用这种研究技术,我们可以方便地找出影响消费者购买、消费以及满意度的主要因素是哪些,以及它们的影响力(权重)运用这种研究技术,我们还可以为市场细分做前期分析。
2.主成分分析主成分分析主要是作为一种探索性的技术,在分析者进行多元数据分析之前,用主成分分析来分析数据,让自己对数据有一个大致的了解是非常重要的.主成分分析一般很少单独使用:a,了解数据。
(screening the data),b,和cluster analysis一起使用,c,和判别分析一起使用,比如当变量很多,个案数不多,直接使用判别分析可能无解,这时候可以使用主成份发对变量简化。
(reduce dimensionality)d,在多元回归中,主成分分析可以帮助判断是否存在共线性(条件指数),还可以用来处理共线性。
主成分分析和因子分析的区别1、因子分析中是把变量表示成各因子的线性组合,而主成分分析中则是把主成分表示成个变量的线性组合。
2、主成分分析的重点在于解释个变量的总方差,而因子分析则把重点放在解释各变量之间的协方差。
3、主成分分析中不需要有假设(assumptions),因子分析则需要一些假设。
因子分析的假设包括:各个共同因子之间不相关,特殊因子(specific fact or)之间也不相关,共同因子和特殊因子之间也不相关.4、主成分分析中,当给定的协方差矩阵或者相关矩阵的特征值是唯一的时候,的主成分一般是独特的;而因子分析中因子不是独特的,可以旋转得到不同的因子。
5、在因子分析中,因子个数需要分析者指定(spss根据一定的条件自动设定,只要是特征值大于1的因子进入分析),而指定的因子数量不同而结果不同。
聚类分析与主成分分析

二、聚类分析的典型(diǎnxíng)应 用
• 作为统计(tǒngjì)学的一个分支,聚类分析已有 多年的研究历史,这些研究主要集中在基于距 离的聚类分析方面。
• 许多统计(tǒngjì)软件包,诸如:SAS、SPSS 和S-PLUS等都包含它许多聚类分析工具。
第八页,共90页。
• 图论法。从几何观点来考虑。将n个样品看成m维空间的n个 点,点与点间用直线连接,从而构成m维空间的点的连接图, 再应用图论的观点将样本点在m维空间作最小支撑(zhī chēng)数,最终达到分类目的。
第十二页,共90页。
六、tree过程(guòchéng)
• 画出用于描述整个聚类过程的树状图
• 两种:
• 如何解释主成分所包含的经济意义。
第四十六页,共90页。
数学模型和几何(jǐ hé)解释
• 为了方便,我们在二维空间中讨论主成分的几何意义。 设有n个样品,每个样品有两个观测变量xl和x2,在 由变量xl和x2 所确定的二维平面中,n个样本点所散 布的情况如椭圆状。由图可以看出(kàn chū)这n个样 本点无论是沿着xl 轴方向或x2轴方向都具有较大的离 散性,其离散的程度可以分别用观测变量xl 的方差和 x2 的方差定量地表示。显然,如果只考虑xl和x2 中 的任何一个,那么包含在原始数据中的经济信息将会 有较大的损失。
第十一页,共90页。
五、聚类分析方法(fāngfǎ)
• 系统聚类法。先将n个元素看成n类,然后将性质最接近(或 相似程度最大)的两类合并为一个新类,得到n-1类。再从 中找出最接近的两类加以合并,变成n-2类。如此下去,最 后所有的元素全聚在一类之中。
• 调优法。先将样品做一个初始的分类,然后按照某种最优的 原则逐步调整,一直调整到分类比较合理为止。
主成分分析和聚类分析报告

北京建筑工程学院理学院信息与计算科学专业 实验报告课程名称〈数据分析》实验名称〈主成分分析和聚类分析》 实验地点:基础楼C-423日期2016.5.5 姓名张丽芝班级 信131 学号 201307010108指导教师 王恒友成绩实验目的】(1) 熟悉利用主成分分析进行数据分析,能够使用SPSS 软件完成数据的主成分分析; (2) 熟悉利用聚类分析进行数据分析,能够运用主成分分析的结果,做进一步分析,如聚类分析、回归分析等,能够使用SPSS 软件完成该任务。
实验要求】根据各个题目的具体要求,分别运用SPSS 软件完成实验任务。
实验内容】1、表4.9 (数据见exercise4_5.txt )给出了 1991年我国30个省市、城镇居民的月平均消 费数据,所考察的八个指标如下:(单位均为元/人)(2)从R 出发做主成分分析,求出各主成分的贡献率及前两个主成分的累积贡献率;2、( 1)对题1中的数据,按照原有的八个指标,对30个省份进行聚类,给出分为3 类的聚类结果X1:人均粮食支出; X3:人均烟酒茶支出; X5:人均衣着商品支出; X7:人均燃料支出;(1)求样本相关系数矩阵RX2:人均副食支出; X4:人均其他副食支出; X6:人均日用品支出; X8:人均非商品支出。
(2)利用题1得到的前2个主成分指标,分别按最短距离法(最近邻居距离)、最长距离法(最远邻居距离)、类平均距离法(组间平均距离)、重心距离法;其中距离均采用欧式平方距离,对样本进行谱系聚类分析,并画出谱系聚类图;给出分为3类的聚类结果。
并与(1)的结果进行比较实验步骤】(此部分主要包括实验过程、方法、结果、对结果的分析、结论等)2)表:方差贡献率和累计贡献率由上图可知,只有前两个成分的特征值大于1,所以只选择前两个主成分。
第一个主成分的 方差贡献率是38.704%,第二个主成分的方差贡献率是29.590%,前两个主成分的方差占所 有主成分方差的64.294% o 前两个主成分的累计贡献率为68.294%,选择前两个主成分即可 代表绝大多数原来的变量。
生物统计学在生态学中的应用

生物统计学在生态学中的应用生物统计学在生态学中有广泛的应用。
下面是一些常见的生态学领域中使用生物统计学的例子:一、群落分析:生物统计方法可用于研究不同种群或物种之间的相互作用以及它们对环境变化的响应。
例如,通过多元统计技术如聚类分析、主成分分析和冗余分析,可以将样地数据转化为具有解释性和预测能力的模型。
群落分析是生态学中常用的研究方法之一。
通过生物统计技术,我们可以对不同种群或物种在特定环境条件下的相互关系进行定量化和解释。
1.聚类分析:聚类分析可用于将相似性较高的样地或个体归为一组。
这种方法基于各个样地(个体)之间的相似性度量,以便识别出具有共同特征和行为模式的群体。
2.主成分分析:主成分分析(PCA)是一种降维技术,它可以将多变量数据转换为更少数量且无相关性的新变量。
这些新变量称为主成分,它们能够捕捉原始数据中最大方差所包含的信息。
通过PCA,我们可以发现隐藏在复杂数据背后存在着哪些关键因素。
3.冗余分析:冗余分析(RDA)结合了多元回归和主坐标轴排序等技术,在考虑环境因子时评估物种结构与环境因素之间是否存在显著关联。
RDA能够帮助我们理解物种组成受到哪些环境因子影响,并揭示潜在驱动机制。
这些生物统计方法可以帮助我们从海量的群落数据中提取和解释有用的信息。
它们为我们揭示了不同种群或物种之间的相互作用、物种对环境变化的响应以及生态系统结构与功能之间的关系,进而促进了保护生态系统和可持续发展等方面的研究。
二、物种多样性评估:利用各种指数(如Shannon-Wiener指数、Simpson指数)和曲线(如稀疏度曲线),可以量化和比较不同区域或样地内的物种丰富度、均匀度和多样性水平。
在物种多样性评估中,各种指数和曲线被广泛应用来量化和比较不同区域或样地内的物种丰富度、均匀度和多样性水平。
以下是一些常见的指数和曲线:1.Shannon-Wiener指数:Shannon-Wiener指数是一种常用于描述生态系统多样性的指标。
主成分分析和聚类分析的比较

主成分分析和聚类分析的比较摘要:主成分分析和聚类分析方多元统计中两种重要的分析方法,但却容易在使用中混淆。
本文从基本思想,应用的优缺点、应用实例中讨论两者的异同,并简述两种方法在实际问题中的应用。
关键词:主成分分析;聚类分析一、引言主成分分析是利用降维的思想,在缺失很少信息的前提下,把多个指标转化为几个综合指标的多元统计方法。
通常把转化生成的综合指标称为主成分,其中每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,使得主成分比原始变量具有某些更优越的性能。
聚类分析是依据实验数据本身所具有的定性或定量的特征来对大量的数据进行分组归类以了解数据集的内在结构,并且对每一个数据集进行描述的过程。
其主要依据是聚到同一个数据集的样本应该性质相似,而属于不同组的样本应该足够不相似。
两种方法既有区别又有联系,本文将两者的异同进行比较,并举例说明两者在实际应用中的联系,以便更好地理解这两种统计方法而为实际所应用。
二、基本思想的异同相同点:主成分分析方法是用少数的几个变量来综合反映原始变量的主要信息,变量虽然较原始变量少,但所包含的信息量却占原始信息的85%以上,因此其可信度很高。
通过主成分分析,可以将事物之间错综复杂的关系中找出一些主要成分,从而能有效利用大量统计数据进行定量分析,解释变量之间的内在关系。
因此主成分变量比原始变量少了很多,从而起到了降维的作用。
聚类分析的基本思想是采用多变量的统计值,定量的确定相互之间的亲疏关系,考虑对象多因素的联系和主导作用。
按它们亲疏差异程度,归类不同的分类中的一元。
使分类更具有客观实际并能反映事物的内在必然联系。
聚类分析是通过一种大的对称矩阵来探索相关关系的一种数学分析方法。
对变量分类后,我们对数据的处理难度也降低,所以从某种意义上说,聚类分析也起到了降维的作用。
不同点:主成分分析是研究如何通过原来变量的少数几个变量组合来解释原来变量绝大多数信息的一种多元统计方法。
主成分和聚类分析
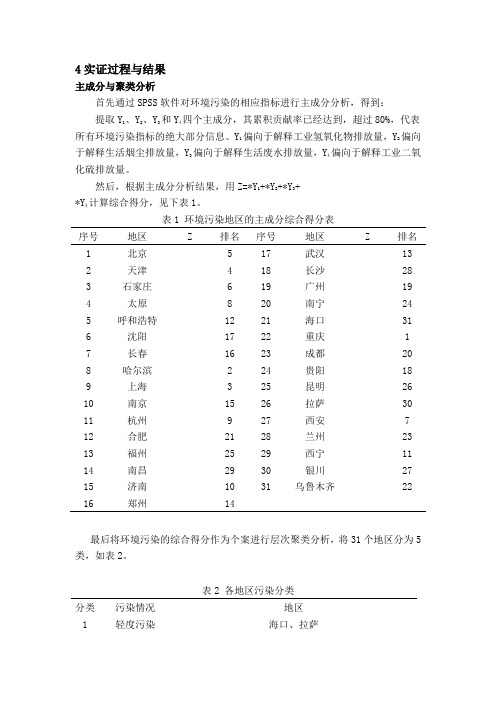
4实证过程与结果主成分与聚类分析首先通过SPSS软件对环境污染的相应指标进行主成分分析,得到:提取Y1、Y2、Y3和Y4四个主成分,其累积贡献率已经达到,超过80%,代表所有环境污染指标的绝大部分信息。
Y1偏向于解释工业氢氧化物排放量,Y2偏向于解释生活烟尘排放量,Y3偏向于解释生活废水排放量,Y4偏向于解释工业二氧化硫排放量。
然后,根据主成分分析结果,用Z=*Y1+*Y2+*Y3+*Y4计算综合得分,见下表1。
表1 环境污染地区的主成分综合得分表序号地区Z排名序号地区Z排名1北京517武汉13 2天津418长沙28 3石家庄619广州19 4太原820南宁24 5呼和浩特1221海口31 6沈阳1722重庆1 7长春1623成都20 8哈尔滨224贵阳18 9上海325昆明26 10南京1526拉萨30 11杭州927西安7 12合肥2128兰州23 13福州2529西宁11 14南昌2930银川27 15济南1031乌鲁木齐22 16郑州14最后将环境污染的综合得分作为个案进行层次聚类分析,将31个地区分为5类,如表2。
表2 各地区污染分类分类污染情况地区1轻度污染海口、拉萨2比较轻度污染合肥、乌鲁木齐、福州、南宁、兰州、,昆明、成都、银川、南昌、长沙、沈阳、长春、南京、广州、贵阳、郑州、武汉、济南、西宁、呼和浩特3污染情况一般太原、杭州、石家庄、西安4污染比较严重北京、天津5污染十分严重上海、哈尔滨、重庆主成分分析和聚类分析在SPSS中的操作过程打开SPSS,“文件-打开-数据”,选中excel,如下图结果。
首先将变量标准化,“分析-描述统计-描述”,将变量全部选入对话框,点上“将标准化得分另存为变量(Z)”,结果如下。
在做主成分分析,“分析-降维-因子分析”,将为标准化的变量选入对话框。
选择右侧“描述”,在弹出来对话框中点上“系数、显著性水平、KMO和Bartlett 的球形度检验”,点“继续”。
主成分分析,聚类分析比较

主成分分析、聚类分析的比较与应用主成分分析、聚类分析的比较与应用摘要:主成分分析、聚类分析是两种比较有价值的多元统计方法,但同时也是在使用过程中容易误用或混淆的几种方法。
本文从基本思想、数据的标准化、应用上的优缺点等方面,详细地探讨了两者的异同,并且举例说明了两者在实际问题中的应用。
关键词:spss、主成分分析、聚类分析一、基本概念主成分分析就是设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。
综合指标即为主成分。
所得出的少数几个主成分,要尽可能多地保留原始变量的信息,且彼此不相关。
因子分析是研究如何以最少的信息丢失,将众多原始变量浓缩成少数几个因子变量,以及如何使因子变量具有较强的可解释性的一种多元统计分析方法。
聚类分析是依据实验数据本身所具有的定性或定量的特征来对大量的数据进行分组归类以了解数据集的内在结构,并且对每一个数据集进行描述的过程。
其主要依据是聚到同一个数据集中的样本应该彼此相似,而属于不同组的样本应该足够不相似。
二、基本思想的异同(一)共同点主成分分析法和因子分析法都是用少数的几个变量(因子) 来综合反映原始变量(因子) 的主要信息,变量虽然较原始变量少,但所包含的信息量却占原始信息的85 %以上,所以即使用少数的几个新变量,可信度也很高,也可以有效地解释问题。
并且新的变量彼此间互不相关,消除了多重共线性。
这两种分析法得出的新变量,并不是原始变量筛选后剩余的变量。
在主成分分析中,最终确定的新变量是原始变量的线性组合,如原始变量为x1 ,x2 ,. . . ,x3 ,经过坐标变换,将原有的p个相关变量xi 作线性变换,每个主成分都是由原有p 个变量线性组合得到。
在诸多主成分Zi中,Z1 在方差中占的比重最大,说明它综合原有变量的能力最强,越往后主成分在方差中的比重也小,综合原信息的能力越弱。
因子分析是要利用少数几个公共因子去解释较多个要观测变量中存在的复杂关系,它不是对原始变量的重新组合,而是对原始变量进行分解,分解为公共因子与特殊因子两部分。
主成分分析和聚类分析的比较

主成分分析和聚类分析的比较一、定义:1.主成分分析:PCA是一种数学方法,通过线性变换将原始数据投影到新的坐标系上,使得投影的数据在新的坐标系下具有最大的方差,从而达到降维和提取数据特征的目的。
2.聚类分析:聚类分析是一种无监督学习方法,通过对样本集合中的数据进行分类,使得同一类别的数据尽量相似,不同类别的数据尽量不相似。
二、目的:1.主成分分析:PCA的主要目的是降低数据的维度,同时保留尽可能多的数据信息。
通过确定主成分,可以选择保留最重要的几个主成分,达到降维的目的,同时避免信息损失。
2.聚类分析:聚类分析的主要目的是发现数据的内在结构和相似性,将数据分成若干个互不交叠的群组,使得同一群组的数据相似度较高,不同群组的数据相似度较低。
三、步骤:1.主成分分析:-对数据进行标准化处理。
-计算数据样本的协方差矩阵。
-对协方差矩阵进行特征值分解,得到特征值和特征向量。
-选择主成分并确定保留的主成分数目。
-根据主成分和原始数据计算得到新的数据集,即降维后的数据集。
2.聚类分析:- 选择合适的聚类算法(如K-means、层次聚类等)。
-初始化聚类中心。
-计算每个样本与聚类中心的距离。
-将样本分配到最近的聚类中心。
-更新聚类中心,重复上述步骤直到满足终止条件。
四、应用领域:1.主成分分析:-数据降维与特征提取:对于高维数据,可以通过PCA将数据降低到较低的维度,并保留主要特征信息。
-数据可视化:通过PCA将高维数据投影到二维或三维空间中,方便数据的可视化展示。
-噪声滤除:PCA可以去除数据中的噪声信息,保留主要特征。
2.聚类分析:-客户细分:在市场营销中,可以通过聚类分析将客户分为不同的群组,根据每个群组的特征制定相应的营销策略。
-图像分割:在图像处理中,可以利用聚类分析对图像进行分割,将图像中的不同物体分别提取出来。
-社交网络分析:通过对社交网络用户之间的关系进行聚类分析,可以发现群组内的用户行为模式和用户兴趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代地理学中的数学方法本次作业数据主要来源于《2013安徽统计年鉴》,由于部分数据缺失,故用《2012年安徽统计年鉴》中的数据进行了选取与处理;本次作业选取的指标有X1(人均GDP/元)、X2(第三产业增加值/千万元)、X3(第三产业占GDP的比重/%)、X4(第三产业从业人员数比重/%)X5(第二产业占GDP的比重/%)、X6(总人口/万人)、X7(农民人均纯收入/元)、X8(城镇居民可支配收入/元)、X9(市区人民人均医疗保健消费支出/元)、X10(非农业人口比重/%)、X11(地方财政收入/万元)、X12(规模以上工业总产值/千万元)、X13(农业总产值/万元)、X14(商品进出口总额/美元)、X15(社会消费品零售总额/万元)、X16(实际利用外资额/万美元)。
运用spss19.0,首先对原始数据进行标准化处理,后经过降维进行因子分析,得到表1相关系数矩阵、表2表征值及贡献率、表3主成分载荷因子矩阵、表4主成分得分。
表1 2012年安徽省各市有关指标相关系数矩阵X1X2X3X4X4X6X7X8X9X10X11X12X13X14X15X16 X1 1.000X20.276 1.000X3-0.309 0.343 1.000X40.79 0.394 0.034 1.000X40.809 0.043 -0.672 0.589 1.000X6-0.417 0.587 0.255 -0.375 -0.516 1.000X70.826 0.192 -0.102 0.733 0.659 -0.549 1.000X80.758 0.343 -0.164 0.61 0.584 -0.254 0.823 1.000X9-0.06 0.018 -0.286 0.013 0.124 -0.024 0.043 0.131 1.000X100.832 0.131 -0.504 0.725 0.916 -0.486 0.62 0.528 0.21 1.000X110.391 0.977 0.274 0.508 0.187 0.451 0.348 0.435 0.038 0.263 1.000X120.474 0.938 0.095 0.532 0.303 0.429 0.376 0.453 0.077 0.343 0.962 1.000X13-0.582 0.341 0.257 -0.51 -0.708 0.913 -0.648 -0.362 0.118 -0.659 0.184 0.17 1.000X140.643 0.901 0.153 0.612 0.346 0.296 0.523 0.635 0.013 0.421 0.93 0.926 0.044 1.000X150.145 0.977 0.338 0.274 -0.054 0.709 0.039 0.22 0.007 0.029 0.936 0.896 0.468 0.822 1.000X160.524 0.806 0.066 0.604 0.358 0.226 0.586 0.729 0.218 0.354 0.86 0.892 0.034 0.871 0.729 1.000表2 表征值及贡献率成份初始特征值提取平方和载入合计方差的% 累积% 合计方差的% 累积%1 7.380 46.128 46.128 7.380 46.128 46.1282 5.003 31.268 77.396 5.003 31.268 77.3963 1.450 9.062 86.458 1.450 9.062 86.4584 0.893 5.579 92.0375 0.608 3.799 95.8376 0.259 1.619 97.4557 0.172 1.077 98.5328 0.126 0.790 99.3219 0.046 0.285 99.60610 0.027 0.171 99.77711 0.015 0.094 99.87112 0.010 0.065 99.93613 0.008 0.047 99.98314 0.002 0.014 99.99715 0 0.003 10016 8.02E-17 5.01E-16 100表3 主成分载荷因子矩阵指标成份1 2 3X140.927 0.311X160.898X120.869 0.435X110.838 0.511X10.802 -0.491X40.795 -0.313X80.769X20.749 0.646X70.73 -0.504X100.66 -0.605X60.93X130.873X150.643 0.742X50.615 -0.673X90.727X30.547 -0.722表4 主成分得分序号区域第一主成分F1第二主成分F2第三主成分F3综合得分ΣF排名7 合肥 3.414 0.212 -0.630 1.584 114 芜湖0.811 0.942 0.662 0.729 212 马鞍山0.238 1.363 0.672 0.597 313 铜陵-0.557 1.998 0.440 0.408 49 淮南-0.581 0.533 0.494 -0.056 52 蚌埠-0.068 -0.246 0.488 -0.064 68 淮北-0.646 0.058 1.863 -0.111 75 滁州-0.121 -0.695 1.305 -0.155 816 宣城-0.386 0.197 -0.835 -0.192 91 安庆0.000 -0.572 -0.179 -0.195 1010 黄山-0.709 0.644 -1.938 -0.301 114 池州-0.881 0.462 -1.704 -0.416 123 亳州-0.217 -1.049 -0.109 -0.438 1315 宿州-0.153 -1.164 -0.065 -0.440 1411 六安-0.213 -0.930 -0.653 -0.448 156 阜阳0.069 -1.753 0.188 -0.499 16由表1可知,在影响经济综合实力的16个变量因子中存在着不同程度的相关,因此也说明运用主成分分析方法分析安徽省各市经济综合实力具有一定的可行性,同时也进步一步说明了主成分分析的必要性。
主成分个数提取原则为主成分对应的特征值大于1的前n个主成分,即特征值在某种程度上可以被看成是表示主成分影响力度大小的指标,如果特征值大于1,说明该主成分的解释力度还不如直接引入一个原变量的平均解释力度大,因此一般可以用特征值大于1作为纳入标准。
从表2特征值及贡献率可以看出特征值大于1的成分有3个,其值分别达到7.38、5.003和1.45。
方差贡献率反映的是某一主成分描述的方差占原有变量总方差的比例,累积方差贡献率表示前n个主成分的总方差占原有变量的总方差的比例。
从表2特征值及贡献率可以看出前3个主成分的累积方差贡献率达到了86.458%,已经超过85%的标准,反映了原有16个变量90%以上的变异信息。
综合以上对特征值和累积方差贡献率的分析,确定选取前3个主成分作为评价安徽省各市综合实力新变量来进行下一步的分析。
在以上分析的基础上,为了进一步说明主成分的实际社会经济意义,体现主成分和原始变量的相关程度,本文采用主成分载荷矩阵来对其加以实际说明。
通过表3主成分载荷因子矩阵可知,其第一主成分概括为宏观经济水平的差异,第二主成分可概括社会结构的差异,第三主成分可概括为生活质量上的差异。
通过以上分析可知,影响地区综合实力的主要因子有经济水平、社会结构、社会质量以及其它,这里的其它包括经济结构、城市化水平、人口结构等。
为了进一步分析安徽省各地区经济发展水平的差异,本次作业用spss19.0数据处理软件,对16个相关指标进行聚类分析,得到图一安徽省16个地区综合实力Ward联接聚类谱系图。
图1 安徽省16个地区综合实力Ward联接聚类谱系图根据图1安徽省16个地区综合实力Ward联接聚类谱系图进一步对安徽省16个地区进行综合评价,可把安徽省各区经济实力分为4大梯度地区:第一梯度:发达地区,以合肥为主的省会。
从表4主成分得分可以看出,合肥主成分得分达到1.584,远远高于其他地区,合肥为安徽省省会,作为全省政治、经济、文化、科教中心,具有得天独厚的区位优势,尤其是2010年把巢湖主要地区并入之后,经济实力大增,经济实力雄厚,产业结构层次较高。
第二梯度:次发达地区,包括铜陵、芜湖、马鞍山。
马芜铜三地区是安徽省三个传统的经济强区,其丰富的自然资源优势为经济的发展打下了坚实的基础;其次,此地区为皖江城市带主要地区,在承接东部产业转移方面扮演重要的角色,是皖江城市带的核心地区;同时,此地区地处长江沿线,区位优势明显,城市化水平高,第二产业比重大,经济实力雄厚,其中芜湖作为安徽省副省会,优势更加明显;从表4主成分得分分析结果中也可以看出,其得分都大于0,排名比较高。
第三梯度:欠发达地区,包括池州、宣城、黄山、蚌埠、滁州、淮北、淮南7市。
其中池州、宣城、黄山地处皖南地区,旅游资源丰富,第三产业比重大,旅游业发展迅速,已形成独特的以发展旅游业为特色、高层次高结构的产业体系;蚌埠市是皖北重要的工业城市,以轻纺工业为主;淮南淮北两地煤炭资源丰富,是华东地区主要的煤炭供应基地,经济较发达;滁州作为皖江城市带城市之一,近几年经济发展也较快。
第四梯度:贫困地区,包括亳州、宿州、安庆、阜阳、六安5个地区。
这几个地区,第一产业比重大,产业基础薄弱,经济发展不平衡,总人口多,经济落后,城市化水平低,主要由于政府对其政策与投资较少,为了全省各地区均衡发展,应给予此地区更多的政策与投资。
为了进一步分析此分类结果的真实性,本文采取判别分析方法对分类结果进行了合理性检验,结果见表5。
表5 判别分析结果分类预测组成员合计1 2 3 4初始计数第一梯度 1 0 0 0 1第二梯度0 3 0 0 3第三梯度0 0 7 0 7第四梯度0 0 0 5 5 % 1 100 0 0 0 1002 0 100 0 0 1003 0 0 100 0 1004 0 0 0 100 100a. 已对初始分组案例中的100.0% 个进行了正确分类。
从表5中可以看出,判别结果与分类结果100%相一致,说明了此次分析结果是比较合理的。
由于是课堂作业,评价指标体系侧重点不同,因此会存在一定的不足之处,但从总体上看基本上反映了安徽省各地区经济发展的现状。
