江苏省扬州中学2013-2014学年高二上学期期末试题 数学 Word版含答案
2013-2014年江苏扬州中学高一(上)数学期末试卷及答案

2013-2014学年江苏省扬州中学高一(上)期末数学试卷一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上)1.(5.00分)已知全集U={1,2,3,4,5,6},A={3,4,5},则∁U A=.2.(5.00分)函数的最小正周期为.3.(5.00分)幂函数f(x)=的定义域为.4.(5.00分)平面直角坐标系xOy中,60°角的终边上有一点P,则实数m的值为.5.(5.00分)已知a=﹣,b=log23,c=sin160°,把a,b,c按从小到大的顺序用“<”连接起来:.6.(5.00分)半径为3cm,圆心角为120°的扇形面积为cm2.7.(5.00分)函数f(x)=log a(x﹣1)(a>0且a≠1)的图象必经过定点P,则点P的坐标为.8.(5.00分)已知||=2,,若,的夹角为60°,则|+2|=.9.(5.00分)已知函数f(x)=x2+(a2﹣1)x+(a﹣2)的一个零点比1大,一个零点比1小,则实数a的取值范围.10.(5.00分)如图,平行四边形ABCD中,E是边BC上一点,G为AC与DE的交点,且,若=,,则用,表示=.11.(5.00分)若x∈(﹣∞,﹣1],不等式(m﹣m2)•2x+1>0恒成立,则实数m的取值范围为.12.(5.00分)将函数y=2sinx的图象先向右平移个单位,再将得到的图象上各点的横坐标变为原来的倍(纵坐标不变),得到函数y=f(x)的图象,若x ∈[0,],则函数y=f(x)的值域为.13.(5.00分)已知△ABC中,BC边上的中线AO长为2,若动点P满足(θ∈R),则(+)•的最小值是.14.(5.00分)已知定义在(0,+∞)上的函数f(x)为单调函数,且f(x)•f (f(x)+)=2,则f(1)=.二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.(14.00分)已知,且α是第一象限角.(1)求cosα的值;(2)求的值.16.(14.00分)已知=(1,1),=(2,3),当k为何值时,(1)k+2与2﹣4垂直?(2)k+2与2﹣4平行?平行时它们是同向还是反向?17.(15.00分)已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<)的部分图象如图所示.(1)求函数y=f(x)的解析式;(2)求函数y=f(x)的单调增区间;(3)求方程f(x)=0的解集.18.(15.00分)已知函数f(x)=log a(a>0且a≠1)的图象经过点P(﹣,2).(1)求函数y=f(x)的解析式;(2)设,用函数单调性的定义证明:函数y=g(x)在区间(﹣1,1)上单调递减;(3)解不等式:f(t2﹣2t﹣2)<0.19.(16.00分)我国加入WTO后,根据达成的协议,若干年内某产品关税与市场供应量P的关系允许近似的满足:(其中t为关税的税率,且).(x为市场价格,b、k为正常数),当t=时的市场供应量曲线如图(1)根据图象求k、b的值;(2)若市场需求量为Q,它近似满足.当P=Q时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率t的最小值.20.(16.00分)已知函数f(x)=x|2a﹣x|+2x,a∈R.(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;(2)若函数f(x)在R上是增函数,求实数a的取值范围;(3)若存在实数a∈[﹣2,2],使得关于x的方程f(x)﹣tf(2a)=0有三个不相等的实数根,求实数t的取值范围.2013-2014学年江苏省扬州中学高一(上)期末数学试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上)1.(5.00分)已知全集U={1,2,3,4,5,6},A={3,4,5},则∁U A={1,2,6} .【解答】解:∵全集U={1,2,3,4,5,6},A={3,4,5},∴∁U A={1,2,6}.故答案为:{1,2,6}2.(5.00分)函数的最小正周期为.【解答】解:因为函数,所以T==.所以函数的最小正周期为.故答案为:.3.(5.00分)幂函数f(x)=的定义域为[0,+∞).【解答】解:∵f(x)==,∴x≥0,∴幂函数f(x)=的定义域为[0,+∞).故答案为:[0,+∞).4.(5.00分)平面直角坐标系xOy中,60°角的终边上有一点P,则实数m的值为1.【解答】解:∵角60°的终边上有一点,∴tan60°==,∴m=1.故答案为:1.5.(5.00分)已知a=﹣,b=log23,c=sin160°,把a,b,c按从小到大的顺序用“<”连接起来:a<c<b.【解答】解:∵a=﹣,b=log23>log22=1,0<c=sin160°<1,∴a<c<b.故答案为:a<c<b.6.(5.00分)半径为3cm,圆心角为120°的扇形面积为3πcm2.【解答】解:扇形的弧长是:3×=2π,则扇形的面积是:×2π×3=3π(cm2).故答案为:3π.7.(5.00分)函数f(x)=log a(x﹣1)(a>0且a≠1)的图象必经过定点P,则点P的坐标为(2,0).【解答】解:根据函数y=log a x的图象经过点(1,0),对于函数f(x)=log a(x﹣1),令x﹣1=1,求得x=2,且f(2)=0,可得点P的坐标为(2,0),故答案为:(2,0).8.(5.00分)已知||=2,,若,的夹角为60°,则|+2|=2.【解答】解:∵||=2,,,的夹角为60°,∴===1.∴|+2|===.故答案为:.9.(5.00分)已知函数f(x)=x2+(a2﹣1)x+(a﹣2)的一个零点比1大,一个零点比1小,则实数a的取值范围(﹣2,1).【解答】解:∵函数f(x)=x2+(a2﹣1)x+(a﹣2)的一个零点比1大,一个零点比1小∴f(1)<0∴1+a2﹣1+a﹣2<0∴a2+a﹣2<0∴﹣2<a<1∴实数a的取值范围为(﹣2,1)故答案为:(﹣2,1)10.(5.00分)如图,平行四边形ABCD中,E是边BC上一点,G为AC与DE的交点,且,若=,,则用,表示=.【解答】解:∵,∴.∵,,∴,∴===.故答案为:.11.(5.00分)若x∈(﹣∞,﹣1],不等式(m﹣m2)•2x+1>0恒成立,则实数m的取值范围为﹣1<m<2.【解答】解:不等式(m﹣m2)•2x+1>0等价为(m﹣m2)•2x>﹣1,即m﹣m2>,当x∈(﹣∞,﹣1]时,,∴,∴要使不等式恒成立,即m﹣m2>﹣2,即m2﹣m﹣2<0,解得﹣1<m<2,故答案为:﹣1<m<2.12.(5.00分)将函数y=2sinx的图象先向右平移个单位,再将得到的图象上各点的横坐标变为原来的倍(纵坐标不变),得到函数y=f(x)的图象,若x ∈[0,],则函数y=f(x)的值域为[﹣1,2] .【解答】解:令y=g(x)=2sinx,则g(x﹣)=2sin(x﹣),∴f(x)=2sin(2x﹣),∵x∈[0,],∴2x﹣∈[﹣,],∴sin(2x﹣)∈[﹣,1],∴2sin(2x﹣)∈[﹣1,2],即函数y=f(x)的值域为[﹣1,2].故答案为:[﹣1,2].13.(5.00分)已知△ABC中,BC边上的中线AO长为2,若动点P满足(θ∈R),则(+)•的最小值是﹣2.【解答】解:由题意可得,∵点P满足(θ∈R),∴.又sin2θ+cos2θ=1,所以P、A、O三点共线,即点P在AO上.∵,∴(+)•=2•=﹣2||•||.∴||+||=|AO|=2,利用基本不等式可得||•||≤=1,∴﹣2||•||≥﹣2,当且仅当|PO|=|PA|时,等号成立,故(+)•的最小值为﹣2,故答案为:﹣2.14.(5.00分)已知定义在(0,+∞)上的函数f(x)为单调函数,且f(x)•f (f(x)+)=2,则f(1)=1±.【解答】解:∵f(x)的定义域为(0,+∞),∴当x=1时,f(1)•f(f(1)+2)=2,∴f(f(1)+2)=;f(1)+2作为f(f(1)+2)的自变量的一个取值,它必须在定义域内,∴f(1)+2>0,即f(1)>﹣2;设f(1)=a,(其中a>﹣2),∴f(a+2)=…①;令x=a+2(其中a>﹣2),代入f(x)•f(f(x)+)=2中,得f(a+2)•f(f(a+2)+)=2…②;把①代入②,得•f(+)=2,即f(+)=a …③;∵a=f(1),∴f(+)=f(1);把+和 1 分别看作函数f(x)的自变量的2个取值,由于函数f(x)是单调函数,要使对应的函数值相等,自变量必须相等;即+=1,解得a=1+或a=1﹣;∵1+和1﹣都大于﹣2,∴两个数值都符合题意;综上,f(1)=1+或f(1)=1﹣;故答案为:1±.二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.(14.00分)已知,且α是第一象限角.(1)求cosα的值;(2)求的值.【解答】解:(1)∵α是第一象限角,∴cosα>0,∵sinα=,∴cosα==;(2)∵tanα==,∴原式=tanα+=tanα+1=.16.(14.00分)已知=(1,1),=(2,3),当k为何值时,(1)k+2与2﹣4垂直?(2)k+2与2﹣4平行?平行时它们是同向还是反向?【解答】解:(1)=k(1,1)+2(2,3)=(4+k,6+k),=2(1,1)﹣4(2,3)=(﹣6,﹣10),由,得:﹣6(4+k)﹣10(6+k)=0,化为﹣16k﹣84=0,解得:.∴当k=﹣时,.(2)由,得﹣6(6+k)+10(4+k)=0,化为4k+4=0,解得:k=﹣1.此时=(3,5)=﹣(﹣6,﹣10)=﹣,∴它们方向相反.17.(15.00分)已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<)的部分图象如图所示.(1)求函数y=f(x)的解析式;(2)求函数y=f(x)的单调增区间;(3)求方程f(x)=0的解集.【解答】解:(1)由图知,A=1,∵周期T=4(﹣)=π,∴ω==2,∴f(x)=sin(2x+φ),又f()=﹣1,∴sin(+φ)=﹣1,∴+φ=2kπ+(k∈Z),∴φ=2kπ+(k∈Z),又|φ|<,∴φ=,∴f(x)=sin(2x+);(2)﹣+2kπ≤2x+≤+2kπ,k∈Z.∴﹣+kπ≤x≤+kπ,k∈Z.∴函数y=f(x)的单调增区间为:[﹣+kπ,+kπ]k∈Z.(3)∵f(x)=0,∴2x+=kπ,k∈Z.∴x=﹣+kπ,k∈Z.∴方程f(x)=0的解集为{x|x=﹣+kπ,k∈Z}.18.(15.00分)已知函数f(x)=log a(a>0且a≠1)的图象经过点P(﹣,2).(1)求函数y=f(x)的解析式;(2)设,用函数单调性的定义证明:函数y=g(x)在区间(﹣1,1)上单调递减;(3)解不等式:f(t2﹣2t﹣2)<0.【解答】解:(1),解得:a2=9,∵a>0 且a≠1,∴a=3;函数y=f(x)的解析式:f(x)=log3…(3分)(2)设x1、x2为(﹣1,1)上的任意两个值,且x1<x2,则x1+1>0,x2+1>0,x2﹣x1>0∵g(x1)﹣g(x2)==…(6分)∴g(x1)﹣g(x2)>0,∴g(x1)>g(x2).∴在区间(﹣,1)上单调递减.…(8分)(3)∵∴…(10分)由,得:t2﹣2t﹣2>0或t2﹣2t﹣2<﹣1;由∴0<t2﹣2t﹣2<1…(13分)∴或.…(15分)19.(16.00分)我国加入WTO后,根据达成的协议,若干年内某产品关税与市场供应量P的关系允许近似的满足:(其中t为关税的税率,且).(x为市场价格,b、k为正常数),当t=时的市场供应量曲线如图(1)根据图象求k、b的值;(2)若市场需求量为Q,它近似满足.当P=Q时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率t的最小值.【解答】解:(1)由图可知,解得(2)当P=Q时,得解得:令,∵x≥9,∴m∈(0,],则t=,∴对称轴m=∈(0,],且开口向下;∴时,t取得最小值,此时x=9∴税率t的最小值为.20.(16.00分)已知函数f(x)=x|2a﹣x|+2x,a∈R.(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;(2)若函数f(x)在R上是增函数,求实数a的取值范围;相等的实数根,求实数t的取值范围.【解答】解:(1)函数y=f(x)为奇函数.当a=0时,f(x)=x|x|+2x,∴f(﹣x)=﹣x|x|﹣2x=﹣f(x),∴函数y=f(x)为奇函数;(2)f(x)=,当x≥2a时,f(x)的对称轴为:x=a﹣1;当x<2a时,y=f(x)的对称轴为:x=a+1;∴当a﹣1≤2a≤a+1时,f(x)在R上是增函数,即﹣1≤a≤1时,函数f(x)在R上是增函数;(3)方程f(x)﹣tf(2a)=0的解即为方程f(x)=tf(2a)的解.①当﹣1≤a≤1时,函数f(x)在R上是增函数,∴关于x的方程f(x)=tf(2a)不可能有三个不相等的实数根;…(9分)②当a>1时,即2a>a+1>a﹣1,∴f(x)在(﹣∞,a+1)上单调增,在(a+1,2a)上单调减,在(2a,+∞)上单调增,∴当f(2a)<tf(2a)<f(a+1)时,关于x的方程f(x)=tf(2a)有三个不相等的实数根;即4a<t•4a<(a+1)2,∵a>1,∴.设,∵存在a∈[﹣2,2],使得关于x的方程f(x)=tf(2a)有三个不相等的实数根,∴1<t<h(a)max,又可证在(1,2]上单调增∴<h(a)max=,∴1<t<∴f (x )在(﹣∞,2a )上单调增,在(2a ,a ﹣1)上单调减,在(a ﹣1,+∞)上单调增,∴当f (a ﹣1)<tf (2a )<f (2a )时,关于x 的方程f (x )=tf (2a )有三个不相等的实数根;即﹣(a ﹣1)2<t•4a <4a , ∵a <﹣1, ∴, 设,∵存在a ∈[﹣2,2],使得关于x 的方程f (x )=tf (2a )有三个不相等的实数根, ∴1<t <g (a )max , 又可证在[﹣2,﹣1)上单调减,∴g (a )max =,∴1<t <; 综上:1<t<.。
江苏省扬州中学2013-2014学年高二下学期阶段测试(5月)数学Word版含答案

江苏省扬州中学2013—2014学年第二学期月考高二数学试卷 2014.5一、填空题:1.已知集合{1,1,2,4},{1,0,2}A B =-=-,则AB = .2.命题“∃x Q ∈,220x -=”的否定为 .3.函数y =的定义域为 .4.若角α的终边过点(5,12)P -,则cos α= .5.“0a =”是复数(,)z a bi a b R =+∈为纯虚数的 条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)6.若曲线x x x f -=4)(在点P 处的切线平行于直线3x -y =0,则点P 的坐标为 .7.复数231i i -⎛⎫ ⎪+⎝⎭的虚部..为 . 8.方程lg(42)lg 2lg 3xx+=+的解集为 . 9.设2()sin f x a x x =+,若(1)0f =,则(1)f -= .10.已知函数2()()ln f x ax x x x =+-在[1,)+∞上单调递增,则实数a 的取值范围是 . 11.在△ABC 中,A B C 、、所对边分别为a 、b 、c .若tan 210tan A cB b++=,则A = .12. 对于函数)(x f ,在使)(x f ≥M 恒成立的所有常数M 中,我们把M 中的最大值称为函数)(x f 的“下确界”,则函数22)1(1)(++=x x x f 的下确界为 .13.求有如下解题思路:则()f x 在R 上单调递减,且(2)1f =,所以原方程有唯一解2x =.类比上述解题思路,方程623(2)2x x x x +=+++的解集为 .14.已知偶函数()f x 满足对任意x R ∈,均有(1)(3)f x f x +=-且2(1),[0,1]()1,(1,2]m x x f x x x ⎧-∈=⎨-∈⎩,若方程3()f x x =恰有5个实数解,则实数m 的取值范围是_ ___.二、解答题:15.设命题p :函数3()1f x x ax =--在区间[1,1]-上单调递减;命题q :函数21y x ax =++的最小值不大于0.如果命题q p 或为真命题,q p 且为假命题,求实数a 的取值范围.高 考 资 源 网16.求证:二次函数2y ax bx c =++的图象与x 轴交于(10),的充要条件为0a b c ++=.17.已知函数.3cos 33cos 3sin)(2xx x x f += (1)将f (x )写成sin()A x ωϕ+的形式,并求其图象对称中心的横坐标;(2)如果△ABC 的三边a 、b 、c 满足b 2=ac ,且边b 所对的角为x ,试求x 的范围及此时函数f(x)的值域.18.如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设α=∠11H AA . (1)试用α表示11H AA ∆的面积;(2)求八角形所覆盖面积的最大值,并指出此时α的大小. 19.设函数()log (2)log (3),a a f x x a x a =-+-其中0a >且1a ≠.(1)已知(4)1f a =,求a 的值;(2)若在区间[3,4]a a ++上()1f x ≤恒成立,求a 的取值范围. 20.函数2()()xf x x a e =-在2x =时取得极小值. (1)求实数a 的值;(2)是否存在区间[,]m n ,使得()f x 在该区间上的值域为44[,]e m e n ?若存在,求出,m n 的值;若不存在,请说明理由.高二数学月考附加题 5.241.求8的展开式中二项式系数最大项.姓名_____________答……………题………………2.(用空间向量解题)如图,四棱锥S ABCD -的高为2,底面ABCD 是边长为22的正方形,顶点S 在底面上的射影是正方形ABCD 的中心O .K 是棱SC 的中点.试求直线AK 与平面SBC 所成角的正弦值.3.甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为231,,342,他们海选合格与不合格是相互独立的.(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量ξ,求随机变量ξ的分布列和数学期望E ξ.4. 已知(x +1)n =a 0+a 1(x -1)+a 2(x -1)2+…+a n (x -1)n ,(其中n ∈N *) (1)求a 0及S n =a 1+a 2+···+a n ; (2)试比较S n 与(n -2)·2n +2n 2的大小,并说明理由.高二数学月考参考答案 2014.51. {1,2}-2. ∀x Q ∈,220x -≠3. [0,2]4. 513- 5. 必要不充分 6. (1,0) 7. 4- 8. {0,1} 9. 2 10.11. 23π 12. 12 13. {1,2}- 14.415)(6+15.解:p 为真命题⇔f ′(x)=32x -a ≤0在[-1,1]上恒成立⇔a ≥32x 在[-1,1]上恒成立⇔a ≥3.q 为真命题⇔Δ=2a -4≥0恒成立⇔a ≤-2或a ≥2. 由题意p 和q 有且只有一个是真命题. p 真q 假⇔⎩⎨⎧<<-≥223a a ⇔a ∈φ;p 假q 真⇔⎩⎨⎧≥-≤<223a a a 或⇔a ≤-2或2≤a <3.综上所述:a ∈(-∞,-2]∪[2,3).16.证明:(1)必要性:由2y ax bx c =++的图象与x 轴交于(10),,可知方程20ax bx c ++=有一个根为1,即0a b c ++=;(2)充分性:若0a b c ++=,则2()(1)()y ax bx c a b c x ax a b =++-++=-++, 当1x =时,0y =,即函数2y ax bx c =++的图象过(10),点.故函数2y ax bx c =++的图象与x 轴交于(10),点的充要条件为0a b c ++=.17. (1)23)332sin(2332cos 2332sin 21)32cos 1(2332sin 21)(++=++=++=πx x x x x x f由)332sin(π+x =0即Z k k x z k k x ∈-=∈=+πππ213)(332得即对称中心的横坐标为Z k k ∈-π213(2)由已知b 2=ac2222222222222222221cos 2222(),2,3,2,23.1cos 102325333952||||sin sin()132923332sin()133a c b a c ac a c x ac ac ac a c b a b ac b a b ac a c ac ac a b ac x x x x x πππππππππππ+-+-+===--<∴+<+∴+<+≥∴≤+<∴≤<<≤<+≤->-∴<+≤<++≤+又即)(x f 的值域为]231,3(+综上所述,]3,0(π∈x )(x f 值域为]231,3(+18.解:(1)设1AH 为x ,∴4sin tan x xx αα++=,4sin sin cos 1x ααα=++,()112218sin cos 2tan sin cos 1AA H x Sααααα=⋅=++,(0,)2πα∈, (2)令sin cos t αα=+∈, 只需考虑11AA H S 取到最大值的情况,即为()()22418411t S t t -==-++,当t =, 即︒=45α时, 11AA H S达到最大此时八角形所覆盖面积的最大值为64-322 . 19.解:(1)12a =. (2)22225()log (56)log [()],24a a a a f x x ax a x =-+=--由2030x a x a ->⎧⎨->⎩得3,x a >由题意知33,a a +>故32a <,从而53(3)(2)022a a a +-=->,故函数225()()24a g x x a =--在区间[3,4]a a ++上单调递增.①若01,a <<则()f x 在区间[3,4]a a ++上单调递减,所以()f x 在区间[3,4]a a ++上的最大值为2(3)log (299)1a f a a a +=-+≤,即2299a a a-+≥,解得a a ≥≤,又01a <<,所以01a <<. ②若31,2a <<则()f x 在区间[3,4]a a ++上单调递增,所以()f x 在区间[3,4]a a ++上的最大值为2(4)log (21216)1a f a a a +=-+≤,221216a a a -+≤,a ≤≤,与312a <<联立无解. 综上:01a <<.20.(1)()e ()(2)x f x x a x a '=--+,由题意知(2)0f '=,解得2a =或4a =.当2a =时,()e (2)x f x x x '=-,易知()f x 在(0,2)上为减函数,在(2,)+∞上为增函数,符合题意; 当4a =时,()e (2)(4)x f x x x '=--,易知()f x 在(0,2)上为增函数,在(2,4),(4,)+∞上为减函数,不符合题意. 所以,满足条件的2a =. (2)因为()0f x ≥,所以0m ≥.① 若0m =,则2n ≥,因为4(0)4e f n =<,所以24(2)e e n n n -=. 设2(2)()e (2)xx g x x x -=≥,则2224(2)()e 0x x x g x xx ⎡⎤--'=+⎢⎥⎣⎦≥, 所以()g x 在[2,)+∞上为增函数.由于4(4)e g =,即方程24(2)e e n n n -=有唯一解为4n =.② 若0m >,则[]2,m n ∉,即2n m >>或02m n <<<.(Ⅰ)2n m >>时,2424()(2)e e ()(2)e e m n f m m mf n n n⎧=-=⎨=-=⎩, 由①可知不存在满足条件的,m n .02m n <<<时,2424(2)e e (2)e e m n m nn m⎧-=⎨-=⎩,两式相除得22(2)e (2)e m n m m n n -=-. 设2()(2)e (02)x h x x x x =-<<,则32()(44)e (2)(1)(2)e x x h x x x x x x x '=--+=+--,()h x 在(0,1)递增,在(1,2)递减,由()()h m h n =得01m <<,12n <<,此时24(2)e 4e e m m n -<<,矛盾.综上所述,满足条件的,m n 值只有一组,且0,4m n ==.高二数学月考附加题参考答案1.解析:展开式中二项式系数最大项是24443541870T T C x +=== 2.解析:,AC BD O ⋂=以O 为坐标原点,OA 为x 轴,OB 为y 轴,OS 为z 轴建立空间坐标系。
江苏省扬州中学2013-2014学年高二4月阶段测试数学(文)试题 Word版含答案

3
.
f ( x), f ( x) K , 5 13.数 f K ( x) (K 为给定常数) , 已知函数 f ( x) x2 3x2 ln x , 若对于任意的 x (0, ) , f ( x) ≤ K 2 K , 恒有 f K ( x) K ,则实数 K 的取值范围为 .
11.
1 1 c b
3 13. [ e 3 , ) 2
15.解: (1)p 是 q 的充分条件,
[ 1, 5 ] [m 1 , m 1 )
(4, ) 则实数 m 的取值范围为
(2) [4, 1) (5,6)
16.解: (1 )定义域为 R 关于原点对称.
f ( x) f ( x)
α
,则 f(4)=
.
6. 已知 y=f(x)是定义在 R 上的偶函数,且当 x<0 时,f(x)=1+2x,则当 x>0 时,f(x)=
.
|x-1|-2,|x|≤1 1 7. 设 f (x)= 1 ,则 f [ f (2)]= 2,|x|>1 1+x
8. 已知集合 A {x | x a}, B {x |1 x 2}, 且A (CR B) R ,则实数 a 的取值范围是
2 2
14. 不等式 a +8b ≥λb(a+b)对于任意的 a,b∈R 恒成立,则实数 λ 的取值范围为
.
二、解答题(总分 90 分) 15.(14 分) 已知命题 p : ( x 1)( x 5) 0 ,命题 q :1 m x 1 m(m 0) 。 (1)若 p 是 q 的充分条件,求实数 m 的取值范围; (2)若 m=5, “ p q ”为真命题, “ p q ”为假命题,求实数 x 的取值范围。
江苏省扬州中学2010-2011学年高二上学期期末考试数学试题(word版有答案)
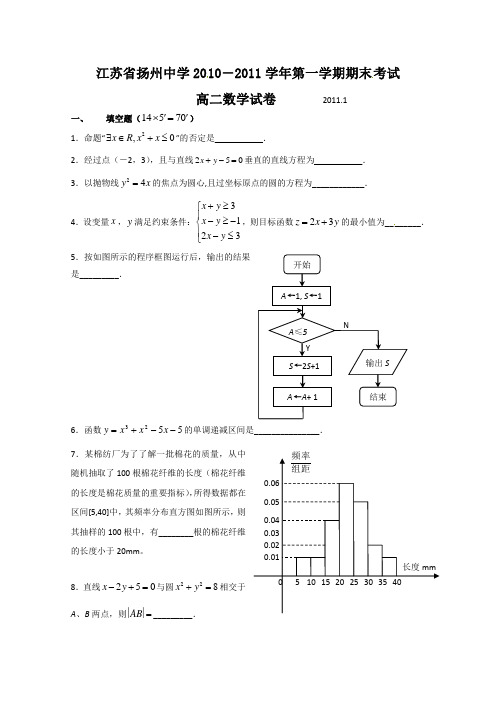
江苏省扬州中学2010―2011学年第一学期期末考试高二数学试卷 2011.1一、填空题(14570''⨯=)1.命题“2,0x R x x ∃∈+≤”的否定是___________.2.经过点(-2,3),且与直线250x y +-=垂直的直线方程为___________. 3.以抛物线24y x =的焦点为圆心,且过坐标原点的圆的方程为____________.4.设变量x ,y 满足约束条件:3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,则目标函数23z x y =+的最小值为________.5.按如图所示的程序框图运行后,输出的结果是_________.6.函数5523--+=x x x y 的单调递减区间是_______________. 7.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有________根的棉花纤维的长度小于20mm 。
8.直线250x y -+=与圆228x y +=相交于A 、B 两点,则AB ∣∣=_________.9.在平面直角坐标系xoy 中,双曲线112422=-y x 上一点M ,点M 的横坐标是3,则M 到双曲线右焦点的距离是_________. 10.设321()252f x x x x =--+,当]2,1[-∈x 时,()f x m <恒成立,则实数m 的取值范围为_________.11.直线3y kx =+与圆22(3)(2)4x y -+-=相交于M ,N 两点,若|MN |≥k 的取值范围_____________.12.已知F 是椭圆C 的一个焦点,B 是短轴的一个端点,线段BF 的延长线交C 于点D ,且FD BF 2=,则椭圆C 的离心率为____________.13.若直线y x b =+与曲线3y =有公共点,则b 的取值范围是__________.14.函数3211()22132f x ax ax ax a =+-++的图像经过四个象限,则a 的取值范围是_____. 二、解答题(15、16每题14',17、18每题15',19、20每题16')15.已知直线1l :(2)(3)50m x m y +++-=和2l :6(21)5x m y +-=。
江苏省扬州中学2013-2014学年高二下学期期中考试数学(理)Word版含答案

2014.4注:本试卷考试时间120分钟,总分值160分一、填空题:本大题共14小题,每小题5分,共70分. 1.已知全集{}0,1,2,3,4U =,集合{}{}1,2,3,2,4A B ==, 则()U C A B ⋃为 ▲ .2.命题“1x ∀>, 21x >”的否定是 ▲ .3. 若函数⎩⎨⎧>≤+=1,lg 1,1)(2x x x x x f ,则f(f(10)= ▲ .4.已知复数z 1=-2+i ,z 2=a +2i(i 为虚数单位,a ∈R ).若z 1z 2为实数,则a 的值为 ▲ . 5.已知()f x 是奇函数,且1)1(=f ,若2()()2g x f x x =+,则=-)1(g ▲ . 6.曲线xe y 2=在0=x 处的切线方程是 ▲ .7.满足{},1,0,1,2a b ∈-,且关于x 的方程220ax x b +-=有实数解的有序数对(,)a b 的个数为 ▲ .8. 322x x ⎛⎫- ⎪⎝⎭的展开式中的常数项为 ▲ .9. 设357log 6,log 10,log 14a b c ===,则,,a b c 的大小关系是 ▲ . 10.利用数学归纳法证明“)(2131211n p n =+⋅⋅⋅⋅⋅⋅+++”,从k n =推导1+=k n 时原等式的左边应增加的项数..是 ▲ . 11.定义域为R 的函数()f x 满足(1)2()f x f x +=,且当(0,1]x ∈时,2()f x x x =-,则当[2,1]x ∈--时,()f x 的最小值为 ▲ .12.对大于或等于2的自然数m 的n 次方幂有如下分解方式:3122+= 53132++=753142+++= 5323+= 119733++=1917151343+++=根据上述分解规律,则9753152++++=,若)(*3N n m ∈的分解中最小的数是91,则m 的值为 ▲ . 13.已知函数1()3xf x x =+,(0)x >,对于*n N ∈,定义11()[()]n n f x f f x +=,则函数()n f x 江苏省扬州中学2013—2014学年度第二学期期中考试高二数学(理)试卷的值域为 ▲ .14.设函数()f x =(a R ∈).若存在(0,1]b ∈使得(())f f b b =,则a 的取值范围是 ▲ .二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤. 15.已知集合A={}2|230x x x --<,B={}|(1)(1)0x x m x m -+--≥, (1)当0m =时,求A B ⋂(2)若p :2230x x --<,q :(1)(1)0x m x m -+--≥, 且p 是q 的充分条件,求实数m 的取值范围.16.已知n n x x f )1()(+=, (1)若20152015012015()f x a a x a x =+++,求1320132015a a a a ++++的值;(2)若)(3)(2)()(876x f x f x f x g ++=,求)(x g 中含6x 项的系数.17.某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r 米,高为h 米,体积为V 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为π12000元(π为圆周率). (1)将V 表示成r 的函数)(r V ,并求该函数的定义域;(2)讨论函数)(r V 的单调性,并确定r 和h 为何值时该蓄水池的体积最大.18.已知 n (2,n n N ≥∈)个半圆的圆心在同一条直线l 上,这n 个半圆每两个都相交,且都在直线l 的同侧,设这n 个半圆被所有的交点最多分成()f n 段圆弧.(1)求(2),(3),(4)f f f ;(2)由(1)猜想()f n 的表达式并用数学归纳法证明.19.设集合},10|{Z x x x A ∈≥=,A B ⊆,且B 中的元素满足:①任意一个元素各数位的数字互不相同;②任意一个元素的任意两个数字之和不等于9. (1)集合B 中的两位数有多少?集合B 中的元素最大的是多少? (2)将B 中的元素从小到大排列,求2015是第几个元素.20. 已知0t >,函数()3x tf x x t-=+. (1)1t =时,写出()f x 的增区间;(2)记()f x 在区间[0,6]上的最大值为()g t ,求()g t 的表达式;(3)是否存在t ,使函数()y f x =在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求t 的取值范围;若不存在,请说明理由.江苏省扬州中学2013~2014学年第二学期期中考试高二数学试卷答题纸成绩一、填空题(每小题5分,计70分)1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.二、解答题(本大题共6小题,计90分) 15.(14分) 16.(14分)17.(14分)考试号________________ 学号_____ 班级___________座位号__________ 姓名_____________…密……………封……………线……………内……………不……………要……………答……………题………………18.(16分) 19.(16分)(请将20题解答写在答题纸反面)高二数学(理)期中试卷参考答案 2014.41.{}0,2,42. 21,1x x ∃>≤ 3.2 4.4 5.1 6.22y x =+ 7.14 8.12 9.a b c >> 10. 2n 11. 116- 12.10 13.2(0,)31n -14.(,0]-∞15、解析(1):{}{}2|230|13A x x x x x =--<=-<<,{}{}|(1)(1)0|11B x x x x x x =+-≥=≥≤-或{}|13A B x x ∴⋂=≤<(2) p 为:(1,3)-而q 为: (,1][1,)m m -∞-⋃++∞,p q ⇒所以 11m +≤-或13m -≥ ⇒ 4m ≥或2m ≤-即实数m 的取值范围为(,2][4,)-∞-⋃+∞。
江苏省扬州市2013-2014学年高二第一学期期末调研考试数学试卷

江苏省扬州市2013-2014学年高二第一学期期末调研考试数学试卷2014.1(满分160分,考试时间120分钟)注意事项:试题答案均写在答题卷相应位置,答在其它地方无效.参考公式:柱体的体积公式:=V Sh 柱体,其中S 是柱体的底面积,h 是高;球的体积公式:34=3V R π球,球的表面积公式:2=4S R π球,其中R 是球的半径; 样本数据12x x ,,…,n x 的方差2211()n i i s x x n ==-∑,其中x =11n i i x n =∑.一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上)1.命题“20,0x x x ∀>+>”的否定是 ▲ .2.右图给出的是一个算法的伪代码,若输入值为3, 2Read If 0Then()2Else()log (1)End If Print()xx x f x f x x f x ≤←←+则输出值()f x = ▲ .3.函数()sin xf x e x =的导数()f x '= ▲ .4.先后抛掷一枚质地均匀的骰子(各面上分别标有点数1,2,3,4,5,6)两次,骰子朝上的面的点数依次记为a 和b ,则双曲线22221x y a b-=为等轴双曲线的概率为 ▲ .5.右边程序输出的结果是 ▲ .6.恒大足球队主力阵容、替补阵容各有4名编号为1,2,3,4的球员进行足球点球练习,每人点球5次,射中的次数如下表:队员\编号 1号 2号 3号 4号 主力45341For From 1 To 5 Step 2 End For Print S I S S I S←←+则以上两组数据的方差中较小的方差2S = ▲ .7.下列有关命题的说法中,错误..的是 ▲ (填所有错误答案的序号). ①命题“若0232=+-x x ,则1=x ”的逆否命题为“若1≠x ,则0232≠+-x x ”; ②“1=x ”是“0232=+-x x ”的充分不必要条件;③若p q 且为假命题,则p 、q 均为假命题.8.已知抛物线x y 82=的焦点是双曲线)0(13222>=-a y a x 的右焦点, 则双曲线的渐近线方程为 ▲ .9.底面边长为2m ,高为1m 的正三棱锥的全面积为 ▲ 2m .10.奇函数32()f x ax bx cx =++在1x =-处有极值,则3a b c ++的值为 ▲ . 11.若,,l m n 是三条互不相同的空间直线,,αβ是两个不重合的平面,则下列命题中为真命题的是 ▲ (填所有正确答案的序号). ①若//,,,l n αβαβ⊂⊂则//l n ; ②若,,l αβα⊥⊂则l β⊥; ③若,,l n m n ⊥⊥则//l m ; ④若,//,l l αβ⊥则αβ⊥.12.设集合{,1},{,1,2},,{1,2,3,4,5,6,7}P x Q y x y ==∈,且P Q ⊆,在直角坐标平面内,从所有满足这些条件的有序实数对(,)x y 所表示的点中任取一个,若该点落在圆2222()x y R R Z +=∈ 内的概率为25,则满足要求的2R 的最小值为 ▲ . 13.如图平面直角坐标系xOy 中,椭圆22221(0)x y a b a b+=>>的离心率3e =,12,A A 分别是椭圆的左、右两个顶点, 圆1A 的半径为a ,过点2A 作圆1A 的切线,切点为P ,替补 5 4 2 5在x 轴的上方交椭圆于点Q .则2PQQA = ▲ . 14.设奇函数()f x 定义在(,0)(0,)ππ-上,其导函数为()f x ',且()02f π=,当0x π<<时,()sin ()cos 0f x x f x x '-<,则关于x 的不等式()2()sin 6f x f x π<的解集为 ▲ .二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) 15.(本小题满分14分)根据我国发布的《环境空气质量指数AQI 技术规定》(试行),AQI 共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200)为中度污染, [200,250),[250,300)均为重度污染,300及以上为严重污染.某市2013年11月份30天的AQI 的频率分布直方图如图所示:⑴该市11月份环境空气质量优或良的共有多少天?⑵若采用分层抽样方法从30天中抽取10天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?⑶空气质量指数低于150时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少? 16.(本小题满分14分)已知命题22:114x y p m m +=--表示双曲线,命题22:124x y q m m +=--表示椭圆. ⑴若命题p 为真命题,求实数m 的取值范围.⑵判断命题p 为真命题是命题q 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个).17.(本小题满分15分)如图,直三棱柱111ABC A B C -中,点D 是BC 上一点. ⑴若点D 是BC 的中点,求证1//A C 平面1AB D ; ⑵若平面1AB D ⊥平面11BCC B ,求证AD BC ⊥.18.(本小题满分15分) 如图,储油灌的表面积S 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.⑴试用半径r 表示出储油灌的容积V ,并写出r 的范围.⑵当圆柱高h 与半径r 的比为多少时,储油灌的容积V 最大?19.(本小题满分16分)如图,椭圆1C 与椭圆2C 中心在原点,焦点均在x 轴上,且离心率相同.椭圆1C 的长轴长为2,且椭圆1C 的左准线:2l x =-被椭圆2C 截得的线段ST 长为23P 是椭圆2C 上的一个动点. ⑴求椭圆1C 与椭圆2C 的方程;⑵设点1A 为椭圆1C 的左顶点,点1B 为椭圆1C 的下顶点,若直线OP 刚好平分11A B ,求点P 的坐标;⑶若点,M N 在椭圆1C 上,点,,P M N 满足2OP OM ON =+,则直线OM 与直线ON 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.20.(本小题满分16分)已知函数x x g bx ax x f ln )(,)(2=+=.⑴当0=a 时,①若)(x f 的图象与)(x g 的图象相切于点00(,)P x y ,求0x 及b 的值;②()()f x g x =在],1[m 上有解,求b 的范围;⑵当1-=b 时,若)()(x g x f ≥在1[,]n e上恒成立,求a 的取值范围.2013—2014学年度第一学期高二数学期末试卷参 考 答 案2014.1一、填空题1.20,0x x x ∃>+≤ 2.2 3.sin cos x x e x e x + 4.61 5.10 6.217.③ 8.x y 3±= 9.33 10.0 11.④ 12.30 13.34 14.(,0)(,)66πππ- 二、解答题15⑴由题意知该市11月份环境空气质量优或良的共有63050)002.0002.0(=⨯⨯+天; ……4分⑵中度污染被抽到的天数共有31050006.0=⨯⨯天; ……9分 ⑶设“市民王先生当天适宜户外晨练”为事件A ,则6.050)008.0002.0002.0()(=⨯++=A P . ……14分16⑴ 命题22:114x y p m m +=--表示双曲线为真命题,则(1)(4)0m m --<, ……3分∴14m <<; ……5分⑵ 命题22:124x y q m m +=--表示椭圆为真命题,204024m m m m->⎧⎪∴->⎨⎪-≠-⎩, ……8分 ∴23m <<或34m <<, ……10分{|14}m m <<{|23m m ⊇<<或34}m <<∴p 是q 的必要不充分条件. ……14分17⑴连接1A B ,设11AB A B E =,则E 为1A B 的中点, ……2分连接DE ,由D 是BC 的中点,得1//DE A C , ……4分 又1DE AB D ⊂面,且11A C AB D ⊄面,所以1//A C 平面1AB D ……7分 ⑵在平面11BCC B 中过B 作1BF B D ⊥,因平面1AB D ⊥平面11BCC B , 又平面1AB D平面111BCC B B D =,所以BF ⊥平面1AB D , ……10分所以BF AD ⊥,在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,所以1BB AD ⊥, ……12分 又1BB BF B =,所以AD ⊥平面11BCC B ,所以AD BC ⊥. ……15分18⑴2222232S r rh r r rh πππππ=++=+,232S r h rππ-∴=, ……3分3223V r r h ππ∴=+353(0)26rS S r r ππ=-<<; ……7分 ⑵2522S V r π'=-,令0V '=,得5S r π=,列表 FE……11分∴当r =时,体积V取得最大值,此时h =:1:1h r ∴=. ……13分答:储油灌容积35(026rS V r r π=-<<,当:1:1h r =时容积V 取得最大值. …15分 19⑴设椭圆1C 方程为221122111(0)x y a b a b +=>>,椭圆2C 方程为222222221(0)x y a b a b +=>>,则12a =1a =2112a x c =-=-,∴11c =,则11b =∴椭圆1C 方程为2212x y +=,其离心率为12e =, ……3分∴椭圆2C 中22222a b =,由线段的ST长为(S -,代入椭圆2C 22224312b b +=, 得225b =,∴2210a =,椭圆2C 方程为221105x y +=; ……6分⑵11((0,1)A B -,则11A B中点为1()2-,∴直线OP为y x =, ……7分由2211052x y y x ⎧+=⎪⎪⎨⎪=⎪⎩,得x y ⎧=⎪⎨=⎪⎩或x y ⎧=⎪⎨=⎪⎩ ∴点P的坐标为22-; ……10分⑶设00(,)P x y ,1122(,),(,)M x y N x y ,则2200210x y +=,2222112222,22x y x y +=+=,由题意001122(,)(,)2(,)x y x y x y =+,∴0121222x x x y y y =+⎧⎨=+⎩ ……12分∴22222222001212112211222(2)2(2)44288x y x x y y x x x x y y y y +=+++=+++++2222112212121212(2)4(2)6(2)106(2)10x y x y x x y y x x y y =+++++=++=……14分∴121220x x y y +=,∴121212y y x x =-,即12OM ON k k ⋅=-, ∴直线OM 与直线ON 的斜率之积为定值,且定值为12-. ……16分20⑴bx x f a =∴=)(0①1(),()f x b g x x ''==000011,,ln b x x e b e bx x ⎧=⎪∴∴=∴=⎨⎪=⎩, ……3分②x x b x x bx x g x f ln )0(ln )()(=∴>=∴= 即b y =与xxx h ln )(=在],1[m 上有交点…4分 2'ln 1)(x x x h -= ,e m ≤∴时)(x h 在],1[m 上递增,]ln ,0[)(mmx h ∈; e m >时)(x h 在],1[e 上递增,在],[m e 上递减且0)(>x h ,]1,0[)(ex h ∈ ……7分e m ≤∴时,]ln ,0[mmb ∈;e m >时,]1,0[e b ∈ ……8分 ⑵)()()(12x g x f x ax x f b ≥∴-=∴-= 即x x ax ln 2≥-,即2ln x x x a +≥在1[,]n e 上恒成立, ……9分 令2ln )(x x x x r +=,3ln 21)('xxx x r --=∴ 令()12ln s x x x =--,则()s x 为单调减函数,且(1)0s =, ……12分 ∴当(0,1)x ∈时,'()0r x >,()r x 单调递增,当(1,)x ∈+∞时,'()0r x <,()r x 单调递减, ……13分若1n ≤,则()r x 在1[,]n e上单调递增,∴2ln ()()max n n r x r n n +==,∴2ln n na n +≥; 若1n >,则()r x 在1[,1]e上单调递增,[1,]n 单调递减,∴()(1)1max r x r ==,∴1a ≥ ……15分 ∴1n ≤时,2ln n na n +≥;1n >时,1a ≥. ……16分。
【首发】江苏省扬州中学2014-2015学年高二上学期10月月考试卷数学Word版含答案

江苏省扬州中学2014—2015学年第一学期质量检测高二数学试卷 2014.10一、填空题:本大题共14个小题;每小题5分,共70分。
1、若直线y =kx +1与直线2x +y -4=0垂直,则k =_______.2、若直线3x +y +a =0过圆x 2+y 2+2x -4y =0的圆心,则a 的值为________. 3、设1AA 是正方体的一条棱,则这个正方体中与1AA 垂直的棱共有 条 4、直线012=-+y x 右上方(不含边界)的平面区域用不等式 表示. 5、若一个球的体积为43π,则它的表面积为__ ______.6、直线a,b 分别是长方体相邻两个面上的对角线所在直线,则a,b 位置关系是7、将一个圆锥的侧面沿一条母线剪开,其展开图是半径为2 的半圆,则该圆锥的高为8、过点C (3,4)且与x 轴,y 轴都相切的两个圆的半径分别为r 1,r 2,则r 1r 2=______.9、已知直线kx -y +1=0与圆C :x 2+y 2=4相交于A ,B 两点,若点M 在圆C 上,且有OM =OA +OB (O 为坐标原点),则实数k =_______.10. 设βα,为两个不重合的平面,n m ,是两条不重合的直线,给出下列四个命题:①若α⊂m ,α⊂n ,//m β,//n β,则//αβ; ②若,,βα⊂⊂m n βα与相交且不垂直,则m n 与不垂直; ③若,,m m n αβαβ⊥=⊥,则n ⊥β;④若βαα//,,//⊥n n m ,则β⊥m .其中所有真命题的序号是 .(写出所有真命题的序号)11、正三棱锥ABC P -高为2,侧棱与底面成045角,则点A 到侧面PBC 的距离是 12、过圆x 2+y 2=4内一点P (1,1)作两条相互垂直的弦AC ,BD ,当AC =BD 时,四边形ABCD 的面积为_______.13、设R n m ∈,,若直线02)1()1(=-+++y n x m 与圆1)1()1(22=-+-y x 相切,则m+n 的取值范围是14、平面直角坐标系中,已知点A (1,-2),B (4,0),P (a,1),N (a +1,1),当四边形PABN 的周长最小时,过三点A ,P ,N 的圆的圆心坐标是________.A BCP (第17题)D二、解答题:本大题共6小题,14+14+14+16+16+16= 90分. 15.如图,在四面体ABCD 中,AB AC DB DC ===,点E 是BC 的中点,点F 在线段AC 上,且AF ACλ=.(1)若EF ∥平面ABD ,求实数λ的值; (2)求证:平面BCD ⊥平面AED .16.已知:无论a 取何值,直线0)1()2(=++++a y a x a 始终平分半径为2的圆C(1)求圆C 的标准方程(2)自点)4,1(-A 作圆C 的切线l ,求切线l 的方程17.如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD , BC //平面PAD ,PBC ∠90=,90PBA ∠≠.求证:(1)//AD 平面PBC ;(2)平面PBC ⊥平面PAB .18、如图所示,在棱长为2的正方体1111ABCD A B C D -中,E 、F 分别为1DD 、DB 的中点.(1)求证:EF //平面11ABC D ;(2)求证:1EF B C ⊥; (3)求三棱锥EFC B V -1的体积.19. 在平面直角坐标系xOy 中,曲线y =x 2-6x +1与坐标轴的交点都在圆C 上.(1)求圆C 的方程;(2)若圆C 与直线x -y +a =0交于A ,B 两点,且OA ⊥OB ,求a 的值.20.在平面直角坐标系xOy 中,已知圆C 1:(x +1)2+y 2=1,圆C 2:(x -3)2+(y -4)2=1.(1)若过点C 1(-1,0)的直线l 被圆C 2截得的弦长为65,求直线l 的方程;(2)设动圆C 同时平分圆C 1的周长、圆C 2的周长. ①证明:动圆圆心C 在一条定直线上运动;②动圆C 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.CDBFED 1C 1B 1A A 1(第15题图)EABCDF高二数学质量检测参考答案 2014.101. 12 2. 1 3. 8 4. 012>-+y x 5. 12π 6.相交或异面 7._25_ 9. 0 10. ④ 11.6 13. ),222[]222,(+∞+⋃--∞ 14. ⎝⎛⎭⎫3,-98 15. 解:(1)因为EF ∥平面ABD ,易得EF ⊂平面ABC ,平面ABC平面ABD AB =,所以//EF AB ,(5分)又点E 是BC 的中点,点F 在线段AC 上, 所以点F 为AC 的中点, 由AF AC λ=得12λ=;(7分)(2)因为AB AC DB DC ===,点E 是BC 的中点,所以BC AE ⊥,BC DE ⊥,(9分) 又AEDE E =,AE DE ⊂、平面AED ,所以BC ⊥平面AED ,(12分) 而BC ⊂平面BCD ,所以平面BCD ⊥平面AED .(14分)16. (1)直线过定点)2,1(-据题意知圆心)2,1(-C ,故圆C 的标准方程为4)2()1(22=++-y x(2)直线l 垂直于x 轴时,合题,方程为1-=x直线l 不垂直于轴时,设方程为)1(4+=-x k y 即04=++-k y kx 由214)2(2=+++--k k k 得34-=k 此时方程为0834=-+y x综上,所求直线方程为1-=x 或0834=-+y x(第15题图)EABC DFA BCPDH17. 【证】(1)因为BC //平面PAD ,而BC ⊂平面ABCD ,平面ABCD I 平面PAD = AD , 所以BC //AD . …………………………………3分 因为AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBC .…………………………………………6分(2)自P 作PH ⊥AB 于H ,因为平面PAB ⊥平面ABCD ,且平面PAB I 平面ABCD =AB ,所以PH ⊥平面ABCD .…………………………………9分 因为BC ⊂平面ABCD ,所以BC ⊥PH . 因为PBC ∠90=,所以BC ⊥PB ,而90PBA ∠≠,于是点H 与B 不重合,即PB I PH = H . 因为PB ,PH ⊂平面PAB ,所以BC ⊥平面PAB .…………12分 因为BC ⊂平面PBC ,故平面PBC ⊥平面PAB .…………… 14分18. 证明:(1)连结1BD ,在B DD 1∆中,E 、F 分别为1D D ,DB 的中点,则11111111////EF D BD B ABC D EF ABC D EF ABC D ⎫⎪⊂⇒⎬⎪⊄⎭平面平面平面(2)1111111,B C ABB C BC AB B C ABC D AB BC B ⊥⎫⎪⊥⎪⎬⊂⎪⎪=⎭平面⇒111111B C ABC D BD ABC D ⊥⎫⇒⎬⊂⎭平面平面111//B C BD EF BD ⊥⎫⎬⎭1EF B C ⇒⊥(3)11CF BDD B ⊥平面CDBFED 1C 1B 1AA 11CF EFB ∴⊥平面 且 C F B F ==112EF BD ==,1B F ===13B E ===∴22211EF B F B E +=即190EFB ∠=11113B EFC C B EF B EF V V S CF --∆∴==⋅⋅=11132EF B F CF ⨯⋅⋅⋅=11132⨯=19. 解:(1)曲线y =x 2-6x +1与y 轴的交点为(0,1), 与x 轴的交点为(3+22,0),(3-22,0). 故可设C 的圆心为(3,t ),则有32+(t -1)2=(22)2+t 2,解得t =1. 则圆C 的半径为32+(t -1)2=3. 所以圆C 的方程为(x -3)2+(y -1)2=9. (2)设A (x 1,y 1),B (x 2,y 2),其坐标满足方程组⎩⎪⎨⎪⎧x -y +a =0,(x -3)2+(y -1)2=9. 消去y ,得方程2x 2+(2a -8)x +a 2-2a +1=0. 由已知可得,判别式Δ=56-16a -4a 2>0. 从而x 1+x 2=4-a ,x 1x 2=a 2-2a +12. ①由于OA ⊥OB ,可得x 1x 2+y 1y 2=0. 又y 1=x 1+a ,y 2=x 2+a , 所以2x 1x 2+a (x 1+x 2)+a 2=0. ② 由①②得a =-1,满足Δ>0,故a =-1.20. [解] (1)设直线l 的方程为y =k (x +1), 即kx -y +k =0.因为直线l 被圆C 2截得的弦长为65,而圆C 2的半径为1,所以圆心C 2(3,4)到l :kx -y+k =0的距离为|4k -4|k 2+1=45. 化简,得12k 2-25k +12=0,解得k =43或k =34.所以直线l 的方程为4x -3y +4=0或3x -4y +3=0. (2)①证明:设圆心C (x ,y ),由题意,得CC 1=CC 2, 即(x +1)2+y 2=(x -3)2+(y -4)2. 化简得x +y -3=0,即动圆圆心C 在定直线x +y -3=0上运动. ②圆C 过定点,设C (m,3-m ), 则动圆C 的半径为1+CC 21 =1+(m +1)2+(3-m )2.于是动圆C 的方程为(x -m )2+(y -3+m )2 =1+(m +1)2+(3-m )2.整理,得x 2+y 2-6y -2-2m (x -y +1)=0.由 ⎩⎪⎨⎪⎧x -y +1=0,x 2+y 2-6y -2=0,得⎩⎨⎧x =1+322,y =2+322或 ⎩⎨⎧x =1-322,y =2-322.所以定点的坐标为⎝⎛⎭⎫1-322,2-322,⎝⎛⎭⎫1+322,2+322.。
江苏省扬州市2013-2014学年高二下学期期末调研测试数学文Word版含答案

2013-2014学年度第二学期高二期末调研测试数 学 (文科)试 题(全卷满分160分,考试时间120分钟)2014.6注意事项:1. 答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷规定的地方.2.试题答案均写在答题卷相应位置,答在其它地方无效.一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应位置)1.设集合{1,2,3}A =,集合{2,2}B =-,则AB = ▲ .2.i 为虚数单位,复数21i-= ▲ . 3.函数()lg(1)f x x =+的定义域为 ▲ . 4.“0ϕ=”是“函数()sin()f x x ϕ=+为奇函数”的▲ 条件.(从“充要”,“充分不必要”,“必要不充分”,“既不充分也不必要”中选择适当的填写) 5.函数xy e =在1x =处的切线的斜率为 ▲ .6.若tan θ+1tan θ=4则sin2θ= ▲ . 7.点A (2,2)关于直线x-y-1=0的对称点'A 的坐标为 ▲ .8.函数()sin cos f x x x =-的值域为 ▲ .9.===⋅⋅⋅=, 则21n m += ▲ . 10.已知函数2|1|=1x y x --的图象与函数=2y kx -的图象恰有两个交点,则实数k 的取值范围是 ▲ .11.已知函数()f x 是定义在[4,)-+∞上的单调增函数,且对于一切实数x ,不等式22(cos )(sin 3)f x b f x b -≥--恒成立,则实数b 的取值范围是 ▲ .12.设T S ,是R 的两个非空子集,如果存在..一个从S 到T 的函数)(x f y =满足;(i)}|)({S x x f T ∈=;(ii)对任意S x x ∈21,,当21x x <时,恒有)()(21x f x f <. 那么称这两个集合“保序同构”.现给出以下4对集合: ①,{1,1}S R T ==-; ②*,S N T N ==;③{|13},{|810}S x x T x x =-≤≤=-≤≤; ④{|01},S x x T R =<<=其中,“保序同构”的集合对的对应的序号是 ▲ (写出所有“保序同构”的集合对的对应的序号).13.已知点(1,2),(1,2),(5,2)A B C --,若分别以,AB BC 为弦作两外切的圆M 和圆N ,且两圆半径相等,则圆的半径为 ▲ .14.若关于x 的不等式2x ax e ≥的解集中的正整数解有且只有3个,则实数a 的取值范围是 ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) 15.(本小题满分14分)已知a R ∈,命题2:"[1,2],0"p x x a ∀∈-≥,命题2:",220"q x R x ax a ∃∈++-=. ⑴若命题p 为真命题,求实数a 的取值范围;⑵若命题""p q ∨为真命题,命题""p q ∧为假命题,求实数a 的取值范围. 16.(本小题满分14分)已知函数()2cos()(0,)6f x x x R πωω=+>∈的最小正周期为10π.⑴求函数()f x 的对称轴方程; ⑵设,[0,]2παβ∈,56516(5),(5)35617f f ππαβ+=--=,求cos()αβ+的值.17.(本小题满分14分)已知函数2()1f x ax bx =++(,a b 为实数,0,a x R ≠∈),(),0()(),0f x x F x f x x >⎧=⎨-<⎩.⑴若(1)0f -=,且函数()f x 的值域为[0,)+∞,求()F x 的表达式;⑵设0,0,0mn m n a <+>>,且函数()f x 为偶函数,求证:()()0F m F n +>. 18.(本小题满分16分)如图,某市新体育公园的中心广场平面图如图所示,在y 轴左侧的观光道曲线段是函数sin()(0,0,0)y A x A ωϕωϕπ=+>><<,[4,0]x ∈-时的图象且最高点B (-1,4),在y 轴右侧的曲线段是以CO 为直径的半圆弧.⑴试确定A ,ω和ϕ的值;⑵现要在右侧的半圆中修建一条步行道CDO (单位:米),在点C 与半圆弧上的一点D 之间设计为直线段(造价为2万元/米),从D 到点O 之间设计为沿半圆弧的弧形(造价为1万元/米).设DCO θ∠=(弧度),试用θ来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)19.(本小题满分16分)如图,圆22:4O x y +=⑴求与直线AC⑵设点M 是圆上任意一点(不在坐标轴上),直线CM 交x 轴于点D ,直线BM 交直线AC 于点N ,①若D 点坐标为,求弦CM 的长; ②求证:2ND MB k k -为定值. 20.(本小题满分16分)已知函数2()(,)f x ax bx a b R =+∈,函数()ln g x x =.⑴当0=a 时,函数)(x f 的图象与函数)(x g 的图象有公共点,求实数b 的最大值; ⑵当0b =时,试判断函数)(x f 的图象与函数)(x g 的图象的公共点的个数;⑶函数)(x f 的图象能否恒在函数()y bg x =的图象的上方?若能,求出,a b 的取值范围;若不能,请说明理由.2014年6月高二期末调研测试文 科 数 学 试 题 参 考 答 案一、填空题:1.{2} 2.1i + 3.(1,)-+∞ 4.充分不必要5.e 6.127.(3,1) 8.[9.2014 10.(0,1)(1,4) 11.1[212.②③④13 14.4[,)16e e二、解答题:15⑴因为命题2:"[1,2],0"p x x a ∀∈-≥,令2()f x x a =-,根据题意,只要[1,2]x ∈时,min ()0f x ≥即可, ……4分 也就是101a a -≥⇒≤; ……7分 ⑵由⑴可知,当命题p 为真命题时,1a ≤,命题q 为真命题时,244(2)0a a ∆=--≥,解得21a a ≤-≥或 ……11分 因为命题""p q ∨为真命题,命题""p q ∧为假命题,所以命题p 与命题q 一真一假,当命题p 为真,命题q 为假时,12121a a a ≤⎧⇒-<<⎨-<<⎩,当命题p 为假,命题q 为真时,11-21a a a a >⎧⇒>⎨≤≥⎩或,综上:1a >或21a -<<. ……14分 16⑴由条件可知,21105T ππωω==⇔=, ……4分则由155()566x k x k k Z ππππ+=⇒=-+∈为所求对称轴方程; ……7分⑵56334(5)cos()sin ,cos352555f ππαααα+=-⇔+=-⇔==, 因为[0,]2πα∈,所以56334)cos()sin ,cos 352555ππααα=-⇔+=-⇔==, 516815(5)cos ,sin 6171717f πβββ-=⇔==,因为[0,]2πβ∈,所以516815(5)cos ,sin 6171717f πβββ-=⇔== ……11分4831513cos()cos cos sin sin 51751785αβαβαβ+=-=⨯-⨯=-. ……14分17⑴由(1)0f -=得10a b -+=,由()f x 值域为[0,)+∞得20,40a b a >⎧⎨∆=-=⎩, ……4分 24(1)02,1b b b a --=⇒==,2()(1)f x x =+,22(1),0()(1),0x x F x x x ⎧+>⎪=⎨-+<⎪⎩;……7分⑵因为偶函数,2()1f x ax =+,又0a >,所以221,0()1,0ax x F x ax x ⎧+>⎪=⎨--<⎪⎩, ……11分因为0mn <,不妨设0m >,则0n <,又0m n +>,所以0m n >->,2222()()11()0F m F n am an a m n +=+--=->,则()()0F m F n +>. …14分 18⑴因为最高点B (-1,4),所以A =4;1(4)3124TT =---=⇒=, 因为2126T ππωω==⇒= ……5分代入点B (-1,4),44sin[(1)]sin()166ππϕϕ=⨯-+⇒-=, 又203πϕπϕ<<⇒=; ……8分⑵由⑴可知:24sin(),[4,0]63y x x ππ=+∈-,得点C (0,即CO = 取CO 中点F ,连结DF ,因为弧CD 为半圆弧,所以2,90DFO CDO θ∠=∠=︒,即2DO θ== ,则圆弧段DO造价预算为万元, Rt CDO ∆中,CD θ=,则直线段CD造价预算为θ万元所以步行道造价预算()g θθ=+,(0,)2πθ∈. ……13分由'()sin )2sin )g x θθ=-+=-得当6πθ=时,'()0g θ=,当(0,)6πθ∈时,'()0g x >,即()g θ在(0,)6π上单调递增; 当(,)62ππθ∈时,'()0g x <,即()g θ在(,)62ππ上单调递减 所以()g θ在6πθ=时取极大值,也即造价预算最大值为(6)万元.……16分19.(2,0),(2,0),(0,2)A B C -,直线:20AC x y -+=, ……2分 ⑴设l :0x y b ++=2=则b =±,所以l:0x y +±=; ……5分⑵①CM:0x +-=,圆心到直线CM的距离d ==所以弦CM的长为2=;(或由等边三角形COM ∆亦可) ……9分 ②解法一:设直线CM 的方程为:2(y kx k =+存在,0,1)k k ≠≠±,则2(,0)D k-由2224y kx x y =+⎧⎨+=⎩,得22(1)40k x kx ++=,所以0x =或241kx k=-+, 将241kx k=-+代入直线CM ,得22221k y k -=+,即222422(,)11k k M k k --++,……12分 则11BMk k k -=+,BM :1(2)1k y x k -=-+,:201:(2)1AC BM l x y k l y x k -+=⎧⎪⎨-=-⎪+⎩,(2,22)N k k -- 得1ND k k k =+,所以212111ND MB k k k k k k --=-=++为定值. ……16分解法二:设00(,)M x y ,则2200002,0,4x x x y ≠±≠+=,直线002:2CM y l y x x -=+, 则002(,0)2x D y -,002MB y k x =-,直线00:(2)2BM y l y x x =--,又:2AC l y x =+AC 与BM 交点00000004224(,)22x y y N x y x y -------,02000022000000000004242242224422NDy x y y y k x x y x x y y y y x y ---==---+------ 将22004x y =-,代入得00022ND y k x y -=+-, ……13分所以200000002000000002(2)248222424ND MBy y x y y x y k k x y x x x x y y ---+--=-=+---+-+, 得220000000000220000000000248248214424842ND MBx y y x y x y y x y k k y x x y y y x x y y --+---+--===--+-+--+-为定值.……16分 20⑴bx x f a =∴=)(0 ,由一次函数与对数函数图象可知两图象相切时b 取最大值, ……1分 设切点横坐标为0x ,1(),()f x b g x x''==,000011,,ln b x x e b e bx x⎧=⎪∴∴=∴=⎨⎪=⎩, 即实数b 的最大值为1b e =; ……4分⑵2ln 0,0,()()xb x f x g x a x =>∴=⇔=, 即原题等价于直线y a =与函数2ln ()xr x x=的图象的公共点的个数, ……5分'432ln 12ln ()x x x xr x x x--==, ()r x ∴在递增且1()(,)2r x e∈-∞,()r x 在)+∞递减且1()(0,)2r x e∈,1(,)2a e∴∈+∞时,无公共点,1(,0]{}2a e ∈-∞⋃时,有一个公共点,1(0,)2a e∈时,有两个公共点; ……9分⑶函数)(x f 的图象恒在函数()y bg x =的图象的上方,即()()f x bg x >在0x >时恒成立, ……10分①0a <时()f x 图象开口向下,即()()f x bg x >在0x >时不可能恒成立, ②0a =时ln bx b x >,由⑴可得ln x x >,0b ∴>时()()f x bg x >恒成立,0b ≤时()()f x bg x >不成立,③0a >时, 若0b <则2ln a x x b x -<,由⑵可得2ln x xx-无最小值,故()()f x bg x >不可能恒成立, 若0b =则20ax >,故()()f x bg x >恒成立,若0b >则2(ln )0ax b x x +->,故()()f x bg x >恒成立, ……15分 综上,0,0a b =>或0,0a b >≥时函数)(x f 的图象恒在函数()y bg x =的图象的上方. ……16分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014.1(满分160分,考试时间120分钟)注意事项:试题答案均写在答题卷相应位置,答在其它地方无效.参考公式:柱体的体积公式:=V Sh 柱体,其中S 是柱体的底面积,h 是高; 球的体积公式:34=3V R π球,球的表面积公式:2=4S R π球,其中R 是球的半径; 样本数据12x x ,,…,n x 的方差2211()n i i s x x n ==-∑,其中x =11n i i x n =∑.一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上) 1.命题“20,0x x x ∀>+>”的否定是 ▲ .2.右图给出的是一个算法的伪代码,若输入值为3, 2Read If 0Then()2Else()log (1)End If Print()xxx f x f x x f x ≤←←+则输出值()f x = ▲ .3.函数()sin xf x e x =的导数()f x '= ▲ .4.先后抛掷一枚质地均匀的骰子(各面上分别标有点数1,2,3,4,5,6)两次,骰子朝上的面的点数依次记为a 和b ,则双曲线22221x y a b-=为等轴双曲线的概率为 ▲ .5.右边程序输出的结果是 ▲ .6.恒大足球队主力阵容、替补阵容各有4名编号为1,2,3,4的球员进行足球点球练习,每人点球5次,射中的次数如下表:则以上两组数据的方差中较小的方差2S = ▲ .1For From 1 To 5 Step 2 End For Print S I S S I S←←+2013—2014学年度第一学期高二数学期末试卷7.下列有关命题的说法中,错误..的是 ▲ (填所有错误答案的序号). ①命题“若0232=+-x x ,则1=x ”的逆否命题为“若1≠x ,则0232≠+-x x ”; ②“1=x ”是“0232=+-x x ”的充分不必要条件; ③若p q 且为假命题,则p 、q 均为假命题.8.已知抛物线x y 82=的焦点是双曲线)0(13222>=-a y a x 的右焦点,则双曲线的渐近线方程为 ▲ .9.底面边长为2m ,高为1m 的正三棱锥的全面积为 ▲ 2m .10.奇函数32()f x ax bx cx =++在1x =-处有极值,则3a b c ++的值为 ▲ . 11.若,,l m n 是三条互不相同的空间直线,,αβ是两个不重合的平面,则下列命题中为真命题的是 ▲ (填所有正确答案的序号). ①若//,,,l n αβαβ⊂⊂则//l n ; ②若,,l αβα⊥⊂则l β⊥; ③若,,l n m n ⊥⊥则//l m ; ④若,//,l l αβ⊥则αβ⊥.12.设集合{,1},{,1,2},,{1,2,3,4,5,6,7}P x Q y x y ==∈,且P Q ⊆,在直角坐标平面内,从所有满足这些条件的有序实数对(,)x y 所表示的点中任取一个,若该点落在圆2222()x y R R Z +=∈ 内的概率为25,则满足要求的2R 的最小值为 ▲ . 13.如图平面直角坐标系xOy 中,椭圆22221(0)x y a b a b+=>>的离心率e =12,A A 分别是椭圆的左、右两个顶点, 圆1A 的半径为a ,过点2A 作圆1A 的切线,切点为P , 在x 轴的上方交椭圆于点Q .则2PQQA = ▲ . 14.设奇函数()f x 定义在(,0)(0,)ππ-U 上,其导函数为()f x ',且()02f π=,当0x π<<时,()sin ()cos 0f x x f x x '-<,则关于x 的不等式()2()sin 6f x f x π<的解集为 ▲ .二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) 15.(本小题满分14分)根据我国发布的《环境空气质量指数AQI 技术规定》(试行),AQI 共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200为中度污染,[200,250),[250,300)均为重度污染,300及以上为严重污染.某市2013年11月份30天的AQI 的频率分布直方图如图所示:⑴该市11月份环境空气质量优或良的共有多少天?⑵若采用分层抽样方法从30天中抽取10天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?⑶空气质量指数低于150时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少? 16.(本小题满分14分)已知命题22:114x y p m m +=--表示双曲线,命题22:124x y q m m +=--表示椭圆. ⑴若命题p 为真命题,求实数m 的取值范围.⑵判断命题p 为真命题是命题q 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个).17.(本小题满分15分)如图,直三棱柱111ABC A B C -中,点D 是BC 上一点. ⑴若点D 是BC 的中点,求证:1//AC 平面1AB D ; ⑵若平面1AB D ⊥平面11BCC B ,求证:AD BC ⊥.18.(本小题满分15分)如图,储油灌的表面积S 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.⑴试用半径r 表示出储油灌的容积V ,并写出r 的范围.⑵当圆柱高h 与半径r 的比为多少时,储油灌的容积V 最大?19.(本小题满分16分)如图,椭圆1C 与椭圆2C 中心在原点,焦点均在x 轴上,且离心率相同.椭圆1C 的长轴长为且椭圆1C 的左准线:2l x =-被椭圆2C 截得的线段ST 长为P 是椭圆2C 上的一个动点.⑴求椭圆1C 与椭圆2C 的方程;⑵设点1A 为椭圆1C 的左顶点,点1B 为椭圆1C 的下顶点,若直线OP 刚好平分11A B ,求点P 的坐标;⑶若点,M N 在椭圆1C 上,点,,P M N 满足2OP OM ON =+,则直线OM 与直线ON 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由. 20.(本小题满分16分)已知函数x x g bx ax x f ln )(,)(2=+=.⑴当0=a 时,①若)(x f 的图象与)(x g 的图象相切于点00(,)P x y ,求0x 及b 的值;②()()f x g x =在],1[m 上有解,求b 的范围;⑵当1-=b 时,若)()(x g x f ≥在1[,]n e上恒成立,求a 的取值范围.2013—2014学年度第一学期高二数学期末试卷参 考 答 案2014.1一、填空题1.20,0x x x ∃>+≤ 2.2 3.sin cos x xe x e x + 4.61 5.10 6.217.③ 8.x y 3±= 9.33 10.0 11.④ 12.30 13.34 14.(,0)(,)66πππ- 二、解答题15⑴由题意知该市11月份环境空气质量优或良的共有63050)002.0002.0(=⨯⨯+天; ……4分⑵中度污染被抽到的天数共有31050006.0=⨯⨯天; ……9分 ⑶设“市民王先生当天适宜户外晨练”为事件A ,则6.050)008.0002.0002.0()(=⨯++=A P . ……14分16⑴ 命题22:114x y p m m +=--表示双曲线为真命题,则(1)(4)0m m --<, ……3分 ∴14m <<; ……5分⑵ 命题22:124x y q m m +=--表示椭圆为真命题,204024m m m m->⎧⎪∴->⎨⎪-≠-⎩, ……8分 ∴23m <<或34m <<, ……10分{|14}m m <<{|23m m ⊇<<或34}m <<∴p 是q 的必要不充分条件. ……14分17⑴连接1A B ,设11AB A B E =,则E 为1A B 的中点, ……2分连接DE ,由D 是BC 的中点,得1//DE AC , ……4分 又1DE AB D ⊂面,且11AC AB D ⊄面, 所以1//AC 平面1AB D ……7分FE⑵在平面11BCC B 中过B 作1BF B D ⊥,因平面1AB D ⊥平面11BCC B , 又平面1AB D平面111BCC B B D =,所以BF ⊥平面1AB D , ……10分所以BF AD ⊥,在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,所以1BB AD ⊥, ……12分 又1BB BF B =,所以AD ⊥平面11BCC B ,所以AD BC ⊥. ……15分18⑴2222232S r rh r r rh πππππ=++=+,232S r h rππ-∴=, ……3分3223V r r h ππ∴=+35(026rS r r π=-<<; ……7分⑵2522S V r π'=-,令0V '=,得5r π=,列表……11分∴当r=时,体积V 取得最大值,此时h =:1:1h r ∴=. ……13分 答:储油灌容积35(0263rS V r r ππ=-<<,当:1:1h r =时容积V 取得最大值. …15分 19⑴设椭圆1C 方程为221122111(0)x y a b a b +=>>,椭圆2C 方程为222222221(0)x y a b a b +=>>,则12a =1a =2112a x c =-=-,∴11c =,则11b =∴椭圆1C 方程为2212xy +=,其离心率为1e =, ……3分 ∴椭圆2C 中22222a b =,由线段的ST长为(S -,代入椭圆2C 22224312b b +=,得225b =,∴2210a =,椭圆2C 方程为221105x y +=; ……6分⑵11((0,1)A B -,则11A B中点为1()22--,∴直线OP为2y x =, ……7分由2211052x y y x ⎧+=⎪⎪⎨⎪=⎪⎩,得x y ⎧=⎪⎨=⎪⎩或x y ⎧=⎪⎨=⎪⎩, ∴点P的坐标为; ……10分 ⑶设00(,)P x y ,1122(,),(,)M x y N x y ,则2200210x y +=,2222112222,22x y x y +=+=,由题意001122(,)(,)2(,)x y x y x y =+,∴01201222x x x y y y =+⎧⎨=+⎩ ……12分∴22222222001212112211222(2)2(2)44288x y x x y y x x x x y y y y +=+++=+++++ 2222112212121212(2)4(2)6(2)106(2)10x y x y x x y y x x y y =+++++=++=……14分∴121220x x y y +=,∴121212y y x x =-,即12OM ON k k ⋅=-,∴直线OM 与直线ON 的斜率之积为定值,且定值为12-. ……16分20⑴bx x f a =∴=)(0①1(),()f x b g x x ''==000011,,ln b x x e b ebx x ⎧=⎪∴∴=∴=⎨⎪=⎩, ……3分②x x b x x bx x g x f ln )0(ln )()(=∴>=∴= 即b y =与xxx h ln )(=在],1[m 上有交点…4分 2'ln 1)(x x x h -= ,e m ≤∴时)(x h 在],1[m 上递增,]ln ,0[)(mmx h ∈; e m >时)(x h 在],1[e 上递增,在],[m e 上递减且0)(>x h ,]1,0[)(ex h ∈ ……7分e m ≤∴时,]ln ,0[mmb ∈;e m >时,]1,0[e b ∈ ……8分⑵)()()(12x g x f x ax x f b ≥∴-=∴-= 即x x ax ln 2≥-,即2ln x x x a +≥在1[,]n e 上恒成立, ……9分 令2ln )(x x x x r +=,3ln 21)('x xx x r --=∴令()12ln s x x x =--,则()s x 为单调减函数,且(1)0s =, ……12分 ∴当(0,1)x ∈时,'()0r x >,()r x 单调递增,当(1,)x ∈+∞时,'()0r x <,()r x 单调递减, ……13分 若1n ≤,则()r x 在1[,]n e上单调递增,∴2ln ()()max n n r x r n n +==,∴2ln n na n+≥; 若1n >,则()r x 在1[,1]e上单调递增,[1,]n 单调递减,∴()(1)1max r x r ==,∴1a ≥ ……15分 ∴1n ≤时,2ln n na n+≥;1n >时,1a ≥. ……16分。
