2017年全国各地市中考数学规律探索归纳探究题汇总(附答案)
2017年各地市中考规律探索归纳探究题汇总有参考答案

精心整理2017年各地市中考规律探索归纳探究题汇总1.在一列数:a1,a2,a3,…,a n中,a1=3,a2=7,从第三个数开始,每一个数都等于它前两个数之积的个位数字,则这一列数中的第2017个数是()A.1B.3C.7D.9【来源】2017年中考真题精品解析数学(江苏扬州卷)精编word版(解析版)【答案】B【解析】依题意得:a1=3,a2=7,a3=1,a4=7,a5=7,a6=9,a7=3,a8=7,……周期为6,2017÷6=336…1,所以a2017=a1=3,故选B.【点睛】本题考查了数字变化类的规律型问题,然后根据所求得的数字发现规律.2A.180B.182C.184D.186【来源】四川省自贡市初2017【答案】C【解析】二、三、四格.等于等于第二、四格数据的积;所以1113m+=⨯故应选C..探寻规律要认真观察、仔细思3.3.4颗星星,第21颗星星,.....按此规律排列下去,第⑨个图A.116B.144【来源】【答案】B第4个图形为:4×5+2+3+4+5,∴第⑨个图形中的颗数为:9×10+2+3+4+5+6+7+8+9+10=144.故选B.考点:规律型:图形的变化类.4.(2017重庆,第10题,4分)下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为()A.73B.81C.91D.109【来源】2017年初中毕业升学考试(重庆A卷)数学(带解析)【答案】C【解析】试题解析:第①个图形中一共有3个菱形,3=12+2;第②个图形中共有7个菱形,7=22+3;第③个图形中共有13个菱形,13=32+4;…,第n 个图形中菱形的个数为:n 2+n+1; 第⑨个图形中菱形的个数92+9+1=91. 故选C .考点:图形的变化规律.5.我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧12PP ,23P P ,34P P ,…得到斐波那契螺旋线,然后顺次连结12P P ,23P P ,34P P ,…得到螺旋折线(如图),已知点1P (0,1),2P (1-,0),3P (0,1-),则该折线上的点9P 的坐标为()A .(6-,24)B .(6-,25)C .(5-,24)D .(5-,25) (第10 所以P 9故选B .61),从点A 经过一次跳马变换可以到达点2), A .13B 过了320+1)÷7×考点:17A .180B .182C .184D .186【来源】2017年初中毕业升学考试(四川自贡卷)数学(带解析) 【答案】C. 【解析】试题解析:由前面数字关系:1,3,5;3,5,7;5,7,9, 可得最后一个三个数分别为:11,13,15, ∵3×5﹣1=14,; 5×7﹣3=32; 7×9﹣5=58;∴m=13×15﹣11=184. 故选C .考点:数字规律.8.如图,将矩形ABCD 绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A 在整个旋转过程中所经过的路径总长为() A.2017πB.2034πC.3024πD.3026π【来源】2017年初中毕业升学考试(四川达州卷)数学(带解析) 【答案】D【解析】解:∵AB =4,BC =3,∴AC =BD =5.转动一次A 的路线长是:904180π⨯=2π,转动第二次的路线长是:905180π⨯=52π,转动第三次的路线长是:903180π⨯=32π,转动第四次的路线长是:0,以此类推,每四次循环.故顶点A 转动四次经过的路线长为:52π+32π+2π=6π.∵2017÷4=504…1,∴顶点A 9.用棋子摆出下列一组图形:按照这种规律摆下去,第n 个图形用的棋子个数为()A .n 3B .n 6 C.63+n D .33+n【来源】2017【答案】D . 【解析】试题解析:∵第一个图需棋子3+3=6; 第二个图需棋子3×2+3=9; 第三个图需棋子3×3+3=12; …∴第n故选:D .10.a 的值为( ) A.23B.75 C.77D.139【来源】 【答案】B1,3,5,7,9,11,左边的数为21,22,23a=11+64=75,故选B .11.(2017中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( ) A.121B.362C.364D.729【来源】2017年初中毕业升学考试(山东德州卷)数学(带解析) 【答案】C【解析】试题分析:①图1,0×3+1=1; ②图2,1×3+1=4; ③图3,4×3+1=13; ④图4,13×3+1=40; ⑤图5,40×3+1=121; ⑥图6,121×3+1=364; 故选C考点:探索规律12.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后三个数的和为768,则n为()A.9B.10C.11D.12【来源】2017年初中毕业升学考试(湖北武汉卷)数学(带解析)【答案】A.【解析】试题解析:设后3个的数和为:(-1)n+1×2n-1+(-1)n+2×2n+(-1)n+3×2n+1=768,当n为偶数:整理得出:-5×(-2)n-1=768,则求不出整数,当n为奇数:整理得出:3×2n-1=768,解得:n=9.故选A.考点:数字变化规律.13.(2017贵州省黔东南州,第10题,4如南宋数学家杨辉(约13世纪)所着的(a+b)n 的展开式的各项系数,此三角形称为“杨辉三角”根据“杨辉三角”请计算(a+b)20A.2017B.2016C.191D.190【来源】2017【答案】D【解析】试题解析:找规律发现(a+b)3(a+b)4的第三项系数为6=1+2+3;(a+b)5的第三项系数为10=1+2+3+4;不难发现(a+b)n的第三项系数为1+2+3+…+(n∴(a+b)20故选D.14.“d”的个数,若第n个图形中“d”的个数是78A.11B.【来源】【答案】B【解析】第四个图形有1+2+3+4=10个○,……第n个图形有1+2+3+……+n=(1)2n n+个○,故(1)2n n+=78,解得n=12或n=-13(舍去).故选:B考点:规律探索15.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB 边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B,M间的距离可能是()A.1.4B.1.1C.0.8D.0.5【来源】2017年初中毕业升学考试(河北卷)数学(带解析)【答案】C.【解析】试题分析:在第一次旋转中BM=1,在第二次旋转中BM=1,在第三次旋转中BM的长从11,在第四次旋转中BM的长从1,在第五次旋转中BM1-变化到1,在第六次旋转中BM=1,故答案选C.16上的点A处,1点出发,沿着射线A O2…按【来源】【答案】A【解析】故选:A17,表示a1=aA.32B.【来源】2017年初中毕业升学考试(湖北十堰卷)数学(带解析)【答案】D.【解析】试题分析:由a1=a7+3(a8+a9)+a10知要使a1取得最小值,则a8+a9应尽可能的小,取a8=2、a9=4,根据a5=a8+a9=6,则a7、a10中不能有6,据此对于a7、a8,分别取8、10、12检验可得.∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3(a8+a9)+a10,∴要使a1取得最小值,则a8+a9应尽可能的小,取a8=2、a9=4,∵a5=a8+a9=6,则a7、a10中不能有6,若a7=8、a10=10,则a4=10=a10,不符合题意,舍去;若a7=10、a10=8,则a4=12、a6=4+8=12,不符合题意,舍去;若a7=10、a10=12,则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40,符合题意;综上,a1的最小值为40,故选:D.考点:数字的变化类18.刘莎同学用火柴棒依图的规律摆六边形图案,用10086根火柴棒摆出的图案应该是第______个.【来源】2017年中考真题精品解析数学(湖南娄底卷) 【答案】2017.【解析】解:由图可知:第1个图形的火柴棒根数为6; 第2个图形的火柴棒根数为11; 第3个图形的火柴棒根数为16; …由该搭建方式可得出规律:图形标号每增加1,火柴棒的个数增加5,所以可以得出规律:搭第n 个图形需要火柴根数为:6+5(n ﹣1)=5n +1,令5n +1=10086,解得:n =2017. 故答案为:2017.点睛:本题考查了图形的变化类问题,遍规律求解即可.19.19.如图,第一个图形中有1按此规律,第n 个图形中有______个点.【来源】2017【答案】()1312n -.【解析】如图,第一个图形中有1按此规律,第n 个图形中有12(3n -1)个点,【点睛】20.201、3、6、10、15、21、…叫做6是第三个三角形数,…,依此类推,第100【来源】 2=3=1+2,a 3=6=1+2+3,a 4=10=1+2+3+4,… ∴a n a 100=()10010012+=5050,故答案为:5050.点睛:本题考查了规律型中的数字的变化类,解题的关键是找出变化规律“a n =1+2+…+n =()12n n +”.21.如图,Rt△OA 0A 1在平面直角坐标系内,∠OA 0A 1=90°,∠A 0OA 1=30°,以OA 1为直角边向外作Rt△OA 1A 2,使∠OA 1A 2=90°,∠A 1OA 2=30°,以OA 2为直角边向外作Rt△OA 2A 3,使∠OA 2A 3=90°,∠A 2OA 3=30°,按此方法进行下去,得到Rt△OA 3A 4,Rt△OA 4A 5,…,Rt△OA 2016A 2017,若点A 0(1,0),则点A 2017的横坐标为______.【来源】山东省济南市槐荫区2018届九年级上学期期中考试数学试题【答案】2016⎝⎭.【解析】由已知可得OA 1OA 2=23⎛ ⎝⎭,OA 3=33⎛ ⎝⎭,……,由此可得OA 2017=20173⎛ ⎝⎭,360°÷30°=12,2017÷12=168…3,由些可知OA 2017所在的射线与OA 1所在射线重合,所以点A 2017的横坐标为:OA 2017×cos30°=2017⎝⎭2016⎝⎭,故答案为:20163⎛⎫⎪ ⎪⎝⎭.【点睛】本题主要考查规律性问题,解题的关键是能根据已知条件先求出一些相关的量,从中发现规律.22.如图,等边△A 1C 1C 2的周长为1,作C 1D 1⊥A 1C 2C 3=D 1C 1,连接D 1C 3,以C 2C 3为边作等边△A 2C 2C 3;作C 2D 2⊥A 2D 2C 4=D 2C 2,连接D 2C 4,以C 3C 4为边作等边△A 3C 3C 4;…且点A 1△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1【来源】2017【答案】1212n n --.【解析】解:∵等边△A 1C 1C 2的周长为1,作C 1D 1⊥12△A 1C 1C 2的周长=12,∴△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4112n -,∴△A 1C 1C 2,22212n -12n -故答案为:1212n n --.灵活运用所学知识,属于中考常考题型.23三角:【来源】 【答案】1a 5+10a 3b 2+10a 2b 3+5ab 4+1b 5. 故答案为:点睛:本题考查了完全平方公式以及规律型中数字的变化,观察图形,找出二项式系数与杨辉三角之间的关系是解题的关键.24.如图,把n 个长为1的正方形拼接成一排,求得71tan ,31tan ,1tan 321=∠=∠=∠C BA C BA C BA ,计算=∠C BA 4tan ,……,按此规律,写出=∠C BA n tan (用含n 的代数式表示). 【来源】2017年初中毕业升学考试(浙江舟山卷)数学(带解析)【答案】113,211n n -+.【解析】试题分析:如图,过点C 作CE ⊥A 4B 于E ,易得∠A 4BC=∠BA 4A 1,故tan ∠A 4BC=tan ∠BA 4A 1=14,在Rt △BCE 中,由tan ∠A 4BC=14,得BE=4CE ,而BC=1,则,,而A 4=所以A 4E=A 4,在Rt △A 4EC 中,tan ∠BA 4C=4113CE A E =;根据前面的规律,不能得出tan ∠BA 1C=1101⨯+,tan ∠BA 2C 1211⨯+,tan ∠BA 3C=1321⨯+,tan ∠BA 4C=1431⨯+,则可得规律tan ∠BA n C=211(1)11n n n n =⨯-+-+.故答案为;考点:解直角三角形.25.如图,正△ABO 的边长为2,O 为坐标原点,作无滑动的翻滚,经第一次翻滚后得△A 1B 1O ,;翻滚2017次后AB 中点M 经过的路径长为【来源】2017【答案】(5;13463(+896)3π.【解析】试题解析:如图,作B 3E ⊥x 轴于E ,考点:点的坐标.26.如图,把n 个边长为1的正方形拼接成一排,求得1tan 1BAC ∠=,21tan 3BA C ∠=,31tan 7BA C ∠=,计算4tan BA C ∠=,……按此规律,写出tan n BA C ∠=(用含n 的代数式表示). 【来源】2017年初中毕业升学考试(浙江嘉兴卷)数学(带解析) 【答案】113,211n n -+. 【解析】试题解析:作CH⊥BA 4于H ,由勾股定理得,BA 4A 4,△BA4C的面积=4-2-32=12,∴1212,解得,则A417,∴tan∠BA4C=4CHA H=113,1=12-1+1,3=22-2+1,7=32-3+1,∴tan∠BAnC=211n n-+.考点:1.解直角三角形;2.勾股定理;3.27.正方形A1B1C1O,A2B2C2C1,A3B3C3C2…C1、C2、C3…在x【来源】【答案】(2【解析】试题分析:(0,1),即OA1=1,∵四边形C1OA1B1是正方形,∴OC1=OA1=11,2),同理A3的坐标为(3,4),…An,12n-).28.设△如图1AE1,BD1交于点F1,得到四边形CD1F1E1,其面积S1=13如图2,分别将AC,BC边3等分,D1,D2,E1,E2是其分点,连接AE2,BD2交于点F2,得到四边形CD2F2E2,其面积S2=16;如图3,分别将AC,BC边4等分,D1,D2,D3,E1,E2,E3是其分点,连接AE3,BD3交于点F3,得到四边形CD3F3E3,其面积S3=110;…按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CD n E n F n,其面积S=.【来源】2017年初中毕业升学考试(山东淄博卷)数学(带解析)【答案】2(1)(2)n n++.【解析】试题分析:如图所示,连接D 1E 1,D 2E 2,D 3E 3,∵图1中,D 1,E 1是△ABC 两边的中点,∴D 1E 1∥AB ,D 1E 1=AB ,∴△CD 1E 1∽△CBA ,且11111DE DE B F A B==12,∴S △CD1E1=14S △ABC =14,∵E 1是BC 的中点,∴S △BD1E1=S △CD1E1=14,∴S △D1E1F1=13S △BD1E1=13×14=112,∴S 1=S △CD1E1+S △D1E1F1=14+112=13,同理可得: 图2中,S 2=S △CD2E2+S △D2E2F2=11918+=16,图3中,S 3=S △CD3E3+S △D3E3F3=131680+=110,以此类推,将AC ,BC边(n+1)等分,得到四边形CD n E n F n ,其面积S n =22111(1)(1)11n n n n +⨯⨯++++=2(1)(2)n n ++,故答11121233,412A B C A B B S S ==30.在平面直角坐标系中,点(,)P x y 经过某种变换后得到点(1,2)P y x '-++,我们把点(1,2)P y x '-++叫做点(,)P x y 的终结点.已知点1P 的终结点为1P ,点2P 的终结点为2P ,点3P 的终结点为4P ,这样依次得到1234n P P P P P L L 、、、、、,若点1P 的坐标为(2,0),则点P 2017的坐标为. 【来源】2017年初中毕业升学考试(内蒙古赤峰卷)数学(带解析)【答案】(2,0). 【解析】试题分析:求得点P 2、P 3、P 4、P 5的值,即可发现其中规律,即可解题. ∵P 1(2,0),则P 2(1,4),P 3(﹣3,3),P 4(﹣2,﹣1),P 5(2,0), ∴P n 的坐标为(2,0),(1,4),(﹣3,3),(﹣2,﹣1)循环,∵2017=2016+1=4×504+1,∴P 2017坐标与P 1点重合, 故答案为(2,0).考点:规律型:点的坐标.31.如图,点(1A 上,过点1A 作111A B l ⊥交直线于点1B ,11A B 为边在11OA B ∆外侧作等边三角形111A B C ,再过点1C 作221A B l ⊥,分别交直线1l 和2l 于22,A B 两点,以22A B 为边在22OA B ∆外侧作等边三角形222,A B C 按此规律进行下去,则第n 个等边三角形n n nA B C 的面积为__________.(用含n 的代数式表示)【来源】2017年初中毕业升学考试(辽宁营口卷)数学(带解析)A 1B 1的A 2B 2的A n B nC n 的∵点A 在Rt ∴A 1B 1∵△A 1∴OA 2∴第n考点:一次函数图象上点的坐标特征;等边三角形的性质;探索规律.32.已知12345357911,,,,,25101726a a a a a =-==-==-,则8a =.【来源】2017年初中毕业升学考试(湖南郴州卷)数学(带解析)【答案】1765.【解析】试题分析:由题意给出的5个数可知:a n =221(1)1nn n +-+,所以当n=8时,a 8=1765.考点:数字规律问题.33.如图,有一条折线A 1B 1A 2B 2A 3B 3A 4B 4…,它是由过A 1(0,0),B 1(2,2),A 2(4,0)组成的折线依次平移4,8,12,…个单位得到的,直线y =kx +2与此折线恰有2n (n ≥1,且为整数)个交点,则k 的值为______.【来源】2017年初中毕业升学考试(湖南常德卷)数学(带解析)【答案】12n-.【解析】试题分析:∵A 1(0,0),A 2(4,0),A 3(8,0),A 4(12,0),…,∴A n (4n ﹣4,0). ∵直线y=kx+2与此折线恰有2n (n≥1,且为整数)个交点,∴点A n+1(4n ,0)在直线y=kx+2上,∴0=4nk+2,解得:k=.故答案为:.34.如图,边长为4的正六边形ABCDEF ABCDEF 绕原点O 顺时针旋转n 次,每次旋转 60,当=n 【来源】2017【答案】(2,【解析】试题分析:2017×60°÷360°=336…11次时点A 作FH ⊥x轴,,∴F (2,.35…….(写出最简计算结果即可)n=2时,结果为:22213=+;n=3时,结果为:33314=+;所以第n 个式子的结果为:1n n +.故答案为:1nn +.考点:规律型:数字的变化类. 36.如图6,在66´的网格内填入1至6的数字后,使每行、每列、每个小粗线宫中的数字不重复,则a c ?.【来源】2017年初中毕业升学考试(湖北恩施卷)数学(带解析) 【答案】2.【解析】试题分析:对各个小宫格编号如下:先看己:已经有了数字3、5、6,缺少1、2、4;观察发现:4不能在第四列,2不能在第五列,而2不能在第六列;所以2只能在第六行第四列,即a=2;则b 和c 有一个是1,有一个是4,不确定,如下:观察上图发现:第四列已经有数字2、3、4、6,缺少1和5,由于5不能在第二行,所以5在第四行,那么1在第二行;如下:再看乙部分:已经有了数字1、2、3,缺少数字4、5、6,观察上图发现:5不能在第六列,所以5在第五列的第一行;4和6在第六列的第一行和第二行,不确定, 分两种情况:①当4在第一行时,6在第二行;那么第二行第二列就是4,如下:再看甲部分:已经有了数字1、3、4、5,缺少数字2、6,观察上图发现:2不能在第三列,所以2在第二列,则6在第三列的第一行,如下:观察上图可知:第三列少1和4,4观察上图可知:第五行缺少1和2,1不能在第1c=1,所以b=4,如下:观察上图可知:第六列缺少1和2,1 再看戊部分:已经有了数字2、3、4、51在第二列,则6在第一列,如下:观察上图可知:第一列缺少3和4,4 观察上图可知:第二列缺少5和6,5 观察上图可知:第三行第五列少6所以,a=2,c=1,ac=2;②当6在第一行,42在第2列,c=4,b=1所以6在第四行,则3在第三行,如下: 所以2在第三行,则1在第四行,如下: 综上所述:37.(20172的等腰直角三角形各边中点得到第1个小三角形,2个小三角形,如此操作下去,则第n 个小三【来源】【答案】2112n .【解析】试题分析:记原来三角形的面积为s ,第一个小三角形的面积为s 1,第二个小三角形的面积为s 2,…, ∵s 1=?s=?s ,s 2=?s=?s ,s 3=?s ,…… ∴s n =?s=??2?2=.考点:1.三角形中位线定理;2.等腰直角三角形.38.如图,在平面直角坐标系中,等腰直角三角形12OA A 的直角边1OA 在y 轴的正半轴上,且1121OA A A ==,以2OA 为直角边作第二个等腰直角三角形23OA A ,以3OA 为直角边作第三个等腰直角三角形20172018OA A ,则点2017A 的坐标为.【来源】2017年初中毕业升学考试(黑龙江齐齐哈尔卷)数学(带解析)【答案】【解析】2为直角∴OA 1=1,∵A 1、A 22017÷∴点A 2017∵OA 2017=∴点A 2017399【来源】【答案】【解析】第2第3…第n 个图形中三角形的个数是1+4(n ﹣1)=4n ﹣3, 当n=2017时,4n ﹣3=8065 考点:图形的变化类40.如图,在平面直角坐标系中,直线l :y=x+2交x 轴于点A ,交y 轴于点A 1,点A 2,A 3,…在直线l 上,点B 1,B 2,B 3,…在x 轴的正半轴上,若△A 1OB 1,△A 2B 1B 2,△A 3B 2B 3,…,依次均为等腰直角三角形,直角顶点都在x 轴上,则第n 个等腰直角三角形A n B n ﹣1B n 顶点B n 的横坐标为. 【来源】2017年初中毕业升学考试(贵州安顺卷)数学(带解析) 【答案】2n+1﹣2. 【解析】试题解析:由题意得OA=OA 1=2, ∴OB 1=OA 1=2,B 1B 2=B 1A 2=4,B 2A 3=B 2B 3=8,∴B 1(2,0),B 2(6,0),B 3(14,0)…, 2=22﹣2,6=23﹣2,14=24﹣2,… ∴B n 的横坐标为2n+1﹣2. 考点:点的坐标. 41.41.如图,把正方形铁片OABC 置于平面直角坐标系中,顶点A 的坐标为(3,0),点P (1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P 的坐标为____________________.【来源】2017年初中毕业升学考试(广西四市卷)数学(带解析) 【答案】(6053,2).【解析】试题分析:第一次P 1(5,2),第二次P 2(5,1),第三次P 3(7,1),第四次P 4(10,2),第五次P 5(14,2),…发现点P42(1(2(3(1)(2x x +-帮助, 【来源】【答案】(【解析】试题分析:432【来源】【答案】【解析】试题解析:∵第1个图形的周长为2+3=5, 第2个图形的周长为2+3×2=8, 第3个图形的周长为2+3×3=11, …∴第2017个图形的周长为2+3×2017=6053 考点:图形的变化规律.44.44.如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第n 个图中正方形和等边三角形的个数之和为______个. 【来源】2017年初中毕业升学考试(山东潍坊卷)数学(带解析) 【答案】9n +3.【解析】试题分析:∵第1个图由1个正六边形、6个正方形和6个等边三角形组成,∴正方形和等边三角形的和=6+6=12=9+3;∵第2个图由11个正方形和10个等边三角形组成,∴正方形和等边三角形的和=11+10=21=9×2+3;∵第3个图由16个正方形和14个等边三角形组成,∴正方形和等边三角形的和=16+14=30=9×3+3,…,∴第n个图中正方形和等边三角形的个数之和=9n+3.故答案为:9n+3.考点:规律型:图形的变化类45.某广场用同一种如图所示的地砖拼图案.第一次拼成形如图1所示的图案,第二次拼成形如图2所示的图案,第三次拼成形如图3的图案,第四次拼成形如图4的图案……按照只有的规律进行下去,第n次拼成的图案用地砖块.…第n46角形A11B2,过点A2作A2B3的横坐标是与1D=30°,再,过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为,A2的横坐标为,A3的横坐标为,进而得到An 的横坐标为,据此可得点A2017的横坐标,故答案为:.考点:1、一次函数图象上点的坐标特征,2、等边三角形的性质47.观察下列运算过程:计算:1+2+22+ (210)解:设S=1+2+22+…+210,① ①×2得2S=2+22+23+…+211,②? ②﹣①得 S=211﹣1.所以,1+2+22+…+210=211﹣1运用上面的计算方法计算:1+3+32+…+32017=.【来源】2017年初中毕业升学考试(贵州毕节卷)数学(带解析)【答案】2018312-.【解析】试题分析:令s=1+3+32+33+…+32017等式两边同时乘以3得:3s=3+32+33+…+32018故答案为:2018312-.考点:规律型:数字的变化类. 48.观察下列图形:它们是按一定规律排列的,依照此规律,第9【来源】【答案】【解析】个点, …第n 3(1)2n n +个点; 当n=9故答案为:135.考点:规律型:图形的变化类49.[探究函数4y x x =+的图象与性质](1)函数4y x x=+的自变量x 的取值范围是;(2)下列四个函数图象中函数4y x x=+的图象大致是;(3)对于函数4y x x=+,求当0x >时,y 的取值范围.请将下列的求解过程补充完整. 解:∵0x >∴()2224y xx=+=+=+∵2≥∴y ≥. [拓展运用](4)若函数259x x y x-+=,则y 的取值范围.【来源】四川省自贡市初2017【答案】(1)0x ≠;(2)C ;(3)4,4;(4)y ≥【解析】试题分析:本题的⑴量的取值范围.本题的⑵问结合第⑴问中的0x ≠的大致取值范围,即可得到函数的大致图象.本题的第⑶”应填写“常数”部分,再根据配方情况可以得到当当x >95y x x=+-的形式,再按⑶故填:x (2)x ≠0x <时,y 所以函数4y x x=+的图象只在直角坐标系的(3)∵∴y x =+故分别填:44,;(4)∵0x >(这里隐含有y 首先是正数)∴2222599551x x y xx x -+==-+=+-=+∵2≥∴1y ≥.50.(2017浙江省台州市)在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程2520x x -+=,操作步骤是:第一步:根据方程的系数特征,确定一对固定点A (0,1),B (5,2);第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A ,另一条直角边恒过点B ; 第三步:在移动过程中,当三角板的直角顶点落在x 轴上点C 处时,点C 的横坐标m 即为该方程的一个实数根(如图1);第四步:调整三角板直角顶点的位置,当它落在x 轴上另一点D 处时,点D 的横坐标n 即为该方程的另一个实数根.(1)在图2中,按照“第四步”的操作方法作出点D (请保留作出点D 时直角三角板两条直角边的痕迹);(2)结合图1,请证明“第三步”操作得到的m (30c +=(a ≠0,24b ac -(4)实际上,(3系时,点P (m 1,n 1),Q (m 2,n 2【来源】2017【答案】(1)作图见解析;(2)证明见解析;(3,B (﹣b a ,c D 即可;(2)过点B ,进而得出,即是方程的实数根;(3)方程(a≠0)可化为,模仿研究小组作法可得一对固定点的坐标;(4)先设方程的根为x ,根据三角形相似可得,进而得到,再根据,可得,最后比较系数可得m 1,n 1,m 2,n 2与a ,b ,c 之间的关系. 试题解析:(1)如图所示,点D 即为所求;(2)如图所示,过点B 作BD⊥x 轴于点D ,根据∠AOC=∠CDB=90°,∠ACO=∠CBD,可得△AOC∽△CDB,∴,∴,∴m(5﹣m )=2,∴,∴m 是方程的实数根;(3)方程(a≠0)可化为,模仿研究小组作法可得:A (0,1),B(﹣,)或A (0,),B (﹣,c )等;,根据三角形相似可得,上式,即,∴比较系数可得= ()2132435(2)n n ⨯⨯⨯+=111111111(1 (23243512)n n n -+-+-+-+-++=111113(1)(2)2(2)2(1)(1221222(1)(2)n n n n n n n n ++-+-++--=⨯++++=2354(1)(2)n n n n +++.52.阅读理解题:定义:如果一个数的平方等于-1,记为21i =-,这个数i 叫做虚数单位,把形如a bi +(,a b 为实数)的数叫做复数,其中a 叫这个复数的实部,b 叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.例如计算:()()()()253251372i i i i -++=++-+=+()()()21212221213i i i i i i i +⨯-=⨯-+⨯-=+-++=+;根据以上信息,完成下列问题:(1)填空:3i =_________,4i =___________;(2)计算:()()134i i +⨯-;(3)计算:232017i i i i ++++.【来源】2017年初中毕业升学考试(湖南张家界卷)数学(带解析)【答案】(1)﹣i ,1;(2)7﹣i ;(3)i .【解析】试题分析:(1)把i 2=﹣1代入求出即可;(2(3试题解析:(1)i 3=i 2i=﹣i ,i 4=(i 2)2=(﹣1)2故答案为:﹣i ,1;(2)(1+i )×(3﹣4i )=3﹣4i+3i ﹣4i 2=3﹣i+4=7﹣i ;(3)i+i 2+i 32017=i ﹣1﹣=i . 53.我们知道,(n n ++=223n +++结果等于多少呢? 在图1所示三角形数阵中,第1,即21;第2行两个圆圈中数的和为22+,即22n ,即2n .这样,该三角形数阵中共有(1)2n n +个【规律探究】将桑拿教学数阵经两次旋转可得如图所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第1n -行的第一个圆圈中的数分别为1n -,2,n ),发现每个位置上三个圆圈中数的和均为.由此可得,这三个三角形数阵所有圆圈中数的总和为:22223(123)n ++++=.因此,2222123n ++++=. 【解决问题】 根据以上发现,计算222212320171232017++++++++的结果为.【来源】2017年初中毕业升学考试(安徽卷)数学(带解析)【答案】21n +()()1212n n n ++?()()11216n n n ++1345 【解析】试题分析:先利用转化的而思想来探究2222123n ++++=()()11216n n n ++;再利用公式解决问题. 试题解析:21n +2222123n ++++=()()11216n n n ++1345 222212320171232017++++++++=12017(20171)(220171)116(220171)40351345(12017)3320172⨯⨯+⨯⨯+=⨯⨯+=⨯=+⨯ 考点:探究问题、解决问题的能力.。
中考数学复习专题——找规律(含答案)

中考数学试复习专题——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有个小圆圈.(1) (2) (3)2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有 个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.1 2 3n … … 第1个图 第2个图 第3个图 …6、如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子枚(用含有n的代数式表示,并写成最简形式).○○○○○○○○○○○○○●●○○●●●○○●○○●●○○●●●○○○○○○○○○●●●○○○○○○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数17的有序实数对是.9、如图2,用n表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n的关系是10、观察图4的三角形数阵,则第50行的最后一个数是()1-2 3-4 5 -67 -8 9 -10。
11、下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第n个图案中白色正方形的个数为.12、观察下列各式:3211=332123+=33221236++=33332123410+++=……猜想:333312310++++=.第一个第二个第三个……第n个第一排第二排第三排第四排6┅┅10 9 8 73 2154答案解析:1解析:1时,5.n再每增加一个数时,m就增加3个数.解答:根据所给的具体数据,发现:8=5+3,11=5+3×2,14=5+3×3,….以此类推,第n个圈中,5+3(1)=32.2解析:分析可得:第1幅图中有1×2-1=1个,第2幅图中有2×2-1=3个,第3幅图中有3×2-1=5个,…,故第n幅图中共有21个3解析:在4的基础上,依次多3个,得到第n个图中共有的棋子数.观察图形,发现:在4的基础上,依次多3个.即第n个图中有4+3(1)=31.当6时,即原式=19.故第6个图形需棋子19枚4解析:此题只要找出截取表一的那部分,并找出其规律即可解.解答:解:表二截取的是其中的一列:上下两个数字的差相等,所以15+3=18.表三截取的是两行两列的相邻的四个数字:右边一列数字的差应比左边一列数字的差大1,所24+25-20+1=30.表四中截取的是两行三列中的6个数字:18是3的6倍,则c应是4的7倍,即28.故选D.认真观察表格,熟知各个数字之间的关系:第一列是1,2,3,…;第二列是对应第一列的2倍;等三列是对应第一列的3倍5解析:据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方,每四个小正方形组成一个完整的圆,从而可得这样的圆是大正方形边长减1的平方,从而可得若这样铺成一个10×10的正方形图案,则其中完整的圆共有102+(10-1)2=181个.解答:解:分析可得完整的圆是大正方形的边长减1的平方,从而可知铺成一个10×10的正方形图案中,完整的圆共有102+(10-1)2=181个.点评:本题难度中等,考查探究图形的规律.本题也只可以直接根据给出的四个图形中计数出的圆的个数,找出数字之间的规律得出答案.6解析:解:第1个正方形图案有棋子共32=9枚,其中黑色棋子有12=1枚,白色棋子有(32-12)枚;第2个正方形图案有棋子共42=16枚,其中黑色棋子有22=4枚,白色棋子有(42-22)枚;…由此可推出想第n个图案的白色棋子数为(2)22=4(1).故第n个图案的白色棋子数为(2)22=4(1).点评:根据图形提供的信息探索规律,是近几年较流行的一种探索规律型问题.解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论7解析:根据题意分析可得:搭第1个图形需12根火柴;搭第2个图形需12+6×1=18根;搭第3个图形需12+6×2=24根;…搭第n个图形需12+6(1)=66根.解答:解:搭第334个图形需6×334+6=2010根火柴棒8解析:寻找规律,然后解答.每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.解答:解:观察图表可知:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.实数15=1+2+3+4+5,则17在第6排,第5个位置,即其坐标为(6,5).故答案填:(6,5).对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.9解析:根据题意分析可得:第n行有n个小圆圈.故f(n)和n的关系是ƒ(n)= (n2).10解析:根据题意可得:第n行有n个数;且第n行第一个数的绝对值为+1,最后一个数的绝对值为;奇数为正,偶数为负;故第50行的最后一个数是1275.解答:解:第n行第一个数的绝对值为+1,最后一个数的绝对值为,奇数为正,偶数为负,第50行的最后一个数是1275第一个图中白色正方形的个数为3×3-1;第二个图中白色正方形的个数为3×5-2第三个图中白色正方形的个数为3×7-3;…当其为第n个时,白色正方形的个数为3(21)5312解析:根据所给的等式,可以发现右边的底数是前边的底数的和,指数是平方,则最后的底数是1+2+310=5×11=55,则原式=552.解答:解:根据分析最后的底数是1+2+310=5×11=55,则原式=552.故答案552。
2017全国中考数学真题 全面调查与抽样调查(选择题+填空题)解析版

2017全国中考数学真题分类知识点40全面调查与抽样调查(选择题+填空题)解析版一、选择题1.(2017重庆,4,4分)下列调查中,最适合采用全面调查(普查)方式的是()A.对重庆初中学生每天阅读时间的调查B.对端午节期间市场上粽子质量情况的调查C.对某批次手机防水功能的调查D.对某校九年级3班学生肺活量情况的调查答案:D解析:选项A对重庆市初中学生每天阅读时间的调查,工作量大,适合于抽样调查;选项B对对端午节期间市场上粽子质量情况的调查,工作量较大,适合于抽样调查;选项C对对某批次手机防水功能的调查,破坏性比较强,所以适合抽样调查;选项D对对某校九年级3班学生肺活量情况的调查,工作量不大,适合于全面调查,故选择D.2.(2017重庆B,4,4分)下列调查中,最适合采用抽样调查的是A.对某地区现有的16名百岁以上老人睡眠时间的调查B.对“神州十一号”运载火箭发射前零部件质量情况的调查C.对某校九年级三班学生视力情况的调查D.对市场上某一品牌电脑使用寿命的调查答案:D,解析:选项A,B,C都属于普查.3.(2017江苏苏州,5,3分)为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,并设置了“赞成、反对、无所谓”三种意见.现从学校所有2400名学生中随机征求了100名学生的意见,其中持“反对”和“无所谓”意见的共有30名学生,估计全校持“赞成”意见的学生人数约为A.70 B.720 C.1680 D.2370答案:C,解析:根据用样本估计总体的统计思想,所以702400=1680100,故答案选C.4.(2017湖南衡阳,6,3分)下面调查方式中,合适的是()A.调查你所在班级同学的身高,采用抽样调查方式B.调查湘江的水质情况,采用抽样调查的方式C.调查CCTV-5《NBA总决赛》栏目在我市的收视率,采用普查的方式D.要了解全市初中学生的业余爱好,采用普查的方式答案:B,解析:所在班的同学不多,调查身高容易操作,用全面调查,故A中错误的;湘江水量多,分布广,调查湘江水质全面调查不容易,应抽样调查,故B是正确的.故选B.5.7.(2017安徽中考·4分)为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了100名学生进行统计,并绘成如图所示的频数直方图,已知该校共有1000名小时。
中考数学规律探索题中考找规律题目有答案

中考规律探索1以下为全部整理类型,规律探索共两套试题,供参考学习使用一.选择题1.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187… 解答下列问题:3+32+33+34…+32013的末位数字是A .0B .1C .3D .72. 把所有正奇数从小到大排列,并按如下规律分组:1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,…,现用等式A M =i,j 表示正奇数M 是第i 组第j 个数从左往右数,如A 7=2,3,则A 2013= A .45,77 B .45,39 C .32,46 D .32,233.下表中的数字是按一定规律填写的,表中a 的值应是 .1 2 3 5 8 13 a (2)358132134…4.下列图形都是由同样大小的矩形按一定的规律组成,其中第1个图形的面积为2cm 2,第2个图形的面积为8 cm 2,第3个图形的面积为18 cm 2,……,第10个图形的面积为A .196 cm 2B .200 cm 2C .216 cm 2D . 256 cm 25.如图,动点P 从0,3出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P 第2013次碰到矩形的边时,点P 的坐标为A 、1,4B 、5,0C 、6,4D 、8,36.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M 与m 、n 的关系是A . M=mnB . M=nm+1C .M=mn+1D .M=mn+17.我们知道,一元二次方程12-=x 没有实数根,即不存在一个实数的平方等于-1,若我们规定一个新数“”,使其满足12-=i 即方程12-=x 有一个根为,并且进一步规定: 一切实数可以与新数进行四则运算,且原有的运算律和运算法则仍然成立,于是有,1i i =12-=i ,,).1(23i i i i i -=-=⋅=.1)1()(2224=-==i i 从而对任意正整数n,我们可得到,.)(.4414i i i i i i n n n ===+同理可得,1,,143424=-=-=++n n n i i i i 那么,20132012432i i i i i i +⋅⋅⋅++++的值为A .0B .1C .-1D .8.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为A .51B .70C .76D .81二.填空题1.观察下列图形中点的个数,若按其规律再画下去,可以得到第n 个图形中所有的个数为 用含n 的代数式表示.2.如图,在直角坐标系中,已知点A ﹣3,0、B 0,4,对△OAB 连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为 .3.如图,正方形ABCD 的边长为1,顺次连接正方形ABCD 四边的中点得到第一个正方形A 1B 1C 1D 1,由顺次连接正方形A 1B 1C 1D 1四边的中点得到第二个正方形A 2B 2C 2D 2…,以此类推,则第六个正方形A 6B 6C 6D 6周长是 .图① 图②图③···第8题图4.直线上有2013个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有个点.5.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是.6 .如图,是用火柴棒拼成的图形,则第n个图形需根火柴棒.7.观察规律:1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,则1+3+5+…+2013的值是.8.如图12,一段抛物线:y=-xx-30≤x≤3,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;……如此进行下去,直至得C13.若P37,m在第13段抛物线C13上,则m =_________.9.直线上有2013个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有个点. 10.观察下列各式的计算过程:5×5=0×1×100+25,15×15=1×2×100+25,25×25=2×3×100+25,35×35=3×4×100+25,…………请猜测,第n个算式n为正整数应表示为____________________________.11.将连续的正整数按以下规律排列,则位于第7行、第7列的数x是__ __.12、如下图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;……按这样的规律下去,则第6幅图中含有 个正方形;13.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆, 第2个图形有10个小圆, 第3个图形有16个小圆, 第4个图形有24个小圆, ……,依次规律,第6个图形有 个小圆.14.已知一组数2,4,8,16,32,…,按此规律,则第n 个数是 . 15、我们知道,经过原点的抛物线的解析式可以是y =ax 2+bxa ≠0 1对于这样的抛物线:当顶点坐标为1,1时,a =__________;当顶点坐标为m ,m ,m ≠0时,a 与m 之间的关系式是__________;2继续探究,如果b ≠0,且过原点的抛物线顶点在直线y =kxk ≠0上,请用含k 的代数式表示b ;3现有一组过原点的抛物线,顶点A 1,A 2,…,A n 在直线y =x 上,横坐标依次为1,2,…,n 为正整数,且n ≤12,分别过每个顶点作x 轴的垂线,垂足记为B 1,B 2,…,B n ,以线段A n B n 为边向右作正方形A n B n C n D n ,若这组抛物线中有一条经过D n ,求所有满足条件的正方形边长.16.如图,所有正三角形的一边平行于x 轴,一顶点在y 轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用1A 、2A 、3A 、4A 、…表示,其中12A A 与x 轴、底边12A A 与45A A 、45A A 与78A A 、…均相距一个单位,则顶点3A 的坐标是 ,22A 的坐标是 .xy A 9A 6A 3A 8A 7A 5A 4A 2A 1O第16题图••••••①② ③17.如图,已知直线l :y=33x ,过点A 0,1作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;……按此作法继续下去,则点A 2013的坐标为 .18、如图,在平面直角坐标系中,一动点从原点O 出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A 10,1,A 21,1,A 31,0,A 42,0,…那么点A 4n +1n 为自然数的坐标为 用n 表示19.当白色小正方形个数n 等于1,2,3…时,由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________.用n 表示,n 是正整数20. 2013衢州4分如图,在菱形ABCD 中,边长为10,∠A=60°.顺次连结菱形ABCD 各边中点,可得四边形A 1B 1C 1D 1;顺次连结四边形A 1B 1C 1D 1各边中点,可得四边形A 2B 2C 2D 2;顺次连结四边形A 2B 2C 2D 2各边中点,可得四边形A 3B 3C 3D 3;按此规律继续下去….则四边形A 2B 2C 2D 2的周长是 ;四边形A 2013B 2013C 2013D 2013的周长是 .21.一组按规律排列的式子:a2,43a ,65a ,87a ,….则第n 个式子是________22.观察下面的单项式:a,﹣2a 2,4a 3,﹣8a 4,…根据你发现的规律,第8个式子是 .23.如图,已知直线l:y=x,过点M2,0作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x 轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M10的坐标为.24.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆第n图,需用火柴棒的根数为.答案:选择题:1、C 2、C 3、21 4、B 5、D 6、D 7、D 8、 C填空题:1、n+122、8052,03、4、160975、516、2n+17、10140498、 29、16097 10、10n-1+52=100nn-1+25 11、85 12、91 13、46 14、2n15、1-1;a =-1m或am +1=0; 2解:∵a ≠0∴y =ax 2+bx =ax +2b a2-24b a∴顶点坐标为-2ba,-24b a∵顶点在直线y =kx 上∴k -2ba=-24b a∵b ≠0∴b =2k3解:∵顶点A n 在直线y =x 上 ∴可设A n 的坐标为n ,n ,点D n 所在的抛物线顶点坐标为t ,t由12可得,点D n 所在的抛物线解析式为y =-1tx 2+2x∵四边形A n B n C n D n 是正方形∴点D n 的坐标为2n ,n ∴-1t2n 2+2×2n =n∴4n =3t∵t 、n 是正整数,且t ≤12,n ≤12∴n =3,6或9∴满足条件的正方形边长为3,6或916、0,31-,-8,-8. 17、()()201340260,40,2或注:以上两答案任选一个都对18、2n,1 19、n 2+4n 20、20;21、221na n n 为正整数22、-128a 823、884736,0 24、6n+2规律探索21、 我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码又叫数字:0,1,2,3,4,5,6,7,8,9;在电子数字计算机中用的是二进制,只要两个数码:0和1;如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数 ;2、 从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…按此规律请你猜想从1开始,将前10个奇数即当最后一个奇数是19时,它们的和是 ; 3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入 (1)2345… 输出…2152 103 174 265…那么,当输入数据是8时,输出的数据是A 、618B 、638C 、658D 、6784、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要 枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n 个小房子用了 块石子6、如下图是用棋子摆成的“上”字:第一个“上”字 第二个“上”字 第三个“上”字如果按照以上规律继续摆下去,那么通过观察,可以发现:1第四、第五个“上”字分别需用 和 枚棋子;2第n 个“上”字需用 枚棋子;7、如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有_______颗.(1)(2)(3)第4题第7题图12 348、根据下列5个图形及相应点的个数的变化规律:猜想第6个图形有 个点,第n 个图形中有 个点;9、下面是按照一定规律画出的一列“树型”图:经观察可以发现:图2比图1多出2个“树枝”;图3比图2多出5个“树枝”;图4比图3多出10个“树枝”;照此规律,图7比图6多出 个“树枝”;10、观察下面的点阵图和相应的等式,探究其中的规律:1在④和⑤后面的横线上分别写出相应的等式;2通过猜想写出与第n 个点阵相对应的等式_____________________;11、用边长为1cm 的小正方形搭成如下的塔状图形,则第n 次所搭图形的周长是_______________cm 用含n 的代数式表示;12、如图,都是由边长为1的正方体叠成的图形;例如第1个图形的表面积为6个平方单位,第2个图形的表面积为18个平方单位,第3个图形的表面积是36个平方单位;依此规律;则第5个图形的表面积 个平方单位13、图1是一个水平摆放的小正方体木块,图2、3是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第…………①1=12; ②1+3=22;③1+3+5=32;④ ;⑤ ;第1次 第2次 第3次 第4次 ······⑴ ⑵ ⑶14题七个叠放的图形中,小正方体木块总数应是A 25B 66C 91D 12014、如图是由大小相同的小立方体木块叠入而成的几何体,图⑴中有1个立方体,图⑵中有4个立方体,图⑶中有9个立方体,……按这样的规律叠放下去, 第8个图中小立方体个数是 .15、图1是棱长为a 的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n 层,第n 层的小正方体的个数为s .解答下列问题:1按照要求填表:2写出当n =10时,s= .16、如图用火柴摆去系列图案,按这种方式摆下去,当每边摆10根时即10 n 时,需要的火柴棒总数为 根;17、用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个三角形需7支火柴棒,照这样的规律下去,搭n 个三角形需要S 支火柴棒,那么用n 的式子表示S 的式子是 _______ n 为正整数.18、如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下图:则第n 个图形中需用黑色瓷砖 ____ 块.用含n 的代数式表示n 1 2 3 4 … s136…(1)(2)(3)图1 图2 图3A B C D19题图19、如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:当黑色瓷砖为20块时,白色瓷砖为 块;当白色瓷砖为n 2n 为正整数块时,黑色瓷砖为 块.20、观察下列由棱长为1的小立方体摆成的图形,寻找规律:如图1中:共有1 个小立方体,其中1个看得见,0个看不见;如图2中:共有8个小立方体,其中7个看得见,1个看不见;如图3中:共有27个小立方体,其中有19个看得8个看不见;……,则第6个图中,看不见的小立方体有 个;21、下面的图形是由边长为l 的正方形按照某种规律排列而组成的.1观察图形,填写下表:图形 ① ② ③ 正方形的个数 8 图形的周长182推测第n 个图形中,正方形的个数为________,周长为______________都用含n 的代数式表示.22、观察下图,我们可以发现:图⑴中有1个正方形;图⑵中有5个正方形,图⑶中共有14个正方形,按照这种规律继续下去,图⑹中共有_______个正方形;23、某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛阴影部分使花坛面积是园地面积的一半,以下图中设计不合要求....的是第22题图 第23题图24、如下图中的四个正方形的边长均相等,其中阴影部分面积最大的图形是25、如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是 A. <1>和<2> B. <2>和<3>C. <2>和<4>D. <1>和<4>ADCB第18题图26、某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;…依此方法,第n 次铺完后,用字母n 表示第n 次镶嵌所使用的木块块数为 . n 为正整数27、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:⑴ 第4个图案中有白色地面砖 块; ⑵ 第n 个图案中有白色地面砖 块;28、分析如下图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.29、将一圆形纸片对折后再对折,得到图2,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是30.如图1,小强拿一张正方形的纸,沿虚线对折一次得图2,再对折一次得图3,然后用剪刀沿图3中的虚线剪去一个角,再打开后的形状是A B C DABCD图3图231、用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,其中∠BAC=度.32、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星正五边形对角线所构成的图形.则∠OCD等于A.108° B.144° C.126° D.129°33、如图,把一个正方形三次对折后沿虚线剪下则得到的图形是A B C D 第35题图34、将一张长方形的纸对折,如图5所示可得到一条折痕图中虚线. 继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到条折痕 .如果对折n次,可以得到_____________条折痕 ;35、观察图形:图中是边长为1,2,3 …的正方形:当边长n=1时,正方形被分成2个大小相等的小等腰直角三角形;当边长n=2时,正方形被分成8个大小相等的小等腰直角三角形;当边长n=3时,正方形被分成18个大小相等的小等腰直角三角形;以此类推:当边长为n时,正方形被分成大小相等的小等腰直角三角形的个数是 ;36、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、“你”、“前”分别表示正方体的___________________._沿虚线剪开祝D SAC SA图1DE BA图237、如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为A5050m2 B4900m2C5000m2D4998m238、读一读,想一想,做一做:国际象棋、中国象棋和围棋号称为世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.①在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“2,3”来表示,请说明“皇后Q”所在的位置“2,3”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.②如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制在图丙中的某四个小方格中标出字母Q即可.3412甲3123行列乙3412丙参考答案1、132、1003、C4、1795、 3n+1-3+nn+1或n+12+2n-16、118、22 24n+27、278、31,n2-n-19、8010、1+3+5+7=42;1+3+5+7+9=52;1+3+5+……+2n-1=n2 11、 4n 12、9013、C 14、64 5、110 21+2+3+……+n=nn+1/2 16、16517、s=2n+1 18、4n+6 19、16,4n+420、125 21、113、18;28、38; 25n+3,10n+8 22 、9123、B 24、B 25、A 26、8n-6 27、118 ;24n+2 28、29、C 30、C 31、 36 32、A 33、C34、15 ;2n-1 35、 2n2 36、后面、上面、左面 37、C38、1 1,1,3,1,4,2,4,4;2。
规律探索--图形规律(解析版)-中考数学重难点题型专题汇总

规律探索-中考数学重难点题型专题汇总图形规律1.如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是A.B.C.D.【答案】D【解析】由题意知,原图形中各行、各列中点数之和为10,符合此要求的只有,故选D.【名师点睛】本题主要考查图形的变化规律,解题的关键是得出原图形中各行、各列中点数之和为10.2.将字母“C”,“H”按照如图所示的规律摆放,依次下去,则第4个图形中字母“H”的个数是()A.9B.10C.11D.12【答案】B【分析】列举每个图形中H的个数,找到规律即可得出答案.【详解】解:第1个图中H的个数为4,第2个图中H的个数为4+2,第3个图中H的个数为4+2×2,第4个图中H的个数为4+2×3=10,故选:B.【点睛】本题考查了规律型:图形的变化类,通过列举每个图形中H 的个数,找到规律:每个图形比上一个图形多2个H 是解题的关键.3.把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为()A.15B.13C.11D.9【答案】C 【分析】根据第①个图案中菱形的个数:1;第②个图案中菱形的个数:123+=;第③个图案中菱形的个数:1225+⨯=;…第n 个图案中菱形的个数:()121n +-,算出第⑥个图案中菱形个数即可.【详解】解:∵第①个图案中菱形的个数:1;第②个图案中菱形的个数:123+=;第③个图案中菱形的个数:1225+⨯=;…第n 个图案中菱形的个数:()121n +-,∴则第⑥个图案中菱形的个数为:()126111+⨯-=,故C 正确.故选:C.【点睛】本题主要考查的是图案的变化,解题的关键是根据已知图案归纳出图案个数的变化规律.4.如图是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为()A.148B.152C.174D.202【分析】观察各图可知,后一个图案比前一个图案多2(n+3)枚棋子,然后写成第n个图案的通式,再取n=10进行计算即可求解.【解析】根据图形,第1个图案有12枚棋子,第2个图案有22枚棋子,第3个图案有34枚棋子,…第n个图案有2(1+2+…+n+2)+2(n﹣1)=n2+7n+4枚棋子,故第10个这样的图案需要黑色棋子的个数为102+7×10+4=100+70+4=174(枚).故选:C.5.把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,…,按此规律排列下去,则第⑤个图案中黑色三角形的个数为()A.10B.15C.18D.21n个图案中黑色三角形的个数为1+2+3+4+……+n,据此可得第⑤个图案中黑色三角形的个数.【解析】∵第①个图案中黑色三角形的个数为1,第②个图案中黑色三角形的个数3=1+2,第③个图案中黑色三角形的个数6=1+2+3,……∴第⑤个图案中黑色三角形的个数为1+2+3+4+5=15,故选:B.Y Y-=()6.观察下列树枝分杈的规律图,若第n个图树枝数用n Y表示,则94A.4152⨯B.4312⨯C.4332⨯D.4632⨯【答案】B【分析】根据题目中的图形,可以写出前几幅图中树枝分杈的数量,从而可以发现树枝分杈的变化规律,进而得到规律21nn Y =-,代入规律求解即可.【详解】解:由图可得到:11223344211213217211521n n Y Y Y Y Y =-==-==-==-==-则:9921Y =-,∴944942121312Y Y -=--+=⨯,故答案选:B.【点睛】本题考查图形规律,解答本题的关键是明确题意,利用数形结合的思想解答.7.用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为()A.32B.34C.37D.41【分析】第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形,……,由此可得:每增加1个图形,就会增加4个正方形,由此找到规律,列出第n 个图形的算式,然后再解答即可.【详解】解:第1个图中有5个正方形;第2个图中有9个正方形,可以写成:5+4=5+4×1;第3个图中有13个正方形,可以写成:5+4+4=5+4×2;第4个图中有17个正方形,可以写成:5+4+4+4=5+4×3;...第n 个图中有正方形,可以写成:5+4(n-1)=4n+1;当n=9时,代入4n+1得:4×9+1=37.故选:C.【点睛】本题主要考查了图形的变化规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键.8.在平面直角坐标系中,等边AOB ∆如图放置,点A 的坐标为()1,0,每一次将AOB ∆绕着点О逆时针方向旋转60︒,同时每边扩大为原来的2倍,第一次旋转后得到11AOB ∆,第二次旋转后得到22A OB ∆,…,依次类推,则点2021A 的坐标为()A.()202020202,2-B.()202120212,2C.()202020202,2⨯D.()201120212,2-【答案】C【分析】由题意,点A 每6次绕原点循环一周,利用每边扩大为原来的2倍即可解决问题.解:由题意,点A 每6次绕原点循环一周,20216371......5÷= ,2021A ∴点在第四象限,202120212OA =,202160xOA ∠=︒,∴点2020A 的横坐标为20212020122=2⨯,纵坐标为20212020=3222-⨯-,()2020202020212,2A ∴,故选:C.【点睛】本题考查坐标与图形变化-旋转,规律型问题,解题的关键是理解题意,学会探究规律的方法,属于中考常考题型.9.如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形…,按这样的方法拼成的第(n+1)个正方形比第n 个正方形多个小正方形.【分析】观察不难发现,所需要的小正方形的个数都是平方数,然后根据相应的序数与正方形的个数的关系找出规律解答即可.【解析】∵第1个正方形需要4个小正方形,4=22,第2个正方形需要9个小正方形,9=32,第3个正方形需要16个小正方形,16=42,…,∴第n+1个正方形有(n+1+1)2个小正方形,第n 个正方形有(n+1)2个小正方形,故拼成的第n+1个正方形比第n 个正方形多(n+2)2﹣(n+1)2=2n+3个小正方形.故答案为:2n+3.10.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形中共有__________个〇.【答案】6058【解析】由图可得,第1个图象中〇的个数为:1+3×1=4,第2个图象中〇的个数为:1+3×2=7,第3个图象中〇的个数为:1+3×3=10,第4个图象中〇的个数为:1+3×4=13,…∴第2019个图形中共有:1+3×2019=1+6057=6058个〇,故答案为:6058.【名师点睛】本题考查图形的变化类,解答本题的关键是明确题意,发现图形中〇的变化规律,利用数形结合的思想解答.11.如图,每一图中有若干个大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,如果第n幅图中有2019个菱形,则n=__________.【答案】1010【解析】根据题意分析可得:第1幅图中有1个.第2幅图中有2×2-1=3个.第3幅图中有2×3-1=5个.第4幅图中有2×4-1=7个.…可以发现,每个图形都比前一个图形多2个.故第n幅图中共有(2n-1)个.当图中有2019个菱形时,2n-1=2019,n=1010,故答案为:1010.【名师点睛】本题考查规律型中的图形变化问题,难度适中,要求学生通过观察,分析、归纳并发现其中的规律.12.观察下列图形规律,当图形中的“○”的个数和“.”个数差为2022时,n的值为____________.【答案】不存在【分析】首先根据n=1、2、3、4时,“•”的个数分别是3、6、9、12,判断出第n 个图形中“•”的个数是3n;然后根据n=1、2、3、4,“○”的个数分别是1、3、6、10,判断出第n 个“○”的个数是()12n n +;最后根据图形中的“○”的个数和“.”个数差为2022,列出方程,解方程即可求出n 的值是多少即可.【详解】解:∵n=1时,“•”的个数是3=3×1;n=2时,“•”的个数是6=3×2;n=3时,“•”的个数是9=3×3;n=4时,“•”的个数是12=3×4;……∴第n 个图形中“•”的个数是3n;又∵n=1时,“○”的个数是1=1(11)2⨯+;n=2时,“○”的个数是32=n=3时,“○”的个数是3(31)62⨯+=,n=4时,“○”的个数是4(41)102⨯+=,……∴第n 个“○”的个数是()12n n +,由图形中的“○”的个数和“.”个数差为2022()1320222n n n +∴-=①,()1320222n n n +-=②解①得:无解解②得:1255,22n n +-==故答案为:不存在【点睛】本题考查了图形类规律,解一元二次方程,找到规律是解题的关键.13.将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为___________.【答案】1275【分析】首先得到前n个图形中每个图形中的黑色圆点的个数,得到第n个图形中的黑色圆点的个数为()12n n+,再判断其中能被3整除的数,得到每3个数中,都有2个能被3整除,再计算出第33个能被3整除的数所在组,为原数列中第50个数,代入计算即可.【详解】解:第①个图形中的黑色圆点的个数为:1,第②个图形中的黑色圆点的个数为:()1222+⨯=3,第③个图形中的黑色圆点的个数为:()1332+⨯=6,第④个图形中的黑色圆点的个数为:()1442+⨯=10,第n个图形中的黑色圆点的个数为()1 2n n+,则这列数为1,3,6,10,15,21,28,36,45,55,66,78,91,,其中每3个数中,都有2个能被3整除,33÷2=161,16×3+2=50,则第33个被3整除的数为原数列中第50个数,即50512⨯=1275,故答案为:1275.【点睛】此题考查了规律型:图形的变化类,关键是通过归纳与总结,得到其中的规律.14.如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有______个交点【答案】190【分析】根据题目中的交点个数,找出n条直线相交最多有的交点个数公式:1(1) 2n n-.【详解】解:2条直线相交有1个交点;3条直线相交最多有1123322+==⨯⨯个交点;4条直线相交最多有11236432++==⨯⨯个交点;5条直线相交最多有1123410542+++==⨯⨯个交点;⋯20条直线相交最多有12019190 2⨯⨯=.故答案为:190.【点睛】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交最多有1(1) 2n n-.15.如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍,拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍;……照这样拼图,则第n 个图形需要___________根火柴棍.【答案】2n+1【分析】分别得到第一个、第二个、第三个图形需要的火柴棍,找到规律,再总结即可.【详解】解:由图可知:拼成第一个图形共需要3根火柴棍,拼成第二个图形共需要3+2=5根火柴棍,拼成第三个图形共需要3+2×2=7根火柴棍,拼成第n 个图形共需要3+2×(n-1)=2n+1根火柴棍,故答案为:2n+1.【点睛】此题考查图形的变化规律,找出图形之间的联系,得出运算规律解决问题.16.如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第___个图形共有210个小球.【答案】20【分析】根据已知图形得出第n 个图形中黑色三角形的个数为1+2+3+ +n=()12n n +,列一元二次方程求解可得.【详解】解:∵第1个图形中黑色三角形的个数1,第2个图形中黑色三角形的个数3=1+2,第3个图形中黑色三角形的个数6=1+2+3,第4个图形中黑色三角形的个数10=1+2+3+4,……∴第n 个图形中黑色三角形的个数为1+2+3+4+5+ +n=()12n n +,当共有210个小球时,()12102n n +=,解得:20n =或21-(不合题意,舍去),∴第20个图形共有210个小球.故答案为:20.【点睛】本题考查了图形的变化规律,解一元二次方程,解题的关键是得出第n 个图形中黑色三角形的个数为1+2+3+……+n.17.如图,由两个长为2,宽为1的长方形组成“7”字图形ABCDEF,其中顶点A 位于x 轴上,顶点B,D 位于y 轴上,O 为坐标原点,则OB OA的值为__________.(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点F 1,摆放第三个“7”字图形得顶点F 2,依此类推,…,摆放第n 个“7”字图形得顶点F n-1,…,则顶点F 2019的坐标为__________.【答案】(1)12;(2)606255(,【解析】(1)∵∠ABO+∠DBC=90°,∠ABO+∠OAB=90°,∴∠DBC=∠OAB,∵∠AOB=∠BCD=90°,∴△AOB∽△BCD,∴OB DC OA BC =,∵DC=1,BC=2,∴OB OA =12,故答案为:12.(2过C 作CM⊥y 轴于M,过M 1作M 1N⊥x 轴,过F 作FN 1⊥x 轴.根据勾股定理易证得BD ==CM=OA=5,DM=OB=AN=5,∴C(5),∵AF=3,M 1F=BC=2,∴AM 1=AF-M 1F=3-2=1,∴△BOA≌ANM 1(AAS),∴NM 1=OA=255,∵NM 1∥FN 1,∴1111251553M N AM FN AF FN ==,,∴FN 1=655,∴AN 1=355,∴ON 1=OA+AN 1=253555555+=,∴F(555,655),同理,F 1(857555,F 2(55,),F 3(1459555,),F 4(17510555,),…F 2019),即(【名师点睛】此题考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳并发现其中的规律,并应用规律解决问题是解题的关键18.如图,正方形1ABCB 中,AB =,AB 与直线l 所夹锐角为60︒,延长1CB 交直线l 于点1A ,作正方形1112A B C B ,延长12C B 交直线l 于点2A ,作正方形2223A B C B ,延长23C B 交直线l 于点3A ,作正方形3334A B C B ,…,依此规律,则线段20202021A A =________.【答案】20203【分析】利用tan30°计算出30°角所对直角边,乘以2得到斜边,计算3次,找出其中的规律即可.【详解】∵AB 与直线l 所夹锐角为60︒,正方形1ABCB 中,AB =,∴∠11B AA =30°,∴11B A =1B A∴111=2=2(3AA -;∵11B A =1,∠122B A A =30°,∴22B A =11B A tan30°=33133⨯=,∴2112=23A A -⨯;∴线段20202021A A =202112020332(33-⨯=,故答案为:2020)3.【点睛】本题考查了正方形的性质,特殊角三角函数值,含30°角的直角三角形的性质,规律思考,熟练进行计算,抓住指数的变化这个突破口求解是解题的关键.19.如图,菱形ABCD 中,120ABC ∠=︒,1AB =,延长CD 至1A ,使1DA CD =,以1AC 为一边,在BC 的延长线上作菱形111ACC D ,连接1AA ,得到1ADA ∆;再延长11C D 至2A ,使1211D A C D =,以21A C 为一边,在1CC 的延长线上作菱形2122A C C D ,连接12A A ,得到112A D A ∆……按此规律,得到202020202021A D A ∆,记1ADA ∆的面积为1S ,112A D A ∆的面积为2S ……202020202021A D A ∆的面积为2021S ,则2021S =_____.【答案】40382【分析】由题意易得60,1BCD AB AD CD ∠=︒===,则有1ADA ∆为等边三角形,同理可得112A D A ∆…….202020202021A D A ∆都为等边三角形,进而根据等边三角形的面积公式可得134S =,2S =242n n S -=,然后问题可求解.【详解】解:∵四边形ABCD 是菱形,∴1AB AD CD ===,//,//AD BC AB CD ,∵120ABC ∠=︒,∴60BCD ∠=︒,∴160ADA BCD ∠=∠=︒,∵1DA CD =,∴1DA AD =,∴1ADA ∆为等边三角形,同理可得112A D A ∆…….202020202021A D A ∆都为等边三角形,过点B 作BE⊥CD 于点E,如图所示:∴3sin 2BE BC BCD =⋅∠=,∴1121133244A D BE A S D =⋅==,同理可得:2222133244S A D ==⨯=,2233233444S A D ==⨯=∴由此规律可得:242n n S -=,∴2202144038202122S ⨯-==⋅;故答案为40382【点睛】本题主要考查菱形的性质、等边三角形的性质与判定及三角函数,熟练掌握菱形的性质、等边三角形的性质与判定及三角函数是解题的关键.20.将一些相同的“〇”按如图所示的规律依次摆放,观察每个“龟图”的“〇”的个数,则第30个“龟图”中有___________个“〇”.【答案】875【分析】设第n 个“龟图”中有a n 个“〇”(n 为正整数),观察“龟图”,根据给定图形中“〇”个数的变化可找出变化规律“a n =n 2−n+5(n 为正整数)”,再代入n=30即可得出结论.【详解】解:设第n 个“龟图”中有a n 个“〇”(n 为正整数).观察图形,可知:a 1=1+2+2=5,a 2=1+3+12+2=7,a 3=1+4+22+2=11,a 4=1+5+32+2=17,…,∴a n =1+(n+1)+(n −1)2+2=n 2−n+5(n 为正整数),∴a 30=302−30+5=875.故答案是:875.【点睛】n =n 2−n+5(n 为正整数)”是解题的关键.21.下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形…,依此规律,则第n 个图形中三角形个数是_______.【答案】21n n +-【分析】此题只需分成上下两部分即可找到其中规律,上方的规律为(n-1),下方规律为n 2,结合两部分即可得出答案.【详解】解:将题意中图形分为上下两部分,则上半部规律为:0、1、2、3、4……n-1,下半部规律为:12、22、32、42……n 2,∴上下两部分统一规律为:21n n +-.故答案为:21n n +-.【点睛】本题主要考查的图形的变化规律,解题的关键是将图形分为上下两部分分别研究22.如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形…按此规律摆下去,第n 个图案有个三角形(用含n 的代数式表示).【分析】根据图形的变化发现规律,即可用含n 的代数式表示.【解析】第1个图案有4个三角形,即4=3×1+1第2个图案有7个三角形,即第3个图案有10个三角形,即10=3×3+1…按此规律摆下去,第n 个图案有(3n+1)个三角形.故答案为:(3n+1).23.如图,四边形ABCD 是矩形,延长DA 到点E,使AE=DA,连接EB,点F 1是CD 的中点,连接EF 1,BF 1,得到△EF 1B;点F 2是CF 1的中点,连接EF 2,BF 2,得到△EF 2B;点F 3是CF 2的中点,连接EF 3,BF 3,得到△EF 3B;…;按照此规律继续进行下去,若矩形ABCD 的面积等于2,则△EF n B 的面积为.(用含正整数n 的式子表示)【分析】先求得△EF 1D 的面积为1,再根据等高的三角形面积比等于底边的比可得EF 1F 2的面积,EF 2F 3的面积,…,EF n﹣1F n 的面积,以及△BCF n 的面积,再根据面积的和差关系即可求解.【解析】∵AE=DA,点F 1是CD 的中点,矩形ABCD 的面积等于2,∴△EF 1D 和△EAB 的面积都等于1,∵点F 2是CF 1的中点,∴△EF 1F 2的面积等于12,同理可得△EF n﹣1F n 的面积为12n−1,∵△BCF n 的面积为2×12n ÷2=12n ,∴△EF n B 的面积为2+1﹣1−12−⋯−12n−1−12n =2﹣(1−12n )=2n +12n .故答案为:2n +12n .。
各地市中考规律探索归纳探究题汇总有答案

2017年各地市中考规律探索归纳探究题汇总1.在一列数:a1,a2,a3,…,a n中,a1=3,a2=7,从第三个数开始,每一个数都等于它前两个数之积的个位数字,则这一列数中的第2017个数是()A. 1B. 3C. 7D. 9【来源】2017年中考真题精品解析数学(江苏扬州卷)精编word版(解析版)【答案】B【解析】依题意得:a1=3,a2=7,a3=1,a4=7,a5=7,a6=9,a7=3,a8=7,……周期为6,2017÷6=336…1,所以a2017=a1=3,故选B.【点睛】本题考查了数字变化类的规律型问题,解题的关键是根据题意先求出一些位置的数字,然后根据所求得的数字发现规律.2.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m的值为()A. 180 B. 182 C. 184 D. 186【来源】四川省自贡市初2017届毕业生学业考试数学试题【答案】C【解析】我们把正方形中的小方格的第一竖列和第二数列的小方格分别一次分别规定第一、二、三、四格.根据前面正方形方格数据排列可以看出第一,二,三格是连续奇数,且第一、三格数据的和等于等于第二、四格数据的积;所以111315+=⨯,解得:184m=.m故应选C.点睛:此题考查了数字的变化规律.首先应找出各个正方形中的哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决问题.3.3.下列图像都是由相同大小的星星按一定规律组成的,其中第①个图形中一共有4颗星星,第②个图形中一共有11颗星星,第③个图形中一共有21颗星星,.....按此规律排列下去,第⑨个图形中星星的颗数为()A. 116B. 144C. 145D. 150【来源】2017年初中毕业升学考试(重庆B卷)数学(带解析)【答案】B【解析】试题分析:∵4=1×2+2,11=2×3+2+321=3×4+2+3+4第4个图形为:4×5+2+3+4+5,∴第⑨个图形中的颗数为:9×10+2+3+4+5+6+7+8+9+10=144.故选B.考点:规律型:图形的变化类.4.(2017重庆,第10题,4分)下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为()A. 73B. 81C. 91D. 109【来源】2017年初中毕业升学考试(重庆A卷)数学(带解析)【答案】C【解析】试题解析:第①个图形中一共有3个菱形,3=12+2; 第②个图形中共有7个菱形,7=22+3; 第③个图形中共有13个菱形,13=32+4; …,第n 个图形中菱形的个数为:n 2+n+1; 第⑨个图形中菱形的个数92+9+1=91. 故选C .考点:图形的变化规律.5.我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧12PP ,23P P ,34P P ,…得到斐波那契螺旋线,然后顺次连结12P P ,23P P ,34P P ,…得到螺旋折线(如图),已知点1P (0,1),2P (1-,0),3P (0,1-),则该折线上的点9P 的坐标为( )A .(6-,24)B .(6-,25)C .(5-,24)D .(5-,25) (第10题图)【来源】2017年初中毕业升学考试(浙江温州卷)数学(带解析) 【答案】B . 【解析】试题解析:由题意,P 5在P 2的正上方,推出P 9在P 6的正上方,且到P 6的距离=21+5=26, 所以P 9的坐标为(﹣6,25), 故选B .考点:点的坐标.6.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移的另一个格点的运动称为一次跳马变换.例如,在44⨯的正方形网格图形中(如图1),从点A 经过一次跳马变换可以到达点B ,C ,D ,E 等处.现有2020⨯的正方形网格图形(如图2),则从该正方形的顶点M 经过跳马变换到达与其相对的顶点N ,最少需要跳马变换的次数是( )A .13B .14 C.15 D .16【来源】2017年初中毕业升学考试(浙江湖州卷)数学(带解析) 【答案】B 【解析】试题分析:根据图一可知,延AC 或AD 可进行下去,然后到CF ,从而求出知跳过了3格,然后依次进行下去,而20×20格共21条线,所以可知要进行下去,正好是(20+1)÷7×2=14. 故答案为:14.考点:1、勾股定理,2、规律探索7.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m 的值为( ) A .180 B .182 C .184 D .186【来源】2017年初中毕业升学考试(四川自贡卷)数学(带解析) 【答案】C. 【解析】试题解析:由前面数字关系:1,3,5;3,5,7;5,7,9,可得最后一个三个数分别为:11,13,15, ∵3×5﹣1=14,; 5×7﹣3=32; 7×9﹣5=58;∴m=13×15﹣11=184. 故选C .考点:数字规律.8.如图,将矩形ABCD 绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A 在整个旋转过程中所经过的路径总长为( ) A. 2017π B. 2034π C. 3024π D. 3026π【来源】2017年初中毕业升学考试(四川达州卷)数学(带解析) 【答案】D【解析】解:∵AB =4,BC =3,∴AC =BD =5.转动一次A 的路线长是: 904180π⨯ =2π,转动第二次的路线长是: 905180π⨯ =52π,转动第三次的路线长是: 903180π⨯ =32π,转动第四次的路线长是:0,以此类推,每四次循环.故顶点A 转动四次经过的路线长为: 52π+32π+2π=6π.∵2017÷4=504…1,∴顶点A 转动四次经过的路线长为:6π×504+2π=3026π,故选D . 9.用棋子摆出下列一组图形:按照这种规律摆下去,第n 个图形用的棋子个数为( ) A .n 3 B .n 6 C.63+n D .33+n【来源】2017年初中毕业升学考试(山东烟台卷)数学(带解析) 【答案】D . 【解析】试题解析:∵第一个图需棋子3+3=6; 第二个图需棋子3×2+3=9; 第三个图需棋子3×3+3=12; …∴第n 个图需棋子3n+3枚. 故选:D .考点:规律型:图形的变化类.10.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a 的值为( ) A. 23 B. 75 C. 77 D. 139【来源】2017年初中毕业升学考试(山东日照卷)数学(带解析) 【答案】B【解析】试题分析:观察可得,上边的数为连续的奇数1,3,5,7,9,11,左边的数为21,22,23,…,所以b=26=64,又因上边的数与左边的数的和正好等于右边的数,所以a=11+64=75,故选B .考点:规律型:数字的变化类.11.(2017德州,第12题,3分)观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( )A. 121B. 362C. 364D. 729【来源】2017年初中毕业升学考试(山东德州卷)数学(带解析)【答案】C【解析】试题分析:①图1,0×3+1=1;②图2,1×3+1=4;③图3,4×3+1=13;④图4,13×3+1=40;⑤图5,40×3+1=121;⑥图6,121×3+1=364;故选C考点:探索规律12.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后三个数的和为768,则n为()A.9 B.10 C.11 D.12【来源】2017年初中毕业升学考试(湖北武汉卷)数学(带解析)【答案】A.【解析】试题解析:设后3个的数和为:(-1)n+1×2n-1+(-1)n+2×2n+(-1)n+3×2n+1=768,当n为偶数:整理得出:-5×(-2)n-1=768,则求不出整数,当n为奇数:整理得出:3×2n-1=768,解得:n=9.故选A.考点:数字变化规律.13.(2017贵州省黔东南州,第10题,4分)我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所着的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为()A. 2017B. 2016C. 191D. 190【来源】2017年初中毕业升学考试(贵州黔东南州卷)数学(带解析)【答案】D【解析】试题解析:找规律发现(a+b)3的第三项系数为3=1+2;(a+b)4的第三项系数为6=1+2+3;(a+b)5的第三项系数为10=1+2+3+4;不难发现(a+b)n的第三项系数为1+2+3+…+(n﹣2)+(n﹣1),∴(a+b)20第三项系数为1+2+3+…+20=190,故选D.考点:完全平方公式.14.将一些相同的“d”按如图所示摆放,观察每个图形中的“d”的个数,若第n个图形中“d”的个数是78,则n的值是()A.11 B.12 C.13 D.14【来源】2017年初中毕业升学考试(山东临沂卷)数学(带解析)【答案】B【解析】试题分析:第一个图形有1个○,第二个图形有1+2=3个○,第三个图形有1+2+3=6个○, 第四个图形有1+2+3+4=10个○, ……第n 个图形有1+2+3+……+n=(1)2n n +个○,故(1)2n n +=78,解得n=12或n=-13(舍去).故选:B考点:规律探索15.已知正方形MNOK 和正六边形ABCDEF 边长均为1,把正方形放在正六边形中,使OK 边与AB 边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B 顺时针旋转,使KM 边与BC 边重合,完成第一次旋转;再绕点C 顺时针旋转,使MN 边与CD 边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B ,M 间的距离可能是( ) A .1.4 B .1.1 C .0.8 D .0.5【来源】2017年初中毕业升学考试(河北卷)数学(带解析) 【答案】C. 【解析】试题分析:在第一次旋转中BM=1,在第二次旋转中BM=1,在第三次旋转中BM 的长从1变化1,在第四次旋转中BM 的长从1-,在第五次旋转中BM 1变化到1,在第六次旋转中BM=1,故答案选C. 考点:正多边形的有关计算.16.如图所示,一动点从半径为2的O ⊙上的0A 点出发,沿着射线0A O 方向运动到O ⊙上的点1A 处,再向左沿着与射线1A O 夹角为60°的方向运动到O ⊙上的点2A 处;接着又从2A 点出发,沿着射线2A O 方向运动到O ⊙上的点3A 处,再向左沿着与射线3A O 夹角为60°的方向运动到O ⊙上的点4A 处;…按此规律运动到点2017A 处,则点2017A 与点0A 间的距离是( ) C.2 D.0【来源】2017年初中毕业升学考试(江苏连云港卷)数学(带解析) 【答案】A 【解析】试题分析:根据题意可知每六次循环一次,可知2017÷6=331……1,所以第2017次为A 1位置,由此可知其到A 0的距离正好等于直径的长4. 故选:A考点:规律探索17.如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如,表示a 1=a 2+a 3,则a 1的最小值为( ) A .32 B .36 C .38 D .40【来源】2017年初中毕业升学考试(湖北十堰卷)数学(带解析) 【答案】D. 【解析】试题分析:由a 1=a 7+3(a 8+a 9)+a 10知要使a 1取得最小值,则a 8+a 9应尽可能的小,取a 8=2、a 9=4,根据a 5=a 8+a 9=6,则a 7、a 10中不能有6,据此对于a 7、a 8,分别取8、10、12检验可得. ∵a 1=a 2+a 3=a 4+a 5+a 5+a 6=a 7+a 8+a 8+a 9+a 8+a 9+a 9+a 10=a 7+3(a 8+a 9)+a 10,∴要使a 1取得最小值,则a 8+a 9应尽可能的小,取a 8=2、a 9=4,∵a 5=a 8+a 9=6,则a 7、a 10中不能有6,若a 7=8、a 10=10,则a 4=10=a 10,不符合题意,舍去;若a 7=10、a 10=8,则a 4=12、a 6=4+8=12,不符合题意,舍去;若a 7=10、a 10=12,则a 4=10+2=12、a 6=4+12=16、a 2=12+6=18、a 3=6+16=22、a 1=18+22=40,符合题意; 综上,a 1的最小值为40, 故选:D .考点:数字的变化类18.刘莎同学用火柴棒依图的规律摆六边形图案,用10086根火柴棒摆出的图案应该是第______个.【来源】2017年中考真题精品解析 数学(湖南娄底卷) 【答案】2017.【解析】解:由图可知:第1个图形的火柴棒根数为6; 第2个图形的火柴棒根数为11; 第3个图形的火柴棒根数为16; …由该搭建方式可得出规律:图形标号每增加1,火柴棒的个数增加5,所以可以得出规律:搭第n 个图形需要火柴根数为:6+5(n ﹣1)=5n +1,令5n +1=10086,解得:n =2017. 故答案为:2017.点睛:本题考查了图形的变化类问题,关键在于通过题中图形的变化情况,通过归纳与总结找出普遍规律求解即可. 19.19.如图,第一个图形中有1个点,第二个图形中有4个点,第三个图形中有13个点,…,按此规律,第n 个图形中有______个点.【来源】2017年中考真题精品解析 数学(广西桂林卷)【答案】()1312n -.【解析】如图,第一个图形中有1个点,第二个图形中有4个点,第三个图形中有13个点,…,按此规律,第n 个图形中有12(3n -1)个点,故答案为: 12(3n -1).【点睛】本题考查了图形类规律题,先确定前几个图形中的点数,然后观察每个图形中的点数与图形次序的关系是解题的关键.20.20.(2017四川省凉山州,第26题,5分)古希腊数学家把1、3、6、10、15、21、…叫做三角形数,其中1是第一个三角形数,3是第二个三角形数,6是第三个三角形数,…,依此类推,第100个三角形数是______.【来源】2017年中考真题精品解析 数学(四川凉山州卷) 【答案】5050.【解析】解:设第n 个三角形数为a n ,∵a 1=1,a 2=3=1+2,a 3=6=1+2+3,a 4=10=1+2+3+4,…∴a n =1+2+…+n =()12n n +,将n =100代入a n ,得:a 100=()10010012+=5050,故答案为:5050.点睛:本题考查了规律型中的数字的变化类,解题的关键是找出变化规律“a n =1+2+…+n =()12n n +”.21.如图,Rt △OA 0A 1在平面直角坐标系内,∠OA 0A 1=90°,∠A 0OA 1=30°,以OA 1为直角边向外作Rt △OA 1A 2,使∠OA 1A 2=90°,∠A 1OA 2=30°,以OA 2为直角边向外作Rt △OA 2A 3,使∠OA 2A 3=90°,∠A 2OA 3=30°,按此方法进行下去,得到Rt △OA 3A 4,Rt △OA 4A 5,…,Rt △OA 2016A 2017,若点A 0(1,0),则点A 2017的横坐标为______. 【来源】山东省济南市槐荫区2018届九年级上学期期中考试数学试题【答案】2016⎝⎭.【解析】由已知可得OA 1=3,OA 2=23⎛ ⎝⎭ ,OA 3=33⎛⎫ ⎪ ⎪⎝⎭ ,……,由此可得OA 2017=20173⎛⎫ ⎪ ⎪⎝⎭,360°÷30°=12,2017÷12=168…3,由些可知OA 2017所在的射线与OA 1所在射线重合,所以点A 2017的横坐标为:OA 2017×cos30°=2017⎝⎭×=2016⎝⎭,故答案为: 20163⎛⎫⎪ ⎪⎝⎭.【点睛】本题主要考查规律性问题,解题的关键是能根据已知条件先求出一些相关的量,从中发现规律.22.如图,等边△A 1C 1C 2的周长为1,作C 1D 1⊥A 1C 2于D 1,在C 1C 2的延长线上取点C 3,使D 1C 3=D 1C 1,连接D 1C 3,以C 2C 3为边作等边△A 2C 2C 3;作C 2D 2⊥A 2C 3于D 2,在C 2C 3的延长线上取点C 4,使D 2C 4=D 2C 2,连接D 2C 4,以C 3C 4为边作等边△A 3C 3C 4;…且点A 1,A 2,A 3,…都在直线C 1C 2同侧,如此下去,则△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长和为______.(n ≥2,且n 为整数)【来源】2017年中考真题精品解析 数学(辽宁抚顺卷)【答案】1212n n --.【解析】解:∵等边△A 1C 1C 2的周长为1,作C 1D 1⊥A 1C 2于D 1,∴A 1D 1=D 1C 2,∴△A 2C 2C 3的周长=12△A 1C 1C 2的周长=12,∴△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长分别为1,12, 212,…, 112n -,∴△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长和为1+12+212+…+112n -=1212n n --.故答案为: 1212n n --.点睛:本题考查等边三角形的性质、解题的关键是理解题意,灵活运用所学知识,属于中考常考题型.23.杨辉三角,又称贾宪三角,是二项式系数在三角形中的一种几何排列,如图,观察下面的杨辉三角:按照前面的规律,则(a +b )5=______.【来源】2017年中考真题精品解析 数学(贵州黔南州卷) 【答案】1a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+1b 5. 【解析】解:观察图形,可知:(a +b )5=1a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+1b 5. 故答案为:1a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+1b 5.点睛:本题考查了完全平方公式以及规律型中数字的变化,观察图形,找出二项式系数与杨辉三角之间的关系是解题的关键.24.如图,把n 个长为1的正方形拼接成一排,求得71tan ,31tan ,1tan 321=∠=∠=∠C BA C BA C BA ,计算=∠C BA 4tan ,……,按此规律,写出=∠C BA n tan (用含n 的代数式表示).【来源】2017年初中毕业升学考试(浙江舟山卷)数学(带解析)【答案】113 , 211n n -+.【解析】试题分析:如图,过点C 作CE ⊥A 4B 于E ,易得∠A 4BC=∠BA 4A 1,故tan ∠A 4BC=tan ∠BA 4A 1=14,在Rt △BCE 中,由tan ∠A 4BC=14,得BE=4CE ,而BC=1,则,, 而A 4B=所以A 4E=A 4, 在Rt △A 4EC 中,tan ∠BA 4C=4113CE A E =;根据前面的规律,不能得出tan ∠ BA 1C=1101⨯+,tan ∠ BA 2C 1211⨯+, tan ∠ BA 3C=1321⨯+,tan ∠ BA 4C=1431⨯+,则可得规律tan ∠ BA n C=211(1)11n n n n =⨯-+-+.故答案为;考点:解直角三角形.25.如图,正△ABO 的边长为2,O 为坐标原点,A 在x 轴上,B 在第二象限。
2017年北京市中考数学一模分类26题探究问题及答案
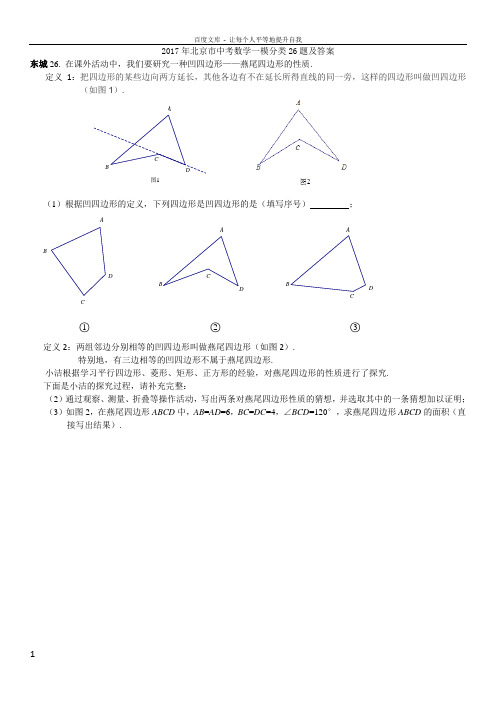
CCB B图1DCB2017年北京市中考数学一模分类26题及答案东城26. 在课外活动中,我们要研究一种凹四边形——燕尾四边形的性质.定义1:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形(如图1).(1)根据凹四边形的定义,下列四边形是凹四边形的是(填写序号);○1○2○3定义2:两组邻边分别相等的凹四边形叫做燕尾四边形(如图2).特别地,有三边相等的凹四边形不属于燕尾四边形.小洁根据学习平行四边形、菱形、矩形、正方形的经验,对燕尾四边形的性质进行了探究.下面是小洁的探究过程,请补充完整:(2)通过观察、测量、折叠等操作活动,写出两条对燕尾四边形性质的猜想,并选取其中的一条猜想加以证明;(3)如图2,在燕尾四边形ABCD中,AB=AD=6,BC=DC=4,∠BCD=120°,求燕尾四边形ABCD的面积(直接写出结果).西城26.阅读下列材料:某种型号的温控水箱的工作过程是:接通电源以后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,……,按照以上方式不断循环.小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究,发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度,x(单位:min)表示接通电源后的时间.下面是小明的探究过程,请补充完整:(1m的值为;(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式;当4<x≤16时,写出一个符合表中数据的函数解析式;②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象;(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源min.海淀26.有这样一个问题:探究函数222x y x =-的图象与性质.下面是小文的探究过程,请补充完整:(1)函数222x y x =-的自变量x 的取值范围是 ;(2)下表是y 与x 的几组对应值.如下图,在平面直角坐标系xOy 中,描出了以上表中各对对应值为坐标的点.①观察图中各点的位置发现:点1A 和1B ,2A 和2B ,3A 和3B ,4A 和4B 均关于某点中心对称,则该点的坐标为 ;②小文分析函数222x y x =-的表达式发现:当1x <时,该函数的最大值为0,则该函数图象在直线1x =左侧的最高点的坐标为 ;(3)小文补充了该函数图象上两个点(1124-,),(3924,), ①在上图中描出这两个点,并画出该函数的图象;②写出该函数的一条性质:________________ .朝阳26. 有这样一个问题:探究函数()262y x =-的图象与性质.小华根据学习函数的经验,对函数()262y x =-的图象与性质进行了探究.下面是小华的探究过程,请补充完整: (1)函数()262y x =-的自变量x 的取值范围是 ;x … -3-2-112 1 3 72 4 5 6 7 … y…625 38 23 3283668332 23 38m…求m 的值;(3)如下图,在平面直角坐标系xOy 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(4)结合函数的图象,写出该函数的一条性质: .丰台26.【问题情境】已知矩形的面积为a (a 为常数,0>a ),当该矩形的长为多少时,它的周长最小?最小值是多少? 【数学模型】设该矩形的长为x ,周长为y ,则y 与x 的函数表达式为⎪⎭⎫ ⎝⎛+=x a x y 2()0>x .【探索研究】小彬借鉴以前研究函数的经验,先探索函数xx y 1+=的图象性质.(1)结合问题情境,函数xx y 1+=的自变量x 的取值范围是0>x ,下表是y 与x 的几组对应值.①写出②画出该函数图象,结合图象,得出当x =______时,y 有最小值,y 最小=________; 【解决问题】(2)直接写出“问题情境”中问题的结论.图1 图2 图3 图4石景山26.(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁, 这样的四边形叫做凹四边形.如图1,四边形ABCD 为凹四边形.(2)性质探究:请完成凹四边形一个性质的证明.已知:如图2,四边形ABCD 是凹四边形. 求证:BCD B A D ∠=∠+∠+∠. (3)性质应用:如图3,在凹四边形ABCD 中,BAD ∠的角平分线与BCD ∠的角平分线交于 点E ,若140ADC ∠=°,102AEC ∠=°,则B ∠= °. (4)类比学习:如图4,在凹四边形ABCD 中,点E ,F ,G ,H 分别是边AD ,AB ,BC ,CD 的中点,顺次连接各边中点得到四边形EFGH .若AB AD =,CB CD =, 则四边形EFGH 是 .(填写序号即可)A .梯形B .菱形C .矩形D .正方形ABD房山26.小东根据学习函数的经验,对函数()2411y x =-+的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:(1)函数()2411y x =-+的自变量x 的取值范围是 ; (2)下表是y 与x 的几组对应值.表中m 的值为________________;(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数()2411y x =-+的大致图象; (4)结合函数图象,请写出函数()2411y x =-+的一条性质:______________________________. (5)解决问题:如果函数()2411y x =-+与直线y=a 的交点有2个, 那么a 的取值范围是______________ .通州26.已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.下面是小风的探究过程,请补充完整:(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)根据画出的函数图象,写出:①x=7对应的函数值y约为______________.②该函数的一条性质:______________________________________________________.门头沟26.在一节数学实践课上,老师出示了这样一道题,如图26-1,在锐角三角形ABC 中,∠A 、∠B 、∠C 所对边分别是a 、b 、c ,请用a 、c 、∠B 表示2b .经过同学们的思考后, 甲同学说:要将锐角三角形转化为直角三角形来解决,并且不能破坏∠B ,因此可以经过点A ,作AD ⊥BC 于点D ,如图26-2,大家认同;乙同学说要想得到2b 要在Rt △ABD 或Rt △ACD 中解决;丙同学说那就要先求出AD =________,BD =_______;(用含c ,∠B 的三角函数表示) 丁同学顺着他们的思路,求出2b =AD 2+DC 2=_____________(其中22sin cos 1αα+=);请利用丁同学的结论解决如下问题:如图26-3,在四边形ABCD 中,90B D ∠=∠=︒,60BAD ∠=︒,4,5AB AD ==. 求AC 的长(补全图形,直接写出结果即可).B26-326-126-2平谷26.有这样一个问题:探究函数+2y x x =-+的图象与性质.小军根据学习函数的经验, 对函数+2y x x =-+的图象与性质进行了探究. 下面是小军的探究过程, 请补充完整:(1)函数+2y x x =-+的自变量x 的取值范围是 ; (2)下表是y 与x 的几组对应值x ﹣2 ﹣ ﹣ ﹣1 ﹣0 1 2 3 4 … y 20 ﹣﹣﹣…在平面直角坐标系xOy 中, 描出了以上表中各对对应值为坐标的点,根据描出的点, 画出该函数的图象;yx–3–2–11234–2–112345O(3)观察图象,函数的最小值是;(4)进一步探究,结合函数的图象,写出该函数的一条..性质(函数最小值除外):.顺义26.某“数学兴趣小组”根据学习函数的经验,对函数()2264 -+-=x xy的图象和性质进行了探究,探究过程如下,请补充完整:(1)该函数的自变量x的取值范围是;(2)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;(3)结合画出的函数图象,写出该函数的一条性质:.怀柔26.已知y是x的函数,下表是y与x的几组对应值.x 2 3 4 5 6 7 …y 0 12325…小聪根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的表达式,图象和性质进行了探究.下面是小聪的探究过程,请补充完整:(1)根据上述表格所反映出的y与x之间的变化规律,写出该函数的表达式: ;(2)该函数自变量x的取值范围是 ;(3)如图,在平面直角坐标系xOy中,描出上表中各对对应值为坐标的点的位置(近似即可),根据描出的点,画出该函数的图象;(4)根据画出的函数图象,写出该函数的一条性质: .燕山26.有这样一个问题:探究函数xx y 22+=的图象和性质. 小奥根据学习函数的经验,对函数xx y 22+=的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:(1)函数xx y 22+=的自变量x 的取值范围是 ;(2)下表是y 与x 的几组对应值:求m 的值;(3)如下图,在平面直角坐标系xoy 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,2).结合函数图象,写出该函数的其他性质(一条即可): .2017年北京市中考数学一模分类26题答案:东城26.解:(1)○2.(2)它是一个轴对称图形;两组邻边分别相等;一组对角相等;一条对角线所在的直线垂直平分另一条对角线等等.已知:如图,在凹四边形ABCD 中,AB =AD ,BC =DC. 求证:∠B =∠D.A证明:连接AC .∵AB=AD,CB=CD,AC=AC , ∴△ABC ≌△ADC. ∴∠B =∠D.(3)燕尾四边形ABCD 的面积为243. 西城26.解:(1)50;(2)①答案不唯一. 如:当0≤x ≤4时,1520y x =+;当4<x ≤16时,y x=; ②(3)56.海淀26.(1)1x ≠;(2)①(1,1); ②(0,0); (3)①xyB 2B 3B 4B 1A 4A 3A 2A 1–1–2–312345–1–2123O②该函数的性质:(ⅰ)当x <0时,y 随x 的增大而增大;当0≤x <1时,y 随x 的增大而减小; 当1<x <2时,y 随x 的增大而减小; 当x ≥2时,y 随x 的增大而增大.(ⅱ)函数的图象经过第一、三、四象限.(ⅲ)函数的图象与直线x =1无交点,图象由两部分组成. (ⅳ)当x >1时,该函数的最小值为1.……(写出一条即可)朝阳26.解:(1)x ≠2(2)当x =7时,y =625.yx363480604020O2323028262422201816141210864图1图2∴625m =.(3)该函数的图象如下图所示:(4)答案不唯一,如:函数图象关于直线x =2对称.丰台26. 解:(1)①m = 4; ②图象如图.1;2.(2)根据小彬的方法可知,当xax =时,y 有最小值,即a x =时,a y 4=最小. 石景山26.(2)证法一:连接AC 并延长到点E ,如图1. ∵13B ∠=∠+∠,24D ∠=∠+∠, ∴1+234B D ∠∠=∠+∠+∠+∠. 即BCD B BAD D ∠=∠+∠+∠. 证法二:延长DC 交AB 于点E ,如图2. ∵1BCD B ∠=∠+∠,1A D ∠=∠+∠, ∴BCD D A B ∠=∠+∠+∠. (3)64°. (4)C . 房山26.(1)全体实数 (2)m=52(3)(4)以下情况均给分:①图象位于第一、二象限 ②当x =1时,函数有最大值4. ③图象有最高点(1,4) ④x >1时,y 随x 增大而减小 ⑤x <1时,y 随x 增大而增大 ⑥图象与x 轴没有交点 ⑦图象与y 轴有一个交点 ⑧图象关于直线x =1对称 …… (5)0<a <4通州26.(1)过点;符合函数概念(2)答案需和图形统一门头沟26.(1)sin AD C B =⋅,cos BD C B =⋅.1xB(2)2222cos b a c ac B =+-⋅ . (3)补全图形正确 . 结果:27AC = 平谷26.(1)2x ≥-;(2)该函数的图象如图所示;yx–3–2–11234–2–112345O(3)-2;(4)该函数的其它性质:当20x -≤<时,y 随x 的增大而减小;(答案不唯一,符合函数性质即可写出一条即可)顺义26.解:(1)自变量x 的取值范围是 2x ≠.(2)(3)该函数的一条性质是:函数有最大值(答案不唯一). 怀柔26.(1)y=2x -;(2)x ≥2;(3) 如图:(4) x ≥2时,函数图形y 随x 的增大而增大. 燕山26. (1) x ≠0(2)将x=3,y=m 代入 22x y x=+ 得m=613(3) (4)当x ﹥2 时,y 随x 的增大而增大等等-5yxO21342134-2-1-3556-4-4-3-1-2。
2017安徽中考数学试卷(含答案).

2017安徽中考数学试卷(含答案).2017年安徽省初中学业水平考试数学(试题卷)一、选择题(本题共10个小题,每小题4分,满分40分)每小题都给出A 、B 、C 、D 四个选项,其中只有一个是正确的.1.12的相反数是() A .12- B .12- C .2D .-22.计算22()a -的结果是() A .6aB .6a -C .5a -D .5a3.如图,一个放置在水平实验台上的锥形瓶,它的俯视图为()A. B. C. D .4.截至2016年底,国家开发银行对“一带一路”沿线国家累积发放贷款超过1600亿美元.其中1600亿用科学计数法表示为()A.101610? B .101.610? C.111.610? D .120.1610?5.不等式320x ->的解集在数轴上表示为()A .B . C. D .6.直角三角板和直尺如图放置.若120∠=?,则2∠的度数为()A.60? B .50? C.40? D.30?7.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数直方图.已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是()A .280B .240C .300D .2608.一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x ,则x 满足() A .16(12)25x += B .25(12)16x -= C.216(1)25x += D .225(1)16x -= 9.已知抛物线2y ax bx c =++与反比例函数by x=的图象在第一象限有一个公共点,其横坐标为1.则一次函数y bx ac =+的图象可能是()A. B . C. D .10.如图,在矩形ABCD 中,5AB =,3AD =.动点P 满足13PAB ABCD S S ?=矩形.则点P 到A ,B 两点距离之和PA PB +的最小值为()A .29B .34 C.52 D .41二、填空题(本大题共4小题,每小题5分,满分20分)11.27的立方根是.12.因式分解:244a b ab b -+= .13.如图,已知等边ABC ?的边长为6,以AB 为直径的⊙O 与边AC ,BC 分别交于D ,E 两点,则劣弧DE 的长为.14.在三角形纸片ABC 中,90A ∠=?,30C ∠=?,30AC cm =.将该纸片沿过点B 的直线折叠,使点A 落在斜边BC 上的一点E 处,折痕记为BD (如图1),剪去CDE ?后得到双层BDE ?(如图2),再沿着边BDE ?某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为 cm.三、(本大题共2小题,每小题8分,满分16分)15.计算:11|2|cos60()3--??-.16.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元.问共有多少人?这个物品的价格是多少?请解答上述问题.四、(本大题共2小题,每小题8分,满分16分)17.如图,游客在点A 处坐缆车出发,沿A B D --的路线可至山顶D 处.假设AB 和BD 都是直线段,且600AB BD m ==,75α=?,45β=?,求DE 的长.(参考数据:sin750.97?≈,cos750.26?≈,2 1.41≈)18. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点ABC ?和DEF ?(顶点为网格线的交点),以及过格点的直线l .(1)将ABC ?向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形;(2)画出DEF ?关于直线l 对称的三角形;(3)填空:C E ∠+∠= ?.五、(本大题共2小题,每小题10分,满分20分)19.【阅读理解】我们知道,(1)1232n n n +++++=,那么2222123n ++++结果等于多少呢?在图1所示三角形数阵中,第1行圆圈中的数为1,即21;第2行两个圆圈中数的和为22+,即22;……;第n 行n 个圆圈中数的和为n nn n n +++个,即2n .这样,该三角形数阵中共有(1)2n n +个圆圈,所有圆圈中数的和为2222123n ++++.【规律探究】将桑拿教学数阵经两次旋转可得如图所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第1n -行的第一个圆圈中的数分别为1n -,2,n ),发现每个位置上三个圆圈中数的和均为 .由此可得,这三个三角形数阵所有圆圈中数的总和为:22223(123)n ++++= .因此,2222123n ++++= .【解决问题】根据以上发现,计算222212320171232017++++++++的结果为 .20.如图,在四边形ABCD 中,AD BC =,B D ∠=∠,AD 不平行于BC ,过点C 作//CE AD 交ABC ?的外接圆O 于点E ,连接AE .(1)求证:四边形AECD 为平行四边形;(2)连接CO ,求证:CO 平分BCE ∠.六、(本题满分12分)21. 甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:甲:9,10,8,5,7,8,10,8,8,7;乙:5,7,8,7,8,9,7,9,10,10;丙:7,6,8,5,4,7,6,3,9,5. (1)根据以上数据完成下表:平均数中位数方差甲 8 8 乙 8 8 2.2 丙 63(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.七、(本题满分12分)22.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元.经市场调查,每天的销售量y (千克)与每千克售价x (元)满足一次函数关系,部分数据如下表:售价x (元/千克) 50 60 70 销售量y (千克)1008060(1)求y 与x 之间的函数表达式;(2)设商品每天的总利润为W (元),求W 与x 之间的函数表达式(利润=收入-成本);(3)试说明(2)中总利润W 随售价x 的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?八、(本题满分14分)23.已知正方形ABCD ,点M 为边AB 的中点.(1)如图1,点G 为线段CM 上的一点,且90AGB ∠=?,延长AG ,BG 分别与边BC ,CD 交于点E ,F .①求证:BE CF =;②求证:2BE BC CE =?.(2)如图2,在边BC 上取一点E ,满足2BE BC CE =?,连接AE 交CM 于点G ,连接BG 延长交CD 于点F ,求tan CBF ∠的值.2017年中考数学参考答案一、1-5:BABCD 6-10:CADBD 二、11、312、()22b a -13、p 14、40或8033三、15、解:原式12322=?=-. 16、解:设共有x 人,根据题意,得8374x x -=+,解得7x =,所以物品价格为87353?=(元). 答:共有7人,物品的价格为53元. 四、17、解:在Rt BDF △中,由sin DFBDb =得, 2sin 600sin 4560030024232DF BD b=°≈(m).在Rt ABC △中,由cos BCABa =可得,cos 600cos756000.26156BC AB a =°(m). 所以423156579DE DF EF DF BC =+=+=+=(m). 18、(1)如图所示;(2)如图所示;(3)45五、19、21n +()()1212n n n ++?()()11216n n n ++ 134520、(1)证明:∵B D =∠∠,B E =∠∠,∴D E =∠∠,∵CE AD ∥,∴180E DAE +=∠∠°.∴180D DAE +=∠∠°,∴AE CD ∥. ∴四边形AECD 是平行四边形.(2)证明:过点O 作OM EC ^,ON BC ^,垂足分别为M 、N . ∵四边形AECD 是平行四边形,∴AD EC =.又AD BC =,∴EC BC =,∴OM ON =,∴CO 平分BCE ∠.六、21、解:(1) 平均数中位数方差甲 2 乙丙6(2)因为2 2.23<<,所以222s s s <<甲乙丙,这说明甲运动员的成绩最稳定.(3)三人的出场顺序有(甲乙丙),(甲丙乙),(乙甲丙),(乙丙甲),(丙甲乙),(丙乙甲)共6种,且每一种结果出现的可能性相等,其中,甲、乙相邻出场的结果有(甲乙丙),(乙甲丙),(丙甲乙),(丙乙甲)共4种,所以甲、乙相邻出场的概率4263P ==. 七、22.解:(1)设y kx b =+,由题意,得501006080k b k b ì+=?í+=??,解得2200k b ì=-?í=??,∴所求函数表达式为2200y x =-+.(2)()()240220022808000W x x x x =--+=-+-.(3)()22228080002701800W x x x =-+-=--+,其中4080x #,∵20-<,∴当4070x ?时,W 随x 的增大而增大,当7080x得最大利润,这时最大利润为1800元.八、23、(1)①证明:∵四边形ABCD 为正方形,∴AB BC =,90ABC BCF ==∠∠°,又90AGB =∠°,∴90BAE ABG +=∠∠°,又90ABG CBF +=∠∠°,∴BAE CBF =∠∠,∴ABE BCF △≌△(ASA),∴BE CF =.②证明:∵90AGB =∠°,点M 为AB 中点,∴MG MA MB ==,∴GAM AGM =∠∠,又∵CGE AGM =∠∠,从而CGE CGB =∠∠,又ECG GCB =∠∠,∴CGE CBG △∽△,∴CE CGCG CB=,即2CG BC CE =?,由CFG GBM CGF ==∠∠∠,得CF CG =. 由①知,BE CF =,∴BE CG =,∴2BE BC CE =?. (2)解:(方法一) 延长AE ,DC 交于点N (如图1),由于四边形ABCD 是正方形,所以AB CD ∥,∴N EAB =∠∠,又CEN BEA =∠∠,∴CEN BEA △∽△,故CE CNBE BA=,即BE CN AB CE ??,∵AB BC =,2BE BC CE =?,∴CN BE =,由AB DN ∥知,CN CG CFAM GM MB==,又AM MB =,∴FC CN BE ==,不妨假设正方形边长为1,设BE x =,则由2BE BC CE =?,得()211x x =?,解得1512x -= ,2512x --=(舍去),∴512BE BC -=,于是51tan 2==∠,(方法二)不妨假设正方形边长为1,设BE x =,则由2BE BC CE =?,得()211x x =?,解得1512x -=,2512x --=(舍去),即512BE -=,作GN BC ∥交AB 于N (如图2),则MNG MBC △∽△,∴12MN MB NG BC ==,设MN y =,则2GN y =,5GM y =,∵GN ANBE AB =,即1221512y y +=-,解得125y =,∴12GM =,从而GM MA MB ==,此时点G 在以AB 为直径的圆上,∴AGB △是直角三角形,且90AGB =∠°,由(1)知BE CF =,于是51 tan 2== ∠.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年各地市中考规律探索归纳探究题汇总1.在一列数:a 1,a 2,a 3,…,a n 中,a 1=3,a 2=7,从第三个数开始,每一个数都等于它前两个数之积的个位数字,则这一列数中的第2017个数是( ) A. 1 B. 3 C. 7 D. 9【来源】2017年中考真题精品解析 数学(江苏扬州卷)精编word 版(解析版) 【答案】B【解析】依题意得:a 1=3,a 2=7,a 3=1,a 4=7,a 5=7,a 6=9,a 7=3,a 8=7,…… 周期为6,2017÷6=336…1,所以a 2017=a 1=3, 故选B .【点睛】本题考查了数字变化类的规律型问题,解题的关键是根据题意先求出一些位置的数字,然后根据所求得的数字发现规律.2.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m 的值为 ( )A. 180B. 182C. 184D. 186【来源】四川省自贡市初2017届毕业生学业考试数学试题 【答案】C 【解析】我们把正方形中的小方格的第一竖列和第二数列的小方格分别一次分别规定第一、二、三、四格.根据前面正方形方格数据排列可以看出第一,二,三格是连续奇数,且第一、三格数据的和等于等于第二、四格数据的积;所以111315m +=⨯,解得:184m =.故应选C.点睛:此题考查了数字的变化规律.首先应找出各个正方形中的哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决问题.3.3.下列图像都是由相同大小的星星按一定规律组成的,其中第①个图形中一共有4颗星星,第②个图形中一共有11颗星星,第③个图形中一共有21颗星星,.....按此规律排列下去,第⑨个图形中星星的颗数为( )A. 116B. 144C. 145D. 150【来源】2017年初中毕业升学考试(重庆B 卷)数学(带解析) 【答案】B【解析】试题分析:∵4=1×2+2,11=2×3+2+3 21=3×4+2+3+4第4个图形为:4×5+2+3+4+5,∴第⑨个图形中的颗数为:9×10+2+3+4+5+6+7+8+9+10=144.故选B .考点:规律型:图形的变化类.4.(2017重庆,第10题,4分)下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )A. 73B. 81C. 91D. 109【来源】2017年初中毕业升学考试(重庆A 卷)数学(带解析) 【答案】C【解析】试题解析:第①个图形中一共有3个菱形,3=12+2; 第②个图形中共有7个菱形,7=22+3; 第③个图形中共有13个菱形,13=32+4; …,第n 个图形中菱形的个数为:n 2+n+1; 第⑨个图形中菱形的个数92+9+1=91. 故选C .考点:图形的变化规律.5.我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧12PP ,23P P ,34P P ,…得到斐波那契螺旋线,然后顺次连结12PP ,23P P ,34P P ,…得到螺旋折线(如图),已知点1P (0,1),2P (1-,0),3P (0,1-),则该折线上的点9P 的坐标为( )A .(6-,24)B .(6-,25)C .(5-,24)D .(5-,25)(第10题图)【来源】2017年初中毕业升学考试(浙江温州卷)数学(带解析) 【答案】B . 【解析】试题解析:由题意,P 5在P 2的正上方,推出P 9在P 6的正上方,且到P 6的距离=21+5=26, 所以P 9的坐标为(﹣6,25), 故选B .考点:点的坐标.6.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格⨯的正方形例如,在44网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现⨯的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其有2020相对的顶点N,最少需要跳马变换的次数是()A.13 B.14 C.15 D.16【来源】2017年初中毕业升学考试(浙江湖州卷)数学(带解析)【答案】B【解析】试题分析:根据图一可知,延AC或AD可进行下去,然后到CF,从而求出这时可知跳过了3格,然后依次进行下去,而20×20格共21条线,所以可知要进行下去,正好是(20+1)÷7×2=14.故答案为:14.考点:1、勾股定理,2、规律探索7.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m的值为()A.180 B.182 C.184 D.186【来源】2017年初中毕业升学考试(四川自贡卷)数学(带解析)【答案】C.【解析】试题解析:由前面数字关系:1,3,5;3,5,7;5,7,9,可得最后一个三个数分别为:11,13,15,∵3×5﹣1=14,;5×7﹣3=32;7×9﹣5=58;∴m=13×15﹣11=184.故选C.考点:数字规律.8.如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A 在整个旋转过程中所经过的路径总长为( )A. 2017πB. 2034πC. 3024πD. 3026π【来源】2017年初中毕业升学考试(四川达州卷)数学(带解析) 【答案】D【解析】解:∵AB =4,BC =3,∴AC =BD =5.转动一次A 的路线长是:904180π⨯ =2π,转动第二次的路线长是: 905180π⨯ =52π,转动第三次的路线长是: 903180π⨯ =32π,转动第四次的路线长是:0,以此类推,每四次循环.故顶点A 转动四次经过的路线长为:52π+32π+2π=6π.∵2017÷4=504…1,∴顶点A 转动四次经过的路线长为:6π×504+2π=3026π,故选D .9.用棋子摆出下列一组图形:按照这种规律摆下去,第n 个图形用的棋子个数为( )A .n 3B .n 6 C.63+n D .33+n【来源】2017年初中毕业升学考试(山东烟台卷)数学(带解析) 【答案】D . 【解析】试题解析:∵第一个图需棋子3+3=6; 第二个图需棋子3×2+3=9; 第三个图需棋子3×3+3=12; …∴第n 个图需棋子3n+3枚. 故选:D .考点:规律型:图形的变化类.10.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a 的值为( )A. 23B. 75C. 77D. 139【来源】2017年初中毕业升学考试(山东日照卷)数学(带解析) 【答案】B【解析】试题分析:观察可得,上边的数为连续的奇数1,3,5,7,9,11,左边的数为21,22,23,…,所以b=26=64,又因上边的数与左边的数的和正好等于右边的数,所以a=11+64=75,故选B .考点:规律型:数字的变化类.11.(2017德州,第12题,3分)观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为()A. 121B. 362C. 364D. 729【来源】2017年初中毕业升学考试(山东德州卷)数学(带解析)【答案】C【解析】试题分析:①图1,0×3+1=1;②图2,1×3+1=4;③图3,4×3+1=13;④图4,13×3+1=40;⑤图5,40×3+1=121;⑥图6,121×3+1=364;故选C考点:探索规律12.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后三个数的和为768,则n为()A.9 B.10 C.11 D.12【来源】2017年初中毕业升学考试(湖北武汉卷)数学(带解析)【答案】A.【解析】试题解析:设后3个的数和为:(-1)n+1×2n-1+(-1)n+2×2n+(-1)n+3×2n+1=768,当n为偶数:整理得出:-5×(-2)n-1=768,则求不出整数,当n为奇数:整理得出:3×2n-1=768,解得:n=9.故选A.考点:数字变化规律.13.(2017贵州省黔东南州,第10题,4分)我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为()A. 2017B. 2016C. 191D. 190【来源】2017年初中毕业升学考试(贵州黔东南州卷)数学(带解析)【解析】试题解析:找规律发现(a+b)3的第三项系数为3=1+2;(a+b)4的第三项系数为6=1+2+3;(a+b)5的第三项系数为10=1+2+3+4;不难发现(a+b)n的第三项系数为1+2+3+…+(n﹣2)+(n﹣1),∴(a+b)20第三项系数为1+2+3+…+20=190,故选D.考点:完全平方公式.14.将一些相同的“d”按如图所示摆放,观察每个图形中的“d”的个数,若第n个图形中“d”的个数是78,则n的值是()A.11 B.12 C.13 D.14【来源】2017年初中毕业升学考试(山东临沂卷)数学(带解析)【答案】B【解析】试题分析:第一个图形有1个○,第二个图形有1+2=3个○,第三个图形有1+2+3=6个○,第四个图形有1+2+3+4=10个○,……第n个图形有1+2+3+……+n=(1)2n n+个○,故(1)2n n+=78,解得n=12或n=-13(舍去).故选:B考点:规律探索15.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B,M间的距离可能是( )A.1.4 B.1.1 C.0.8 D.0.5【来源】2017年初中毕业升学考试(河北卷)数学(带解析)【答案】C.试题分析:在第一次旋转中BM=1,在第二次旋转中BM=1,在第三次旋转中BM 的长从11,在第四次旋转中BM 的长从1,在第五次旋转中BM 的1变化到1,在第六次旋转中BM=1,故答案选C. 考点:正多边形的有关计算.16.如图所示,一动点从半径为2的O ⊙上的0A 点出发,沿着射线0A O 方向运动到O ⊙上的点1A 处,再向左沿着与射线1A O 夹角为60°的方向运动到O ⊙上的点2A 处;接着又从2A 点出发,沿着射线2A O 方向运动到O ⊙上的点3A 处,再向左沿着与射线3A O 夹角为60°的方向运动到O ⊙上的点4A 处;…按此规律运动到点2017A 处,则点2017A 与点0A 间的距离是( )A.4B.C.2D.0【来源】2017年初中毕业升学考试(江苏连云港卷)数学(带解析) 【答案】A 【解析】试题分析:根据题意可知每六次循环一次,可知2017÷6=331……1,所以第2017次为A 1位置,由此可知其到A 0的距离正好等于直径的长4. 故选:A考点:规律探索17.如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如, 表示a 1=a 2+a 3,则a 1的最小值为( )A .32B .36C .38D .40【来源】2017年初中毕业升学考试(湖北十堰卷)数学(带解析)【解析】试题分析:由a1=a7+3(a8+a9)+a10知要使a1取得最小值,则a8+a9应尽可能的小,取a8=2、a9=4,根据a5=a8+a9=6,则a7、a10中不能有6,据此对于a7、a8,分别取8、10、12检验可得.∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3(a8+a9)+a10,∴要使a1取得最小值,则a8+a9应尽可能的小,取a8=2、a9=4,∵a5=a8+a9=6,则a7、a10中不能有6,若a7=8、a10=10,则a4=10=a10,不符合题意,舍去;若a7=10、a10=8,则a4=12、a6=4+8=12,不符合题意,舍去;若a7=10、a10=12,则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40,符合题意;综上,a1的最小值为40,故选:D.考点:数字的变化类18.刘莎同学用火柴棒依图的规律摆六边形图案,用10086根火柴棒摆出的图案应该是第______个.【来源】2017年中考真题精品解析数学(湖南娄底卷)【答案】2017.【解析】解:由图可知:第1个图形的火柴棒根数为6;第2个图形的火柴棒根数为11;第3个图形的火柴棒根数为16;…由该搭建方式可得出规律:图形标号每增加1,火柴棒的个数增加5,所以可以得出规律:搭第n个图形需要火柴根数为:6+5(n﹣1)=5n+1,令5n+1=10086,解得:n=2017.故答案为:2017.点睛:本题考查了图形的变化类问题,关键在于通过题中图形的变化情况,通过归纳与总结找出普遍规律求解即可.19.19.如图,第一个图形中有1个点,第二个图形中有4个点,第三个图形中有13个点,…,按此规律,第n个图形中有______个点.【来源】2017年中考真题精品解析数学(广西桂林卷)【答案】()1312n-. 【解析】如图,第一个图形中有1个点,第二个图形中有4个点,第三个图形中有13个点,…,按此规律,第n 个图形中有12(3n -1)个点, 故答案为:12(3n -1). 【点睛】本题考查了图形类规律题,先确定前几个图形中的点数,然后观察每个图形中的点数与图形次序的关系是解题的关键. 20.20.(2017四川省凉山州,第26题,5分)古希腊数学家把1、3、6、10、15、21、…叫做三角形数,其中1是第一个三角形数,3是第二个三角形数,6是第三个三角形数,…,依此类推,第100个三角形数是______.【来源】2017年中考真题精品解析 数学(四川凉山州卷) 【答案】5050. 【解析】解:设第n 个三角形数为a n ,∵a 1=1,a 2=3=1+2,a 3=6=1+2+3,a 4=10=1+2+3+4,… ∴a n =1+2+…+n =()12n n +,将n =100代入a n ,得:a 100=()10010012+=5050,故答案为:5050.点睛:本题考查了规律型中的数字的变化类,解题的关键是找出变化规律“a n =1+2+…+n =()12n n +”.21.如图,Rt △OA 0A 1在平面直角坐标系内,∠OA 0A 1=90°,∠A 0OA 1=30°,以OA 1为直角边向外作Rt △OA 1A 2,使∠OA 1A 2=90°,∠A 1OA 2=30°,以OA 2为直角边向外作Rt △OA 2A 3,使∠OA 2A 3=90°,∠A 2OA 3=30°,按此方法进行下去,得到Rt △OA 3A 4,Rt △OA 4A 5,…,Rt △OA 2016A 2017,若点A 0(1,0),则点A 2017的横坐标为______.【来源】山东省济南市槐荫区2018届九年级上学期期中考试数学试题【答案】2016⎝⎭.【解析】由已知可得OA 1OA 2=2⎝⎭ ,OA 3=3⎝⎭ ,……,由此可得OA 2017=2017⎝⎭,360°÷30°=12,2017÷12=168…3,由些可知OA 2017所在的射线与OA 1所在射线重合,所以点A 2017的横坐标为:OA 2017×cos30°=20173⎛⎫⎪ ⎪⎝⎭=20163⎛ ⎝⎭,故答案为: 2016⎝⎭.【点睛】本题主要考查规律性问题,解题的关键是能根据已知条件先求出一些相关的量,从中发现规律.22.如图,等边△A 1C 1C 2的周长为1,作C 1D 1⊥A 1C 2于D 1,在C 1C 2的延长线上取点C 3,使D 1C 3=D 1C 1,连接D 1C 3,以C 2C 3为边作等边△A 2C 2C 3;作C 2D 2⊥A 2C 3于D 2,在C 2C 3的延长线上取点C 4,使D 2C 4=D 2C 2,连接D 2C 4,以C 3C 4为边作等边△A 3C 3C 4;…且点A 1,A 2,A 3,…都在直线C 1C 2同侧,如此下去,则△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长和为______.(n ≥2,且n 为整数)【来源】2017年中考真题精品解析 数学(辽宁抚顺卷)【答案】1212n n --.【解析】解:∵等边△A 1C 1C 2的周长为1,作C 1D 1⊥A 1C 2于D 1,∴A 1D 1=D 1C 2,∴△A 2C 2C 3的周长=12△A 1C 1C 2的周长=12,∴△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长分别为1, 12, 212,…, 112n -,∴△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长和为1+12+212+…+112n -=1212n n --.故答案为: 1212n n --.点睛:本题考查等边三角形的性质、解题的关键是理解题意,灵活运用所学知识,属于中考常考题型.23.杨辉三角,又称贾宪三角,是二项式系数在三角形中的一种几何排列,如图,观察下面的杨辉三角:按照前面的规律,则(a +b )5=______.【来源】2017年中考真题精品解析 数学(贵州黔南州卷) 【答案】1a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+1b 5. 【解析】解:观察图形,可知:(a +b )5=1a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+1b 5.故答案为:1a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+1b 5.点睛:本题考查了完全平方公式以及规律型中数字的变化,观察图形,找出二项式系数与杨辉三角之间的关系是解题的关键.24.如图,把n 个长为1的正方形拼接成一排,求得71tan ,31tan ,1tan 321=∠=∠=∠C BA C BA C BA ,计算=∠C BA 4tan ,……,按此规律,写出=∠C BA n tan (用含n 的代数式表示).【来源】2017年初中毕业升学考试(浙江舟山卷)数学(带解析) 【答案】113 , 211n n -+. 【解析】试题分析:如图,过点C 作CE ⊥A 4B 于E ,易得∠A 4BC=∠BA 4A 1,故tan ∠A 4BC=tan ∠BA 4A 1=14,在Rt △BCE 中,由tan ∠A 4BC=14,得BE=4CE ,而BC=1,则,, 而A 4B=,所以A 4E=A 4B-BE=, 在Rt △A 4EC 中,tan ∠BA 4C=4113CE A E =;根据前面的规律,不能得出tan ∠ BA 1C=1101⨯+,tan ∠ BA 2C 1211⨯+, tan ∠ BA 3C=1321⨯+,tan ∠ BA 4C=1431⨯+,则可得规律tan ∠BA n C=211(1)11n n n n =⨯-+-+.故答案为;考点:解直角三角形.25.如图,正△ABO 的边长为2,O 为坐标原点,A 在x 轴上,B 在第二象限。
