2014年成考高起点《数学(理科)》考试真题及答案
2014年普通高等学校招生全国统一考试数学理试题(四川卷,解析版)

2014年普通高等学校招生全国统一考试理科参考答案〔四川卷〕一.选择题:本大题共10小题,每一小题5分,共50分.在每一小题给出的四个选项中,只有一个是符合题目要求的。
1.集合2{|20}A x x x =--≤,集合B 为整数集,如此A B ⋂= A .{1,0,1,2}- B .{2,1,0,1}-- C .{0,1} D .{1,0}- 【答案】A【解析】{|12}A x x =-≤≤,B Z =,故A B ⋂={1,0,1,2}- 2.在6(1)x x +的展开式中,含3x 项的系数为A .30B .20C .15D .10 【答案】C【解析】含3x 项为24236(1)15x C x x ⋅=3.为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上 所有的点A .向左平行移动12个单位长度B .向右平行移动12个单位长度C .向左平行移动1个单位长度D .向右平行移动1个单位长度 【答案】A【解析】因为,故可由函数sin 2y x =的图象上所有的点向左平行移动12个单位长度得到4.假设0a b >>,0c d <<,如此一定有A .a b c d >B .a b c d <C .a b d c >D .a b d c < 【答案】D【解析】由1100c d d c <<⇒->->,又0a b >>,由不等式性质知:0a b d c ->->,所以a bd c <5.执行如图1所示的程序框图,如果输入的,x y R ∈,如此输出的S 的最大值为A .0B .1C .2D .3 【答案】C【解析】当001x y x y ≥⎧⎪≥⎨⎪+≤⎩时,函数2S x y =+的最大值为2,否如此,S 的值为1.6.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能拍甲,如此不同的排法共有 A .192种 B .216种 C .240种 D .288种 【答案】B【解析】当最左端为甲时,不同的排法共有55A 种;当最左端为乙时,不同的排法共有14C 44A 种。
成考数学2014年理工类试题和答案(1--21题有详细答案)

,
,选 B
D
乙:a������ 2 + ������������+c=0 有实根,则
甲是乙的必要条件,但不是乙的充分条件 甲是乙的充分的条件,但不是乙的必要条件 甲既不是乙的充分的条件,也不是乙的必要条件
D 甲是乙的充分必要条件 解:显然甲是乙的充分条件,且有实数根,也必须������ 2 − 4������������ > 0, 即甲是乙的充分必要条件。应选择 D 8、二次函数y = ������ 2 + ������ − 2 的图像与x 轴的交点坐标为 A: −2, 0 和 1, 0 C 2, 0 和 1, 0 B −2, 0 和 −1, 0 D 2, 0 和 −1, 0 A
解方程������ 2 + ������ − 2 = 0,其根为������1 = −2,������2 = 1, 所以交点坐标选 A 9、设z = 1 + A
1+ 3������ 4
3 i i 是虚数单位,则 z = B
B
1− 3������ 4
1
C
2+ 3������ 4 1 ������
D
1
2− 3������ 4 1− 3������ 4
3 2
3,0 ,其长轴长为 4,
������ + ������与椭圆有两个不同的交点,求m的取值范围
解:1、长轴长为 4,则a = 2 由焦点坐标知c = 3 所以b = ������2 − ������ 2 = 4 − 3 = 1 所以本椭圆的方程为: 4 + ������ 2 = 1 2、 将y =
3 2 x2
������ + ������ 代入椭圆方程 4 + ������ 2 = 1 可得
2014成人高等学校招生全国统一考试数学真题(理工类)

附录 2014年成人高等学校招生全国统一考试(高起点)数学试题(理工农医类)第Ⅰ卷(选择题,共85分)一、选择题(本大题共17小题,每小题5分,共85分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}21|<≤-=x x M ,{}1|≤=x x N ,则集合=N MA . {}1|->x xB .{}1|>x xC .{}11|≤≤-x xD .{}21|≤≤x x 2.函数51-=x y 的定义域为 A . ()5,∞- B . ()+∞∞-, C . ()+∞,5 D .()()+∞∞-,55, 3.函数x y 6sin 2=的最小正周期为A . 3πB .2πC . π2D .π34.下列函数为奇函数的是A . x y 2log =B . x y sin =C . 2x y =D .x y 3=5.过点()1,2 且与直线x y =垂直的直线方程为A . 2+=x yB . 1-=x yC . 3+-=x yD .2+-=x y6.函数12+=x y 的反函数为A .21+=x yB .21-=x y C .12-=x y D .x y 21-= 7.若c b a ,,为实数,且0≠a .设甲:042≥-ac b ,乙:02=++c bx ax 有实数根,则A .甲是乙的必要条件,但不是乙的充分条件B .甲是乙的充分条件,但不是乙的必要条件C .甲既不是乙的充分条件,也不是乙的必要条件D .甲是乙的充分必要条件8. 二次函数22-+=x x y 的图像与x 轴的交点坐标为A . ()0,2- 和()0,1B .()0,2- 和()0,1-C .()0,2 和()0,1D .()0,2 和()0,1-9.设i z 31+=,i 是虚数单位,则=z 1 A .431i + B .431i - C .232i + D .232i - 10.设1>>b a ,则A .44b a ≤B .4log 4log b a >C .22--<b aD .b a 44<11.已知平面向量()1,1=a ,()1,1-=b ,则两向量的夹角为A . 6πB .4πC . 3πD .2π 12.3)1(xx -的展开式中的常数项为A .3B .2C .2-D .3-13.每次射击时,甲击中目标的概率为8.0,乙击中目标的概率为6.0,甲、乙各自独立地向目标射击一次,则恰有一人击中的概率为A .44.0B .6.0C .8.0D .1 14.已知一个球的体积为π332,则它的表面积为 A . π4 B .π8 C .π16 D .π2415.在等腰三角形ABC 中,A 是顶角,且21cos -=A ,则=B cos A .23 B .21 C . 21- D .23- 16. 四棱锥ABCD P -的底面为矩形,且4=AB ,3=BC ,⊥PD 底面ABCD ,5=PD ,则PB与底面所成角为A .︒30B .︒455.1C .︒60D .︒7517.将5本不同的历史书和2本不同的数学书排成一行,则2本数学书恰好在两端的概率为A .101 B .141 C .201 D .211第Ⅱ卷(非选择题,共65分)二、填空题(本大题共4小题,每小题4分,共16分) 18.已知空间向量()3,2,1=a ,()3,2,1-=b ,则=+b a 2 .19.曲线x x y 23-=在点()1,1-处的切线方程为 .20.设函数()11+=+x x x f ,则()=3f . 21.某运动员射击10次,成绩(单位:环)如下8 10 9 9 10 8 9 9 8 7则该运动员的平均成绩是 环.三、解答题(本大题共4小题,共49分.解答应写出推理、演算步骤)22.(本小题满分12分)已知ABC ∆中,︒=110A ,5=AB ,6=AC ,求BC .(精确到01.0)23.(本小题满分12分)已知数列{}n a 的前n 项和n n S 211-=,求 (Ⅰ) {}n a 的前三项;(Ⅱ) {}n a 的通项公式. 24.(本小题满分12分)设函数()x x x x f 9323--=,求(Ⅰ)函数()x f 的导数;(Ⅱ)函数()x f 在区间[]4,1的最大值与最小值.25.(本小题满分13分) 设椭圆的焦点为()0,31-F ,()0,32F ,其长轴长为4. (Ⅰ)求椭圆的方程;(Ⅱ) 若直线m x y +=23与椭圆有两个不同的交点,求m 的取值范围.参考答案一、 选择题(每小题5分,共85分)1 . C 2.D 3.A 4.B 5.C 6.B 7.D 8.A 9.B 10.C 11.D 12.D 13.A 14.C 15.A 16.B 17.D二、填空题(每小题4分,共16分,)18. ()9,2,3 19. 2-=x y 20.32 21. 7.8 三、解答题(共49分.)22.解:根据余玄定理 A AC AB AC AB BC cos 222∙∙-+=︒∙∙∙-+=110cos 652652203.9≈23.解:(Ⅰ)因为n n S 211-=,则 2121111=-==S a 41212112122=--=-=a S a 8141218112133=---=--=a a S a (Ⅱ)当2≥n 时,1--=n n n S S a⎪⎭⎫ ⎝⎛---=-1211211n n ⎪⎭⎫ ⎝⎛-=-211211n n 21=当1=n 时,211=a ,满足公式n n a 21= 所以数列的通项公式为n n a 21=. 24.解:(Ⅰ) 因为函数()x x x x f 9323--=,所以963)(2'--=x x x f(Ⅱ) 令0)('=x f ,解得3=x 或1-=x ,比较()1f ,()3f ,()4f 的大小,()111-=f ,()273-=f ,()204-=f所以函数()x x x x f 9323--=在区间[]4,1的最大值为11-,最小值为27-. 25.解:(Ⅰ)由已知,椭圆的长轴长42=a ,焦距322=c ,设其短半轴长为b ,则 13422=-=-=c a b所以椭圆的方程为1422=+y x (Ⅱ) 将直线方程m x y +=23代入椭圆方程可得01322=-++m mx x因为直线与椭圆有两个不同交点,所以()014322>--=∆m m解得 22<<-m所以m 的取值范围为()2,2-.。
历年成人高考《数学》真题及答案汇总(高起点)

☆★☆倾情收集☆★☆历年成人高考《数学》真题及答案汇总(高起点)2002年——2011年2002年全国成人高等学校(高起点)招生统一数学(理)试卷和参考答案2003年全国成人高等学校(高起点)招生统一数学(理)试卷及答案2004年全国成人高等学校(高起点)招生统一数学(理)试卷及答案2005年全国成人高考(高起点)数学(理)试卷和参考答案2006年全国成人高考高起点数学(理)真题及答案2007年全国成人高考高起点数学(理)真题及答案2008年(高起点)数学(理)成人高考考试试题及答案2009年成人高等学校招生全国统一考试数 学 (理工农医类)1.答案必须答在答题卡上指定的位置,答在试卷上无效。
2.在本试卷中, tan a 表示角a 的正切, cot a 表示角a 的余切.一、选择题:本大题共17小题,每小题5分,共85分.在每小题给出的四个选项中,只有一项是符合题目要求的; 将所选项前的字母填涂在答题卡相应题号的信息点上。
(1)集合A 是不等式310x +≥的解集,集合{}|x1B x =,则集合A ∩B= (A) {}|-11x x ≤ (B) 1|-13x x ⎧⎫≤⎨⎬⎩⎭(C) {}|-11x x ≤ (D) 1|-13x x ⎧⎫≤⎨⎬⎩⎭ (2)设Z=l+2i ,i 为虚数单位,则Z Z +=(A) -2i (B) 2i (C) -2 (D)2(3)函数1(1)1y x x =≠-+的反函数为 (A) 1()y x x R =+∈ (B) 1()x x R -∈(c) 11(0)y x x =+≠ (D) 11(0)y x x=-≠ (4)函数y=log 2(x 2-3x+2)的定义域为(A) {}|x2x (B) {}|x 3x (c) {}|x 1x 2x 或 (D) {}|x 1x - (5)如果04πθ,则(A) cos θ<sin θ (B) sin θ<tan θ(C) tan θ<cos θ (D) cos θ<tan θ(6)下列函数中,在其定义域上为减函数的是 (A )212x y ⎛⎫= ⎪⎝⎭(B )y=2x (C )12x y ⎛⎫= ⎪⎝⎭(D )y=x 2(7)设甲:22a b , 乙:a b ,则(A )甲是乙的必要条件,但不是乙的充分条件(B )甲是乙的充分条件,但不是乙的必要条件(C )甲不是乙的充分条件,也不是乙的必要条件(D )甲是乙的充分必要条件(8)直线x+2y+3=0经过(A )第一、二、三象限 (B )第二、三象限(C )第一、二、四象限 (D )第一、三、四象限(9)若θ为第一象限角,且sin θ-cos θ=0,则sin θ+cosθ=(A (B (C (D (10)正六边形中,由任意三个顶点连线构成的三角形的个数为(A ) 6 (B ) 20 (C ) 120 (D )720(11)向量a=(1,2),b=(-2,1),则a 与b 的夹角为(A )300 (B )450 (C )600 (D )900(12)l 为正方体的一条棱所在的直线,则该正方体各条棱所在的直线中,与l 异面的共有(A )2条 (B )3条 (C )4条 (D )5条(13)若(1+x )n 展开式中的第一、二项系数之和为6,则r=(A )5 (B ) 6 (C ) 7 (D )8(14)过点(1,2)且与直线2x+y-3=0平行的直线方程为(A )2x+y-5=0 (B )2y-x-3=0 (C )2x+y-4=0 (D )2x-y=0(15) x=1+rcos ,y=-1+rcos ,θθ⎧⎨⎩(0r ,θ为参数)与直线x-y=0相切,则r=(A (B (C )2 (D )4(16)若三棱锥的本个侧面都是边长为1的等边三角形,则该三棱锥的高为(A )2 (B )3 (C ) 3(D )12(17)某人打耙,每枪命中目标的概率都是0.9,则4枪中恰有2枪命中目标的概率为(A )0.0486 (B )0.81 (C )0.5 (D )0.0081二、填空题;本大题共4小题,每小题4分,共16分.把答案写在答题卡相应题号后。
2014年成人高考专升本高等数学一考试真题及详解

2014年成人高考专升本高等数学一考试大纲本大纲适用于工学、理学(生物科学类、地理科学类、环境科学类心理学类等四个级学科除外)专业的考生.总要求考生应按本大纲的要求,了解或理解“高等数学”中极限和连续、一元函数微分学、一元函数积分学、空间解析几何、多元函数微积分学、无穷级数、常微分方程的基本概念与基本理论,学会、掌握或熟练掌握上述各部分的基本方法应注意各部分知识的结构及知识的内在联系;应具有一定的抽象思维能力、逻辑推理能力、运算能力、空间想象能力,能运用基本概念、基本理论和基奉方法正确地推理证明,准确地计算;能综合运用所学知识分析并解决简单的实际问题。
本大纲对内容的要求由低到高,对概念和理论分为“了解”和“理解”两个层次;对方法和运算分为“会”、“掌握”和“熟练掌握”三个层次.复习考试内容一、极限1.知识范围(1)数列极限的概念与性质数列极限的定义唯一性,有界性,四则运算法则,夹逼定理,单调有界数列,极限存在定理(2)函数极限的概念与性质函数在一点处极限的定义左、右极限及其与极限的关系x趋于无穷(x一∞,x→+∞,x →—∞)时函数的极限,唯一性,法则,夹逼定理(3)无穷小量与无穷大量无穷小量与无穷大量的定义,无穷小量与无穷大量的关系,无穷小量的性质,无穷小量的比较(4)两个重要极限2.要求(1)理解极限的概念(对极限定义中等形式的描述不作要求)会求函数在一点处的左极限与右极限,了解函数在一点处极限存在的充分必要条件(2)了解极限的有关性质,掌握极限的四则运算法则(3)理解无穷小量、无穷大量的概念,掌握无穷小量的性质、无穷小量与无穷大量的关系会进行无穷小量的比较(高阶、低阶、同阶和等价)会运用等价无穷小量代换求极限(4)熟练掌握用两个重要极限求极限的方法二、连续1知识范围(1)函数连续的概念函数在一点处连续的定义,左连续与右连续,函数在一点处连续的充分必要条件,函数的间断点(2)函敖在一点处连续的性质连续函数的四则运算,复台函数的连续性,反函数的连续性(3)闭区间上连续函数的性质有界性定理,最大值与最小值定理,介值定理(包括零点定理)(4)初等函数的连续性2.要求(1)理解函数在一点处连续与间断的概念,理解函数在一点处连续与极限存在的关系,掌握函数(含分段函数)在一点处的连续性的判断方法(2)会求函数的间断点(3)掌握在闭区间上连续函数的性质,会用介值定理推证一些简单命题(4)理解初等函数在其定义区间上的连续性,会利用连续性求极限,一元函数微分学三、导数与微分1知识范围(1)导数概念导数的定义,左导数与右导数,函数在一点处可导的充分必要条件,导数的几何意义与物理意义,可导与连续的关系(2)求导法则与导数的基本公式导数的四则运算反函数的导数导数的基本公式(3)求导方法复合函数的求导法,隐函数的求导法,对数求导法,由参数方程确定的函数的求导法,求分段函数的导数(4)高阶导数高阶导数的定义高阶导数的计算(5)微分微分的定义,微分与导数的关系,微分法则,一阶微分形式不变性2.要求(l)理解导数的概念及其几何意义,了解可导性与连续性的关系,掌握用定义求函数在一点处的导散的方法(2)会求曲线上一点址的切线方程与法线方程(3)熟练掌握导数的基本公式、四则运算法则及复合函数的求导方法,会求反函数的导数(4)掌握隐函数求导法、对数求导法以及由参数方程所确定的函数的求导方法,会求分段函数的导数(5)理解高阶导数的概念,会求简单函数的n阶导数(6)理解函数的微分概念,掌握微分法则,了解可微与可导的关系,会求函数的一阶微分(二)微分中值定理及导致的应用1.知识范围(l)微分中值定理罗尔(Rolle)定理拉格朗日(Lagrange)中值定理(2)洛必迭(I,’Hospital)法则(3)函数单调性的判定法(4)函数的极值与极值点、最大值与最小值(5)曲线的凹凸性、拐点(6)曲线的水平渐近线与铅直渐近线2.要求(l)理解罗尔定理、拉格朗日中值定理及它们的几何意义会用拉格朗日中值定理证明简单的不等式(2)熟练掌握用洛必达法则求型未定式的极限的方法(3)掌握利用导数判定函数的单调性及求函数的单调增、减区间的方法,会利用函数的单调性证明简单的不等式(4)理解函数扳值的概念掌握求函数的驻点、极值点、极值、最大值与最小值的方法,会解简单的应用问题(5)会判断曲线的凹凸性,会求曲线的拐点(6)会求曲线的水平渐近线与铅直渐近线2、一元函数积分学(一)不定积分1.知识范围(1)不定积分原函数与不定积分的定义原函数存在定理不定积分的性质(2)基本积分公式(3)换元积分法第一第换元法(凑微分法)第二换元法(4)分部积分法(5) -些简单有理函数的积分2.要求(1)理解原函数与不定积分的概念及其关系,掌握不定积分的性质,了解原函数存在定理(2)熟练掌握不定积分的基本公式(3)熟练掌握不定积分第-换元法,掌握第二换元法(限于三角代换与简单的根式代换)(4)熟练掌握不定积分的分部积分法(5)会求简单有理函数的不定积分(二)定积分1.知识范围(1)定积分的概念定积分的定义及其几何意义可积条件(2)定积分的性质(3)定积分的计算变上限积分牛顿莱布尼茨(Newton-Leibniz)公式换元积分法分部积分法(4)无穷区间的反常积分(5)定积分的应用平面图形的面积旋转体的体积2.要求(1)理解定积分的概念及其几何意义,了解函数可积的条件(2)掌握定积分的基本性质.(3)理解变上限积分是变上限的函数,掌握对变上限积分求导数的方法(4)熟练掌握牛顿一莱布尼茨公式(5)掌握定积分的换元积分法与分部积分法(6)理解无穷区间的反常积分的概念,掌握其计算方法(7)掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生成的旋转体的体积。
2014年全国高考理科数学试题及答案-新课标1

2014年普通高等学校招生全国统一考试全国课标1理科数学注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2. 回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效. 3. 回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效. 4. 考试结束,将本试题和答题卡一并交回.第Ⅰ卷一.选择题:共12小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1. 已知集合A={x |2230x x --≥},B={x |-2≤x <2=,则A B ⋂=A .[-2,-1]B .[-1,2)C .[-1,1]D .[1,2) 2. 32(1)(1)i i +-=A .1i +B .1i -C .1i -+D .1i --3. 设函数()f x ,()g x 的定义域都为R ,且()f x 时奇函数,()g x 是偶函数,则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数4. 已知F 是双曲线C :223(0)x m y m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为A B .3 C D .3m5. 4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .786. 如图,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线O A ,终边为射线O P ,过点P 作直线O A 的垂线,垂足为M ,将点M 到直线O P 的距离表示为x 的函数()f x ,则y =()f x 在[0,π]上的图像大致为7. 执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =A .203B .165C .72D .1588. 设(0,)2πα∈,(0,)2πβ∈,且1s in ta n c o s βαβ+=,则A .32παβ-=B .22παβ-= C .32παβ+=D .22παβ+=9. 不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:1p :(,),22x y D x y ∀∈+≥-,2p :(,),22x y D x y ∃∈+≥, 3P :(,),23x y D x y ∀∈+≤,4p :(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ,3PB .1p ,4pC .1p ,2pD .1p ,3P10. 已知抛物线C :28y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线P F 与C 的一个焦点,若4F P F Q =,则||Q F =A .72B .52C .3D .211. 已知函数()f x =3231a x x -+,若()f x 存在唯一的零点0x ,且0x >0,则a 的取值范围为A .(2,+∞)B .(-∞,-2)C .(1,+∞)D .(-∞,-1) 12. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A .B .C .6D .4第Ⅱ卷本卷包括必考题和选考题两个部分。
数学理。2014年普通高等学校招生全国统一考试题及参考答案

2014年普通高等学校招生全国统一考试理科数学(四川卷)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合2{|20}A x x x =--≤,集合B 为整数集,则A B ⋂=A .{1,0,1,2}-B .{2,1,0,1}--C .{0,1}D .{1,0}-2.在6(1)x x +的展开式中,含3x 项的系数为A .30B .20C .15D .103.为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点A .向左平行移动12个单位长度 B .向右平行移动12个单位长度 C .向左平行移动1个单位长度 D .向右平行移动1个单位长度 4.若0a b >>,0c d <<,则一定有A .a b c d >B .a b c d <C .a b d c >D .a b d c<5.执行如图1所示的程序框图,如果输入的,x y R ∈,则输出的S 的最大值为A .0B .1C .2D .36.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能拍甲,则不同的排法共有A .192种B .216种C .240种D .288种7.平面向量(1,2)a =,(4,2)b =,c ma b =+(m R ∈),且c 与a 的夹角等于c 与b 的夹角,则m = A .2- B .1- C .1 D .28.如图,在正方体1111ABCD A BC D -中,点O 为线段BD 的中点。
设点P 在线段 1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是A .B .C .D . 9.已知()ln(1)ln(1)f x x x =+--,(1,1)x ∈-。
现有下列命题:①()()f x f x -=-;②22()2()1xf f xx =+;③|()|2||f x x ≥。
2014年普通高等学校招生全国统一考试数学理试题(四川卷,含答案)
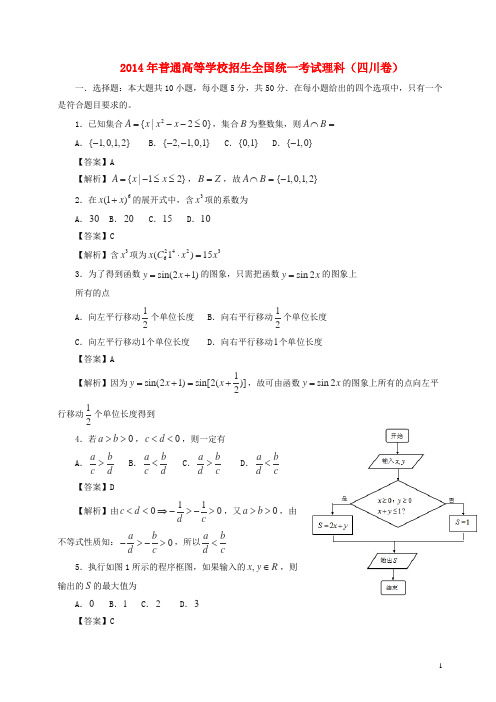
2014年普通高等学校招生全国统一考试理科(四川卷)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合2{|20}A x x x =--≤,集合B 为整数集,则A B ⋂= A .{1,0,1,2}- B .{2,1,0,1}-- C .{0,1} D .{1,0}- 【答案】A【解析】{|12}A x x =-≤≤,B Z =,故A B ⋂={1,0,1,2}- 2.在6(1)x x +的展开式中,含3x 项的系数为 A .30 B .20 C .15 D .10 【答案】C【解析】含3x 项为24236(1)15x C x x ⋅=3.为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上 所有的点 A .向左平行移动12个单位长度 B .向右平行移动12个单位长度 C .向左平行移动1个单位长度 D .向右平行移动1个单位长度 【答案】A【解析】因为1sin(21)sin[2()]2y x x =+=+,故可由函数sin 2y x =的图象上所有的点向左平行移动12个单位长度得到4.若0a b >>,0c d <<,则一定有 A .a b c d > B .a b c d < C .a b d c > D .a b d c< 【答案】D【解析】由1100c d d c<<⇒->->,又0a b >>,由不等式性质知:0a b d c ->->,所以a bd c< 5.执行如图1所示的程序框图,如果输入的,x y R ∈,则输出的S 的最大值为A .0B .1C .2D .3 【答案】C【解析】当001x y x y ≥⎧⎪≥⎨⎪+≤⎩时,函数2S x y =+的最大值为2.6.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有 A .192种 B .216种 C .240种 D .288种 【答案】B【解析】当最左端为甲时,不同的排法共有55A 种;当最左端为乙时,不同的排法共有14C 44A 种。
