数学广场——植树问题
三年级上册数学教案- 《数学广场——植树问题》沪教版(2015秋)

数学广场——植树问题教学目标:1. 知识目标:在学生对对实际问题的具体操作和观察中,探索并体会段数和剪的次数、段数和树的棵数的关系,并能以此分析和解决实际问题。
2. 能力目标:经历观察、比较、概括、归纳等数学活动,获得物体的个数和段数之间的关系,建立初步的观察、推理、和探究的能力。
3. 情感目标:通过同桌活动、小组活动的形式,体验合作的快乐,激发学习兴趣。
教学重点:从对实际问题的具体操作和观察中,探索并体会间隔数与间隔物体的个数的关系,并能以此分析和解决实际问题。
教学难点:运用探索的知识解决生活中的一些问题。
教学准备:绳子、剪刀、多媒体。
教学过程:一、探索段数和剪的次数之间的关系1. 情景引入(1)学生动手剪绳子,把剪到的结果填在表格中。
(生独立完成)(2)交流:(指名口答)(3)观察:你能发现什么?(单独思考,再同桌交流)(4)交流:(抽生回答,不同意见的补充)师板书:剪的次数=绳子的段数-1绳子的段数=剪的次数+1【设计意图:通过动手操作,让生直观感知剪的次数与绳子的段数之间的关系。
】2. 练一练:(1)小亚要剪50段,需要剪()次。
(2)小亚剪50次,得到()段。
3. 揭示课题:(板书:分段)二、探究树的棵数和间隔数之间的关系1. 出示植树图和表格。
2. 小组合作学习。
3. 交流。
板书:树的棵数=间隔数+1间隔数=树的棵数-14. 小结。
5. 练习。
(1)一条马路的一侧有11棵树,共有()个间隔。
(2)小朋友排队做操,一列队伍中有12个间隔,这列队伍有()个小朋友。
(3)从一楼到五楼要走()层。
【设计意图:学生从剪绳子过渡到种树问题,只要通过合作学习、交流,很容易探究出间隔数与棵数之间的关系。
】三、沟通、比较1. 师:“剪绳子”和“植树”之间有什么联系?(四人小组讨论)2. 交流:板书:两端都没有物体:物体的个数=段数-1两端都有物体:物体的个数=段数+13. 小结:四、练习:1. 选择题:(1)把一根木头锯4次,可以锯成()段。
三年级数学教案 数学广场——植树问题-一等奖

植树问题教学内容:教科书例1及相关内容教学目标:1 通过猜测、验证等数学探究活动,使学生初步体会两端都栽的植树问题的规律,构建数学模型,解决实际生活中的有关问题。
2培养学生通过“化繁为简”从简单问题中探索规律,找出解决问题的有效方法的能力,逐步培养学生的模型思想和化归思想。
教学重点:发现并理解两端都栽的植树问题中间隔数与棵树的规律。
教学难点:运用“植树问题”的解题思想解决生活中的实际问题。
教学准备:课件、直尺、学习纸。
教学过程:一、谜语导入,引入新课师:同学们,你们喜欢猜谜语吗?生:喜欢。
师:两棵小树十个杈,不长叶子不开花,能写会算还会画,天天干活不说话。
打一人体的组成部分。
是什么呢?你说说看?生:是手。
师:对了,就是我们的手。
我们的手作用可真大,又会写又会画还会算,而且我们的手上还有许多的数学奥秘,仔细看老师的手,你看到了数字几呢?生:5师:哦,你说的数字5表示的是什么啊?能告诉我们吗?生:手指的个数。
师:除了手指的个数外你还能看到什么呢?生:还能看到手指之间的间隔。
师:哦,手指之间还有一个个的间隔。
同学们,老师五个手指之间到底有几个间隔呢?生:4个。
师:(课件出示)手指间的空隙,在数学上我们叫做间隔。
(板书:间隔。
)一只手上有四个间隔,我们就说它的间隔数是4。
(板书:“间隔”后加“数”)师:生活中间隔无处不在。
(课件出示:人民大会堂柱子、路灯杆、摆花盆、钟声等),师边放课件边叙述说明。
师:想一想,生活中还有哪些地方有间隔?生充分交流二、充分经历,探究新知1、大胆猜测,引发冲突。
(1)读一读,说一说。
课件出示例1,引导学生获取相关数学信息,让学生读题,然后指名说一说:从题中你了解到了哪些信息?重点帮助学生弄清楚下列数学信息含义:“每隔5米栽一棵“是什么意思?使学生明确“每隔5米栽一棵”就是指每两棵树之间的距离都是5米,每两棵树之间的距离也叫间隔长度,也可以说成“两棵树之间的间隔是5米”。
“两端要栽”是什么意思?“一边”是什么意思?可以先让学生说一说,然后教师拿出实物演示。
2023-2024学年三年级下学期数学《智慧广场-植树问题》(教案)

2023-2024学年三年级下学期数学《智慧广场-植树问题》一、教学目标1. 让学生理解植树问题的基本概念,掌握解决植树问题的方法。
2. 培养学生运用数学知识解决实际问题的能力。
3. 培养学生合作、探究的学习精神。
二、教学内容1. 植树问题的基本概念。
2. 植树问题的解决方法。
3. 植树问题在实际生活中的应用。
三、教学重点与难点1. 教学重点:植树问题的解决方法。
2. 教学难点:如何将植树问题与实际生活相结合。
四、教学准备1. 教师准备:课件、教具、实例等。
2. 学生准备:学习用品、已掌握的数学知识。
五、教学过程1. 导入:通过一个实例引入植树问题,激发学生的兴趣。
2. 新课导入:讲解植树问题的基本概念,让学生了解植树问题的背景。
3. 解决方法:讲解植树问题的解决方法,让学生掌握如何解决植树问题。
4. 实例讲解:通过实例讲解,让学生了解植树问题在实际生活中的应用。
5. 练习:让学生独立完成一些植树问题的练习题,巩固所学知识。
6. 小组讨论:让学生分组讨论,探讨植树问题在实际生活中的应用。
7. 总结:总结本节课所学内容,强调植树问题的解决方法和实际应用。
六、作业布置1. 让学生完成一些植树问题的练习题。
2. 让学生观察生活中遇到的植树问题,并尝试解决。
七、教学反思1. 教师应关注学生在课堂上的反应,及时调整教学方法和节奏。
2. 教师应注重培养学生的实际操作能力,让学生在解决植树问题的过程中,提高自己的数学素养。
八、教学评价1. 通过课堂提问、练习题和小测验等方式,了解学生对植树问题的掌握程度。
2. 观察学生在解决植树问题时的思路和方法,评价学生的数学思维能力。
3. 关注学生在小组讨论中的表现,评价学生的合作能力和探究精神。
九、教学延伸1. 让学生了解更多的植树问题,拓展学生的知识面。
2. 引导学生关注环保问题,培养学生的环保意识。
十、教学资源1. 教师用书:《小学数学教学指导》。
2. 学生用书:《小学数学课本》。
7《数学广角——植树问题》(教案)2023-2024学年数学五年级上册 人教版

《数学广角——植树问题》一、教学目标1. 让学生了解植树问题的背景,理解在一条线段上两端都要栽树的情况下,植树棵数与间隔数的关系。
2. 培养学生动手操作、观察、猜想、归纳总结的能力,渗透“化繁为简”的数学思想。
3. 通过解决生活中的实际问题,让学生感受数学与生活的紧密联系,培养学生的数学应用意识。
二、教学内容1. 在一条线段上两端都要栽树的情况下,植树棵数与间隔数的关系。
2. 解决生活中的实际问题。
三、教学重难点教学重点:理解在一条线段上两端都要栽树的情况下,植树棵数与间隔数的关系。
教学难点:解决生活中的实际问题。
四、教学准备课件、操作材料。
五、教学过程1. 情境导入课件呈现“环保小卫士”评选活动的情境,让学生说说环保小卫士应该做些什么?引入植树。
2. 探究新知(1)出示例1:在一条直线上,间隔5米栽一棵树,如果两棵树之间的距离是5米,从第1棵到第100棵树之间一共有多少米?引导学生用小棒代替小树,实际操作一下,学生汇报操作结果。
根据学生的回答,课件演示:1--2 2--3 3--4 4--5 5--6100-99 99-98 98-97 97-96 96-95让学生数一数,一共有多少个间隔,引导学生发现间隔数比棵数少1。
(2)完成做一做第1题。
学生独立完成,指名回答,集体订正。
(3)出示例2:同学们在全长100米的小路两旁植树,每隔20米栽一棵,一共需要多少棵树?学生独立完成,指名回答,集体订正。
3. 巩固练习完成教材第108页“练习二十三”第1题。
4. 课堂小结这节课你有什么收获?5. 课后作业教材第108页“练习二十三”第2题。
六、板书设计植树问题两端都要栽:棵数=间隔数 1两端都不栽:棵数=间隔数-1只栽一端:棵数=间隔数两端都要栽:棵数=间隔数×2七、课后反思本节课通过让学生动手操作、观察、猜想、归纳总结,使学生理解了植树棵数与间隔数的关系。
但在解决生活中的实际问题时,部分学生还存在困难,需要在今后的教学中加强练习。
三年级上册数学整理与提高(数学广场-植树问题)沪教版 (14)

5
4
5
20
我们发现的间隔数和棵数关系是:
在两端都植的情况下#43; 1 间隔数 = 棵数 - 1
抢答:看谁速度快
1.一条路共40米,如果每10米种一棵 树,有( 4 )个间隔。
2.一排树两头都种,有10个间隔,能 种( 11)棵树。
3.一排树两头都种,共种35棵树,那 么间隔数是(34)。
例1: 同学们在全长100米的小路一边植树,每隔5米栽 一棵(两端要栽)。一共需要栽多少棵树苗?
100÷5=20(个) 20+1=21(棵) 答:一共需要栽21棵树苗。
练习一:
张村的村道长1000米,在村道 一旁从头到尾安装路灯,每隔20米安 装一盏,根据这些信息,你能算出这 条村道一共安装了多少盏路灯吗?
3-1=2(个) 24×2=48 (个) 答:一共走了48个台阶。
今天这节课你们 知道了哪些新知识?
考考你
要把一根木头锯成相等 的5段,锯一次需要8分钟, 锯完一共要花多少分钟?
谢谢大家!
再
见!
2 1
3 4
手指数和间隔数之间的关系:
手指数 = 间隔数 + 1
间隔数 = 手指数 - 1
我来做绿化小设计师
张爷爷计划要在全长20 米的小路一边植树搞绿化 (两端都植)。请你设计一 个合理的植树方案。
每隔5米植一棵
起
点
5米
5米
5米
终
点
5米
总距离(米)
20米
间距(米) 间隔数(个)
棵数(棵)
1000÷20=50(个) 50+1=51(盏)
答:一共安装了51盏路灯。
练习二:
走廊长80米,在走廊两边每隔2米 摆一盆花(两端都摆),一共摆了多少 盆花?
2023-2024年小学数学五年级上册高频考点精讲精练 第7讲 数学广角—植树问题(人教版含解析)
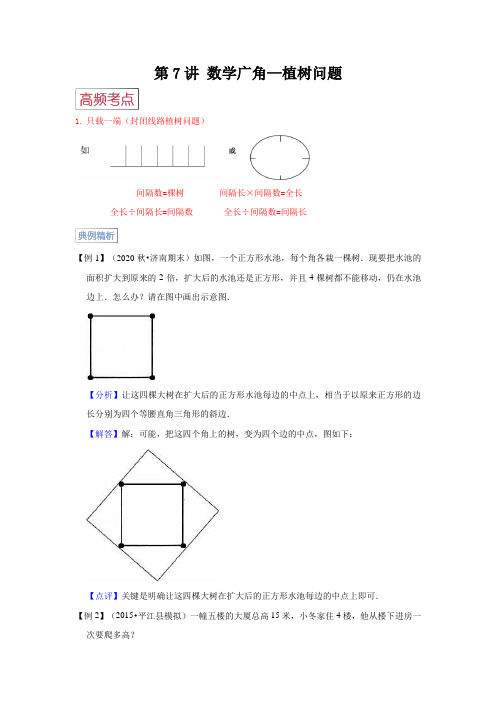
第7讲数学广角—植树问题1.只载一端(封闭线路植树问题)间隔数=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长【例1】(2020秋•济南期末)如图,一个正方形水池,每个角各栽一棵树.现要把水池的面积扩大到原来的2倍,扩大后的水池还是正方形,并且4棵树都不能移动,仍在水池边上.怎么办?请在图中画出示意图.【分析】让这四棵大树在扩大后的正方形水池每边的中点上,相当于以原来正方形的边长分别为四个等腰直角三角形的斜边.【解答】解:可能,把这四个角上的树,变为四个边的中点,图如下:【点评】关键是明确让这四棵大树在扩大后的正方形水池每边的中点上即可.【例2】(2015•平江县模拟)一幢五楼的大厦总高15米,小冬家住4楼,他从楼下进房一次要爬多高?【分析】五层楼总高15米,那么每层的高度是15÷5=3米,小冬家住4楼,他从楼下进房一次要爬4﹣1=3个楼间距,然后用3乘每层的高度即可解决问题.【解答】解:15÷5×(4﹣1)=3×3=9(米)答:他从楼下进房一次要爬9米高.【点评】本题属于植树问题的实际应用,关键是明确:间隔数=层数﹣1.【例3】(2014春•杭州期末)为了保护公园里的一棵千年古树,园林局决定为它做一个圆形防护栏.如果护栏有10个间隔,一共需要打多少根木桩?【分析】根据植树的知识知道,在圆形的周围植树,间隔数就是植树的棵数,而本题中的防护栏是个圆形的,护栏有10个间隔,所以即可得出需要打木桩的根数.【解答】解:因为在圆形的防护栏周围打木桩,有几个间隔就必须打几个木桩,所以如果护栏有10个间隔,一共需要打10根木桩;答:一共需要打10根木桩.【点评】此题属于在圆形的物体周围植树的问题,即在圆形的周围植树,间隔数就是植树的棵数.2.两端都载:如图:间隔数+1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔长+1=棵数全长÷间隔数=间隔长全长÷(棵树-1)=间隔长【例4】(2015•平江县模拟)在一段路的路边每隔20米栽一棵树,包括这段路两端在内栽10棵树,这段路长多少米?【分析】由于从一端到另一端一共栽了10棵树,共有间隔数为:10﹣1=9个;又由于间距是20米,根据总距离=间距×间隔数可以求出这条路的长度,列式为:20×9=180(米);据此解答.【解答】解:根据分析可得,20×(10﹣1)=20×9=180(米);答:这段路长180米.【点评】本题考查了植树问题,知识点是:栽树的棵数=间隔数+1(两端都栽),总距离=间距×间隔数.【例5】(2015春•长春校级期末)工人叔叔要在马路的一侧安装路灯,从头开始每隔4米安一个,共安装了30个,这条路长米.【分析】因为间隔数=路灯的盏数﹣1,所以先求出马路边路灯的间隔数,再乘4即可.【解答】解:(30﹣1)×4=29×4=116(米)答:这条路长116米.故答案为:116.【点评】本题主要考查了间隔数=树的棵数﹣1,再根据基本的数量关系解决问题.【例6】(2015春•务川县期中)小朋友们在路的一边植树,先植一棵树,以后每隔3米植一棵,已经植了9棵,问第一棵和第九棵树相距多少米?【分析】此题属于植树问题中的两端都要栽的情况:间隔数=植树棵数﹣1,据此可得一共有9﹣1=8个间隔,再乘每个间隔的长度3米,即可得出第一棵和第九棵树相距多少米.【解答】解:(9﹣1)×3,=8×3,=24(米);答:第一棵和第九棵树相距24米.【点评】植树问题中:两端都要栽时,间隔数=植树棵数﹣1.3.两端都不载如图:间隔数-1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长全长÷间隔长-1=棵数全长÷(棵树+1)=间隔长【例7】(2016春•魏县校级月考)某木工把一根长4米的圆柱形木料锯成80厘米的小段,需40分钟;如果改锯成50厘米的小段,需要多少时间?【分析】根据题意,先求出长4米的圆柱形木料锯成80厘米的小段需要锯多少次,再求出每锯一次所需要的时间,即可求出锯成50厘米的小段所需要的时间.【解答】解:4米=400厘米,400÷80﹣1=4(次),40÷4=10(分钟),400÷50﹣1=7(次),10×7=70(分钟),答:需要70分钟.【点评】解答此题的关键是,要知道锯木料的次数比锯成的段数少1,再根据题中的数量关系即可解答.【例8】(2015春•永胜县月考)一根钢管,把它锯成7段,需要18分钟,照这样计算,如果锯成16段需要多少分钟?【分析】锯两段只需要锯1次,所以锯成7段,需要锯(7﹣1)次,用18分钟除以这个时间,就是锯一次用的时间;锯16段只需要锯16﹣1=15次,用锯一次用的时间乘上15就是锯成9段需要的时间.【解答】解:18÷(7﹣1)=18÷6=3(分钟)3×(16﹣1)=3×15=45(分钟)答:如果锯成16段需要45分钟.【点评】本题关键是要理解锯1次就可以锯成2段,存在这个关系:锯成的段数=锯的次数+1.【例9】(2013秋•即墨市期末)崂山举行登山大赛,组委会在长达845米的山路中,每隔65米设置一个服务站(起点和终点不设).共设多少个服务站?【分析】先用全程除以间隔的长度,求出一共有多少段,再用段数减去1就是需要设服务站的数量.【解答】解:845÷65﹣1=13﹣1=12(个)答:共设12个服务站.【点评】本题属于植树问题中的两段都不栽的情况:植树的棵数=间隔数﹣1.一.选择题(共8小题)1.(2021秋•盐都区期末)把一根电缆截成2段需要4分钟,如果截成5段需要()分钟.A.10B.20C.162.(2020秋•黔西南州期末)一根绳子长15米,剪了三刀剪成()段.A.3B.4C.53.(2019秋•东海县期中)大上海国际公寓步行街上两边张灯结彩,从这头到那头每隔4米挂一个红灯笼(两端都挂),步行街全长600米,一共挂了多少个红灯笼?()A.150B.151C.302D.3004.(2021秋•巴马县期末)一根钢筋锯成6段,共需30分钟,平均锯一次需要()分钟.A.5B.7C.6D.45.(2015秋•利川市月考)圆形滑冰场的一周全长180m.在这个滑冰场的一周每隔12m安装一盏灯,一共要安装()盏灯.A.14B.15C.166.(2021秋•老城区期末)公园内一条林荫大道全长800米,在它的两侧从头到尾每隔20米放一个垃圾桶,一共需要()个垃圾桶。
2023-2024学年三年级下学期数学《智慧广场——植树问题》(教案)

2023-2024学年三年级下学期数学《智慧广场——植树问题》(教案)一、教学目标1. 知识与技能:学生能够理解植树问题的基本概念,掌握植树问题的解题方法,并能运用所学知识解决实际问题。
2. 过程与方法:通过观察、分析、讨论等环节,培养学生独立思考、合作交流的能力,提高学生解决问题的能力。
3. 情感态度与价值观:培养学生对数学的兴趣,激发学生探索未知、勇于创新的意识。
二、教学内容1. 植树问题的基本概念:理解植树问题的定义,明确问题中的数量关系。
2. 植树问题的解题方法:掌握植树问题的解题步骤,学会运用公式进行计算。
3. 植树问题的应用:将植树问题与实际生活相结合,解决相关问题。
三、教学重点与难点1. 教学重点:植树问题的解题方法及步骤,公式的运用。
2. 教学难点:理解植树问题中的数量关系,将植树问题与实际生活相结合。
四、教具与学具准备1. 教具:PPT课件,黑板,粉笔。
2. 学具:草稿纸,计算器。
五、教学过程1. 导入:通过PPT展示植树节的图片,引导学生关注植树问题。
2. 新课导入:讲解植树问题的基本概念,分析问题中的数量关系。
3. 解题方法:介绍植树问题的解题步骤,引导学生运用公式进行计算。
4. 例题讲解:通过典型例题,展示植树问题的解题过程,引导学生独立思考。
5. 小组讨论:分组讨论植树问题在实际生活中的应用,培养学生合作交流的能力。
6. 课堂小结:总结本节课所学内容,强调重点与难点。
7. 课后作业:布置相关练习题,巩固所学知识。
六、板书设计1. 植树问题2. 重点内容:植树问题的定义,解题步骤,公式运用。
3. 板书布局:清晰明了,突出重点。
七、作业设计1. 基础题:巩固植树问题的基本概念和解题方法。
2. 提高题:运用植树问题解决实际问题。
3. 拓展题:研究植树问题在其他领域的应用。
八、课后反思1. 教学效果:分析学生对植树问题的掌握程度,调整教学策略。
2. 学生反馈:关注学生在学习过程中的困惑,及时解答疑问。
五年级上数学广角—植树问题1

五年级上数学广角—植树问题1在我们的日常生活中,植树是一项充满意义的活动。
而在数学的世界里,“植树问题”则是一个有趣且实用的数学模型。
今天,就让我们一起来深入探索五年级上册数学广角中的“植树问题”。
首先,我们来思考一个简单的场景:在一条笔直的道路上植树。
假设这条路长 100 米,每隔 5 米种一棵树(两端都种),那么一共需要种多少棵树呢?要解决这个问题,我们可以通过画图来帮助理解。
先画出 100 米的道路,然后每隔 5 米标记一个点,表示种树的位置。
通过画图,我们可以清晰地看到,100 米被分成了 100 ÷ 5 = 20 段,但是因为两端都种树,所以树的数量比段数多 1,即需要种 20 + 1 = 21 棵树。
这就是“植树问题”中最基本的一种情况:两端都种。
其数量关系是:棵数=间隔数+ 1。
那如果道路的两端都不种树呢?比如还是 100 米的道路,每隔 5 米种一棵树,两端都不种。
同样,我们先算出间隔数为100 ÷5 =20 段,因为两端都不种,所以树的数量比段数少 1,即需要种 20 1 = 19 棵树。
这种情况的数量关系是:棵数=间隔数 1。
还有一种情况是,道路只有一端种树。
例如 100 米的道路,每隔 5米种一棵树,只有一端种。
此时,树的数量就等于间隔数,即 100 ÷ 5= 20 棵。
数量关系为:棵数=间隔数。
为了更好地理解这些数量关系,我们可以通过一些实际的例子来巩固。
假设在一个圆形的花园周围种树。
因为圆形是一个封闭图形,起点和终点重合,所以它的数量关系和只有一端种树是一样的,即棵数=间隔数。
如果花园的周长是 60 米,每隔 6 米种一棵树,那么一共需要种 60÷ 6 = 10 棵树。
再比如,在一条走廊上挂灯笼,走廊长 30 米,每隔 3 米挂一个灯笼。
如果两端都挂,那么灯笼的数量为 30 ÷ 3 + 1 = 11 个。
如果两端都不挂,灯笼的数量为 30 ÷ 3 1 = 9 个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3段
4段
剪的次数 1 2 3 4 5 6 7 8 纸条的段数 2 3 4 5 6 7 8 9
纸条的段数 = 剪的次数 +1
植树问题
植树问题
植树问题
小探究
我选取每隔( )米种一棵,先把总 长度平均分成( )段。
两端都种 0
24
只种一端
两端都不种
总长度
每一段的 长度
(A)
A4 B5 C 6
(2)一根木头据一次需要2分钟,
如果把它锯成10段,需要几分钟?
( C )10-1=9(次) 9 x 2=18(分钟) A 22 B 20 C 18
(3)在一根12米长的彩带上每隔3
米挂一个气球,从头挂到尾,一共挂
了几个气球?
(C)
A3 B4 C5
(4)轨道1号线行驶路线全长30千米, 相邻两站的距离是2千米。一共要设多 少个车站?( C)
段数
两端都种 只种一端 两端都不
的棵数
的棵数 种的棵数
验证
我选取每隔( 5)米种一棵,先把总长 度平均分成( )段。
两端都种 0
15
只种一端
两端都不种
总长度
每一段的 长度
段数
两端都种 只种一端 两端都不
的棵数
的棵数 种的棵数
15 5
植树问题
植树问题
选一选:
(1)一根彩带长15米,把它剪成
了5段,剪了几次?
想一想:
盆数 = 段数 8(盆)= 8(段)
起点站
终点站
2千米
两端都种 段数+1=个数
30÷2=15段 A 14 B 15
15 + 1=16个 C 16
(5)轨道4号线是条环城轨道线行驶
路线全长30千米,相邻两站的距离是2
千米,要设多少个车站呢?( B )
起点站 终点站 起点站
终点站
2千米
只种一端 30÷2=15段 段数 = 个数 15 段=15个
A 14 B 15 C 16
练一练:
1、教学楼的走廊长56米,如果 在走廊上等间隔地摆放8盆花, 并且走廊的两端都放,那么每两 盆花间隔多少米?
练一练:
2、校门到教学楼有30米,如果 每隔3米插一面彩旗,需要多少 面彩旗?(两头都要插)
想一想:
小区的环形花坛上要放8盆 红花,会把花坛分成几段呢?
