三角形中位线定理
三角形中位线定理课件
在几何学、代数和三角学等领域，三角形中位线定理被广泛应用于证明和计算 。
三角形中位线定理的历史
该定理最早可追溯到古希腊数学家欧几里得，后来被其他数学家不断完善和证 明。
02
三角形中位线定理的证明
证明方法一：通过相似三角形证明
总结词
利用相似三角形的性质，通过一系列推导证明中位线定理。
VS
建筑学中的应用
在建筑设计或施工时，可以利用三角形中 位线定理来确保结构的稳定性和安全性。 例如，在桥梁或高层建筑的设计中，可以 利用该定理来分析结构的受力情况。
04
三角形中位线定理的拓展
三角形中位线定理的推广
三角形中位线定理的逆定理
如果一条线段平行于三角形的一边，并且通过三角形的另一边的 中点，那么这条线段就是三角形的中位线。
THANKS
感谢观看
在多边形中的应用
对于任意多边形，如果一条线段平行于一边，并且等于另一边的一半，那么这条线段就是多边形的中 位线。
中位线定理与其他几何定理的关系
与平行线性质定理的关系
三角形中位线定理的应用需要平行线的性质 定理来证明线段平行。
与勾股定理的关系
在直角三角形中，中位线定理可以与勾股定 理结合使用，以证明某些几何关系。
证明方法三：通过向量证明
总结词
利用向量的性质和运算规则，通过向量的表示和推导证明中位线定理。
详细描述
首先，利用向量的表示方法，我们可以将三角形的边表示为向量。然后，通过向量的加法和数乘运算，以及向量 的模长和夹角计算，我们可以推导出中位线定理。这种方法需要熟悉向量的性质和运算规则，但可以提供一种全 新的证明角度。
三角形中位线定理ppt课件
目录
三角形中位线定理的推论
三角形中位线定理的推论
1. 三条中位线交于一点，称为重心。
2. 重心所在的中位线距离对应顶点的距离的比例为2：1。
3. 中位线长度为底边长度的一半。
4. 重心到对边中点的距离为一半对边长。
5. 以三角形的重心为圆心，以重心到顶点的距离为半径作圆，可圆上的任意点对三角形三个顶点的距离相等。
6. 以两个中点为圆心，中位线长度为半径作圆，则两圆交点与对边中点重合。
7. 以重心为圆心，以重心到任意顶点为半径作圆，圆心角等于顶点所对的角。
8. 以中线为直径作圆，则圆心在三角形外接圆上。
中位线定理
中位线定理中位线定理是指一个三角形的三条中线交于一点且这个点离三角形三个顶点的距离相等，这个点就是三角形的重心。
这个定理是三角形的基本定理之一，能够应用到许多数学问题中。
中位线的定义是连接三角形一边的中点和对面顶点的线段，一个三角形有三条中线。
所有三角形的中线交于一点，这个点被称为三角形的重心。
三角形的重心在中位线上的比例是2:1，即重心距离每条中位线的距离为中点距离这条中线的距离的两倍。
中位线定理的证明可以通过相似三角形和平行四边形的性质来得到。
设ABC是一个三角形，D、E和F分别是AB、BC和AC上的中点，G是三条中线的交点。
我们需要证明GD和EF平行且相等。
首先，我们知道DG和GE分别是DC和EB的一半，因为D和E是AB的中点，也就是说DE是AB的一半。
同样地，CG和GF分别是BE和AF的一半，因为F和B是AC的中点，所以FB的长度等于AC的一半，也就是GF和CG的长度。
因为DG和CG交于点G，所以DGCG是一个平行四边形。
同样地，GE和GF交于点G，所以GEFG也是一个平行四边形。
DG和GE的长度相等，CG和GF的长度也相等。
由平行四边形的性质可以得到，GD和EF平行且相等。
三角形的重心还有一些特殊的性质，比如它是三角形内心、外心和垂心的平均点，也是三条中线所构成的小三角形的面积最小的点。
这些性质可以通过三角形的其他定理和性质来证明。
在实际应用中，中位线定理可以用于计算三角形的重心的位置。
如果已知三角形的三个顶点的坐标，可以用中点公式计算中点的坐标，然后用重心的性质计算重心的坐标。
这对于计算三角形的重量、质心、离心率等问题非常有用。
此外，中位线定理还有一些扩展，比如垂径定理、角平分线定理、内心坐标公式等。
这些扩展定理都与三角形相关，可以用于解决各种数学问题。
三角形中位线定理
1 EF= 1 BC 2 2
三角形的中位线的性质
三角形的中位线平行于第三边， 并且等于它的一半 A 用符号语言表示
∵DE是△ABC的中位线
E B
D C
1 ∴ DE∥BC， DE= BC. 2
① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
初试身手
A D
练习1.如图，在△ABC中，D、E分别是 、F分别 AB 、、 AC 的中点 是 AB AC 、BC的中点
∴ DF=1/2BC，DE=1/2AC。 ∴ 四边形DECF的周长是 B DF+DE+EC+CF=16/2+12/2+1 6/2+12/2=28
D
F
E
C
拓展应用：
在△ABC中，∠BAC=90°，延长BA到点D，使 AD=1/2AB，点E,F分别为BC,AC的中点，试说DF=BE理 D 由
理由： ∵ 点E,F分别为BC,AC的中点
B三角 形的周长与原三角形的周长有什么 关系？ 2、三角形三条中位线围成的三角形的面积与原三角 形的面积有什么关系？
演练
已知：如果，点D、E、F分别是△ABC的三边 的中点． （1）若AB=8cm，求EF的长； （2）若DE=5cm，求BC的长． （3）若增加M、N分别是BD、BF的中点， A 问MN与AC有什么关系？为什么？
例1、求证三角形的一条中位线与第三边上 的中线互相平分. A
E
C
14
定 理 应 用：
⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍 或 1/2提供了一个新的途径
⑶解决“中点问题”
注意：在处理这些问题时,要求出现三角形及中位线
三角形中位线定理的证明及其应用
例 ｌ 如 图，在 四边形Ａ Ｂ Ｃ Ｄ中， Ａ Ｂ ＝ Ｃ Ｄ， Ｅ、 盼 别
是Ｂ Ｃ 、 Ａ Ｄ的 中点 ，延长Ｂ Ａ和Ｃ Ｄ分别 与Ｅ Ｆ 的延 长线 交 于Ｋ、 日， 求证 ： ／ ＿ ＿ Ｂ Ｋ Ｅ＝ Ｃ Ｈ Ｅ ． （ ２ ０ ０ ６ 年 内 蒙 古 呼 和 浩 特市初 中数学 竞赛题 ）
样 取 中点 比作平行 线好 ． 证明： 连 接Ｂ Ｄ并取Ｂ Ｄ的中 点Ｇ， 连Ｆ Ｇ、 Ｇ Ｅ， 在 △Ｄ Ａ Ｂ 和 △Ｂ Ｃ Ｄ 中，
・ ．
・
Ｆ 是ＡＤ的中 点， Ｅ 是Ｂ Ｃ 的 中点 ，
・ ． ．
Ｆ Ｇ ／ ／ Ａ Ｂ Ｊ ￣ Ｆ Ｇ ＝ Ａ ， Ｅ Ｇ ／ ／ ／ Ｄ Ｇ Ｊ ￣ Ｅ Ｇ ＝ 二Ｄ Ｃ ．
・ ．
．
Ａ ＡＥ Ｆ￣ Ａ ＡＢＣ ＥＦ ＝
＝
＝
Ｅ Ｆ ／ ／ Ｂ Ｃ Ｊ ｔ Ｅ Ｆ ＝Ｉ － － Ｂ Ｃ
２ ．
ＢＣ Ａ Ｂ ２
以
Ｉ
Ａ（ ０，口）
‘ 、
＼
钳 ／
童（ｂ ，ｏ’
＼ ‘ 专 ｆ口
．
、
Ｃ‘ ｃ－ Ｏ）
证 明 二 ： ’ 诜 ４ （ ｏ ， ， 日 （ ６ ， ０ ） ， ｃ （ ｃ ， ｏ ） ． 贝 Ｊ ｌ Ｅ （ 告 ， 号 ） ， 畸， 号 ） ．
求证： Ｅ Ｆ ＜２ １（ ＡＢ ＋ Ｃ Ｄ） ． （ ２ ０ １ １ 年银 川市 中考 题）
￣
分 析 ： 利 用 中 位 线 ， 将 矾吉 Ｂ ＋ ｃ Ｄ ） 转 移 到 同 一 三 角 形 中 ．
・ 。
・
直 线 Ｅ Ｆ 的 方 程 为 ） ， ＝ 号 ，
三角形中位线证明6种方法
三角形中位线证明6种方法三角形是几何学中最基本的图形之一，具有许多特性和性质。
三角形中位线是三角形内部一条特殊的线段，连接三角形两边中点的直线称为三角形中位线。
本文将介绍10条关于三角形中位线的证明方法，并对每一种方法进行详细阐述。
1. 三角形中位线长相等证明：对于任意三角形ABC，连接AC的中点E和BC的中点F，连接BE并延长至D，使得AD与CF相交于点G。
则有：CE=EA (连接AC的中点E)BF=FC (连接BC的中点F)EF=EF （共同边）在三角形BEF和CEF中，有EF、BE、FC互相平行，并按比例划分。
根据平行线定理，有BE/EF=BG/GF和FC/EF=CG/GF。
由此可得：BE/FC=BG/CG2BE/2FC=2BG/2CGAB/AC=BG/CG同理可证出，AC/BC=AH/HB和BC/AB=CI/IA。
即中位线长相等。
2. 三角形中位线堆垛证明：对于任意三角形ABC，连接AC的中点E和BC的中点F。
则有：EF∥ABEB=FAEC=FC在三角形AEC和BFC中，有EC=FC，∠EAC=∠FBC，∠CAE=∠CBF。
由此可得：三角形AEC与三角形BFC全等（AAS）AE=BF。
同理可证出BE=CF，因此中位线堆垛。
3. 三角形中位线垂直证明：对于任意三角形ABC，连接AC的中点E和BC的中点F。
则有：EF∥ABEB=FAEC=FC在三角形AEC和BFC中，有EC=FC，∠EAC=∠FBC，∠CAE=∠CBF。
由此可得：三角形AEC与三角形BFC全等（AAS）AE=BF。
连接EF并绘制ED⊥EF和FG⊥EF，分别交于点D和G。
则有：ED=GFEB=FC在三角形EBD和FCG中，有ED=FG，∠EDB=∠FGC，∠EBD=∠FCG。
由此可得：三角形EBD与三角形FCG全等（HL）BD=CG。
同理可证出AD=BG和AC=2DE，BC=2FG。
中位线垂直。
4. 三角形中位线和周长的关系证明：对于任意三角形ABC，连接AC的中点E和BC的中点F。
三角形中位线定理
因此DE∥BC。
如图，过D作DFAC，交BC于F，则 D BF=FC。
E （E′ ）
∵四边形DFCE是平行四边形，
∴DE=FC。 ∵FC=1 BC，
B
F
C
∴DE=2 BC。因此得：三角形中位线定理：
三 角 形 的 中 位 线 平 行 于 第 三 边，并 且 等于它的 一半。
4.10 三角形中位线定理
D
E
B
C
4.10 三 角 形 中 位 线
1、 连结三角形两边中点的线段叫做三角形的中位线。 A
2、观察右图，点D、E是线段AB、AC的中点
则 线段DE 是ABC的中位线。
D 3、如果再取线段BC的中点F，
E
则ABC还能画出 两 条中位
线，它们分别是 .10 三 角 形 中 位 线
初二几何
4.10 三角形的中位线
编辑: 邓 登 制作: 邓 登
4.10 三 角 形 中 位 线
1、 连结三角形两边中点的线段叫做三角形的中位线。
4.10 三 角 形 中 位 线
1、 连结三角形两边中点的线段叫做三角形的中位线。 A
2、观察右图，点D、E是线段AB、AC的中点
则 线段DE 是ABC的中位线。
4.10 三角形中位线定理
4.10 三角形中位线定理
4.10 三角形中位线定理
3、如图，点D、E、F分别是△ABC各边的中点，则ABC的中位线
是 线段 DE、线段DF 。
C
4、图中CF是△ABC的中位线吗？
它是△ABC的中线。
D
F
A
E
B
4.10 三角形中位线定理
如图，DE是△ABC的一条中位线。如果过D作
三角形中位线定理
三角形的中位线平行于第三边且等于第三边的一半
中位线定理的证明
如图，在△ABC中，D、E分别为AB、AC
的中点，连接DF.
求证：（1） DE ∥ BC 辅助线：延长DF至点F， 使EF=DF，连接FC △AED≌△CEF
1 2） DE （BC 2
一题多解
思考1
△ABC与△DEF的周长、面积有什么等量关系？
取AE中点G，连接DG
△DGF≌△CEF
四边形ABCD,AB与DC不平行,点E、F分别是
BC、AD的中点.求证: EF 1 AB CD
连接AC,取AC中点G 1 1 ∵FG=2 CD GE= AB 2
∴FG+GE>EF
1 EF ∴2 AB CD
2
∴平行四边形ABEC ∴F为BC中点，O为AC中 即：AB=2OF 点
如图，四边形ABCD中，E、F、G、H分别 是AB、BC、CD、DA的中点．求证:四边形EFGH 是平行四边形．
∵HG∥AC∥EF;EH∥BD∥F
GLeabharlann ∴EFGH为平行四边形题型二
增设中点，构造中位线
如图，已知△ABC中，D 是AB的中点， E是BC的三等分点（BE＞CE），AE、CD相交于F. 求证:F是DC的中点.
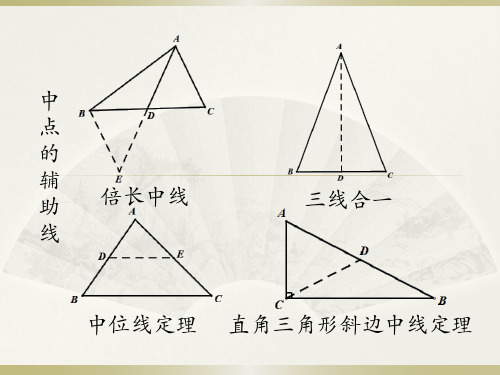
中 点 的 辅 助 线
倍长中线
三线合一
中位线定理
直角三角形斜边中线定理
三角形中位线的定义
连接三角形两边中点的线段叫做三角形的中位线 注意中线和中位线的区别！
中线：
一个顶点和对边的中点连线
中位线：
两个中点的连线
三角形中位线定理
观察并猜想DE与BC的关系
位置关系
数量关系
三角形的中位线定理
太奇教育深圳分校沙井校区
三角形的中位线定理
太奇教育深圳分校沙井校区
• 一、三角形的中位线
• 连接三角形两边的中点的线段叫做三角形的中位 线．
• 二、三角形中位线定理
• 三角形的中位线平行于三角形的第三边，且等于 第三边的一半．
太奇教育深圳分校沙井校区
• 三、由三角形中位线定理可以推出：
• 1、三角形三条中位线组成一个三角形，其周长为 原三角形周长一半． • 2、三角形三条中位线将原三角形分割成四个全等 的三角形． • 3、三角形三条中位线可以从原三角形中划分出面 积相等的三个平行四边形．
• 例3、如图，△ABC中，D、E分别在AB、 AC上，且BD=CE，F、G分别为BE、CD的 中点，过F、G的直线交AB于点P，交AC于 点Q．求证：AP=AQ．
太奇教育深圳分校沙井校区
• 例4、如图所示，O为等边三角形ABC内的 任意一点，且OD∥BC，交AB于D， OF∥AB，交AC于F，OE∥AC，交BC于 E．求证：OD＋OE＋OF=BC．
太奇教育深圳分校沙井校区
• 例1、如图，在四边形ABCD中，E、F、G、 H分别是AB、BC、CD、DA的中点．求证： 四边形EFGH是平行四边形．
太奇教育深圳分校沙井校区
• 例2、已知，如图，E、F分别为四边形 ABCD的对角线AC、BD的中点．求证： EF<(AB＋CD)．
太奇教育深圳分校沙井校区
太奇教育深圳分校沙井校区
• 例5、已知：如图，△ABC是等边三角形，过AB 边上的点D作DG∥BC，交AC于点G，在GD的延 长线上取点E，使DE=BD，连接AE、CD． （1）求证：△AGE≌△DAC； （2）过点E作EF∥DC，交BC于点F，请你连 接AF，并判断△AEF是怎样的三角形，试证明你 的结论．
三角形中位线定理图解说明
∵AD=BD边形
∴BC∥DF BC=DF
∴DE∥BC 且 DE=1/2BC
中位线特点
三角形中位线性质：三角形的中位线平行于第三边并且等于第三边的一半．
三角形三条中位线所构成的三角形是原三角形的相似形。
若在一个三角形中，一条线段是平行于一条边，且等于这条边的一半（这条 线段的端点必须是交 另外两条边上），这条线段就是这个三角形的中位线。
三角形中位线定义：连接三角形两边中点的线段角三角形的中位线。如图中线段 DE。
中位线定理 定理：三角形的中位线平行于第三边，并且等于第三边的一半 证明 1：如图，延 长 DE 到 F，使 EF=DE ，连 接 CF. ∵DE=EF 、∠AED=∠CEF 、AE=EC ∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF ∴AB∥FC
误区
要把三角形的中位线与三角形的中线区分开．三角形中线是连结一顶点和它 对边的中点，而三角形中位线是连结三角形两边中点的并且与底边平行且等于底 边的 1/2 的线段。
三角形的中线定义：
连接三角形顶点与对边中点的连线段。如图： BE 都是三角形的中线。
AE、CF、
三角形中位线
又 AD=DB ∴BD∥CF, BD=CF
所以 ，四边形 BCFD 是平行四边形
∴DE∥BC 且 DE=1/2BC
证明 2：
如图，延 长 DE 到 F，使 EF=DE ，连 接 CF、DC、AF
∵AE=CE DE=EF
∴四边形 ADCF 为平行四边形
∴AD∥CF AD=CF
三角形中位线
三角形中位线定理：
三角形中位线定理：
三角形中位线定理是指一个三角形的三条中位线交于一点，且该点距离三个顶点的距离相等。
具体来说，若在三角形ABC中，D、E和F分别是AB、BC和CA 的中点，则它们交于一点G，且AG=BG=CG。
中位线定理是三角形中的基本定理之一，它可以用于解决许多与三角形有关的问题。
例如，可以利用中位线定理证明三角形内任意一条线段的中点与三角形的三个顶点连线的交点共线；也可以利用中位线定理证明三角形的面积公式S=（1/2）×底边×高。
中位线定理还有一些其他有趣的应用，例如可以用它来构造一个等面积的平行四边形，或者用它来解决一些几何推理问题。
总之，中位线定理是三角形中的一个重要工具，它能够帮助我们更好地理解和解决与三角形有关的各种问题。
- 1 -。
中位线的判定定理
中位线的判定定理
中位线是一个数学术语，是平面几何内的三角形任意两边中点的连线或梯形两腰中点的连线。
1判定方法
1,根据定义：三角形两边中点之间的线段为三角形的中位线。
2.经过三角形一边中点与另一边平行的直线与第三边相交,交点与中点之间的线段为三角形的中位线。
3.端点在三角形的两边上与第三边平行且等于第三边的一半的线段为三角形的中位线。
2中位线定义
三角形：连结三角形两边中点的线段叫做三角形的中位线。
三角形的中位线平行于第三边，其长度为第三边长的一半，通过相似三角形的性质易得。
其两个逆定理也成立，即经过三角形一边中点平行于另一边的直线，必平分第三边；以及三角形内部平行于一边且长度为此边一半的线段必为此三角形的中位线。
但是注意过三角形一边中点作一长度为底边一半的线段有两个，不一定与底边平行。
梯形：连结梯形两腰中点的线段叫做梯形的中位线。
梯形的中位线平行于上底和下底，其长度为上、下底长度和的一半，可将梯形旋转180°、将其补齐为平行四边形后易证。
其逆定理正确与否与上相仿。
1,根据定义：三角形两边中点之间的线段为三角形的中位线.
2.经过三角形一边中点与另一边平行的直线与第三边相交,交点与中
点之间的线段为三角形的中位线.
3.端点在三角形的两边上与第三边平行且等于第三边的一半的线段为三角形的中位线.
三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线．
平行于第三边,并且是一边的中点的线段是中位线.这条还是一个定理,可以证明出来。
三角形中位线证明6种方法
三角形中位线证明6种方法以下是6种证明三角形中位线的方法：方法1：套用中线定理根据中线定理，三角形中位线所构成的三角形，面积是原来三角形的1/4，因此中位线的长度为(1/2)其所对应的边长。
因此，对于三角形ABC，若D、E、F分别为AB、BC、CA上的中点，则DE=1/2AC，EF=1/2AB，FD=1/2BC。
我们可以用勾股定理证明这些相等关系，从而证明三角形的中位线。
方法2：利用向量根据向量的性质，若d、e、f分别为v1、v2、v3的中点，则三角形DEF的质心G=v1+v2+v3。
因此，若d、e、f分别为向量a、b、c的中点，则三角形DEF的质心为G=(a+b+c)/3。
因此，DE=1/2AC，EF=1/2AB，FD=1/2BC。
可以使用向量的加减和数量积证明这些相等关系。
方法3：利用勾股定理根据勾股定理，若a、b、c分别为三角形ABC的边长，则a^2=b^2+c^2-2bc*cosA。
因此，若D、E、F分别为AB、BC、CA的中点，则DE=1/2AC=sqrt[(b^2+c^2)/4]-bc*cosA/2。
同样地，EF=1/2AB=sqrt[(c^2+a^2)/4]-ca*cosB/2，FD=1/2BC=sqrt[(a^2+b^2)/4]-ab*cosC/2。
根据余弦定理，可以证明这些相等关系。
方法4：利用相似三角形根据相似三角形的性质，若D、E、F分别为AB、BC、CA上的中点，则三角形DEF与三角形ABC相似。
因此，DE=1/2AC，EF=1/2AB，FD=1/2BC。
可以使用相似三角形的性质证明这些相等关系。
方法5：利用三角形面积公式根据三角形面积公式，若D、E、F分别为AB、BC、CA上的中点，则S(DEF)=1/4S(ABC)，其中S表示面积。
因此，DE=1/2AC，EF=1/2AB，FD=1/2BC。
可以使用三角形面积公式证明这些相等关系。
方法6：利用垂直平分线根据垂直平分线的性质，若D、E、F分别为AB、BC、CA上的中点，则AD、BE、CF相互垂直。
八年级数学-三角形中位线定理
八年级数学-三角形中位线定理三角形的中位线平行于第三边，并且等于它的一半。
运用这个定理，可以证明线与线的平行关系；证明线段之间的相等或倍分关系；还可将分散的已知条件集中起来发挥作用。
例1：如图P3-3，已知△ABC中，D是AB中点，O是CD中点，BO延长后交AC于E．证明：取AE中点F，连结DF．∵D是AB中点，∵O是CD中点，例2：已知：如图P3-4，在四边形ABCD中，AD=BC，M、N分别是AB.DC的中点，延长AD.MN 交于E，延长BC.MN交于F．求证：∠AEM=∠BFM．证明：连BD，取中点O，连ON、OM，在△ABD与△BDC中，M、O为AB.BD边中点；N、O为DB.DC 边中点．∵AD=BC．∴OM＝ON．∴∠1＝∠2．而∠1=∠BFM，∠2=∠AEM，∴∠AEM＝∠BFM．例3：选择题：(1)一个三角形三个内角度数的比为1∶2∶3，则这个三角形是 [ ](A)锐角三角形 (B)钝角三角形(C)直角三角形 (D)无法确定解：(C)．设三个内角的度数分别为k、2k、3k，24根据三角形内角和定理，有k+2k+3k＝180°解得 k=30°．∴三角形的三个内角分别为30°、60°、90°．故选(C)．(2)如果等腰三角形的顶角为40°，那么其中一个底角的度数为[ ](A)50° (B)70°(C)100° (D)140°解：(B)．(3)钝角三角形的三条高 [ ](A)相交于三角形内部的一点(B)相交于大边上的一点(C)相交于三角形外部的一点(D)不能相交于一点解：(C)．(4)在△ABC中，AB＞BC＞CA，那么在①∠C=60°，②∠B=60°，③∠A=60°中，可能成立的是 [ ](A)③ (B)②(C)②③ (D) ①③解：(A)．在△ABC中，∵ AB＞BC＞CA，∴∠C＞∠A＞∠B．若∠C=60°，则∠A与∠B的均小于60°，这与三角形内角和等于180°矛盾．若∠B=60°，则∠C和∠A均大于60°，这也与三角形内角和等于180°矛盾．∴∠A=60°，应选(A)．(5)顺次连结周长为a的三角形三边中点所得三角形的周长为 [ ]解：(D)．(6)在△ABC中，∠B.∠C的外角平分线相交于D，那么∠BDC等于 [ ]解：(C)．如图P3-5，∵∠EBC＋∠FCB=(180°-∠ABC)＋(180°-∠ACB)=360°-(∠ABC＋∠ACB)．又∵∠A=180°-(∠ABC＋∠ACB)，∴∠ABC＋∠ACB＝180°-∠A．∴∠EBC＋∠FCB＝360°-180°+∠A=180°+∠A．∵BD.CD分别平分∠EBC.∠FCB，∴∠BDC=180°-(∠1+∠2)(7)下列命题中的假命题是 [ ]（A)有一个内角是60°的等腰三角形是等边三角形（B)等边三角形是等腰三角形（C）等腰直角三角形中，斜边是任一直角边2倍。
三角形中位线定理
F
C
∴DE∥BC,
1 1 DE DF BC . 2 2
定义：连接三角形两边中点的线
段 叫做三角形的中位线. 定理:三角形的中位线平行于第三 边, 且等于第三边的一半.
练习
• 已知:在△ABC中,D,E,F分别是边 • BC,CA,AB的中点. • 求证：EF+FD+ED=(AB+BC+AC)÷2
三角形中位线定理
作者：无敌的人
三角形中位线的性质定理
证明:如图,延长DE至F,使EF=DE,连接CF. A ∵ AE=CE,∠AED=∠CEF, EF=DE
∴△ADE≌△CFE(SAS).
D E
∴AD=CF,∠ADE=∠F. ∴BD∥CF. B ∵AD=BD, ∴BD=CF, 又∵ BD∥CF. ∴四边形DBCF是平行四边形. ∴DF∥BC,DF=BC.
A
F
B
E
C
D
A
连结三角形两边中点的线段 叫做三角形的中位线
D
E
三角形中位线定理： 三角形的中位线平行于 第三边，并且等于它的一半。
C
B
DE=2BC DE∥BC
Hale Waihona Puke
3角形中位线定理
3角形中位线定理三角形中位线定理，是在三角形中，与三条相邻边的中点相连的线段，它们构成的三个交点都在同一点上。
本文将从定理的证明、推广应用、例题等三个方面进行阐述。
一、定理的证明证明思路：设三角形ABC的三边分别为a、b、c，D为BC的中点，E为AC的中点，F 为AB的中点，则连接AD、BE、CF的交点为G。
则需证明AD、BE、CF三条线段的交点G是一个固定点。
证明：由于D、E、F都是各边中点，可得：∵ D是BC的中点，∴ BD = DC；又∵ G是AD与BE的交点，故可以得出：∵ D、E分别为BC和AC的中点，∴ DE // AC，同时AE = EC，∴ △AED与△CEB 相似。
$\frac{GA}{BD}=\frac{GC}{CE}$又 $\because BD=DC$ ， $\therefore GA=GC$同理可得：于是，我们得到了两个相等的值：GA=GC，GB=GC。
由此，可知三角形GAC是一个等腰三角形，且AG与CF之间的线段垂直于CF，同理可得：因为三角形GAC、GBA、CBG均拥有最长边CG，所以它们就构成了一个共同的圆，而这个圆的中心就是点G。
因此可以得知：三角形ABC的三边中位线的交点G是一个固定点。
二、推广应用利用中位线定理，我们可以推导容易证明的三条定理和一个相关问题：中位线长定值定理、七分线长定值定理、以及在四边形中应用中位线定理、解决中位线问题。
1. 中位线长定值定理在三角形中，如果其中一条中位线相等，那么这个三角形就是等边三角形。
设△ABC为等边三角形，则BD、AE、CF三条中位线的长度均为$\frac{1}{2}$边长，又 $\because BD=AE=CF$ ，所以可以得到：BD=AE=CF=$\frac{1}{2}$a=a，同理可得：b=c=a。
在三角形中，三条中位线可将它们所在线段的长分为1:2:3的比例。
首先，由于三角形的三角形内部对角线互不交于同一点，那么三角形内部的线段AB、AC、BC是不会共线的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课 题： 三角形中位线定理
教学目标：
1． 理解三角形中位线的概念，掌握它的性质．
2． 能较熟练地应用三角形中位线性质进行有关的证明和计算．
3．经历探索、猜想、证明的过程，进一步发展推理论证的能力．
4．能运用综合法证明有关三角形中位线性质的结论．理解在证明过程中所运用的归纳、类比、转化等思想方法．
重点、难点
1．重点：掌握和运用三角形中位线的性质．
2．难点：三角形中位线性质的证明（辅助线的添加方法）．
（1）强调三角形的中位线与中线的区别：
（2）要把三角形中位线性质的特点、条件、结论及作用交代清楚：
学习过程：
一、情景创设
实验：请同学们思考：将任意一个三角形分成四个全等的三角形，你是如何切割的？（答案如图）
图中有几个平行四边形？你是如何判断的？
二、引入新课
1． 三角形中位线： ．
2． 三角形中位线性质
三角形中位线定理： ． 定理符号语言的表达：
如图，在△ABC 中
∵D 、E 是AB 、AC 的中点
∴
应注意的两个问题：①第一个结论是表明中位线与第三边的位置关系，第二个结论是说明中位线与第三边的数量关系，在应用时可根据需要来选用其中的结论（可以单独用其中结论）．②这个定理的证明方法很多，关键在于如何添加辅助线．
三探索活动
已知： 如图，点D 、E 、分别为△ABC 边AB 、AC 的中点，求证：DE ∥BC 且DE=21BC ． 分析：所证明的结论既有平行关系，又有数量关系，联想已学过的知识，可以把要证明的内容转化到一个平行四边形中，利用平行四边形的对边平行且相等的性质来证明结论成立，从而使问题得到解决，这就需要添加适当的辅助线来构造平行四边形．
方法1：如图（1），延长DE 到F ，使EF=DE ，连接CF ，（也可以过点C 作CF
A B C D
E
∥AB 交DE 的延长线于F 点，证明方法与上面大体相同）
CD 方法2：如图（2），延长DE 到F ，使EF=DE ，连接CF 、
和AF ，
【思考】：
（1）想一想：①一个三角形的中位线共有几条？②三角形的中位线与中线有什么区别？
（2）三角形的中位线与第三边有怎样的关系？
三角形中位线的性质：三角形的中位线平行与第三边，且等于第三边的一半．
〖拓展〗已知：△ABC 的周长为a ，面积为s ，连接各边中点得△A 1B 1C 1，再连接△A 1B 1C 1各边中点得△A 2B 2C 2……，
则（１） 第３次连接所得△A 3B 3C 3的周长＝ ，面积＝
（２）第n 次连接所得△A n B n C n 的周长＝ ，面积＝ 四典型例题
1、 如图，△ABC 中，AD 是BC 的中线，EF 是中位线，
求证：AD 、EF 互相平分。
2、已知，在三角形ABC 中，BD 平分∠ABC ，AD ⊥BD ，F 为AC 的中点，
求证：DE ∥BC ，DF=
21（BC －AB ）
3 求证：顺次连结四边形四条边的中点，所得的四边形是平行四边形．
已知：如图所示，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点． D E B C A
求证：四边形EFGH 是平行四边形．‘
思 顺次连结矩形菱形正方形各边中点所得的四边形是什么四边形？等腰梯形呢？ （学生边画图边观察，请学生猜想）
2、猜测：当四边形满足什么条件时，四边形EFGH 为矩形、菱形、正方形？
五、课堂练习
（一）填空
1如图，A 、B 两点被池塘隔开，在AB 外选一点C ，连结AC 和BC ，并分别找
出AC 和BC 的中点M 、N ，如果测得MN=20 m ，那么A 、B 两点的距离是 m ，
理由是 ．
2．△ABC 中，D 、E 、F 分别是AB 、AC 、BC 的中点，
（1）若EF=5cm ，则AB= cm ；若BC=9cm ，则DE= cm ；
（2）中线AF 与DE 中位线有什么特殊的关系？证明你的猜想．
3．一个三角形的周长是135cm ，过三角形各顶点作对边的平行线，则这三条平行线所组成的三角形的周长是 cm ．
(二)解答
1已知：如图点E. F .G . H 分别是线段 AB. BC. C D. AD 的中点
当四边形DBCA 满足什么条件时，四边形EFGH 是菱形？
六小结与作业
D G
E B
F C A
H
评价与反思。