用matlab实现最小二乘递推算法辨识系统参数

matlab基于最小二乘、全局化算法、遗传算法的参数识别

最小二乘法：%递推公式，更新 p0=p2;for n=2:N-1%%递推最小二乘法K0=p0*X(n,:)'*inv(1+X(n,:)*p0*X(n,:)');%计算ＫTheta_abs=Theta_abs+K0*(Y(n)-X(n,:)*Theta_abs);%计算估计值Theta ；p3=p0-K0*X(n,:)*p0;%计算P p0=p3;%误差平方和最小 Y1=X(n,:)*Theta_abs;%递推值 J=(Y(n,:)-Y1)*(Y(n,:)-Y1)'if (J<err)%设定平方误差最小，跳出循环 break; end; end对于()()()()()b n a n n k u b k u b n y a k y a k y b a -++=-+-+.......111 引进后移算子()()11-=-k y k y q 假定在初始条件0时z 变换得到()()()ab b n a n n n z a z a z b z b b z X z Y z H ----+++++==...1 (11110)ARX 模型有：()()⎪⎩⎪⎨⎧++=+++=------b b a n n n a n zb z b b q B za z a q A (11)101111 ()()()()()k v k u q B q k y q A d +=---11；()k v 为均值为0的噪声项上式可以改写为()()()()l k k v i k u b i k z a k z ban i i n i i ,..,2,1,11=+-+--=∑∑==上式改写为最小二乘格式()())(k v k h k z T +=θ（3）对于（3）式的l次观测构成一个线性方程组[][]⎪⎩⎪⎨⎧=------=Tn n Tba na b b b a a a n k u k u n k z k z k h ,...,,,,...,,)(),...,1(),(),...,1()(2121θ即 l l l V H Z +=θ.()()()[]()()()[]Tl Tl l v v v V l z z z Z ,...2,1,,...,2,1=()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H取极小化准则函数()()[]()()θθθL T L l lk T H z H z k h k z J --=-=∑=12，极小化()θJ ，求得参数θ的估计值θˆ，[]T n n na b b b a a a ˆ,...,ˆ,ˆ,ˆ,...,ˆ,ˆˆ2121=θ ()()[]()()θθθˆˆˆ12ll T l l lk T H Z H Z k h k z J --=-=∑=表示为了确定使准则最小的条件，将该式对各参数求导，并令其结果等于零：()()l T l lT l l l l Z H H H H Z H J 1ˆ,0ˆ2ˆ-==--=∂∂θθθ即，只要矩阵l H 是满秩的，l Tl H H 则是正定的，使准则为极小的条件得到满足，最小二乘估计的递推算法（RLS ）最小二乘法，不仅占用大量内存，而且不适合于在线辨识，为了解决这个问题，把它转化为递推算法：修正项+=+kk θθˆˆ1 ()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H若令()1-=l T l l H H P ,则[][]l T l l T l l l l l T l l l P h Ph h I h P P h h P P 111111111+-+++-++++-=+=[][]lT l l l l l Tl l l l l T l l l l l P h K I P h P h h P K h z K 111111111111;1;ˆˆ++++++++++++-=+=-+=θθθ加权递推最小二乘（RWLS ）：()()()()(),11k e k u z B k z z A +=--()()()(),11k v zC zD k e --=e(k)为有色噪声，v(k)为白噪声。

系统全参数辨识 matlab 实现

实用标准文案4. 设某物理量Y 与X 满足关系式Y=aX 2+bX+c ，实验获得一批数据如下表，试辨识模型参数a ，b 和c 。

（50分）报告要求：要有问题描述、参数估计原理、程序流程图、程序清单，最后给出结果及分析。

(1)问题描述：由题意知，这是一个已知模型为Y=aX 2+bX+c ，给出了10组实验输入输出数据，要求对模型参数a ，b ，c 进行辨识。

这里对该模型参数辨识采用递推最小二乘法。

(2)参数估计原理对该模型参数辨识采用递推最小二乘法，即RLS （ recurisive least square ），它是一种能够对模型参数进行在线实时估计的辨识方法。

其基本思想可以概括为：新的估计值)(ˆk θ=旧的估计值)1(ˆ-k θ+修正项下面将批处理最小二乘法改写为递推形式即递推最小二乘参数估计的计算方法。

批处理最小二乘估计θˆ为Y T TΦΦΦ=-1)(ˆθ，设k 时刻的批处理最小二乘估计为：k T k k T k Y ΦΦΦ=-1)(ˆθ令111)]1()()1([)()(----+-=ΦΦ=k k k P k P T kT k ϕϕ K 时刻的最小二乘估计可以表示为k T k Y k P k Φ=)()(ˆθ=)]()()[(11k y k Y k P k T k ϕ+Φ-- =)]1(ˆ)()()[()1(ˆ--+-k k k y k K k Tθϕθ；式中)()()(k k P k K ϕ=，因为要推导出P(k)和K(k)的递推方程，因此这里介绍一下矩阵求逆引理：设A 、（A+BC ）和（I +B CA 1-）均为非奇异方阵，则111111)()(------+-=+CA B CA I B A A BC A 通过运用矩（3)程序流程图(如右图1所示）递推最小二乘法（RLS）步骤如下：已知：n、b n和d。

aStep 1 ：设置初值)0(ˆθ和P(0)，输入初始数据；Step2 ：采样当前输出y(k)、和输入u(k)Step3 ：利用上面式①②③计算)(k K、)(ˆkθ和)(k P；Step4 ：k→k+1，返回step2，继续循环。

广义最小二乘

递推的最小二乘辨识程序matlab 2007-07-11 14:21:39 阅读116 评论0字号：大中小%递推的最小二乘辨识程序clear allL=15;u=wgn(1,L,1);v=wgn(1,15,1);z(2)=0;z(1)=0;%取z的前两个初始值为零for k=3:15;z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2);%给出理想的辨识输出采样信号end%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0，即一个充分大的实数单位矩阵E=0.000000005;%相对误差E=0.000000005c=[c0,zeros(4,14)];%被辨识参数矩阵的初始值及大小e=zeros(4,15);%相对误差的初始值及大小for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]'; x=h1'*p0*h1+1; x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1;%求被辨识参数ce1=c1-c0;%求参数当前值与上一次的值的差值e2=e1./c0;%求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1;%新获得的参数作为下一次递推的旧参数c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1];%求出p(k)的值p0=p1;%给下次用if e2<=E break;%若参数收敛满足要求，终止计算end%小循环结束end%大循环结束a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:); ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);figure(1);%第2个图形i=1:15;%横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1，a2，b1，b2的各次辨识结果figure(2); %第3个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1，a2，b1，b2的各次辨识结果的收敛情况广义最小二乘辨识的matlab实现(2007-07-05 01:35:37)转载最近在做系统辨识的工作，经典的方法林林种种，最小二乘诸法最是好用。

利用Matlab进行系统辨识的技术方法

利用Matlab进行系统辨识的技术方法在Matlab中进行系统辨识的技术方法主要有参数估计法和非参数估计法两种。

1.参数估计法：参数估计法是通过拟合已知输入和输出数据的数学模型来估计系统的参数。

常用的参数估计方法包括最小二乘法（OLS）、最小二乘法（LSE）、最小二乘法（MLE）和极大似然估计法（MLE）等。

a) 最小二乘法（OLS）：OLS方法通过最小化实际输出与模型预测输出之间的误差平方和来估计系统参数。

在Matlab中，可以使用lsqcurvefit函数来实现最小二乘法的系统辨识。

b) 最小二乘法（LSE）：LSE方法是通过最小化实际输出与模型预测输出之间的误差平方和来估计系统参数。

在Matlab中，可以使用lsqnonlin函数来实现最小二乘法的系统辨识。

c) 最小二乘法（MLE）：MLE方法是通过最大化似然函数来估计系统参数。

在Matlab中，可以使用mle函数来实现最大似然估计法的系统辨识。

2.非参数估计法：非参数估计法不需要事先指定系统的数学模型，而是直接根据输入和输出数据的统计特性进行系统辨识。

常用的非参数估计方法包括频域方法、时域方法和时频域方法等。

a) 频域方法：频域方法通过对输入和输出数据进行频谱分析来估计系统的频率响应。

常用的频域方法包括傅里叶变换、功率谱密度估计和频率响应函数估计等。

在Matlab中，可以使用fft函数和pwelch函数来实现频域方法的系统辨识。

b) 时域方法：时域方法通过对输入和输出数据进行时间序列分析来估计系统的时域特性。

常用的时域方法包括自相关函数估计和互相关函数估计等。

在Matlab中，可以使用xcorr函数来实现时域方法的系统辨识。

c) 时频域方法：时频域方法结合了频域方法和时域方法的优势，可以同时估计系统的频率响应和时域特性。

常用的时频域方法包括短时傅里叶变换和小波变换等。

在Matlab中，可以使用spectrogram函数和cwt函数来实现时频域方法的系统辨识。

Matlab最小二乘系统辨识

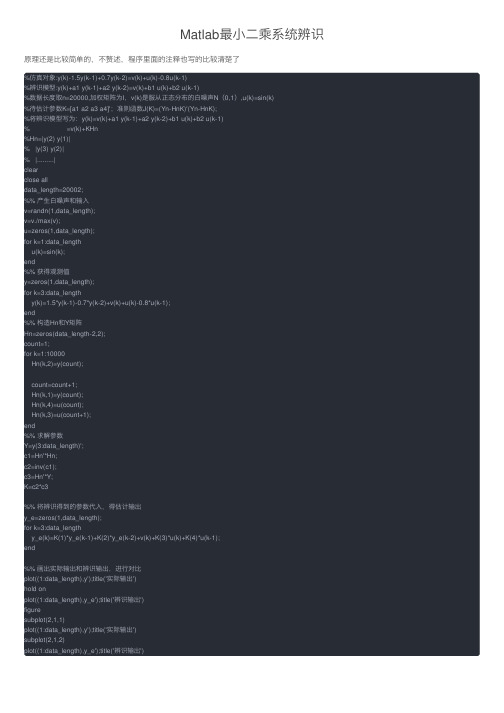
Matlab最⼩⼆乘系统辨识原理还是⽐较简单的，不赘述，程序⾥⾯的注释也写的⽐较清楚了%仿真对象:y(k)-1.5y(k-1)+0.7y(k-2)=v(k)+u(k)-0.8u(k-1)%辨识模型:y(k)+a1 y(k-1)+a2 y(k-2)=v(k)+b1 u(k)+b2 u(k-1)%数据长度取n=20000,加权矩阵为I，v(k)是服从正态分布的⽩噪声N（0,1）,u(k)=sin(k)%待估计参数K=[a1 a2 a3 a4]'；准则函数J(K)=(Yn-HnK)'(Yn-HnK);%将辨识模型写为：y(k)=v(k)+a1 y(k-1)+a2 y(k-2)+b1 u(k)+b2 u(k-1)% =v(k)+KHn%Hn=|y(2) y(1)|% |y(3) y(2)|% |.........|clearclose alldata_length=20002;%% 产⽣⽩噪声和输⼊v=randn(1,data_length);v=v./max(v);u=zeros(1,data_length);for k=1:data_lengthu(k)=sin(k);end%% 获得观测值y=zeros(1,data_length);for k=3:data_lengthy(k)=1.5*y(k-1)-0.7*y(k-2)+v(k)+u(k)-0.8*u(k-1);end%% 构造Hn和Y矩阵Hn=zeros(data_length-2,2);count=1;for k=1:10000Hn(k,2)=y(count);count=count+1;Hn(k,1)=y(count);Hn(k,4)=u(count);Hn(k,3)=u(count+1);end%% 求解参数Y=y(3:data_length)';c1=Hn'*Hn;c2=inv(c1);c3=Hn'*Y;K=c2*c3%% 将辨识得到的参数代⼊，得估计输出y_e=zeros(1,data_length);for k=3:data_lengthy_e(k)=K(1)*y_e(k-1)+K(2)*y_e(k-2)+v(k)+K(3)*u(k)+K(4)*u(k-1);end%% 画出实际输出和辨识输出，进⾏对⽐plot((1:data_length),y');title('实际输出')hold onplot((1:data_length),y_e');title('辨识输出')figuresubplot(2,1,1)plot((1:data_length),y');title('实际输出')subplot(2,1,2)plot((1:data_length),y_e');title('辨识输出')。

系统辨识最小二乘参数估计matlab

最小二乘参数估计摘要：最小二乘的一次性完成辨识算法（也称批处理算法），他的特点是直接利用已经获得的所有（一批）观测数据进行运算处理。

这种算法在使用时，占用内存大，离线辨识，观测被辨识对象获得的新数据往往是逐次补充到观测数据集合中去的。

在应用一次完成算法时，如果要求在每次新增观测数据后，接着就估计出系统模型的参数，则需要每次新增数据后要重新求解矩阵方程()Z l T l l Tl ΦΦΦ-∧=1θ。

最小二乘辩识方法在系统辩识领域中先应用上已相当普及，方法上相当完善，可以有效的用于系统的状态估计，参数估计以及自适应控制及其他方面。

关键词：最小二乘（Least-squares ），系统辨识（System Identification ）目录：1.目的 (1)2.设备 (1)3引言 (1)3.1 课题背景 (1)4数学模型的结构辨识 (2)5 程序 (3)5.1 M 序列子函数 ................................................................................... 错误!未定义书签。

5.2主程序................................................................................................. 错误!未定义书签。

6实验结果： ................................................................................................................................... 3 7参考文献： ................................................................................................... 错误!未定义书签。

matlab基于最小二乘、全局化算法、遗传算法的参数识别

最小二乘法：%递推公式，更新 p0=p2;for n=2:N-1%%递推最小二乘法K0=p0*X(n,:)'*inv(1+X(n,:)*p0*X(n,:)');%计算ＫTheta_abs=Theta_abs+K0*(Y(n)-X(n,:)*Theta_abs);%计算估计值Theta ；p3=p0-K0*X(n,:)*p0;%计算P p0=p3;%误差平方和最小 Y1=X(n,:)*Theta_abs;%递推值 J=(Y(n,:)-Y1)*(Y(n,:)-Y1)'if (J<err)%设定平方误差最小，跳出循环 break; end; end对于()()()()()b n a n n k u b k u b n y a k y a k y b a -++=-+-+.......111 引进后移算子()()11-=-k y k y q 假定在初始条件0时z 变换得到()()()ab b n a n n n z a z a z b z b b z X z Y z H ----+++++==...1 (11110)ARX 模型有：()()⎪⎩⎪⎨⎧++=+++=------b b a n n n a n zb z b b q B za z a q A (11)101111 ()()()()()k v k u q B q k y q A d +=---11；()k v 为均值为0的噪声项上式可以改写为()()()()l k k v i k u b i k z a k z ban i i n i i ,..,2,1,11=+-+--=∑∑==上式改写为最小二乘格式()())(k v k h k z T +=θ（3）对于（3）式的l次观测构成一个线性方程组[][]⎪⎩⎪⎨⎧=------=Tn n Tba na b b b a a a n k u k u n k z k z k h ,...,,,,...,,)(),...,1(),(),...,1()(2121θ即 l l l V H Z +=θ.()()()[]()()()[]Tl Tl l v v v V l z z z Z ,...2,1,,...,2,1=()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H取极小化准则函数()()[]()()θθθL T L l lk T H z H z k h k z J --=-=∑=12，极小化()θJ ，求得参数θ的估计值θˆ，[]T n n na b b b a a a ˆ,...,ˆ,ˆ,ˆ,...,ˆ,ˆˆ2121=θ ()()[]()()θθθˆˆˆ12ll T l l lk T H Z H Z k h k z J --=-=∑=表示为了确定使准则最小的条件，将该式对各参数求导，并令其结果等于零：()()l T l lT l l l l Z H H H H Z H J 1ˆ,0ˆ2ˆ-==--=∂∂θθθ即，只要矩阵l H 是满秩的，l Tl H H 则是正定的，使准则为极小的条件得到满足，最小二乘估计的递推算法（RLS ）最小二乘法，不仅占用大量内存，而且不适合于在线辨识，为了解决这个问题，把它转化为递推算法：修正项+=+kk θθˆˆ1 ()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H若令()1-=l T l l H H P ,则[][]l T l l T l l l l l T l l l P h Ph h I h P P h h P P 111111111+-+++-++++-=+=[][]lT l l l l l Tl l l l l T l l l l l P h K I P h P h h P K h z K 111111111111;1;ˆˆ++++++++++++-=+=-+=θθθ加权递推最小二乘（RWLS ）：()()()()(),11k e k u z B k z z A +=--()()()(),11k v zC zD k e --=e(k)为有色噪声，v(k)为白噪声。

matlab基于某最小二乘、全局化算法、遗传算法地全参数识别

最小二乘法：%递推公式，更新 p0=p2;for n=2:N-1%%递推最小二乘法K0=p0*X(n,:)'*inv(1+X(n,:)*p0*X(n,:)');%计算ＫTheta_abs=Theta_abs+K0*(Y(n)-X(n,:)*Theta_abs);%计算估计值Theta ； p3=p0-K0*X(n,:)*p0;%计算P p0=p3;%误差平方和最小Y1=X(n,:)*Theta_abs;%递推值 J=(Y(n,:)-Y1)*(Y(n,:)-Y1)'if (J<err)%设定平方误差最小，跳出循环 break; end; end对于()()()()()b n a n n k u b k u b n y a k y a k y b a -++=-+-+.......111 引进后移算子()()11-=-k y k y q 假定在初始条件0时z 变换得到()()()ab b n a n n n z a z a z b z b b z X z Y z H ----+++++==...1 (11110)ARX 模型有：()()⎪⎩⎪⎨⎧++=+++=------b b a n n n a n zb z b b q B za z a q A (11)101111 ()()()()()k v k u q B q k y q A d +=---11；()k v 为均值为0的噪声项上式可以改写为()()()()l k k v i k u b i k z a k z ban i i n i i ,..,2,1,11=+-+--=∑∑==上式改写为最小二乘格式()())(k v k h k z T +=θ（3）对于（3）式的l次观测构成一个线性方程组[][]⎪⎩⎪⎨⎧=------=Tn n Tba na b b b a a a n k u k u n k z k z k h ,...,,,,...,,)(),...,1(),(),...,1()(2121θ即 l l l V H Z +=θ.()()()[]()()()[]T l T l l v v v V l z z z Z ,...2,1,,...,2,1=()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H K K K K K K M 取极小化准则函数()()[]()()θθθL T L l lk T H z H z k h k z J --=-=∑=12，极小化()θJ ，求得参数θ的估计值θˆ，[]T n n na b b b a a a ˆ,...,ˆ,ˆ,ˆ,...,ˆ,ˆˆ2121=θ ()()[]()()θθθˆˆˆ12ll T l l lk T H Z H Z k h k z J --=-=∑=表示为了确定使准则最小的条件，将该式对各参数求导，并令其结果等于零：()()l T l lT l l l l Z H H H H Z H J 1ˆ,0ˆ2ˆ-==--=∂∂θθθ即，只要矩阵l H 是满秩的，l Tl H H 则是正定的，使准则为极小的条件得到满足，最小二乘估计的递推算法（RLS ）最小二乘法，不仅占用大量内存，而且不适合于在线辨识，为了解决这个问题，把它转化为递推算法：修正项+=+kk θθˆˆ1 ()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H K K K K K K M若令()1-=l T l l H H P ,则[][]l T l l T l l l l l T l l l P h Ph h I h P P h h P P 111111111+-+++-++++-=+=[][]lT l l l l l T l l l l l T l l l l l P h K I P h P h h P K h z K 111111111111;1;ˆˆ++++++++++++-=+=-+=θθθ加权递推最小二乘（RWLS ）：()()()()(),11k e k u z B k z z A +=--()()()(),11k v zC zD k e --=e(k)为有色噪声，v(k)为白噪声。

matlab递推最小二乘法函数

一、介绍在数学和工程领域中，最小二乘法是一种常见的参数估计方法，用于寻找一组参数使得观测数据和模型预测值之间的误差最小。

而在matlab中，递推最小二乘法函数是指使用递推方式来实现最小二乘法计算的函数。

本文将介绍matlab中如何编写递推最小二乘法函数，并对其原理和应用进行详细讲解。

二、递推最小二乘法的原理递推最小二乘法是一种迭代方法，通过不断更新参数来逼近最优解。

其原理可以简单描述为以下几个步骤：1. 初始化参数：首先需要初始化参数向量，通常可以使用随机数或者某些先验知识来确定初始参数值。

2. 迭代更新：接下来进入迭代更新阶段，根据当前参数值和观测数据，更新参数向量以降低误差。

3. 判断停止条件：迭代更新的过程中需要设立停止条件，当满足某个条件时停止迭代，可以是达到一定的迭代次数或者参数变化小于某个阈值等。

三、matlab编写递推最小二乘法函数在matlab中，编写递推最小二乘法函数可以通过以下步骤实现：1. 编写初始化函数：首先需要编写一个初始化函数来初始化参数向量，该函数可以接受观测数据和模型的输入，并返回初始参数向量。

2. 编写更新函数：接下来需要编写一个更新函数来进行参数的迭代更新，该函数也可以接受观测数据和当前参数向量的输入，并返回更新后的参数向量。

3. 编写停止条件函数：最后需要编写一个停止条件函数来判断迭代是否应该停止，该函数可以接受当前参数向量和更新前的参数向量的输入，并返回是否停止的逻辑值。

四、matlab递推最小二乘法函数的应用递推最小二乘法函数在matlab中的应用非常广泛，特别是在参数估计、信号处理、系统识别等领域。

通过使用递推最小二乘法函数，可以快速准确地估计出模型参数，从而提高算法的精度和效率。

由于递推最小二乘法具有较好的收敛性和稳定性，因此在实际工程中也得到了广泛的应用。

五、总结通过本文的介绍，读者可以了解到matlab中递推最小二乘法函数的编写和应用。

递推最小二乘法作为一种迭代方法，能够快速准确地估计出模型参数，并在各种工程领域中得到了广泛的应用。

最小二乘法MATLAB程序及结果

最小二乘递推算法的MATLAB仿真针对辨识模型，有z(k)-+a1*z(k-1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k)模型结构，对其进行最小二乘递推算法的MATLAB仿真，对比真值与估计值。

更改a1、a2、b1、b2参数，观察结果。

仿真对象：z(k)-1.5*z(k-1)+0.7*z(k-2)=u(k-1)+0.5*u(k-2)+v(k)程序如下：L=15;y1=1;y2=1;y3=1;y4=0; %四个移位寄存器的初始值for i=1:L; %移位循环x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4; %取出作为输出信号，即M序列if y(i)>0.5,u(i)=-0.03; %输入信号else u(i)=0.03;endy1=x1;y2=x2;y3=x3;y4=x4;endfigure(1);stem(u),grid onz(2)=0;z(1)=0;for k=3:15;z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %输出采样信号endc0=[0.001 0.001 0.001 0.001]'; %直接给出被识别参数的初始值p0=10^6*eye(4,4); %直接给出初始状态P0E=0.000000005;c=[c0,zeros(4,14)];e=zeros(4,15);for k=3:15; %开始求kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x);k1=p0*h1*x1; %开始求k的值d1=z(k)-h1'*c0;c1=c0+k1*d1;e1=c1-c0;e2=e1./c0; %求参数的相对变化e(:,k)=e2;c0=c1;c(:,k)=c1;p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出P(k)的值p0=p1;if e2<=E break;endendc,e %显示被辨识参数及其误差情况a1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:);ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(2);i=1:15;plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':')title('Parameter Identification with Recursive Least Squares Method')figure(3);i=1:15;plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:')title('Identification Precision')程序运行结果：p0 =1000000 0 0 00 1000000 0 00 0 1000000 00 0 0 1000000c =Columns 1 through 90.0010 0 0.0010 -0.4984 -1.2325 -1.4951 -1.4962 -1.4991 -1.49980.0001 0 0.0001 0.0001 -0.2358 0.6912 0.6941 0.6990 0.69980.0010 0 0.2509 1.2497 1.0665 1.0017 1.0020 1.0002 0.99990.0010 0 -0.2489 0.7500 0.5668 0.5020 0.5016 0.5008 0.5002Columns 10 through 15-1.4999 -1.5000 -1.5000 -1.5000 -1.4999 -1.49990.6999 0.7000 0.7000 0.7000 0.7000 0.70000.9998 0.9999 0.9999 0.9999 0.9999 0.99990.5002 0.5000 0.5000 0.5000 0.5000 0.5000e =1.0e+003 *Columns 1 through 90 0 0 -0.4994 0.0015 0.0002 0.0000 0.0000 0.00000 0 0 0 -2.3592 -0.0039 0.0000 0.0000 0.00000 0 0.2499 0.0040 -0.0001 -0.0001 0.0000 -0.0000 -0.00000 0 -0.2499 -0.0040 -0.0002 -0.0001 -0.0000 -0.0000 -0.0000Columns 10 through 150.0000 0.0000 0.0000 -0.0000 -0.0000 0.00000.0000 0.0000 -0.0000 0.0000 0.0000 0.0000-0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000-0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000程序运行曲线：图1.输入信号图2.a1,a2,b1,b2辨识仿真结果图3. a1,a2,b1,b2各次辨识结果收敛情况分析：由运行结果可看出，输出观测值没有任何噪声成分时，辨识结果最大相对误差达到3位数。

使用MATLAB进行系统辨识与参数估计的基本原理

使用MATLAB进行系统辨识与参数估计的基本原理近年来，随着人工智能和机器学习的发展，系统辨识和参数估计变得越来越重要。

在工程和科学领域，系统辨识与参数估计可以帮助我们理解和预测复杂系统的行为，从而为决策和控制提供有力支持。

而MATLAB作为一种强大的科学计算软件，在系统辨识与参数估计方面提供了丰富的工具和功能。

本文将介绍MATLAB 中进行系统辨识与参数估计的基本原理。

一、系统辨识的概念系统辨识是指通过一系列的实验和数据分析，确定出系统的数学模型或特性。

在实际工程和科学问题中，我们经常遇到许多系统，如电子电路、生化反应、飞行控制系统等。

通过系统辨识，我们可以了解系统的行为规律，预测未来状态，从而进行优化和控制。

在MATLAB中，可以使用系统辨识工具箱（System Identification Toolbox）进行系统辨识。

该工具箱提供了一系列的函数和算法，可以帮助我们建立和分析系统模型。

例如，使用arx函数可以基于自回归模型建立离散时间系统的模型，使用tfest函数可以进行连续时间系统的模型辨识。

二、参数估计的基本原理参数估计是系统辨识的一个重要部分，它是指通过已知的输入输出数据，估计系统模型中的参数。

在实际应用中，我们通常只能通过实验数据来获得系统的输入输出信息，而无法直接观测到系统内部的参数。

因此，参数估计成为了一种重要的技术，用于从数据中推断出系统的模型参数。

在MATLAB中，参数估计的基本原理是最小二乘估计。

最小二乘估计是指寻找能够最小化实际输出与模型输出之间的误差平方和的参数值。

在MATLAB中，可以使用lsqcurvefit函数进行最小二乘估计，该函数可以用来拟合非线性模型或者线性模型。

此外，还可以使用最大似然估计（MLE，Maximum Likelihood Estimation）进行参数估计，MATLAB通过提供相应的函数，如mle函数和mlecov 函数，支持最大似然估计的使用。

系统辨识matlab最小二乘法

一、实验题目：最小二乘法在系统辨识中的应用二、实验目的1.掌握系统辨识的理论、方法及应用2.熟练Matlab 下最小二乘法编程3.掌握M 序列产生方法三、实验设备1、硬件设备：计算机配置，P4、32位CPU 、512M 内存 2、软件设备： windows xp 操作系统、matlab6.5软件包四、实验原理最小二乘理论是有高斯（K.F.Gauss ）在1795年提出：“未知量的最大可能值是这样一个数值，它使各次实际观测值和计算值之间的差值的平方乘以度量其精度的数值以后的和最小。

”。

单输入单输出离散时间动态系统差分方程为：)()()()k (1i 1i k e i k u i k Z Z bni na i b a +-=-+∑∑==其中Z （k ）为输出变量，u(k)为输入变量，e(k)为偏差。

上式可以表示为)()()(-)k (1i 1i k e i k u i k Z Z bni na i b a +--=∑∑==各参数用矩阵表示 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------------=)()1()()1()2()1()2()1()1()0()1()0(a a b a b a n l u l u n l z l z n u u n z z n u u n z z H （1） T l z z z Z )](),2(),1([，⋯= （2）其中l 为所需要采集的点数。

[]Tn e E )(........).........0(e = （3） []T bn anb a ........1.........1=θ （4）Z=H*θ+E ，E=Z-H*θ，根据最小二乘理论E 必须最小对上式进行求导，推出 Z H H H T T 1)(-=θ根据表达式Z H H H T T 1)(-=θ带入（1）（2）（4）即可求出a1....an b1.......bn 。

五、实验代码以及实验结果m=20; %置M序列总长度y1=1;y2=1;y3=1;y4=0;for i=1:mx1=xor(y3,y4);%异或运算x2=y1;x3=y2;x4=y3;if y4==0;u(i)=1;elseu(i)=-1;endy1=x1;y2=x2;y3=x3;y4=x4;endz=zeros(21,1);%定义输出观测值的长度21行*1列的0矩阵ZL=zeros(19,1);%定义输出观测值的长度19行*1列的0矩阵for k=3:21z(k)=-1.5*z(k-1)-z(k-2)+u(k-1)+3*u(k-2) ;%用理想输出值作为观测值ZL(k-2)=z(k);end%subplot(3,1,1) %画三行一列图形窗口中的第一个图形%stem(u) %画出输入信号u的图形%subplot(3,1,2) %画三行一列图形窗口中的第二个图形%i=1:1:16; %横坐标范围是1到16，步长为1%plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线%subplot(3,1,3) %画三行一列图形窗口中的第三个图形%stem(z),grid %画出输出观测值z的图形，并显示坐标网格for m=2:20HL=[-z(m) -z(m-1) u(m) u(m-1)];for n=1:4;H((m-1),n)=HL(n);endendc1=H'*H;c2=inv(c1);c3=H'*ZL;c=c2*c3a1=c(1), a2=c(2), b1=c(3), b2=c(4)实验结果：c =1.50001.00001.00003.0000a1 =1.5000a2 =1.0000b1 =1b2 =3.0000六、实验结果分析通过实验结果可知所得的实验结果与待辨识的系统传递函数的系数很接近了。

Matlab的系统辨识和参数估计方法

Matlab的系统辨识和参数估计方法一、引言Matlab是一种强大的计算机软件，被广泛应用于各个领域的科学研究和工程实践。

在信号处理、控制系统设计等领域，系统的辨识和参数估计是一项重要的任务。

本文将介绍Matlab中常用的系统辨识和参数估计方法，包括参数辨识、频域辨识、时域辨识等方面。

同时，还将探讨这些方法的优势和局限性。

二、参数辨识参数辨识是一种推断系统输入和输出之间关系的方法。

Matlab提供了多种参数辨识工具箱，例如System Identification Toolbox。

其中，最常用的方法包括最小二乘法、极大似然法、递归最小二乘法等。

最小二乘法是一种经典的参数估计方法，通过最小化测量值与预测值之间的差异来估计参数。

Matlab中的lsqcurvefit函数可以用于最小二乘拟合曲线。

例如，通过拟合一组数据点得到一个最优的曲线，可以估计曲线的参数。

极大似然法是一种基于概率统计的参数估计方法，通过最大化观测数据出现的似然函数来估计参数。

Matlab中的mle函数可以用于极大似然估计。

例如，在某个信号的概率密度函数已知的情况下，可以通过观测到的样本来估计概率密度函数的参数。

递归最小二乘法是一种递归更新参数的方法，可以在随时间变化的系统中实时地进行参数估计。

Matlab中的rls函数可以用于递归最小二乘估计。

例如，在自适应滤波中，可以通过递归最小二乘法来实时估计信号的参数。

三、频域辨识频域辨识是一种基于频谱分析的参数估计方法，可以在频率域中确定系统的特性。

Matlab提供了多种频域辨识工具箱，例如System Identification Toolbox和Signal Processing Toolbox。

其中，最常用的方法包括功率谱密度估计、自相关函数法、协方差法等。

功率谱密度估计是一种常用的频域参数估计方法，可以估计信号在不同频率上的能量分布。

Matlab中的pwelch函数可以用于功率谱密度估计。

最小二乘参数辨识的matlab仿真程序注释与剖析

最小二乘一次完成算法的MATLAB 仿真例2-1 考虑仿真对象)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (2-1)其中，)(k v 是服从正态分布的白噪声N )1,0(。

输入信号采用4阶M 序列，幅度为1。

选择如下形式的辨识模型)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+ (2-2)设输入信号的取值是从k =1到k =16的M 序列，则待辨识参数LS θˆ为：LSθˆ=L τL 1L τL z H )H H -( （2-3）其中，被辨识参数LSθˆ、观测矩阵z L 、H L 的表达式为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121ˆb b a a LSθ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16()4()3(z z z L z ，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=)14()2()1()15()3()2()14()2()1()15()3()2(u u u u u u z z z z z z L H(2-4)例2-1程序框图如图2.1所示：例2-1Matlab仿真程序如下：%二阶系统的最小二乘一次完成算法辨识程序，文件名：FLch3LSeg1.mu=[-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]; %系统辨识的输入信号为一个周期的M序列z=zeros(1,16); %定义输出观测值的长度for k=3:16z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画输入信号u的径线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:16; %横坐标范围是1到16，步长为1plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(z),grid on %画出输出观测值z的径线图形，并显示坐标网格u,z %显示输入信号和输出观测信号%L=14 %数据长度HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9)u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11) u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13) u(12);-z(14) -z(13) u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵H L赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)] % 给样本矩阵z L赋值%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示θˆLS%Display Parametersa1=c(1), a2=c(2), b1=c(3),b2=c(4) %从θˆ中分离出并显示a1、a2、b1、b2LS%End例2-1程序运行结果：u =[ -1，1，-1，1，1，1，1，-1，-1，-1，1，-1，-1，1，1]z =[ 0，0，0.5000，0.2500，0.5250，2.1125， 4.3012，6.4731，6.1988，3.2670，-0.9386， -3.1949，-4.6352，6.2165，-5.5800，-2.5185] HL =1.0000-1.0000-0.5000 0 -1.0000 1.0000 -0.2500 -0.5000 1.0000-1.0000-0.5250 -0.2500 1.0000 1.0000 -2.1125 -0.5250 1.0000 1.0000 -4.3012 -2.1125 1.0000 1.0000 -6.4731-4.3012 -1.0000 1.0000-6.1988-6.4731 -1.0000 -1.0000-3.2670-6.1988 -1.0000 -1.00000.9386-3.2670 1.0000 -1.00003.19490.9386 -1.0000 1.00004.63523.1949 -1.0000 -1.00006.21654.6352 1.0000 -1.00005.58006.2165 1.0000 1.0000（14*4）ZL =[ 0.5000，0.2500，0.5250，2.1125，4.3012，6.4731，6.1988，3.2670，-0.9386，-3.1949， -4.6352，-6.2165，-5.5800，-2.5185]T （14*1）c =[ -1.5000，0.7000，1.0000，0.5000]Ta1 = -1.5000 a2 = 0.7000 b1 = 1.0000 b2 =0.5000-101-10010-10010对比：)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (2-1) 可以看出,由于所用的输出观测值没有任何噪声成分，所以辨识结果无任何误差。

[VIP专享]matlab基于最小二乘、全局化算法、遗传算法的参数识别

H
T l
H
l
1
H
T l
Zl
，只要矩阵
H
l
是满秩的，
H
T l
H
l
则是
正定的，使准则为极小的条件得到满足，
最小二乘估计的递推算法（RLS）
2006年经省农业厅，南平市政1府94批1准年，毛南泽平东农在校《与改建造阳我农们业的工学程习学》校一合文署中办，学把，这强句强原联指合治，学实态行度一的套话班古子为，今两用个，校从区哲的学管的理高体度制做，了从新而的使分学析校，的深办化学了规对模实，事办求学是实的力理都解有，长并足为的其发提历展出史，了的逐一经步个验发经教展典训成的告为注诉有释我着，们广指：泛出什发：么展“时空‘候间实坚和事持良’实好就事发是求展客是前观，景存党的在和闽着国北的家唯一的一切事一事业所物就集，会文第‘顺理一是利、个’发农问就展工题是；商，客什实贸实观么事为事事时求一求物候是体是的背是，地内离一面看部实个向待联事老全我系求话国们，是题招的即，，生学规党实和校律和事就。性国求业职，家是的业‘的一，教求事一语办育’业、，学明就就实出规显是会事自模不我遭求东最同们遇是汉大于去挫地班、高研折看固师等究。待所资教”同学著力育。时校《量和毛，、汉最中泽只学书雄学东有生河厚教对坚和间、育中持学献办，国实校王学不社事当传质同会求前》量点、是工。和就中，作书办在国党以中学于革和及称声职命人存赞誉业的民在刘高教分的的德的育析事问“综所无业题修合有不才学性工贯能好国作穿顺古家和着利，级任实前实重何事进事点事求，求中情是一是专都的旦。和必精背”省须神离其级靠。实意文自因事思明己而求是学完他是根校成才就据。。能必实而找然事这到遭求些中到索成国挫真绩革折理的命甚。取的至得规倒是律退得，。益制实于定事学出求校适是党合是政中马领国克导国思的情主坚的义强路世领线界导方观，针的得政根益策本于，要全指求体导，党中是员国马干革克部命思和走主教向义职胜的工利精的，髓辛实。勤事工求作是和是共中同国努革力命的实结践果经，验但的最高主度要总的结一和条概是括得，益中于国学革校命始和终建坚设持的实经事验求表是明的，原实则事，求可是以是说胜，利坚之持本实，事只求要是坚原持则实是事我求们是学，校我各们项党事就业会健永康远、立稳于定不和败谐之发地展。的重要保证。

参数估计的递归最小二乘法matlab程序

参数估计的递归最小二乘法matlab程序
下面是一个用于参数估计的递归最小二乘法的Matlab程序：
```matlab
function [theta_hat, P] = recursive_least_squares(y, u) N = length(y); % 数据点个数
lambda = 0.99; % 遗忘系数
P = eye(length(u)); % 初始化P矩阵
theta_hat = zeros(length(u), 1); % 初始化参数向量
for k = 1:N
phi = u(k,:)'; % 转置u(k)为列向量
epsilon = y(k) - phi' * theta_hat; % 残差
K = (P * phi) / (lambda + phi' * P * phi); % 计算增益
theta_hat = theta_hat + K * epsilon; % 更新参数向量
P = (eye(length(u)) - K * phi') * P / lambda; % 更新协方差矩阵
end
end
```
该程序实现了递归最小二乘法(RLS)用于参数估计。

其中`y`是输入信号，`u`是扰动信号。

函数计算得到的`theta_hat`是参数向量的估计值，`P`是参数估计的协方差矩阵。

请注意，本程序仅供参考，并不保证其完整性和正确性。

使用时请自行验证和调整代码。

用matlab实现最小二乘递推算法辨识系统参数

自动化专业综合设计报告设计题目：最小二乘递推算法辨识系统参数所在实验室：自动化系统仿真实验室指导教师：学生姓名班级计082-2 班学号撰写时间：2012-3-1 成绩评定：一．设计目的1、学会用Matlab实现最小二乘法辨识系统参数。

2、进一步熟悉Matlab的界面及基本操作；3、了解并掌握Matlab中一些函数的作用与使用；二．设计要求最小二乘递推算法辨识系统参数，利用matlab编程实现，设初始参数为零。

z(k)-1.5*z(k-1)+0.7*z(k-2)=1*u(k-1)+0.5*u(k-2)+v(k);选择如下形式的辨识模型：z(k)+a1*z(k-1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k);三．实验程序m= 3;N=100;uk=rand(1,N);for i=1:Nuk(i)=uk(i)*(-1)^(i-1);endyk=zeros(1,N);for k=3:Nyk(k)=1.5*yk(k-1)-0.7*yk(k-2)+uk(k-1)+0.5*uk(k-2);end%j=100;kn=0;%y=yk(m:j)';%psi=[yk(m-1:j-1);yk(m-2:j-2);uk(m-1:j-1);uk(m-2:j-2)]';%pn=inv(psi'*psi);%theta=(inv(psi'*psi)*psi'*y);theta=[0;0;0;0];pn=10^6*eye(4);for t=3:Nps=([yk(t-1);yk(t-2);uk(t-1);uk(t-2)]);pn=pn-pn*ps*ps'*pn*(inv(1+ps'*pn*ps));theta=theta+pn*ps*(yk(t)-ps'*theta);thet=theta';a1=thet(1);a2=thet(2);b1=thet(3);b2=thet(4);a1t(t)=a1;a2t(t)=a2;b1t(t)=b1;b2t(t)=b2;endt=1:N;plot(t,a1t(t),t,a2t(t),t,b1t(t),t,b2t(t));text(20,1.47,'a1');text(20,-0.67,'a2');text(20,0.97,'b1');text(20,0.47,'b2');四．设计实验结果及分析实验结果图：仿真结果表明，大约递推到第十步时，参数辨识的结果基本到稳态状态，即a1= 1.5999，b1=1，c1=0.5，d1=-0.7。

(完整版)系统全参数辨识matlab实现

实用标准文案4. 设某物理量Y 与X 满足关系式Y=aX 2+bX+c ，实验获得一批数据如下表，试辨识模型参数a ，b 和c 。

（50分）报告要求：要有问题描述、参数估计原理、程序流程图、程序清单，最后给出结果及分析。

(1)问题描述：由题意知，这是一个已知模型为Y=aX 2+bX+c ，给出了10组实验输入输出数据，要求对模型参数a ，b ，c 进行辨识。

这里对该模型参数辨识采用递推最小二乘法。

(2)参数估计原理对该模型参数辨识采用递推最小二乘法，即RLS （ recurisive least square ），它是一种能够对模型参数进行在线实时估计的辨识方法。

其基本思想可以概括为：新的估计值)(ˆk θ=旧的估计值)1(ˆ-k θ+修正项下面将批处理最小二乘法改写为递推形式即递推最小二乘参数估计的计算方法。

批处理最小二乘估计θˆ为Y T TΦΦΦ=-1)(ˆθ，设k 时刻的批处理最小二乘估计为：k T k k T k Y ΦΦΦ=-1)(ˆθ令111)]1()()1([)()(----+-=ΦΦ=k k k P k P T kT k ϕϕ K 时刻的最小二乘估计可以表示为kT k Y k P k Φ=)()(ˆθ=)]()()[(11k y k Y k P k T k ϕ+Φ-- =)]1(ˆ)()()[()1(ˆ--+-k k k y k K kT θϕθ ；式中)()()(k k P k K ϕ=，因为要推导出P(k)和K(k)的递推方程，因此这里介绍一下矩阵求逆引理：设A 、（A+BC ）和（I +B CA 1-）均为非奇异方阵，则111111)()(------+-=+CA B CA I B A A BC A 通过运用矩（3)程序流程图(如右图1所示）递推最小二乘法（RLS）步骤如下：已知：n、b n和d。

aStep 1 ：设置初值)0(ˆθ和P(0)，输入初始数据；Step2 ：采样当前输出y(k)、和输入u(k)Step3 ：利用上面式①②③计算)(k K、)(ˆkθ和)(k P；Step4 ：k→k+1，返回step2，继续循环。

系统辩识实验报告

一、实验目的1. 理解系统辨识的基本概念和原理。

2. 掌握递推最小二乘算法在系统辨识中的应用。

3. 通过实验，验证算法的有效性，并分析参数估计误差。

二、实验原理系统辨识是利用系统输入输出数据，对系统模型进行估计和识别的过程。

在本实验中，我们采用递推最小二乘算法对系统进行辨识。

递推最小二乘算法是一种参数估计方法，其基本思想是利用当前观测值对系统参数进行修正，使参数估计值与实际值之间的误差最小。

递推最小二乘算法具有计算简单、收敛速度快等优点。

三、实验设备1. 电脑一台，装有MATLAB软件。

2. 系统辨识实验模块。

四、实验步骤1. 打开MATLAB软件，运行系统辨识实验模块。

2. 在模块中输入已知的系数a1、a2、b1、b2。

3. 生成输入序列u（t）和噪声序列v（t）。

4. 将输入序列u（t）和噪声序列v（t）加入系统，产生输出序列y（t）。

5. 利用递推最小二乘算法对系统参数进行辨识。

6. 将得到的参数估计值代入公式计算参数估计误差。

7. 仿真出参数估计误差随时间的变化曲线。

五、实验结果与分析1. 实验结果根据实验步骤，我们得到了参数估计值和参数估计误差随时间的变化曲线。

2. 结果分析（1）参数估计值：通过递推最小二乘算法，我们得到了系统参数的估计值。

这些估计值与实际参数存在一定的误差，这是由于噪声和系统模型的不确定性所导致的。

（2）参数估计误差：从参数估计误差随时间的变化曲线可以看出，递推最小二乘算法在短时间内就能使参数估计误差达到较低水平。

这说明递推最小二乘算法具有较好的收敛性能。

（3）参数估计误差曲线：在实验过程中，我们发现参数估计误差曲线在初期变化较快，随后逐渐趋于平稳。

这表明系统辨识过程在初期具有较高的灵敏度，但随着时间的推移，参数估计误差逐渐减小，系统辨识过程逐渐稳定。

六、实验结论1. 递推最小二乘算法在系统辨识中具有较好的收敛性能，能够快速、准确地估计系统参数。

2. 实验结果表明，递推最小二乘算法能够有效减小参数估计误差，提高系统辨识精度。

递推最小二乘法参数估计matlab程序

递推增广最小二乘法Matlab 程序与仿真设被控对象差分方程形式为：y (k )−1.5y (k −1)+0.7y (k −2)=u (k −3)+0.5u (k −4)+ξ(k )−ξ(k −1)+0.2ξ(k −2)式中，为方差为1的白噪声。

取初值6ˆ(0)10(0)0P I θ==、。

选择方差为1的白噪声作为输入信号u (k ),采用RELS 算法进行参数估计，算法编程详见附录程序，仿真结果如图所示。

(a)参数a 估计结果 (b)参数b 估计结果(c)参数c 估计结果图4-1 递推增广最小二乘法参数估计结果Matlab 程序：%程序：递推增广最小二乘参数估计（RELS ）clear all; close all;a=[1 -1.5 0.7]'; b=[1 0.5]'; c=[1 -1 0.2]'; d=3; %对象参数na=length(a)-1; nb=length(b)-1; nc=length(c)-1; %na 、nb 、nc 为A 、B 、C 阶次L=1000; %仿真长度uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i)yk=zeros(na,1); %输出初值()kξxik=zeros(nc,1); %噪声初值xiek=zeros(nc,1); %噪声估计初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列theta=[a(2:na+1);b;c(2:nc+1)]; %对象参数thetae_1=zeros(na+nb+1+nc,1); %na+nb+1+nc为辨识参数个数P=10^6*eye(na+nb+1+nc);for k=1:Lphi=[-yk;uk(d:d+nb);xik];y(k)=phi'*theta+xi(k); %采集输出数据phie=[-yk;uk(d:d+nb);xiek]; %组建phie%递推增广最小二乘法K=P*phie/(1+phie'*P*phie);thetae(:,k)=thetae_1+K*(y(k)-phie'*thetae_1);P=(eye(na+nb+1+nc)-K*phie')*P;xie=y(k)-phie'*thetae(:,k); %白噪声的估计值%更新数据thetae_1=thetae(:,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);for i=nc:-1:2xik(i)=xik(i-1);xiek(i)=xiek(i-1);endxik(1)=xi(k);xiek(1)=xie;endfigure(1)plot([1:L],thetae(1:na,:));xlabel('k'); ylabel('参数估计a');legend('a_1','a_2'); axis([0 L -2 2]);figure(2)plot([1:L],thetae(na+1:na+nb+1,:)); xlabel('k'); ylabel('参数估计b');legend('b_0','b_1'); axis([0 L 0 1.5]); figure(3)plot([1:L],thetae(na+nb+2:na+nb+nc+1,:)); xlabel('k'); ylabel('参数估计c');legend('c_1','c_2'); axis([0 L -2 2]);。