第九章统计热力学小结
07_统计热力学基础小结

核的总配分函数等于各原子的核配分函数的乘积。 q n ,total = (2s n + 1)(2 s n '+1)(2 s n "+1)... = ∏ (2 s n + 1) i
i
仅在此种近似下,核配分函数才与温度 T 无关,此时有: H n = U n = CV (n) = 0 p = -(∂An/∂V)T,n=0 An = − NkT ln qn ∂A S n = − n = Nk ln q n ∂T V , N Gn = − NkT ln qn = An 分子全配分函数 q = q t ⋅ q r ⋅ qV ⋅ qe ⋅ q n 化学反应体系的公共能量标度 按公共能量标度, q ' = ∑ g i e −(ε 0 +εi ) / kT =e −ε 0 / kT ∑ g i e −ε i / kT = e −ε 0 / kT ⋅ q 能量标度的改变只对具能量单位的量 U、H、F、G 有影响,即多一项 U0 例如:对非定位系 A = − kT ln qN + U0 N!
1
二.波尔兹曼能量分布式 N i* = N gi e − εi / kT ∑ gi e−εi /kT
i
最可几分布时 i 能级上的粒子数 e −ε i / kT 称波尔兹曼因子
Ni g e − ε i / kT = i − ε i / kT N ∑ gie
i
i 能级上的粒子数占总粒子数之比,也称能级分布数
同左
同左
CV =
∂ ln q p = NkT ∂V T , N
同左
对来自第一定律的函数(H、U、CV、p)表达式相同 对来自第二定律的函数(S、A、G)表达式不同
(完整word版)统计热力学--小结与习题

第9章统计热力学初步小结与练习核心内容:配分函数(q )及其与热力学函数(U,S …)之间的关系 主要内容:各种运动形式的q 及由q 求U,S …的计算公式 一、内容提要1微观粒子的运动形式和能级公式式中,;:粒子的总能量,;t :粒子整体的平动能,;r :转动能, 振动能,;e:电子运动能,;n:核运动能。
(1) 三维平动子,2 2 22 J(八与 c式中,h :普朗克常数;m :粒子的质量;a , b , c :容器的三个 边长,n x , n y , n z 分别为x , y , z 轴方向的平动量子数,取值1, 2, 3……。
对立方容器(2) 刚性转子8m a 2 bh 2 28mV 32 2 2、(n x f +n z )基态 n x = 1, n y = 1, n z = 1,简并度久。
二1,而其他能级的简并度要具体情况具体分析,如26h %的能级,其简并度g = 3。
8mV双原子分子 h2rj (J 1)式中,J :转动量子数,取值0,1, 2……,I :转动惯量,I 一R 02, 分子的折合质量, 凹叱,R o :分子的平衡键长,能级.的mn +m 2简并度g r = 2J+1 (3) —维谐振子;v=( )h 、式中,“分子的振动频率,::振动量子数,取值0, 1, 2……, 各能级都是非简并的,g, = 1 对三维谐振子, ;v = ( x 「y 「z ■ 3)h \gv =(S 1)(s 2)2,其中 s= x + y + - z(4) 运动自由度:描述粒子的空间位置所必须的独立坐标的数目。
2、能级分布的微态数和 Boltzmann 分布(1)能级分布的微态数能级分布:N 个粒子分布在各个能级上的粒子数,叫做能级 分布数,每一套能级分布数称为一种分布。
微态数:实现一种分布的方式数。
n ;定域子系统能级分布微态数g niW D = N
值的推导
S kN ln
e
e
i
k U
U T
1 kT
S k N ln
i / kT
A U TS
所以
A N k T ln
i
e
i / kT
这就是定位体系的熵和Helmholtz自由能的 计算公式
27
Boltzmann 公式的讨论
7
统计体系的分类
目前,统计主要有三种:
一种是Maxwell-Boltzmann统计,通常称为 Boltzmann统计。 1900年Planck提出了量子论,引入了能量 量子化的概念,发展成为初期的量子统计。 在这时期中,Boltzmann有很多贡献,开始 是用经典的统计方法,而后来又有发展,加以改 进,形成了目前的Boltzmann统计。
10
统计体系的分类
非定位体系(non-localized system) 非定位体系又称为离域子体系,基本粒子之
间不可区分。例如,气体的分子,总是处于混乱
运动之中,彼此无法分辨,所以气体是非定位体
系,它的微观状态数在粒子数相同的情况下要比
定位体系少得多。
11
统计体系的分类
根据统计单位之间有无相互作用,又可把统
化学原理第九章
统计热力学简介
1
主线
S k ln
Ω
i i
A U TS
ti
G, H ,C p
NiN N i i U
等同性修正 非定位体系
S
ln Ω ln t m
t N!
i
N i!
tm
热力学与统计物理第九章答案

热力学与统计物理第九章答案【篇一:热力学统计物理课后答案12】=txt>2.2 设一物质的物态方程具有以下形式:p?f(v)t,试证明其内能与体积无关.解:根据题设,物质的物态方程具有以下形式:故有??p????f(v). (2) ??t?v??u???p??t?????p, (3) ??v?t??t?vp?f(v)t,(1)但根据式(2.2.7),有所以??u????tf(v)?p?0. (4) ?v??t这就是说,如果物质具有形式为(1)的物态方程,则物质的内能与体积无关,只是温度t的函数.2.3 求证: (a)???0; (b??p?h解:焓的全微分为令dh?0,得内能的全微分为令du?0,得p??s???0. (4) ????v?utdu?tds?pdv. (3) ??s?v???0. (2) ???pt??h??s???s?)?????v?u0.dh?tds?vdp. (1)2.6 试证明在相同的压强降落下,气体在准静态绝热膨胀中的温度降落大于在节流过程中的温度降落.解:气体在准静态绝热膨胀过程和节流过程中的温度降落分别由偏导数???t???t?和???描述. 熵函数s(t,p)的全微分为 ?p?p??s??h??s???s?ds??dt???dp. ???t?p??p?t在可逆绝热过程中ds?0,故有??s???v?t???p????t??t?p???t?. (1) ?????s?pc????sp????t?p最后一步用了麦氏关系式(2.2.4)和式(2.2.8).焓h(t,p)的全微分为??h???h?dh??dt???dp. ???t?p??p?t在节流过程中dh?0,故有??h???v?t???p???v??t??t??t???p. (2) ?????h?pc????hp????t?p最后一步用了式(2.2.10)和式(1.6.6). 将式(1)和式(2)相减,得??t???t?v???0.(3) ??????p?s??p?hcp所以在相同的压强降落下,气体在绝热膨胀中的温度降落大于节流过程中的温度降落. 这两个过程都被用来冷却和液化气体.由于绝热膨胀过程中使用的膨胀机有移动的部分,低温下移动部分的润滑技术是十分困难的问题,实际上节流过程更为常用. 但是用节流过程降温,气体的初温必须低于反转温度. 卡皮查(1934年)将绝热膨胀和节流过程结合起来,先用绝热膨胀过程使氦降温到反转温度以下,再用节流过程将氦液化.2.9 证明范氏气体的定容热容量只是温度t的函数,与比体积无关.解:根据习题2.8式(2)??2p???cv????t?2?, (1) ?v??t??t?v范氏方程(式(1.3.12))可以表为nrtn2ap??. (2) v?nbv2由于在v不变时范氏方程的p是t的线性函数,所以范氏气体的定容热容量只是t的函数,与比体积无关.不仅如此,根据2.8题式(3)??2p?cv(t,v)?cv(t,v0)?t??2?dv, (3) v0?t??vv我们知道,v??时范氏气体趋于理想气体. 令上式的v0??,式中的cv(t,v0)就是理想气体的热容量. 由此可知,范氏气体和理想气体的定容热容量是相同的.顺便提及,在压强不变时范氏方程的体积v与温度t不呈线性关系. 根据2.8题式(5)2??cv???p?????2?, (2) ??v?t??t?v这意味着范氏气体的定压热容量是t,p的函数.2.16 试讨论以平衡辐射为工作物质的卡诺循环,计算其效率. 解:根据式(2.6.1)和(2.6.3),平衡辐射的压强可表为1p?at4, (1) 3因此对于平衡辐射等温过程也是等压过程. 式(2.6.5)给出了平衡辐射在可逆绝热过程(等熵过程)中温度t与体积v的关系t3v?c(常量).(2)将式(1)与式(2)联立,消去温度t,可得平衡辐射在可逆绝热过程中压强p与体积v的关系pv?c?(常量).(3)43下图是平衡辐射可逆卡诺循环的p?v图,其中等温线和绝热线的方程分别为式(1)和式(3).下图是相应的t?s图. 计算效率时应用t?s图更为方便.在由状态a等温(温度为t1)膨胀至状态b的过程中,平衡辐射吸收的热量为出的热量为循环过程的效率为q2?t2?s2?s1?.(5) q1?t1?s2?s1?. (4)在由状态c等温(温度为t2)压缩为状态d的过程中,平衡辐射放t2?s2?s1?q2t??1??1??1?2. (6)q1t1s2?s1t12.19 已知顺磁物质遵从居里定律:m?ch(居里定律). t若维物质的温度不变,使磁场由0增至h,求磁化热.解:式(1.14.3)给出,系统在可逆等温过程中吸收的热量q与其在过程中的熵增加值?s满足q?t?s. (1)在可逆等温过程中磁介质的熵随磁场的变化率为(式(2.7.7)) ??s???m???0????.(2) ?h?t??t??hcvh?c是常量?, (3) t如果磁介质遵从居里定律易知所以cv?0h??s???.(5) ??2?ht??thm?cv??m???h, (4) ??2t??t?h在可逆等温过程中磁场由0增至h时,磁介质的熵变为吸收的热量为补充题1 温度维持为25?c,压强在0至1000pn之间,测得水的实验数据如下:??v??3?63?1?1????4.5?10?1.4?10p?cm?mol?k. ??t?p?s??cv?0h2??s?(6) ??dh??2?h2t??tcv?0h2q?t?s??. (7)2t【篇二:热力学统计物理课后习题答案】t>8.4求弱简并理想费米(玻色)气体的压强公式.解:理想费米(玻色)气体的巨配分函数满足ln?????lln1?e?????ll??在弱简并情况下:2?v2?v3/23/22ln???g3?2m???1/2ln1?e?????ld???g3?2m???d?3/2ln1?e??? ??l30hh0????????2?v3/22?3/2??g3?2m????ln1?e?????l3?h?????0?3/2dln1?e???????l???? ?2?vd?3/22 ??g3?2m????3/2????l30he?1与(8.2.4)式比较,可知ln??再由(8.2.8)式,得3/23/2??1n?h2??1?h2?????????nkt?1??ln???nkt?1?????v2?mkt??2?mkt?????42???42???2?u 3?e??n?h2?????v?2?mkt??3/2?3/2h2???n????? ????e?????v?t?2?mkt??n?n v3/23/2??1?n?h2????n?n?h2?????????p?ln??kt?1???nkt?1???????v2?mkt?t2?mkt?t???? ???42????42??8.10试根据热力学公式 s?熵。
第9章统计热力学初步

上一内容 下一内容 回主目录
返回
2021/2/9
9.1 粒子各运动形式的能级及能级的简并度
(5)简并度(统计权重,Degeneration):某一能级所 对应的所有不同的量子状态 (简称量子态) 的数目。以符 号 g 表示。
能级,量子状态及简并度的关系:
一个能级相当于一个楼层,简并度相当于该楼层的房间 数目,一个粒子只要处于同一楼层,无论哪个房间,能量都 相等,但由于处于不同房间,因此处于不同的量子状态.
f转振3n3
例:单原子分子 双原子分子
n1 fr 0 fv 0 n2 fr 2 fv 1
线型多原子分子 nnfr 2 fv 3n5 非线型多原子分子 nn fr 3 fv 3n6
C2(O 3,2,4)、 N3(H 3,3,6) CH4(3,3,9)
上一内容 下一内容 回主目录
返回
2021/2/9
2
定域子系统
gv 1
根据
εv
υ 1hν 2
可能的能级:
v,0
1 2
h
v,1
3 2
h
v,2
5 2
h
v,3
7 2
h
上一内容 下一内容 回主目录
返回
2021/2/9
9.2 能级分布的微态数及系统的总微态数
v,0
1 2
hv
v,1
3 2
hv
v,2
5 2
hv
v,3
7 2
hv
能级 能级分布数
分布 n0 n1 n2 n3
注意:三者的大小关系!
上一内容 下一内容 回主目录
返回
2021/2/9
9.2 能级分布的微态数及系统的总微态数
第9章 统计热力学
( N , U ,V ) : 为系统的一个状态函数
3、系统的总微态数()
能级分布 能级分布数 n0 0 2 ab ac bc 1 a a b b c c n1 3 0 n2 0 0 n3 0 1 c b a 等同粒子 微态数 (WD) 1 1
WD
D
可别粒子 微态数 (W D) 1 3
2、能级简并度(degeneration)
h2 2 2 2 n x n y nz (nx,n y ,nz 1,2, ) ε t 2/3 8mV
举例
nx
2 y 2 z
ny
nz
n n n 14
2 x
这时同一能级下有6种不 同的微观状态,则 gi = 6。
3、刚性转子
i
独立子系统是本 章主要研究对象
•相依子系统(assembly of interacting particles): 系统中粒子之间的相互作用不能忽略:
U
n
i i
i
U (位能)
3、统计热力学基本概念
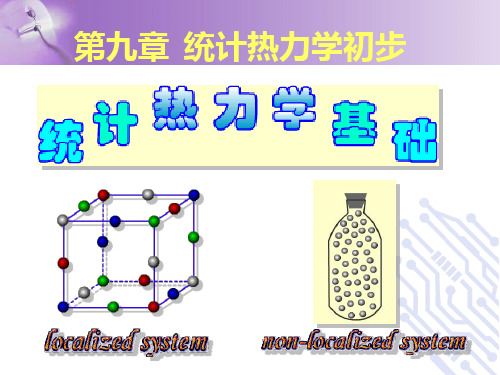
系统按粒子运动情况分类: •定域子系统 •离域子系统
(可辨粒子系统)
(全同粒子系统)
本章主要内容
h2 n x2 n y2 nz2 (nx,n y ,nRTz ln( J1/,K2,) ) ε t 2/3 8mV h2 r J ( J 1) 2 J 0,2, gr (2 J 1) 1, 8 I
0 P
2、能级分布与状态分布
Δ G G Δ 1 RT ln J v h ( 0,2, ) 1, 2
2、统计热力学与经典热力学的异同
• 研究对象相同:
大量粒子构成的宏观平衡系统。 • 研究方法不同: 经典热力学:三大实验定律 统计热力学:粒子微观结构与运动、力学规律、 统计方法等。
第9章_统计热力学初步-wfz-1

§9.2 能级分布的微观状态数及系统的总微态数
1. 能级分布
平衡系统中, 粒子各能级的能量值只与粒子的性质及 V有关,所 以平衡系统中各能级的能量也完全确定
任何一种能级分布均应服从 粒子数及能量守恒关系:
ì U = ï ï ï í ï N = ni
å
i
由于粒子的不停运动并彼此交换 能量 , 使 N 、 U 、 V 确定的系统并非 只有一种能级分布。
h2 et = 8m
2 骣 2 2 ny nx nz 琪 琪 + + 琪 2 2 琪 a b c2 桫
(n x , n y , n z
势箱边长
= 1, 2, L
量子数
)
m 为分子质量 a、b、c 为容器边长 h 为Planck常数
yn
x ,n y ,n z
对应于量子数
n x , n y , n z的量子态
3
量子态: 系统中粒子所处的各种不同的微观状态. 能级: 粒子能量相同的一组量子态组成一个能级.不同能级的 能量 i值是不连续的, 即量子化的. 在一定宏观状态的独立子系统中, 系统的总粒子数N 和总能量U 是不变的, 若处于能级i的粒子数目为 ni ,必然有 N ni U ni i
11.622
10-
40
J
e t, 1 - e t, 0 = (11.622 - 5.811 )? 10-
40
J
5.811
10-
40
J
由以上计算知:平动子相邻能级的能量差Δ 非常小,所以平动子 很容易受激发而处于各能级。在常温下,平动子的量子化效应不突出, 可近似用经典力学方法处理。
10
2. 分子转动 双原子分子可近似看作原子间距 d 保持不变的刚性转子 . 转子的转动惯量 I :
01热力学与统计物理大总结范文

01热力学与统计物理大总结范文热力学与统计物理总复习一、填空题1、理想气体满足的条件:①玻意耳定律温度不变时,PVC②焦耳定律理想气体温标的定义PT在相同的温度和压强下③阿伏伽德罗定律,相等体积所含各种气体的物质的量相等,即nV11等于kT,即:a某i2kT222、能量均分定理:对于处在温度为T的平衡状态的经典系统,粒子能量中每一个平方项的平均值广义能量均分定理:某i某jijkT3、吉布斯相律:fk2其中k是组元数量,是相的数量。
4、相空间是2Nr维空间,研究的是:一个系统里的N个粒子;空间是2r维空间,研究的是:1个粒子二、简答题1、特性函数的定义。
答:适当选择独立变量,只要知道一个热力学函数,就可以通过求偏导数而求得均匀系统的全部热力学函数,从而把均匀系统的平衡性质完全确定。
这个热力学函数即称为特性函数。
2、相空间的概念。
答:为了形象地描述粒子的力学运动状态,用q1,,qr;p1,,pr共2r 个变量为直角坐标,构成一个2r维空间,称为空间。
根据经典力学,系统在任一时刻的微观运动状态由f个广义坐标q1,q2,,qf及与其共轭的f个广义动量p1,p2,,pf在该时刻的数值确定。
以q1,,qf;p1,,pf共2f个变量为直角坐标构成一个2f维空间,称为相空间或空间。
3、写出热力学三大定律的表达和公式,分别引出了什么概念?答:热力学第零定律:如果物体A和物体B各自与处在同一状态的物体C达到热平衡,若令A与B-1-进行热接触,它们也将处在热平衡,这个经验事实称为热平衡定律。
即gA(PA,VA)gB(PB,VB),并引出了“温度T”这概念。
热力学第一定律:自然界一切物质都具有能量,能量有各种不同形式,可以从一种形式转化为另一种形式,从一个物体传递到另一个物体,在传递与转化中能量的数量不变。
即dUdQdW,并引出了“内能U”的概念。
热力学第二定律:克氏表述:不可能把热量从低温物体传到高温物体而不引起其他变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∏ ∏ ∏ WD =
N! × ni ! i
g ni i
=
N!
i
g ni i
ni!
i
∏ ∏ WD =
i
(ni + gi − 1)! ≈ ni !×( gi − 1)!
i
g ni i
ni !
(3)系统的总微态数
Ω = ∑WD
D
3. 玻尔兹曼分布
nj
=
N q
e −ε j / kT ;
ni
=
N q
gi e −εi / kT
qv0
=
1 1− e−hν
/ kT
qe = ge,0e−ε e,0 / kT qe0 = eε e,0 / kT qe = ge,0 = 常数
qn = gn,0e −ε n,0 / kT qn0 = eε n,0 / kT qn = gn,0 = 常数
7
7. 热力学函数的计算 (1)热力学能
U0
=
/
2
U
0 r
=
NkT
U
0 v
=
NkΘ
v
1 eΘ v /T
−1
8
(2)摩尔定容热容
CV ,m
=
∂ ∂T
⎡ ⎢ RT ⎢⎣
2 ⎜⎛ ⎜⎝
∂
ln q 0 ∂T
⎟⎞ ⎟⎠V
⎤ ⎥ ⎥⎦V
CV ,t
=
3 2
R
C V ,r = R
CV ,v
=
R⎜⎛ Θ v
⎝T
⎟⎞ 2 eΘ ⎠
v /T (eΘ
v /T
− 1)−2
NkT
2
⎜⎜⎝⎛
∂
ln q ∂T
0
⎟⎞ ⎟⎠V
=
U
0 t
+
U
0 r
+
U
0 v
+
Ue0
+
Un0
U 0 = U − Nε 0 = U − U0.
U
0 t
≈
Ut
;
U
0 r=Ur; NhomakorabeaU
0 v
=
Uv
−
Nh ν
2
U
0 e
=
0;
U
0 n
=
0.
(电子和核运动处于基态 )
U
0 t
=
3 NkT
/2
或
U
0 t,
m
=
3 RT
利用配分函数的析因子性质,将配分函数分解为独立 的平动、转动、振动、电子运动及核运动的配分函数。对 平动、转动和振动分别应用势箱中粒子、刚性转子及谐振 子模型加以处理,得到了配分函数与分子的转动惯量、分 子振动基频的关系式,使得应用分子光谱数据直接计算粒 子配分函数,从而计算系统热力学性质成为可能。
HmΘ ,T − U0,m T
=
RT⎜⎜⎝⎛
∂
ln q0 ∂T
⎟⎞ ⎟⎠V
+
R
(3)理想气体反应的标准平衡常数
− ln
KΘ
=
1 R
Δr ⎜⎜⎝⎛ GmΘ
− U0,m T
⎟⎟⎠⎞ +
1 RT
Δ rU 0,m
Δ rU 0,m
=
Δ
r
H
Θ
m,298K
−
Δ
r
(
H
Θ
m,298K
− U0,m )
∑ =
Δ
r
H
Θ
m,298K
+
RΘ v
(eΘ v / T − 1)T
8. 玻耳兹曼熵定理
SS== kkllnnΩΩ
摘取最大项原理
llnnWWBB≈≈llnnΩΩ
9. 理想气体反应的标准平衡常数
(1)理想气体的标准摩尔吉布斯自由能函数
G
Θ
m
,T
− U 0,m
T
=
−
R
ln ⎜⎜⎝⎛
q0 N
⎟⎞ ⎟⎠
10
(2)理想气体的标准摩尔焓函数
4
4. 粒子的配分函数 (1)定义式
∑ q def e −ε j / kT ;
j
q ∑ def
gi e −ε i / kT
i
(2)析因子性质
qq== qqttqqrrqqvvqqeeqqnn
(3)能量零点的选择对配分函数的影响
qt0 = qteε t,0 kT ≈ qt
qr0 = qreε r,0 kT = qr
−
ν
B
B
(
H
Θ
m,298K,B
−
U 0,m,B
)
11
2
1.粒子各种运动形式的能级及能级的简并度
(1) 分子的平动
εt
=
h2 8m
⎜⎛ ⎜⎝
nx2 a2
+
ny2 b2
+
nz 2 c2
⎟⎞ ⎟⎠
nx, ny, nz = 1, 2, 3, …,
(2)双原子分子的转动
εr
=
J(J
+ 1)
h2
8π 2 I
J = 0, 1, 2, …, gr ,J = 2J + 1
⎝ ∂V ⎠T
将上述公式中配分函数 q 乘以 e/N ,即可得到离域子系统 相应热力学函数与配分函数间的关系式。
6
6. 粒子配分函数的计算
qt
=
qt,x qt, y qt,z
=
⎜⎛ ⎝
2πmkT
h2
⎟⎞ 3 / 2V ⎠
qr
=
T
σΘ r
=
8π 2IkT σ h2
qv
=
e hν / 2kT
1 − e−hν / 2kT
(3)双原子分子的振动
(4)电子及核运动
εv
=
(υ
+
1 )hν
2
υ = 0, 1, 2, …,
gv,v = 1
电电子子运运动动基基态态简简并并度度ggee,0,0==常常数数
核核运运动动基基态态简简并并度度ggnn,0,0==常常数数
3
2. 能级分布的微观状态数及系统的总微态数
(1) 定域子系统 (2)离域子系统
(为温度的函数 )
(3)统计熵 SS==SStt++SSrr ++SSvv
St, m
=
R⎜⎜⎝⎛
3 ln 2
M kg ⋅ mol −1
+
5 2
ln
T K
−
ln
p Pa
+
20.723 ⎟⎟⎠⎞
9
Sr, m = R ln(T / σΘ r ) + R
S v,m
=
1 R ln 1 − e −Θ v / T
第九章 统计热力学初步
本章总结
统计热力学的目标是为宏观系统的平衡性质提供分子理论或 解释。其出发点是等概率原理(假设),即对U,N,V 有确定值的 系统,系统的每一个微态出现的概率相同;或在足够长的时间内 系统处于每个微态的时间相同。
根据等概率原理,系统每个量子态出现的概率为 P =1/Ω, Ω 为系统总的微态数。借助于量子力学的概念,对独立子系
p = NkT ⎜⎛ ∂ ln q ⎟⎞ ⎝ ∂V ⎠T
S = N k lnq + U T
A = - N kT lnq
G = − NkT ln q + NkTV ⎜⎛ ∂ ln q ⎟⎞ ⎝ ∂V ⎠T
H = NkT 2 ⎜⎛ ∂ ln q ⎟⎞ + NkTV ⎜⎛ ∂ ln q ⎟⎞
⎝ ∂T ⎠V
q
0 v
=
qveε v,0
kT
= qvehν
2kT
qe0 = qeeε e,0 kT qn0 = qneε v,0 kT
(常温下 ε t,0 ≈ 0)
(ε r,0 = 0)
(ε
v,0
=
1 2
hν
)
5
5. 热力学函数与配分函数间的关系
定域子系统 U = NkT 2 ⎜⎛ ∂ ln q ⎟⎞ ⎝ ∂T ⎠V
统,通过能级分布计算系统能够达到的微态数,并由此得到系 统总的微态数。但由于宏观系统包含数量级达 1024 的粒子,要 求得系统所有的能级分布是不可能的也是不必要的:因为能使 系统具有最多微态的能级分布实际代表了系统总的微态分布。
1
应用拉格朗日待定乘数法确定了上述能级分布,并因 其出现的的概率最大,故称为最概然分布(又称平衡分布、 玻耳兹曼分布);在最概然分布中引出了粒子配分函数的概 念。系统平衡热力学性质均可用配分函数或配分函数的导 数表示,因此配分函数起到了联系系统宏观性质与微观性 质的桥梁作用。
