重力势能曲线引力势能曲线弹性势能曲线

合集下载

大学物理功-动能定理-保守力的功

解：抛体在重力场中运动，
m g 是一恒量，
y
但m 的轨迹是一抛物线，取一元位移d r
dr b
a
m g 与位移的夹角θ时时在变在这一元段内写出元功
mg
x
dA Fdrmgdr
m gdscosmgdy
b
b
b
A
Fdr
a
Fcosds mg
a
a
dy
m g(ybya) 9
解：(1)建坐标系如图
l-a O
fμ m(lg x)/l l l μmg
A f afdra l (lx)dx μm(g lx)2l μm(g la)2
a x
2l
a 2l
注意：摩擦力作负功！ 21
(2)对链条应用动能定理：
l-x O
A＝ AP＋ Af 1 2m2v 1 2m0 2v
x
v0
0AP＋ Af
1m2v 2
x
A Pa lp d r a lm l x gd m x(l2 2 g l a 2 )
前已得出： Af
μm (gl a)2
2l
m(lg 2a2)μ m(lg a)21m2v
2l
2l
2
得 v
g l
1
(l2 a 2)μ (l a )22
13
3） A为合外力作功的代数和，不是合外力中某一个力的功。动能定理中的速度必须相对同一个惯性系。
4）通过作功，质点与外界进行能量交换。如果外力对物体做正功，质点动能增加；如果外力对物体做负功，质点的动能减少，
即物体克服外力作功，是以减少自身的动能为代价。
所以，动能是物体因运动而具有的作功的本领。

大学物理第三章动量守恒定律和能量守恒定律 3-5 保守力与非保守力

①引力势能引力势能
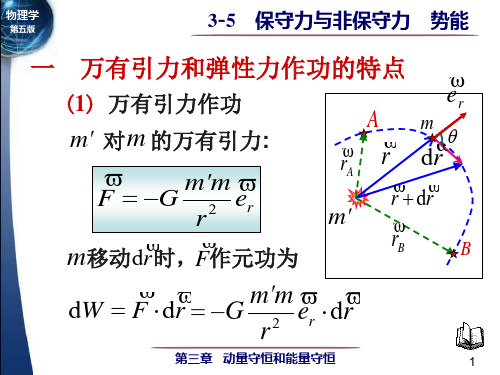
m' m m' m 引力的功引力的功 WAB = −(−G r ) − (−G r ) B A
A点势能：点势能：且令E 设B点为无限远即rB=∞ 且令 PB=0 点为无限远
m' m WAB = −G rA
= − ( E pB − E pA ) = E pA
功与路径无关，只决定于初末位置。功与路径无关，只决定于初末位置。第三章动量守恒和能量守恒
4
} ⇒ dW
物理学
第五版
3-5 保守力与非保守力势能 -
F
dW
O
x1
x2
dx
x2 x
W = ∫ Fdx = ∫
x1
x2
x1
1 2 1 2 − kxdx = −( kx2 − kx1 ) 2 2
5
第三章动量守恒和能量守恒
W p → p0 = −( Ep0 − Ep ) = −∆Ep
E p ( x, y, z) =
∫
E p0 = 0
( x, y,z )
F ⋅ dr
任意一点的势能等于在保守力作用下从该点到势能零点保守力所作的功
第三章动量守恒和能量守恒 10
物理学
第五版
3-5 保守力与非保守力势能 -
W AB = − ( E pB − E pA ) = − ∆ E P
引力的功引力的功
m' m m' m WAB = −(−G ) − (−G ) rB rA
引力势能引力势能
m' m Ep = −G r
弹性势能弹性势能
弹力的功弹力的功
W AB 1 1 2 2 = − ( kx B − kx A ) 2 2

大学物理-保守力与非保守力

第三章动量守恒和能量守恒
4/12
物理学
第五版
3-5 保守力与非保守力势能 2 保守力作功的数学表达式
∫
(The mathematical expression of work by the conservative force)
ACB
F ⋅ dr = ∫
F ⋅ dr =
ADB
F ⋅ dr
∫
BDA
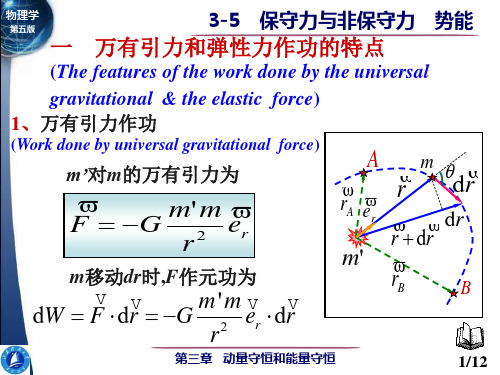
m 从 A 到 B 的过程中作功：的过程中F作功作功：
A mθ m'm W = ∫ F ⋅ dr = ∫ − G 2 er ⋅ dr dr r A r rA e r dr er ⋅ dr = er ⋅ dr cos θ = dr r + dr
B
rB m'm B W = ∫ − G 2 dr rA r 1 1 m'm W = Gm′m( − ) W = −G dr = 0 2 rB rA l r
Elastic potential energy
m' m Ep = −G r
1 E p = kx 2 2
6/12
第三章动量守恒和能量守恒
物理学
第五版
3-5 保守力与非保守力势能物体在地球表面附近距地面高为y时具有的引力物体在地球表面附近距地面高为时,具有的引力势能称为重力势能重力势能(Gravity potenial) Ep = −mgy 重力势能保守力的功(Work of conservative force) 保守力的功
第三章动量守恒和能量守恒
z = 0, Ep = 0
11/12
物理学
第五版
本章目录
选择进入下一节：选择进入下一节：

SCUT-3_5保守力与非保守力

ex in
m1
v ex Fi
外力功
内力功
v in m i m2 Fi
对质点系，有对质点系，
∑W
i
ex
i
+ ∑Wi = ∑ Eki − ∑ Eki 0 = Ek − Ek 0
in i i i
质点系动能定理质点系动能定理
W
ex
+W
in
= Ek − Ek0
第三章三大守恒定律
值得注意：
内力做功可以改变系统的总动能。内力做功可以改变系统的总动能。
第三章三大守恒定律
3.5 势能功能原理机械能守恒万有引力、重力、一万有引力、重力、弹性力作功的特点 1）万有引力作功
v m 为参考系，以 m' 为参考系，的位置矢量为 r . m' 对 m 的万有引力为
v m' m v F = −G 3 r r v
作功为
m
m'
O
A
v v dr r (t)
m' m Ep = −G r
Ep
O
Ep
x
O
z
O
x
弹性势能曲线弹性势能曲线引力势能曲线引力势能曲线
重力势能曲线重力势能曲线
z = 0, Ep = 0
x = 0, Ep = 0
r → ∞, Ep = 0
第三章三大守恒定律
三质点系的动能定理个质点，对第 i 个质点，有
Wi + Wi = E ki − E ki 0
第三章三大守恒定律
有一轻弹簧, 例 8 有一轻弹簧其一端系在铅直放置的圆环的顶点P, 另一端系一质量为m 的小球, 顶点另一端系一质量为的小球小球穿过圆环并在圆环上运动(不计摩擦开始小球静止于点不计摩擦) 在圆环上运动不计摩擦 .开始小球静止于点 A, 弹簧处于自然状态,其长度为圆环半径当小球运动到圆环处于自然状态其长度为圆环半径R; 其长度为圆环半径的底端点B时小球对圆环没有压力求弹簧的劲度系数. 小球对圆环没有压力. 的底端点时,小球对圆环没有压力求弹簧的劲度系数解以弹簧、小球和地球为一系统，以弹簧、小球和地球为一系统，

重力势能和弹性势能(A级)

重力势能和弹性势能考试要求内容基本要求略高要求较高要求重力势能理解重力势能的概念会用重力势能的定义进行计算重力做功与重力势能改变的关系弹性势能理解弹性势能的概念计算变力做功框架知识点1 重力势能定义：物体由于被举高而具有的能叫做重力势能．对于重力势能，其大小由地球和地面上物体的相对位置决定．物体质量越大、位置越高、做功本领越大，物体具有的重力势能就越多．公式：重力势能的公式：E p=mgh（E p为重力势能，m为质量，g为重力系数，等于9.8N/kg）物理学中，物体具有的重力势能的大小与物体的质量成正比，与物体被举高的高度成正比．所以得出E p=mgh．重力势能是标量，单位为焦（J）．与功不同的是，功的正负号表示作用效果，比较大小时仅比较数值；而重力势能中正数一律大于负数．在重力势能的表示式中，由于高度h是相对的，因此重力势能的数值也是相对的．我们说某个物体具有重力势能mgh，这是相对于某一个水平面来说的，把这个水平面的高度取做零，这个水平面称为参考平面，物体位于这个参考平面上时，重力势能为零，因此参考平面也称为零势能平面．经典物理对重力势能的理解就是当一个物体处在一个位置，相对于参照平面，重力可以对物体做多少功，使物体获得多少其他形式的能量，就说重力势能是多少．但并不是说重力势能为0就不具备做功的能力，这是由其的相对性决定的．重力做正功时，重力势能减小，反之，则增大．由于重力和万有引力是同性质的力，因此在物体的高度不能忽略时，将重力势能称作引力势能更合适些，也就是说，重力势能就是引力势能，在目前的考纲中，除专门讨论重力随物体在地球上的位置（纬度和高度）变化而变化外，认为重力等于万有引力，因此也可以认为物体的重力势能等于引力势能．如果考虑g是变量的话，那么重力势能就过渡到引力势能，引力势能表达式是GMmr，不过零势能处在无穷远．重力做功与重力势能的关系：W=E P1-E P2，规律：重力做正功时，重力势能减少重力做负功时，重力势能增加．知识点2 弹性势能定义：发生弹性形变的物体各部分之间，由于有弹力的相互作用而具有势能，这种势能就是叫做弹性势能势能的单位与功的单位是一致的．确定弹力势能的大小需选取零势能的状态，一般选取弹簧未发生任何形变，而处于自由状态的情况下其弹力势能为零．弹力对物体做功等于弹力势能增量的负值．即弹力所做的功只与弹簧在起始状态和终了状态的伸长量有关，而与弹簧形变过程无关．弹性势能是以弹力的存在为前提，所以弹性势能是发生弹性形变，各部分之间有弹性力作用的物体所具有的．如果两物体相互作用都发生形变，那么每一物体都有弹性势能，总弹性势能为二者之和．弹性势能的计算及公式在拉伸弹簧的过程中，弹簧弹力是随弹簧的形变量的变化而变化的，弹簧弹力还因弹簧的不同而不同．因此，弹簧弹力做功不能直接用功的公式W =Flcosα．与研究匀变速直线运动的位移方法类似，就是将弹簧的形变过程分成很多小段，每一小段中近似认为拉力是不变的．所以，每一小段的功分别为：W 1=F 1△l 1，W 2=F 2△l 2，W 3=F 3△l 3，……弹簧弹力在整个过程中所做的功为：W =W 1+W 2+W 3+……=F 1△l 1+F 2△l 2+F 3△l 3+……要直接计算上述各小段功的求和式是较困难的．与匀变速直线运动中利用v-t 图象求位移x 相似，我们可以画出F-l 图象，如图1所示．每段弹簧弹力的功就可用图中细窄的矩形面积表示，对这些矩形面积求和，就得到了由F 和l 围成的三角形的面积如图2所示，这块三角形面积就表示弹簧弹力在整个过程中所做的功．弹簧弹力在整个过程中所做的功为： W=221l k ∆ （其中，k 是弹簧的劲度系数，Δl 是弹簧的伸长量或压缩量）弹力做功与弹性势能变化的关系：弹力做正功，弹性势能减少，弹力做负功，弹性势能增加．o l F 图1o l F l ∆图2 kΔl例题【例1】如图所示，某物块分别沿三条不同的轨道由离地高h 的A 点滑到同一水平面上，轨道1、2是光滑的，轨道3是粗糙的，则（）A ．沿轨道1滑下重力做功多B ．沿轨道2滑下重力做功多C ．沿轨道3滑下重力做功多D ．沿三条轨道滑下重力做的功一样多【例2】物体1的重力势能E p 1=3J ，物体2的重力势能E p 2=－3J ，则（）A ．E p 1=E p 2B ．E p 1＞E p 2C ．E p 1＜E p 2D ．无法判断【例3】将同一物体分两次举高，每次举高的高度相同，则（）A ．不论选取什么参考平面，两种情况中，物体重力势能的增加量相同B ．不论选取什么参考平面，两种情况中，物体最后的重力势能相等C ．不同的参考平面，两种情况中．重力做功不等D ．不同的参考平面，两种情况中．重力最后的重力势能肯定不等【例4】下列说法中正确的是（）A ．物体克服重力做功，物体的重力势能增加B ．物体克服重力做功，物体的重力势能减少C ．重力对物体做正功，物体的重力势能增加D ．重力对物体做负功，物体的重力势能减少【例5】物体在运动过程中，克服重力做功50J ，则（）A ．物体的重力势能一定为50JB ．物体的重力势能一定增加50JC ．物体的重力势能一定减少50JD ．物体的重力势能可能不变【例6】下列叙述中，正确的是（）A ．做自由落体运动的物体，在第1s 内与第2s 内重力势能的减少量之比为1:3B ．做竖直上抛运动的物体，从抛出到返回到抛出点的过程中，重力对物体所做的功为零C ．物体做匀速直线运动时重力势能一定不变D ．在平衡力作用下运动的物体，重力势能一定改变【例7】一个质量为m 的物体，在吊绳拉力的作用下，沿竖直方向由静止开始以加速度a 匀速上升了t s ，则在这一过程中，该物体增加的重力势能为（）A ．2221t maB ．2221t mgC ．221mgatD ．()221at a g m + 【例8】关于重力势能的说法中不正确的是（）A ．物体重力势能的值随参考平面的选择不同而不同B ．物体的重力势能严格说是属于物体和地球这个系统的 3 1 2 A hC．重力对物体做正功，物体的动能一定增加D．物体位于参考面之下其重力势能取负值【例9】用起重机将质量为m的物体匀速地吊起一段距离，那么作用在物体上各力的做功情况应该是下面的哪种说法（）A．重力做正功，拉力做负功，合力做功为零B．重力做负功，拉力做正功，合力做正功C．重力做负功，拉力做正功，合力做功为零D．重力不做功，拉力做正功，合力做正功【例10】一质量为m的物体被人用手由静止竖直向上以加速度a匀加速提升h，关于此过程下列说法中不正确的是（）A．提升过程中手对物体做功m（a+g）hB．提升过程中合外力对物体做功mahC．提升过程中物体的动能增加m（a+g）hD．提升过程中物体克服重力做功mgh【例11】水塔是在空中的盛水容器，有两个注水口，一个在顶部，一个在底部，注满一水塔水，则（）A．从顶部注水做功多B．从底部注水做功少C．从两注水口注水一样多D．条件不足不能比较从上下注水做功多少AhBH【例12】井深8m，井上支架高2m，在支架上用一根长3m的绳子系住一个重100N的物体，若以地面为参考平面，则物体的重力势能有_____________；若以井底面为参考平面，则物体的重力势能是____________．【例13】质量为5kg的钢球，从离地15m高处自由下落1s，其重力势能变为_____________（g取10m/s2，取地面为参考平面）．【例14】一物体做自由落体运动．在第1s内和第2s内，重力对该物体做的功之比为________；在第1s 末和第2s末，重力做功的即时功率之比为________．【例15】如图所示，质量为m的小球从高为h的斜面的A点滚下经水平面BC后，再滚上另一斜面，当它到达h/3高度的D点时的速度为零，此过程中物体重力做的功是多少?【例16】一质量为1kg物体，位于离地面高1.5m处，比天花板低2.5m．以地面为零势能位置时，物体的重力势能等于________J；以天花板为零势能位置时，物体的重力势能等于_______J（g取10m/s2）．【例17】甲、乙两物体，质量大小关系为m甲=5m乙，从很高的同一高度处自由下落2s，重力做功之比为_____，对地面而言的重力势能之比为_______．【例18】关于弹性势能，以以下说法正确的是（）A．任何发生弹性形变的物体都具有弹性势能B．物体只要发生形变，就一定具有弹性势能C．外力对弹性物体做功，物体的弹性势能就发生变化D．弹簧的弹性势能只由弹簧的形变量决定【例19】关于弹力做功与弹性势能的说法正确的是（）A．弹力对物体所做的功等于物体所具有的弹性势能B．物体克服弹力所做的功等于物体所具有的弹性势能C．弹力对物体所做的功等于物体弹性势能的减少D．物体克服弹力所做的功等于物体弹性势能的增加【例20】弹簧的一端固定，原处于自然长度．现对弹簧的另一端施加一个拉力，关于拉力做功（或弹簧克服拉力做功）与弹性势能变化的关系，以下说法中正确的是（）A．拉力对弹簧做正功，弹簧的弹性势能增加B．拉力对弹簧做正功，弹簧的弹性势能减少C．弹簧克服拉力做功．弹簧的弹性势能增加D．弹簧克服拉力做功，弹簧的弹性势能减少【例21】如图所示，一弹簧竖直固定在地面上，一小球自弹簧正上方自由下落，从小球落上弹簧到弹簧压缩到最低点的过程中，小球的重力势能将______，弹簧的弹性势能将______．【例22】在光滑水平面上有两个小球，如图所示，假设它们之间存在着相互排斥的力，也具有一种势能，我们把它叫做x势能，当A小球不动，B小球在外力作用下向A靠近，试分析它们间的x势能将如何变化？【例23】一竖直弹簧下端固定于水平地面上，如图所示，小球从弹簧的正上方高为h的地方自由下落到弹簧上端，经几次反弹以后小球最终在弹簧上静止于某一点A处，则（）A．h愈大，弹簧在A点的压缩量愈大B．弹簧在A点的压缩量与h无关C．h愈大，最终小球静止在A点时弹簧的弹性势能愈大D．小球第一次到达A点时弹簧的弹性势能比最终小球静止在A点时弹簧的弹BA性势能大【例24】一个质量为m 的物体以某一速度从固定斜面底端冲上倾角α＝30°的斜面．已知该物体做匀减速运动的加速度为34g ，在斜面上上升的最大高度为h ，则此过程中（） A ．物体的动能增加32mgh B ．物体的重力做功mgh C ．物体的机械能损失了12mgh D ．物体克服摩擦力做功12mgh 【例25】如图，长为L 的细线拴一个质量为m 的小球悬挂于O 点，现将小球拉至与O 点等高的位置且线恰被拉直．求放手后小球摆到O 点正下方的过程中：（1）球的重力做的功；（2）线的拉力做的功；（3）外力对小球做的总功．【例26】起重机以4g 的加速度将质量为m 的物体匀减速地沿竖直方向提升高度h ，则起重机钢索的拉力对物体做的功为多少？物体克服重力做功为多少？物体的重力势能变化了多少．【例27】如图所示，一个质量为m 的木块，以初速度v 0冲上倾角为θ的固定斜面，沿斜面上升L 的距离后又返回运动．若木块与斜面间的动摩擦因数为μ，求：（1）木块上升过程克服重力做功的平均功率；木块的重力势能变化了多少？（2）木块从开始运动到返回到出发点的过程中，滑动摩擦力做的功是多少？（3）木块从开始运动到返回到出发点的过程中，重力做的功是多少？重力势能变化了多少？θ v 0O【例28】在空中将物体M以初速度v平抛，不计阻力，则t s末的重力的瞬时功率为多少?t s内重力的平均功率为多少?【例29】如图所示，一个质量为m、半径为r、体积为V的铁球，用一细线拴住，慢慢地放入截面积为S、深度为h的水中．已知水的密度为ρ，求铁球从刚与水面接触至与杯底接触的过程中，水与铁球的重力势能分别变化了多少？水与铁球组成的系统总的重力势能变化了多少？【例30】如图所示，劲度系数为k的轻质弹簧一端固定，另一端与物块拴接，物块放在光滑水平面上．现用外力缓慢拉动物块，若外力所做的功为W，则物块移动了多大的距离？F【例31】地面上竖直放置一根劲度系数为k，原长为L0的轻质弹簧，在其正上方有一质量为m的小球从h 高处自由落到下端固定于地面的轻弹簧上，弹簧被压缩，求小球速度最大时重力势能是多少？（以地面为参考平面）检测1、以下关于重力势能的说法中，正确的是（）A．地面上的物体的重力势能一定为零B．质量大的物体重力势能一定大C．高处物体的重力势能一定大D．重力做正功时，物体的重力势能一定变化2、关于重力势能，下列说法中正确的是（）A．物体的位置一旦确定，它的重力势能的大小也随之确定B．物体与零势面的距离越大，它的重力势能也越大C．一个物体的重力势能从﹣5J变化到﹣3J，重力势能变小了D．重力势能的减少量等于重力对物体做的功3、选择不同的水平面作参考平面，物体在某一位置的重力势能和某一过程中重力势能的改变量（）A．都具有不同的数值B．都具有相同的数值C．前者具有相同数值，后者具有不同数值D．前者具有不同数值，后者具有相同数值4、一实心的正方体铁块与一实心的正方体木块质量相等，将它们放在水平地面上，下列结论正确的（）A．铁块的重力势能大于木块的重力势能B．铁块的重力势能等于木块的重力势能C．铁块的重力势能小于木块的重力势能D．上述三种情况都有可能5、关于弹性势能，以下说法中正确的是（）A．发生弹性形变的物体一定具有弹性势能B．发生弹性形变的物体不一定具有弹性势能C．发生形变的物体一定具有弹性势能D．发生形变的物体不一定具有弹性势能6、在地面附近一个质量为5kg的物体，从零势面以上8m处下落到零势面以下2m处的过程中，重力势能的最大值是________J，重力做功是________J．（g=10m／s2）7、探究弹性势能的表达式的依据是弹簧增加的弹性势能等于_________________．8、简述我们在探究弹性势能的表达式过程中主要难点在哪里?我们如何克服这个难点?9、如图所示，表示撑杆跳运动的几个阶段：助跑、撑杆起跳、越横杆．试定性地说明在这几个阶段中能量的转化情况．作业1、关于重力势能的下列说法中正确的是（）A．重力势能的大小只由重物本身决定B．重力势能恒大于零C．在地面上的物体，它具有的重力势能一定等于零D．重力势能实际上是物体和地球所共有的2、关于重力势能的几种理解，正确的是（）A．重力势能等于零的物体，一定不会对别的物体做功B．放在地面上的物体，它的重力势能一定等于零C．在不同高度将某一物体抛出，落地时重力势能相等D．相对不同的参考平面，物体具有不同数值的重力势能，但并不影响研究有关重力势能的问题3、如图所示，桌面高为h，质量为m的小球从离桌面高H处自由落下，假设桌面处的重力势能为0，则小球落到地面前瞬间的重力势能为（）A．mgh B．mgHC．mg（h+H）D．-mgh4、如图所示一物体从A点沿粗糙面AB与光滑面AC分别滑到同一水平面上的B点与C点，则下列说法中正确的是（）A．沿AB面重力做功多B．沿两个面重力做的功相同C．沿AB面重力势能减少多D．沿两个面减少的重力势能相同5、关于弹性势能，下列说法中正确的是（）A．任何发生弹性形变的物体，都具有弹性势能B．任何具有弹性势能的物体，一定发生了弹性形变C．物体只要发生形变，就一定具有弹性势能D．弹簧的弹性势能只跟弹簧被拉伸或压缩的长度有关6、如图所示，一质量为m 的小球，用长为L 的轻绳悬挂于O 点．小球在水平力F 的作用下从最低点缓慢地移到图示位置，则此过程中力F 所做的功为多少？7、物体从斜面上高度为h 的地方，由静止释放沿斜面下滑又在水平面上运动到P 点停下来，用推力把物体推回到斜面上同一位置，推力做功至少为多少？Pm hFFO。

大学物理第二章动能定理

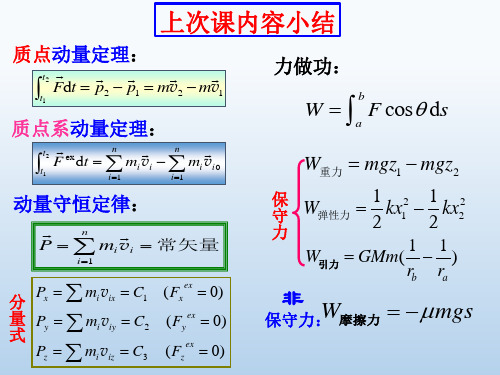
例题3. 如图，一轻绳跨过一定滑轮，两边分别拴有质量
为m及M的物体，M离地面的高度为h: (1)若滑轮质量及
摩擦力不计，m与桌面的摩擦也不计，开始时两物体均静
止，求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为，结果又如何？
解：
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理：
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得：
t2 t1
M外dt
L2
L1
注意：只有外力矩对质点系的角动量变化有贡献，
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d

机械能角动量守恒

探路者无人飞船俯视火星
探路者飞船在火星着陆点地貌
海盗号和凤凰号
碰撞两物体互相接触时间极短而互作用力较大的相互作用 .
ex in F F pi C
i
完全弹性碰撞两物体碰撞之后，它们的动能之和不变 .
Ek Ek1 Ek 2 C
非弹性碰撞由于非保守力的作用，两物体碰撞
例 2 设有两个质量分别为 m1 和 m2 , 速度分别为 v10 和 v20 的弹性小球作对心碰撞 , 两球的速度方向相同. 若碰撞是完全弹性的, 求碰撞后的速度 v1 和 v2 . 解取速度方向为正向，由动量守恒定律得碰前
m1v10 m2 v20 m1v1 m2 v2 m1 (v10 v1 ) m2 (v2 v20 )
土星五号火箭
美国的土星 5 号是人类历
史上使用过的最高、最重、
推力最强的运载火箭，高达110.6米，起飞重量 3038吨，总推力达3400吨左右，可将 127 吨的有效
载重送上近地轨道。
中国神州飞船
空间实验室（Space Laboratory）是一种可重复使用和多用途的载人航天科学实验空间站。前苏联、美国和欧洲航天局已于20世纪七八十年代率先研制成功出空间实验室。中国首个空间实验室的主体“天宫一号”已于2011年9月29日21时16 分在酒泉发射升空。
v1
1 1 1 2 2 2 m mv1 m mv2 K l l0 2 2 2
一、质点系角动量定理
质点系统所受外力矩之和等于系统总角动量的变化率。
t M 外dt dL 或： t M 外dt L L0
0
注：内力矩不改变系统总角动量，但使得角动量系统内部重新分配。

第4章1 功动能定理

得
mg
T v dr

l
v 2 gl(cos cos 0 )
1.53 m s
1
8
例2. 如图，长为 L ，质量为 m 的匀质链条，置于水平桌面上，链条与桌面之间的摩擦系数为μ，下垂部分的长度为 a 。链条由静止开始运动，求在链条滑离桌面的过程中，重力和摩擦力所作的功和链条离开桌面时的速率。解: （1）重力所作的功：链条下端在y时，重力所作元功
x y z
3
A Ax Ay Az
功的单位 1J 1N m 做功的三个要素：力、物体、过程 3. 功率平均功率瞬时功率
A P t
A dA P lim F v t 0 t dt
P Fv cos
功率的单位：瓦特（W） 1W 1J s 1
vB
2
2
定义：动能（状态函数）—— E 1 mv 2 E p k k
2
2
5 2m
动能定理 ——合力对质点所作的功数值上等于该质点动能的增量。
A EkB E kA
注意：功和动能都与参考系有关；动能定理仅适用于惯性系。
6
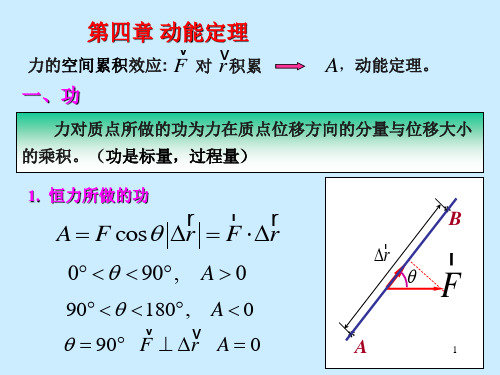
例 1 一质量为1.0kg 的小球系在长为1.0m 细绳下端 , 绳的上端
18
1 引力势能
rB Gm1m2 AAB f dr rA r 3 r dr ( L) A ( L) rB Gm1m2 Gm1m2 Gm1m2 dr 2 ( L ) rA r rB rA AAB E p EPA E pB 选 rB= 为零势点,EpB=0 m1m2 m1 , m2 两质点引力势能 E p r G r 重力势能:
固定在天花板上。起初把绳子放在与竖直线成 30 角处, 然后放

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

v2

v
2
ds) ds)

３-３质点在保守力场中的势能一、势能的引入
保守力的功等于势能坛量的负值! 保守力---------势能
a
b
重力
引力
弹性力
注： 1、势能属于系统。 2、势能零点。重力势能引力势能
弹性势能
二、己知保守力场确定势能函数
E p F (r ) dr V (r ) C
：为横向单位矢量
o b
圆弧ab o r
a
A=0
回旋力做功与路径有关！
5、摩擦力
b
a
摩擦力做功与路径有关！
三、保守力非保守力和耗散力
c a d
b
保守力（场）的数学判据 :
(任意)
[例3-3] 有两个力场: F1 ayj ( y 0) F2 bxj ( x 0) 判断它们是保守力还是非保守力。 (a, b 0)
机械能守恒定律
与参无关与参有关
E守恒
E不守恒
v
V
4、弧立系统
[例3-11] P71
x
Ａ
o
取Ａ的平衡位置为Ｘ轴的原点Ｏ及势能零点Ａ在任一位置 x 处时系统的
Fi
Fi ri
i
i
a( xa , ya , za )
b A F dr F cosds
b a a
注： 1、功与力、路径有关。
F 与参照系无关，位移与参照系有关， 2、
故 A与参照系有关。
3、合力之功：
b a i
f
v 0 F v 0
(1) 对沙箱, 应用动能定理：
(2) 对弹丸，应用动能定理：
s s+l
(3) 机械能变化：
s 一对非保守内力(耗散力)做负功，使系统动能减少。 s+l
3 -- 5
功能原理能量守恒定律
一、质点系动能定理
二、功能原理
保守内力的总功
内力做的总功
非保守内力的总功
注： 1、取好系统及初、末状态。 2、惯性系。 3、If
4、功率：
单位： J/s or W
动能定理:
b A F dr F cosds
b a a
dr
b
Vb

dV F cos ma t m dt b b dV ds A m ds mdV dt dt a a
b Vb
Va
F
a
1 1 2 2 mVdV mVdV mV b mV a Ekb Eka 2 2 a Va
质点动能的增量等于作用在质点上的合力对质点所做的功．
注： 1. A 0 E k
A 0 Ek
A Ekb Eka
能量衡量物体的作功本领，功是能量转化的量度。
2. A, Ek 与参有关，动能定理在惯系中成立。
3. A Ek
4.微分形式
[例3-1] 柔软匀质物体以初速送上平台，物体前端在平台上滑行 s 距离后停止．设滑道上无摩擦，物体与台面间的摩擦系数为，且ｓ＞Ｌ．求初速度． L 水平平台解：
传送机滑道
o x
L
s x
动能定理
[例3-２] 小球在水平变力F作用下缓慢移动，即在所有位置上均近似处于力平衡状态，直到绳子与竖直方向成角。求：(1) F的功， (2) 重力的功。 A 解： l F mgtg m F
Ft mgtg cos mg sin

0
mg
AF Ft ds mg sin ld mgl (1 cos ) Amg mg sin ld mgl (1 cos )
解：
３－４内力的功一、质点系
内力
外力
二、内力的功
：相对元位移
注： 1、一对内力做功之和一般不为零

j
i

j
与参照系无关 2、一对内力做功之和与所选的参照系无关
[例3-6] 光滑水平面上放有质量为m1的沙箱，由左方飞来质量为m2的弹丸从箱左侧击入，在沙箱中前进 l 距离后停止。在这段时间中沙箱向右运动了距离 s ，此后沙箱带着弹丸以匀速 v 运动。求(1) 沙箱对弹丸的平均阻力F；(2) 弹丸初速v0 ；(3) 沙箱--弹丸系统损失的机械能。解：
第三章机械能和功
3-1 功动能定理空间上的累积
力的累积效应时间上的累积恒力之功：
F
功
冲量

r
A F cos r F r
变力之功：
Ai Fi cosi ri
A Fi cos i ri
b( xb , yb , zb )
ri
i
例：
三、已知势能函数确定保守力场
而
故：
力沿某方向分力等于势能函数沿该方向空间变化率负值！
式中
称为矢量微分算子
称为势能函数的梯度
例：
则重力
例：
四、势能曲线
ＯＺＯ重力势能曲线ｒ x Ｏ弹性势能曲线
引力势能曲线
双原子分子的势能曲线
Ｏ
ｒ
[例3-5] 已知地球半径 R，物体质量 m，处在地面 2R 处。求势能:（1）地面为零势能点；（2）无限远处为零势能点。
0
3-2 保守力非保守力耗散力
一、力场
F (r , t,V )
z
m
r
F (r )
力矢
y
y x
力矢在空间的分布形象反映了力场
x
二、几种力的功 1、重力
z
a o
b
x
重力做功与路径无关！
2、引力
b
a
引力做功与路径无关！
3、弹性力
m Ｏ
a
x
b
Ｘ
弹性力做功与路径无关！
4、回旋力
b A ( Fi ) dr Fi dr Ai i a i
直角坐标系：单位：N· m or J
b b 自然坐标系： A F dr Ft dr Ft ds
b a a a
A P t A dA F dr P lim F v dt dt t 0 t
y
C B D
y
y2 B y1 A
F2
C
A
D
F1
(任意)
x
x1
x2 x
Hale Waihona Puke [例3-4] P 58h
l
dS
h
l
(2)
h
l
(3)
(1)
(1)
dA ds mg cosds 1 mg sin mgdh mgdl
m g cos m g cos m
v2
(2) (3)
dA2 mgdh m( gdl dA3 mgdh m( gdl