(完整版)三角函数公式默写模版(可编辑修改word版)
(完整word版)三角函数公式全集合

三角函数1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b)cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)] tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)]3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) - sin(b) = 2sin[(a - b)/2]cos[(a + b)/2]cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2]cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(a)cos 2a = cos2a - sin2a = 2cos2a - 1= 1 - 2sin2a6.半角公式sin2a = (1 – cos 2a)/ 2cos2a = (1 + cos 2a)/ 2tan a = [1 – cos 2a] /sin 2a = sin 2a / [1 + cos 2a ]7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]三角函数公式三角函数是数学中属于初等函数中的超越函数的一类函数。
(完整word版)三角函数公式大全

(完整word版)三⾓函数公式⼤全⾼中三⾓函数公式⼤全[图]1 三⾓函数的定义1.1 三⾓形中的定义图1 在直⾓三⾓形中定义三⾓函数的⽰意图在直⾓三⾓形ABC,如下定义六个三⾓函数:正弦函数余弦函数正切函数余切函数正割函数余割函数1.2 直⾓坐标系中的定义图2 在直⾓坐标系中定义三⾓函数⽰意图在直⾓坐标系中,如下定义六个三⾓函数:正弦函数余弦函数正切函数余切函数正割函数余割函数2 转化关系2.1 倒数关系2.2 平⽅关系2 和⾓公式3 倍⾓公式、半⾓公式3.1 倍⾓公式3.2 半⾓公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式证明过程⾸先,sin(α+β)=sinαcosβ+sinβcosα(已证。
证明过程见《和⾓公式与差⾓公式的证明》)因为sin(α+β)=sinαcosβ+sinβcosα(正弦和⾓公式)则sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosα于是sin(α-β)=sinαcosβ-sinβcosα(正弦差⾓公式)将正弦的和⾓、差⾓公式相加,得到sin(α+β)+sin(α-β)=2sinαcosβ则sinαcosβ=sin(α+β)/2+sin(α-β)/2(“积化和差公式”之⼀)同样地,运⽤诱导公式cosα=sin(π/2-α),有cos(α+β)=sin[π/2-(α+β)]=sin(π/2-α-β)=sin[(π/2-α)+(-β)]=sin(π/2-α)cos(-β)+sin(-β)cos(π/2-α)=cosαcosβ-sinαsinβ于是cos(α+β)=cosαcosβ-sinαsinβ(余弦和⾓公式)那么cos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβcos(α-β)=cosαcosβ+sinαsinβ(余弦差⾓公式)将余弦的和⾓、差⾓公式相减,得到cos(α+β)-cos(α-β)=-2sinαsinβ则sinαsinβ=cos(α-β)/2-cos(α+β)/2(“积化和差公式”之⼆)将余弦的和⾓、差⾓公式相加,得到cos(α+β)+cos(α-β)=2cosαcosβ则cosαcosβ=cos(α+β)/2+cos(α-β)/2(“积化和差公式”之三)这就是积化和差公式:sinαcosβ=sin(α+β)/2+sin(α-β)/2sinαsinβ=cos(α-β)/2-cos(α+β)/2cosαcosβ=cos(α+β)/2+cos(α-β)/24.2 和差化积公式部分证明过程:sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosαcos(α+β)=sin[90-(α+β)]=sin[(90-α)-β]=sin(90-α)cosβ-sinβcos(90-α)=cosαcosβ-sinαsinβcos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβtan(α+β)=sin(α+β)/cos(α+β)=(sinαcosβ+sinβcosα)/(cosαcosβ-sinαsinβ)=(cosαtanαcosβ+cosβtanβcosα)/(cosαcosβ-cosαtanαcosβtanβ)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=tan[α+(-β)]=[tanα+tan(-β)]/[1-tanαtan(-β)]=(tanα-tanβ)/(1+tanαtanβ)诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tgA=tanA=sinA/cosA两⾓和与差的三⾓函数si n(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b)sin(a-b)=sin(a)cos(b)-cos(a)sin(b)cos(a-b)=cos(a)cos(b)+sin(a)sin(b)tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))三⾓函数和差化积公式sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)sin(a)sin(b)=2cos((a+b)/2)sin((a-b)/2)cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]⼆倍⾓公式sin(2a)=2sin(a)cos(a)cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)半⾓公式sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中,tan(c)=b/a] a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中,tan(c)=a/b]1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2其他⾮重点三⾓函数csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=(e^a-e^(-a))/2cosh(a)=(e^a+e^(-a))/2tgh(a)=sinh(a)/cosh(a)常⽤公式表(⼀)1。
(完整word版)三角函数常用公式表
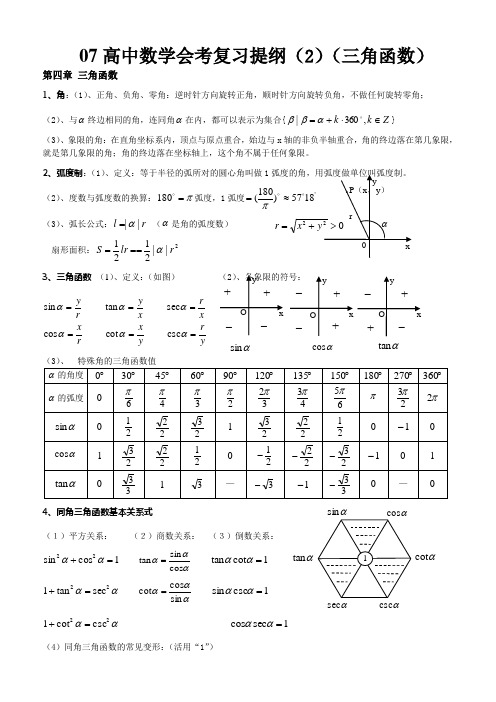
07高中数学会考复习提纲(2)(三角函数)第四章 三角函数1、角:(1)、正角、负角、零角:逆时针方向旋转正角,顺时针方向旋转负角,不做任何旋转零角; (2)、与α终边相同的角,连同角α在内,都可以表示为集合{Z k k ∈⋅+=,360|αββ}(3)、象限的角:在直角坐标系内,顶点与原点重合,始边与x 轴的非负半轴重合,角的终边落在第几象限,就是第几象限的角;角的终边落在坐标轴上,这个角不属于任何象限。
2、弧度制:(1)、定义:等于半径的弧所对的圆心角叫做1(2)、度数与弧度数的换算:π= 180弧度,1弧度)180( =π(3)、弧长公式:r l ||α= (α是角的弧度数) 扇形面积:2||2121r lr S α===3、三角函数 (1)、定义:(如图) (2)、各象限的符号: yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin (3)、 特殊角的三角函数值4、同角三角函数基本关系式(1)平方关系: (2)商数关系: (3)倒数关系:1cos sin 22=+αα αααcos sin tan = 1cot tan =αα αα22sec tan 1=+ αααsin cos cot =1csc sin =αα αα22csc cot 1=+ 1sec cos =αα(4)同角三角函数的常见变形:(活用“1”)αsinx y++ _ _ O xy++__ αcosOαtanxy+ +__O=r αsec αsinαtan αcotcsc①、αα22cos 1sin -=, αα2cos 1sin -±=;αα22sin 1cos -=, αα2sin 1cos -±=;②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+,αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±, |cos sin |2sin 1ααα±=± 5、诱导公式:(奇变偶不变,符号看象限)公式一: ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k 公式二: 公式三: 公式四: 公式五:ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充:ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切)(βα+S :βαβαβαsin cos cos sin )sin(+=+ )(βα-S :βαβαβαsin cos cos sin )sin(-=- )(βα+C :βαβαβsin sin cos cos )cos(-=+a )(βα-C :βαβαβsin sin cos cos )cos(+=-a )(βα+T : βαβαβαtan tan 1tan tan )tan(-+=+ )(βα-T : βαβαβαtan tan 1tan tan )tan(+-=-)(βα+T 的整式形式为:)tan tan 1()tan(tan tan βαβαβα-⋅+=+例:若︒=+45B A ,则2)tan 1)(tan 1(=++B A .(反之不一定成立) 7、辅助角公式:⎪⎪⎭⎫⎝⎛++++=+x b a b x b a a b a x b x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a(其中ϕ称为辅助角,ϕ的终边过点),(b a ,ab =ϕtan ) (多用于研究性质) 8、二倍角公式:(1)、α2S : αααcos sin 22sin = (2)、降次公式:(多用于研究性质) α2C : ααα22sin cos2cos -= ααα2sin 21cos sin =1cos 2sin2122-=-=αα 212cos 2122cos 1sin 2+-=-=ααα α2T : ααα2tan 1tan 22tan -= 212cos 2122cos 1cos 2+=+=ααα (3)、二倍角公式的常用变形:①、|sin |22cos 1αα=-, |cos |22cos 1αα=+;②、|sin |2cos 2121αα=-, |cos |2cos 2121αα=+③、22sin 1cos sin 21cos sin 22244ααααα-=-=+; ααα2cos sin cos 44=-;④半角:2cos 12sinαα-±=,2cos 12cos αα+±=,αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-= 9、三角函数的图象性质(1)、函数的周期性:①、定义:对于函数f (x ),若存在一个非零常数T ,当x 取定义域内的每一个值时,都有:f (x +T )= f (x ),那么函数f (x )叫周期函数,非零常数T 叫这个函数的周期;②、如果函数f (x )的所有周期中存在一个最小的正数,这个最小的正数叫f (x )的最小正周期。
高中数学必修一三角函数知识点默写稿

高中数学必修一三角函数知识点默写稿
以下是高中数学必修一三角函数知识点默写稿,供您参考:
1. 角度与弧度的关系:1弧度等于度,反之,1度等于弧度。
2. 三角函数的基本性质:
奇偶性:正弦、余弦为偶函数,正切为奇函数。
周期性:正弦、余弦、正切函数的周期均为2π。
有界性:正弦、余弦函数的值域为[-1,1],正切函数的值域为R。
3. 诱导公式:
奇变偶不变,符号看象限。
对于任意角θ,有sin(π+θ)=-sinθ,cos(π+θ)=-cosθ,tan(π+θ)=tanθ。
对于任意角θ,有sin(-θ)=-sinθ,cos(-θ)=cosθ,tan(-θ)=-tanθ。
4. 两角和与差的三角函数公式:
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)
5. 倍角公式:
sin2α=2sinαcosα
co s2α=cos²α-sin²α
tan2α=(2tanα)/(1-tan²α)
6. 辅助角公式:对于任意角θ,有sinθ=(2tan(θ/2))/(1+tan²(θ/2)),cosθ=(1-tan²(θ/2))/(1+tan²(θ/2))。
7. 三角函数的图像与性质:
正弦函数图像为周期函数,在[0,π]上单调递增,在[π,2π]上单调递减。
余弦函数图像为周期函数,在[0,π]上单调递减,在[π,2π]上单调递增。
正切函数图像为周期函数,在R上单调递增。
高中三角函数公式大全整理版(可编辑修改word版)

高中三角函数公式大全sin30°=1/2sin45°=√2/2 sin60°=√3/2 cos30°=√3/2cos45°=√2/2 cos60°=1/2 tan30°=√3/3tan45°=1 tan60°=√3 cot30°=√3cot45°=1 cot60°=√3/3 sin15°=(√6-√2)/4 sin75°=(√6+√2)/4 cos15°=(√6+√2)/4cos75°=(√6-√2)/4(这四个可根据 sin (45°±30°)=sin45°cos30°±cos45°sin30°得出) sin18°=(√5-1)/4 (这个值在高中竞赛和自招中会比较有用,即黄金分割的一半)正弦定理:在△ABC 中,a / sin A = b / sin B = c / sin C = 2R (其中,R 为△ABC 的外接圆的半径。
)两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) = tanA + tanB 1- tanAtanBtan(A-B) = tanA - tanB 1+ tanAtanBcot(A+B) = cotAcotB-1 cotB + c otAcot(A-B) = cotAcotB +1 cotB - cotA 倍角公式 tan2A =2tanA1- tan 2ASin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosATan3A= 3 t an 3A - (tan A )3 1- (tan A )2tan A t an( 3 A ) tan( 3 + A ) 半角公式= -sin( A )= 2 cos( A )= 2 tan( A )= 2 cot( A )= 2 tan( A )= 1- cos A =sin A2 sin A 和差化积 1+ cos Asina+sinb=2sin a + b cos a - b2 2 sina-sinb=2cos a + b sin a - b22cosa+cosb = 2cos a + b cos a - b2 2cosa-cosb = -2sin a + b sin a - b2 2tana+tanb= sin(a + b )cos a cos b积化和差1sinasinb = - [cos(a+b)-cos(a-b)]2 cosacosb = sinacosb = cosasinb = 诱导公式1 [cos(a+b)+cos(a-b)]21 [sin(a+b)+sin(a-b)]21 [sin(a+b)-sin(a-b)]2sin(-a) = -sinacos(-a) = cosasin( -a) = cosa2cos( -a) = sina2sin( +a) = cosa2 1- cos A 2 1+ cos A 2 1- cos A 1+ cos A 1+ cos A1- cos A(a 2 + b 2 ) (a 2 + b 2 ) cos( +a) = -sina 2sin(π-a) = sinacos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA = sin acos a万能公式 2 tan a sina=2 1+ (tan a )2 21- (tan a )2cosa=2 1+ (tan a )2 2 2 tan a tana=2 1- (tan a )2 2其它公式 a•sina+b•cosa= ×sin(a+c) [其中b tanc= ] aa•sin(a)-b•cos(a) = ×cos(a-c) [其中 a tan(c)= ] b a a 2 1+sin(a) =(sin +cos )2 2 a a 2 1-sin(a) = (sin -cos ) 2 2其他非重点三角函数csc(a) = sec(a) = 1 sin a 1 cos a公式一:设 α 为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα公式二:设 α 为任意角,π+α 的三角函数值与 α 的三角函数值之间的关系: sin (π+α)= -sinαA 2 +B 2 + 2A B c os(⋅) t + arcsin[(Asin + Bsin ) A 2 + B 2 + 2 A B c os(⋅)cos (π+α)= -cosαtan (π+α)= tanαcot (π+α)= cotα公式三:任意角 α 与 -α 的三角函数值之间的关系:sin (-α)= -sinαcos (-α)= cosαtan (-α)= -tanαcot (-α)= -cotα公式四:利用公式二和公式三可以得到 π-α 与 α 的三角函数值之间的关系: sin (π-α)= sinαcos (π-α)= -cosαtan (π-α)= -tanαcot (π-α)= -cotα公式五:利用公式-和公式三可以得到 2π-α 与 α 的三角函数值之间的关系: sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotαA•sin(ωt+θ)+ B•sin(ωt+φ) = ×sin。
三角函数公式总表(完美版)

三角函数公式总表一、角的概念的拓展1.与α终边相同的角的集合:{}|2,k k Z ββαπ=+∈ 二、弧度制1.长度等于半径长的弧所对的圆心角叫做1弧度的角,在弧度制下,1弧度记作1rad (rad 可以省略). 弧度制下的弧长公式:l rα=,即l r α=.扇形面积公式: 222111.||22222l S r r r lr r απααππ====≤. ㈠将角度化为弧度:3602rad π=;180rad π=;11rad 0.01745rad 180π=≈㈡将弧度化为角度:2rad 360π=;rad 180π=;1801rad 57.3π=≈三、三角函数的定义1.sin cos tan cot sec csc y x y x r r r r x y x yαααααα======、、、、、 2.三角函数线:角α与单位圆的交点P (x ,y )过P 点向x 轴引垂线,垂足叫M ,过A 点向x 轴 引垂线,交角的终边或反向延长线与点T ,则sin 1y yy MP r α====,cos 1x x x OM r α====,tan y MP ATAT x OM OAα====.有向线段MP ,OM ,AT 分别称为正弦线,余弦线,正切线.3. 三角函数符号:一正二正弦,三切四余弦. 四、同角三角函数基本关系式六边形记忆法图形结构“上弦中切下割左正右余中间1”xy oMTPA(1)oxy MTPA(2) xyoMTPA(3) oxyM TP A(4)1.记忆方法“对角线上两个函数的积为12.阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方3.任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积 四、诱导公式公式组一 (k Z ∈):sin(2)sin ,cos(2)cos ;tan(2)tan k x x k x x k x x πππ+=+=+=公式组二:sin()sin tan()tan ,cos()cos x xx x x x -=--=--=公式组三:sin()sin ,cos()cos ,tan()tan x x x x x x πππ+=-+=-+= 公式组四:sin()sin ,tan()tan ,cos()cos x x x x x x πππ-=-=--=-公式组五:sin(2)sin ,cos(2)cos ,tan(2)tan x x x x x x πππ-=--=-=-公式组六:sin cos ,cos sin ,tan cot 222πππαααααα⎛⎫⎛⎫⎛⎫-=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭公式组七:sin cos ,cos sin ,tan cot 222πππαααααα⎛⎫⎛⎫⎛⎫+=+=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭公式组八:333sin cos ,cos sin ,tan cot 222πππαααααα⎛⎫⎛⎫⎛⎫-=--=--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 公式组九:333sin cos ,cos sin ,tan cot 222πππαααααα⎛⎫⎛⎫⎛⎫+=-+=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭四、两角和与差公式 βαβαβαsin sin cos cos )cos(-=+βαβαβαsin sin cos cos )cos(+=-βαβαβαsin cos cos sin )sin(+=+βαβαβαsin cos cos sin )sin(-=-βαβαβαtan tan 1tan tan )tan(-+=+βαβαβαtan tan 1tan tan )tan(+-=-五、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-= ααα2tan 1tan 22tan -= 常用数据: 30456090、、、的三角函数值6sin15cos 754-==,42615cos 75sin +==3275cot 15tan -== ,3215cot 75tan +==注: ⑴以上公式务必要知道其推导思路,从而清晰地“看出”它们之间的联系,它们的变化形式.如tan()(1tan tan )tan tan αβαβαβ+-=+221cos 1cos cos ,sin 2222αααα+-==等. 从而可做到:正用、逆用、变形用自如使用各公式.⑵三角变换公式除用来化简三角函数式外,还为研究三角函数图象及性质做准备. ⑶三角函数恒等变形的基本策略。
三角函数公式默写

三角函数公式默写(一)1、弧长公式: ;扇形面积公式:2、终边在y 轴上的角的集合是: ;终边在x 轴上的角的集合是3、第三象限角的集合:4、与已知角α终边相同的角β的集合是5、若角α在第三象限,则2α在 象限 6、三角函数的定义:(1)已知α角终边任意一点(,)p x y ,则sin _____,cos _____,tan _____(______)r ααα====。
(2)三角函数的符号y y y0 x 0 x 0 xsinx cosx tanx 7、若角α终边与单位圆交于点P ,则点P 的坐标为 8、特殊角的三角函数值9、同角三角函数的基本关系式(1)平方关系: (2)商数关系: 10、诱导公式(1)sin(2k π+α)= (2)sin(π-α)= (3)sin(π+α)= cos(2k π+α)= cos(π-α)= cos(π+α)=tan(2k π+α)= tan(π-α)= tan(π+α)= (4)sin (2π-α)= (5)sin (-α)= cos (2π-α)= cos (-α)=tan (2π-α)= tan (-α)=11、(1)sin (π2 -α)= (2)sin (π2 +α)= (3)sin (3π2 -α)= (4)sin (3π2 +α)=cos (π2 -α)= cos (π2 +α)= cos (3π2 -α)= cos (3π2 +α)=三角函数公式默写(二)——三角函数的图像与性质三角函数公式默写(三)——三角恒等变换两角和与差的三角函数公式及倍角公式1、sin(α+β)=sin(α—β)=cos(α+β)=cos(α—β)=tan(α+β)=tan(α-β)=2、sin2α=cos2α= = =tan2α=3、公式的变形1+tanα1-tanα=1-tanα1+tanα=tanα +tanβ = tanα-tanβ = 1+cos2α= 1-cos2α= cos2α= sin2α=4、根式的化简1+sinα= 1-sinα=1+cosα= 1-cosα=。
(完整word)三角函数诱导公式大全,推荐文档

三角函數誘導公式大全三角函数诱导公式常用的诱导公式有以下几组:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为:对于k·π/2±α(k∈Z)的个三角函数值,①当k是偶数时,得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan.(奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)例如:sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
