spss多因素方差分析报告例子
spss多因素方差分析报告例子

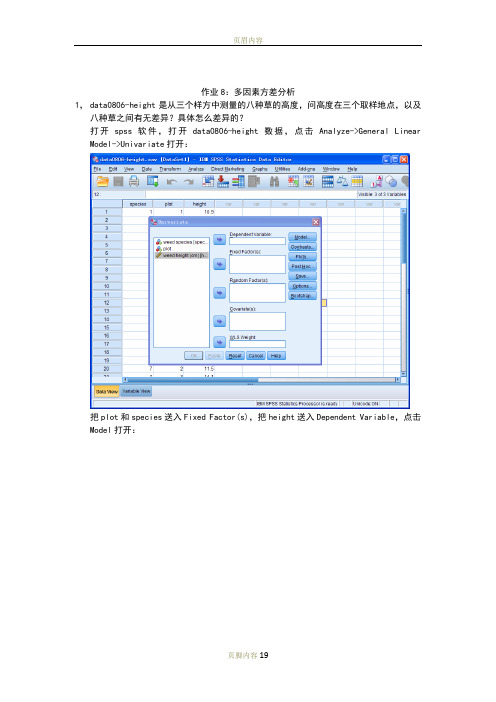
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
spss 方差分析(多因素方差分析)实验报告

大学经济管理学院学生实验报告实验课程名称:统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质:演示性 验证性综合性设计性实验项目名称方差分析(多因素方差分析)指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法,并能够解释软件运行结果。
二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例:为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数据。
销售量日期周一至周三周四至周五周末地区一5000 6000 4000 6000 8000 3000 4000 7000 5000地区二700080008000500050006000500060004000地区三300020004000600060005000800090006000(1)选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。
在SPSS输入数据。
(2)利用多因素方差分析法,分析不同地区和不同日期对该商品的销售是否产生了显著影响。
1. 选择菜单Analyze,General Linear Model,Univariate;2. 指定观测变量销售额到Dependant Variable框中;3. 指定固定效应的控制变量到Fixed Factors框中,4. OK,得到分析结果。
(3)地区和日期是否对该商品的销售产生了交互影响?若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
三、实验结论(包括SPSS输出结果及分析解释)SPSS输出的多因素方差分析的饱和模型分析:表的第一列是对观测变量总变差分解的说明;第二列是观测变量变差分解的结果;第三列是自由度;第四列是方差;第五列是F检验统计量的观测值;第六列是检验统计量的概率P-值。
F日期,,F地区,F日期*地区概率P-值分别为0.254,0.313,0.000。
如果显著性水平α为0.05,由于F日期、,F地区大于显著性水平α,所以不应拒绝原假设,不同地区和不同日期对该商品没有显著性影响。
spss多因素方差分析报告例子
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction 的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
spss 方差分析(多因素方差分析)实验报告

大学经济管理学院学生实验报告实验课程名称:统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质:演示性 验证性综合性设计性实验项目名称方差分析(多因素方差分析)指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法,并能够解释软件运行结果。
二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例:为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数据。
销售量日期周一至周三周四至周五周末地区一5000 6000 40006000 8000 30004000 7000 5000地区二700080008000 500050006000500060004000地区三300020004000 600060005000800090006000(1)选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。
在SPSS输入数据。
(2)利用多因素方差分析法,分析不同地区和不同日期对该商品的销售是否产生了显著影响。
1. 选择菜单Analyze,General Linear Model,Univariate;2. 指定观测变量销售额到Dependant Variable框中;3. 指定固定效应的控制变量到Fixed Factors框中,4. OK,得到分析结果。
(3)地区和日期是否对该商品的销售产生了交互影响?若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
三、实验结论(包括SPSS输出结果及分析解释)。
spss多因素方差分析报告例子

作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate 打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算rror,即无法分开intercept和error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate主对话框,点击Plots:Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
《2024年使用SPSS软件进行多因素方差分析》范文

《使用SPSS软件进行多因素方差分析》篇一一、引言随着社会发展和科研进步,数据已经成为学术研究和工程领域不可或缺的部分。
对于处理复杂的多个因素之间关系的探究,多因素方差分析成为了一种常见的数据分析方法。
本文旨在展示如何使用SPSS软件进行多因素方差分析,以便读者能更好地理解和掌握其使用方法和过程。
二、数据与方法本节将介绍数据的来源、背景和采集方式,以及采用多因素方差分析的原因。
此外,也将简单介绍SPSS软件的相关知识和其在本次分析中的使用方式。
1. 数据来源本次研究使用的数据来自于一项实地调查。
数据涉及了不同区域、不同教育程度和不同经济水平的参与者,每个参与者均进行了特定的实验操作,产生了多个因变量和自变量的数据。
2. 方法我们选择使用SPSS软件进行多因素方差分析,该软件是当前广泛使用的统计分析工具之一。
其功能强大且操作简便,可以很好地处理复杂的多因素数据。
三、实验设计与变量本部分将详细介绍实验设计及所涉及的变量。
1. 实验设计实验设计为完全随机设计,涉及两个主要自变量(因素A和因素B)和多个因变量(如结果Y1、Y2等)。
2. 变量说明因素A包括三个水平:水平1、水平2、水平3;因素B同样包括三个水平:水平A、水平B、水平C。
因变量为各组在实验操作后的结果,包括但不限于特定任务完成度、准确度等。
四、数据分析与结果解读本部分将详细描述使用SPSS软件进行多因素方差分析的步骤及结果解读。
1. 数据录入与整理将收集到的数据录入SPSS软件中,并进行必要的整理和清洗,确保数据的准确性和完整性。
2. 多因素方差分析步骤(1)打开SPSS软件,选择“分析”菜单中的“一般线性模型”选项,然后选择“单变量”。
(2)在弹出的对话框中,将因变量放入“因变量”框中,将两个自变量放入“固定因子”框中。
(3)点击“运行”,SPSS将自动进行多因素方差分析,并生成相应的结果表格和图表。
3. 结果解读通过查看SPSS生成的结果表格和图表,我们可以得到以下信息:各因素的主效应、各因素之间的交互效应以及因变量的变化情况等。
《2024年使用SPSS软件进行多因素方差分析》范文

《使用SPSS软件进行多因素方差分析》篇一一、引言在社会科学研究中,多因素方差分析是一种常用的统计方法,用于探究多个自变量对一个因变量的影响。
这种分析方法能够帮助研究者理解多个因素如何同时作用于因变量,以及它们之间是否存在交互效应。
本文将详细介绍如何使用SPSS软件进行多因素方差分析,以期为相关领域的研究提供方法和参考。
二、方法2.1 研究设计本部分首先介绍了研究目的、研究问题和研究对象等基本情况。
针对特定问题,研究者应事先进行适当的文献回顾,以便更好地理解和把握所研究问题的现状。
接着确定了使用多因素方差分析作为主要的统计分析方法,因为它能够探究多个因素同时作用于因变量的影响及其之间的交互效应。
2.2 数据收集在数据收集阶段,应遵循科学的研究设计和样本选择原则,确保数据的可靠性和有效性。
收集的数据应包括自变量和因变量的观测值,以及可能影响分析结果的协变量。
此外,还需要收集有关样本特征的信息,如性别、年龄、教育背景等。
2.3 SPSS软件操作(1)数据录入:将收集到的数据录入SPSS软件中,确保数据格式正确、无缺失值和异常值。
(2)定义变量:在SPSS中定义自变量、因变量和协变量,为后续分析做好准备。
(3)多因素方差分析:选择“分析”菜单中的“一般线性模型”选项,进行多因素方差分析。
在分析过程中,需要设置好因素、水平、因变量和协变量等参数。
(4)结果解读:根据SPSS输出的结果,解读各因素对因变量的影响程度、交互效应以及统计显著性等信息。
三、结果与分析3.1 描述性统计首先对数据进行描述性统计分析,包括计算各变量的均值、标准差、最大值、最小值等统计量,以便初步了解数据的分布特征和变化规律。
3.2 多因素方差分析结果通过SPSS软件进行多因素方差分析后,得到以下结果:(1)各因素对因变量的影响:从输出结果中可以看出,哪些因素对因变量的影响显著,哪些因素的影响不显著。
这有助于研究者了解各因素对因变量的独立作用。
spss多因素方差分析例子

作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业8:多因素方差分析1,data0806-height 是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss 软件,打开data0806-height 数据,点击Analyze->General Linear Model->Univariate 打开:把plot 和species 送入Fixed Factor(s) ,把height 送入Dependent Variable ,点击Model 打开:选择Full factorial ,Type III Sum of squares ,Include intercept in model (即全部默认选项),点击Continue 回到Univariate 主对话框,对其他选项卡不做任何选择,结果输出:因无法计算?? rror ,即无法分开?? intercept 和?? error ,无法检测interaction 的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate 打开:选择好Dependent Variable 和Fixed Factor(s) ,点击Model 打开:点击Custom,把主效应变量species 和plot 送入Model 框,点击Continue 回到Univariate 主对话框,点击Plots :把date 送入Horizontal Axis ,把depth 送入Separate Lines ,点击Add,点击Continue回到Univariate 对话框,点击Options :把OVERALL,species, plot 送入Display Means for 框,选择Compare main effects ,Bonferroni ,点击Continue 回到Univariate 对话框,输出结果:可以看到:SS species =33.165 ,df species =7,MS species=4.738 ;SS plot =33.165 ,df plot =7,MS plot=4.738 ;SS error =21.472 ,df error =14,MS error=1.534 ;Fspecies=3.089 ,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
该表说明:SSspecies=33.165,dfspecies=7,MSspecies=4.738;SSerror=21.472,dferror=14,MSerror=1.534;Fspecies=3.089,p=0.034<0.05;物种间存在差异:SSplot=33.165,dfplot=7,MSplot=4.738;SSerror=21.472,dferror=14,MSerror=1.534;Fplot=12.130,p=0.005<0.01;不同的物种间在差异:由边际分布图可知:类似结论:草的高度在不同样地的条件之间有差异(Fplot=12.130,p=0.005<0.01 ),具体是,样地一和样地三之间存在的差异最大;八种不同草的高度也存在差异(Fspecies=3.089 ,p=0.034<0.05 ),具体是第四种草和第五种草的差异最大。
再次检验不同种类草的高度差异:重新进行方差分析,A nalyze->General LinearModel->Univariate :把species 送入Fixed Factor(s) ,把high 送入DependentVariable ,点击Plots :把species 送入Horizontal Axis ,点击Add,点击Continue 回到Univariate ,点击Post Hoc (因为我们已经知道species 效应显著):把species 送入Post Hoc Tests for 框,选择Tukey,输出结果:各组均值从小到大向下排列。
最大的是第五组,最小的是第四组,其中有些种类草的高度存在差异,有些不存在。
再次检验不同样地草的高度差异:过程和上相似:结果如下不同样地的草高度存在差异,其中一样地的草高度最短,3样地的草高度最高,且三组之间都存在差异。
2,data0807-flower ,某种草的开花初期高度在两种温度和两个海拔之间有无差异?具体怎么差异的?多因素单因变量方差分析通过Analyze->General Linear Model->Univariate 实现,把因变量height 送入Dependent Variable 栏,把因素变量temperature 和attitude 送入Fixed Factor(s) 栏点击Model 选项卡,打开:选着full factorial ,type 3,点击)Include intercept in model。
点击Plots 对话框,打开::可选择attitude 到Horizontal Axis ,然后选择temperature 到Horizontal Axis ,再选择attitude 到Separate Lines ,Plots 框显示attitude,temperature, attitude * temperature ,Estimated Marginal Means选择OVERALL,产生边际均值的均值Display 框选择要输出的统计量,Descriptive statistics 描述统计量,Homogeneity tests 方差齐性检验。
结果输出:主效应各因素各水平以及样本量,各水平的均值和标准差。
把样本分为四组,进行方差齐性检验,方差不一致。
可以看到:SSaltitude=503.167 ,dfaltitude=1 ,MSaltitude=503.167 ;SStemperature=1149.798 ,dftemperature=1 ,MStemperature=1149.798 ;SSinteraction=338.486 ,dfinteraction=1 ,MSinteraction=338.486 ;SSerror=935.748 ,dferror=83 ,MSerror=935.748 ;Faltitude=44.63 ,p=0.034<0.001;Ftemperature=101.986,p=0.005<0.001;Ftemperature=101.986,<0.001;Finteraction=34.458 ,p<0.001;所以故认为在0.1%的置信水平上,不同温度,不同海拔之间的草高度是存在差异的。
在四个样本总体中,在95%的置信区间,花的平均高度范围为137.719 到139.172 之间。
在海拔为3200 米处,在95%的置信区间,花的平均高度范围为139.852 到141.920 之间。
在海拔为3400 米处,在95%的置信区间,花的平均高度范围为134.985 到137.036 之间。
aititude 各水平的边际均值的多重比较,在本试验中,事实上0: 平均aititude (3200)= aititude (3400);但是平均aititude (3200)花高度—平均aititude (3400)花高度,在95%置信区间为 3.427 到6.333. 故均值存在差异。
,SSaltitude=503.167 ,dfaltitude=1 ,MSaltitude=503.167 ;SSerror=935.748 ,dferror=83 ,MSerror=935.748 ;Faltitude=44.63 ,P<0.001. 不同海拔的花高度不存在差异的的概率<0.001.在温度为T1 处,在95%的置信区间,花的平均高度范围为141.149 到143.119 之间。
在温度为T2 处,在95%的置信区间,花的平均高度范围为133.689 到135.825 之间。
温度各水平的边际均值的多重比较,在本试验中,事实上0: (T1时,平均花高度)= (T2 时,平均花高度);但是(T1 时,平均花高度)—(T2 时,平均花高度),在95%置信区间为 5.924 到8.830 ,故均值存在差异,不接受H0 假设。
SStemperature=1149.798 ,dftemperature=1 ,MStemperature=1149.798 ;SSerror=935.748 ,dferror=83 ,MSerror=935.748 ;Ftemperature=101.986,p<0.001;不同温度下,花的高度存在差异。
在温度为T1,海拔3200 米处,在95%的置信区间,花的平均高度范围为145.433 到148.004 之间。
在温度为T2处,海拔3200 米处在95%的置信区间,花的平均高度范围为133.433 到136.673 之间。
在温度为T1 处,海拔3400 米处,在95%的置信区间,花的平均高度范围为136.057 到139.043 之间。
在温度为T2 处,海拔3400 米处,在95%的置信区间,花的平均高度范围为133.068 到135.853 之间。
不同海拔下的的边际均值图两个因素的边际均值交互效应图,该图直线相互交叉(即斜率不一样)表明有交互效应。
结论如下:某种草的开花初期高度在两种温度之间有差异(Ftemperature=101.986,p<0.001; ),T1 时草的开花初期高度高于T2 时草的开花初期高度.某种草的开花初期高度在两种海拔之间有差异(Faltitude=44.63 ,P<0.001. ),海拔3200 时草的开花初期高度高于海拔3400 时草的开花初期高度.温度和海拔对草的开花初期高度的影响存在交互效应(Finteraction=34.458 ,p<0.001) 。
