高等数学上6.2定积分在几何学上的应用PPT课件
合集下载
高等数学上62定积分在几何学上的应用

16 a2 2 sin4 u d u 0
o (令u t )
2
3 a2
2 a x
首页
上页
返回
下页
结束
2. 极坐标情形
求由曲线
及
在区间
围成的曲边扇形的面积 . 上任取小区间
则对应该小区间上曲边扇形面积的近似值为
dA 1 ( )2 d
2
所求曲边扇形的面积为
r ( ) d
首页
上页
返回
下页
结束
P277-5
例6. 计算心形线
面积 . 解:
1 a2 (1 cos )2 d
2
a2 4 cos4 d
0
2
令
t
2
8a2 2 cos4t dt 0
8a2 3 1 3 a2
422 2
所围图形的
(利用对称性)
d
o
2a x
0
2
令u t 2
16
a
3
0
(2u
sin
2u)
sin
4
u
d
u
令v u
2
16
a3
2
2
(2v
sin 2v) cos4 v d v
偶函数
奇函数
首页
上页
返回
下页
结束
P281-9
例15. 一平面经过半径为R 的圆柱体的底圆中心 , 并
与底面交成 角, 计算该平面截圆柱体所得立体的体积 .
30
y
ox
R x
定积分在几何中的应用 课件

1.由抛物线y2=x与直线x=2所围成的图形的面积为_______.
2.求y=-x2与y=x-2围成图形的面积S.
【解析】1.由
y2
得x,其交点为(2,
),(22,
),所 以2 结合
x 2,
抛物线的对称性和定积分的概念,所围成的图形的面积
为 2 2 0
xdx
4 3
3
x.2
|02
8
2 3
答案:8 2
①当曲边梯形的面积在x轴上方时,如图1,则
b
a
f
x dx
=S上.
②当曲边梯形的面积在x轴下方时,如图2,则
b
a
f
x
dx
=-S下.
③当曲边梯形的面积在x轴上方、x轴下方均存在时,如图3,
则
b
a
f
x
dx
=S上-S下,若S上=S下,则
b
a
f
x dx
=0.
(2)由两条曲线f(x),g(x)和直线x=a,x=b(a<b)所围成的平面 图形的面积S.
0
1
2.求由曲线y=
x
,y=2-x,y=-1
3
x所围成图形的面积.
【解析】1.选C.阴影部分的面积
S= [1 x2 1 ]dx 2 x2 1 dx
0
1
= 2 x2 ,1 d故x 选C. 0
2.方法一:解题流程:
画图形
画出草图,如图所示.
求交点
用积分 表示
计算
解方程组
y
x,
x y 2,
3
2.如图,由
y y
Байду номын сангаас
精品课件-高等数学定积分在几何上的应用ppt

第二节 定积分在几何上的应用
例3 求由 y=cosx, y=sinx 在区间 [0, ] 上所围成的图 形的面积.
两曲线的交点
y sin x
y
cos
x
( , 4
2) 2
A1
A2
A A1 A2
4 (cos x sin x)dx
0
(sin x cos x)dx
x(t) ye of Information and Technology
y2 2x
y x4
A42y4y22dy1.8
Nanjing College of Information and Technology
第五章 定积分及其应用
第二节 定积分在几何上的应用
问题 若选x为积分变量呢? 4
SS1 S2
2
[
2x (
2 x )]dx
第二节 定积分在几何上的应用
应用微元法解决定积分应用问题的步骤是:
1) 选取积分变量, 确定它的变化区间[a,b];
2) 在区间[a, b]上任取一个小区间[x,x+dx], 并在小区
间上找出所求量F的微元 dF = f(x)dx (局部近似值) ;
3) 求定积分 F
b
f (x)dx
a
Nanjing College of Information and Technology
ΔA≈ f(x)dx
面积元素
dA
yf(x)
记作dA
o a xxdbxx
(2) 将这些面积元素在[a,b]上“无限累加”得
b
b
Alim f(x)dx f ( x)dx d A
定积分的应用课件

液体静压力计算步骤
详细阐述液体静压力计算的步骤,包 括确定计算区域、选择坐标系、列出 被积函数等。
其他物理问题中定积分应用
引力计算
通过定积分求解质点系或连续体 之间的引力问题。
波动问题
将波动问题转化为定积分问题, 进而求解波动过程中的各种物理 量。
01
02
电场强度计算
利用定积分求解电荷分布连续体 所产生的电场强度。
消费者剩余和生产者剩余计算
消费者剩余计算
消费者剩余是消费者愿意支付的价格与实际支付价格之间的差额。在需求曲线和价格线之间的面积表示消费者 剩余,可以通过定积分计算。
生产者剩余计算
生产者剩余是生产者实际得到的价格与愿意接受的最低价格之间的差额。在供给曲线和价格线之间的面积表示 生产者剩余,同样可以通过定积分计算。
01
通过定积分求解绕x轴或y轴旋转一周所得旋转体的体积。
平行截面面积为已知的立体体积计算
02
利用定积分将立体划分为无数个平行截面,通过截面面积和高
度求解体积。
参数方程表示立体体积计算
03
将参数方程转化为普通函数形式,再利用定积分求解体积。
曲线弧长求解方法
1 2
直角坐标下曲线弧长计算
通过定积分求解曲线在直角坐标系下的弧长。
参数方程表示曲线弧长计算
将参数方程转化为普通函数形式,再利用定积分 求解弧长。
3
极坐标下曲线弧长计算
通过定积分求解曲线在极坐标系下的弧长。
03
定积分在物理学中应用
变力做功问题求解方法
微元法求解变力做功
通过将变力做功的过程划分为无数个微小的 元过程,每个元过程中力可视为恒力,从而 利用定积分求解变力做功。
高等数学(第三版)课件:定积分的应用

线 y f ( x,) 直线 x a, x b (a b) 与
• x 轴围成的面积是在x 轴上方和下方曲边梯形
面积的差.
• • 同样可由微元法分析
•⒉ 一般地,根据微元法由曲线 y f ( x), y g( x),
• ( f ( x) g( x)) 及直线x a, x b 所围的图形
• 面积.(右图所示)
• 解: 取 为积分变量,
•
面积微元为
d
A
1 2
(a )2
d
• 于是
A 2 1 (a )2d a 2 2
02
23
2 4 a 2 3
03
• 例5 计算双纽线 r 2 a2 cos2 (a 0)
•
所围成的平面图形的面积(下图所示)
• 解 因 r 2 0,故 的变化范围是 [ 3 , 5 ,]
• ⑴分割区间[a,b],将所求量(曲边梯形面积 A )
分为部分量(小曲边梯形面积 Ai)之和;
• ⑵确定各部分量的近似值(小矩形面积);
Ai f (i )xi
• ⑶求和得所求量的近似值(各小矩形面积之和);
n
A f (i )xi
i 1
• ⑷对和式取极限得所求量的精确值(曲边梯形面积).
n
A lim 0
• 它表示高为f ( x) 、底为 dx 的一个矩形面积.
• ⑵由定积分几何意义可知,当 f (x) 0 时,由曲
线 y f (x),直线 x a, x b (a b) 与 x 轴所围成
的曲边梯形的面积A为
A
b
f (x)dx
.
a
• ⑶当 f ( x)在区间 [a, b]上的值有正有负时,则曲
•
定积分在几何中的应用 课件

y=x2-3围成平面图形的面积是
S [3 2x (x2 3)]dx 3 (3 2x x2 )dx
1
1
(3x
x2
1 3
x3
31
(3 3 32 1 33) [1 3 (1)2 1 (1)3]
3
3
9 2 1 32 . 33
【拓展提升】求函数图象围成平面图形面积的方法 (1)画出两个函数的图象,先将两个函数方程联立方程组求 解,得到函数图象的交点的横坐标a,b(a<b),确定积分区间 [a,b]. (2)在公共的积分区间上,由上界函数减去下界函数作为被积 函数,定积分的值就等于两个函数图象围成平面图形的面
积,即 S a[b f1(x) (f其2 (中x)]fd1x(x)>f2(x)).
类型 二 计算复杂平面图形的面积 【典型例题】 1.由两条曲线y=x2, y 1 x2与直线y=1围成平面区域的面积
4
是_______.
2.求曲线 y x 与直线y=2-x,y 1 x 围成图形的面积.
3
【解题探究】1.题1中怎样确定积分变量的区间? 2.如何将图形的面积转化为定积分计算? 探究提示: 1.由直线y=1分别与曲线y=x2y, 1 x联2 立,求出交点坐标,
(2x
1 2
x2
1 6
x2)
13
=2 3
1 6
(2x
1 3
x2
)
13
=5 6 1 9 21 1 1=2 1 .
63
36
【互动探究】若将题2中条件变为如图由直线y=x-2,曲线 y2=x所围成图形,试求其面积S.
【解析】由
y2
x得, x=1或x=4,
y x 2,
故A(1,-1),B(4,2),如图所示:
高等数学第六章第二节定积分在几何学上的应用课件.ppt
解:
cos x 0,
2
x
2
s
2
2
2 2 0
1 y2 dx 1 ( cos x)2 dx
2 2
2 cos x dx
0
2
2
2
2
sin
x 2
2
0
4
的弧长.
例11. 计算摆线
一拱
的弧长 .
y
解: ds
(dd
x t
)2
(
d d
y t
)
2
d
t
o
a2 (1 cos t)2 a2 sin2 t d t
1 y2 dx
因此所求弧长
s b 1 y2 dx a
b
a
1 f 2(x) dx
y
y f (x)
ds
o a xxdxb x
(2) 曲线弧由参数方程给出:
弧长元素(弧微分) :
ds (dx)2 (dy)2
2 (t) 2 (t) dt
因此所求弧长
s
2 (t) 2 (t) d t
(3) 曲线弧由极坐标方程给出:
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
方法2 利用椭圆参数方程
则 V 20a y2 dx 2 ab2 sin3t d t
2 ab2 2 1
3
4 ab2
3
特别当b
=
a
( 人教A版)定积分在几何中的应用课件 (共36张PPT)

A.b[f(x)-g(x)]dx a
C.b|f(x)-g(x)|dx a
B.b[g(x)-f(x)]dx a
D.b[fx-gx]dx
a
解析:因为 f(x),g(x)两条曲线上下位置关系不确定,故选 C.
答案:C
2.曲线 y=x2 与直线 x+y=2 围成的图形面积为( )
A.5
9 B.2
C.4 解析:如图,解方程组y=x2,
t 0,12
1 2
12,1
S′ -
0
+
S
极小值
所以当t=12时,S最小,且Smin=14.
怎样解答与曲边图形有关的综合问题? 解决与曲边图形有关的综合问题,关键是要正确分析题意,先分清是求曲边 图形面积,还是利用曲边图形面积解决其他问题,再正确作出图形,确定积 分区间和被积函数,然后根据条件,建立等量关系或方程进行求解.
x
∴S=
2 x2dx+
x0 x0
[x2-(2x0x-x02)]dx
0
2
=112x30.
∴112x30=112,x0=1. ∴切点为(1,1),切线方程为 y=2x-1.
因对图形特征认识不清致误
[典例] 求由抛物线 y2=8x(y>0)与直线 x+y-6=0 及 y=0 所围成图形的面积 S.
[解析] 由题意,作出简图(如图)并解方程组y2=8xy>0 x+y-6=0 得 x=2, 所以 y2=8x(y>0)与直线 x+y-6=0 的交点坐标为(2,4).
0
0
8x)dx. (2)应用定积分求平面图形的面积时,正确分析图形特征,将复杂的面积问题分为
几部分来求解,若更换积分变量应相应的将被积函数及积分界限均改变.
[随堂训练] 1.若 y=f(x)与 y=g(x)是[a,b]上的两条光滑曲线的方程,则这两条曲线及直线 x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
边长 →0 时, 折线的长度趋向于一个确定的极限 , 则称
此极限为曲线弧 AB 的弧长 , 即
n
s lim 0
M i1M i
i1
并称此曲线弧为可求长的.
y M i1
A M0 o
定理: 任意光滑曲线弧都是可求长的.
(证明略)
Mi
B Mn x
首页
上页
返回
下页
结束
(1) 曲线弧由直角坐标方程给出: y f (x) (a x b)
弧长元素(弧微分) :
ds (dx)2 (dy)2 1 y2 dx (P170)
因此所求弧长
s b 1 y2 dx a b 1 f 2 (x) dx a
y
y f (x)
ds
o a xxdx b x
首页
上页
返回
下页
结束
(2) 曲线弧由参数方程给出:
x y
(t) (t)
( t )
弧长元素(弧微分) :
ds (dx)2 (dy)2
2 (t) 2 (t) dt
因此所求弧长
s
2 (t) 2 (t) d t
首页
上页
返回
下页
结束
(3) 曲线弧由极坐标方程给出:
r r( ) ( ) 令 x r( )cos , y r( )sin , 则得
0
4
a
2
b
12
2
ab
当 a = b 时得圆面积公式
首页
上页
返回
下页
结束
一般地 , 当曲边梯形的曲边由参数方程
x y
(t) (t)
给出时, 按顺时针方向规定起点和终点的参数值 t1 , t2
y
y
a
b
o
x
oa
bx
(t1 对应 x a)
(t1 对应 x b)
则曲边梯形面积
首页
上页
A t 2 (t) (t) dt t1
a2 4 cos 2 d (2 ) 0
a2sin 2 4 a2
0
y
4
o
ax
4
思考: 用定积分表示该双纽线与圆 r a 2 sin
所围公共部分的面积 .
答案:
A 2
6 a2 sin 2 d
0
4 6
1 2
a
2
cos 2
d
首页
上页
返回
下页
结束
二、平面曲线的弧长
定义: 若在弧 AB 上任意作内接折线 , 当折线段的最大
y2 b2
1
所围图形的面积
.
解: 利用对称性 , 有 d A y dx
y b
a
A 40 y d x
利用椭圆的参数方程
o xxdxa x
x y
a cost b sin t
(0 t 2 )
应用定积分换元法得
A 4
0
b sin t (a sin t) dt
4ab
2 sin 2 t dt
8a2 3 1 3 a2
422 2
(利用对称性)
d
o
2a x
首页
上页
返回
下页
结束
例7.的面积 .
1 2cos cos2
解: 利用对称性 , 所求面积
A 1a2 2
2
2
1 2
a
2
(1
cos
)2 d
1 2
(1
2
8a2 sin4 u d u 0
16 a2 2 sin 4 u d u 0
o
(令u t ) 2
16a2 3 1 3 a2
42 2
2 a x
首页
上页
返回
下页
结束
2. 极坐标情形
设 ( ) C[ , ] , ( ) 0 , 求由曲线 r ( ) 及
射线 , 围成的曲边扇形的面积 . 在区间[ , ]上任取小区间 [ , d ]
a2 2
13
3
2
0
2 a
o
x
d
4 3 a2
3
点击图片任意处 播放开始或暂停
首页
上页
返回
下页
结束
P277-5
例6. 计算心形线 r a(1 cos ) (a 0) 所围图形的
面积 .
解: A 2 1 a2 (1 cos )2 d 02
a2 4 cos4 d
0
2
令t
2
8a2 2 cos4t dt 0
第二节
第六章
定积分在几何学上的应用
一、 平面图形的面积
二、 平面曲线的弧长 三、已知平行截面面积函数的
立体体积
四、 旋转体的侧面积 (补充)
首页
上页
返回
下页
结束
一、平面图形的面积
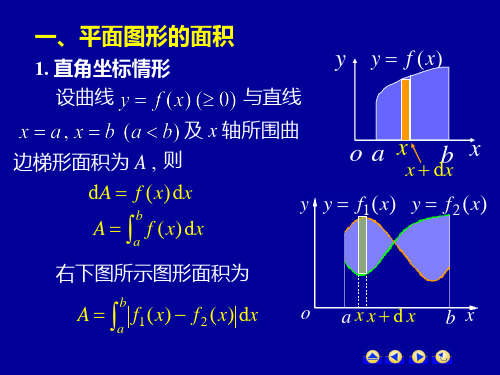
1. 直角坐标情形
设曲线 y f (x) ( 0) 与直线
y y f (x)
x a , x b (a b) 及 x 轴所围曲
所围图形的面积 .
解: 由
y2 x y x2
y
得交点 (0, 0) , (1, 1)
y2 x (1,1)
1
AdA0
x x2 dx
2
3
x2
1
x3
1
3 30
1
3
y x2 ox 1 x
xdx
首页
上页
返回
下页
结束
P275-2
例2. 计算抛物线 y2 2x 与直线 y x 4 所围图形 的面积 .
边梯形面积为 A , 则
oa x b x
x dx
dA f (x)dx
b
A a f (x) dx
y y f1(x) y f2 (x)
右下图所示图形面积为
b
A a f1(x) f2 (x) dx
o axxdx b x
首页
上页
返回
下页
结束
P274-1
例1. 计算两条抛物线 y2 x , y x2 在第一象限所围
返回
下页
结束
例4. 求由摆线 x a (t sin t), y a (1 cost) (a 0)
的一拱与 x 轴所围平面图形的面积 .
解:
2
AdA0 a (1 cost) a (1 cost) d t
a2 2 (1 cos t)2 d t 0
y
4a2 2 sin 4 t d t
0
cos
2
)
1 a2 a2 2
2
(3 2
2
cos
1 2
cos
2 )
y
d
1 a2 a2 (3 2)
2
4
5 a2 2a2
4
o
a 2a x
首页
上页
返回
下页
结束
例8. 求双纽线 r 2 a 2cos 2 所围图形面积 .
解: 利用对称性 , 则所求面积为
A 4
4
1 a2
cos2
d
02
解: 由 y2 2x 得交点 y x4
y yd y
y2 2x
(8, 4)
(2, 2) , (8, 4)
y
为简便计算, 选取 y 作积分变量,
则有
AdA
4
2
(
y
4
1 2
y
2
)
dy
o
yx4 x
(2, 2)
1 2
y
2
4
y
1 6
y3
4 2
18
首页
上页
返回
下页
结束
P276-3
例3. 求椭圆
x2 a2
则对应该小区间上曲边扇形面积的近似值为
dA 1 ( )2 d
2
所求曲边扇形的面积为
r ( ) d
A 1 2 ( ) d 2
x
首页
上页
返回
下页
结束
P277-4
例5. 计算阿基米德螺线 r a (a 0) 对应 从 0 变
到 2 所围图形面积 .
解: A 2 1 (a )2 d 02
