Buck电路设计与MATLAB仿真
电力电子课程设计-BUCK电路闭环PID控制系统的MATLAB仿真

电力电子课程设计-BUCK电路闭环PID控制系统的MATLAB仿真CHANGZHOU INSTITUTE OF TECHNOLOGY课程设计说明书课程设计名称:电力电子题目:BUCK电路闭环PID控制系统的MATLAB仿真—15V/5V二级学院(直属学部): 电子信息与电气工程学院专业:电气工程及其自动化班级:07电单学生姓名: 学号:指导教师姓名: 职称:讲师2011 年 1 月电力电子课程设计任务书二级学院(直属学部):电子信息与电气工程学院专业:电气工程及其自动化班级:学生姓名指导教师韩霞职称讲师课题名称 BUCK电路闭环PID控制系统的MATLAB仿真-15V/5V1、根据设计要求计算滤波电感和滤波电容的参数值,设计PID补偿网络2、采用MATLAB中simulink中的simpowersystems模型库搭建闭环降压式变换器的仿真模型3、观察系统在额定负载以及突加、突卸80%额定负载时的输出电压和负载电课流的波形4、撰写课程设计说明书,要求包括:题一、封面二、目录工三、正文1、降压变换器的基本原理作2、BUCK变换器主电路参数设计2.1设计内容及要求内 2.2主电路设计(占空比、滤波电感、滤波电容的设计)3、BUCK变换器闭环PID控制的参数设计容 3.1主电路传函分析3.2补偿环节的设计4、BUCK变换器闭环系统的仿真4.1仿真参数及过程描述4.2仿真模型图及仿真结果5、总结(含心得体会)6、参考文献(不少于6篇)21、输入直流电压(V):15V IN2、输出电压(Vo):5V3、输出电流(I):10A N指标4、输出电压纹波峰-峰值 Vpp?50mV)5、锯齿波幅值Um=1.5V 目标6、开关频率(fs):100kHZ )要7、采样网络传函H(s)=0.3 求8、BUCK主电路二极管的通态压降V=0.5V,电感中的电阻压降V=0.1V,开DL关管导通压降V=0.5V,滤波电容C与电解电容R的乘积为75uΩ*F ONC第1天阅读课程设计指导书,熟悉设计要求和设计方法第2天根据设计原理计算相关主要元件参数以及完成PID系统的设计进第3天熟悉MATLAB仿真软件的使用,构建系统仿真模型程安第4天仿真调试,记录要求测量波形排第5天撰写课程设计说明书1、电力电子课程设计任务书本院编2、电力电子课程设计指导书本院编3、王创社,乐开端等,开关电源两种控制模式的分析与比较,电力电子技术,1998,3,78一81; 主4、徐辅东,电流型控制开关变换器的研究与优化,西南交通大学硕士论文,要2000年4月。
BUCK电路的PID控制设计及仿真

BUCK电路的PID控制设计一、实验目的DC/DC 变换器可将不可控的直流输入变为可控的直流输出,广泛应用于可调直流开关电源及直流电机驱动中. Buck 变换器是DC/DC 变换器中最具代表性的拓扑结构之一.在工程实际中, Buck变换器的控制方式可以开环和闭环来实现。
其中闭环控制方式又可分为PI校正,PID控制,fuzzy控制等方式。
本文首先会建立Buck 变换器的模型,然后会分别进行开环、PI控制器校正,PID控制器校正,并在MATLAB/SIMULINK上进行仿真,最后对得出的结果进行比较。
二、设计内容及要求U):24V( 20%)1、输入电压(iU):12V(1%稳定度)2、输出电压(oI):1A3、额定电流(oV≤70mV4、输出电压纹波峰-峰值ppV≤150mV 6、开关5、满载与半载之间的切换时,输出电压纹波峰-峰值pp频率(f):无要求,本设计设定为20kHz三、Buck 主拓扑电路3.1开环Buck 电路图图(1)开环Buck 电路3.2 参数计算与选择(1)占空比 50%o i U D U == (2)滤波电感滤波电感的选择与负载电流的变化范围及希望的工作状态有关,假设电路要求工作在电感电流连续工作状态,则临界电感(1)2f o s oD U L I -= 根据公式代入计算可得:-4s (1)(10.5)*12 1.5*102f 2*20000o o U D L H I --===此时L 值为电感电流连续与否的临界值,实际电感值可选为(2~3)倍的临 界电感。
这里L 取4*104H 。
(3)滤波电容 电容的容量,会影响输出纹波电压和超调量的大小。
在开关关断时为负载供电和减小输出电压的纹波,滤波电容C 的选择直接关系开关稳压电源输出中纹波电压分量o U 大小。
滤波电容C2(1)8o o U D C U Lf-= 根据纹波要求代入计算-42-442(1)12*0.5==1.79*1088*0.07*1.5*10*(2*10)o o U D C U Lf -= F 这里电容C 取7.5*104F 。
基于MATLABSIMULINK的buck变换器的设计与分析
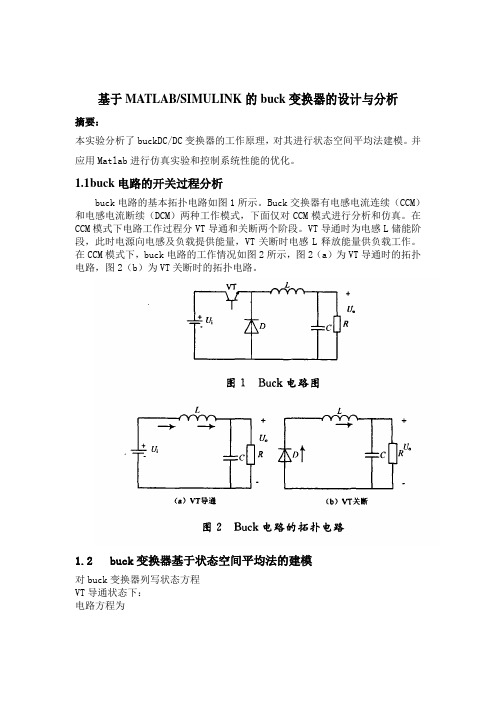
基于MATLAB/SIMULINK的buck变换器的设计与分析摘要:本实验分析了buckDC/DC变换器的工作原理,对其进行状态空间平均法建模。
并应用Matlab进行仿真实验和控制系统性能的优化。
1.1b uck电路的开关过程分析buck电路的基本拓扑电路如图1所示。
Buck交换器有电感电流连续(CCM)和电感电流断续(DCM)两种工作模式,下面仅对CCM模式进行分析和仿真。
在CCM模式下电路工作过程分VT导通和关断两个阶段。
VT导通时为电感L储能阶段,此时电源向电感及负载提供能量,VT关断时电感L释放能量供负载工作。
在CCM模式下,buck电路的工作情况如图2所示,图2(a)为VT导通时的拓扑电路,图2(b)为VT关断时的拓扑电路。
1.2buck变换器基于状态空间平均法的建模对buck变换器列写状态方程VT导通状态下:电路方程为状态方程为VT关断状态下:电路方程为状态方程为根据状态空间平均法,可以得到buck变换器的状态空间平均模型。
其基本思想是根据开关处于通态和断态时各自的状态方程及所占的时间比例,将两个不同时间段的方程按各自的时间比例加权平均,即可得到一个开关周期内,系统近似的平均状态方程。
因此设占空比为D,D*VT导通状态下的电路方程+(1-D)*VT断开状态下的电路方程得:由此得平均状态方程:因此应用现代控制理论得出buck电路的数学模型式中:状态变量X1为buck变换器输出电压,即电容两端电压;X2为电感电流;D为占空比。
1.3 buck变换器的MATLAB/SIMULINK仿真分析(1) 仿真程序(2) 进行参数的设定设定输入电压u=100V,R=0.5欧姆,D=40%,L=0.01H,C=0.1F电感L越小,电容C越大,震荡周期越小。
下图为不同的电感值和电容值对应的阶跃响应曲线改变L=0.001改变C=0.75占空比D影响输出电压的稳定值的大小,D越大稳定值越大。
改变D=0.5(3)利用配置零极点法设计控制器,优化系统性能1.极点配置法当系统参数为u=100V,R=0.5欧姆,D=40%,L=0.01H,C=0.1F时,对系统进行极点配置法优化。
Buck电路的闭环设计及仿真分析

Buck电路的闭环设计及仿真分析一、本文概述随着电力电子技术的飞速发展,电源转换技术已成为现代电子设备不可或缺的一部分。
其中,Buck电路作为一种基本的直流-直流(DC-DC)转换器,因其结构简单、效率高、调节范围宽等优点,在电子设备中得到了广泛应用。
然而,为了确保Buck电路在各种环境和负载条件下的稳定性和高效性,闭环设计显得尤为重要。
本文旨在探讨Buck电路的闭环设计方法,并通过仿真分析验证设计的有效性。
文章首先简要介绍了Buck电路的基本原理和应用背景,然后重点阐述了闭环设计的重要性及常用方法。
在闭环设计部分,文章详细分析了反馈网络的选取、控制策略的制定以及功率级和控制级的协同工作等问题。
同时,结合具体的设计实例,阐述了闭环设计在实际应用中的具体实现过程。
为了验证设计的有效性,文章采用了仿真分析的方法。
通过搭建基于MATLAB/Simulink的仿真模型,对设计的Buck闭环电路进行了全面的仿真分析。
仿真结果证明了闭环设计的有效性,同时也为实际电路的制作和调试提供了重要参考。
文章对闭环设计的Buck电路进行了总结,并指出了未来研究方向和潜在的应用前景。
通过本文的研究,旨在为从事电源转换技术研究和应用的工程师和学者提供有益的参考和启示。
二、Buck电路的基本原理Buck电路,也称为降压转换器,是一种基本的直流-直流(DC-DC)转换电路,其主要功能是将较高的直流电压降低到所需的较低直流电压。
其名称来源于电路中开关元件(如MOSFET或晶体管)的操作,类似于"bucking"(减少或抑制)输入电压。
Buck电路的基本构成包括一个开关(通常是MOSFET),一个电感(或称为线圈),一个二极管(也称为整流器或续流二极管),以及一个输出电容器。
在开关打开时,电流通过电感从输入源流向输出,此时电感储存能量。
当开关关闭时,电感释放其储存的能量,通过二极管向输出电容器和负载供电。
Buck电路的工作原理基于电感的电压-电流关系。
Buck电路设计与MATLAB仿真

Buck电路设计与MATLAB仿真LT利用simpowersystems中的模块建立所设计降压变换器的仿真电路。
输入电压为20V的直流电压源,开关管选MOSFET模块(参数默认),用Pulse Generator模块产生脉冲驱动开关管。
分别做两种开关频率下的仿真。
(1)使用理论计算的占空比(D=0.25),记录直流电压波形,计算稳态直流电压值,计算稳态直流纹波电压,并与理论公式比较,验证设计指标。
4、仿真过程::A.建立模型:建立仿真模型如下如所示:B. 记录数据:仿真算法选择ode23tb,最大步长为0.1s,占空比D=0.25进行仿真,记录数据如下表所示:开关频率f s(K Hz) 电感L(mH)电容C(μF)输出电压稳态值V o(V)输出电压纹波值ΔV o(V)电感电流波动值ΔI o(A)10 0.375500 4.736 0.0267 1 0.45 417 4.339 0.0275 0.875 0.1875500 6.435 0.0510 1.850 0.075100 4.745 0.0197 1.0140.09 83.3 4.396 0.0224 0.875与理论值对比开关频率f s(K Hz) 电感L(mH)电容C(μF)输出电压稳态值V o(V)输出电压纹波值ΔV o(V)电感电流波动值ΔI o(A)100.375500 5 0.025 1 0.45 417 5 0.025 0.833 0.1875 5005 0.025 2 500.075 100 5 0.025 1 0.09 83.3 50.0250.833C .仿真过程:当f s =10KHz,L=0.375mH C=500μF , 占空比D=0.25,电流连续的临界状态时,记录稳态直流电压值V o =4.736V ,稳态直流电压理论值5V计算稳态直流纹波电压的理论值2(1D)0.025V8s o o T V V CL-∆==,通过图中得到直流纹波电压为0.0267V当fs=10KHz,L=0.375mH, C=500μF,占空比D=0.25,电流连续的临界状态时,由(1)o SLV D T IL-∆=,得电感电流波动理论值是1A ,由图像得到电感电流波动值是1A ,与理论计算相符合Time/sP u l s e /VSwitch (fs=10KHz,L=0.375mH,C=500uF)Time/sI L /VInductor Current(fs=10KHz,L=0.375mH,C=500uF)Time/sU o /VUo (fs=10KHz,L=0.375mH,C=500uF)Figure-1 fs=10K Hz,L=0.375mH, C=500μF,占空比D=0.25,电流连续的临界状态取1.2倍临界电感值时,输出电压稳态值是4.399V ,理论值是5V ,纹波电压理论值0.025V记录波形测得纹波电压为0.0275V 电感电流波动理论值为0.833A ,由图像得到电感电流波动值是0.875ATime/sP u l s e /VPulse (fs=10KHz,L=0.45mH,C=417uF)Time/sI L /AInductor Current(fs=10KHz,L=0.45mH,C=417uF)取1.2倍电感值时0.1970.19750.1980.19850.1990.19950.20.20050.2010.2015Time/sU o /VUo (fs=10KHz,L=0.45mH,C=417uF)f s =50KHz,L=0.075mH, C=100μF, 占空比D=0.25,电流连续的临界状态时,记录稳态直流电压值V o =4.745V ,理论值是5V ,稳态直流纹波电压理论值0.025V ,由输出电压波形得到实际值为0.0197V电感电流波动理论值为1A ,测量值为1.014AFigure-2取1.2倍电感Time/sP u l s e /VPulse (fs=50KHz,L=0.075mH,C=100uF)Time/sI L /AInductor Current(fs=50KHz,L=0.075mH,C=100uF)x 10-3Time/sU o /VUo (fs=50KHz,L=0.075mH,C=100uF)Figure-3 f s =50KHz,L=0.075mH, C=100μF,占空比D=0.25,电流连续的临界状态取 1.2倍临界电感时,输出电压平均值为4.396V,理论值是5V,纹波电压理论值为0.025V,实际为0.0224V电感电流波动理论值为0.833A,实际值为0.875ATime/sP u l s e /VPulse (fs=50KHz,L=0.09mH,C=83.3uF)Time/sI L /AIductor Current(fs=50KHz,L=0.09mH,C=83.3uF)4.524.54 4.564.58 4.6 4.62 4.64x 10-3Time/sU o /VUo (fs=50KHz,L=0.09mH,C=83.3uF)Figure-4 取1.2倍电感时(2)画出电感电流波形,计算电流波动值并与理论公式对比记录数据如下表 开关频率f s (K Hz) 电感L(m H)电容C(μF)电感电流波动值ΔI o (A) 电感电流波动实际值ΔI o (A)100.375500 110.45 417 0.833 0.875 0.1875 500 2 1.8 500.07510011.014 0.09 83.3 0.8330.8750.10880.10890.1090.10910.10920.10930.10940.1095-1-0.50.511.52Time/sP u l s e /VSwitch (fs=10KHz,L=0.375mH,C=500uF)Time/sI L /VInductor Current(fs=10KHz,L=0.375mH,C=500uF)Figure-5 fs=10KHz,L=0.375mH, C=500μF,占空比D=0.25,电流连续的临界状态0.0250.02550.026-1-0.500.511.52Time/sP u l s e /VPulse (fs=10KHz,L=0.45mH,C=417uF)Time/sI L /AInductor Current(fs=10KHz,L=0.45mH,C=417uF)Figure-6 fs=10KH z,L=0.45mH, C=417μF,占空比D=0.250.02480.02490.025-1-0.500.51Time/sP u l s e /VTime/sI L /AInductor Current(fs=50KHz,L=0.075mH,C=100uF)Figure-7 f s =50KHz,L=0.075mH, C=100μF,占空比D=0.25,电流连续的临界状态0.02480.02490.025-1-0.500.511.52Time/sP u l s e /VPulse (fs=50KHz,L=0.09mH,C=83.3uF)Time/sI L /AIductor Current(fs=50KHz,L=0.09mH,C=83.3uF)Figure-8 f s =50KHz,L=0.09mH, C=83.3μF,占空比D=0.25(3)修改占空比,观察直流电压值的变化。
MatlabBuck电路的仿真

MatlabBuck电路的仿真MATLAB 仿真报告 2题目:Buck 电路的仿真一降压变换器,输入电压为600V,输出电压450V,电感值2mH、电容值1mF,负载电阻 3 ,开关频率为 2kHz。
用 SimPowerSystems 中的模块建立仿真电路。
开关管选 IGBT 模块。
(1) 计算开关器件的占空比。
D4 506 00=75%(2)对电路进行仿真。
(a)记录电容电压波形,计算稳态电压值,计算启动时的超调量;解:电容电压波形如下图所示,稳态电压值如上图 V=。
启动时的超调量如下图所示,Matlab给出启动时超调量为 %b)记录电感电流波形,计算稳态电流平均值,记录启动时的电流瞬时峰值;由图 1可以得出,稳态电流平均值为 I=,启动时电流瞬时峰值为.c)测量纹波电压和纹波电流;纹波电压波形如图 1,纹波电流波形如图 2。
图 1中电压最大值 Umax = ;电压最小值为 Umin = .图 2中电流最大值 Imax = ;电流最小值 Imin = .d)用理论分析上述结果。
在开关管打开的时候,电压加在电感两端给电感充电,在开关管闭合的时候,电感两端放电,被电容吸收,无功功率在电路中传输,造成了 V ripple以及 I ripple,导致纹波的产生。
(3) 将电感值修改为。
比较开关管分别选择为IGBT 和IGBT/Diode 时,波形有什么差别,并解释原因。
电感减少以后,将 IGBT换成 IGBT/Diode,电路的波形由原来的CCM工作在了DCM,电路超调量减小,稳定性上升,原因是 IGBT/Diode在 CE 点之间接入一个二极管,似的电路的电流电压被钳制在一个稳定值,电路启动时,不会拥有过大的超调量,电路的稳定性上升。
(4) 以(2)中的仿真为基础,不改变主电路的拓扑和参数,试通过控制手段,降低电路启动时电压电流的超调量。
在电路中加入一个串联校正控制器,电路的超调量有着明显的下降。
基于MATLAB的并联Buck_均流仿真

基于MATLAB的并联Buck均流仿真张莹文(洛阳师范学院物理与电子信息学院)摘 要: Buck是电源设计中常见的拓扑结构,使用多个Buck模块并联供电时会存在均流问题。
本文基于MATLAB设计一款并联Buck变换器,并基于串电阻法和平均电流法两种均流控制策略进行仿真分析。
首先提出并联电源模块的均流问题并对并联Buck变换器及均流控制策略进行简介,然后基于MATLAB搭建并联Buck电源模块的仿真模型,分别就串电阻法和平均电流法两种均流策略对并联Buck模块进行均流控制仿真,最后通过仿真结果的对比分析,发现并联Buck采用平均电流法时其均流效果更好。
关键词: Buck;并联; MATLAB;均流0 引言军工、工业、科研等领域的设备对电源的要求越来越高,电源模块正朝着大功率和大电流方向不断跨越,通过利用多个模块并联供电,还可以有效的减少电容、电感、变压器的尺寸,以及抑制干扰改善系统性能[1]。
在多个模块并联供电中,由于多个模块的外特性不同,每个模块分担电流也不同。
这会导致外特性差的模块可靠性降低。
并联运行技术中均流控制是研究的重点之一,即对负载电流的平均分配[2-4]。
通过利用均流控制策略来控制电源模块电流的均匀分配,实现稳定可靠的冗余系统[5, 6]。
本文针对开关电源Buck变换器进行并联均流控制策略的设计,采用双Buck并联电路,基于此进行串电阻法和平均电流法的并联均流控制策略的Buck变换器进行电路设计。
1 并联Buck变换器及均流控制策略简介如图1所示为两个降压斩波电路并联供电的原理图,图中包括两个MOSFET管分别是V1、 V2,两个储能电感分别是L1、 L2,两个续流二极管分别是VD1、VD2,一个滤波电容C和负载电阻R。
该电路在一个开关周期内共有4种模态[7, 8]。
目前常见的均流控制策略包括串电阻法、主从均流法、最大电流法和平均电流法等。
本文将对串电阻法和平均电流法进行设计与比较。
buck的pid-fuzzy控制matlab仿真
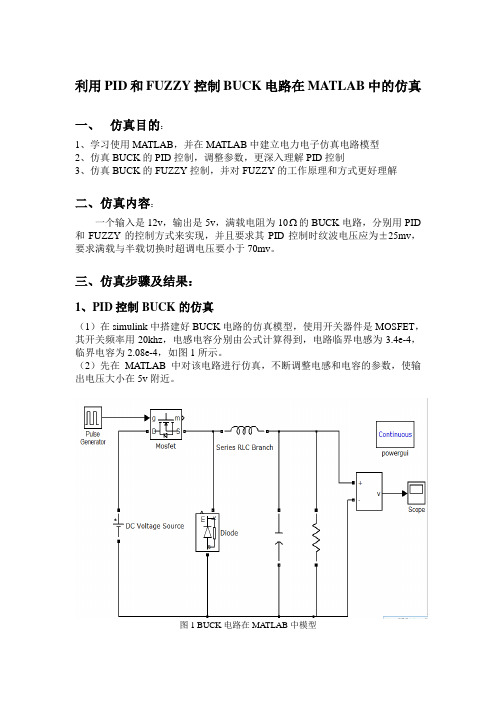
利用PID和FUZZY控制BUCK电路在MATLAB中的仿真一、仿真目的:1、学习使用MATLAB,并在MATLAB中建立电力电子仿真电路模型2、仿真BUCK的PID控制,调整参数,更深入理解PID控制3、仿真BUCK的FUZZY控制,并对FUZZY的工作原理和方式更好理解二、仿真内容:一个输入是12v,输出是5v,满载电阻为10 的BUCK电路,分别用PID 和FUZZY的控制方式来实现,并且要求其PID控制时纹波电压应为±25mv,要求满载与半载切换时超调电压要小于70mv。
三、仿真步骤及结果:1、PID控制BUCK的仿真(1)在simulink中搭建好BUCK电路的仿真模型,使用开关器件是MOSFET,其开关频率用20khz,电感电容分别由公式计算得到,电路临界电感为3.4e-4,临界电容为2.08e-4,如图1所示。
(2)先在MATLAB中对该电路进行仿真,不断调整电感和电容的参数,使输出电压大小在5v附近。
图1 BUCK电路在MA TLAB中模型(3)然后,在MATLAB中利用PID模块搭建反馈环节,建立PID的控制模块。
加了PID控制模块的电路如图2所示。
图2 PID控制的BUCK电路模型其中,PID模块选取了MATLAB中一个给出的模块,没有自己再搭建,工作过程是这样的:首先测量电路输出电压,然后和给定电压比较,得出差值信号,送给PID模块,通过PID调节输出的值再与三角波进行逻辑比较,输出的信号给MOSFET的门极,控制MOSFET的通断,实现对BUCK电路的控制。
其中,换载切换是通过接入和断开并联的电阻来实现的。
(4)电路一开始的输出电压是很不理想的,需要对PID的参数作调整,即调节Kp、Ki 、Kd以使输出达到题目要求的指标。
在调整的过程中,我首先调的是Kp,一开始按10的倍数变,然后找到一个相对好一点的范围在按3的倍数变,同理,最后调到了0.1的倍数,用这种方式先找出一个比较好的Ki的较小范围,然后在这个范围里,再调节Kd,调节Kd 的方法我用的和调Kp的一样,最后调的Ki。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Buck电路设计与仿真*名:***班级:电气1102学号:********日期:2014年5月10日指导老师:***北京交通大学计算机仿真技术作业四题目:Buck 电路的设计与仿真 1、Buck 电路设计:设计一降压变换器,输入电压为20V ,输出电压5V ,要求纹波电压为输出电压的0.5%,负载电阻10欧姆,求工作频率分别为10kHz 和50kHz 时所需的电感、电容。
比较说明不同开关频率下,无源器件的选择。
2、Buck 电路理论计算: 由以下公式计算:20.252.0.5A (1)3.5%8()4.2odoo o s o s d o LB OB V D V V I RV T D V LCDT V V I I L====∆-==-==1.占空比: 负载电流: 纹波电压: 电流连续条件:得到下列计算结果3、Buck 电路仿真:利用simpowersystems 中的模块建立所设计降压变换器的仿真电路。
输入电压为20V 的直流电压源,开关管选MOSFET 模块(参数默认),用Pulse Generator 模块产生脉冲驱动开关管。
分别做两种开关频率下的仿真。
(1)使用理论计算的占空比(D=0.25),记录直流电压波形,计算稳态直流电压值,计算稳态直流纹波电压,并与理论公式比较,验证设计指标。
4、仿真过程::A .建立模型:建立仿真模型如下如所示:B. 记录数据:仿真算法选择ode23tb,最大步长为0.1s ,占空比D=0.25进行仿真,记录数据如下表所C .仿真过程:当f s =10KHz,L=0.375mH C=500μF, 占空比D=0.25,电流连续的临界状态时,记录稳态直流电压值V o =4.736V ,稳态直流电压理论值5V计算稳态直流纹波电压的理论值2(1D)0.025V 8s o o T V V CL-∆==,通过图中得到直流纹波电压为0.0267V当fs=10KHz,L=0.375mH, C=500μF,占空比D=0.25,电流连续的临界状态时, 由(1)o SL V D T I L-∆=,得电感电流波动理论值是1A ,由图像得到电感电流波动值是1A ,与理论计算相符合Time/sP u l s e /VSwitch (fs=10KHz,L=0.375mH,C=500uF)Time/sI L /VInductor Current(fs=10KHz,L=0.375mH,C=500uF)0.04360.04380.0440.04420.04440.04460.04480.0450.04520.0454Time/sU o /VUo (fs=10KHz,L=0.375mH,C=500uF)Figure-1 fs=10KHz,L=0.375mH, C=500μF,占空比D=0.25,电流连续的临界状态取1.2倍临界电感值时,输出电压稳态值是4.399V ,理论值是5V ,纹波电压理论值0.025V 记录波形测得纹波电压为0.0275V 电感电流波动理论值为0.833A ,由图像得到电感电流波动值是0.875ATime/sP u l s e /VPulse (fs=10KHz,L=0.45mH,C=417uF)Time/sI L /AInductor Current(fs=10KHz,L=0.45mH,C=417uF)0.1970.19750.1980.19850.1990.19950.20.20050.2010.2015Time/sU o /VUo (fs=10KHz,L=0.45mH,C=417uF)f s =50KHz,L=0.075mH, C=100μF, 占空比D=0.25,电流连续的临界状态时,记录稳态直流电压值V o =4.745V ,理论值是5V ,稳态直流纹波电压理论值0.025V ,由输出电压波形得到实际值为0.0197V电感电流波动理论值为1A ,测量值为1.014ATime/sP u l s e /VPulse (fs=50KHz,L=0.075mH,C=100uF)Time/sI L /AInductor Current(fs=50KHz,L=0.075mH,C=100uF)66.026.04 6.066.086.1x 10-3Time/sU o /VUo (fs=50KHz,L=0.075mH,C=100uF)Figure-3 f s =50KHz,L=0.075mH, C=100μF, 占空比D=0.25,电流连续的临界状态取 1.2倍临界电感时,输出电压平均值为4.396V ,理论值是5V ,纹波电压理论值为0.025V ,实际为0.0224V电感电流波动理论值为0.833A ,实际值为0.875ATime/sP u l s e /VPulse (fs=50KHz,L=0.09mH,C=83.3uF)Time/sI L /AIductor Current(fs=50KHz,L=0.09mH,C=83.3uF)4.524.54 4.564.584.6 4.62 4.64x 10-3Time/sU o /VUo (fs=50KHz,L=0.09mH,C=83.3uF)Figure-4 取1.2倍电感时(2)画出电感电流波形,计算电流波动值并与理论公式对比 记录数据如下表Time/sP u l s e /VSwitch (fs=10KHz,L=0.375mH,C=500uF)Time/sI L /VInductor Current(fs=10KHz,L=0.375mH,C=500uF)Figure-5 fs=10KHz,L=0.375mH, C=500μF,占空比D=0.25,电流连续的临界状态0.0250.02550.026-1-0.5Time/sTime/sI L /AInductor Current(fs=10KHz,L=0.45mH,C=417uF)Figure-6 fs=10KHz,L=0.45mH, C=417μF,占空比D=0.250.02480.02490.025-1-0.500.511.52Time/sP u l s e /V0.02470.02480.02490.025Time/sI L /AInductor Current(fs=50KHz,L=0.075mH,C=100uF)Figure-7 f s =50KHz,L=0.075mH, C=100μF, 占空比D=0.25,电流连续的临界状态0.02480.02490.025-1-0.500.5Time/sP u lTime/sI L /AIductor Current(fs=50KHz,L=0.09mH,C=83.3uF)Figure-8 f s =50KHz,L=0.09mH, C=83.3μF, 占空比D=0.25DV o /VVo-D(Vd=20V)Figure-9 输出电压与占空比关系曲线(4)将电感改为临界电感值的一半,运行仿真模型(只仿真开关频率10k 时的情况,使用理论计算的占空比):记录电感电流波形,电感电流波动值为1.8A 观察不连续电流的波形;记录直流电压波形,计算稳态直流电压值,与理论公式6.67V 对比,,实际值6.435V 并与同一占空比下电流连续时的直流电压值4.736V 进行比较;计算稳态直流纹波电压,由图中得到纹波电压为0.0510V 并与理论公式比较(需根据电流波形计算D2的大小)。
理论值计算:1875.0101010875.144=⨯⨯==S RT L τ 5.0281212=-+=C C CD D D τ则 : V U D D D U S C C C 67.6205.025.025.01210=⨯+=+=2,max 22,max=0.00003 s 1.8A,0.645A 1()4LB o o o d LB I I V DI V D I ∆===+,[()][()()(())]2()0.0373Vs d o o s d o o o o d o s d o o o o d o o DT V V LI DT V V V LI V V V DT V V LI V LCV V V V ----+---∆=-∆=实际仿真值:6.435V V可见理论公式算出来的值比实际仿真出来的值要大一些,是由于反并联二极管作用导致。
但是,在同一占空比情况下,电流不连续情况下比连续情况的输出电压大, 比较稳态直流纹波电压:由图像得到输出电压的纹波为0.0510V在同一占空比的情况下,电流不连续情况下的纹波电压比连续情况明显增大。
Time/sP u l s e /VPulse (fs=10KHz,L=0.1875mH,C=500uF,D=0.25)Time/sI L /AIductor Current (fs=10KHz,L=0.1875mH,C=500uF,D=0.25)Time/sU o /VUo (fs=10KHz,L=0.1875mH,C=500uF,D=0.25)Figure-10 fs=10KHz,L=0.1875mH, C=500μF,占空比D=0.254、实验总结::通过本次的实验,使我在原有的基础上对MA TLAB有了更深一步的了解,不仅熟练了操作,而且也学会用仿真方法发现问题,并解决问题。
本次实验与电力电子学知识紧密结合,通过实际的仿真现象,使我更加熟知了课本中的原理概念,更加形象的理解了Buck变换器的工作原理。
