市说课比赛:山东卷圆锥曲线说课稿(定稿)(word和ppt配套,同名)..15页PPT
圆锥曲线定义的应用94111PPT精品文档18页

两点,若|AB|=m ,求ΔF2 AB 的周长 .
y
A
F1 o
F2 x
B
三、规律总结
1、在求轨迹方程时先利用定义判断曲线 形状可避免繁琐的计算. 2、涉及椭圆双曲线上的点与两个焦点构 成的三角形问题,常用第一定义结合正、 余弦定理来解决. 3、涉及焦点、准线、离心率、圆锥曲线上 的点中的三者,常用统一定义解决问题.
青并没有因为那天的小小不愉快,再表现出什么不高兴的和反常的举动来。108第三十四回 东伢子照面起风波|(兴冲冲前往 小树林,东伢子照面起风波;兴致全无扫兴归,小青耍小性真懊悔。)看到小青、耿英和耿直都不想再待在床上休息了,耿正 就对他们说:“我是一点儿也不累了。如果你们也不想再睡觉,不如和我一起到小树林那边去吧。咱们去告诉淋灰的人,来拉 他们的家伙什儿,顺便还可以在林子里边走一走呢!”大家都拍手称好。尤其是耿直,还高兴地蹦了一个高,大声说:“太好 了,到小树林里玩儿去喽,我看能不能抓到一只小兔子!”看他一边高兴地叫着,一边蹦跳着跑去开门了,小青笑着对耿英说: “直子小弟可真可爱啊,还顽皮呢!”耿英也笑着说:“他就是一个永远长不大的样子!”耿正高兴地一挥手,痛痛快快地大 声说:“小青姐,英子,咱们也走!”说着话,耿正领头出了过厅,忽然想起来没有带上那天卖石灰膏的头儿开的收据,就回 头对小青说:“对啦小青姐,你去向娘娘要上那个收据,我们好取回来押金!”小青恍然大悟,赶快回屋里跟姆妈要上收据, 出来了递给耿正,大家一起高高兴兴地出发了。不成想,四个人刚出院门儿,迎面就碰上了对门儿的东伢子正好挑着空水桶出 来。耿正和耿英同时向东伢子点点头打招呼:“嗨,东伢子,打水去啊?”东伢子憨厚地笑一笑,说:“啊,打水去。你们这 是要去哪里呀?”耿正和耿英还没有来得及回答呢,耿直就抢着说:“我们要去小树林里玩儿!”耿正也笑一笑,说:“我们 去小树林那边叫淋灰的人来拉他们的家伙什儿,顺便在林子里边走一走。”东伢子说:“小树林里是挺不错呢。天儿暖和了, 树上已经长出了新叶子,树下也有了小草小花儿的。走一走好哇,叫什么来着?”看他那可爱的憨厚样子,耿英忍不住笑了, 说:“你是想说‘踏青’吧?”东伢子说:“啊,对对对,踏青,踏青。春日里踏青,挺有意思的,我也很喜欢呢!”看耿正 兄妹三人和东伢子聊得很热乎,小青不乐意了。她偷偷地拽一拽耿英的衣角,大声说:“咱们快走啊,怎么说起来还没完了 呢!”耿正不解地看着小青,问:“小青姐,你这是怎么了?”小青赌气地一扭头,说:“没什么。你们去吧,我不去了,回 家去!”说着转身就要走,耿英赶快伸手拉住她,陪着笑脸说:“小青姐,这就是你的不对了。说好了一起去走一走的。你这 样赌气不去了,我们也玩儿不好啊!”抬头一看,东伢子已经很识趣儿地走了,就继续低声对她说:“人家东伢子又没有惹你, 你干吗要那样对待人家呢?”耿直也眨巴着眼睛说:“我也觉得刚才是小青姐姐不对。我很喜欢这个东伢子,他很像我们的大 壮哥哥呢!”耿直的后半句话让耿英心里一
2020年山东高考数学冲刺讲义-第5讲 圆锥曲线基础(教师版)
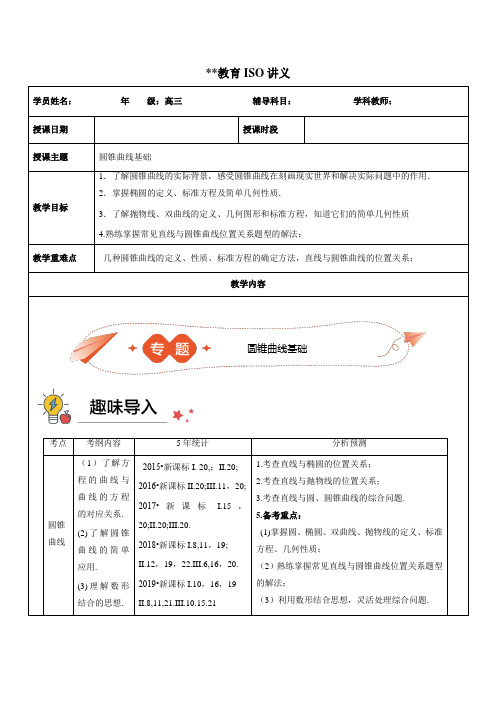
**教育ISO讲义学员姓名:年级:高三辅导科目:学科教师:授课日期授课时段授课主题圆锥曲线基础教学目标1.了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用.2.掌握椭圆的定义、标准方程及简单几何性质.3.了解抛物线、双曲线的定义、几何图形和标准方程,知道它们的简单几何性质4.熟练掌握常见直线与圆锥曲线位置关系题型的解法;教学重难点几种圆锥曲线的定义、性质、标准方程的确定方法,直线与圆锥曲线的位置关系;教学内容考点考纲内容5年统计分析预测圆锥曲线(1)了解方程的曲线与曲线的方程的对应关系.(2)了解圆锥曲线的简单应用.(3)理解数形结合的思想.2015•新课标I. 20,;II.20;2016•新课标II.20;III.11,20;2017•新课标I.15,20;II.20;III.20.2018•新课标I.8,11,19;II.12,19,22.III.6,16,20.2019•新课标I.10,16,19II.8,11,21.III.10.15.211.考查直线与椭圆的位置关系;2.考查直线与抛物线的位置关系;3.考查直线与圆、圆锥曲线的综合问题.5.备考重点:(1)掌握圆、椭圆、双曲线、抛物线的定义、标准方程、几何性质;(2)熟练掌握常见直线与圆锥曲线位置关系题型的解法;(3)利用数形结合思想,灵活处理综合问题.圆锥曲线基础【知识梳理】1. 圆锥曲线的定义、标准方程与几何性质名称椭圆双曲线抛物线定义|PF1|+|PF2|=2a(2a>|F1F2|)||PF1|-|PF2||=2a(2a<|F1F2|)|PF|=|PM|,点F不在直线l 上,PM⊥l于M标准方程x2a2+y2b2=1(a>b>0)x2a2-y2b2=1(a>0,b>0)y2=2px(p>0)图形几何性质范围|x|≤a,|y|≤b |x|≥a x≥0顶点(±a,0)(0,±b)(±a,0)(0,0)对称性关于x轴,y轴和原点对称关于x轴对称焦点(±c,0))0,2(p几何性质轴长轴长2a,短轴长2b实轴长2a,虚轴长2b离心率e=ca=1-b2a2(0<e<1)e=ca=1+b2a2(e>1)e=1 准线x=-p2渐近线y =±b ax2.直线圆锥曲线的位置关系判断直线l 与圆锥曲线C 的位置关系时,通常将直线l 的方程Ax +By +C =0(A ,B 不同时为0)代入圆锥曲线C 的方程F (x ,y )=0,消去y (也可以消去x )得到一个关于变量x (或变量y )的一元方程.即⎩⎨⎧==++0),(0y x F C By Ax 消去y ,得ax 2+bx +c =0. (1)当a ≠0时,设一元二次方程ax 2+bx +c =0的判别式为Δ,则Δ>0⇔直线与圆锥曲线C 相交; Δ=0⇔直线与圆锥曲线C 相切;Δ<0⇔直线与圆锥曲线C 相离.(2)当a =0,b ≠0时,即得到一个一次方程,则直线l 与圆锥曲线C 相交,且只有一个交点,此时,若C 为双曲线,则直线l 与双曲线的渐近线的位置关系是平行;若C 为抛物线,则直线l 与抛物线的对称轴的位置关系是平行或重合. 3.“弦”的问题 1.弦长公式设斜率为k (k ≠0)的直线l 与圆锥曲线C 相交于A ,B 两点,A (x 1,y 1),B (x 2,y 2),则2122122122122122124)(11114)(11y y y y ky y k x x x x k x x k AB -++=-+=-++=-+=2.处理中点弦问题常用的求解方法 (1).点差法:即设出弦的两端点坐标后,代入圆锥曲线方程,并将两式相减,式中含有x 1+x 2,y 1+y 2,y 1-y 2x 1-x 2三个未知量,这样就直接联系了中点和直线的斜率,借用中点公式即可求得斜率. (2).根与系数的关系:即联立直线与圆锥曲线的方程得到方程组,化为一元二次方程后由根与系数的关系求解.注意:中点弦问题常用的两种求解方法各有弊端:根与系数的关系在解题过程中易产生漏解,需关注直线的斜率问题;点差法在确定范围方面略显不足.考点一 圆锥曲线的定义与标准方程【例1】 (1)椭圆x 25+y 24=1的左焦点为F ,直线x =m 与椭圆相交于点M ,N ,当△FMN 的周长最大时,△FMN的面积是( )A .55B .655C .855D .455(2)设F 1,F 2分别是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,P 是C 上一点,若|PF 1|+|PF 2|=6a ,且△PF 1F 2最小内角的大小为30°,则双曲线C 的渐近线方程是( )A .2x ±y =0B .x ±2y =0C .x ±2y =0D .2x ±y =0【解析】 (1)如图,设椭圆的右焦点为F ′,连接MF ′,NF ′.因为|MF |+|NF |+|MF ′|+|NF ′|≥|MF |+|NF |+|MN |,所以当直线x =m 过椭圆的右焦点时,△FMN 的周长最大. 此时|MN |=2b 2a =855,又c =a 2-b 2=5-4=1,所以此时△FMN 的面积S =12×2×855=855.故选C.(2)不妨设P 为双曲线C 右支上一点,由双曲线的定义,可得|PF 1|-|PF 2|=2a .又|PF 1|+|PF 2|=6a ,解得|PF 1|=4a ,|PF 2|=2a ,又|F 1F 2|=2c ,则|PF 2|=2a 最小,所以∠PF 1F 2=30°. 在△PF 1F 2中,由余弦定理,可得cos 30°=|PF 1|2+|F 1F 2|2-|PF 2|22|PF 1||F 1F 2|=16a 2+4c 2-4a 22×4a ×2c =32,整理得c 2+3a 2=23ac ,解得c =3a ,所以b =c 2-a 2=2a .所以双曲线C 的渐近线方程为y =±2x .故选A.【答案】 (1)C (2)A 【总结】(1)圆锥曲线的定义①椭圆:|MF 1|+|MF 2|=2a (2a >|F 1F 2|). ②双曲线:||MF 1|-|MF 2||=2a (2a <|F 1F 2|). ③抛物线:|MF |=d (d 为M 点到准线的距离).[注意] 应用圆锥曲线定义解题时,易忽视定义中隐含条件导致错误.A .2B . 3C .2D . 5(2)(2019·济南市模拟考试)设F 1,F 2分别是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,过F 2的直线交椭圆于A ,B 两点,且AF →1·AF →2=0,AF →2=2F 2B →,则椭圆E 的离心率为( )A .23B .34C .53D .74【解析】 (1)如图,由题意,知以OF 为直径的圆的方程为2)2(c x -+y 2=c 24①,将x 2+y 2=a 2记为②式,①-②得x =a 2c ,则以OF 为直径的圆与圆x 2+y 2=a 2的相交弦所在直线的方程为x =a 2c ,所以|PQ |=222)(2c a a -由|PQ |=|OF |,得222)(2ca a -=c ,整理得c 4-4a 2c 2+4a 4=0,即e 4-4e 2+4=0,解得e =2,故选A.(2)设|BF 2|=m ,则|AF 2|=2m .连接BF 1,由椭圆的定义可知|AF 1|=2a -2m ,|BF 1|=2a -m .由AF →1·AF →2=0知AF 1⊥AF 2,故在Rt △ABF 1中,(2a -2m )2+(3m )2=(2a -m )2,整理得m =a 3.故在Rt △AF 1F 2中,|AF 1|=4a3,|AF 2|=2a 3,故22)34()32(a a +=4c 2,解得e =53. 【答案】 (1)A (2)C【总结】(1)椭圆、双曲线的离心率(或范围)的求法求椭圆、双曲线的离心率或离心率的范围,关键是根据已知条件确定a ,b ,c 的等量关系或不等关系,然后把b 用a ,c 代换,求ca的值.(2)双曲线的渐近线的求法及用法①求法:把双曲线标准方程等号右边的1改为零,分解因式可得. ②用法:(i)可得b a 或ab的值.(ii)利用渐近线方程设所求双曲线的方程.【变式训练1】(2019·广州市调研测试)已知抛物线y 2=2px (p >0)与双曲线x 2a 2-y 2b2=1(a >0,b >0)有相同的焦点F ,点A 是两曲线的一个交点,且AF ⊥x 轴,则双曲线的离心率为( )A .2+1B .3+1C .5+1D .2+2解析:选A.如图,结合题意画出图形,因为抛物线的焦点坐标为)0,2(p ,所以由题设知双曲线的右焦点的坐标为)0,2(p ,所以a 2+b 2=p 24①.因为AF ⊥x 轴,所以由点A 在抛物线上可得A )p ,2(p (取A 在第一象限),又点A 在双曲线上,所以p =b 2a ②.将②代入①得a 2+b 2=b 44a 2,即b 4=4a 4+4a 2b 2,所以44)(b a +42)(b a -1=0,所以2)(ba =2-12,从而e 2=c 2a 2=2-1+22-1=(2+1)2,故e =2+1.故选A.【变式训练2】(2019·济南一模改编)抛物线y 2=8x的焦点到双曲线x 216-y 29=1渐近线的距离为________,双曲线右焦点到抛物线准线的距离为________.解析:抛物线y 2=8x的焦点F (2,0),双曲线 x 216-y 29=1的一条渐近线方程为y =34x ,即3x -4y =0,则点F (2,0)到渐近线3x -4y =0的距离为|3×2-4×0|32+42=65.双曲线右焦点的坐标为(5,0),抛物线的准线方程为x =-2,所以双曲线右焦点到抛物线准线的距离为7.答案:657考点三 直线与圆锥曲线的位置关系 角度一 位置关系的判断及应用【例3】 在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :y 2=2px (p >0)于点P ,M 关于点P 的对称点为N ,连接ON 并延长交C 于点H .(1)求|OH ||ON |; (2)除H 以外,直线MH 与C 是否有其他公共点?说明理由.【解】 (1)由已知得M (0,t ),P ),2(2t pt 又N 为M 关于点P 的对称点,故N ),(2t pt ,ON 的方程为y =pt x ,代入y 2=2px ,整理得px 2-2t 2x =0,解得y 1+y 2,y 1y 2,则弦长|AB |=1+k 2·(x 1-x 2)2=1+k 2·(x 1+x 2)2-4x 1x 2=1+1k2·|y 1-y 2|=1+1k 2·(y 1+y 2)2-4y 1y 2(k 为直线的斜率且k ≠0),当A ,B 两点坐标易求时也可以直接用|AB |=(x 1-x 2)2+(y 1-y 2)2求之.【变式训练1】.过点P (4,2)作一直线AB 与双曲线C :x 22-y 2=1相交于A 、B 两点,若P 为AB 中点,则|AB |=( )A .22B .2 3C .3 3D .4 3解析:易知直线AB 不与y 轴平行,设其方程为y -2=k (x -4),代入双曲线C :x 22-y 2=1,整理得(1-2k 2)x 2+8k (2k -1)x -32k 2+32k -10=0,设此方程两实根为x 1,x 2,则x 1+x 2=8k (2k -1)2k 2-1,又P (4,2)为AB 的中点,所以8k (2k -1)2k 2-1=8,解得k =1,当k =1时,直线与双曲线相交,即上述二次方程的Δ>0,所求直线AB 的方程为y -2=x -4化成一般式为x -y -2=0,x 1+x 2=8,x 1x 2=10, |AB |=2|x 1-x 2|=2·82-40=4 3.故选D.答案:D【变式训练2】(2019·内江模拟)设椭圆x 2a 2+y 2b 2=1(a >b >0)的左右焦点分别为F 1、F 2,上下顶点分别为A 、B ,直线AF 2与该椭圆交于A 、M 两点.若∠F 1AF 2=120°,则直线BM 的斜率为( )A.14 B.34C.32D. 3解析:由题意,椭圆x 2a 2+y 2b2=1(a >b >0),且满足∠F 1AF 2=120°,如图所示,则在△AF 2O 中,|OA |=b ,|AF 2|=a ,且∠OAF 2=60°,所以a =2b , 不妨设b =1,则a =2,所以c =a 2-c 2=3,则椭圆的方程为x 24+y 2=1,由题意知圆心(0,0)到直线l 的距离d =|-m |2<1,得|m |< 2.|AB |=21-d 2=21-m 22=2×2-m 2,联立得⎩⎪⎨⎪⎧x 24+y 23=1,y =-x +m ,消去y ,得7x 2-8mx +4m 2-12=0,由题意得Δ=(-8m )2-4×7(4m 2-12)=336-48m 2=48(7-m 2)>0,解得m 2<7, 设C (x 1,y 1),D (x 2,y 2),则x 1+x 2=8m7,x 1x 2=4m 2-127,|CD |=2|x 1-x 2|=2×(8m 7)2-4×4m 2-127=2× 336-48m 249=467×7-m 2=837|AB |=837×2×2-m 2,解得m 2=13<7,得m =±33.即存在符合条件的直线l ,其方程为y =-x ±33.【总结】【变式训练1】(2019·大连模拟)已知抛物线C :x 2=2py (p >0),其焦点到准线的距离为2,直线l 与抛物线C 交于A ,B 两点,过A ,B 分别作抛物线C 的切线l 1,l 2,l 1与l 2交于点M .(1)求p 的值;(2)若l 1⊥l 2,求△MAB 面积的最小值. 解析:(1)由题意知,抛物线焦点为:)2,0(p ,准线方程为:y =-p2,焦点到准线的距离为2,即p =2. (2)抛物线的方程为x 2=4y ,即y =14x 2,所以y ′=12x ,设A (x 1,y 1),B (x 2,y 2),l 1:y -x 214=x 12(x -x 1),l 2:y -x 224=x 22(x -x 2),由于l 1⊥l 2,所以x 12·x 22=-1,即x 1x 2=-4.设直线l 方程为y =kx +m ,与抛物线方程联立,得⎩⎪⎨⎪⎧y =kx +m x 2=4y,所以x 2-4kx -4m =0,依题意,y 1+y 2=-2tm t 2+4,所以m -2t 2mt 2+4=0,又m ≠0,所以t 2=4,因为t >0,故得t =2,所以k l =1t =12,即直线l 的斜率为12.【变式训练3】已知抛物线C :y =2x 2,直线l :y =kx +2交抛物线C 于A ,B 两点,M 是线段AB 的中点,过点M 作x 轴的垂线交C 于点N .(1)证明:抛物线C 在点N 处的切线与AB 平行;(2)是否存在实数k ,使得以AB 为直径的圆M 经过点N ?若存在,求出k 的值;若不存在,请说明理由. 解析:(1)证明:设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =kx +2,y =2x 2得2x 2-kx -2=0, 则x 1+x 2=k2,x 1·x 2=-1,因为M 是线段AB 的中点,所以M (k 4,k 24+2),又过点M 作x 轴的垂线交C 于点N ,所以N (k 4,k 28).因为y =2x 2,所以y ′=4x ,则抛物线C 在点N 处的切线的斜率为4×k4=k ,故抛物线C 在点N 处的切线与AB 平行.(2)假设存在实数k ,使得以AB 为直径的圆M 经过点N ,则|MN |=12|AB |.由(1)知y M =k 24+2,又MN 垂直于x 轴,所以|MN |=y M -y N =k 24+2-k 28=k 2+168.由(1)知,x 1+x 2=k2,x 1x 2=-1,所以|AB |=1+k 2|x 1-x 2|=1+k 2·(x 1+x 2)2-4x 1x 2=1+k 2·(k 2)2+4=121+k 2·16+k 2, 所以k 2+168=141+k 2·16+k 2,即k 4+12k 2-64=0,解得k =±2.故存在实数k =±2,使得以AB 为直径的圆M 经过点N .一、选择题1.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的焦点到渐近线的距离为3,且离心率为2,则该双曲线的实轴的长为( )A .1B . 3解析:选C.由题意知双曲线的焦点(c ,0)到渐近线bx -ay =0的距离为bca 2+b2=b =3,即c 2-a 2=3,又e =ca=2,所以a =1,该双曲线的实轴的长为2a =2. 2.若抛物线y 2=4x 上一点P 到其焦点F 的距离为2,O 为坐标原点,则△OFP 的面积为( ) A .12B .1C .32D .2解析:选B.设P (x 0,y 0),依题意可得|PF |=x 0+1=2,解得x 0=1,故y 20=4×1,解得y 0=±2,不妨取P (1,2),则△OFP 的面积为12×1×2=1.3.(2019·高考全国卷Ⅲ)双曲线C :x 24-y 22=1的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点.若|PO |=|PF |,则△PFO 的面积为( )A .324B .322C .2 2D .3 2解析:选A.不妨设点P 在第一象限,根据题意可知c 2=6,所以|OF |= 6.又tan ∠POF =b a =22,所以等腰三角形POF 的高h =62×22=32,所以S △PFO =12×6×32=324.4.(2019·昆明模拟)已知F 1,F 2为椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,B 为C 的短轴的一个端点,直线BF 1与C 的另一个交点为A ,若△BAF 2为等腰三角形,则|AF 1||AF 2|=( )A .13B .12C .23D .3解析:选A.如图,不妨设点B 在y 轴的正半轴上,根据椭圆的定义,得|BF 1|+|BF 2|=2a ,|AF 1|+|AF 2|=2a ,由题意知|AB |=|AF 2|,所以|BF 1|=|BF 2|=a ,|AF 1|=a 2,|AF 2|=3a 2.所以|AF 1||AF 2|=13.故选A.5.(2019·湖南湘东六校联考)已知椭圆Γ:x 2a 2+y 2b 2=1(a >b >0)的长轴长是短轴长的2倍,过右焦点F 且斜率为k (k >0)的直线与Γ相交于A ,B 两点.若AF →=3FB →,则k =( )k 1=y 1x 1+3=26(x 1+1)x 1+3=469,k 2=-y 2-x 2-3=26(x 2+1)x 2+3=-263, 所以3k 1+2k 2=3×469+2×)362( =0,即3k 1+2k 2的值为0.通过本节课的学习,你掌握了哪些内容?。
山东省各地市高考数学(文科)最新试题分类大汇编21:圆锥曲线(1)讲课教案
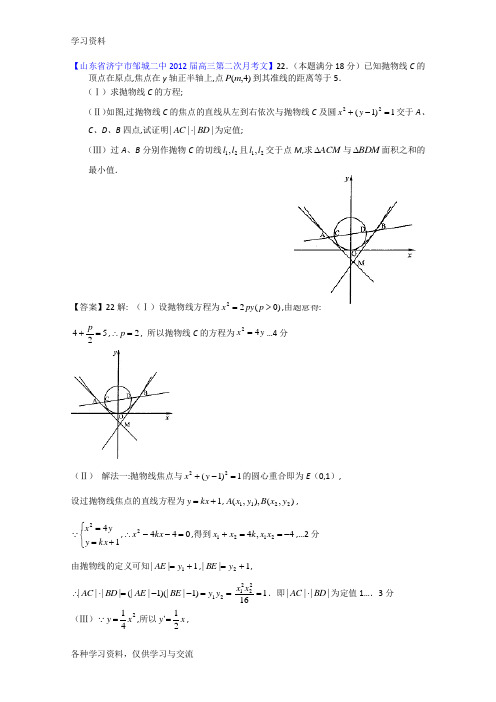
【山东省济宁市邹城二中2012届高三第二次月考文】22.(本题满分18分)已知抛物线C 的顶点在原点,焦点在y 轴正半轴上,点)4,(m P 到其准线的距离等于5. (Ⅰ)求抛物线C 的方程;(Ⅱ)如图,过抛物线C 的焦点的直线从左到右依次与抛物线C 及圆1)1(22=-+y x 交于A 、C 、D 、B 四点,试证明||||BD AC ⋅为定值;(Ⅲ)过A 、B 分别作抛物C 的切线21,l l 且21,l l 交于点M ,求ACM ∆与BDM ∆面积之和的最小值.【答案】22解: (Ⅰ)设抛物线方程为)0(22>=p py x ,由题意得:524=+p,2=∴p , 所以抛物线C 的方程为y x 42=…4分(Ⅱ) 解法一:抛物线焦点与1)1(22=-+y x 的圆心重合即为E (0,1), 设过抛物线焦点的直线方程为1+=kx y ,),(),,(2211y x B y x A ,⎩⎨⎧+==142kx y yx ,0442=--∴kx x ,得到4,42121-==+x x k x x ,…2分 由抛物线的定义可知1||1+=y AE ,1||2+=y BE ,==--=⋅∴21)1|)(|1|(|||||y y BE AE BD AC 1162221=x x .即||||BD AC ⋅为定值1 (3)(Ⅲ)241x y = ,所以x y 21'=,所以切线AM 的方程为)(2141121x x x x y -=-,切线BM 的方程为)(2142222x x x x y -=-,解得)4,2(2121x x x x M +即)1,2(-k M ……2分所以点M 到直线AB 的距离为221|22|kk d ++=.设=++⋅+=+=+=∆∆2221122)(21|)||(|21kk y y d BD AC S S y BDMACM1)24(11]2)([222221++=++⋅++=k k k k x x k (2)令),1[12+∞∈=+t k ,所以t t y 243-=,0212'2>-=∴t y ,所以t t y 243-=在),1[+∞上是增函数,当1=t ,即0=k 时,2min =y ,即ACM ∆与BDM ∆面积之和的最小值为2…3分(Ⅱ)解法二:设过抛物线焦点的直线方程为1+=kx y ,),(),,(2211y x B y x A ,不妨设0,021><x x .⎩⎨⎧+==142kx y yx ,0442=--∴kx x ,得到4,42121-==+x x k x x ,.2分 12121||1||x k x k AE ⋅+-=+=∴,22221||1||x k x k BE ⋅+=+=,1)(1)1()11)(11(||||2122122212+-+++-=-⋅+-⋅+-=⋅∴x x k x x k x k x k BD AC 1116161)1(4222=++⋅+++=k k k ,即||||BD AC ⋅为定值 (3)(Ⅲ)241x y = ,所以x y 21'=,所以切线AM 的方程为)(2141121x x x x y -=-,切线BM 的方程为)(2142222x x x x y -=-,解得)4,2(2121x x x x M +即)1,2(-k M ……….3分 所以点M 到直线AB 的距离为221|22|kk d ++=.设222212122)1111(21|)||(|21kk x k x k d BD AC S S y BDMACM ++⋅-⋅++-⋅+-=+=+=∆∆1]2)1(4[11]2)(1[2222122+⋅-+=++⋅--+=k k k k x x k …3分令),1[12+∞∈=+t k ,所以t t y 243-=,0212'2>-=∴t y ,所以t t y 243-=在),1[+∞上是增函数,当1=t ,即0=k 时,2min =y ,即ACM ∆与BDM ∆面积之和的最小值为2【山东省济宁市金乡二中2012届高三11月月考文】2.已知双曲线22221x y a b-=,过其右焦点且垂直于实轴的直线与双曲线交于M 、N 两点,O 是坐标原点.若OM ON ⊥,则双曲线的离心率为( )A. 122+B. 13+C. 15+D. 17+ 【答案】C【山东省济宁市金乡二中2012届高三11月月考文】17.(本题满分14分)已知双曲线1:2222=-b y a x C 的一个焦点是抛物线x y 522=的焦点,且双曲线C 经过点)3,1(,又知直线1:+=kx y l 与双曲线C相交于A 、B 两点.(1)求双曲线C 的方程; (2)若OB OA ⊥,求实数k 值.【答案】17(1) 412x 112=-y (2) 2±=k (验证0≥∆)【山东省济宁市金乡二中2012届高三11月月考文】19.(本小题满分13分)已知抛物线C :2y mx =(0m >),焦点为F ,直线220x y -+= 交抛物线C 于A 、B 两点,P 是线段AB 的中点,过P 作x 轴的垂线交抛物线C 于点Q . (1)求抛物线C 的焦点坐标;(2)若抛物线C 上有一点(,2)R R x 到焦点F 的距离为3,求此时m 的值;(3)是否存在实数m ,使△ABQ 是以Q 为直角顶点的直角三角形?若存在,求出m 的值;若不存在,说明理由。
圆锥曲线与方程说课稿高三数学二轮复习(1)

《圆锥曲线与方程》说课稿单元教学有利于整体规划学生核心素养的发展,有利于借助于大背景、大问题、大思路、大框架进行高观点统领、思想性驾驭、结构化关联,能有效规避传统的课时教学整体感不强、知识分解过度、学习碎片化、教学效益低下的现象。
但数学单元教学同时也要求课时教学,它应该在核心素养和课程目标的指引下,设计单元教学目标和课时教学目标,使之成为一个前后联系、相互支撑的整体,今天,我就“圆锥曲线与方程”的二轮复习进行单元设计与课时实施的说课。
1 单元教学的整体设计圆锥曲线包含椭圆、双曲线、抛物线,从知识技能角度看,三者的知识结构相近,知识间存在内在的必然联系,具有统一性,一轮复习我们采用了“总——分—总”的方式,把三者整合在一起,即先通过曲线与方程部分总体建构几何与代数的轨迹关系,引出大单元的学习内容。
然后分三个小单元进行学习,每个单元的研究结构是一致的,均从定义、标准方程和几何性质三个方面展开研究。
最后在知识学习的基础上,进行直线与圆锥曲线的位置关系的整体教学,形成圆锥曲线学习与研究的大框架。
经过一轮复习,学生掌握了圆锥曲线基础知识,学生初步建立了利用圆锥曲线知识解决解问题的基本思路及模式,但是在解题过程中,学生往往急于求成或者套用现成的模式,分析解决问题的能力较弱;主动把题目与相关概念建立联系的意识比较淡薄,表现在选填题目不能深入挖掘已知条件,将已知和所学知识建立联系的能力不足;而对于圆锥曲线的学习,知识的内在统一性是一条明线,内隐的用代数的方法研究几何,深刻认识数和形的辩证统一是一条暗线。
所以在二轮复习时,我们从思想方法视角对传统的知识单元进行重整,更为上位地认识学科知识。
重整后的三个小单元的做法和目标各不相同,如果说一轮复习进行的是横向到边的广度学习,那么二轮复习我希望以核心素养为立意,以整体设计为入口,进行纵向到底的深度学习。
“核心素养一课程标准一单元设计—课时计划”是环环相扣的教师教育活动的基本环节,单元设计下的课时教学不同于传统的以知识传授为主的学习,强调将教学内容置于整体内容中去把控,更多地关注教学内容的本质及其蕴含的数学思想。
2010年山东省烟台市数学圆锥曲线练习上课教案2

顶点: ,特殊点:
实轴: 长为2a, a叫做半实轴长;虚轴: 长为2b,b叫做虚半轴长,双曲线只有两个顶点,而椭圆则有四个顶点,这是两者的又一差异。
(3)渐近线
过双曲线 的渐近线 ( )(4)离心率
双曲线的焦距与实轴长的比 ,范围:
7.等轴双曲线
(1)渐近线方程为 ;(2)渐近线互相垂直;(3)离心率
技能情感目
结合教学内容对学生进行运动变化和对立统一的观点的教育;培养学生抽象概括能力和逻辑思维能力
重难点
教学重点:三种曲线的标准方程和图形、性质;
教学难点:做好思路分析,引导学生找到解题的落足点。
教学方法
与教具、教材
多媒体、展台、几何画板
启发式教学、学生自主讨论
人教选修1-1
板书设计
备课组长签字:__________________
教师指导内容
学生活动内容
2.已知抛物线方程为 ,直线 过抛物线的焦点F且被抛物线截得的弦长为3,求p的值.
解:设 与抛物线交于
由距离公式
|AB|= =
则有
由
从而 由于p>0,解得
三、课堂小结(用时分钟)
四、随堂作业(用时分钟)
如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为 ,以x轴为对称轴,过A,O,B三点作抛物线
教师指导内容
学生活动内容
一、知识归类(用时分钟)
4.双曲线的定义:平面内到两定点 的距离的差的绝对值为常数(小于 )的动点的轨迹叫双曲线即 这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距
5.双曲线的标准方程:
( , ); ( , )
(2) 有关系式 成立,且
山东省泰安市高考一轮复习金榜聚焦:第17讲 圆锥曲线

圆锥曲线经典精讲主讲教师:王春辉 北京数学特级教师引入从一道题谈起:若椭圆22221(0)x y a b a b+=>>上存在一点,使得,则椭圆离心率的取值范围是 .归纳与总结 (1)从椭圆01:2222>>=+b a by a x C ,上的点P 看长轴两端点的视角达最大时,点P 位于 ; (2)从椭圆01:2222>>=+b a by a x C ,上的点P 看两焦点的视角达到最大时,点位于 ; (3)从椭圆01:2222>>=+b a by a x C ,上的点P 看短轴两端点的视角达最小时,点P 位于 .重难点突破题一:已知椭圆22221(0)x y a b a b+=>>和圆O :,过椭圆上一点P 引圆O 的两条切线,切点分别为A 、B .(1)①若圆O 过椭圆的两个焦点,求椭圆的离心率e ;②若椭圆上存在点P ,使得∠APB =90°,求椭圆离心率的取值范围;(2)直线AB 与x 轴、y 轴分别交于点M 、N ,求证:为定值.金题精讲题一:过抛物线的焦点的直线与抛物线交于,两点,过,两点分别作抛物线的切线,这两条切线的交点为.(Ⅰ)求的值;(Ⅱ)求证:是和的等比中项.题二:已知双曲线2222:1(0,0)x yC a ba b-=>>,分别为C的左、右焦点.P为C右支上一点,且的面积为.(Ⅰ)求C的离心率e;(Ⅱ)设A为C的左顶点,Q为第一象限内C上的任意一点,问是否存在常数,使得恒成立.若存在,求出的值;若不存在,请说明理由.引入题一:重难点突破题一:(1)①,②;(2)定值为,证明略金题精讲题一:(Ⅰ)0;(Ⅱ)证明略题二:(Ⅰ)2;(Ⅱ)存在,=2.。
圆锥曲线学生公开课教案教学设计课件资料

圆锥曲线学生公开课教案教学设计课件资料一、教学目标1. 知识与技能:理解圆锥曲线的概念和性质。
掌握圆锥曲线的标准方程及其求法。
学会运用圆锥曲线解决实际问题。
2. 过程与方法:培养学生的观察、分析和解决问题的能力。
培养学生的逻辑思维能力和数学美感。
培养学生的合作交流和表达能力。
3. 情感态度与价值观:激发学生对圆锥曲线的兴趣和好奇心。
培养学生对数学美的感知和欣赏能力。
培养学生勇于探索和创新的思维精神。
二、教学内容1. 圆锥曲线的概念与性质引导学生通过观察圆锥的切割和展开,理解圆锥曲线的形成过程。
引导学生探究圆锥曲线的几何性质,如曲率、渐近线等。
2. 圆锥曲线的标准方程引导学生利用圆锥曲线的性质推导出标准方程。
引导学生理解不同类型的圆锥曲线(如椭圆、双曲线、抛物线)的标准方程及其特点。
3. 圆锥曲线的应用引导学生运用圆锥曲线解决实际问题,如测量问题、轨迹问题等。
引导学生运用圆锥曲线方程进行优化问题求解。
三、教学过程1. 导入通过展示圆锥曲线在现实生活中的应用实例,引发学生对圆锥曲线的兴趣。
引导学生回顾之前的数学知识,为新课的学习做好铺垫。
2. 知识讲解利用多媒体课件,生动形象地展示圆锥曲线的形成过程。
引导学生通过合作交流,探究圆锥曲线的几何性质。
利用数学软件,动态展示圆锥曲线的变化,增强学生对圆锥曲线的理解。
3. 例题讲解与练习讲解典型例题,引导学生掌握解题方法。
安排适量练习题,巩固所学知识。
4. 课堂小结总结本节课的主要内容和知识点。
强调圆锥曲线在实际生活中的应用价值。
四、教学评价1. 课堂表现评价:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态。
2. 练习题评价:通过学生完成的练习题,评估学生对圆锥曲线知识点的掌握程度。
3. 小组讨论评价:评估学生在合作交流中的表现,如观点阐述、团队协作等。
五、教学资源1. 多媒体课件:展示圆锥曲线的形成过程、几何性质和应用实例。
2. 数学软件:动态展示圆锥曲线的变化,增强学生直观感受。
山东省胶州市高考数学二轮复习第12讲圆锥曲线的定义、方程、几何性质学案(无答案)文(2021年整理)

山东省胶州市2018届高考数学二轮复习第12讲圆锥曲线的定义、方程、几何性质学案(无答案)文编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山东省胶州市2018届高考数学二轮复习第12讲圆锥曲线的定义、方程、几何性质学案(无答案)文)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山东省胶州市2018届高考数学二轮复习第12讲圆锥曲线的定义、方程、几何性质学案(无答案)文的全部内容。
第12讲圆锥曲线的定义、方程、几何性质学习目标【目标分解一】圆锥曲线的定义、标准方程【目标分解二】圆锥曲线的几何性质重点圆锥曲线的定义、标准方程及几何性质【课前自主复习区】■核心知识储备提炼1 圆锥曲线的重要性质(1)椭圆、双曲线中a,b,c之间的关系①在椭圆中:a2=b2+c2;离心率为e=错误!=错误!;②在双曲线中:c2=a2+b2;离心率为e=错误!=错误!.(2)双曲线的渐近线方程与焦点坐标①双曲线错误!-错误!=1(a>0,b>0)的渐近线方程为y=±错误!x;焦点坐标F1(-c,0),F2(c,0);②双曲线错误!-错误!=1(a>0,b>0)的渐近线方程为y=±错误!x,焦点坐标F1(0,-c),F2(0,c).(3)抛物线的焦点坐标与准线方程①抛物线y2=±2px(p>0)的焦点坐标为错误!,准线方程为x=∓错误!;②抛物线x2=±2py(p>0)的焦点坐标为错误!,准线方程为y=∓错误!。
提炼2 弦长问题(1)直线与圆锥曲线相交时的弦长斜率为k的直线与圆锥曲线交于点A(x1,y1),B(x2,y2)时,|AB|=或|AB|=(2)抛物线焦点弦的几个常用结论设AB是过抛物线y2=2px(p>0)焦点F的弦,若A(x1,y1),B(x2,y2),则①x1x2=错误!,y1y2=-p2;②弦长|AB|=x1+x2+p=错误!(α为弦AB的倾斜角);③错误!+错误!=2p;④以弦AB为直径的圆与准线相切.[高考真题回访]1.(2013·全国卷Ⅰ改编)已知圆M :(x +1)2+y 2=1,圆N :(x -1)2+y 2=9,动圆P 与圆M外切并且与圆N 内切,圆心P 的轨迹为曲线C ,则C 的方程为________. 2。
