2012年北京市高考试题集锦理数(含答案)
2012年理数高考试题答案及解析北京

2012年普通高等学校招生全国统一考试数学 (理 )(北京卷 )本试卷共 5 页 . 150 分 .考试时长 120 分钟 .考试生务必将答案答在答题卡上 .在试卷上作答无效 .考试结束后,将本试卷和答题卡一并交回.第一部分 ( 选择题共 40 分 )一、选择题共 8 小题。
每小题 5 分 .共 40 分 .在每小题列出的四个选项中, 选出符合胜目要求的一项 .1.已知集合 A={x ∈ R|3x+2> 0} B={x ∈ R|( x+1 ) (x-3) > 0} 则 A ∩ B=A ( -, -1) B ( -1, -2) C( -2,3)D (3,+ )33【解析】和往年一样,依然的集合 (交集 )运算,本次考查的是一次和二次不等式的解法。
因为 A{ x R | 3x 20}x2 B{ x | x1或 x 3} 画出数,利用二次不等式可得3轴易得: A B { x | x 3} .故选 D .【答案】 D2.设不等式组0 x2,D ,在区域 D 内随机取一个点,则此点到坐标y,表示平面区域为2原点的距离大于 2 的概率是(A )(B ) 2( C )( D ) 44246【解析】题目中0 x 2 D0 y表示的区域如图正方形所示,而动点2可以存在的位置为正方形面积减去四分之一圆的面积部分,因此2 2 1224P4,故选 D 。
2 24【答案】 D3.设 a , b ∈R 。
“ a=0”是“复数 a+bi 是纯虚数”的( )A. 充分而不必要条件B.必要而不充分条件C.充分必要条件D. 既不充分也不必要条件【解析】当 a0 时,如果 b0同时等于零,此时 a bi0 是实数,不是纯虚数,因此不是充分条件;而如果 a bi 已经为纯虚数,由定义实部为零,虚部不为零可以得到a 0 ,因此想必要条件,故选 B 。
【答案】 B4.执行如图所示的程序框图,输出的 S 值为( )A. 2 B .4 C.8 D. 16【解析】 k 0 , s1k 1, s 1 k 2 , s 2k 2 , s 8 ,循环结束,输出的 s 为 8,故选 C。
2012年高考数学北京(理)

2012年普通高等学校招生全国统一考试数学(理)(北京卷)解析本试卷共5页. 150分.考试时长120分钟.考试生务必将答案答在答题卡上.在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、 选择题共8小题.每小题5分.共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1、已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B= (A ) (-∞,-1) (B )(-1,-23) (C )(-23,3) (D )(3,+∞) [答案]D[解析]和往年一样,依然是集合(交集)运算,本题考查的是一次和二次不等式的解法.因为A={x ∈R|3x+2>0}32->⇒x ,利用二次不等式的解法可得{}31>-<=x x x B 或,画出数轴易得:A ∩B={x|x >3}.[点评]集合的运算往往与解不等式联系在一起考查,属低档题.(2)设不等式组,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是(A )4π (B )22π- (C )6π(D )44π-[答案]D[解析]题目中表示区域如下图正方形所示,而动点D 可以存在的位置为正方形面积减去四分之一圆的面积,因此P=4422241222ππ-=⨯-⨯[点评]这是道微综合题,它涉及到的知识包括:线性规划,圆的概念和面积公式,概率.与面积、体积、长度有关的概率问题属于几何概型.3.设a,b∈R.“a=O”是“复数a+bi是纯虚数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件[答案]B[解析]a=O,b=0时,a+bi=0是实数,不是纯虚数;而如果a+bi是纯虚数,一定有a=O.[点评]纯虚数的概念要理解到位.(4)执行如图所示的程序框图,输出S值为(A)2(B)4(C)8(D)16[答案]C[解析]本题考查程序框图,设计到判断循环结束的时刻,以及简单整数指数幂的计算,k=o,s=1⇒k=1,s=1⇒k=2,s=2⇒k=3,s=8,结束[点评]读懂程序,做好循环结束的判断.本题属低档题.5.如图. ∟ACB=90º.CD⊥AB于点D,以BD为直径的圆与BC交于点E.则( )A. CE·CB=AD·DBB. CE·CB=AD·ABC. AD·AB=CD ²D.CE·EB=CD ²[答案]A[解析]这是平面几何题,主要考查射影定理的各种情况,要求学生对垂直的变化要有深入了解.[点评]平面几何中三角形相似的知识不容忽视.6.从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A. 24B. 18C. 12D. 6 [答案]B[解析]分两类:(1)奇偶奇形式:3×2×2=12;偶奇奇形式:3×2=6,共有12+6=18 [点评]排列组合题要注意合理分类.(7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A )28+B )30+C )56+D )60+[答案]B[解析]本题考查的是三棱锥的三视图问题,问题变化为求表面积,因此对学生的计算基本功以及空间想象能力都存在着综合性的考查.从所给的三视图可以得到该几何体的直观图,如下图所示,结合图中的数据,利用勾股定理计算出各边的长度,进而求出面积.563056101010+=+++=+++=左右后底表S S S S S[点评]把三视图正确地转化为直观图是解决问题的关键.(8)某棵果树前n 年的总产量S n 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为(A )5(B )7(C )9(D )11 [答案]C[解析]该题考查知识点很灵活,要根据图像看出变化趋势,由于目的是看年平均产量最高,就需要随着n 的增大,总年产量变化超过平均值的加入,随着n 的增大,由图可知6,7,8,9这几年增长最快,超过平均值,所以应该加入,因此选C.[点评]考察阅读理解能力,这也对数学的学习平时要求不能过于僵化,要灵活. 第二部分(非选择题共110分)二.填空题(共6小题,每小题5分,共30分). 9.直线(t 为参数)与曲线(“为多α数)的交点个数为[答案]2[解析]直线方程为x+y=1,圆方程为x 2+y 2=9,画出图形易得两个交点.[点评]把参数方程化为普通方程是解决该问题关键.(10)已知{a n }为等差数列,S n 为其前n 项和,若a 1= ,S 2=a 3,则a 2=_________,S n =_________________.[答案]1,42n n[解析]本题考查等差数列的基本计算,难度不大,因为d a d a a a S 211132+=++⇒=211==⇒a d ,所以42)1(,12112n n d n n na S d a a n +=-+==+= [点评]等差、等比数列的通项公式、前n 项和公式是必须要掌握的内容,并会熟练应用.11.在△ABC 中,若α=2,b+c=7,cos B =14-,则b= [答案]4[解析]在⊿ABC 中,由余弦定414)(744))((42cos 222-=-+=-++=-+=c b c c b c b c ac b c a B化简得8c-7b+4=0,又b+c=7,解得b=4.[点评]正余弦定理是解三角形的有力工具,要烂熟于心.12.在直角坐标系xOy 中.直线l 过抛物线24y x =的焦点F.且与该撇物线相交于A 、B两点.其中点A 在x 轴上方.若直线l 的倾斜角为60º.则△OAF 的面积为[答案]3[解析]根据y 2=4x 得焦点坐标F (1,0),因为直线l 的倾斜角为60º,所以直线的斜率为K=tan600=3,利用点斜式,直线方程为y=3x-3,将直线和曲线联立⇒⎪⎩⎪⎨⎧=-=xy x y 4)1(32A (3,23)B (332,31-),因此33212121=⨯⨯=⨯⨯=∆A OAF y OF S [点评]直线与抛物线的关系可以转化为求交点坐标问题.(13)已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则∙的值为________, ∙的最大值为 .[答案]1,1[解析]CB DE ∙=〉〈=∙DE cos ,而DA DE =〉〈,cos ,所以∙=1=;容易发现当E 点移动到B 点时,∙取最大值1.[点评]向量问题应多在数形结合上做文章.14.已知f(x)=m(x-2m )(x+m+3),g(x)=2x -2,若同时满足条件: ①x ∈R ,f(x) <0或g(x) <0 ②x ∈(﹣∝, ﹣4),f(x)g(x) <0则m 的取值范围是 [答案](-4,-2)[解析]根据g(x)= 2x -2<0,可解的x<1.由于x ∈R ,f(x) <0或g(x) <0成立,导致f(x)在x ≥1时,必须是f(x)<0的,因此f(x)的开口必须向下,m<0,且此时两个根为x 1=2m,x 2=-m-3,为保证条件①成立,需要⇒⎩⎨⎧<--=<=131221m x m x ⎪⎩⎪⎨⎧-><421m m ,又m<0,故结果为-4<m<0;又②x ∈(﹣∝, ﹣4),f(x)g(x) <0,得x ∈(-∞,-4)时,g(x)<0恒成立,因此就需要在这个范围内f(x)有取正数的可能,即-4应该比x 1,x 2中的小根大,当m ∈(-1,0)时,-m-3<-4,此时不成立;当m=-1时,有两相等根-2,此时不成立;当m ∈(-4,-1)时,2m<-4,得m<-2. 综上可知:m ∈(-4,-2)[点评]本题考查学生函数的综合能力,涉及到二次函数图像的开口,根的大小,涉及到指数函数的平移的单调性,还涉及到简易逻辑中的“或”,典型的“小题大做”.三、解答题公6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分) 已知函数(sin cos )sin 2()sin x x x f x x-=.(1) 求f (x )的定义域及最小正周期; (2) 求f (x )的单调递增区间.[解析] (1)由sinx ≠0得,x ≠πk ,即函数定义域为{x |x ≠πk ,k ∈Z}(sin cos )2sin cos()sin 2cos 21)1sin 4x x x x f x x x x x π-==--=--,所以T=π(2)由πππππk x k 224222+≤-≤+-,即ππππk x k +≤≤+-838,又x ≠πk , 故单调增区间是Z k k k k ∈⎥⎦⎤ ⎝⎛+⎪⎭⎫⎢⎣⎡-83,,8πππππ [点评]本题是三角函数题,考查知识比较基础,属容易题. 16. (本小题共14分)如图1,在Rt △ABC 中,∟C=90°,BC=3,AC=6,D ,E 分别是AC ,AB 上的点,且DE ∠BC ,DE=2,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1C ⊥CD,如图2.(1) 求证:A 1C ⊥平面BCDE ;(2) 若M 是A 1D 的中点,求CM 与平面A 1BE 所成角的大小;(3) 线段BC 上是否存在点P ,使平面A 1DP 与平面A 1BE 垂直?说明理由[解析](1)∵DE ⊥A 1D ,且DE ⊥CD,∴DE ⊥底面A 1D C, ∴DE ⊥A 1C,又因为A 1C ⊥CD, A 1C ⊥平面BCDE.(2)以C 点为坐标原点,CA 1为竖轴,CB 为横轴,CD 为纵轴建立空间直角坐标系,则C (0,0,0)M (0,1,3),=CM (0,1,3), =BE (-1,2,0),)32,0,3(1=B A ,设平面A 1BE 的法向量为),,(111z y x =,解得)23,21,1(=n ,设所求线面角为α,sin α=4,22πα=∴(3)设点P 坐标为(m,0,0), )32,0,(1-=m P A ,)32,2,0(1-=D A ,设平面A 1DP 的法向量为2n ,解得)63,2,1(2m m n =,又平面A 1BE 与平面A 1DP 垂直,02=∙n ,解得m=-2,故在BC 上不存在这样的点P.[点评]立体几何问题的考查往往以垂直、平行为重点,进一步考查三种角,我们可以充分利用好垂直条件,建立空间直角坐标系求解或证明.17(本小题共13分)近年来,某市为了促进生活垃圾的风分类处理,将生活垃圾分为厨余垃圾、可回收和其他垃圾三类,并分别设置了相应分垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):(Ⅰ)试估计厨余垃圾投放正确的概率; (Ⅱ)试估计生活垃圾投放错误的概率;(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c 其中a >0,a+b+c=600.当数据a,b,c 的方差s 2最大时,写出a,b,c 的值(结论不要求证明),并求此时s 2的值.(注:2222121()()()n s x x x x x x n ⎡⎤=-+-++-⎣⎦ ,其中x 为数据x 1,x 2…,x n 的平均数).[解析](1)P=32600400= (2)P=1031000300=(3)a=600,b=0,c=0,方差最大值为8万[点评]本题第三问考查学生的能力很强,化简计算观察的考查非常到位. 18.(本小题共13分)已知函数f (x )=ax 2+1(a>0),g(x)=x 3+bx.(1) 若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c )处具有公共切线,求a 、b 的值; (2) 当a 2=4b 时,求函数f(x)+g(x)的单调区间,并求其在区间(-∞,-1)上的最大值.[解析](1)∵)1()1(g f '='∴2a=3+b , ∵f(1)=g(1),∴a=b , ∴a=b=3.(2)令F(x)=f(x)+g(x)= x 3+ax 2+42a x+1∴6,20423)(2122a x a x a ax x x F -=-==++=',得由于a>0,所以-2a <-6a∴(-∞,-2π),(- 6π,+∞)为增区间,(-2π,- 6π)为减区间,F(-1)=a-42a ,F(-2a )=1,且 F(-1) ≤F(-2a) ② -2a>-1,即a<2时,最大值为F(-1)=a-42a②当-2a ≤-1,即a ≥2时,最大值为F(-1)=a-42a 或F(-2a )=1,而F(-1)=a-42a =-(2a-1)2+1≤1,所以最大值为1.[点评]本题考查的是导数中较为常规的题目,切线、单调性、极值和最值这些内容也都是学习的重点,难点在第二问中的讨论,思维含量要求很高.19.(本小题共14分)已知曲线C:(5-m)x 2+(m-2)y 2=8(m ∈R)(1) 若曲线C 是焦点在x 轴上的椭圆,求m 的取值范围;(2) 设m=4,曲线c 与y 轴的交点为A ,B (点A 位于点B 的上方),直线y=kx+4与曲线C 交于不同的两点M 、N ,直线y=1与直线BM 交于点G.求证:A ,G ,N 三点共线.[解析](1)利用椭圆的标准方程,易解得27<m<5 (2) 由得消去y y x kx y ⎩⎨⎧=++=82422(2k 2+1)x 2-16kx+24=0 ∴1224,1216222211+=+=+k x x k k x x 直线BM 的方程为)1,23(221111+⇒+=+y x G x x y y三点共线可以用2211223x y y x k k AN AG -=+⇒=,结合韦达定理代入化简可得结论. [点评]此题难度在于运算,思维含量适中,对学生来讲易于解答.20.(本小题共13分)设A 是由m ×n 个实数组成的m 行n 列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记s(m ,n)为所有这样的数表构成的集合.对于A ∈S(m,n),记r i (A)为A 的第ⅰ行各数之和(1≤ⅰ≤m ),C j (A)为A 的第j 列各数之和(1≤j ≤n ):记K(A)为∣r 1(A)∣,∣R 2(A)∣,…,∣Rm(A)∣,∣C 1(A)∣,∣C 2(A)∣,…,∣Cn(A)∣中的最小值.(1) 对如下数表A ,求K (A )的值;(2)设数表A ∈S (2,3)形如求K (A )的最大值;(3)给定正整数t ,对于所有的A ∈S (2,2t+1),求K (A )的最大值.[解析](1)k (A )=0.7;[点评]本题第二、三问难度较大,不易解决,属难题.。
2012年理数高考试题答案及解析-北京-(5446)

2012年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页. 150分.考试时长120分钟.考试生务必将答案答在答题卡上.在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题。
每小题5分.共40分.在每小题列出的四个选项中,选出符合胜目要求的一项.1.已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B= A (-,-1)B (-1,-23) C (-23,3)D (3,+)【解析】和往年一样,依然的集合(交集)运算,本次考查的是一次和二次不等式的解法。
因为32}023|{xx R x A,利用二次不等式可得1|{x x B 或}3x 画出数轴易得:}3|{xx BA .故选D .【答案】D 2.设不等式组2,20yx ,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是(A )4(B )22(C )6(D )44【解析】题目中220yx 表示的区域如图正方形所示,而动点D可以存在的位置为正方形面积减去四分之一圆的面积部分,因此4422241222P,故选D 。
【答案】D3.设a ,b ∈R 。
“a=0”是“复数a+bi 是纯虚数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解析】当0a时,如果0b同时等于零,此时0bi a 是实数,不是纯虚数,因此不是充分条件;而如果bi a已经为纯虚数,由定义实部为零,虚部不为零可以得到0a,因此想必要条件,故选B 。
【答案】B4.执行如图所示的程序框图,输出的S 值为()A. 2 B .4 C.8 D. 16【解析】0k ,11k s ,21k s ,22k s ,8s ,循环结束,输出的s 为8,故选C 。
【答案】5.如图. ∠ACB=90o ,CD ⊥AB 于点D ,以BD 为直径的圆与BC 交于点 E.则()A. CE ・CB=AD ・DBB. CE ・CB=AD ・ABC. AD ・AB=CD 2D.CE ・EB=CD 2【解析】在ACB 中,∠ACB=90o ,CD ⊥AB 于点D ,所以DB AD CD 2,由切割线定理的CB CECD2,所以CE ・CB=AD ・DB 。
北京市高考数学理科试卷及答案解析

北京市高考数学理科试卷及答案解析2012 北京理科高考试卷及答案分析精校版一、选择题共 8小题。
每题5分.共 40分 .在每题列出的四个选项中,选出吻合胜目要求的一项.1.已知会集 A={x ∈ R | 3x+2>0﹜, B={x ∈ R | (x+1)(x-3)>0﹜则 A ∩B=( ) A .(﹣∞,﹣ 1)B.{ 1,2} C. ﹙2,3 ﹚ D.( 3,+∝)332. 设不等式组0 x 2表示的平面地域为 D ,在地域 D 内随机取一个0 y 2点,则此点到坐标原点的距离大于 2的概率是()A.B.2 4C.D.42643.设a,b R .“0 ”是 ‘复数a bi是纯虚数 ”的()aA.充分而不用要条件B.必需而不充分条件C.充分必需条件D.既不充分也不用要条件4.履行以下列图的程序框图,输出的 S 值为( )A. 2B .4D. 165.如图 . ∠ ACB=90o , CD ⊥ AB 于点 D ,以 BD 为直径的圆与 BC 交于点 E.则( )A. CE · CB=AD · DBB. CE · CB=AD · ABC. AD AB CD 2D.CE EB CD 26.从0, 2中选一个数字 .从中选两个数字,构成无重复数字的三位数.此中奇数的个数为 ( )7.某三梭锥的三视图以下列图,该三梭锥的表面积是( )A.286 5 B.30 65C.56 12 5D. 60 12 5S n8.某棵果树前 n 前的总产量 S 与 n 之间的关系以下列图 . 从目前记录的结果 看,前 m 年的年均匀产量最高。
m 值为()O1 2 3 4 5 6 7 8 9 10 11n152二 .填空题共 6小题。
每题 5分。
共 30分 .x 2 t x3cos9.直线1 ( t 为参数 )与曲线y( 为参数 )的交点个数为yt3sin10.已知 { a n } 等差数列 S n 为其前 n 项和,若 a 11 a 3 ,则 a2 = , S n, S 2211.在△ ABC 中,若 a 2 , b c 7, cos B1,则 b =412.在直角坐标系 xOy 中,直线 l 过抛物线 y 2 4x 的焦点 F ,且与该抛物线订交于A 、B 两点,此中点 A 在 x 轴上方,若直线l 的倾斜角为 60o.则 OAF 的面积为13.己知正方形 ABCD 的边长为 1,点 E 是 AB 边上的动点 .则 DE CB 的值为14. 已知 f ( x) m( x 2m)( x m 3), g( x)2x 2 ,若同时满足条件:① x R ,有 f ( x)0 或g (x) 0;② x (, 4) ,使得 f (x) g( x)则 m 的取值范围是三、解答题公 6小题,共 80分。
理数高考试题答案及解析-北京

2012年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页. 150分.考试时长120分钟.考试生务必将答案答在答题卡上.在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题。
每小题5分.共40分.在每小题列出的四个选项中,选出符合胜目要求的一项.1.已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B= A (-∞,-1)B (-1,-23) C (-23,3)D (3,+∞) 【解析】和往年一样,依然的集合(交集)运算,本次考查的是一次和二次不等式的解法。
因为32}023|{->⇒>+∈=x x R x A ,利用二次不等式可得1|{-<=x x B 或}3>x 画出数轴易得:}3|{>=x x B A .故选D . 【答案】D2.设不等式组⎩⎨⎧≤≤≤≤20,20y x ,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是 (A )4π (B )22π- (C )6π (D )44π-【解析】题目中⎩⎨⎧≤≤≤≤2020y x 表示的区域如图正方形所示,而动点D可以存在的位置为正方形面积减去四分之一圆的面积部分,因此4422241222ππ-=⨯⋅-⨯=P ,故选D 。
【答案】D3.设a ,b ∈R 。
“a=0”是“复数a+bi 是纯虚数”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件【解析】当0=a 时,如果0=b 同时等于零,此时0=+bi a 是实数,不是纯虚数,因此不是充分条件;而如果bi a +已经为纯虚数,由定义实部为零,虚部不为零可以得到0=a ,因此想必要条件,故选B 。
【答案】B4.执行如图所示的程序框图,输出的S 值为( )A. 2 B .4 C.8 D. 16【解析】0=k ,11=⇒=k s ,21=⇒=k s ,22=⇒=k s ,8=s ,循环结束,输出的s 为8,故选C 。
理数高考试题答案及解析-北京

2012年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页. 150分.考试时长120分钟.考试生务必将答案答在答题卡上.在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题。
每小题5分.共40分.在每小题列出的四个选项中,选出符合胜目要求的一项.1.已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B= A (-∞,-1)B (-1,-23) C (-23,3)D (3,+∞) 【解析】和往年一样,依然的集合(交集)运算,本次考查的是一次和二次不等式的解法。
因为32}023|{->⇒>+∈=x x R x A ,利用二次不等式可得1|{-<=x x B 或}3>x 画出数轴易得:}3|{>=x x B A I .故选D . 【答案】D2.设不等式组⎩⎨⎧≤≤≤≤20,20y x ,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是 (A )4π (B )22π- (C )6π (D )44π-【解析】题目中⎩⎨⎧≤≤≤≤2020y x 表示的区域如图正方形所示,而动点D可以存在的位置为正方形面积减去四分之一圆的面积部分,因此4422241222ππ-=⨯⋅-⨯=P ,故选D 。
【答案】D3.设a ,b ∈R 。
“a=0”是“复数a+bi 是纯虚数”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件【解析】当0=a 时,如果0=b 同时等于零,此时0=+bi a 是实数,不是纯虚数,因此不是充分条件;而如果bi a +已经为纯虚数,由定义实部为零,虚部不为零可以得到0=a ,因此想必要条件,故选B 。
【答案】B4.执行如图所示的程序框图,输出的S 值为( )A. 2 B .4 C.8 D. 16【解析】0=k ,11=⇒=k s ,21=⇒=k s ,22=⇒=k s ,8=s ,循环结束,输出的s 为8,故选C 。
2012年北京高考数学真题及答案(理科)

绝密★使用完毕前2012年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合{A x=∈R|320}x+>,{B x=∈R|(1)(3)0}x x+->,则A B=I(A)(,1)-∞-(B)2(1,)3--(C)2(,3)3-(D)(3,)+∞(2)设不等式组2,2xy⎧⎨⎩≤≤≤≤表示的平面区域为D.在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是(A)π4(B)π22-(C)π6(D)4π4-(3)设,a b∈R.“0a=”是“复数ia b+是纯虚数”的(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(4)执行如图所示的程序框图,输出的S值为(A)2(B)4(C)8(D)16数学(理)(北京卷)第1 页(共11 页)(5)如图,90ACB∠=︒,CD AB⊥于点D,以BD为直径的圆与BC交于点E.则(A)CE CB AD DB⋅=⋅(B)CE CB AD AB⋅=⋅(C)2AD AB CD⋅=(D)2CE EB CD⋅=(6)从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为(A)24(B)18(C)12(D)6(7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A)28+(B)30+(C)56+(D)60+(8)某棵果树前n年的总产量nS与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高,m的值为(A)5(B)7(C)9(D)11BA DCE正(主)视图侧(左)视图俯视图42 3 4数学(理)(北京卷)第2 页(共11 页)数学(理)(北京卷) 第 3 页(共 11 页)第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2012年高考(北京理)(试题与答案纯WORD,逐题详解)
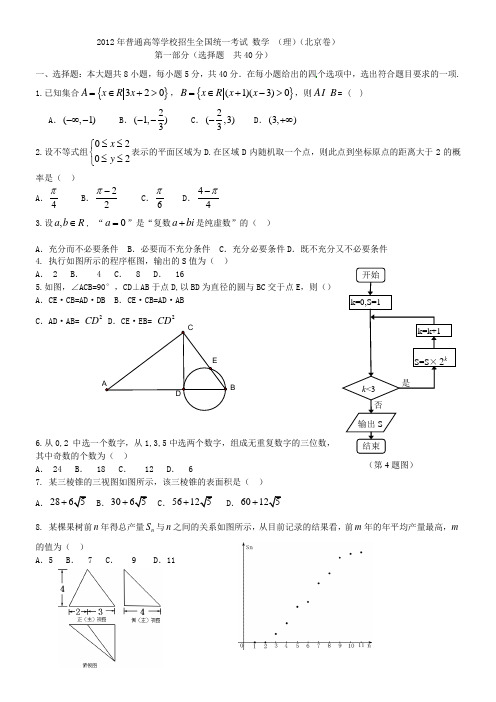
2012年普通高等学校招生全国统一考试 数学 (理)(北京卷)第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知集合{}320A x R x =∈+>,{}(1)(3)0B x R x x =∈+->,则A B = ( ) A .(,1)-∞- B .2(1,)3-- C .2(,3)3- D .(3,)+∞2.设不等式组0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D.在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( ) A .4π B .22π- C .6π D .44π- 3.设,a b R ∈, “0a =”是“复数a bi +是纯虚数”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分又不必要条件4. 执行如图所示的程序框图,输出的S 值为( ) A . 2 B . 4 C . 8 D . 165.如图,∠ACB=90°,CD ⊥AB 于点D,以BD 为直径的圆与BC 交于点E ,则() A .CE ·CB=AD ·DB B .CE ·CB=AD ·AB C .AD ·AB= 2CD D .CE ·EB= 2CD6.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数, 其中奇数的个数为( )A . 24B . 18C . 12D . 67. 某三棱锥的三视图如图所示,该三棱锥的表面积是( ) A.28+ B.30+ C.56+.60+8. 某棵果树前n 年得总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为( )A .5B . 7C . 9D .11(第4题图)B第二部分(非选择题 共110分) 二、填空题:本大题共6小题,每小题5分,共30分. 9. 直线2,1x t y t =+⎧⎨=--⎩(t 为参数)与曲线3cos 3sin x y =α⎧⎨=α⎩(α为参数)的交点个数为 .10.已知{}n a 为等差数列,n S 为其前n 项和.若112a =,23S a =,则2a = . 11.在△ABC 中,若2a =,7bc +=,1cos 4B =-,则b = . 12.在直角坐标系xoy 中,直线l 过抛物线24y x =的焦点F,且与该抛物线相较于A 、B 两点,其中点A 在x 轴上方,若直线l 的倾斜角为60°,则△OAF 的面积为 .13.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为 ; DE DC ⋅的最大值为 .14.已知()(2)(3)f x m x m x m =-++,()22x g x =-.若同时满足条件:①,()0x R f x ∀∈<或()0g x <;②(,4)x ∃∈-∞- ,()()0f x g x <. 则m 的取值范围是 . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题13分) 已知函数(sin cos )sin 2()sin x x xf x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递增区间.16. (本小题14分)如图1,在Rt △ABC 中,∠C=90°,BC=3,AC=6,D,E 分别是AC ,AB 上的点, 且DE ∥BC ,DE=2,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1C ⊥CD ,如图2. (1)求证:A 1C ⊥平面BCDE;(2)若M 是A 1D 的中点,求CM 与平面A 1BE 所成角的大小;(3)线段BC 上是否存在点P,使平面A 1DP 与平面A 1BE 垂直?说明理由.17.(本小题13分)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):(1)试估计厨余垃圾投放正确的概率; (2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为,,a b c ,其中0a >,600a b c ++=.当数据,,a b c 的方差2S 最大时,写出,,a b c 的值(结论不要求证明),并求此时2S 的值. (注:方差2222121[()()()]n s x x x x x x n=-+-++- ,其中x 为12,,n x x x 的平均数)18.(本小题13分)已知函数2()1f x ax =+(0a >),3()g x x bx =+.(1)若曲线()y f x =与曲线()y g x =在它们的交点(1,c )处具有公共切线,求,a b 的值; (2)当24a b =时,求函数()()f x g x +的单调区间,并求其在区间(,1]-∞-上的最大值.19.(本小题14分)已知曲线C: 22(5)(2)8()m x m y m R -+-=∈ (1)若曲线C 是焦点在x 轴的椭圆,求m 的范围;(2)设4m =,曲线C 与y 轴的交点为A,B (点A 位于点B 的上方),直线4y kx =+与曲线C 交于不同的两点M,N,直线1y =与直线BM 交于点G 求证:A,G,N 三点共线.20.(本小题13分)设A 是由m n ⨯个实数组成的m 行n 列的数表,满足:每个数的绝对值不大于1,且所有数的和为零.记(,)S m n 为所有这样的数表构成的集合.对于(,)A S m n ∈,记()i r A 为A 的第i 行各数之和1i m ≤≤,()j c A 为A 的第j 列各数之和1j n ≤≤; 记()k A 为1|()|r A ,2|()|r A ,…,|()|m r A ,1|()|c A ,2|()|c A ,…,|()|n c A 中的最小值. (1)对如下数表A,求()k A 的值;(2)设数表A=(2,3)S 形如求()k A 的最大值;(3)给定正整数t ,对于所有的A ∈S(2,21t +),求()k A 的最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年高考试题 数学(理)【北京市试题卷】本试卷共5页,150分.考试时长120分钟.考试生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}|320A x x =∈+>R ,()(){}|130B x x x =∈+->R ,则A B =I ( )A.()1-∞-,B.213⎧⎫--⎨⎬⎩⎭,C.233⎛⎫- ⎪⎝⎭, D.()3+∞,2.设不等式组0202x y ⎧⎨⎩≤≤,≤≤表示的平面区域为D .在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( )A.π4B.π22- C.π6D.4π4- 3.设a b ∈R ,.“0a =”是“复数i a b +是纯虚数”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.执行如图所示的程序框图,输出的S 值为( )A.2B.4C.8D.165.如图,90ACB ∠=︒,CD AB ⊥于点D ,以BD 为直径的圆与BC 交于点E ,则( )A.CE CB AD DB ⋅=⋅B.CE CB AD AB ⋅=⋅C.2AD AB CD ⋅=D.2CE EB CD ⋅=EBDAC6.从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( ) A.24 B.18 C.12 D.67.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A.28+B.30+C.56+D.60+8.某棵果树前n 前的总产量n S 与n 之间的关系如图所示.从目前记录的结果看,前m 年的年平均产量最高,m 值为( )A.5B.7C.9D.11344正(主)视图侧(左)视图俯视图第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9直线21x t y t =+⎧⎨=--⎩(t 为参数)与曲线3cos 3sin x y αα=⎧⎨=⎩(α为参数)的交点个数为 .10.已知{}n a 为等差数列,n S 为其前n 项和.若112a =,23S a =,则2a = . 11.在ABC △中,若2a =,7b c +=,1cos 4B =-,则b = .12.在直角坐标系xOy 中,直线l 过抛物线24y x =的焦点F ,且与该抛物线相交于A ,B 两点,其中点A 在x 轴上方,若直线l 的倾斜角为60︒.则OAF △的面积为 . 13.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅u u u r u u u r的值为 ;DE DC ⋅u u u r u u u r的最大值为 .14.已知()()()23f x m x m x m =-++,()22x g x =-.若同时满足条件:①x ∀∈R ,()0f x <或()0g x <; ②()()()40x f x g x ∃∈-∞-<,,, 则m 的取值范围是 .三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数()()sin cos sin 2sin x x x f x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递增区间. 16.(本小题共14分)如图1,在Rt ABC △中,90C ∠=︒,3BC =,6AC =.D ,E 分别是AC ,AB 上的点,且DE BC ∥,2DE =,将ADE △沿DE 折起到1A DE △的位置,使1AC CD ⊥,如图2. (1)求证:1A C ⊥平面BCDE ;(2)若M 是1A D 的中点,求CM 与平面1A BE 所成角的大小;ACDEBA 1MCBE D图1图2(3)线段BC 上是否存在点P ,使平面1A DP 与平面1A BE 垂直?说明理由.17.(本小题共13分)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):(1)试估计厨余垃圾投放正确的概率; (2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a b c ,,,其中0a >,600a b c ++=.当数据a b c ,,的方差2s 最大时,写出a b c ,,的值(结论不要求证明),并求此时2s 的值.(求:()()()2222121n s x x x x x x n ⎡⎤=-+-++-⎢⎥⎣⎦L ,其中x 为数据1x ,2x ,…,n x 的平均数)18.(本小题共13分)已知函数()()210f x ax a =+>,()3g x x bx =+.(1)若曲线()y f x =与曲线()y g x =在它们的交点()1c ,处具有公共切线,求a ,b 的值; (2)当24a b =时,求函数()()f x g x +的单调区间,并求其在区间(]1-∞-,上的最大值.19.(本小题共14分)已知曲线()()()22:528C m x m y m -+-=∈R (1)若曲线C 是焦点在x 轴上的椭圆,求m 的取值范围;(2)设4m =,曲线C 与y 轴的交点为A B ,(点A 位于点B 的上方),直线4y kx =+与曲线C 交于不同的两点M ,N ,直线1y =与直线BM 交于点G .求证:A G N ,,三点共线.20.(本小题共13分)设A 是由m n ⨯个实数组成的m 行n 列的数表,满足:每个数的绝对值不大于1,且所有数的和为零.记()S m n ,为所有这样的数表构成的集合.对于()A S m n ∈,,记()i r A 为A 的第i 行各数之和()1i m ≤≤,()j c A 为A 的第j 列各数之和()1j n ≤≤;记()k A 为()1||r A ,()2||r A ,…,()||m r A ,()1||c A ,()2||c A ,…,()||n c A 中的最小值. (1)对如下数表A ,求()k A 的值;(2)设数表A求()k A (3)给定正整数t ,对于所有的()221A S t ∈+,,求()k A 的最大值.答案一、选择题二、填空题三、解答题 15. 解: (sin cos )sin 2(sin cos )2sin cos ()2(sin cos )cos sin sin x x x x x x xf x x x x x x--===-{}πsin 21cos 221|π4x x x x x k k ⎛⎫=-+=--≠∈ ⎪⎝⎭Z ,,(1)原函数的定义域为{}|πx x k k ≠∈Z ,,最小正周期为π.(2)原函数的单调递增区间为πππ8k k ⎡⎫-+⎪⎢⎣⎭,k ∈Z ,3πππ8k k ⎛⎤+ ⎥⎝⎦,k ∈Z16. 解:(1)Q CD DE ⊥,1A E DE ⊥∴DE ⊥平面1ACD , 又Q 1A C ⊂平面1ACD , ∴1A C ⊥DE又1AC CD ⊥, ∴1A C ⊥平面BCDEy C(2)如图建系C xyz -,则()200D -,,,(00A ,,,()030B ,,,()220E -,, ∴(103A B =-u u u r,,,()1210A E =--u u u u r ,,设平面1A BE 法向量为()n x y z =r,,则1100A B n A E n ⎧⋅=⎪⎨⋅=⎪⎩u u u r r u u u u r r∴3020y x y ⎧-=⎪⎨--=⎪⎩∴2z y y x ⎧=⎪⎪⎨⎪=-⎪⎩ ∴(12n =-r,又∵(10M-, ∴(10CM =-u u u u r,∴cos 2||||CM n CM n θ⋅====⋅u u u u r ru u u u r r∴CM 与平面1A BE 所成角的大小45︒(3)设线段BC 上存在点P ,设P 点坐标为()00a ,,,则[]03a∈,则(10A P a =-u u u r,,,()20DP a =u u u r ,,设平面1A DP 法向量为()1111n x y z =u u r,,则1111020ay x ay ⎧-=⎪⎨+=⎪⎩ ∴111112z x ay⎧=⎪⎪⎨⎪=-⎪⎩∴()136n a =-u u r,假设平面1A DP 与平面1A BE 垂直 则10n n ⋅=u u r r,∴31230a a ++=,612a =-,2a =-∵03a <<∴不存在线段BC 上存在点P ,使平面1A DP 与平面1A BE 垂直 17.(1)由题意可知:4002=6003(2)由题意可知:200+60+403=100010(3)由题意可知:22221(120000)3s a b c =++-,因此有当600a =,0b =,0c =时,有280000s =.18. 解:(1)由()1c ,为公共切点可得:2()1(0)f x ax a =+>,则()2f x ax '=,12k a =, 3()g x x bx =+,则2()=3f x x b '+,23k b =+,∴23a b =+⎺又(1)1f a =+,(1)1g b =+,∴11a b +=+,即a b =,代入①式可得:33a b =⎧⎨=⎩. (2)Q 24a b =,∴设3221()()()14h x f x g x x ax a x =+=+++则221()324h x x ax a '=++,令()0h x '=,解得:12a x =-,26ax =-;Q 0a >,∴26aa -<-,∴原函数在2a ⎛⎫-∞- ⎪⎝⎭,单调递增,在26a a ⎛⎫-- ⎪⎝⎭,单调递减,在6a ⎛⎫-+∞ ⎪⎝⎭,上单调递增①若12a--≤,即2a ≤时,最大值为2(1)4a h a =-;②若126a a -<-<-,即26a <<时,最大值为12a h ⎛⎫-= ⎪⎝⎭③若16a --≥时,即6a ≥时,最大值为12a h ⎛⎫-= ⎪⎝⎭. 综上所述:当(]02a ∈,时,最大值为2(1)4a h a =-;当()2,a ∈+∞时,最大值为12a h ⎛⎫-= ⎪⎝⎭.19.(1)原曲线方程可化简得:2218852x y m m +=-- 由题意可得:8852805802m m mm ⎧>⎪--⎪⎪>⎨-⎪⎪>⎪-⎩,解得:752m <<(2)由已知直线代入椭圆方程化简得:22(21)16240k x kx +++=,2=32(23)k ∆-,解得:232k >由韦达定理得:21621M N k x x k +=+①,22421M Nx x k =+,② 设(,4)N N N x k x +,(,4)M M M x kx +,(1)G G x ,MB 方程为:62M M kx y x x +=-,则316M M x G kx ⎛⎫⎪+⎝⎭,, ∴316M M x AG x k ⎛⎫=- ⎪+⎝⎭u u u r ,,()2N N AN x x k =+u u ur ,,欲证A G N ,,三点共线,只需证AG u u u r ,AN u u u r共线即3(2)6MN N M x x k x x k +=-+成立,化简得:(3)6()M N M N k k x x x x +=-+将①②代入易知等式成立,则A G N ,,三点共线得证。
