2机翼和叶栅的升力理论
机翼和叶栅工作原理

机翼和叶栅工作原理机翼和叶栅是飞行器中最重要的部件之一,它们的工作原理直接影响着飞机的稳定性和飞行性能。
机翼和叶栅的设计和构造非常复杂,需要考虑多种因素,如气动力学、材料力学、热力学等,同时也需要使用高科技的材料和先进的制造工艺。
本文将详细介绍机翼和叶栅的工作原理。
一、机翼的工作原理机翼是飞机最重要的部件之一,它的主要作用是提供升力和推力,让飞机能够飞行。
机翼的基本结构包括大翼板、前缘板、后缘板和翼肋等。
在飞行时,机翼的上表面比下表面更加弯曲,使得上表面的气流速度要比下表面的气流速度更快,从而形成了压力差,产生了升力。
机翼的前缘板和后缘板也起到了非常重要的作用,它们能够使气流保持在合适的角度,避免气流的分离和逆流,从而增加了升力的产生。
机翼的工作原理也与伯努利原理密切相关。
伯努利原理是流体力学中的一个重要原理,它描述了流体在速度和压力之间的关系。
在机翼的上表面,气流的速度更快,压力更小,而在机翼的下表面,气流的速度较慢,压力较大。
这种速度和压力的差异使得机翼产生了升力。
机翼的设计也是非常关键的。
对于不同的飞行器和飞行条件,机翼的设计也需要有所不同。
机翼的形状、厚度、长度、后缘角度等都需要考虑到不同的因素,如飞行速度、气流参数、飞机质量等。
现代飞机的机翼也使用了尖锐的前缘、切削的后缘和复杂的结构,以提高机翼的流线型和气动效率。
二、叶栅的工作原理叶栅是飞机发动机的关键部件之一,它起到了限制和调节气流的作用。
叶栅的主要结构由多个叶片组成,叶栅内有高温高压的气流通过,叶片的开启和关闭可以调节气流的流量和速度。
叶栅的作用除了控制气流外,还可以起到控制噪音和降低引擎的燃油消耗等作用。
叶栅的工作原理也与伯努利原理有关。
在叶栅内,气流的速度和压力也存在着差异。
当叶栅的叶片打开时,气流能够顺畅地通过,气体速度增加,压力下降。
当叶栅的叶片关闭时,气流被限制,气体的速度减小,压力升高。
通过控制叶栅的叶片开合,能够达到有效地控制气流的目的。
翼型与叶栅理论..

故在 b 处:
d d W 1 2 v 01 e 2 i( ) 2 i 2 R ie i( ) i 0
解得:
2R v0sin()
有时称 ( ) 为绝对攻角
二元机翼中:
CL
FL
b
•
v
2 0
2
对于儒可夫斯基翼型:
b 4R
故升力系数为:
C Lv024 R R v 0v s0 2 in /(2 )()
非定常速度的演化-旋转框架下
Ry vx
此为作用在叶型上的力之两个坐标分量,合力大小为:
R Rx2Ry2 v
由于:
R w w y w x w x w y 0
可见两者相垂直,合力方向为将 w 逆环量方向转90度。
如果令两叶片间距无穷大,而环量不变,此时叶型受力?
等价平板叶栅 栅距相同,但叶型不同的两个叶栅,如果对无论怎样的来流,二栅中
2) 同一叶型单独绕流和置于叶栅中在同一攻角下被绕流时,其动力 特性也不同。加速叶栅中叶型,其升力系数大于单独叶型的升力系 数,但减速叶栅中叶型升力系数恒小于单独叶型的升力系数。
离心泵及内流图例
绝对速度分布的变化
压强分布的变化
初始场的非定常模拟
某一时刻的流动
非定常速度的演化-固定框架下
对控制线内流体列出沿坐标方向动量方程
(p' p'')tRx q(wx'' wx' )
Ry q(w'y' w'y)
(a)
由连续性方程得:
qwx' t wx''t 从而: wx' wx'' wx
代入方程(a): Rx (p' p'')t
04.PDF文档(第四章 轴流式通风机)

第四章 轴流式通风机图4-1为轴流式风机,由集风器1,、叶轮2,、导叶3,、扩散筒4等组成。
叶轮和导叶组成级,轴流通风机,因为压力较低,一般都用单级,例如低压轴流通风机在490Pa 以下,高压轴流通风机一般在4900Pa 以下。
其特点:压力系数低ψ<0.6,流量系数高φ=0.3~0.6,比转速高n s =18~90(100~500)(单级)全压效率高达η=90%以上,单向扩散筒的单级风机效率为83~85%。
不过目前轴流风机逐渐向高压发展,例如国际上已造出动叶可调轴流通风机ΔP =14210Pa,许多大型离心式风机有被轴流式风机取代的趋势。
图4-1轴流式风机§1 基元级一、基元级上的速度三角形图4-2 轴流式通风机的基元级轴流式通风机的基元级由叶轮和导叶所组成的。
对于不同半径的圆柱面上,由于离心力不同,那么气流的参数是变化的,叶片沿叶高方向(径向)是扭曲的。
为了研究不同半径上的流动,用一圆柱面去切开轴流式通风机,会得到圆柱面上的环形叶删,可以展开成平面叶栅,如图4-2所示,这种平面动叶和导叶所组成的叶栅,称为基元级 与离心通风机一样,在动叶前后形成速度三角形:不过在圆柱面上:u 1 = u 2 = u ,C 1z = C 2z = C z ,ρ1 = ρ2 = ρ(β2 >β1,α2 < α1)对于多级轴流风机,一般要求后导叶出口的流速C 3和气流角α3等于叶轮前的状态C 3 = C 1,α3 =α1可以得出叶流前后平均的相对速度W m 及方向角βmβm = tg(C z / W mu ) (4-1) W mu = u – ΔW u /2 –C 1u (4-2)22muZ W C Wm +=式(5-2)的推导可出图3-2b 时:u = u 1 = u 2 ΔW u = W 1u – W 2u = C 2u - C 1u = ΔC u (4-3) ΔW u 或ΔC u 称为相速。
机翼及叶栅理论共29页PPT

谢谢
11、越是没有欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
机翼及叶栅理论
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
翼型及叶栅理论

换,并进行傅立叶级数展开,可得涡强分布的
积分方程为:
()2v(A0cot2n 1Ansin)
又有:
A0
n1
Ancosnddyx
式中:
解题步骤
——攻角
dy
——x 或 的已知函数
dx
x,关关系系—— x b (1cos)
2
傅立叶系数
A0
1
dyd
0 dx
An
2
0
dycosnd
dx
解题步骤
z c ( 1 2 )c 2 c ( 1 2 ) c 1 2 O (2 ) 2 c c ( 1 2 )
上式表明,在计算中只保留大于ε一次方量级的 各项时,z平面上的变换曲线的弦长为b≈4c。
解题步骤
2.求取变换曲线的方程
设 Rei 为ζ平面圆周上的任一点,则在z平面相
xA ,B 2cco,y sA ,B0
题目
设在ζ平面有一圆心在坐标原点左面的实轴上,圆 周过ζ=c的圆,无穷远来流速度大小为v∞,其方向与 实轴夹角为α。试求其在物理平面z上的流动边界。(
设m<<c)
解题步骤
解:
1. 由于m<<c,故其半径将是a=c+m=c(1+ε),式中 ε=m/c<<1。此时圆周只过一个变换奇点ζ=c。在z 平面上其对应点z=2c处不保角,故圆弧变换成一 夹角为零的尖角。在圆周上其它各点对应的点在z 平面上将构成一平滑曲线,它与负实轴的交点是
2c 2c
解题步骤
变换曲线的形状如图。
极点分布法
MF2Hg17
题目
设一长为b的平板被一小攻角α的均匀来流v∞绕过, 试用薄翼理论求其表面的速度分布、升力系数及力矩 系数,及其分布曲线。 (xx),,vxx
华北水利水电大学955-工程流体力学2021年考研专业课初试大纲

华北水利水电大学2021年硕士研究生入学考试初试科目考试大纲工程流体力学(科目代码:955)考试大纲一、试卷分值及考试时间考试时间180分钟(3个小时),满分150分。
二、考试基本要求本考试大纲适用于报考华北水利水电大学“动力工程及工程热物理”、“流体机械及工程”、“动力机械及工程”、“水利工程”等学术型硕士和“能源动力(专业学位)”研究生入学考试。
闭卷考试,允许使用计算器,但不得使用带有公式和文本存储功能的计算器。
本科目考试主要测试考生掌握流体力学的基本概念、基本理论的扎实程度,考查考生能熟练运用这些概念与理论分析解决现实生产中流体力学相关问题的能力。
考察范围包括流体静力学、流体运动学、流体动力学、量纲分析、流动测量与显示技术、理想流体运动以及边界层理论、黏性流体流动基础以及流体力学工程应用等方面。
要求考生掌握流体力学的基础概念、基本原理、基本计算方法和基本方程的推导,并具有综合运用所学知识分析问题和解决问题的能力。
三、试卷内容及结构(一)流体的定义和特征(约占5%)1.流体作为连续介质的假设;2.流体的定义和特征;3.作用在流体上的力;4.流体的物理性质。
(二)流体静力学(约占10%)1.流体静压强及其特性;2.流体平衡微分方程式;3.流体静力学基本方程;4.绝对压强,相对压强;5.液柱式测压计;6.静止液体作用在平面、曲面上的总压力;7.液体的相对平衡。
(三)流体运动的基本概念和基本方程(约占15%)1.研究流体流动的两种方法、流动的分类;2.流动概念如迹线与流线、流速、流量、系统与控制体等;3.连续方程、动量方程、能量方程;4.伯努利方程及其意义和应用,动量方程及其应用;5.动量矩方程、叶轮机械欧拉方程、速度三角形及其应用等。
(四)相似原理和量纲分析(约占10%)1.模型试验、量纲分析法;2.相似原理、重要相似准则。
(五)管流损失和水力计算(约占15%)1.粘性流体的两种流动状态:层流、紊流,雷诺数;2.沿程损失、局部损失的实验研究;3.管内流动的能量损失,沿程损失、局部损失的计算;4.圆管中的层流、湍流流动理论分析;5.管道水力计算;6.水击现象;7.管嘴与孔口的出流。
飞机机翼产生升力的原理

飞机机翼产生升力的原理飞机机翼产生升力的原理是基于伯努利定律和牛顿第三定律。
机翼与气流之间存在一个由上下表面之间的压差所产生的升力。
首先,根据伯努利定律,当气流通过机翼上下表面时,由于机翼上表面更加凸起,气流在上表面流动速度较快,而在下表面流动速度较慢。
根据伯努利定律,流动速度较快的区域气流压力较低,而流动速度较慢的区域气流压力较高。
因此,在机翼上表面的气流速度较快,气流压力较低,在机翼下表面的气流速度较慢,气流压力较高。
根据牛顿第三定律,当气流与机翼表面发生相互作用时,产生一个与气流作用方向相反的等大反作用力。
气流在机翼的上表面流动时,由于流动速度快,压力低,从而使机翼表面受到向下的压力。
同样,在机翼的下表面,气流流动速度慢,压力高,因此机翼下表面受到向上的压力。
这两个力的合力即为升力。
此外,还需要考虑机翼形状对升力的影响。
机翼通常采用个人梯形翼型,即厚度向前增大,厚度向后逐渐减小,同时上表面与下表面都呈现出一定的曲率。
这样的设计有利于增加升力的产生。
当气流通过机翼时,由于上表面的曲率较大,气流流速相对较快,导致压力较低。
而下表面的曲率较小,气流流速相对较慢,导致压力较高。
这种形状设计使得机翼上表面产生的压差更大,从而增加了升力的大小。
升力的大小还与机翼的攻角有关。
攻角是机翼与来流气流方向之间的夹角。
当攻角增大时,气流相对机翼的上表面流动的速度也会增大,从而压差增大,升力也会增大。
然而,当攻角过大时,气流会分离并形成气流脱落区域,进而导致升力的减小和失速。
除了上述原理外,还有一种解释机翼产生升力的理论,即“流下假设”。
根据流下假设,机翼上下表面之间的气体流动是分离的。
当空气从机翼上表面流向下表面时,会形成一个叫做流下层的气流。
而在下表面,由于气流速度较慢,流下层会分离并向下流动,形成一个被称为下层的气流。
而在上表面,由于气流速度较快,受到上层气流的引导,附着在机翼上表面,形成一个叫做上层的层流。
02 第二节 机翼与叶栅的升力理论
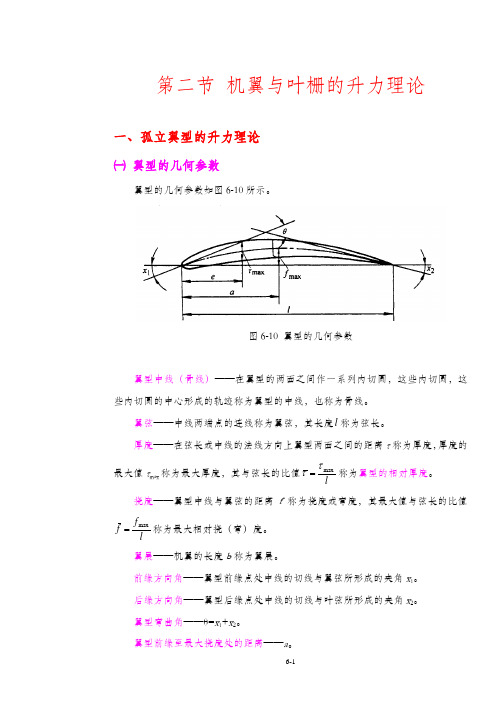
w∞ ——翼型前后无穷远处未受翼型影响的来流速度。 ▲说明
△如果介质是实际流体,则 F 力的大小与式(6-37)所计算的值有所偏差。
3、升力和阻力 ▲F 力可以看作是垂直于 w∞ 的升力 Fy 和平行于 w∞ 的阻力 Fx 的合力,如图 6-11 所示。
6-2
▲攻角 △来流 w∞ 与翼弦的夹角 α 称为攻角,如图 6-11 所示。
Fy
=
ρ mtw∞z ∆wu cos λ sin(b ∞ + λ)
b
(6 − 47)
由式(6-43)和式(6-47)可得
cy
l t
=
2 cos l sin 2 β ∞ ∆wu sin(β ∞ + l)w∞z
(6 − 48)
根据三角恒等式,上式还可以写成
cy
λ t
=
2∆wu w∞z
sin β ∞ 1 + tan λ / tan β ∞
参数。 ◇其倒数 t/l 称相对栅距。
翼型安放角——翼弦与列线方向之夹角 βb。 进口安放角——翼型前缘点中线的切线与圆周方向之夹角 βb1。 出口安放角——翼型后缘点中线的切线与圆周方向之夹角 βb2。 翼型弯曲角——θ=βb2-βb1。
⑵ 叶栅的动力特性 ▲叶栅绕流如图 6-17 所示。
▲说明 △叶栅绕流与孤立翼型绕流不同,由于栅中翼型有无穷多,因此对流场的扰 动可以传播到无穷远的地方,这样流场中就不再有未受扰动的流动速度 w∞,栅前 栅后足够远处的速度 w1 和 w2 的大小和方向都是不同的。
⑵ 平面直列叶栅 ▲ 圆柱面沿母线割开后,可以展开在平面上。 ▲圆柱面和各叶片相交,其截面(翼型剖面或翼型)在平面上构成一组叶栅。如 图:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§6-1
基本名词术语
WUHAN UNIVERSITY
• 1.叶轮轮毂半径 • 2.叶片外缘半径 • 3.基元(基元级)叶片:在叶片的任意半径 r 及 r+dr 处将两个同 心圆柱面切开,则这两个面之间的部分称为基元叶片。 • 4.翼型:设dr很小,基元叶片展开成平面,其中一个叶片的翼型 断面 • 5.工作面:翼型凹面——正压力面 • 6.背面:翼型凸面——负压力面 “三创”教育工作座谈会·张澍 • 7.翼型中线(骨架线、骨线):翼型两面间内切圆圆心的连线
WUHAN
Fy C y 1 tg Fx Cx
—滑翔角 升阻比(翼形的质量系数)
UNIVERSITY
“三创”教育工作座谈会·张澍
§6-2 机翼和叶栅的升力理论
WUHAN UNIVERSITY
WUHAN UNIVERSITY
“三创”教育工作座谈会·张澍
§6-2 机翼和叶栅的升力理论
二、叶栅 1.速度 已知:Q, A, , D, n 对于等半径的叶栅: 圆周速度 u1 u 2 u 相对速度的轴向分速
2 w dF , dFy C y bdr cos 2 dQT Ztdr c m
WUHAN UNIVERSITY
dFy
C y l u 2 sin( ) HT w 2 g t cm cos
WUHAN UNIVERSITY
“三创”教育工作座谈会·张澍
WUHAN
UNIVERSITY
§6-1
基本名词术语
WUHAN UNIVERSITY
• 8.翼弦和弦长:中线端点的连线,长度L称为弦长 • 9.前缘点和后缘点:中线有两个端点,迎着来流方向的端点另一 端点称为后缘点,翼型前缘是圆滑的,后缘是尖锐的 • 10.前驻点和后驻点:来流接触翼型后开始分离的点称为前驻点 ,绕流翼型后在后端会合的点称为后驻点 • 11.翼型厚度:与骨线垂直的翼形两面间的距离 , max —最 大厚度。相对厚度 max
基本名词术语
WUHAN UNIVERSITY
15.后缘方向角:翼型后缘点处中线的切线与翼弦所形成的夹角 x2 x1 x2 16.翼形弯曲角: 17.叶栅:相同翼型等距排列的翼型系列 18.叶栅列线:叶栅中各翼型的相对应点的连线 19.平面直列叶栅:叶栅列线为直线 t 2r / z 20.栅距:两相邻翼型在叶栅列线方向上的距离t, r—为圆柱切面的半径
WUHAN
Hale Waihona Puke l• 12.挠度:翼型中线与翼弦的距离f,相对挠度 b • 13.翼展:垂直于纸面的翼型长度称为翼长或翼展b,相对翼展 l • 14.前缘方向角:翼型前缘点处中线的切线与翼弦所形成的夹角 x1
“三创”教育工作座谈会·张澍
UNIVERSITY
f f max l
§6-1
• • • • • • •
2
§6-2 机翼和叶栅的升力理论
WUHAN UNIVERSITY
2.动力学基本方程式——叶栅 ①作用在基元上的力有升力 dFy ,和阻力 dFx 其合力为 dF ②dF与圆周方向一夹角为 90 ( ) ③dF的圆周分量为 ④使翼型dr转动的推动功率 ⑤叶片数为Z,则所需总功率
dFu dF cos 90 dF sin( )
WUHAN
UNIVERSITY
dP udFsin( )
ZdP z u uF sin( )
z u dF sin( ) “三创”教育工作座谈会·张澍 ⑥流经dr段的流量为,则功率为 dQT H T
§6-2 机翼和叶栅的升力理论
WUHAN
UNIVERSITY
l • z—为叶片数 “三创”教育工作座谈会·张澍 • 21.叶栅稠密度:弦长l与栅距t之比 t
§6-1
• • • • •
基本名词术语
WUHAN UNIVERSITY
22.冲角:来流 w 与弦的夹角 称为冲角 23.正冲角:冲角在翼弦以下(工作面迎着来流) 24.进口安放角:翼型前缘点处中线的切线与列线的夹角 b1 25.出口安放角:翼型后缘点处中线的切线与列线的夹角 b 2 26.翼形弯曲角: b2 b1
WUHAN
UNIVERSITY
“三创”教育工作座谈会·张澍
§6-2 机翼和叶栅的升力理论
一、弧立翼型的升力理论 Fy : 垂直于w ①升力 ②阻力 Fx : 平行于w ③ ④ ⑤
w Fy C y bl 2 2 w Fx C x bl 2
2
WUHAN UNIVERSITY
C y — 升力系数 与断面形状,冲角, 表面粗糙度,雷诺数有 关 C x — 阻力系数
WUHAN UNIVERSITY
wu
w1 u w 2 u 2
w2
w1
w
1
WUHAN
cm
c1
c2
2
w1u
w2u
w1m w2m wm
QT QT cm 2 A 2 ( D2 d h ) 4
UNIVERSITY
2
u
c u1 c u 2 w1u w2u 2 2 w w c u m m 2 2 w 2 wm cm tg u c cu 2 wu w1u w2u u u1 2 “三创”教育工作座谈会·张澍
WUHAN UNIVERSITY
0101000110010101
轴流式流体机械的叶轮理论 10010101
WUHAN UNIVERSITY
•对于轴流式流体机械,同样可采用欧拉方程来分 0101000110010101 析,但由于轴流式流体机械的叶轮数较少,叶片 间的流道较宽,分析其实际能头时,要做很多修 10010101 正。因而,其叶轮理论一般是用机翼理论来分析
2 C y 1 ucm sin( ) HT sin 2 2 g t cm cos
u (cu 2 cu1 ) ucu HT , c m w / sin g g sin cos l 2cu Cy t w sin cos cos sin 2cu 1 w 1 tg / tg
