机翼设计公式
展弦比计算范文

展弦比计算范文展弦比是指飞机机翼的根部弦长与翼尖弦长之间的比值。
在航空工程中,展弦比是设计和评估机翼性能的重要参数之一、通过选择合理的展弦比,可以实现机翼的良好气动性能和结构强度,同时影响飞机的速度性能、操纵性能和燃油效率等方面。
展弦比的计算公式为:展弦比=翼根弦长/翼尖弦长展弦比越大,表示翼尖弦长相对于翼根弦长来说更长,这意味着翼面积从根部到尖端的变化更大。
相对较大的展弦比可以延缓绕流分离,减少阻力,提高升力和气动效率。
此外,对于高速飞机来说,大展弦比可以减小翼面积,在一定程度上减小巡航阻力。
计算展弦比的过程取决于翼根弦长和翼尖弦长的测量方法和精度。
通常情况下,翼根弦长是指机翼最内部的梢宽,而翼尖弦长是指机翼最外部的梢宽。
这两个数值可以通过飞机设计文档或者机翼工程图纸来获取。
对于直线机翼,可以直接量取翼根弦长和翼尖弦长,然后带入上述的公式计算展弦比。
然而,对于翼型复杂、非直线的飞机机翼,展弦比的计算则需要通过工程方法或者计算机模拟进行。
工程方法通常是将翼面积在机翼弦长方向上分割为若干矩形或梯形,然后计算每个矩形或梯形的弦长,并将其平均值作为翼根弦长和翼尖弦长来计算展弦比。
展弦比的选择取决于飞机的设计需求和性能指标。
一般来说,低速飞机如直升机和一些运输飞机,其翼面积和气动性能要求较高,通常选择较小的展弦比,一般范围为3到5之间。
而高速战斗机、喷气式民航飞机等需要更好速度性能的飞机,通常选择较大的展弦比,一般范围为7到10之间。
展弦比的优化设计是一个复杂而重要的问题,需要综合考虑飞机的综合性能指标、目标任务和操作环境等因素。
在实际设计中,设计师会结合飞机的布局、结构和气动特性来确定最佳的展弦比。
同时,展弦比的选择还会受到制造成本、材料重量和工艺要求等因素的限制。
总之,展弦比是飞机机翼设计过程中的重要参数之一,对于飞机的性能和经济性都有着重要影响。
通过合理选择展弦比,可以实现最佳的气动和结构性能,提高飞机的整体性能指标。
三角翼图纸与相关参数计算
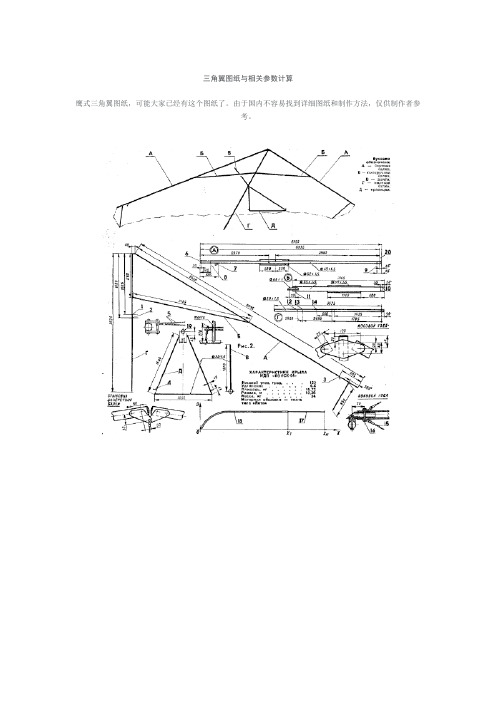
三角翼图纸与相关参数计算鹰式三角翼图纸,可能大家已经有这个图纸了。
由于国内不容易找到详细图纸和制作方法,仅供制作者参考。
滑翔比达到10的无动力三角翼图,点击看大图,有详细尺寸。
升阻比:又称“举阻比”、“空气动力效率”。
飞机飞行中,在同一迎角的升力与阻力的比值。
其值随迎角的变化而变化,此值愈大愈好,低速和亚声速飞机可达17~18,跨声速飞机可达10~12,马赫数为2的超声速飞机约为4~8。
展弦比:翼展(机翼的长度)的平方除以机翼面积,如圆形机翼就是直径的平方除以圆面积,用以表现机翼相对的展张程度。
小展弦比机翼导致大诱导阻力,进而使升阻比小,航程性能不好,但机动性好。
如大航程、低机动性飞机——B-52轰炸机展弦比为6.滑翔比:飞行器每下沉1米,所滑翔前进距离,称作滑翔比。
最好的滑翔机升阻比达到100以上,滑翔比高达40以上。
决定滑翔比大小的因素取决于以下几点。
①大展弦比大展弦比的机翼,诱导阻力小,机翼效率高,滑翔比就大。
还有的增加翼尖小翼,进一步消除诱导阻力。
②流线型除了诱导阻力,另一个功率损失就是压差阻力。
前进的物体,前面压力大,形成阻挡,后面压力小,形成拖拽。
如果以一个平板圆形为基础,阻力为1,那么圆柱形阻力为0.6,圆球形为0.3,鸡蛋形可以减小到0.1,水滴形可以减小到0.04,拉长的水滴形甚至可以做到0.01以下。
水滴拉长的水滴阻力极小的鲨鱼形高级滑翔机机身一般都是拉长水滴状,机翼则是半个拉长水滴状,所以,阻力极小。
③减轻重量。
重量和阻力一样,是航空器的设计的首要问题。
重量增大直接导致下沉率增大,间接造成滑翔比大大减小。
途径是采用大强度比的材料,如铝,镁,钛等金属的合金以及碳纤维,玻璃钢等材料。
机翼升力计算公式(转):升力L=1/2 *空气密度*速度的平方*机翼面积*机翼升力系数(N)机翼升力系数曲线如下注解:在小迎角时曲线斜率是常数。
在标识的1位置是抖振点,2位置是自动上仰点,3位置是反横操纵和方向发散点,4位置是失速点。
斯托克斯公式stokes定律

斯托克斯公式stokes定律斯托克斯公式(Stokes定律)是描述流体运动的基本定律之一,它被广泛应用于流体力学和电磁学等领域。
斯托克斯公式是以英国物理学家乔治·斯托克斯(George Stokes)的名字命名的,他在19世纪中叶首次提出了这个公式。
斯托克斯公式是由麦克斯韦方程组推导而来的,它描述了流体中的速度场与涡旋场之间的关系。
根据斯托克斯公式,涡旋场的环流与速度场通过曲面的面积分之间存在线性关系。
换句话说,斯托克斯公式给出了速度场在曲面上的环量与曲面边界上的环量之间的关系。
斯托克斯公式的数学表达形式如下:∮C F·ds = ∬S (∇ × F)·dS其中,C是曲面S的边界曲线,F是速度场,ds是边界曲线上的微元弧长,S是曲面S的面积,∇ × F是速度场F的旋度,dS是曲面S上的面积元。
斯托克斯公式的应用非常广泛。
在流体力学中,斯托克斯公式被用来计算旋转流体中涡旋的强度和分布情况。
在电磁学中,斯托克斯公式被用来计算磁场沿闭合回路的环量,从而计算磁场的旋度。
此外,斯托克斯公式还被应用于固体力学、量子力学等领域。
对于流体力学中的应用,斯托克斯公式可以帮助我们理解涡旋的生成和演化过程。
涡旋是流体中的一种特殊流动形式,它具有旋转的性质。
通过斯托克斯公式,我们可以计算涡旋的强度,并进一步研究其对流体运动的影响。
斯托克斯公式的应用还可以帮助我们解决一些工程和科学问题。
例如,在空气动力学中,我们可以利用斯托克斯公式来计算飞机机翼周围的气流情况,从而优化机翼的设计。
在电磁学中,我们可以利用斯托克斯公式来计算闭合电路中的电磁感应强度,从而分析电磁场的分布情况。
斯托克斯公式是流体力学和电磁学等领域中非常重要的定律之一。
它描述了速度场与涡旋场之间的关系,可以帮助我们理解和分析涡旋的形成和演化过程。
斯托克斯公式的应用广泛,可以帮助我们解决一些工程和科学问题。
通过学习和应用斯托克斯公式,我们可以深入理解流体力学和电磁学等领域的原理和现象。
翼型倾角计算公式

翼型倾角计算公式翼型倾角是飞机机翼与水平线的夹角,也称为攻角。
它是飞机飞行中非常重要的一个参数,对飞机的飞行性能和稳定性有着重要的影响。
翼型倾角的大小直接影响着升力和阻力的产生,因此翼型倾角的计算是飞机设计和飞行控制中的重要问题之一。
下面我们将介绍翼型倾角的计算公式及其相关知识。
翼型倾角的计算公式可以通过几何关系和三角函数来推导得出。
在飞机飞行中,翼型倾角可以分为几种不同的情况来进行计算,包括静止状态下的翼型倾角、飞行状态下的翼型倾角以及攻角的变化等情况。
下面我们将逐一介绍这些情况下的翼型倾角计算公式。
首先是静止状态下的翼型倾角计算公式。
在飞机静止的情况下,翼型倾角可以通过机翼的设计参数来计算。
一般来说,飞机的设计参数中会包含翼型倾角的数值,设计师可以根据飞机的设计要求和性能指标来确定翼型倾角的大小。
翼型倾角的大小会直接影响飞机的起降性能和飞行稳定性,因此设计师需要根据实际情况来确定翼型倾角的数值。
其次是飞行状态下的翼型倾角计算公式。
在飞机飞行的过程中,翼型倾角会随着飞机的姿态和飞行状态而发生变化。
一般来说,飞机的姿态会通过飞行控制系统来调节,以保持飞机的平衡和稳定。
在这种情况下,翼型倾角可以通过飞机的姿态角和攻角来计算。
翼型倾角与攻角之间的关系可以通过三角函数来描述,一般来说,翼型倾角等于飞机的姿态角加上攻角。
最后是攻角的变化情况。
在飞机飞行的过程中,攻角会随着飞机的飞行状态和飞行任务而发生变化。
攻角的变化会直接影响翼型倾角的大小,因此在飞机设计和飞行控制中需要对攻角的变化进行合理的考虑。
一般来说,攻角的变化会通过飞行控制系统来实现,飞行员可以通过操纵飞机的控制杆来调节飞机的攻角,从而实现飞机的飞行任务。
综上所述,翼型倾角的计算公式可以通过几何关系和三角函数来推导得出,它是飞机飞行中非常重要的一个参数,对飞机的飞行性能和稳定性有着重要的影响。
在飞机的设计和飞行控制中,需要对翼型倾角进行合理的计算和调节,以保证飞机的飞行安全和性能指标的实现。
飞机机翼面积计算公式

飞机机翼面积计算公式嘿,咱们来聊聊飞机机翼面积的计算公式这事儿。
你想啊,飞机能在天上飞,那机翼的作用可太大啦!而要算出机翼的面积,这里面可是有不少门道。
先来说说常见的机翼形状,有平直的,有后掠的,还有各种奇奇怪怪的形状。
但不管啥形状,咱们都能找到办法算出它的面积。
一般来说,对于简单的矩形机翼,那计算就比较容易,长乘以宽就搞定啦。
可现实中的机翼大多不是这么规整的。
比如说,梯形机翼。
这时候,咱们就得用梯形面积的计算公式:(上底 + 下底)×高 ÷ 2 。
这里的上底和下底就是机翼前后缘的长度,高就是机翼的展长。
但实际情况往往更复杂,机翼可能会有各种曲线和弧度。
这时候,可能就得用到积分的方法来计算了。
这听起来是不是有点头疼?别担心,我给您举个例子。
有一次我去参观一个飞机模型展览,看到一个特别漂亮的飞机模型,那机翼的形状很独特。
我就好奇这机翼面积咋算呢。
工作人员就跟我解释,他们先把机翼分成了很多小的部分,每个部分都近似看成一个简单的形状,然后分别计算这些小部分的面积,最后加起来。
这就像是把一个大难题分解成了很多小问题,逐个解决。
再说说在实际的飞机设计中,机翼面积的计算可太重要了。
它直接关系到飞机的升力、阻力和飞行性能。
如果机翼面积算小了,飞机可能就飞不起来;算大了,又会增加重量和阻力,影响飞行效率。
所以啊,工程师们在计算机翼面积的时候,那可是要反复斟酌,考虑各种因素。
他们得根据飞机的用途、速度、重量等等来确定最合适的机翼面积。
总之,飞机机翼面积的计算虽然有点复杂,但只要掌握了方法,也不是啥难事。
希望您通过我的介绍,对这方面能有更清楚的了解!。
naca四位翼型公式_解释说明以及概述

naca四位翼型公式解释说明以及概述1. 引言1.1 概述本文旨在详细讨论和解释NACA四位翼型公式,并对其进行概述。
NACA (National Advisory Committee for Aeronautics)四位翼型公式是一套用于描述飞行器翼型外形的数学方程,它广泛应用于航空领域的翼型设计与分析中。
1.2 文章结构本文主要包括五个部分:引言、NACA四位翼型公式的背景、NACA四位翼型公式的解释说明、NACA四位翼型公式的概述与分类,以及结论及展望。
接下来将逐一介绍每个部分所涵盖的内容。
1.3 目的通过本文,读者将对NACA四位翼型公式有一个全面的理解,包括其背景、发展历史以及重要性。
同时,我们还将详细讨论该公式的基本原理、参数含义和影响因素,并提供使用方法和应用案例作为实际应用指导。
此外,在对不同类型和特征的NACA四位翼型进行分类和概述时,我们将探讨选择考虑因素并分析其区别。
最后,文章将总结主要观点和发现结果,并探讨NACA四位翼型公式未来的发展趋势,并提供改进方向的建议。
随着本文的阅读,读者将了解到NACA四位翼型公式在航空领域中的重要性,以及其对飞行器设计和性能分析所产生的积极影响。
2. NACA四位翼型公式的背景2.1 航空领域中的重要性在航空领域中,飞行器必须具备良好的气动性能,才能实现稳定和高效的飞行。
其中翼型是影响飞行器气动性能最重要的因素之一。
翼型的设计直接决定了飞行器在不同飞行状态下的升力、阻力以及操纵特性等方面表现。
2.2 NACA四位翼型公式的发展历史NACA(National Advisory Committee for Aeronautics)是成立于1915年的美国国家航空咨询委员会。
在20世纪初期,研究人员意识到改善翼型形状对于提高飞机性能至关重要。
为了得到更好的翼型形状,NACA组织开始进行大量实验和理论分析,并最终开发出了一系列适用于不同应用场景的数学公式,即NACA四位翼型公式。
机翼力矩中心计算

机翼力矩中心计算【一、机翼力矩中心概述】机翼力矩中心,简称CM(Center of Moment),是指在飞机飞行过程中,机翼所产生的力矩作用的中心点。
它是飞机设计、飞行控制和飞行性能分析的重要参数。
了解机翼力矩中心的计算方法及其在飞行中的应用,对于飞行员和飞机设计者来说具有重要意义。
【二、机翼力矩中心的计算方法】1.基本公式:机翼力矩中心的位置可以通过以下公式计算:CM = (M1 * d1 + M2 * d2) / (M1 + M2)其中,M1为机翼根部弯矩,d1为机翼根部到力矩中心的距离;M2为机翼尖部弯矩,d2为机翼尖部到力矩中心的距离。
2.修正系数:实际计算中,需要考虑机翼的扭转、弹性变形等因素,因此需要引入修正系数。
修正系数通常包括:扭转修正系数、弹性修正系数等。
3.实例计算:以某型飞机为例,根据设计参数和飞行条件,可以计算出机翼力矩中心的位置。
【三、机翼力矩中心在飞行中的应用】机翼力矩中心在飞行中的应用主要体现在以下几个方面:1.飞行稳定性分析:机翼力矩中心的位置关系着飞机的稳定性,对于飞机的操控性和安全性具有重要意义。
2.飞行性能计算:机翼力矩中心的位置会影响飞机的升力、阻力等性能参数,从而影响飞行性能。
3.飞行控制系统设计:机翼力矩中心是飞行控制系统设计的重要依据,如飞行控制律设计、飞行控制系统硬件布局等。
【四、影响机翼力矩中心的因素】1.机翼几何参数:机翼的形状、尺寸等几何参数会影响机翼力矩中心的位置。
2.飞行条件:飞行速度、高度、温度等条件会对机翼力矩中心产生影响。
3.机翼材料和结构:机翼的材料和结构属性也会对力矩中心产生影响。
【五、总结与建议】机翼力矩中心是飞机设计和飞行控制的关键参数,掌握其计算方法和应用对于飞机性能分析和飞行安全至关重要。
在实际设计和飞行过程中,要充分考虑各种因素对机翼力矩中心的影响,合理调整机翼力矩中心的位置,以提高飞机的飞行性能和安全性。
机翼尾翼设计

少阻力。图如下:
9.内翼后缘扩展:可以增加根部弦长,便于起落架布置,降低根 部弦剖面升力系数,便于气动设计。如下图:
10.增升装置选择:
=
= 可以选择三缝襟翼和前缘缝翼结合。 11.副翼选择: 根据统计,可取如下数据: S 副/S=0.05 c 副/c=0.20 L 副/L=0.25 偏角=30°
12.扰流片布置在后缘襟翼前面 13.燃油容积计算,根据公式: =22914.8kg 符合要求。
14.机翼到机身前头距离: X.25 m.a.c=46%xLFus=18.34m
三.尾翼 1.平尾外形参数: 纵向机身容量参数:
=0.925
其中:
由纵向机身容量参数与平尾容量的关系:
可以得到:平尾容量 VH=3.5*32%=1.12
3.后掠角:Λ =25° 后掠角不能太多太小,变化如下图:.405 时阻力发散 M 大约是 0.81>0.8。
5.机翼参数如下: 面积 S=147.6m2 展长 L= AR ∗ S=37.45m 弦长 =2.25m 气动弦长: 前缘后掠角: 平均气动弦长到翼根距离为 8.25m 机翼平面图如下: =4.18m =0.511 =5.63m
其中:c 为平尾弦长,t 为厚度
所以平尾图如下:
2.垂尾尾外形参数: 航向机身容量参数:
=0.218
其中:
由航向机身容量参数与垂尾容量的关系:
可以得到:垂尾容量Vv=0.105 取尾臂力LV=50%LFUS=19.9m,AR=2.2,λ =0.7,χ =40° 由公式:
其中:机翼面积S=147.6M ,机翼展长bw=37.45m
2
可得: Sv/S=19.7%,垂尾面积 Sv=29.16m2,展长 l=8m, c 根=4.28m, c 尖=3m,垂尾 MAC=3.67m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机翼设计公式
飞机翼的设计公式是航空工程的基础,它关系到飞机的安全性、性能和飞行性能。
飞机翼的设计计算公式是由有效升力系数CL、实际升力L和气动力学加速度
γ所确定的:CL=2L/γV2S,其中γ是空气或其他速度膜的流体动力学加速度,V
是飞机阵风前后壁面的速度,S是单位表面积。
在飞行动力学中,翼型性能主要体现在有效升力、有效推力和有效尾抗三个方面。
有效升力系数CL是应用计算中最重要的参数。
根据力学方程,CL的取值范围
可以从0到翼型的升力系数最大值Cmax。
有效升力系数CL的增加能够提高飞机的
升力场而减小滑行比。
有效推力系数CD是研究飞机滑行性能的另一个重要参数,
它由飞机实际推力和飞行速度所决定。
有效尾抗系数Cm可以用来表征飞机滑行时
气动结构对飞行器姿态的影响。
当翼型设计出来后,通过试验测量得到翼型的三个动力学参数,并与计算值进行对比,以评价计算的精度和可靠性。
在有限的迭代过程中,不断改进翼型,确定最终的设计参数。
以确保飞机翼形
性能满足要求,并能兼顾一定的安全限制,以满足飞行运行要求。
总之,飞机翼设计公式是设计航空器翼型的重要依据,它由有效升力系数CL、实际升力L和气动力学加速度γ确定,根据力学方程,经过反复迭代,得出翼型
的最终设计参数,以确保飞机翼形性能符合预期安全要求,从而满足飞行运行要求。
