清华大学范钦珊版理论力学复习材料共79页
3理论力学 课后答案 (范钦珊 刘燕 王琪 著) 清华大学出版社
RC
FR D
FR G
H
FR H
— 6 —
第 3 章 静力学平衡问题
3-1 图示两种正方形结构所受荷载 F 均已知。试求其中 1,2,3 各杆受力。
: 2 F3 cos 45° − F = 0 解:图(a)
F3 =
2 F (拉) 2
F1 = F3(拉)
F2 − 2 F3 cos 45° = 0
F2 = F(受压) 图(b) : F3 = F3′ = 0 F1 = 0 F2 = F(受拉)
由于 FBC = FCB ; FEC = FCE ,联立式(1)、( 2)、( 3)解得: FH =
(3)
F 2 sin 2 α
3–7 三个半拱相互铰接,其尺寸、支承和受力情况如图所示。设各拱自重均不计,试计算支座 B 的 约束力。
FD′ FD FCx FCy FAy
习题 3-7 图 (a) (b)
习题 1-3 图
F
(a-1) (b-1) 或(b-2)
FAx
F
或(a-2) (c-1)
D B
F
C C
A
C
FAy
α
B
D
(d-1)
或(d-2)
FD
FD
(e-2)
FA FB (e-3)
FA
(e-1)
— 2 —
A F Ax
D A
D
(f-1)
(f-2)
(f-3)
1-4 图 a 所示为三角架结构。荷载 F1 作用在铰 B 上。杆 AB 不计自重,杆 BC 自重为 W。试画出 b、 c、d 所示的隔离体的受力图,并加以讨论。
F
(b)
A
FA
(c)
清华大学范钦珊版理论力学复习材料-第1章

FRy
FRx
止推轴承
机器中常见各类轴承,如 滑动轴承或径向轴承等。这些 轴承允许轴承转动,但限制与 轴线垂直方向的运动和位移。 轴承约束力的特点与光滑圆柱 铰链相同,因此,这类约束可 归入固定铰支座。受力分析Fra bibliotek受力图F
怎样确定O、B二处的受力?
A 处固定
怎样确定 A 处
F
的受力?
D、E 二处为活页铰链
第1章 受力分析概述
本章主要介绍静力学模型—物体的模型、连接 与接触方式的模型、载荷与力的模型,同时介绍物体 受力分析的基本方法。
静力学模型 力的基本概念 工程常见约束与约束力 受力分析与受力图 结论与讨论
静力学模型
物体的抽象与简化-刚体 集中力和分布力 约束
F D
E
怎样确定 D、E 二处的受力?
对于一定 的牵引力
怎样确定配重 W 或滑轮位置?
G B F
对于处于某一 位置的机械臂
A
怎样确定A、B、G三处的受力?
分析力学问题时,往往必须首先根据问题的性 质、已知量和所要求的未知量,选择某一物体(或 几个物体组成的系统)作为研究对象,并假想地将 所研究的物体从与之接触或连接的物体中分离出来, 即解除其所受的约束而代之以相应的约束力。
解除约束后的物体,称为分离体(isolated body)。
分析作用在分离体上的全部主动力和约束力,画 出分离体的受力简图-受力图。这一过程即为受力分 析。
受力分析是求解静力学和动力学问题的 重要基础。具体步骤如下:
选定合适的研究对象,确定分离体; 画出所有作用在分离体上的主动力(一般皆为 已知力);
柔索约束 刚性约束
理论力学课后答案范钦珊)
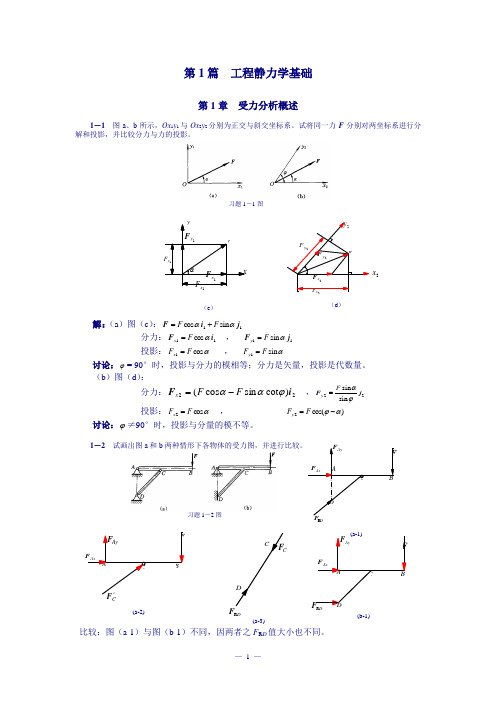
C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c )2x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1-4图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1(f-3)F F'F 1(d-2)AF yB 21(c-1)F A B1FDx y(b-2)1(b-3)F yB 2 F A B1B F习题1-5图AxF'(b-3)E D(a-3)B(b-2)(b-1)F 'CDDF EFBC(c)AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
南航理论力学范钦珊PPT第章力系的等效与简化

2014年10月10日基础部分——静力学第2 章力系的等效与简化力系分类:平面力系空间力系第2章力系的等效和简化力在平面上的投影F xy矢量力在坐标轴上的投影z标量?o90=γzzF xyϕ(二次投影法(二次投影法)(一次投影法(一次投影法)ik jkj i F z y x F F F ++=OxyAF思考:投影与分力间的联系?k j i F z y x F F F ++=zy x F F F F ++=ik j即:对正交坐标系,分力的大小和投影的大小相等。
?即代数和合力投影定理合力投影定理⎪⎭⎪⎬⎫2-1-1 力对点之矩(力矩)xy zOhz)y,A(x,BF矢量r 即矩心z z)(F MOxyzOhz)y,A(x,BFr矩心)(F M O zz)(F M O z定位矢zyxF F F z y x k j i ikjxyzOhz)y,A(x,BFr矩心)(F M OzyxF F F z y x k j i y z z x ?0,0==z F z定义zz代数量力F 对z 轴的矩2-1-2 力对轴之矩力对轴之矩是力使物体绕某一轴F xy在什么情况下M Oz (F )= 0?[思考]0F平行于z 轴F通过z轴)(FOzM hFxy±=当力与轴共面时,力对该轴之矩等于零。
解析表达式另定义xyzOhz)y,A(x,BFr)(F M O )(F Oz M []zO )(F M =力对点之矩与力对轴之矩的关系?[例2-1] xyzOA BFxyF [解法1] 按定义计算[解法2] 按解析式计算2)0,,(a a FF F F F z y x 22,22,0=−==22?)(=F Ox M ?)(=F Oy M2-1-3 合力矩定理定理矢量和点合力矩定理z汇交力系存在合力;那其它力系呢?z轴合力矩定理[例2-2] O )(F M ?[]ααsin cos )(231l l l F −−解:合力矩定理平面力对点之矩OAr yF xF ?=d如何判断两力系等效?M CF BF A力系1F CM EM D力系22-2-1 力系的特征量——主矢与主矩主矢力系中所有力的矢量和。
清华大学《材料力学》(第2版)范钦珊)英文版解题指南-chap.2 Diagram of Internal Forces

Determine the bending moment of point e M(e) through
integrating the differential equation.
Solution:
A
B
C
D
FQ ql
2
Oa e
a
e
O
M
ql 2 8
?
dM dx
FQ
dM FQdx
e
e
dM a
a FQdx
TSINGHUA UNIVERSITY
The Third Kind of Exercise: The counter-operation of differential equation of equilibrium
Problem 5
TSINGHUA UNIVERSITY
Back to the first page
below and determine the values of M max
and| FQ |max
.
2M MM
a
a
a
a
The Second Kind of Exercise: Utilize the differential equation of equilibrium to draw the shear and bending moment diagrams (1)
TSINGHUA UNIVERSITY
Fan’s Studio for Education and Teaching
HIGHER EDUCATION PRESS BEIJING CHINA
Q.S.Fan Tsinghua University P.R.CHINA
名师名校精品课件清华大学《材料力学》(第2版)范钦珊)英文版解题指南-chap.7 Composite Forces

TSINGHUA UNIVERSITY
Back to the first page
τx´y´
α=-15° x
σx´
x´
Solution: 2. The normal stress perpendicular to the direction of grain of timber
where
x
x
y 2
Back to the first page
Problem:The stresses, which are applied to the element of the component of timber, are shown in the figure. The angle shown in the figure is the included angle of the direction of grain of timber with the vertical direction.
Extensive Problem
hydraulic vessel
column plunger
In this case, why do not we consider the radial stress in the wall?
The Second Kind of Exercise: The Application of Strain Energy Density
0
0
100 2
sin(
2
30)
xycos(2 30)
x 33.3MPa xy yx 57.7MPa
The First Kind of Exercise: The Analysis of the Stress-State
清华大学材料力学习题详解(范钦珊) 第13章

eBook材料力学习题详细解答教师用书(第13章)2006-01-18范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan’s Education & Teaching Studio习题13-1 习题13-2 习题13-3 习题13-4 习题13-5 习题13-6 习题13-7 习题13-8第13章 动载荷与疲劳强度概述13-1 图示的No.20a 普通热轧槽钢以等减速度下降,若在0.2s 时间内速度由1.8m/s 降至0.6m/s ,已知l =6m ,b =1m 。
试求槽钢中最大的弯曲正应力。
解:No.20a 槽钢的线密度63.22=ρkg/m槽钢的加速度62.08.16.0−=−=a m/s 2 由自重引起的均布载荷集度:g q ρ=1(↓)由惯性力引起的均布载荷集度: a q ρ=2(↓) (加速度↑)总的均布载荷集度:)(21a g q q q +=+=ρ由总载荷(动载荷+静载荷)引起的弯矩:)(4432824max a g q q q M M C +=×=××+××−==ρ=4×22.63(9.8+6)=1430 N ·m于是,槽钢横截面上的最大正应力MPa 1591022414306min dmax ..=×==−W M C σ13-2 钢制圆轴AB 上装有一开孔的匀质圆盘如图所示。
圆盘厚度为δ,孔直径300mm 。
圆盘和轴一起以匀角速度ω转动。
若已知:δ=30mm ,a =1000mm ,e =300mm;轴习题13-1图习题13-2图直径d =120mm ,ω=40rad/s ;圆盘材料密度33m kg 108.7×=ρ。
试求由于开孔引起的轴内最大弯曲正应力(提示:可以将圆盘上的孔作为一负质量(-m ),计算由这一负质量引起的惯性力)。
解:将圆盘上的孔作为一负质量(-m ),计算由这一负质量引起的惯性力:222I π4F me D e ==××××ωρδω由此引起的附加动约束力:2IF F F B A == 动载荷引起的附加最大动弯矩发生在C 截面,其值为:a F a F M A I max 21== 于是,最大附加弯曲动应力:22dmax dmax 3π24672MPa π32.a D e M d W⋅⋅===ρδωσ13-3 质量为m 的匀质矩形平板用两根平行且等长的轻杆悬挂着,如图所示。
范钦珊版材料力学习题全解 第2章 拉伸与压缩杆件的应力变形分析与强度计算

习题 2-2 习题 2-4 习题 2-6 习题 2-8 习题 2-10 习题 2-12 习题 2-14 习题 2-16 习题 2-18
2
材料力学习题详细解答之二 第 2 章 拉伸与压缩杆件的应力变形分析与强度计算
2-1 两根直径不同的实心截面杆,在 B 处焊接在一起,弹性模量均为 E=200 GPa, 受力和尺寸等均标在图中。
习题 2-8 图
解:由图(a):
8
∑ F y = 0 , F3 =
3 FP 5
4 5 4 3
∑ Fx = 0 , F1 = − F3 = − FP
由图(b):
∑ Fx = 0 , F4 = 4 F3 = 4 FP
5 3
5 ∑ F y = 0 , F2 = − F3 = − FP 3
| F1 |>| F2 |
m2,l=2
习题 2-4 图
解:根据已知条件,用截面法求得
5
FNA = 40 kN, FNB = 20 kN, FNE = 30 kN FNA 40 × 10 3 = = 200 MPa (1) σ A = A 2.0 × 10 − 4 F σ B = NB = 100 MPa A F NE σE = = 150 MPa A (2) σ max = σ A = 200 MPa(A 截面)
σa =
2. σ s =
FNa Ea FP =− Aa b0 hEs + 2b1hEa
− 200 × 109 × 385 × 103 0.03 × 0.05 × 200 × 109 + 2 × 0.02 × 0.05 × 70 × 109
= −175 MPa(压)
σa =
−175E a 70 = −175 = −61.25 MPa(压) Es 200
