简单理解泊松分布
工业设计概论 泊松

工业设计概论导言工业设计是以实现产品的功能、美学和经济效益为目标的设计过程。
它涵盖了产品的外观设计、结构设计、材料选择等方面。
在工业化时代,工业设计对于企业的竞争力和产品的市场反应能力起着至关重要的作用。
本文将重点介绍泊松分布在工业设计中的应用。
泊松分布的概念泊松分布是一种概率分布,描述了在给定时间或空间范围内,事件发生的次数的概率分布。
泊松分布最早由法国数学家勒朗德·泊松在1837年发表的论文中介绍。
泊松分布的特点1.事件在给定时间或空间范围内是独立发生的。
2.事件在给定时间或空间范围内的概率是相等的。
3.事件的平均发生率是已知的。
泊松分布在工业设计中的应用泊松分布在工业设计中有多种应用,主要体现在以下几个方面:1. 产品瑕疵率的估计在工业生产中,产品的瑕疵率是一个重要的指标。
通过对产品瑕疵率的估计,企业可以评估生产过程中的质量控制情况,并及时采取措施进行调整。
泊松分布可以用于对产品瑕疵率的统计分析,帮助企业判断产品的质量水平,进而提高产品的竞争力。
2. 设备维修时间的预测在工业生产过程中,设备的损坏和维修是不可避免的。
泊松分布可以用于对设备维修时间的预测和规划,帮助企业合理安排维修计划,提高设备利用率和生产效率。
3. 生产线上的故障排查在产品生产线上,经常会出现一些故障,而这些故障往往会导致生产线的停工和生产效率的降低。
泊松分布可以用于对生产线上故障发生的概率进行分析,帮助企业及时排查故障,并改进生产线的设计和操作,提高生产效率和产品质量。
4. 产品需求量的预测在产品设计和生产过程中,准确预测产品的需求量对于企业的运营和市场营销至关重要。
泊松分布可以用于对产品需求量的预测,帮助企业合理安排生产计划和库存管理,降低生产成本和库存风险。
总结泊松分布在工业设计中具有重要的应用价值。
通过对产品瑕疵率的估计、设备维修时间的预测、生产线上的故障排查以及产品需求量的预测等方面的分析,企业可以提高产品质量、生产效率和市场反应能力,增强竞争力。
泊松分布的概念及表和查表方法
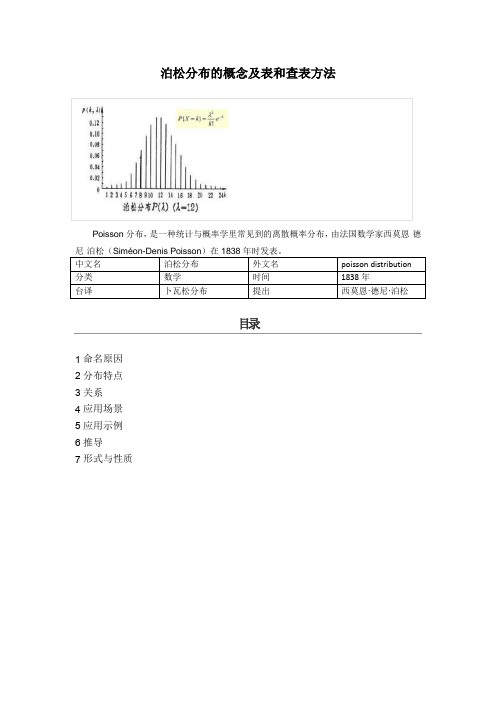
泊松分布的概念及表和查表方法目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。
泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)命名的,他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。
通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。
应用场景在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。
因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性)。
应用示例泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。
泊松分布的概念及表和查表方法

泊松分布的概念及表和查表方法Poisson分布,是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。
中文名泊松分布外文名poisson distribution 分类数学时间1838年台译卜瓦松分布提出西莫恩·德尼·泊松目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。
泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Sim éon-Denis Poisson)命名的,他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。
通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。
应用场景在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。
4.3.2泊松分布

生物统计学
二项分布
一、泊松分布:二项式分布的极限分布
二、分布参数
三、分布形状
一、泊松分布:二项式分布极限分布
应用二项式分布时,往往遇到一个概率p或q是很小
的值,例如小于0.1,另一方面n又相当大,这样以
上二项分布将为另一种分布所接近,或者为一种极
限分布。
这一种分布称泊松概率分布,简称泊松分
布(Poisson distribution)。
二、分布参数
三、分布形状这一分布包括一个参
数m,由m的大小决
定其分布形状如图4.4。
当m值小时分布呈很
偏斜形状,m增大后
则逐渐对称,趋近于
以下即将介绍的正态
分布
观察值:单位空间上的个数
例如,在一定面积上的害昆虫个数的分布;病害作物个数(单株数)的分布。
谢谢!。
保险学泊松分布

保险学泊松分布保险学泊松分布是指在保险行业中,用泊松分布来计算风险事件的发生率和评论事故的频次。
本文将介绍泊松分布在保险领域的应用以及如何使用泊松分布来计算保险的风险和概率。
一、泊松分布在保险领域的应用泊松分布是一种用于描述稀有事件发生率和时序独立的概率分布。
在保险领域中,泊松分布常用于计算各种类型的风险,如车祸率、火灾率、自然灾害率等。
保险公司可以使用泊松分布来计算遇到这些风险的概率,以评估自己的风险暴露水平,并为下一步的风险管理决策提供有力的支持。
泊松分布在商业保险业务中的应用也比较广泛。
例如,生命保险公司可以使用泊松分布来估计特定年龄组人士死亡的数量。
对于车险公司来说,他们可以使用泊松分布来估计在特定地点和特定时间的车祸数量。
只要保险公司有充足的数据,泊松分布可以用于估计和预测任何类型的保险事件。
二、如何使用泊松分布来计算风险和概率在保险行业中,泊松分布常常用于计算保险事件的预期频率。
为了计算预期频率,需要了解以下四个要素:1. 保险事件的时间段,如一个月或一年;2. 该时间段内具有该风险的总数量,比如说一个月内发生车祸的次数;3. 整个保险事件历史数据;4. 次数的平均数(称为泊松速率),通常利用历史数据得出。
对于一个不那么明显的例子,如计算建筑物失火的可能性,请看以下步骤:第一步:确定事件的时间段。
例如,你想计算1年内建筑物失火的可能性。
第二步:使用历史数据计算事件的平均发生率。
例如,如果你发现过去10年,共发生了150起建筑物失火事件,那么平均每年发生的失火次数是15次。
第三步:使用泊松分布来计算预期建筑物失火事件的数量。
密度函数p(k)告诉我们在一年内k次事件发生的概率。
p(k)由以下公式计算其中,n是平均每年发生的失火次数。
例如,在上述示例中,n = 15。
k是你想知道的每年发生的失火事件的数量。
第四步:根据泊松分布计算得出,1年内发生建筑物失火的概率分布如下表所示:从表中可以看出,在1年中,发生0次建筑物失火的概率是0.0232,几乎是非常小的概率。
泊松分布的概念及表和查表方法

泊松分布的概念及表和查表方法目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。
泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)命名的,他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。
通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。
应用场景在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。
因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性)。
应用示例泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。
泊松分布定理

泊松分布定理泊松分布定理又称为泊松定理,是概率论中的一条重要定理,它描述了随机事件在单位时间内发生的次数服从泊松分布的概率分布。
泊松分布定理的数学表达式为:P(k) = λ^k * e^(-λ) / k!其中,P(k)表示事件发生k次的概率,λ为单位时间内事件平均发生的次数。
首先,我们来解释一下泊松分布的背景和基本概念。
泊松分布是一种描述离散随机变量的概率分布,它适用于具有以下特点的事件:1. 事件是独立发生的,每次事件的发生与其他事件的发生无关。
2. 事件在单位时间内发生的次数是有限的,没有上限。
3. 事件平均发生的次数在单位时间内是相对稳定的,不会随时间发生变化。
泊松分布定理给出了计算事件发生概率的具体公式,可以通过该公式计算出任意次数事件发生的概率。
泊松分布定理的证明主要基于数学方法,其中用到了高等数学中的泰勒级数展开和极限的概念。
证明的过程比较抽象和复杂,对于一般读者来说可能较难理解。
然而,对于实际应用中的问题,我们可以通过具体的例子来更好地理解和应用泊松分布定理。
例如,假设一个电话交换台每分钟接收的电话次数平均为3次,现在我们希望知道在30分钟内接收到5次电话的概率是多少。
根据泊松分布定理,我们可以计算出这个概率。
首先,将λ=3代入泊松分布定理公式,得到事件发生k=5次的概率P(5):P(5) = 3^5 * e^(-3) / 5!接下来,我们希望计算在30分钟内接收到5次电话的概率,这相当于在30个单位时间内接收到5次电话的概率。
由于事件是独立发生的,我们可以将30分钟内接收到5次电话的概率表示为:P = P(5)^30将前面计算得到的P(5)代入上式,即可计算出在30分钟内接收到5次电话的概率。
通过这个例子,我们可以看到泊松分布定理的应用具有一定的实用性。
在实际问题中,例如交通流量的分析、疾病的发病率研究等,都可以采用泊松分布定理进行概率计算。
总结起来,泊松分布定理是概率论中的一条重要定理,用于描述随机事件在单位时间内发生的次数服从泊松分布的概率分布。
泊松分布的理解

泊松分布的理解一、什么是泊松分布泊松分布是一种概率分布,它描述了在一定时间或空间范围内,事件发生的次数。
它得名于法国数学家西蒙泊松(Siméon Denis Poisson),他在研究天文学时发现了这种分布。
泊松分布的特点是:事件的发生是随机的,且任意两个事件之间是独立的。
它通常用于描述一些稀有事件的发生概率,例如地震、车祸、电话呼叫等。
二、泊松分布的公式泊松分布的概率质量函数为:P(X=k)=e^(-λ) * λ^k / k!其中,X表示事件发生的次数,λ表示单位时间或单位空间内事件的平均发生次数,k表示事件发生的次数。
三、泊松分布的实际应用1. 网络攻击网络攻击是一种随机事件,它的发生概率符合泊松分布。
例如,黑客攻击某个网站的次数就可以用泊松分布来描述。
在网络安全领域,泊松分布被广泛应用于预测网络攻击的发生概率和频率,以便采取相应的防御措施。
2. 电话呼叫电话呼叫也符合泊松分布的特点。
例如,某个电话服务中心在一个小时内接到的呼叫次数就可以用泊松分布来描述。
这种分布可以帮助电话服务中心预测客户呼叫的数量,以便安排足够的客服人员来处理呼叫。
3. 交通事故交通事故也可以用泊松分布来描述。
例如,在一个路口发生的交通事故数量就可以用泊松分布来表示。
这种分布可以帮助交通管理部门预测交通事故的发生概率和频率,以便采取相应的交通安全措施。
四、泊松分布的优点和缺点泊松分布的优点是:它简单易用,适用于描述稀有事件的发生概率。
它的概率质量函数只有一个参数λ,可以通过样本数据来估计。
此外,泊松分布具有无记忆性,即事件的发生概率与之前的事件无关,这使得它在实际应用中更加方便。
泊松分布的缺点是:它只适用于描述稀有事件,当事件的发生次数较多时,它的拟合效果就会变差。
此外,泊松分布假设事件的发生是随机独立的,但在实际应用中,事件之间可能存在一定的相关性,这也会影响泊松分布的拟合效果。
五、总结泊松分布是一种描述稀有事件发生概率的概率分布,它可以应用于很多领域,例如网络安全、电话服务、交通管理等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正确理解泊松分布 很多人在上概率论这门课的时候就没搞明白过泊松分布到底是怎么回事,至少我就是如此。
虽然那个时候大家都会背“当试验的次数趋于无穷大,而乘积np 固定时,二项分布收敛于泊松分布”,大部分的教科书上也都会给出这个收敛过程的数学推导,但是看懂它和真正理解还有很大距离。
如果我们学习的意义是为了通过考试,那么我们大可停留在“只会做题”的阶段,因为试卷上不会出现“请发表一下你对泊松公式的看法”这样的题目,因为那样一来卷子就变得不容易批改。
所以现在的大部分考试都会出一些客观题,比如到底是泊松分布还是肉松分布。
而如果我们学习的目的是为了理解一样东西,那么我们就有必要停下来去思考一下诸如“为什么要有泊松分布?”、“泊松分布的物理意义是什么?”这样的“哲学”问题。
如果我们要向一个石器时代的人解释什么是电话,我们一定会说:“电话是一种机器,两个距离很远的人可以通过它进行交谈”,而不会说:“电话在1876年由贝尔发明,一台电话由几个部分构成……”(泊松分布在1876年由泊松提出,泊松分布的公式是……)所以我们问的第一个问题应该是“泊松分布能拿来干嘛?”
泊松分布最常见的一个应用就是,它作为了排队论的一个输入。
什么是排队论?比如我们每天去食堂打饭,最头疼的一个问题就是排队,之所以要排队是因为食堂打饭的大叔有限,假设学校有1000个学生,而食堂恰好配了1000个大叔和打饭的窗口,那么就永远不会有人排队。
但是出于经营成本方面的考虑食堂通常不会这么干,因此如何控制窗口的数量并且保证学生不会因为排队时间太长而起义是一门很高深的学问。
在一段时间t (比如1个小时)内来到食堂就餐的学生数量肯定不会是一个常数,(比如一直是200人),而应该符合某种随机规律:比如1个小时内来200个学生的概率是10%,来180个学生的概率是20%……一般认为,这种随机规律服从的就是泊松分布。
也就是在单位时间内有k 个学生到达的概率为:
,...1,0,!
)(==-k k e k f k
λλ 其中λ为单位时间内学生的期望到达人数。
问题是“这个式子是怎么来的呢?”——我们知道泊松分布是二项分布满足某种条件的一个特殊形式,因此可以先从简单的二项分布入手,寻找两者之间的联系。
二项分布很容易理解,比如一个牛仔一枪打中靶子的概率是p ,如果我们让他开10枪,如果每击中一次目标就得一分,问他一共能得几分?虽然我们不能在牛仔射击前准确地预测出具体的得分k ,但可以求出k 的概率分布,比如k=9的概率是50%,k=8的概率是30%……并且根据k 的分布来判断他的枪法如何,这便是概率统计的思想。
具体计算的方法就是求出“得k 分”的概率。
比如“得9分”可以是“射失第一发,而命中其余的9发”,它的概率是p 的9次方乘上(1-p ),当然,可能情况不只这种,我们用X 代表“没命中”,O 代表“命中”,“得9分”所有的可能的情况如下: XOOOO OOOOO
OXOOO OOOOO
OOXOO OOOOO
OOOXO OOOOO
OOOOX OOOOO
OOOOO XOOOO
OOOOO OXOOO
OOOOO OOXOO
OOOOO OOOXO
OOOOO OOOOX
根据组合数性质,在
C 910种情况下,牛仔都可以得到9分。
因此牛仔“得9分”的概率是9-1099
10)1(p p C -。
同理,“射击n 次,得k 分”的概率就是k n k k
n p p C --)1(。
对于一个神枪手(p=1)来
讲,他“射击10次,得10分”的概率就是1.
二项分布和泊松分布最大的不同是前者的研究对象是n 个离散的事件(10次射击),而后者考察的是一段连续的时间(单位时间)。
因此泊松分布就是在二项分布的基础上化零为整。
如果我们把单位时间划分成n 个细小的时间片,假设在每个时间片内牛仔都在射击,只是这次他发射的不是子弹,而是学生——“命中目标”就代表向食堂成功地发射出一个学生,如果“没有命中”就表示学生被打到了食堂之外的地方。
如果n 不是无穷大,那么在某个时间片内可能出现两个学生同时进入食堂的状况,这样的话就和我们假设任意的时间片内只可能发生“一个学生出现”或“没有学生出现”不符,为了能用二项分布去近似泊松分布,因此n 必须趋于无穷,时间片必须无穷小,这也是为什么泊松分布的前提之一是“n 很大” 的原因!(另一个前提是“p 很小”)
这样一来我们就可以用二项分布的公式表示单位时间到来k 个学生的概率了。
在单位时间内发生n 次独立的“发射学生”试验,把学生“发射”到食堂的概率是p :
那么单位时间内食堂到来k 个学生的概率:
k n k k n
p p C --)1( 当np 固定时,设np=λ,故n p λ
=,原式子可变为:
k n k
k n n n C --⎪⎭⎫ ⎝⎛)1(λλ 把组合数展开:
k n k
n n k k n n n n --⎪⎭
⎫ ⎝⎛+⋅⋅⋅--)1(!)1-()2)(1(λλ 调整式子: k n k k n n k n n n n k --+⋅⋅⋅--)1()
1-()2)(1(!
λλ 将k n 拆成k 个n 连乘的形式:
k n k n n n n k n n n n k --⋅⋅⋅⋅+⋅⋅⋅--)1()
1-()2)(1(!λ
λ: 将每一个n 和分子的一个因式合并为一项可得:
k n k n
n k n n k ---⋅⋅⋅)1)](1-1()2-1(1-1[!λλ)( 由于∞→n ,即:
k n n k n
n k n n k -∞→--⋅⋅⋅)1)](1-1()2-1(1-1[lim !λλ)( 因为:1)1-1()2-1(1-1lim
=-⋅⋅⋅∞→n k n n n )( λλ
λ-∞→-∞→=-=-e n n n n k n n )1(lim )1(lim 所以原式λλ-⋅=e k k
!
这就是我们熟悉的泊松公式,其中λ的物理意义就是单位时间内学生到来的数量,也就是平均到达率,是一个常数。
