统计学案例——相关回归分析
简单线性回归分析2

)
lXY lXX
a Y bX
03:56
24
b=0.1584,a=-0.1353
Yˆ 0.1353 0.1584X
03:56
25
回归直线的有关性质
(1) 直线通过均点 ( X ,Y )
(2) 各点到该回归线纵向距离平方和较到其它任何直线小。
(Y Yˆ)2 [Yˆ a bX ]2
03:56
残 差 0.0282 22 0.0013
总变异 0.0812 23
R2=SS回归/SS总=0.0530/0.0812=0.6527 说明在空气中NO浓度总变异的65.27%与车流量有关。
03:56
48
二、简单线性回归模型
两变量关系的定量描述 统计推断 统计应用
统计预测
Y 的均值的区间估计:总体回归线的95%置信带(相应X 取值水平下,) ;
回归模型 (regression model):
描述变量之间的依存关系的函数。
简单线性回归(simple linear regression):
模型中只包含两个有“依存关系”的变量,一个变量随 另外一个变量的变化而变化,且呈直线变化趋势,称之 为简单线性回归。
03:56
9
例如,舒张压和血清胆固醇的依存性
统计推断 通过假设检验推断NO平均浓度是否随着车 流量变化而变化;
统计应用 利用模型进行统计预测或控制。
03:56
13
两变量关系的定量描述
散点图 简单线性回归方程 回归系数的计算——回归系数的最小二乘估计 线性回归分析的前提条件
03:56
14
1. 散点图
0.25
0.2
NO浓度/×10-6
正态 (normal)假定是指线性模型的误差项服从正态 分布 。
统计学案例——相关回归分析报告
统计学案例——相关回归分析报告《统计学》案例——相关回归分析案例⼀质量控制中的简单线性回归分析1、问题的提出某⽯油炼⼚的催化装置通过⾼温及催化剂对原料的作⽤进⾏反应,⽣成各种产品,其中液化⽓⽤途⼴泛、易于储存运输,所以,提⾼液化⽓收率,降低不凝⽓体产量,成为提⾼经济效益的关键问题。
通过因果分析图和排列图的观察,发现回流温度是影响液化⽓收率的主要原因,因此,只有确定⼆者之间的相关关系,寻找适当的回流温度,才能达到提⾼液化⽓收率的⽬的。
经认真分析仔细研究,确定了在保持原有轻油收率的前提下,液化⽓收率⽐去年同期增长1个百分点的⽬标,即达到12.24%的液化⽓收率。
2、数据的收集⽬标值确定之后,我们收集了某年某季度的回流温度与液化⽓收率的30组数据(如上表),进⾏简单直线回归分析。
3.⽅法的确⽴设线性回归模型为εββ++=x y 10,估计回归⽅程为x b b y10?+= 将数据输⼊计算机,输出散点图可见,液化⽓收率y 具有随着回流温度x的提⾼⽽降低的趋势。
因此,建⽴描述y 与x 之间关系的模型时,⾸选直线型是合理的。
从线性回归的计算结果,可以知道回归系数的最⼩⼆乘估计值b 0=21.263和b 1=-0.229,于是最⼩⼆乘直线为x y229.0263.21?-= 这就表明,回流温度每增加1℃,估计液化⽓收率将减少0.229%。
(3)残差分析为了判别简单线性模型的假定是否有效,作出残差图,进⾏残差分析。
从图中可以看到,残差基本在-0.5—+0.5左右,说明建⽴回归模型所依赖的假定是恰当的。
误差项的估计值s=0.388。
(4)回归模型检验 a.显著性检验在90%的显著⽔平下,进⾏t 检验,拒绝域为︱t ︱=︱b 1/ s b1︱>t α/2=1.7011。
由输出数据可以找到b 1和s b1,t=b 1/ s b1=-0.229/0.022=-10.313,于是拒绝原假设,说明液化⽓收率与回流温度之间存在线性关系。
spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析案例。
在统计学中,多元回归分析是一种用于探究多个自变量与因变量之间关系的方法。
通过多元回归分析,我们可以了解不同自变量对因变量的影响程度,以及它们之间的相互作用情况。
在本篇文档中,我将通过一个实际案例来介绍如何使用SPSS软件进行多元回归分析。
案例背景:假设我们是一家电子产品公司的市场营销团队,在推出新产品之前,我们希望了解不同因素对产品销量的影响。
我们收集了一些数据,包括产品的售价、广告投入、竞争对手的售价、季节等因素,以及产品的销量作为因变量。
数据准备:首先,我们需要将数据录入SPSS软件中。
在SPSS中,我们可以通过导入Excel文件的方式将数据导入到软件中,并进行必要的数据清洗和处理。
确保数据的准确性和完整性对于后续的多元回归分析非常重要。
模型建立:接下来,我们需要建立多元回归模型。
在SPSS中,我们可以通过依次选择“分析”-“回归”-“线性回归”来进行多元回归分析。
在“因变量”栏中输入销量,然后将所有自变量依次输入到“自变量”栏中。
在建立模型之前,我们还需要考虑是否需要进行变量转换或交互项的添加,以更好地拟合数据。
模型诊断:建立模型后,我们需要对模型进行诊断,以确保模型的准确性和有效性。
在SPSS中,我们可以通过查看残差的正态性、异方差性以及自相关性来进行模型诊断。
如果模型存在严重的偏差或违反了多元回归分析的假设,我们需要进行相应的修正或改进。
模型解释:最后,我们需要解释多元回归模型的结果。
在SPSS的输出结果中,我们可以看到各个自变量的系数、显著性水平、调整R方等统计指标。
通过这些指标,我们可以了解不同自变量对销量的影响程度,以及它们之间的相互作用情况。
同时,我们还可以进行各种假设检验,来验证模型的有效性和可靠性。
结论:通过以上多元回归分析,我们可以得出不同自变量对产品销量的影响程度,以及它们之间的相互作用情况。
这些结果对于我们制定产品的定价策略、广告投放策略以及市场营销策略都具有重要的指导意义。
相关分析回归分析案例

相关分析
概念
种类
线性相关
变量之间关系
函数关系
相关关系
因果关系
互为因果关系
共变关系
确定性依存关系
随机性依存关系
种类
一元相关
多元相关
负 相 关
正 相 关
线性相关
曲线相关
x
y
正 相 关
x
y
负 相 关
x
y
曲线相关
x
y
不 相 关
Hale Waihona Puke 线性相关相关系数测定两变量是否线性相关?
定义式:
(2)D.W检验 D.W检验用于检验残差序列的自相关性。自相关性会影响模型参数估计值不具有最优性,使区间估计和预测区间的精度较低。J.Durbin和 G.S.Watson 于1951年提出的一种序列自相关的方法。简称DW检验。DW检验目前是检验自相关性的最常用方法,但它只适用于检验一阶自相关性。一般只需考察计算得到的DW值落入的区间,以确定模型自相关状态。判别准则 若0≤D.W ≤d,序列存在正相关; 若d< D.W <4- d ,序列无自相关; 若4-dL < D.W ≤4,序列存在负相关
3·相关分析测定相关程度和方向,回归分析用回归模型进行预测和控制。
y与x之间是一种相关关系,即当自变量x变化时,因变量y大体按某规律变化,两者之间的关系不能直观地看出来,需要用统计学的办法加以确定,回归分析就是研究随机现象中变量间关系的一种数理统计方法,相关关系存在着某种程度的不确定性。 身高与体重;矿物中A组分含量与B组分含量间的关系;分析化学制备标准工作曲线,浓度与吸光度间的关系。 求回归方程的方法,通常是用最小二乘法,其基本思想就是从并不完全成一条直线的各点中用数理统计的方法找出一条直线,使各数据点到该直线的距离的总和相对其他任何线来说最小,即各点到回归线的差分和为最小,简称最小二乘法。
相关性与回归分析
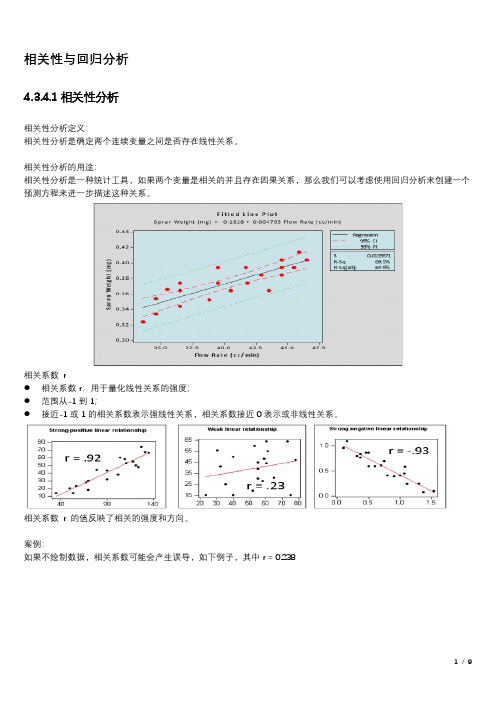
相关性与回归分析4.3.4.1相关性分析相关性分析定义:相关性分析是确定两个连续变量之间是否存在线性关系。
相关性分析的用途:相关性分析是一种统计工具,如果两个变量是相关的并且存在因果关系,那么我们可以考虑使用回归分析来创建一个预测方程来进一步描述这种关系。
相关系数r●相关系数r:用于量化线性关系的强度;●范围从-1到1;●接近-1或1的相关系数表示强线性关系,相关系数接近0表示或非线性关系。
相关系数r 的值反映了相关的强度和方向。
案例:如果不绘制数据,相关系数可能会产生误导,如下例子,其中r = 0.238尽管相关系数表示弱线性关系,但图形显示强曲线关系-始终绘制数据相关VS因果例如,犯罪率和冰淇淋销售之间的相关系数为r=0.96,那么强相关系数是否意味着因果关系?高冰激凌销量会导致高犯罪率吗?相关性只意味着存在一种线性关系,而未必是因果关系。
相关性分析案例:黑带想知道在更高的流速和更多附着在灯丝上的物质之间是否存在线性关系?收集历史数据并计算相关系数。
相关检验的原假设是相关系数r=0(更高的流速和更多附着在灯丝上的物质之间无线性关系),备择假设是相关系数r ≠0(更高的流速和更多附着在灯丝上的物质之间有线性关系)。
●p > 0.05,无法拒绝原假设,更高的流速和更多附着在灯丝上的物质之间无线性关系(无显著性差异);●p < 0.05,拒绝原假设,更高的流速和更多附着在灯丝上的物质之间有线性关系(有显著性差异)。
复制数据-统计(S)-基本统计(B)-相关(C):变量(V):点击C15、C16?-方法(M):选择pearson相关系数-点击显示P值(D)-确定P值决定了统计的显著性,皮尔逊相关系数r = 0.834为正,正相关,中等强度(较强)相关性。
判定准则(结论):p值= 0.000 < 0.05,拒绝原假设,接收备择假设,更高的流速和更多附着在灯丝上的物质之间有线性关系。
皮尔逊相关系数r = 0.834,为较强的正相关。
统计学案例分析

统计学案例分析(总3页)
--本页仅作为文档封面,使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
统计学期末考试
y=a+bx
关于江西省GDP与全国GDP的数据分析
一:相关于回归分析
由上图可知:y=
相关系数:R=5836
所以江西省GDP与全国GDP确实存在着线性相关关系
二:时间趋势分析
对比上列数据图表可知:江西省GDP增速在2005年低于全国平均水平,随后逐渐赶超,至2008-
2009年时增速差距最明显,至2014-2015年,江西省GDP增
速又遇到阻碍,低于全国均值
y=a+bx b=
a=y=
故y=+
三:图表分析
对比上列数据图表可知:江西省GDP增速在2005年低于全国平均水平,随后逐渐赶超,至2008-2009年时增速差距最明显,至2014-2015年,江西省GDP增速又遇到阻碍,低于全国均值。
多元线性回归分析案例

多元线性回归分析案例多元线性回归分析是统计学中常用的一种分析方法,它可以用来研究多个自变量对因变量的影响,并建立相应的数学模型。
在实际应用中,多元线性回归分析可以帮助我们理解变量之间的关系,预测未来的趋势,以及制定相应的决策。
本文将通过一个实际案例来介绍多元线性回归分析的基本原理和应用方法。
案例背景。
假设我们是一家电子产品制造公司的市场营销团队,我们想要了解产品销量与广告投入、产品定价和市场规模之间的关系。
我们收集了过去一年的数据,包括每个月的产品销量(千台)、广告投入(万元)、产品定价(元/台)和市场规模(亿人)。
数据分析。
首先,我们需要对数据进行描述性统计分析,以了解各变量的分布情况和相关性。
我们计算了产品销量、广告投入、产品定价和市场规模的均值、标准差、最大最小值等统计量,并绘制了相关性矩阵图。
通过分析发现,产品销量与广告投入、产品定价和市场规模之间存在一定的相关性,但具体的关系还需要通过多元线性回归分析来验证。
多元线性回归模型。
我们建立了如下的多元线性回归模型:\[Sales = \beta_0 + \beta_1 \times Advertising + \beta_2 \times Price + \beta_3 \times MarketSize + \varepsilon\]其中,Sales表示产品销量,Advertising表示广告投入,Price表示产品定价,MarketSize表示市场规模,\(\beta_0, \beta_1, \beta_2, \beta_3\)分别为回归系数,\(\varepsilon\)为误差项。
模型验证。
我们利用最小二乘法对模型进行参数估计,并进行了显著性检验和回归诊断。
结果表明,广告投入、产品定价和市场规模对产品销量的影响是显著的,模型的拟合效果较好。
同时,我们还对模型进行了预测能力的验证,结果表明模型对未来产品销量的预测具有一定的准确性。
决策建议。
统计学原理 相关与回归分析

粮食产量y 随机的
降雨量
土质
种子 耕作技术
X3
X4 X5
可 控 的
(二)相关的种类
完全相关 函数关系是相关关系的一种特例。 不完全相关 相关分析的基本内容
度相 关 密 切 程
y 完全由x的数值唯一确定,函数关系。
不相关
相 关 的 性 质
x、y值变化各自独立,变量间没有相关
关系
正相关 x 负相关
y
x
x2 26896 28900 31329 24336 25600 27556
y2
62540 73695 420857
70225 83521 463382
55696 65025 382469
合计
2114
从表上可以看出,随着个人收入的增加,消 费支出有明显的增长趋势,二者存在一定的依存 关系。正相关关系。 2、相关图(散点图) 直角坐标系第一象限
1、相关表
单变量分组相关表
分组相关表
双变量分组相关表
先做定性分析——相关资料排序——列在一张表上
个人收入x 164 170 177 182 192 207 225 243 265 289
消费支出y 156 160 166 170 178 188 202 218 236 255 1929
xy 25584 27200 29382
yc = 25.32 + 0.7927 300 = 263.13万元
(三)估计标准误差Syx P197
Syx = Syx =
=
(y - yc) 2 n-2 y2 - a y -b xy n-2
382469 -25.32 1929 -0.7927 420857
10 - 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《统计学》案例——相关回归分析案例一质量控制中的简单线性回归分析1、问题的提出某石油炼厂的催化装置通过高温及催化剂对原料的作用进行反应,生成各种产品,其中液化气用途广泛、易于储存运输,所以,提高液化气收率,降低不凝气体产量,成为提高经济效益的关键问题。
通过因果分析图和排列图的观察,发现回流温度是影响液化气收率的主要原因,因此,只有确定二者之间的相关关系,寻找适当的回流温度,才能达到提高液化气收率的目的。
经认真分析仔细研究,确定了在保持原有轻油收率的前提下,液化气收率比去年同期增长1个百分点的目标,即达到12.24%的液化气收率。
2、数据的收集目标值确定之后,我们收集了某年某季度的回流温度与液化气收率的30组数据(如上表),进行简单直线回归分析。
3.方法的确立设线性回归模型为εββ++=x y 10,估计回归方程为x b b y10ˆ+= 将数据输入计算机,输出散点图可见,液化气收率y 具有随着回流温度x 的提高而降低的趋势。
因此,建立描述y 与x 之间关系的模型时,首选直线型是合理的。
从线性回归的计算结果,可以知道回归系数的最小二乘估计值b 0=21.263和b 1=-0.229,于是最小二乘直线为x y229.0263.21ˆ-= 这就表明,回流温度每增加1℃,估计液化气收率将减少0.229%。
(3)残差分析为了判别简单线性模型的假定是否有效,作出残差图,进行残差分析。
从图中可以看到,残差基本在-0.5—+0.5左右,说明建立回归模型所依赖的假定是恰当的。
误差项的估计值s=0.388。
(4)回归模型检验 a.显著性检验在90%的显著水平下,进行t 检验,拒绝域为︱t ︱=︱b 1/ s b1︱>t α/2=1.7011。
由输出数据可以找到b 1和s b1,t=b 1/ s b1=-0.229/0.022=-10.313,于是拒绝原假设,说明液化气收率与回流温度之间存在线性关系。
b.拟合度检验判定系数r 2=0.792。
这意味着液化气收率的样本变差大约有80%可以由它与回流温度的线性关系来解释。
2r r ==-0.89这样,r 值为y 与x 之间存在中高度的负线性关系提供了进一步的证据。
由于n ≥30,我们近似确定y 的90%置信区间为:s z y)(ˆ2α±=21.263-0.229x ±1.282×0.388 = 21.263-0.229x ± 0.4974、结果分析由回归直线图可知,要保持液化气收率在12.24%以上,回流温度必须控制在34℃以下。
因为装置工艺卡片要求回流温度在33—40℃之间,为确保液化气质量合格,可以将回流温度控制在33—34℃之间。
为此,应当采取各项有效措施,改善外部操作环境,将液化气收率控制在目标值范围内。
案例二:轿车生产与GDP等关系研究中国的轿车生产是否与GDP、城镇居民人均可支配收入、城镇居民家庭恩格尔系数、私人载客汽车拥有量、公路里程等都有密切关系?如果有关系,它们之间是种什么关系?关系强度如何?(数据见《中国统计年鉴》)(1)分析轿车生产量与私人载客汽车拥有量之间的关系:首先,求的因变量轿车生产量y和自变量私人载客汽车拥有量x1的相关系数r=0.992018,说明两者间存在一定的线性相关关系且正相关程度很强。
然后以轿车生产量为因变量y,私人载客汽车拥有量x1为自变量进行一元线性回归分析,结果如下:①由回归统计中的R=0.984101看出,所建立的回归模型对样本观测值的拟合程度很好;②估计出的样本回归函数为:ŷ=1.775687+0.206783x1,说明私人载客汽车拥有量每增加1万辆,轿车生产量增加2067.83辆;③由上表中â和βˆ的p值分别是0.709481543和6.60805E-15,显然â的p值大于显著性水平α=0.05,不能拒绝原假设α=0,而βˆ的p值远小于显著性水平α=0.05,拒绝原假设β=0,说明私人载客汽车拥有量对轿车生产量有显著影响。
(2)分析轿车生产量与城镇居民家庭恩格尔系数之间的关系:首先,求的因变量轿车生产量y和自变量城镇居民家庭恩格尔系数x2的相关系数r=-0.77499,说明两者间存在一定的线性相关关系但负相关程度一般。
然后以轿车生产量为因变量y,城镇居民家庭恩格尔系数x2为自变量进行一元线性回归分析,结果如下:由回归统计中的R=0.600608看出,所建立的回归模型对样本观测值的拟合程度一般,综合其相关系数值可知此二者关系不太符合所建立的线性模型,说明二者间没有密切的线性相关关系。
(3)分析轿车生产量与公路里程之间的关系:首先,求的因变量轿车生产量y和自变量公路里程x3的相关系数r=0.941214,说明两者间存在一定的线性相关关系且正相关程度较强。
然后以轿车生产量为因变量y,公路里程x3为自变量进行一元线性回归分析,结果如下:①由回归统计中的R=0.885883看出,所建立的回归模型对样本观测值的拟合程度较好;②估计出的样本回归函数为:ŷ=-125.156+1.403022x3,说明公路里程每增加1万公里,轿车生产量增加1.403022万辆;③由上表中â和βˆ的p值分别是5.64E-05和1.82E-08,显然â和βˆ的p 值均远小于显著性水平α=0.05,拒绝原假设α=0、β=0,但由于β对两者的影响更为显著,所以可以说明公路里程对轿车生产量有显著影响。
(4)分析轿车生产量与GDP之间的关系:首先,求的因变量轿车生产量y和自变量GDP x4的相关系数r=0.939995,说明两者间存在一定的线性相关关系且正相关程度较强。
然后以轿车生产量为因变量y,GDP x4为自变量进行一元线性回归分析,结果如下:①由回归统计中的R=0.88359看出,所建立的回归模型对样本观测值的拟合程度较好;②估计出的样本回归函数为:ŷ=-70.7127+0.001829x4,说明GDP每增加1亿元,轿车生产量增加18.29辆;③由上表中â和βˆ的p值分别是0.001534和2.11E-08,显然â和βˆ的p 值均小于显著性水平α=0.05,拒绝原假设α=0、β=0,但由于β对两者的影响更为显著,所以可以说明GDP对轿车生产量有较显著影响。
(5)分析轿车生产量与城镇居民人均可支配收入x5之间的关系:首先,求的因变量轿车生产量y和自变量城镇居民人均可支配收入x5的相关系数r=0.917695,说明两者间存在一定的线性相关关系且正相关程度较强。
然后以轿车生产量为因变量y,城镇居民人均可支配收入x5为自变量进行一元线性回归分析,结果如下:①由回归统计中的R=0.842164看出,所建立的回归模型对样本观测值的拟合程度较好;②估计出的样本回归函数为:ŷ=-92.9054+0.032928x5,说明城镇居民人均可支配收入每增加1元,轿车生产量增加329.28辆;③由上表中â和βˆ的p值分别是0.001444和2.12E-07,显然â和βˆ的p 值均小于显著性水平α=0.05,拒绝原假设α=0、β=0,但由于β对两者的影响更为显著,所以可以说明城镇居民人均可支配收入对轿车生产量有显著影响。
案例三:子女身高与父母身高的回归分析1、问题的提出早在19世纪后期,英国生物学家Galton通过观察1078个家庭中父亲、母亲身高的平均值x和其中一个成年儿子身高y,建立了关于父母身高与子女身高的线性方程:y=33.73+0.516x从方程可以看出,子女身高有回归平均的倾向。
那么,时隔一百多年后的今天,人类的物质生活和精神生活都已发生巨大的变化,父母身高与子女身高之间将呈现出什么样的关系呢?在现实生活中,我们都知道父母身高对子女身高是有影响的,但父亲与母亲的影响分别有多大?他们对儿子和女儿的影响程度是否相同?能否用定量的形式回答这个问题呢?如果可以利用回归方法,进一步揭示父亲身高、母亲身高与子女身高之间量化关系的秘密,将有助于那些关注自己后代身高的年轻父母们进行早期预测,同时也可为那些未婚青年男女在选择理想配偶时提供科学的参考依据。
2、数据的收集为了问题的研究,我们要求所调查的家庭满足下列条件:(1)家庭中有一个或多个子女(2)家庭成员身体健康,发育正常,无先天性和遗传性疾病,无残疾(3)子女的年龄均在23岁(含23岁)以上。
考虑到调查范围的广泛性,我们随机抽取了机关干部、职员、工人、农民、城市居民、军人、大学生家庭,并特意选择了一所全国招生的院校应届毕业生,他们来自于全国各地,家庭背景相对复杂,这样使得样本更具代表性。
在收回的410份(发放460份)调查表中,符合要求的有290个家庭,其中,有儿子405人,有女儿270人。
3、方法的确定根据所收集的数据,应用二元回归分析方法,研究父亲身高、母亲身高与儿子或女儿身高的关系。
(1)建立回归方程设X1为父亲身高,X2为母亲身高,Y为儿子或女儿身高。
则父母身高与子女身高的回归模型为:Y=β0+β1X1+β2X2+ε根据样本数据建立估计二元回归方程:yˆ=b0+b1x1+b2x2(2)显著性检验对回归方程进行F检验,拒绝区域为F﹥Fα(2,n-3);对回归系数进行t检验,拒绝区域为t﹥tα/2(n-3)。
(3)预测若某一家庭父亲和母亲身高分别为x10和x20,则子女身高的点估计为:yˆ=b0+b1x10+b2x20区间估计方法已超出大纲要求,在此不要求。
4、结果分析(1)父母身高对儿子身高的影响yˆ=53.640+0.368x1+0.349x2显著性检验:在α=0.01的显著水平下,F=62.714﹥Fα(2,400)=4.68t1=7.85﹥tα/2(400)=2.689t2=6.71﹥tα/2(400)=2.689结果说明回归方程显著,两个偏回归系数显著。
因此,所建立回归方程是有意义的,即父母身高与儿子身高有显著的线性关系。
(2)父母身高对女儿身高的影响yˆ=47.140+0.249x1+0.455x2显著性检验:在α=0.01的显著水平下,F=46.81﹥Fα(2,300)=4.68t1=4.92﹥tα/2(300)=2.68t2=7.61﹥tα/2(300)=2.689结果说明回归方程显著,回归系数显著,故所建立回归方程有效,即女儿身高与父母身高有显著的线性关系,特别是母亲身高对女儿身高的影响更为重要。
(3)从以上结果可以看出,在某种程度上,父母身高对子女身高有重要影响,且在不同时期,子女身高有回归平均身高的趋势,即个子矮的父母,其子女身高未必低于自己,个子高的父母,其子女身高未必高于自己。
下表给出了部分家庭子女身高的预测值,其中,区间估计的把握程度为95%。
