2021年高三数学总复习-数列
2021届高考数学一轮复习第七章数列数学归纳法第5节数学归纳法选用含解析

第5节数学归纳法(选用)考试要求 1.了解数学归纳法的原理;2.能用数学归纳法证明一些简单的数学命题.知识梳理1。
数学归纳法证明一个与正整数n有关的命题,可按下列步骤进行:(1)(归纳奠基)证明当n取第一个值n0(n0∈N*)时命题成立;(2)(归纳递推)假设n=k(k≥n0,k∈N*)时命题成立,证明当n =k+1时命题也成立。
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立。
2。
数学归纳法的框图表示[常用结论与易错提醒]1。
数学归纳法证题时初始值n0不一定是1.2.推证n=k+1时一定要用上n=k时的假设,否则不是数学归纳法.诊断自测1。
判断下列说法的正误。
(1)用数学归纳法证明等式“1+2+22+…+2n+2=2n+3-1”,验证n=1时,左边式子应为1+2+22+23.()(2)所有与正整数有关的数学命题都必须用数学归纳法证明.()(3)用数学归纳法证明问题时,归纳假设可以不用.()(4)不论是等式还是不等式,用数学归纳法证明时,由n=k到n=k+1时,项数都增加了一项。
()解析对于(2),有些命题也可以直接证明;对于(3),数学归纳法必须用归纳假设;对于(4),由n=k到n=k+1,有可能增加不止一项.答案(1)√(2)×(3)×(4)×2。
(选修2-2P99B1改编)在应用数学归纳法证明凸n边形的对角线为错误!n(n-3)条时,第一步检验n等于()A.1B.2C。
3 D.4解析三角形是边数最少的凸多边形,故第一步应检验n=3。
答案C3。
已知f(n)=错误!+错误!+错误!+…+错误!,则()A.f(n)中共有n项,当n=2时,f(2)=错误!+错误!B.f(n)中共有n+1项,当n=2时,f(2)=错误!+错误!+错误!C.f(n)中共有n2-n项,当n=2时,f(2)=错误!+错误!D。
f(n)中共有n2-n+1项,当n=2时,f(2)=错误!+错误!+错误!解析f(n)共有n2-n+1项,当n=2时,错误!=错误!,错误!=错误!,故f(2)=错误!+错误!+错误!.答案D4.用数学归纳法证明1+错误!+错误!+…+错误!<n(n∈N,且n〉1),第一步要证的不等式是________。
2021年高考数学专题复习:数列(含答案解析)

(1)求{an}的通项公式;
(2)设bn=2 an,求{bn}的前n项和Tn.
3.已知等比数列{an}的各项均为正数,且a1+16a3=1,a1a5=16a42.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an,求数列{ }的前n项和Tn.
(1)求数列{an}的通项公式;
(2)证明: .
13.设数列{an}满足a1=2,an+1=an+2n.
(1)求数列{an}的通项公式;
(2)设bn=log2(a1•a2…an),求数列{ }的前n项和Sn.
14.已知等比数列{an}的各项都为正数,Sn为其前n项和,a3=8,S3=14.
(1)求数列{an}的通项公式;
(2)记Tn ,求使得Tn 成立的正整数n的最小值.
15.设数列{an}的前n项和为Sn(n∈N*),且满足an+Sn=2n+1.
(1)证明数列{an﹣2}是等比数列,并求数列{an}的通项公式;
(2)若bn=n(2﹣an),求数列{bn}的前n项和Tn.
16.已知{an}是等差数列,{bn}是等比数列,b1=a5,b2=3,b5=﹣81.
(1)求数列{an},{bn}的通项公式;
(2)设cn an,数列{cn}的前n项和为Tn,若不等式 1 恒成立,求λ的取值范围.
18.已知递增的等比数列{an}的前n项和为Sn,S3 ,a3a4=a5.
(1)求数列{an}的通项公式;
(2)若4an=3Sn,求正整数n的值.
19.已知等差数列{an}中,a2=3,a4=7.等比数列{bn}满足b1=a1,b4=a14.
2021年高考数学解答题专项复习-《数列》(含答案)

2021年高考数学解答题专项复习-《数列》1.设{a}是等差数列,a1=–10,且a2+10,a3+8,a4+6成等比数列.n(1)求{a n}的通项公式;(2)记{a n}的前n项和为S n,求S n的最小值.2.设{a}是等差数列,且a1=ln2,a2+a3=5ln2.n(1)求{a n}的通项公式;(2)求错误!未找到引用源。
.3.设数列{a}的前n项和为S n.已知2S n=3n+3.n(1)求{a n}的通项公式;(2)若数列{b n}满足a n·b n=log3a n,求{b n}的前n项和T n.4.已知{a}是公差为1的等差数列,且a1,a2,a4成等比数列.n(1)求{a n}的通项公式;(2)求数列的前n项和.5.已知数列{a}前n项和为S n,且S n=2n2+n,n∈N+,数列{b n}满足a n=4log2b n+3,n∈N+.n(1)求a n和b n的通项公式;(2)求数列{a n·b n}的前n项和T n.6.已知数列{a}和{b n}满足a1=1,b1=0,,.n(1)证明:{a n+b n}是等比数列,{a n–b n}是等差数列;(2)求{a n}和{b n}的通项公式.7.S为数列{a n}的前n项和.已知a n>0,=.n(1)求{a n}的通项公式;(2)设 ,求数列{b n}的前n项和.8.已知等差数列{a}满足a3=6,前7项和为S7=49.n(1)求{a n}的通项公式(2)设数列{b n}满足b n=(a n-3)·3n,求{b n}的前n项和T n.9.设数列{a}满足a1+3a2+...+(2n-1)a n=2n.n(1)求{a n}通项公式;(2)求数列的前n项和.10.已知等比数列{a}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项.数列{b n}满足b1=1,n数列{(b n+1-b n)a n}的前n项和为2n2+n.(1)求q的值;(2)求数列{b n}的通项公式.11.已知数列{a}是递增的等比数列,且a1+a4=9,a2a3=8.n(1)求数列{a n}的通项公式;(2)设S n为数列{a n}的前n项和,,求数列{b n}的前n项和T n.12.已知数列{a}为递增的等差数列,其中a3=5,且a1,a2,a5成等比数列.n(1)求{a n}的通项公式;(2)设记数列{b n}的前n项和为T n,求使得成立的m的最小正整数.13.等比数列{a}的各项均为正数,且.n(1)求数列{a n}的通项公式;(2)设,求数列的前n项和T n.14.已知数列{a}是首项为正数的等差数列,数列的前n项和为.n(1)求数列{a n}的通项公式;(2)设错误!未找到引用源。
2021届新高考数学总复习:等比数列的通项及其性质(附答案解析)

10.在等比数列{an}中,若a5=2a4,a2=2,则a6=( )
A.64B.16C.8D.32
11.若等比数列{an}满足:a1=1,a1+a2+a3=7,则a4=( )
A.8B.﹣27C.8或﹣27D.﹣8或﹣27
12.已知各项均为正数的等比数列{an}中,a2=2,a3a4a5=29,则a3=( )
【解答】解:设等比数列{an}的公比为q,则a1a3a5= •a2q•a2q3=(a2q)3=8,则a2q=a3=2.
又a2a4= •a3q=a32=22=4.
故选:B.
4.在等比数列{an}中,a3=2,a7=18,则a3与a7的等比中项为( )
A.4B.6C.±6D.±4
【解答】解:∵等比数列{an}中,a3=2,a7=18,
A. B.2C.±2D.
7.等比数列{an}中,an∈R+,a5•a6=32,则log2a1+log2a2+…+log2a10的值为( )
A.10B.20C.25D.160
8.已知各项均为正数的等比数列{an}中,a2=2,a5=2a4+3a3,则a6=( )
A.2B.54C.162D.243
9.设{an}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=( )
A.16B.32C.64D.256
16.在正项等比数列{an}中,若a3a7=4,则 =( )
A.16B.8C.4D.2
17.在等比数列{an}中,已知a1a3=4,a9=256,则a8=( )
A.128或﹣128B.128C.64或﹣64D.64
2021届高考数学(新课标) 题型全归纳 数列要点讲解

数 列一、高考要求理解数列的有关概念,了解递推公式是给出数列的一种方法,并能依据递推公式写出数列的前n 项.理解等差(比)数列的概念,把握等差(比)数列的通项公式与前n 项和的公式. 并能运用这些学问来解决一些实际问题.了解数学归纳法原理,把握数学归纳法这一证题方法,把握“归纳—猜想—证明”这一思想方法. 二、热点分析1.数列在历年高考中都占有较重要的地位,一般状况下都是一个客观性试题加一个解答题,分值占整个试卷的10%左右.客观性试题主要考查等差、等比数列的概念、性质、通项公式、前n 项和公式、极限的四则运算法则、无穷递缩等比数列全部项和等内容,对基本的计算技能要求比较高,解答题大多以考查数列内容为主,并涉及到函数、方程、不等式学问的综合性试题,在解题过程中通常用到等价转化,分类争辩等数学思想方法,是属于中高档难度的题目.2.有关数列题的命题趋势 (1)数列是特殊的函数,而不等式则是深刻生疏函数和数列的重要工具,三者的综合求解题是对基础和力气的双重检验,而三者的求证题所显现出的代数推理是近年来高考命题的新热点 (2)数列推理题是新毁灭的命题热点.以往高考常使用主体几何题来考查规律推理力气,近两年在数列题中也加强了推理力气的考查。
(3)加强了数列与极限的综合考查题3.娴熟把握、机敏运用等差、等比数列的性质。
等差、等比数列的有关性质在解决数列问题时应用格外广泛,且格外机敏,主动发觉题目中隐含的相关性质,往往使运算简洁秀丽 .如243546225a a a a a a ++=,可以利用等比数列的性质进行转化:从而有223355225a a a a ++=,即235()25a a +=. 4.对客观题,应留意寻求简捷方法 解答历年有关数列的客观题,就会发觉,除了常规方法外,还可以用更简捷的方法求解.现介绍如下: ①借助特殊数列. ②机敏运用等差数列、等比数列的有关性质,可更加精确 、快速地解题,这种思路在解客观题时表现得更为突出,很多数列客观题都有机敏、简捷的解法5.在数列的学习中加强力气训练 数列问题对力气要求较高,特殊是运算力气、归纳猜想力气、转化力气、规律推理力气更为突出.一般来说,考题中选择、填空题解法机敏多变,而解答题更是考查力气的集中体现,尤其近几年高考加强了数列推理力气的考查,应引起我们足够的重视.因此,在平常要加强对力气的培育。
2021届高三数学总复习第一轮——等差数列
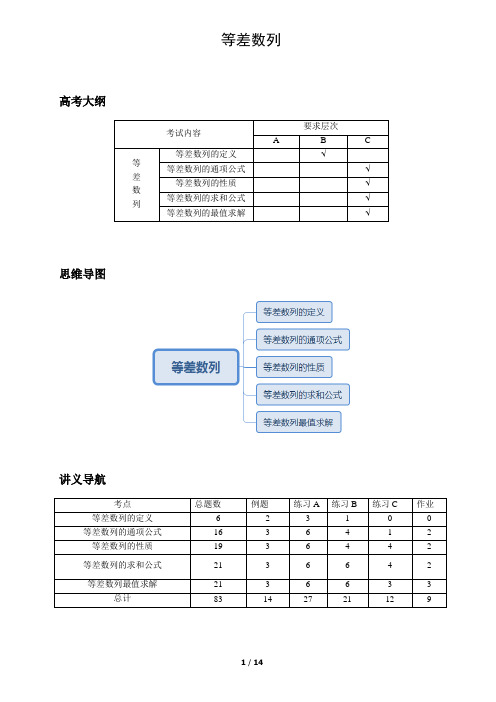
等差数列高考大纲思维导图讲义导航知识梳理一、等差数列的定义如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列.这个常数叫做等差数列的公差,公差常用字母d表示二、等差数列的通项公式等差数列是常见数列的一种,数列从第二项起,每一项与它的前一项的差等于同一个常数,已知等差数列的首项a1,公差d,那么第n项为a n=a1+(n﹣1)d,或者已知第m项为a m,则第n项为a n=a m+(n﹣m)d.三、等差数列的性质(1)若公差d>0,则为递增等差数列;若公差d<0,则为递减等差数列;若公差d=0,则为常数列;(2)有穷等差数列中,与首末两端“等距离”的两项和相等,并且等于首末两项之和;(3)m,n∈N+,则a m=a n+(m﹣n)d;(4)若s,t,p,q∈N*,且s+t=p+q,则a s+a t=a p+a q,其中a s,a t,a p,a q是数列中的项,特别地,当s+t=2p时,有a s+a t=2a p;(5)若数列{a n},{b n}均是等差数列,则数列{ma n+kb n}仍为等差数列,其中m,k均为常数.(6)a n,a n﹣1,a n﹣2,…,a2,a1仍为等差数列,公差为﹣d.(7)从第二项开始起,每一项是与它相邻两项的等差中项,也是与它等距离的前后两项的等差中项,即2a n+1=a n+a n+2,2a n=a n﹣m+a n+m,(n≥m+1,n,m∈N+)(8)a m,a m+k,a m+2k,a m+3k,…仍为等差数列,公差为kd(首项不一定选a1).四、等差数列的求和公式等差数列的前n项和公式等差数列的前n项和的公式:①()12nnn a aS+=;②()112nn nS na d-=+.五、等差数列最值求解等差数列前n项和的最值问题可转化为项的正负问题,也可转化为二次函数最值问题.例题讲解一、等差数列定义的理解例1.下面数列中,是等差数列的有( ) ①4,5,6,7,8…②3,0,-3,0,-6,…③0,0,0,0…④110,210,310,410,… A .1个 B .2个C .3个D .4个例2.下列数列中不是等差数列的为( ) A.0,0,0,0,0 B.0,1-,2-,3-,4- C.2,3,4,5,6 D.0,1,2,1,0二、等差数列通项公式例1.在等差数列{}n a 中,已知32a =,5815a a +=,则10(a = ) A .64 B .26C .18D .13例2.在等差数列{}n a 中,214a =,55a =,则公差(d = )A .2-B .3-C .2D .3例3.已知{}n a 是等差数列,124a a +=,7828a a +=,则公差等于( ) A .2 B .4 C .6 D .8三、等差数列的性质例1.等差数列{}n a 中,已知21016a a +=,则468(a a a ++= ) A .16 B .20 C .24 D .28例2.等差数列{}n a 中,若4681012120a a a a a ++++=,则91113a a -的值是( )A .14B .15C .16D .17例3.已知等差数列{}n a 单调递增且满足1104a a +=,则8a 的取值范围是( )A .(2,4)B .(,2)-∞C .(2,)+∞D .(4,)+∞四、等差数列的求和公式例1.已知等差数列{}n a 的前n 项和为n S ,若33S a =,且30a ≠,则43(S S = ) A .1B .53C .83D .3例2.等差数列{}n a 中,14739a a a ++=,36927a a a ++=,则数列{}n a 前9项的和9S 等于( ) A .99 B .66C .144D .297例3.设{}n a 是任意等差数列,它的前n 项和、前2n 项和与前4n 项和分别为X ,Y ,Z ,则下列等式中恒成立的是( )A .23X Z Y +=B .44X Z Y +=C .237X Z Y +=D .86X Z Y +=六、等差数列最值求解例1.已知等差数列{}n a 中,39a a =,公差0d <,则使其前n 项和n S 取得最大值的自然数n 是( ). A.4或5 B.5或6 C.6或7 D.不存在例2.设等差数列{a n }的前n 项和为S n ,若a 2=−3,S 5=−10,则a 5=__________,S n 的最小值_______.例3.在各项均为正数的等比数列{a n }中,214a =,且a 4+a 5=6a 3.练习A1.下列说法中正确的是( )A.若a ,b ,c 成等差数列,则222,,a b c 成等差数列B.若a ,b ,c 成等差数列,则222log ,log ,log a b c 成等差数列C.若a ,b ,c 成等差数列,则a+2,b+2,c+2成等差数列D.若a ,b ,c 成等差数列,则2,2,2a b c 成等差数列2.已知下列各数列,其中为等差数列的个数为( ) 1 4,5,6,7,8,... 2 3,0,-3,0,-6,... 3 0,0,0,0, (4)1234,,,,10101010… A.1 B.2C.3D.43.已若{}n a 是等差数列,则由下列关系确定的数列{}n b 也一定是等差数列的是( )A. 2n n b a =B. 2n n b a n =+C. 1n n n b a a +=+D. n n b na =4.已知数列{}n a 为等差数列,且39a =,53a =,则9a 等于( )A .9-B .6-C .3-D .275.已知等差数列{}n a 中,1232a a a ++=,3456a a a ++=,则91011a a a ++的值为( ) A .18 B .16 C .14 D .126.等差数列{}n a 中,若46101290a a a a +++=,则10141(3a a -= )A .15B .30C .45D .607.等差数列{}n a 中,31a =-,1117a =-,则7a 等于( )A .9-B .8-C .92-D .4-8.在等差数列{}n a 中,公差为12,1359960a a a a +++⋯+=,则246100(a a a a +++⋯+= ) A .60 B .70 C .75 D .859.已知等差数列{}n a 满足12910a a a ++⋯+=,则有( )A .3890a a +=B .2900a a +<C .1910a a +>D .4646a =10.已知数列{}n a 为等差数列,且17132a a a π++=,则7tan (a = )A.BC. D.11.已知0a >,0b >,并且1a ,12,1b成等差数列,则9a b +的最小值为( ) A .16 B .9C .5D .412.等差数列{}n a 中,已知21016a a +=,则468(a a a ++= ) A .16 B .20C .24D .2813.在等差数列{}n a 中,若4681012120a a a a a ++++=,则10122a a -的值为( ) A .20 B .22C .24D .2814.等差数列{}n a 中,156a a +=,65a =,那么9a 的值是( ) A .7- B .7 C .113-D .11315.已知等比数列{}n a 中,各项都是正数,且1321,,22a a a 成等差数列,则8967a a a a ++等于( )A.1+B.1-C.3+D.3-16.已知等差数列{}n a 的前n 项和为n S ,若33S a =,且30a ≠,则43(S S = ) A .1B .53C .83D .317.设等差数列{}n a 的前n 项和n S ,若4104a a +=,则13(S = ) A .13 B .14C .26D .5218.设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5(S = ) A .5 B .7C .9D .1019.在等差数列{}n a 中,若351024a a a ++=,则此数列的前13项的和等于( ) A .8 B .13C .16D .2620.在等差数列{}n a 中,若14739a a a ++=,36927a a a ++=,则9(S = ) A .66 B .99C .144D .29721.已知{}n a 为等差数列,n S 为其前n 项和.若312S =,244a a +=,则6(S = ) A .6 B .12C .15D .1822.等差数列{}n a 前n 项和为n S ,111a =-,466a a +=-.则当n S 取最小值时,(n = ) A .6 B .7C .8D .923.数列{}n a 的通项公式为2328n a n n =-,则数列{}n a 各项中最小项是( )A .第4项B .第5项C .第6项D .第7项24.已知数列{}n a 是等差数列,若91130a a +<,10110a a <,且数列{}n a 的前n 项和n S 有最大值,那么当n S 得最小正值时,n 等于( ) A .20 B .17 C .19 D .2125.已知n S 是等差数列*{}()n a n N ∈的前n 项和,且564S S S >>,以下有四个命题:①数列{}n a 中的最大项为10S ②数列{}n a 的公差0d < ③100S >④110S <其中正确的序号是( )A .②③B .②③④C .②④D .①③④26.在等差数列{}n a 中,128a =-,公差4d =,若前n 项和n S 取得最小值,则n 的值为( ) A .7 B .8C .7或8D .8或927.数列{}n a 是首项为111a =,公差为2d =-的等差数列,那么使前n 项和n S 最大的n 值为( ) A .4 B .5C .6D .7练习B1.设{}n a 为等差数列,则下列数列中,成等差数列的个数为( )①2{}na ②{}n pa ③{}n pa q + ④{}(n na p 、q 为非零常数) A .1 B .2C .3D .42.等差数列{}n a 的公差0d >,前n 项和为n S ,则对2n >时有( ) A .1nn S a a n<< B .1nn S a a n <<C .1n n Sa a n<<D .1,,n n Sa a n的大小不确定3.设等差数列{}n a 的前n 项和为n S ,在同一个坐标系中,()n a f n =及()n S g n =的部分图象如图所示,则( )A .当4n =时,n S 取得最大值B .当3n =时,n S 取得最大值C .当4n =时,n S 取得最小值D .当3n =时,n S 取得最小值4.已知数列{}n a 是等差数列,n S 为其前n 项和.若3916S S =,则612(S S = )A .110B .310C .510D .7105.设等差数列{}n a 的前n 项和为n S ,且满足100S >,110S <,则下列数值最大的是( )A .4SB .5SC .6SD .7S6.等差数列{}n a 与{}n b 的前n 项和分别为n S 与n T ,若3221n n S n T n -=+,则77(ab = ) A .3727B .3828C .3929D .40307.一个有限项的等差数列,前4项之和为40,最后4项之和是80,所有项之和是210,则此数列的项数为( ) A .10 B .12 C .14 D .168.已知点(n ,*)()n a n N ∈都在直线3240x y --=上,那么在数列n a 中有79(a a += )A .790a a +>B .790a a +<C .790a a +=D .790a a =9.已知等差数列{}n a 满足3243a a =,则{}n a 中一定为零的项是( )A .6aB .8aC .10aD .12a10.在等差数列{}n a 中,15a =,470a a +=,则数列{}n a 中为正数的项的个数为( ) A .4 B .5 C .6 D .711.已知数列{}n a 中,132(3n n a a ++= *)n N ∈,且356820a a a a +++=,那么10a 等于( ) A .8 B .5 C .263D .712.若等差数列{}n a 的公差为d ,前n 项和为n S ,记nn S b n=,则( ) A .数列{}n b 是等差数列,{}n b 的公差也为dB .数列{}n b 是等差数列,{}n b 的公差为2dC .数列{}n n a b +是等差数列,{}n n a b +的公差为dD .数列{}n n a b -是等差数列,{}n n a b -的公差为2d13.等差数列{}n a 中,已知113a =,254a a +=,33n a =,则n 为( )A .48B .49C .50D .5114.若等差数列的首项是24-,且从第10项开始大于零,则公差d 的取值范围是( )A .83d > B .3d < C .833d < D .833d <15.在数列{}n a 中,若1332()n n a a n N +=+∈,且247920a a a a +++=,则10a 为( ) A .5 B .7C .8D .1016.等差数列{}n a 前n 项和为n S ,111a =-,466a a +=-.则当n S 取最小值时,(n = ) A .6 B .7C .8D .917.在各项均为正数的等比数列{}n a 中,63a =,则48(a a += )A .有最小值6B .有最大值6C .有最大值9D .有最小值318.已知实数序列1a ,2a ,⋯,n a 满足:任何连续3项之和均为负数,且任何4项之和均为正数,则n 的最大值是( ) A .4 B .5C .6D .719.已知n S 是等差数列*{}()n a n N ∈的前n 项和,且564S S S >>,以下有四个命题:①数列{}n a 中的最大项为10S ②数列{}n a 的公差0d < ③100S >④110S <其中正确的序号是( )A .②③B .②③④C .②④D .①③④20.已知各项均为正数的等比数列{}n a 中,如果21a =,那么这个数列前3项的和3S 的取值范围是( )A .(-∞,1]-B .[1,)+∞C .[2,)+∞D .[3,)+∞21.已知等差数列{}n a 的前n 项和为n S ,且110a =,56S S ,下列四个命题中,假命题是( )A .公差d 的最大值为2-B .70S <C .记n S 的最大值为K ,K 的最大值为30D .20162017a a >练习C1.已知||0x y >>.将四个数,,x x y x y -+( )A .当0x >时,存在满足已知条件的x ,y ,四个数构成等比数列B .当0x >时,存在满足已知条件的x ,y ,四个数构成等差数列C .当0x <时,存在满足已知条件的x ,y ,四个数构成等比数列D .当0x <时,存在满足已知条件的x ,y ,四个数构成等差数列2.等差数列{}n a 的公差0d >,前n 项和为n S ,则对2n >时有( )A .1nn S a a n<< B .1nn S a a n<<C .1nn S a a n<< D .1,,nn S a a n的大小不确定3.设等差数列{}n a 的前n 项和为n S ,在同一个坐标系中,()n a f n =及()n S g n =的部分图象如图所示,则( )A .当4n =时,n S 取得最大值B .当3n =时,n S 取得最大值C .当4n =时,n S 取得最小值D .当3n =时,n S 取得最小值4.等差数列,的前项和分别为,,若,则 A . B .C .D .5.在等差数列中,,其前项和为,若,则 A . B .C .2008D .20096.设为等差数列,则下列数列中,成等差数列的个数为① ② ③ ④、为非零常数) A .1 B .2 C .3 D .47.设表示等差数列的前项和,已知,那么等于 A .B .C .D .8.等差数列中,,,则该数列前项之和为{}n a {}n b n n S n T 231n n S n T n =+(n na b =)232131n n --2131n n ++2134n n -+{}n a 12007a =-n n S 20082006220082006S S -=2009(S =)2009-2008-{}n a ()2{}na {}n pa {}n pa q +{}(n na p q n S {}n a n 51013S S =1020SS ()193101813{}n a 1m a k =1()k a m k m=≠mk ()A .B .C .D .9.设数列为等差数列,其前项和为,已知,,若对任意,都有成立,则的值为A .22B .21C .20D .1910.设等差数列的公差为,前项和为.若,则的最小值为 A .10 B .C .D .二.填空题(共2小题) 11.在等差数列中,,若它的前项和有最大值,则使取得最小正数的 19 .12.已知两个等差数列、的前项和分别为和,若,则使为整数的正整数的个数是 5个 .课后练习1.等差数列中,若,则 .2.设等差数列的前项和为,若,,则 0 ,的最小值为 .3.等差数列中,,,则取最大值时, 6或7 .4.已知等差数列的前项和为,能够说明“若数列是递减数列,则数列是递减数列”是假命题的数列的一个通项公式为 (答案不唯一) .5.设等差数列的前项和为,若,,则数列的公差等于 .6.若等差数列满足,则12mk-2mk12mk +12mk+{}n a n n S 14799a a a ++=25893a a a ++=*n N ∈n k S S k (){}n a d n n S 11a d ==8n nS a +()927212+{}n a 11101a a <-n n S n S n ={}n a {}n b n n A n B 7453n n A n B n +=+n na b {}n a 31110a a +=678a a a ++={}n a n n S 23a =-510S =-5a =n S {}n a 10a >49S S =n S n ={}n a n n S {}n a {}n S {}n a 27n a n =-+{}n a n n S 1122S =71a ={}n a 1-{}n a 1461,52a a a =+=2019a =20192二.解答题(共3小题)7.在等差数列中,已知,,. (Ⅰ)求数列的通项公式; (Ⅱ)求.8.设等差数列满足,. (1)求的通项公式;(2)求的前项和及使得最大的序号的值.9.已知为等差数列,,. ( I ) 求数列的通项公式以及前项和. (Ⅱ)求使得的最小正整数的值.{}n a 1312a a +=2418a a +=*n N ∈{}n a 3693n a a a a +++⋯+{}n a 35a =109a =-{}n a {}n a n n S n S n {}n a 112a =-562a a ={}n a n n S 14n S >n。
2021版高考数学一轮总复习第六章数列题组训练34数列的基本概念理20210515482

2021版高考数学一轮总复习第六章数列题组训练34数列的基本概念理202105154821.在数列1,1,2,3,5,8,13,x ,34,55,…中,x 应取( ) A .19 B .20 C .21 D .22答案 C解析 a 1=1,a 2=1,a 3=2,∴a n +2=a n +1+a n ,∴x =8+13=21,故选C. 2.数列13,18,115,124,…的一个通项公式为( )A .a n =12n +1B .a n =1n +2C .a n =1n (n +2)D .a n =12n -1答案 C解析 观看知a n =1(n +1)2-1=1n (n +2). 3.(2020·济宁模拟)若S n 为数列{a n }的前n 项和,且S n =n n +1,则1a 5等于( )A.56 B.65 C.130 D .30 答案 D解析 ∵当n≥2时,a n =S n -S n -1=n n +1-n -1n =1n (n +1),∴1a 5=5×(5+1)=30.4.若数列{a n }满足a 1=2,a n +1a n =a n -1,则a 2 017的值为( ) A .-1 B.12 C .2 D .3 答案 C解析 因为数列{a n }满足a 1=2,a n +1a n =a n -1,因此a n +1=1-1a n ,因此a 2=12,a 3=1-2=-1,a 4=1+1=2,可知数列的周期为3.而2 017 =3×672+1,因此a 2 017=a 1=2.故选C. 5.(2020·辽宁省实验中学月考)设数列{a n }的前n 项和为S n ,且S n =2(a n -1),则a n =( )A .2nB .2n -1C .2nD .2n-1答案 C解析 当n =1时,a 1=S 1=2(a 1-1),可得a 1=2;当n≥2时,a n =S n -S n -1=2a n -2a n -1,∴a n =2a n -1,∴数列{a n }为等比数列,公比为2,首项为2,∴通项公式为a n =2n.故选C. 6.(2020·辽宁)设等差数列{a n }的公差为d ,若数列{2a 1a n }为递减数列,则( ) A .d<0 B .d>0 C .a 1d<0 D .a 1d>0答案 C解析 ∵数列{2a 1a n }为递减数列,∴2a 1a n >2a 1a n +1,n ∈N *,∴a 1a n >a 1a n +1,∴a 1(a n +1-a n )<0.∵{a n }为公差为d 的等差数列,∴a 1d<0.故选C.7.若数列{a n }的前n 项和S n =n 2-10n(n∈N *),则数列{na n }中数值最小的项是( ) A .第2项 B .第3项 C .第4项 D .第5项答案 B解析 ∵S n =n 2-10n ,∴当n≥2时,a n =S n -S n -1=2n -11;当n =1时,a 1=S 1=-9也适合上式.∴a n =2n -11(n∈N *).记f(n)=na n =n(2n -11)=2n 2-11n ,此函数图像的对称轴为直线n =114,但n∈N *,∴当n =3时,f(n)取最小值.因此,数列{na n }中数值最小的项是第3项. 8.数列53,108,17a +b ,a -b 24,…中,有序实数对(a ,b)能够是( ) A .(21,-5) B .(16,-1) C .(-412,112)D .(412,-112)答案 D解析 由数列中的项可观看规律,5-3=10-8=17-(a +b)=(a -b)-24=2,⎩⎪⎨⎪⎧a +b =15,a -b =26,解得a =412,b =-112.故选D.9.(2021·山东荷泽重点高中联考)观看下列的图形中小正方形的个数,则第n 个图中的小正方形的个数f(n)为( )A.(n +1)(n +2)2B.(n +2)(n +3)2C.n 2D.n 2+n 2答案 A解析 由题意可得f(1)=2+1;f(2)=3+2+1;f(3)=4+3+2+1;f(4)=5+4+3+2+1;f(5)=6+5+4+3+2+1;…;∴f(n)=(n +1)+n +(n -1)+…+1=(n +1)(n +2)2.10.(2020·郑州第二次质量推测)已知数列{a n }满足a n +1=a n -a n -1(n≥2),a 1=m ,a 2=n ,S n 为数列{a n }的前n 项和,则S 2 017的值为( ) A .2 017n -m B .n -2 017m C .m D .n答案 C解析 依照题意运算可得a 3=n -m ,a 4=-m ,a 5=-n ,a 6=m -n ,a 7=m ,a 8=n ,…,因此数列{a n }是以6为周期的周期数列,且a 1+a 2+…+a 6=0,因此S 2 017=S 336×6+1=a 1=m.故选C.11.(2020·湖南长沙模拟)已知S n 是各项均为正数的数列{a n }的前n 项和,S n >1且S n =(a n +3)(a n +1)8(n∈N *),则a n =( )A .4n -1B .4n -3C .4n -3或4n -1D .n +2 答案 A解析 当n =1时,a 1=S 1=(a 1+3)(a 1+1)8,解得a 1=1或a 1=3,∵S n >1,∴a 1=3,当n≥2时,a n =S n -S n -1=(a n +3)(a n +1)8-(a n -1+3)(a n -1+1)8,即(a n +a n -1)(a n -a n-1-4)=0,∵a n >0,故a n -a n -1=4,∴{a n }是首项为3,公差为4的等差数列,∴a n =3+4(n-1)=4n -1.12.(2020·湖北宜昌一中月考)定义a n =5n+(15)n ,其中n∈{110,15,12,1},则a n 取最小值时,n 的值为( ) A.110 B.15 C.12 D .1答案 A解析 令5n=t>0,考虑函数y =t +1t (t>0),易知其中(0,1]上单调递减,在[1,+∞)上单调递增,且当t =1时,y 的值最小.再考虑函数t =5n,当0<n≤1时,t ∈(1,5],可知当n =110时,a n 取得最小值.故选A.13.用火柴棒按下图的方法搭三角形:按图示的规律搭下去,则所用火柴棒数a n 与所搭三角形的个数n 之间的关系式能够是________. 答案 a n =2n +114.(2020·课标全国Ⅰ)若数列{a n }的前n 项和S n =23a n +13,则{a n }的通项公式a n =________.答案 (-2)n -1解析 由S n =23a n +13,得当n≥2时,S n -1=23a n -1+13,∴当n≥2时,a n =-2a n -1.又n =1时,S 1=a 1=23a 1+13,a 1=1,∴a n =(-2)n -1.15.已知数列{a n }满足:a 4n -3=1,a 4n -1=0,a 2n =a n ,n ∈N *,则a 2 013=________;a 2 014=________. 答案 1,0解析 a 2 013=a 504×4-3=1,a 2 014=a 2×1 007=a 1 007=a 4×252-1=0.16.(2020·广东梅州质量检测)已知数列2 016,2 017,1,-2 016,-2 017,…,那个数列的特点是从第二项起,每一项都等于它的前后两项之和,则那个数列的前2 017项之和S 2 017等于________. 答案 2 016解析 依照题意可将该数列多写几项出来,以便观看:2 016,2 017,1,-2 016,-2 017,-1,2 016,2 017,1,….观看发觉该数列是周期为6的周期数列,且前6项的和为0.而要求的2 017=6×336+1,则S 2 017=0×336+a 2 017=0+a 1=2 016.17.(2020·广州一模)设数列{a n }的各项差不多上正数,且对任意n∈N *,都有4S n =a n 2+2a n ,其中S n 为数列{a n }的前n 项和,则数列{a n }的通项公式为a n =________. 答案 2n解析 当n =1时,由4S 1=a 12+2a 1,a 1>0,得a 1=2; 当n≥2时,由4a n =4S n -4S n -1=(a n 2+2a n )-(a n -12+2a n -1), 得(a n +a n -1)(a n -a n -1-2)=0.因为a n +a n -1>0, 因此a n -a n -1=2,则数列{a n }是首项为2,公差为2的等差数列, 故a n =2+(n -1)×2=2n.18.(2020·北京海淀区一模)数列{a n }的通项为a n =⎩⎪⎨⎪⎧2n-1,n ≤4,-n 2+(a -1)n ,n ≥5,(n∈N *),若a 5是{a n }中的最大值,则a 的取值范畴是________. 答案 [9,12]解析 当n≤4时,a n =2n-1单调递增,因此n =4时取最大值,a 4=24-1=15. 当n≥5时,a n =-n 2+(a -1)n =-(n -a -12)2+(a -1)24.∵a 5是{a n }中的最大值,∴⎩⎪⎨⎪⎧a -12≤5.5,-52+5(a -1)≥15,解得9≤a≤12.∴a 的取值范畴是[9,12].19.已知在数列{a n }中,a 1=1,前n 项和S n =n +23a n .(1)求a 2,a 3; (2)求{a n }的通项公式.答案 (1)a 2=3,a 3=6 (2)a n =n (n +1)2解析 (1)由S 2=43a 2,得3(a 1+a 2)=4a 2,解得a 2=3a 1=3;由S 3=53a 3,得3(a 1+a 2+a 3)=5a 3,解得a 3=32(a 1+a 2)=6.(2)由题设知a 1=1. 当n>1时,有a n =S n -S n -1=n +23a n -n +13a n -1, 整理,得a n =n +1n -1a n -1.因此a 1=1,a 2=31a 1,a 3=42a 2,…,a n -1=n n -2a n -2,a n =n +1n -1a n -1.将以上n 个等式两端分别相乘,整理,得a n =n (n +1)2.综上,{a n }的通项公式a n =n (n +1)2.1.已知数列12,23,34,45,…,那么0.94,0.96,0.98,0.99中属于该数列中某一项值的有( ) A .1个 B .2个 C .3个 D .4个答案 C2.关于数列{a n },“a n +1>|a n |(n =1,2,…)”是“{a n }为递增数列”的( ) A .必要不充分条件 B .充分不必要条件 C .充要条件 D .既不充分也不必要条件答案 B解析 当a n +1>|a n |(n =1,2,…)时,∵|a n |≥a n ,∴a n +1>a n ,∴{a n }为递增数列.当{a n }为递增数列时,若该数列为-2,0,1,则a 2>|a 1|不成立,即a n +1>|a n |(n =1,2,…)不一定成立.故综上知,“a n +1>|a n |(n =1,2,…)”是“{a n }为递增数列”的充分不必要条件. 3.已知数列2,5,22,…,则25是该数列的( ) A .第5项 B .第6项 C .第7项 D .第8项答案 C解析 由数列2,5,22,…的前三项2,5,8可知,数列的通项公式为a n =2+3(n -1)=3n -1,由3n -1=25,可得n =7.4.已知数列{a n }满足a 0=1,a n =a 0+a 1+…+a n -1(n≥1),则当n≥1时,a n 等于( ) A .2nB.12n(n +1) C .2n -1D .2n-1答案 C解析 由题设可知a 1=a 0=1,a 2=a 0+a 1=2. 代入四个选项检验可知a n =2n -1.故选C.5.(2021·上海松江一模)在一个有穷数列每相邻两项之间添加一项,使其等于两相邻项的和,我们把如此的操作叫做该数列的一次“H 扩展”.已知数列1,2.第一次“H 扩展”后得到1,3,2;第二次“H 扩展”,后得到1,4,3,5,2.那么第10次“H 扩展”后得到的数列的项数为( ) A .1 023 B .1 025 C .513 D .511答案 B解析 设第n 次“H 扩展”后得到的数列的项数为a n ,则第n +1次“H 扩展”后得到的数列的项数为a n +1=2a n -1,∴a n +1-1=2(a n -1).∴a n +1-1a n -1=2.又∵a 1-1=3-1=2,∴{a n -1}是以2为首项,2为公比的等比数列,∴a n -1=2·2n -1,∴a n =2n +1,∴a 10=210+1=1 025.故选B.6.(2020·辽宁沈阳二中月考)数列{a n }中,a n =n - 2 016n - 2 017,则该数列前100项中的最大项与最小项分别是( ) A .a 1,a 50 B .a 1,a 44 C .a 45,a 44 D .a 45,a 50答案 C 解析 a n =1+2 017- 2 016n - 2 017,∴a 44<0,a 45>0,且从a 1到a 44递减,从a 45到a 100递减.7.(2020·河北省衡水中学模拟)数列{a n }满足a 1=2,a n +1=a n 2(a n >0,n ∈N *),则a n =( ) A .10n -2B .10n -1C .102n -1D .22n -1答案 D解析 因为数列{a n }满足a 1=2,a n +1=a n 2(a n >0,n ∈N *), 因此log 2a n +1=2log 2a n ,即log 2a n +1log 2a n =2.又a 1=2,因此log 2a 1=log 22=1.故数列{log 2a n }是首项为1,公比为2的等比数列. 因此log 2a n =2n -1,即a n =22n -1.故选D.8.设数列{a n }的前n 项和S n =n 2,则a 7+a 8的值为________. 答案 28解析 a 7+a 8=S 8-S 6=82-62=28.9.(2021·广东广州5月月考)已知数列{a n }满足a 1=1,a n +1=a n 2+a n ,用[x]表示不超过x 的最大整数,则[1a 1+1+1a 2+1+…+1a 2 017+1]=________.答案 0解析 因为a n +1=a n 2+a n ,因此1a n +1=1a n (a n +1)=1a n -1a n +1,即1a n +1=1a n -1a n +1,因此1a 1+1+1a 2+1+…+1a 2021+1=(1a 1-1a 2)+(1a 2-1a 3)+…+(1a 2 017-1a 2 018)=1a 1-1a 2 018.因为a 1=1,a 2=2>1,a 3=6>1,…,可知1a 2 018∈(0,1),则1a 1-1a 2 018∈(0,1),因此[1a 1-1a 2 018]=0.10.(2020·安徽屯溪一中月考)已知函数f(x)=2x -2-x,数列{a n }满足f(log 2a n )=-2n(n∈N *).(1)求数列{a n }的通项公式;(2)讨论数列{a n }的单调性,并证明你的结论. 答案 (1)a n =n 2+1-n (2)略解析 (1)因为f(x)=2x-2-x,f(log 2a n )=-2n , 因此2log 2a n -2-log 2a n =-2n ,即a n -1a n =-2n ,因此a n 2+2na n -1=0, 解得a n =-n±n 2+1. 因为a n >0,因此a n =n 2+1-n. (2)数列{a n }是递减数列.证明如下: 因为a n +1a n =(n +1)2+1-(n +1)n 2+1-n =n 2+1+n(n +1)2+1+(n +1)<1, 又a n >0,因此a n +1<a n ,即数列{a n }是递减数列.11.(2020·河南洛阳第二次统一考试)已知数列{a n }中,a 1=1,其前n 项和为S n ,且满足2S n =(n +1)a n (n∈N *). (1)求数列{a n }的通项公式;(2)记b n =3n-λa n 2,若数列{b n }为递增数列,求λ的取值范畴. 答案 (1)a n =n(n∈N *) (2)(-∞,2)解析 (1)∵2S n =(n +1)a n ,∴2S n +1=(n +2)a n +1, ∴2a n +1=(n +2)a n +1-(n +1)a n , 即na n +1=(n +1)a n ,∴a n +1n +1=a nn ,∴a n n =a n -1n -1=…=a 11=1, ∴a n =n(n∈N *). (2)b n =3n-λn 2. b n +1-b n =3n +1-λ(n+1)2-(3n -λn 2)=2·3n-λ(2n+1).∵数列{b n }为递增数列,∴2·3n-λ(2n+1)>0,即λ<2·3n2n +1.令c n =2·3n2n +1,则c n +1c n =2·3n +12n +3·2n +12·3n =6n +32n +3>1.∴{c n}为递增数列,∴λ<c1=2,即λ的取值范畴为(-∞,2).。
最新-2021届高三数学理一轮总复习江苏专用课件:第六章第二节 等差数列及其前n项和 精品

=a1+(n-1)-631a1≥0,可得 n≤634=2113,所以数列
{an}的前 21 项都是正数,以后各项都是负数,故 Sn 取
最大值时,n 的值为 21.
答案:21
2.已知数列{an}的前 n 项和 Sn=n2-6n,则{|an|}的 前 6 项和 T6=________. 解析:由 Sn=n2-6n 得{an}是等差数列,且首项为-5, 公差为 2.所以 an=-5+(n-1)×2=2n-7,当 n≤3 时, an<0;当 n>3 时,an>0;所以 T6=-a1+(-a2)+(-a3) +a4+a5+a6=5+3+1+1+3+5=18. 答案:18
2.求等差数列前 n 项和 Sn 最值的 2 种方法 (1)函数法:利用等差数列前 n 项和的函数表达式 Sn= an2+bn,通过配方或借助图象求二次函数最值的方法求解. (2)邻项变号法:
nan=1,∴2an=an-1+an+1(n≥2),
∴数列{an}为等差数列.
[变式 3] 若母题变为:已知数列{an}中,a1=2,an=2-an1-1 (n≥2,n∈N*),设 bn=an-1 1(n∈N*).求证:数列{bn}是 等差数列.
证明:∵an=2-an1-1,∴an+1=2-a1n. ∴bn+1-bn=an+11-1-an-1 1 =2-a11n-1-an-1 1=aann--11=1, ∴{bn}是首项为 b1=2-1 1=1, 公差为 1 的等差数列.
考点一 等差数列的基本运算基础送分型考点——自主练透 [题组练透]
1.(2015·全国卷Ⅰ改编)已知{an}是公差为 1 的等差数列, Sn 为{an}的前 n 项和,若 S8=4S4,则 a10=________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)求数列 , 的通项公式;(2)令 ,证明: .
16.已知 为等差数列 的前 项和,满足 , . 为数列 的前 项和,满足 , .(1)求 和 的通项公式;
(2)设 ,若数列 的前 项和 ,求 的最大值.
17.已知数列 为递增的等差数列,其中 ,且 成等比数列.
2020-2021学年度10月月考卷
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.已知数列 的前 项和为 , .
(1)证明数列 为等比数列并求其通项公式;
(2)若 ,求数列 的前 项和 .
2.已知公差不为0的等差数列 的前三项和为6,且 , , 成等比数列.
(1)求 的通项公式;
(2)设 记数列 的前n项和为 ,求使得 成立的m的最小正整数.
18.已知等差数列 中, ,且 , , 成等比数列.
(1)求数列 的通项公式;
(2)若数列 满足 ,求数列 的前 项和 .
19.已知等差数列 是单调递增数列, ,且 , 成等比数列, 是数列 的前 项和.(1)求数列 的通项公式;
27.已知数列 的前 项和为 ,且 ,(其中 为常数),又 .
(1)求数列 的通项公式;(2)设 ,求数列 的前 项和 .
28.已知数列 的前 项和为 ,且 .
(1)求数列 的通项公式;(2)若数列 的前 项和为 ,证明: .
29.在等差数列 和等比数列 中, ,且 。
(1)求 和 ;(2)求数列 的前n项和Sn。
(2)求数列 的前 项和.
10.在数列 , 中,已知 ,且 .
(Ⅰ)求数列 和 的通项公式;(Ⅱ)求数列 的前 项和 .
11.已知数列 满足: ,数列 满足 .(1)求数列 的通项 ,并求证:数列 为等比数列;
(2)求数列 的通项公式及其前n项和 .
12.已知数列 满足 ,且 成等差数列.(Ⅰ)求 的值和 的通项公式;
(1)求数列{ }的通项公式;
(2)若 成等比数列,求
25.已知各项均为正数的数列 中, 是数列 的前 项和,对任意 ,有 (1)求常数 的值;
(2)求数列 的通项公式;
26、已知Sn为数列{an}的前n项和,且a1<2,an>0,6Sn=an2+3an+2,n∈N*.
(1)求数列{an}的通项公式;
(2)设 ,求证:数列 的前 项和 .
22.已知正项数列 的前 项和为 是 与 的等比中项.
(1)求证:数列 是等差数列;
(2)若 ,数列 的前 项和为 ,求 .
(2)求证:
24.已知数列{ }的前n项和为 ,数列 的前n项和为 , 为等差数列且各项均为正数,
(2)若数列 满足 ,求数列 的前 项和 .
5.已知数列 为等差数列,数列 为等比数列,满足
(1)求数列 通项公式;(2)令 ,求数列 的前 项和 .
6.已知 是各项均为正数的等比数列, .
(1)求 的通项公式;(2)设 ,求数列 的前n项和.
7.已知等差数列 满足 , ,又数列 中, 且 ( ).(1)求数列 , 的通项公式;
(1)求数列 的通项公式;
(2)设 ,数列 的前 项和为 ,求使 的 的最大值.
3.已知数列 满足: , ;数列 是等比数列,并满足 ,且 , , 成等差数列.(1)求数列 , 的通项公式;
(2)若数列 的前 项和是 ,数列 满足 ,求证: .
4.已知正项等比数列 的前 项和为 ,且满足关于 的不等式 的解集为 .(1)求数列 的通项公式;
(2)若数列 , 的前n项和分别是 , ,且 .求数列 的前n项和 .(3)若 ( ,且 )对一切正整数n恒成立,求实数m的取值范围.
8.已知数列 是首项为 的等比数列,前 项和 中, , , 成等差数列.(1)求数列 的通项公式;
(2)设 ,若 ,求证 .
9.已知等差数列 的前 项和为 ,等比数列 的前 项和为 .若 , , .(1)求数列 与 的通项公式;
(2)设 , 是数列 的前 项和,求满足 的最小的 的值.
20.若 是公差不为0的等差数列 的前n项和, , , 成等比数列.
(1)求等比数列 , , 的公比;(2)若 ,求数列 的通项公式;
(3)在(2)的条件下,设 , 是数列 的前n项和,求使得 对所有 都成立的最小正整数m.
21.已知数列 的前 项和 = ,数列 为等差数列,且 (1)求数列 , 的通项公式;
(Ⅱ)设 ,求数列 的前 项和.
13.已知正项等比数列{an}中,a1,2a2,a3+6成等差数列,且a42=4a1a5.
(1)求数列{an}的通项公式;
(2)若Sn是数列{an}的前n项和,设bn= ,求数列{bn}的前n项和Tn.
14.已知数列 满足 .
(1)证明 是等比数列,并求 的通项公式;(2)证明: .
