中考数学证明题
2023年数学中考试题精选:几何综合证明(一)

1.(2023.营口24题)在平行四边形ABCD中,∠ADB=90°,点E在CD 上,点G在AB上,点F在BD的延长线上,连接EF,DG, ∠FED=∠ADG,ADBD =DG EF=k.(1)如图1,当k=1时,请用等式表示线段AG与线段DF的数量关系________;(2)如图2,当k=√(3)时,写出线段AD,DE和DF之间的数量关系,并说明理由;(3)在(2)的条件下,当点G是AB的中点时,连接BE,求tan∠EBF的值2.(2023.本溪铁岭辽阳25题)在Rt△ABC中,∠ACB=90°,CA=CB,点O为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.(1)如图1,当点D与点O重合时,请直接写出线段AD与线段EF 的数量关系;(2)如图2,当点D在线段AB上时,求证:CG+BD=√2BC;(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出S1S2的值.3.(2023.大连25题)综合与实践问题情境:数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质。
已知AB=AC,∠A>90°,点E为AC上一动点,将△ABE以BE为对称轴翻折,同学们经过思考后进行如下探究:独立思考:小明:“当点D落在BC上时,∠EDC=2∠ACB.”小红:“若点E为AC中点,给出AC与DC的长,就可求出BE的长.”补足探究:奋进小组的同学们经过探究后提出问题1,请你回答:问题1:在等腰△ABC中,AB=AC,∠A>90°,△BDE由△ABE翻折得到.(1)如图1,当点D落在BC上时,求证:∠EDC=2∠ACB;(2)如图2,若点E为AC中点,AC=4,CD=3,求BE的长.问题解决:小明经过探究发现:若将问题1中的等腰三角形换成∠A<90°的等腰三角形,可以问题进一步拓展.问题2:如图3,在等腰△ABC中,∠A<90°,AB=AC=BD=4,2∠D=∠ABD.若CD=1,则求BC的长.4.(2023.牡丹江26题)平行四边形ABCD中,AE⊥BC,垂足为E,连接DE,将ED绕点E逆时针旋转90°,得到EF,连接BF.(1)当点E在线段BC上,∠ABC=45°时,如图1,求证:AE+EC=BF;(2)当点E在线段BC延长线上,∠ABC=45°时,如图2,当点E在线段CB延长线上,∠ABC=135°时,如图3,请猜想并直接写出线段AE,EC,BF的数量关系;(3)在(1)、(2)的条件下,若BE=3,DE=5,则CE=______.5.(2023.贵州省25题)如图1,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.(1)【动手操作】如图2,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为______度;(2)【问题探究】根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;(3)【拓展延伸】如图3,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD将于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.6.(2023.沈阳24题)如图1.在平行四边形纸片中,AB=10,AD=6,∠DAB=60°,点E为BC边上的一点(点E不与点C重合),连接AE,将平行四边形ABCD纸片沿AE所在直线折叠,点C,D的对应点分别为C`,D`,射线C`E与射线AD将于点F.(1)求证:AF=EF;(2)如图2,当EF⊥AF时,DF的长为______;(3)如图3,当CE=2时,过点F作FM⊥AE,垂足为点M,延长FM 交C`D`于点N,连接AN,EN,求△ANE的面积。
2023年数学中考真题:圆的有关计算及证明精选(一)

圆的有关计算及证明2023年数学中考试题精选(一)1.(2023.营口23题)如图,在△ABC中,AB=BC,以BC为直径作圆O与AC将于点D,过点D作DE⊥AB,交CB延长线于点F,垂足为点E.(1)求证:DF为圆O的切线;,求BF的长。
(2)若BE=3,cosC=452.(2023.本溪铁岭辽阳24题)如图,AB是圆O的直径,点C,E在圆O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.(1)求证:EF与圆O相切;,求BC的长。
(2)若BF=1,sin∠AFE=453.(2023.沈阳22题)如图,BE是圆O的直径,点A和点D是圆O上的两点,过点A作圆O的切线交BE延长线于点C.(1)若∠ADE=25°,求∠C的度数;(2)若AB=AC,CE=2,求圆O半径的长.4.(2023.大连市23题)如图1,在圆O中,AB为圆O的直径,点C为圆O上一点,AD为∠CAB的平分线交圆O于点D,连接OD交BC于点E.(1)求∠BED的度数;(2)如图2,过点A作圆O的切线BC延长线于点F,过点D作DG ∥AF交AB于点G.若AD=2√35,DE=4,求DG的长。
5.(2023.湖北省恩施州23题)如图,△ABC是等腰直角三角形,∠ACB=90°,点O为AB的中点,连接CO交圆O于点E,圆O与AC 相切于点D.(1)求证:BC是圆O的切线;(2)延长CO交圆O于点G,连接AC交圆O于点F,若AC=4√(2),求FG的长.6.(2023.贵州省23题)如图,已知圆O是等边三角形ABC的外接圆,连接CO并延长交AB于点D,交圆O于点E,连接EA,EB.(1)写出图中一个度数为30°的角;____,图中与△ACD全等的三角形是______;(2)求证:△AED∽△CEB;(3)连接OA,OB,判断四边形OAEB的形状,并说明理由。
7.(2023.江苏省24题)如图,在△ABC中,AB=AC,以AB为直径的圆O交边AC于点D,连接BD,过点C作CE∥AB.(1)请用无刻度的直尺和圆规作图:过点B作圆O的切线,交CE 于点F;(不写作法,保留作图痕迹,标明字母)(2)在(1)的条件下,求证:BD=BF.8.(2023.江西省20题)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的圆O与AC相交于点D,E为优弧ABD上一点,且∠ADE=40°.(1)求BE的长;(2)若∠EAD=76°,求证:CB为圆O的切线.9.(2023.沈阳22题)如图,AB是圆O的直径,点C是圆O上的一点(点C不与点A,B重合),连接AC,BC,点D是AB上的一点,AC=AD,BE交CD的延长线于点E,且BE=BC.(1)求证:BE是圆O的切线;(2)若圆O的半径为5,tanE=1,则BE的长为_____.210.(2023.扬州市25题)如图,在△ABC中,∠ACB=90°,点D是AB∠A,点O在BC上,以点O为圆心的圆经过C、上一点,且∠BCD=12D两点.(1)试判断直线AB与圆O的位置关系,并说明理由;,圆O的半径为3,求AC的长.(2)若sinB=3511.(2023.广西壮族自治区23题)如图,PO平分∠APD,PA与圆O相切于点A,延长AO交PD于点C,过点O作OB⊥PD,垂足为B.(1)求证:PB是圆O的切线;(2)若圆O的半径为4,OC=5,求PA的长.12.(2023.广东省22题)如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A`,连接AA`交BD于点E,连接CA`.(1)求证:AA`⊥CA`;(2)以点O为圆心,OE为半径作圆.①如图2,圆O与CD相切,求证:AA`=√3CA`;②如图3,圆O与CA`相切,AD=1,求圆O的面积.13.(2023.安徽省20题)已知四边形ABCD内接于圆O,对角线BD是圆O的直径.(1)如图1,连接OA,CA,若OA⊥BD,求证:CA平分⊥BCD; (2)如图2,E为圆O内一点,满足AE⊥BC,CE⊥AB,若BD=3√3,AE=3.求弦BC的长.14.(2023.湖北黄冈市20题)如图,⊥ABC 中,以AB 为直径的圆O 交BC 于点D ,DE 是圆O 的切线 ,且DE⊥AC ,垂足为E ,延长CA 交圆O 于点F.(1)求证:AB=AC ;(2)若AE=3,ED=6,求AF 的长。
中考数学证明题集锦及答案
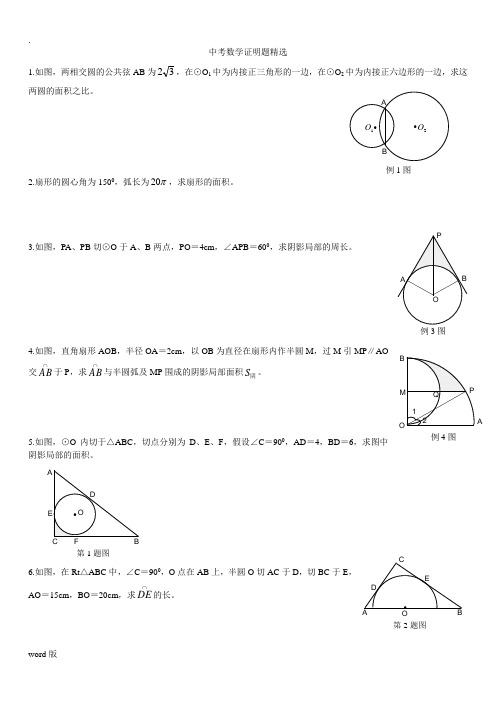
中考数学证明题精选1.如图,两相交圆的公共弦AB为32,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比。
2.扇形的圆心角为1500,弧长为π20,求扇形的面积。
3.如图,PA、PB切⊙O于A、B两点,PO=4cm,∠APB=600,求阴影局部的周长。
4.如图,直角扇形AOB,半径OA=2cm,以OB为直径在扇形内作半圆M,过M引MP∥AO交⋂AB于P,求⋂AB与半圆弧及MP围成的阴影局部面积阴S。
5.如图,⊙O内切于△ABC,切点分别为D、E、F,假设∠C=900,AD=4,BD=6,求图中阴影局部的面积。
第1题图6.如图,在Rt△ABC中,∠C=900,O点在AB上,半圆O切AC于D,切BC于E,AO=15cm,BO=20cm,求⋂DE的长。
2O1O••例1图BA例3图例4图OBA•第2题图EA BOCD7.如图,有一个直径是1米圆形铁皮,要从中剪出一个最大的圆心角为900的扇形ABC ,求:〔1〕被剪掉〔阴影〕局部的面积;〔2〕用所留的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?8.如图,⊙O 与⊙O '外切于M ,AB 、CD 是它们的外公切线,A 、B 、C 、D 为切点,E O '⊥OA 于E ,且∠AOC =1200。
〔1〕求证:⊙O '的周长等于⋂AMC 的弧长;〔2〕假设⊙O '的半径为1cm ,求图中阴影局部的面积。
9.如图,在梯形ABCD 中,AB ∥CD ,∠BCD=90°,且AB=1,BC=2,tan ∠ADC=2. (1) 求证:DC=BC;(2) E 是梯形内一点,F 是梯形外一点,且∠E DC=∠F BC ,DE=BF ,试判断△E CF 的形状,并证明你的结论; (3) 在〔2〕的条件下,当BE :CE=1:2,∠BEC=135°时,求sin ∠BFE 的值.10.:如图,在□ABCD 中,E 、F 分别为边AB 、CD 的中点,BD 是对角线,AG ∥DB 交CB 的延长线于G . 〔1〕求证:△ADE ≌△CBF ;〔2〕假设四边形 BEDF 是菱形,那么四边形AGBD 是什么特殊四边形?并证明你的结论.11.如图13-1,一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O 〔点O 也是BD 中点〕按顺时针方向旋转.〔1〕如图13-2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜测BM ,FN 满足的数量关系,并证明你的猜测; 〔2〕假设三角尺GEF 旋转到如图13-3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD的延长线与GF 的延长线相交于点N ,此时,〔1〕中的猜测还成立吗?假设成立,请证明;假设不成立,请说明理由. E BF CD A D F O N D FN CO•第3题图AB OCO '第4题图MDEA B O C12.如图,⊙O 的直径AB 垂直于弦CD 于E ,连结AD 、BD 、OC 、OD ,且OD =5。
中考复习初中数学几何证明 试题(含答案)
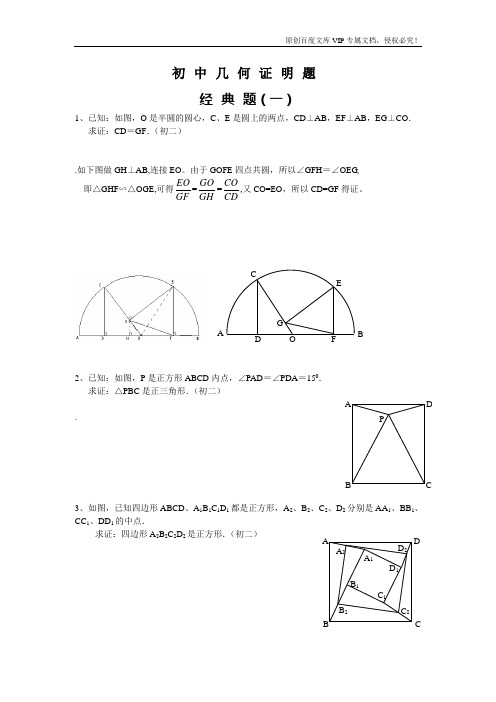
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.BF求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
【中考数学】2022-2023学年易错常考专题训练—切线的证明(含解析)

【中考数学】2022-2023学年易错常考专题训练—切线的证明一、综合题1.如图,⊙O 是Rt △ABC 的外接圆,∠ABC =90°,BD =BA ,BE ⊥DC 交DC 的延长线于点E .(1)若∠BAD =70°,则∠BCA = °;(2)若AB =12,BC =5,求DE 的长: (3)求证:BE 是⊙O 的切线.2.如图,AB 为 的直径,C 为 上一点,D 为BA 延长线上一点, .⊙O ⊙O ∠ACD =∠B(1)求证:DC 为 的切线;⊙O (2)线段DF 分别交AC ,BC 于点E ,F 且 , 的半径为5, ,求∠CEF =45∘⊙O sinB =35CF 的长.3.如图,四边形ABCD 的顶点在⊙O 上,BD 是⊙O 的直径,延长CD 、BA 交于点E ,连接AC 、BD 交于点F ,作AH ⊥CE ,垂足为点H ,已知∠ADE =∠ACB .(1)求证:AH 是⊙O 的切线;(2)若OB =4,AC =6,求sin ∠ACB 的值;(3)若 = ,求证:CD =DH .DF FO 234.如图,⊙ 是△ 的外接圆, 为直径,弦 , 交 的延长线于点O ABC AC BD =BA BE ⊥DC DC ,求证:E(1) ;∠ECB =∠BAD (2) 是⊙ 的切线.BE O 5.如图,已知Rt △ABC ,∠C=90°,D 为BC 的中点,以AC 为直径的⊙O 交AB 于点E .(1)求证:DE 是⊙O 的切线;(2)若AE :EB=1:2,BC=6,求AE 的长.6.如图,在Rt △ABC 中,∠C=90°,∠BAC 的角平分线AD 交BC 边于D .以AB 上某一点O 为圆心作⊙O ,使⊙O 经过点A 和点D .(1)判断直线BC 与⊙O 的位置关系,并说明理由;(2)若AC=3,∠B=30°.①求⊙O 的半径;②设⊙O 与AB 边的另一个交点为E ,求线段BD 、BE 与劣弧DE 所围成的阴影部分的图形面积.(结果保留根号和π)7.如图,等腰三角形ABC 中,AC=BC=10,AB=12,以BC 为直径作⊙O 交AB 于点D ,交AC 于(1)求证:直线EF 是⊙O 的切线;(2)求cos ∠E 的值.8.如图,已知△ABC 是等边三角形,以AC 为直径的⊙O 分别交AB ,BC 于点D ,E ,点F 在AB的延长线上,2∠BCF=∠BAC .(1)求∠ADE 的度数.(2)求证:直线CF 是⊙O 的切线.9.如图,AB 是⊙O 的直径,弦CD ⊥AB 于H ,G 为⊙O 上一点,连接AG 交CD 于K ,在CD 的延长线上取一点E ,使EG=EK ,EG 的延长线交AB 的延长线于F.(1)求证:EF 是⊙O 的切线; (2)连接DG ,若AC ∥EF 时.①求证:△KGD ∽△KEG ;②若,AK= ,求BF 的长.cosC =451010.在 中, , , 是 边上的点,⊙O 与 相切,切点Rt △ABC ∠A =90°AB =AC =4O BC AB 为 , 与⊙O 相交于点 ,且 .D ACE AD =AE(1)求证: 是⊙O 的切线;AC (2)如果 为 弧上的一个动点(不与 、 重合),过点 作⊙O 的切线分别与边 F DE D E F 、 相交于 、 ,连接 、 ,有两个结论:①四边形 的周长不变,②AB AC G H OG OH BCHG 的度数不变.已知这两个结论只有一个符合题意,找出正确的结论并证明;∠GOH (3)探究:在(2)的条件下,设 , ,试问 与 之间满足怎样的函数关系,BG =x CH =y y x 写出你的探究过程并确定变量 的取值范围,并说明当 时 点的位置.x x =y F 11.如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 交BC 于点D ,连接AD ,过点D 作DM ⊥AC ,垂足为M ,AB 、MD 的延长线交于点N.(1)求证:MN 是⊙O 的切线;(2)求证:DN 2=BN•(BN+AC );(3)若BC =6,cosC = ,求DN 的长.3512.如图,AB 为⊙O 的直径,P 为BA 延长线上一点,点C 在⊙O 上,连接PC ,D 为半径OA 上一点,PD =PC ,连接CD 并延长交⊙O 于点E ,且E 是 的中点.AB(1)求证:PC 是⊙O 的切线;(2)若AB =8,CD•DE =15,求PA 的长.13.如图,内接于⊙,⊙的直径AD 与弦BC 相交于点E ,BE =CE ,过点D 作交△ABC O O DF ∥BC AC 的延长线于点F .(1)求证:DF 是⊙的切线;O (2)若,AB =6,求DF 的长.sin∠BAD =1314.如图,在中,,,以边上一点为圆心,为半径作,RtΔABC ∠BAC =90°∠C =30°AC O OA ⊙O 恰好经过边的中点,并与边相交于另一点.⊙O BC D AC F(1)求证:是的切线.BD ⊙O (2)若,是半圆上一动点,连接,,.填空: AB =3E AGF AE AD DE ①当的长度是 时,四边形是菱形;AE ABDE ②当的长度是 时,是直角三角形.AE ΔADE15.已知AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ,切点为G ,连接AG 交CD 于K .(1)如图1,求证:KE=GE ;(2)如图2,连接CA ,BG ,若∠FGB= ∠ACH ,求证:CA ∥FE ;12(3)如图3,在(2)的条件下,连接CG 交AB 于点N ,若sinE= ,AK= ,求CN 的3510长.16.如图,已知在 Rt △ABC 中, ∠C=90° ,点D 为AC 的中点.(1)请利用尺规作出以BC 为直径的⊙O ; (保留作图痕迹 )(2)AB 交⊙O 于点 E ,连接 DE ,求证: DE 是 ⊙O 的切线.(3)若 ∠ABC=30° , BC=6 ,求⊙O 与 DE 、 DC 组成的阴影部分面积.答案解析部分1.【正确答案】(1)70(2)解:在Rt △ABC 中,AC = =13, ∠BDE =∠BAC ,∠BED =∠CBA =90°,BC 2+AB 2∴△DEB ∽△ABC ,∴ ,即 , 解得,DE = ;DE AB =BD AC DE 12=121314413(3)证明:连接OB , ∵OB =OC ,∴∠OBC =∠OCB , ∵四边形ABCD 内接于⊙O , ∴∠BAD+∠BCD =180°, ∵∠BCE+∠BCD =180°,∴∠BCE =∠BAD ,∵BD =BA , ∴∠BDA =∠BAD ,∵∠BDA =∠ACB ,∴∠ACB =∠BAD ,∴∠OBC =∠BCE ,∴OB ∥DE ,∵BE ⊥DC , ∴BE ⊥OB ,∴BE 是⊙O 的切线.2.【正确答案】(1)解:如图,连接OC ,为 的直∵AB ⊙O 径,, ∴∠ACB =∠BCO +∠OCA =90°,∴∠B =∠BCO ,∵∠ACD =∠B ,∴∠ACD =∠BCO ,即 ,∴∠ACD +∠OCA =90∘∠OCD =90∘ 为 的切线∴DC ⊙O (2)解: 中, ,, , ,(2)Rt △ACB AB =10sinB =35=ACAB ∴AC =6BC =8 , ,∵∠ACD =∠B ∠ADC =∠CDB ∽ ,∴△CAD △BCD ,∴AC BC =AD CD =68=34设 , ,AD =3x CD =4x 中, , ,Rt △OCD OC 2+CD 2=OD 252+(4x)2=(5+3x)2 舍 或 ,x =0()307 , ,∵∠CEF =45∘∠ACB =90∘ ,∴CE =CF 设 ,CF =a ,∵∠CEF =∠ACD +∠CDE ,∠CFE =∠B +∠BDF ,∴∠CDE =∠BDF ,∵∠ACD =∠B ∽ ,∴△CED △BFD ,∴CE CD =BF BD ,,∴a 4×307=8−a 10+3×307a =247∴CF =2473.【正确答案】(1)证明:连接OA ,由圆周角定理得,∠ACB =∠ADB , ∵∠ADE =∠ACB ,∴∠ADE =∠ADB ,∵BD 是直径, ∴∠DAB =∠DAE =90°, 在△DAB 和△DAE 中,,{∠BAD =∠EADDA =DA∠BDA =∠EDA ∴△DAB ≌△DAE ,∴AB =AE ,又∵OB =OD , ∴OA ∥DE ,又∵AH ⊥DE ,∴OA ⊥AH ,∴AH 是⊙O 的切线(2)解:由(1)知,∠E =∠∠DBE =∠ACD , ∴∠E =∠ACD ,∴AE =AC =AB =6.在Rt △ABD 中,AB =6,BD =8,∠ADE =∠ACB ,∴sin ∠ADB = = ,即sin ∠ACB = 683434(3)证明:由(2)知,OA 是△BDE 的中位线,∴OA ∥DE ,OA = DE .12∴△CDF ∽△AOF , ∴ = = , CD AO DF OF 23∴CD = OA = DE ,即CD = CE ,231314∵AC =AE ,AH ⊥CE ,∴CH =HE = CE ,12∴CD = CH ,12∴CD =DH .4.【正确答案】(1)证明:∵四边形ABCD 是圆内接四边形,∴∠ECB=∠BAD.(2)证明:连结OB ,OD ,在△ABO 和△DBO 中, ,∴△ABO ≌△DBO (SSS ),{AB =BDBO =BOOA =OD ∴∠DBO=∠ABO ,∵∠ABO=∠OAB=∠BDC ,∴∠DBO=∠BDC , ∴OB ∥ED ,∵BE ⊥ED ,∴EB ⊥BO , ∴BE 是⊙O 的切线5.【正确答案】(1)证明:连接OE 、EC ,∵AC 是⊙O 的直径,∴∠AEC=∠BEC=90°,∵D 为BC 的中点,∴ED=DC=BD ,∴∠1=∠2,∵OE=OC ,∴∠3=∠4,∴∠1+∠3=∠2+∠4,即∠OED=∠ACB ,∵∠ACB=90°,∴∠OED=90°,∴DE 是⊙O 的切线(2)解:由(1)知:∠BEC=90°,∵在Rt △BEC 与Rt △BCA 中,∠B=∠B ,∠BEC=∠BCA ,∴△BEC ∽△BCA ,∴ = ,BE BC BC BA ∴BC 2=BE•BA ,∵AE :EB=1:2,设AE=x ,则BE=2x ,BA=3x ,∵BC=6,∴62=2x•3x ,解得:x= ,6即AE= 66.【正确答案】(1)解:(1)直线BC 与⊙O 相切;连结OD ,如图所示,∵OA=OD ,∴∠OAD=∠ODA ,∵∠BAC 的角平分线AD 交BC 边于D ,∴∠CAD=∠OAD ,∴∠CAD=∠ODA ,∴OD ∥AC ,∴∠ODB=∠C=90°,即OD ⊥BC .又∵直线BC 过半径OD 的外端,∴直线BC 与⊙O 相切.(2)解:①设OA=OD=r ,在Rt △BDO 中,∠B=30°,∴OB=2r ,在Rt △ACB 中,∠B=30°,∴AB=2AC=6,∴3r=6,解得r=2.②在Rt △ACB 中,∠B=30°,∴∠BOD=60°.∴.∴所求图形面积为.7.【正确答案】(1)证明:如图,方法1:连接OD 、CD .∵BC 是直径,∴CD ⊥AB .∵AC=BC .∴D 是AB 的中点.∵O 为CB 的中点,∴OD ∥AC .∵DF ⊥AC ,∴OD ⊥EF .∴EF 是圆O 的切线.方法2:∵AC=BC ,∴∠A=∠ABC ,∵OB=OD ,∴∠DBO=∠BDO ,∵∠A+∠ADF=90°∴∠EDB+∠BDO=∠A+∠ADF=90°.即∠EDO=90°,∴OD ⊥ED∴EF 是圆O 的切线.(2)解:连BG .∵BC 是直径,∴∠BDC=90°.∴CD= =8.AC 2−AD 2∵AB•CD=2S △ABC =AC•BG ,∴BG= = = .AB ⋅CD AC 9610485∴CG= = .BC 2−BG 2145∵BG ⊥AC ,DF ⊥AC ,∴BG ∥EF .∴∠E=∠CBG ,∴cos ∠E=cos ∠CBG= = .BG BC 24258.【正确答案】(1)解:∵△ABC 是等边三角形,∴∠ACB=∠ACE=60°,∴∠ADE=180°﹣∠ACE=120°(2)解:∵⊙O 的直径是AC , ∴∠AEC=90°,即AE ⊥BC .又∵AB=AC ,∴∠BAE=∠CAE .∵2∠BCF=∠BAC ,∴∠BCF=∠CAE .∵∠CAE+∠ECA=90°,∴∠BCF+∠ECA=90°,即∠ACF=90°.又AC 是直径,∴直线CF 是⊙O 的切线9.【正确答案】(1)证明:如图,连接OG.∵EG=EK ,∴∠KGE=∠GKE=∠AKH ,又OA=OG ,∴∠OGA=∠OAG , ∵CD ⊥AB ,∴∠AKH+∠OAG=90°,∴∠KGE+∠OGA=90°,∴EF 是⊙O 的切线.(2)解:①∵AC ∥EF ,∴∠E=∠C , 又∠C=∠AGD ,∴∠E=∠AGD ,又∠DKG=∠CKE ,∴△KGD ∽△KGE.②连接OG ,如图所示.∵,AK= ,cosC =4510设 ,∴ , ,则 cosC =45=CHAC =kCH =4k AC =5k AH =3k KE=GE ,AC ∥EF ,∴CK=AC=5k ,∴HK=CK -CH=k.在Rt △AHK 中,根据勾股定理得AH 2+HK 2=AK 2,即 , , , ,则 ,(3k)2+k 2=(10)2k =1CH =4AC =5AH =3设⊙O 半径为R ,在Rt △OCH 中,OC=R ,OH=R -3k ,CH=4k ,由勾股定理得:OH 2+CH 2=OC 2, ,∴(R−3)2+42=R 2R =256在Rt △OGF 中,,∴ ,cosC =cos∠GOF =45=OG OF OF =12524∴BF =OF−OB =12524−256=252410.【正确答案】(1)解:如图,连接OA ,OD ,OE ,∵AB 是⊙O 的切线,点D 为切点,∴∠ADO=90°,∵AD=AE ,OD=0E ,AO=AO ,∴△AOD ≌△AOE ,∴∠ADO=∠AEO=90°,∴AC 是⊙O 的切线,点E 为切点;(2)解:根据题意,四边形BCHG 的周长为BC+CH+BG+HG , ∵ , ,∠A =90°AB =AC =4∴∠B=∠C=45°,BC=4 ,2∵∠ADO=∠AEO=90°,OD=0E ,∴∠DOB=∠EOC=45°,△BOD ≌△COE ,∴OB=OC ,BD=CE ,∴∠EOD=90°,∠AOB=90°,∠BAO=45°,∴BD=OD=DA=CE= AB=2,12∵AB ,AC ,GH 都是⊙O 的切线,∴HF=HE ,GD=GF ,∴四边形BCHG 的周长为BC+CE+EH+GH+BD+GD =BC+CE+BD+GH+HF+FG = BC+CE+BD+2GH =4+4 +2GH ,2∵GH 是变量,∴四边形BCHG 的周长不是定值,这个结论不符合题意;∵AB ,AC ,GH 都是⊙O 的切线,根据切线长定理,得GO 平分∠DOF ,HO 平分∠EOF ,∴∠GOH=∠GOF+∠HOF= ∠DOF+ ∠EOF= (∠DOF+∠EO )121212= ∠EOD ,12∵∠EOD=90°,∴∠GOH=45°,是个定值,故该结论符合题意(3)解:根据题意,GD=GF=x-2,HE=HF=y-2, ∴GH=x+y-4,AG=4-x ,AH=4-y ,在直角三角形AGH 中, ,AG 2+AH 2=GH 2∴ ,(x−2)2+(y−2)2=(x +y−4)2整理,得y= ,且2<x <4,8x 当x=y 时,∴AG=AH ,∴AG :AB=AH :AC ,∴GH ∥BC ,∴OF ⊥GH ,∵BG=CH ,∠B=∠C ,BO=CO ,∴△BOG ≌△COH ,∴GO=HO ,∴GF=FH ,∴A ,F ,O 三点一线,∴∠DOF=∠EOF , ∴弧DF=弧EF ,故点F 是弧DE 的中点.11.【正确答案】(1OD ,∵AB 是直径,∴∠ADB =90°,又∵AB =AC ,∴BD =CD ,∠BAD =∠CAD ,∵AO =BO ,BD =CD ,∴OD ∥AC ,∵DM ⊥AC ,∴OD ⊥MN ,又∵OD 是半径,∴MN 是⊙O 的切线;(2)证明:∵AB =AC , ∴∠ABC =∠ACB ,∵∠ABC+∠BAD =90°,∠ACB+∠CDM =90°,∴∠BAD =∠CDM ,∵∠BDN =∠CDM ,∴∠BAD =∠BDN ,又∵∠N =∠N ,∴△BDN ∽△DAN ,∴,BN DN =DNAN ∴DN 2=BN•AN =BN•(BN+AB )=BN•(BN+AC );(3)解:∵BC =6,BD =CD , ∴BD =CD =3,∵cosC = = ,35CD AC ∴AC =5,∴AB =5,∴AD = = =4,AB 2−BD 225−9∵△BDN ∽△DAN ,∴ = = ,BN DN =DN AN BD AD 34∴BN = DN ,DN = AN ,3434∴BN = ( AN )= AN ,3434916∵BN+AB =AN ,∴ AN+5=AN 916∴AN = ,807∴DN = AN = .3460712.【正确答案】(1)证明:连接OC ,OE ,∵OC=OE ,∴∠OEC=∠OCE ,∵E 是 的中点,AB ∴ ,AE =BE ∴∠AOE=∠BOE=90°,∴∠OEC+∠ODE=90°,∵PC=PD ,∴∠PCD=∠PDC ,∵∠PDC=∠ODE ,∴∠PCD=∠ODE ,∴∠PCD+∠OCD=∠ODE+∠OEC=90°,∴OC ⊥PC ,∴PC 是⊙O 的切线;(2)解:连接AC ,BE ,BC , ∵∠ACD=∠DBE ,∠CAD=∠DEB ,∴△ACD ∽△EBD ,∴,AD DE =CDBD ∴CD•DE=AD•BD=(AO-OD )(AO+OD )=AO 2-OD 2;∵AB 为⊙O 的直径,∴∠ACB=90°,∵∠PCO=90°,∴∠ACP=∠BCO ,∵∠BCO=∠CBO ,∴∠ACP=∠PBC ,∵∠P=∠P ,∴△ACP ∽△CBP ,∴ ,PC PB =PA PC ∴PC 2=PB•PA=(PD+DB )(PD-AD )=(PD+OD+OA )(PD+OD-OA )=(PD+OD )2-OA 2=PD 2+2PD•OD+OD 2-OA 2,∵PC=PD ,∴PD 2=PD 2+2PD•OD+OD 2-OA 2,∴OA 2-OD 2=2OD•PD ,∴CD•DE=2OD•PD ;∵AB=8,∴OA=4,由CD•DE=AO 2-OD 2;∵CD•DE=15,∴15=42-OD 2,∴OD=1(负值舍去),∴AD=3,由CD•DE=2OD•PD ,∴PD= ,CD•DE 2OD =152∴PA=PD-AD= .9213.【正确答案】(1)证明:∵AD 为的直径,BE =CE ,⊙O ∴,AD ⊥BC ∴,∠AEC =90°∵,DF ∥BC ∴,∠ADF =∠AEC =90°∴,且OD 是的半径,DF ⊥AD ⊙O ∴DF 是的切线;⊙O (2)解:连接CD ,∵,AB =6,sin∠BAD =13∴CE =BE =2,∴,AE =AB 2−BE 2=42∵,AD ⊥BC ∴AC =AB =6,∵,cos∠CAD =AE AC =AC AD ∴,426=6AD ∴,AD =922∵,tan∠CAD =DF AD =CEAE ∴,DF922=242∴(注:答案不唯一,可利用两个三角形相似进行解答).DF =9414.【正确答案】(1,OD ∵在中,,,RtΔABC ∠BAC =90°∠C =30°∴,AB =12BC∵是的中点,∴,D BC BD =12BC∴,∴,AB =BD ∠BAD =∠BDA ∵,∴,OA =OD ∠OAD =∠ODA ∴,即,∠ODB =∠BAO =90°OD ⊥BC(2);或23π13ππ15.【正确答案】(1)证明:如图1,连接OG .∵EF 切⊙O 于G ,∴OG ⊥EF ,∴∠AGO+∠AGE=90°,∵CD ⊥AB 于H ,∴∠AHD=90°,∴∠OAG+∠AKH=90°,∵OA=OG ,∴∠AGO=∠OAG ,∴∠AGE=∠AKH ,∵∠EKG=∠AKH ,∴∠EKG=∠AGE ,∴KE=GE(2)证明:设∠FGB=α,∵AB 是直径,∴∠AGB=90°,∴∠AGE=∠EKG=90°﹣α,∴∠E=180°﹣∠AGE﹣∠EKG=2α,∵∠FGB= ∠ACH ,12∴∠ACH=2α,∴∠ACH=∠E ,∴CA ∥FE(3)解:作NP ⊥AC 于P .∵∠ACH=∠E ,∴sin ∠E=sin ∠ACH= ,AH AC =35设AH=3a ,AC=5a ,则CH= ,tan ∠CAH= ,AC 2−CH 2=4a CH AH =43∵CA ∥FE ,∴∠CAK=∠AGE ,∵∠AGE=∠AKH ,∴∠CAK=∠AKH ,∴AC=CK=5a ,HK=CK﹣CH=4a ,tan ∠AKH= =3,AK= ,AH HK AH 2+HK 2=10a ∵AK= ,10∴ ,10a =10∴a=1.AC=5,∵∠BHD=∠AGB=90°,∴∠BHD+∠AGB=180°,在四边形BGKH 中,∠BHD+∠HKG+∠AGB+∠ABG=360°,∴∠ABG+∠HKG=180°,∵∠AKH+∠HKG=180°,∴∠AKH=∠ABG ,∵∠ACN=∠ABG ,∴∠AKH=∠ACN ,∴tan ∠AKH=tan ∠ACN=3,∵NP ⊥AC 于P ,∴∠APN=∠CPN=90°,在Rt △APN 中,tan ∠CAH=,设PN=12b ,则AP=9b ,PN AP =43在Rt △CPN 中,tan ∠ACN= =3,PNCP ∴CP=4b ,∴AC=AP+CP=13b ,∵AC=5,∴13b=5,∴b= ,∴CN= = = .513PN 2+CP 2410⋅b 20131016.【正确答案】(1)解:如图 ,作 的垂直平分线,交 于 ,以 为半径作⊙O , 1BC BC O OB 则 ⊙O 即为所作;OD OE(2)解:如图2,连接,,∵O BC D AC是的中点,是的中点,∴OD△ACB是的中位线,∴OD//AB,∴∠COD=∠B∠DOE=∠OEB,,∵OE=OB,∴∠OEB=∠B,∴∠COD=∠DOE,∵OC=OE OD=OD,,∴△OCD△OED(SAS)≌,∴∠OED=∠OCD=90°,∵OE⊙O是的半径,∴DE⊙O是的切线;(3)解:如图2,,∵OB =OE ,∴∠OEB =∠B =30° ,∴∠COE =∠OEB +∠B =60°由(2)知: ≌ ,△OCD △OED ,∴∠COD =∠DOE =30° ,∵BC =6 ,∴OC =3 中, ,Rt △OCD CD =3 与 、 组成的阴影部分面积∴⊙O DE DC .=2S △OCD −S 扇形OCE =2×12×3×3−60π×32360=33−3π2。
中考数学-几何证明

2020年-春季-初三下-【入学考试】1.(初2020级BZ初三下入学测试)如图,正方形ABCD中,对角线AC, BD交于点。
,点E.点OB ,线段AB上,且AF OE ,连接AE交OF于G , 连接DG交AO于H.F分别在线段⑴如图1,若点E为线段BO中点,AE J5,求BF的长:(2)如图2,若AE平分BAC,求证:FG HG;(3)如图3,点E在线段BO (含端点)上运动,连接HE,当线段HE长度取得最大值时,直接写出cos HDO的值.2.(初2020级BS初三下入学测试)如图,平行四边形ABCD中,AB=2BC, B 60 . 曲 DC中点,连接AE . F为AD上一点,连接CF交AE与点G , CM平分FCB交AB于点M .(1)如图1,若BC 3,AF 1 求sin DCF 的值.(2)求证:EG BM CG(3)如图2, CN AB于点N ,若AG=4, MN : BN=3: 5.求CG 的长度.3.(初2020级YZ初三下入学测试)在0ABCD中BAC=90 , AB=AE,延长BE交CD 于点F . AG BE交BE于点H点,M是BC边上的点.(1)如图1,若点M与点G重合,AH 5, AD 显26 ,求CF的长:2(2)如图2.若AM是BAD的角平分线,连接MH , HMG MAH ,求证:AM 2 .2HM(3)如图3,若点M为BC的中点,作点B关于AM的对称点N,连接AN、MN、EN,请直接写出AMH、NAE、MNE之间的角度关系.4.(初2020级YZ 初三下入学测试)在正方形 ABCD 中,E 为边CD 上一点(不与点 C 、D 第4页共34重合),垂直于BE 的一条直线 MN 分别交BC 、BE 、AD 于点M 、P 、N,正方形ABCD 的边长为6.(1)如图1,当点M 和点C 重合时,若AN =4,求线段PM 的长度;(2)如图2,当点M 在边BC 上时,判断线段AN 、MB 、EC 之间的数量关系,并说明理由;(3)如图3,当垂足P 在正方形 ABCD 的对角线 AC 上运动时,连接 NB,将^ BPN 沿着BN 翻折,点P 落在点P 处,AB 的中点为Q,直接写出PQ 的最小值.5.(万二中初2020级初三下入学测试)在4ABC与4ADF中,/BAC=/DAF=90° ,AB=AC,AD=AF, DF的延长线交BC于点E,连接DB、CF.(1)如图1,当点C、A、D三点在同一直线上,且AC=g AF, AF=超时,求CE的长;(2)如图2,当/ AFC = 90°时,求证:E是BC的中点;(3)如图3,若CF平分/ ACB,且CF的延长线与DB交于点G,请直接写出BG、DG、FG之间的数量关系.[ D6.(万中初2020级初三下入学测试) 如图,在?ABCD中,/ACB = 45° , AEXBC于点E, 过点C 作CFLAB于点F,交AE于点M.点N在边BC上,且AM = CN ,连结DN .(1)若AB= 10Q , AC = 4,求BC 的长;(2)求证:AD+AM= 22DN .(3)如图,连接EF、探究AF、EF、CF之间存在的数量关系,直接写出数量关系不需要证明.2020年-春季-初三下-【第一次诊断】1.(初2020级YW初三下第一次诊断)如图,在平行四边形ABCD中,AC为对角线,过点D作DELDC交直线AB于点E,过点E作EHXAD于点H,过点B作BFXAD于点F.(1)如图,若/ BAD=60° , AF=3, AH=2,求AC 的长.(2)如图,若BF=DH,在AC上取一点G,连接DG、GE, 若/ DGE=75° ,/CDG=45° -/CAB,求证:DG 立CG22.如图,已知ABCD中,/ B=45° , CE^AD于G,交BA延长线E, CF平分/ DCE ,连接EF, ED.(1)如果AB=5, AD = 372,求线段DE的长.(2)如果/ CFE=90° ,求证:CD 2DF 版AG .(3)如图,在(2)的条件下,若FG J5,点M、N是线段CF、CD上的动点,DM+MN 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由 ^3.(初2020级BZ初三下第一次诊断)已知△ ABC是等边三角形,CD,AB交AB于M, DBXBC, E是AC上一点,EHXBC,垂足为H, EH与CD交于点F,连接BE.(1)如图,若EC=-AC , EH=6,求BE 的长. 5(2)如图,连接AF,将AF绕点A顺时针旋转,使F点落在BD边上的G点处,AG交CD 于Q,求证:BG=CF.(3)如图,在(2)的条件下,连接FG,交BE于N,连接MN,若竺勺,4AGF的面QG 3积为49户,求MN的长.3.(万州国本中学初三下期中考试)已知,在0ABCD中,AB BD, AB BD, E为射线BC上一点,连接AE交BD于点F .(1)如图1,若点E与点C重合,且AF 2胫,求AD的长;(2)如图2,当点E在BC边上时,过点D作DG AE于G ,延长DG交BC于H ,连接FH ,求证:AF DH FH ;(3)如图3,当点E在射线BC上运动时,过点D作DG AE于G , M为AG的中点,点N在BC边上且BN 1 ,已知AB 4 J2 ,请直接写出MN的最小值.4 .(万州国本中学初三下第一次诊断) 【问题背景】如图1所示,在gABC 中,AB= BC, ABC=90,点D 为直线BC 上的一个动点(不与 B 、C 重合),连结AD,将线段AD 绕点D 按顺时针方向旋转90。
2024年中考数学复习重难点题型训练—简单几何证明题(含答案解析)

2024年中考数学复习重难点题型训练—简单几何证明题(含答案解析)类型一三角形全等1.(2022·西藏)如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.【答案】证明:∵AD平分∠BAC,∴∠BAD=∠CAD,在△ABD和△ACD中,AB=AC∠BAD=∠CADAD=AD,∴△ABD≌△ACD(SAS).2.(2022·湖南省益阳市)如图,在Rt△ABC中,∠B=90°,CD//AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.【答案】证明:∵DE⊥AC,∠B=90°,∴∠DEC =∠B =90°,∵CD//AB ,∴∠A =∠DCE ,在△CED 和△ABC 中,∠DCE =∠A CE =AB ∠DEC =∠B ,∴△CED≌△ABC(ASA).3.(2022·江苏省南通市)如图,AC 和BD 相交于点O ,OA =OC ,OB =OD .(1)求证:∠A =∠C ;(2)求证:AB//CD .【答案】证明:(1)在△AOB 和△COD 中,OA =OC ∠AOB =∠COD OB =OD ,∴△AOB≌△COD(SAS),∴∠A =∠C ;(2)由(1)得∠A =∠C ,∴AB//CD .4.(2022·上海市)如图所示,在等腰三角形ABC 中,AB =AC ,点E ,F 在线段BC 上,点Q 在线段AB 上,且CF =BE ,AE 2=AQ ⋅AB .求证:(1)∠CAE =∠BAF ;(2)CF ⋅FQ =AF ⋅BQ .【答案】证明:(1)∵AB=AC,∴∠B=∠C,∵CF=BE,∴CF−EF=BE−EF,即CE=BF,在△ACE和△ABF中,AC=AB∠C=∠BCE=BF,∴△ACE≌△ABF(SAS),∴∠CAE=∠BAF;(2)∵△ACE≌△ABF,∴AE=AF,∠CAE=∠BAF,∵AE2=AQ⋅AB,AC=AB,∴AE AQ=AC AF,∴△ACE∽AFQ,∴∠AEC=∠AQF,∴∠AEF=∠BQF,∵AE=AF,∴∠AEF=∠AFE,∴∠BQF=∠AFE,∵∠B=∠C,∴△CAF∽△BFQ,∴CF BQ=AF FQ,即CF⋅FQ=AF⋅BQ.5.(2022·贵州省铜仁市)如图,点C在BD上,AB⊥BD,ED⊥BD,AC⊥CE,AB=CD.求证:△ABC≌△CDE.【答案】证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠B=∠D=∠ACE=90°,∴∠DCE+∠DEC=90°,∠BCA+∠DCE=90°,∴∠BCA=∠DEC,在△ABC和△CDE中,∠BCA=∠DEC∠B=∠DAB=CD,∴△ABC≌△CDE(AAS).6.(2022·广东省云浮市)如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.【答案】证明:∵∠AOC=∠BOC,PD⊥OA,PE⊥OB,∴PD=PE,在Rt△OPD和Rt△OPE中,OP=OPPD=PE,∴Rt△OPD≌Rt△OPE(HL).7.(2022·四川省宜宾市)已知:如图,点A、D、C、F在同一直线上,AB//DE,∠B=∠E,BC=EF.求证:AD=CF.【答案】证明:∵AB//DE,∴∠A=∠EDF.在△ABC和△DEF中,∠A=∠EDF∠B=∠EBC=EF,∴△ABC≌△DEF(AAS).∴AC=DF,∴AC−DC=DF−DC,即:AD=CF.8.(2022·陕西省)如图,在△ABC中,点D在边BC上,CD=AB,DE//AB,∠DCE=∠A.求证:DE=BC.【答案】.证明:∵DE//AB,∴∠EDC=∠B,在△CDE和△ABC中,∠EDC=∠BCD=AB∠DCE=∠A,∴△CDE≌△ABC(ASA),∴DE=BC.9.(2022·湖南省衡阳市)如图,在△ABC中,AB=AC,D、E是BC边上的点,且BD=CE.求证:AD=AE.【答案】证明:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中,AB=AC∠B=∠CBD=CE,∴△ABD≌△ACE(SAS),∴AD=AE.10.(2022·四川省乐山市)如图,B是线段AC的中点,AD//BE,BD//CE.求证:△ABD≌△BCE.【答案】证明:∵点B为线段AC的中点,∴AB=BC,∵AD//BE,∴∠A =∠EBC ,∵BD//CE ,∴∠C =∠DBA ,在△ABD 与△BCE 中,∠A =∠EBC AB =BC ∠DBA =∠C ,∴△ABD≌△BCE.(ASA).11.(2021·湖南衡阳市·中考真题)如图,点A 、B 、D 、E 在同一条直线上,,//,//AB DE AC DFBC EF =.求证:ABC DEF △≌△.【答案】见解析【分析】根据//,//AC DF BC EF ,可以得到,A FDE ABC DEF ∠=∠∠=∠,然后根据题目中的条件,利用ASA 证明△ABC ≌△DEF 即可.【详解】证明:点A ,B ,C ,D ,E 在一条直线上∵//,//AC DF BC EF∴,A FDE ABC DEF∠=∠∠=∠在ABC 与DEF 中CAB FDE AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ABC DEF ASA △≌△【点睛】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,本题是一道较为简单的题目.12.(2021·四川乐山市·中考真题)如图,已知AB DC =,A D ∠=∠,AC 与DB 相交于点O ,求证:OBC OCB ∠=∠.【答案】证明见解析【分析】根据全等三角形的性质,通过证明ABO DCO △≌△,得OB OC =,结合等腰三角形的性质,即可得到答案.【详解】∵A D AOB DOC AB DC ∠=∠∠=∠=⎧⎪⎨⎪⎩,∴ABO DCO △≌△(AAS ),∴OB OC =,∴OBC OCB ∠=∠.【点睛】本题考查了全等三角形、等腰三角形的知识;解题的关键是熟练掌握全等三角形、等腰三角形的性质,从而完成求解.13.(2021·四川泸州市·中考真题)如图,点D 在AB 上,点E 在AC 上,AB=AC ,∠B=∠C ,求证:BD=CE【答案】证明见详解.【分析】根据“ASA”证明△ABE ≌△ACD ,然后根据全等三角形的对应边相等即可得到结论.【详解】证明:在△ABE 和△ACD 中,∵A A AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩,△ABE ≌△ACD (ASA),∴AE=AD ,∴BD=AB–AD=AC-AE=CE .【点睛】本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.14.(2021·云南中考真题)如图,在四边形ABCD 中,,,AD BC AC BD AC ==与BD 相交于点E .求证:DAC CBD ∠=∠.【答案】见解析【分析】直接利用SSS 证明△ACD ≌△BDC ,即可证明.【详解】解:在△ACD 和△BDC 中,AD BC AC BD CD DC =⎧⎪=⎨⎪=⎩,∴△ACD ≌△BDC (SSS ),∴∠DAC=∠CBD .【点睛】本题考查了全等三角形的判定和性质,解题的关键是根据题意灵活运用SSS 的方法.15.(2020•菏泽)如图,在△ABC 中,∠ACB =90°,点E 在AC 的延长线上,ED ⊥AB 于点D ,若BC =ED ,求证:CE =DB.【分析】由“AAS ”可证△ABC ≌△AED ,可得AE =AB ,AC =AD ,由线段的和差关系可得结论.【解答】证明:∵ED ⊥AB ,∴∠ADE =∠ACB =90°,∠A =∠A ,BC =DE ,∴△ABC ≌△AED (AAS ),∴AE =AB ,AC =AD ,∴CE =BD .16.(2020•南充)如图,点C 在线段BD 上,且AB ⊥BD ,DE ⊥BD ,AC ⊥CE ,BC =DE .求证:AB =CD .【分析】证明△ABC≌△CDE(ASA),可得出结论.【解答】证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠ACE=∠ABC=∠CDE=90°,∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,∴∠ACB=∠CED.在△ABC和△CDE中,∠ACB=∠CEDBC=DE∠ABC=∠CDE,∴△ABC≌△CDE(ASA),∴AB=CD.17.(2020•硚口区模拟)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE.【分析】要证BD=CE只要证明AD=AE即可,而证明△ABE≌△ACD,则可得AD=AE.【解答】证明:在△ABE与△ACD中∠A=∠AAB=AC∠B=∠C,∴△ABE≌△ACD.∴AD =AE .∴BD =CE .18.(2020•铜仁市)如图,∠B =∠E ,BF =EC ,AC ∥DF .求证:△ABC ≌△DEF .【分析】首先利用平行线的性质得出∠ACB =∠DFE ,进而利用全等三角形的判定定理ASA ,进而得出答案.【解答】证明:∵AC ∥DF ,∴∠ACB =∠DFE ,∵BF =CE ,∴BC =EF ,在△ABC 和△DEF 中,∠B =∠E BC =EF ∠ACB =∠DFE ,∴△ABC ≌△DEF (ASA ).19.(2020•无锡)如图,已知AB ∥CD ,AB =CD ,BE =CF .求证:(1)△ABF ≌△DCE ;(2)AF ∥DE .【分析】(1)先由平行线的性质得∠B =∠C ,从而利用SAS 判定△ABF ≌△DCE ;(2)根据全等三角形的性质得∠AFB =∠DEC ,由等角的补角相等可得∠AFE =∠DEF ,再由平行线的判定可得结论.【解答】证明:(1)∵AB ∥CD ,∴∠B =∠C ,∵BE =CF ,∴BE ﹣EF =CF ﹣EF ,即BF =CE ,在△ABF 和△DCE 中,∵AB =CD ∠B =∠C BF =CE ,∴△ABF ≌△DCE (SAS );(2)∵△ABF ≌△DCE ,∴∠AFB =∠DEC ,∴∠AFE =∠DEF ,∴AF ∥DE .20.(2020•台州)如图,已知AB =AC ,AD =AE ,BD 和CE 相交于点O .(1)求证:△ABD ≌△ACE ;(2)判断△BOC 的形状,并说明理由.【分析】(1)由“SAS ”可证△ABD ≌△ACE ;(2)由全等三角形的性质可得∠ABD =∠ACE ,由等腰三角形的性质可得∠ABC =∠ACB ,可求∠OBC=∠OCB,可得BO=CO,即可得结论.【解答】证明:(1)∵AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS);(2)△BOC是等腰三角形,理由如下:∵△ABD≌△ACE,∴∠ABD=∠ACE,∵AB=AC,∴∠ABC=∠ACB,∴∠ABC﹣∠ABD=∠ACB﹣∠ACE,∴∠OBC=∠OCB,∴BO=CO,∴△BOC是等腰三角形.21.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD;(2)若AB=CF,∠B=40°,求∠D的度数.【分析】(1)根据平行线的性质求出∠B=∠C,根据AAS推出△ABE≌△DCF,根据全等三角形的性质得出即可;(2)根据全等得出AB=CD,BE=CF,∠B=∠C,求出CF=CD,推出∠D=∠CFD,即可求出答案.【解答】(1)证明:∵AB∥CD,∴∠B=∠C,在△ABE和△DCF中,∠A=∠D∠B=∠CAE=DF,∴△ABE≌△DCF(AAS),∴AB=CD;(2)解:∵△ABE≌△DCF,∴AB=CD,BE=CF,∠B=∠C,∵∠B=40°,∴∠C=40°∵AB=CF,∴CF=CD,∴∠D=∠CFD=12×(180°﹣40°)=70°.类型二特殊四边形判定及性质22.(2022·广西壮族自治区河池市)如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.(1)求证:∠ACB=∠DFE;(2)连接BF,CE,直接判断四边形BFEC的形状.【答案】(1)证明:∵AF=CD,∴AF+CF=CD+CF,即AC=DF,在△ABC和△DEF中,AB=DEBC=EFAC=DF,∴△ABC≌△DEF(SSS),∴∠ACB=∠DFE;(2)解:如图,四边形BFEC是平行四边形,理由如下:由(1)可知,∠ACB=∠DFE,∴BC//EF,又∵BC=EF,∴四边形BFEC是平行四边形.23.(2022·青海省西宁市)如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F.(1)求证:△ABE≌△ADF;(2)若AE=4,CF=2,求菱形的边长.【答案】(1)证明:∵四边形ABCD 是菱形,∴AB =BC =CD =AD ,∠B =∠D ,∵AE ⊥BC ,AF ⊥CD ,∴∠AEB =∠AFD ,在△ABE 和△ADF 中,∠AEB =∠AFD ∠B =∠D AB =AD ,∴△ABE≌△ADF(AAS);(2)解:设菱形的边长为x ,∵AB =CD =x ,CF =2,∴DF =x −2,∵△ABE≌△ADF ,∴BE =DF =x −2,在Rt △ABE 中,根据勾股定理得,AE 2+BE 2=AB 2,即42+(x −2)2=x 2,解得x =5,∴菱形的边长是5.24.(2022·江苏省无锡市)如图,已知四边形ABCD为矩形,AB=22,BC=4,点E在BC 上,CE=AE,将△ABC沿AC翻折到△AFC,连接EF.(1)求EF的长;(2)求sin∠CEF的值.【答案】解:(1)∵CE=AE,∴∠ECA=∠EAC,根据翻折可得:∠ECA=∠FCA,∠BAC=∠CAF,∵四边形ABCD是矩形,∴DA//CB,∴∠ECA=∠CAD,∴∠EAC=∠CAD,∴∠DAF=∠BAE,∵∠BAD=90°,∴∠EAF=90°,设CE=AE=x,则BE=4−x,在△BAE中,根据勾股定理可得:BA2+BE2=AE2,即:(22)2+(4−x)2= x2,解得:x=3,在Rt△EAF中,EF=AF2+AE2=17.(2)过点F作FG⊥BC交BC于点G,设CG=x,则GB=3−x,∵FC=4,FE=17,∴FG2=FC2−CG2=FE2−EG2,即:16−x2=17−(3−x)2,解得:x=43,∴FG=FC2−CG2∴sin∠CEF=FG EF=25.(2022·湖北省荆门市)如图,已知矩形ABCD中,AB=8,BC=x(0<x<8),将△ACB 沿AC对折到△ACE的位置,AE和CD交于点F.(1)求证:△CEF≌△ADF;(2)求tan∠DAF的值(用含x的式子表示).【答案】(1)证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,BC=AD,根据折叠的性质得:BC=CE,∠E=∠B=90°,∴∠E=∠D=90°,AD=CE,在△CEF与△ADF中,∠ CFE=∠AFD∠D=∠E=90°AD=CE,∴△CEF≌△ADF(AAS);(2)解:设DF=a,则CF=8−a,∵四边形ABCD是矩形,∴AB//CD,AD=BC=x,∴∠DCA=∠BAC,根据折叠的性质得:∠EAC=∠BAC,∴∠DCA=∠EAC,∴AF=CF=8−a,在Rt△ADF中,∵AD2+DF2=AF2,∴x2+a2=(8−a)2,∴a=64−x216,∴tan∠DAF=DF AD=64−x216x.26.(2022·四川省遂宁市)如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF//AC交OE的延长线于点F,连接AF.(1)求证:△AOE≌△DFE;(2)判定四边形AODF的形状并说明理由.【答案】(1)证明:∵E是AD的中点,∴AE=DE,∵DF//AC,∴∠OAD=∠ADF,∵∠AEO=∠DEF,∴△AOE≌△DFE(ASA).(2)解:四边形AODF为矩形.理由:∵△AOE≌△DFE,∴AO=DF,∵DF//AC,∴四边形AODF为平行四边形,∵四边形ABCD为菱形,∴AC⊥BD,即∠AOD=90°,∴平行四边形AODF为矩形.27.(2022·湖北省)如图,已知E、F分别是▱ABCD的边BC,AD上的点,且BE=DF(1)求证:四边形AECF是平行四边形;(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD//BC,且AD=BC,∴AF//EC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形;(2)如图所示:∵四边形AECF是菱形,∴AE=EC,∴∠1=∠2,∵∠3=90°−∠2,∠4=90°−∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE=12BC=5.28.(2022·云南省)如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE 与CD的延长线交于点F,连接AF,∠BDF=90°.(1)求证:四边形ABDF是矩形;(2)若AD=5,DF=3,求四边形ABCF的面积S.【答案】.(1)证明:∵四边形ABCD是平行四边形,∴BA//CD,∴∠BAE=∠FDE,∵点E是AD的中点,∴AE=DE,在△BEA和△FED中,∠BAE=∠FDEAE=DE∠BEA=∠FED,∴△BEA≌△FED(ASA),∴EF=EB,又∵AE=DE,∴四边形ABDF是平行四边形,∵∠BDF=90°.∴四边形ABDF是矩形;(2)解:由(1)得四边形ABDF是矩形,∴∠AFD=90°,AB=DF=3,AF=BD,∴AF=AD2−DF2=52−32=4,∴S矩形ABDF=DF⋅AF=3×4=12,BD=AF=4,∵四边形ABCD是平行四边形,∴CD=AB=3,∴S△BCD=12BD⋅CD=12×4×3=6,∴四边形ABCF的面积S=S矩形ABDF+S△BCD=12+6=18,答:四边形ABCF的面积S为18.29.(2022·广西壮族自治区河池市)如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.(1)求证:∠ACB=∠DFE;(2)连接BF,CE,直接判断四边形BFEC的形状.【答案】(1)证明:∵AF=CD,∴AF+CF=CD+CF,即AC=DF,在△ABC和△DEF中,AB=DEBC=EFAC=DF,∴△ABC≌△DEF(SSS),∴∠ACB=∠DFE;(2)解:如图,四边形BFEC是平行四边形,理由如下:由(1)可知,∠ACB=∠DFE,∴BC//EF,又∵BC=EF,∴四边形BFEC是平行四边形.30.(2022·湖南省郴州市)如图,四边形ABCD是菱形,E,F是对角线AC上的两点,且AE=CF,连接BF,FD,DE,EB.求证:四边形DEBF是菱形.【答案】证明:∵四边形ABCD是菱形,∴AB=BC=CD=AD,∠DAB=∠DCB,AC平分∠DAB,AC平分∠DCB,∴∠DAC=∠BAC=12∠DAB,∠DCA=∠ACB=12∠DCB,∴∠DAC=∠BAC=∠DCA=∠ACB,∵AE=CF,∴△DAE≌△BAE≌△BCF≌△DCF(SAS),∴DE=BE=BF=DF,∴四边形DEBF是菱形.31.(2022·山东省聊城市)如图,△ABC中,点D是AB上一点,点E是AC的中点,过点C 作CF//AB,交DE的延长线于点F.(1)求证:AD=CF;(2)连接AF,CD.如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF 是菱形,证明你的结论.【答案】(1)证明:∵CF//AB,∴∠ADF=∠CFD,∠DAC=∠FCA,∵点E是AC的中点,∴AE=CE,∴△ADE≌△CFE(AAS),∴AD=CF;(2)解:当AC⊥BC时,四边形ADCF是菱形,证明如下:由(1)知,AD=CF,∵AD//CF,∴四边形ADCF是平行四边形,∵AC⊥BC,∴△ABC是直角三角形,∵点D是AB的中点,∴CD=12AB=AD,∴四边形ADCF是菱形.32.(2022·北京市)如图,在▱ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.【答案】证明:(1)在▱ABCD中,OA=OC,OB=OD,∵AE=CF.∴OE=OF,∴四边形EBFD是平行四边形;(2)∵四边形ABCD是平行四边形,∴AB//DC,∴∠BAC=∠DCA,∵∠BAC=∠DAC,∴∠DCA=∠DAC,∴DA=DC,∵OA=OC,∴DB⊥EF,∴平行四边形EBFD是菱形.33.(2022·湖南省张家界市)如图,菱形ABCD的对角线AC、BD相交于点O,点E是CD的中点,连接OE,过点C作CF//BD交OE的延长线于点F,连接DF.(1)求证:△ODE≌△FCE;(2)试判断四边形ODFC的形状,并写出证明过程.【答案】.(1)证明:∵点E是CD的中点,∴CE=DE,又∵CF//BD∴∠ODE=∠FCE,在△ODE和△FCE中,∠ODE=∠FCEDE=CE∠DEO=∠CEF,∴△ODE≌△FCE(ASA);(2)解:四边形ODFC为矩形,证明如下:∵△ODE≌△FCE,∴OE=FE,又∵CE=DE,∴四边形ODFC为平行四边形,又∵四边形ABCD为菱形,∴AC⊥BD,即∠DOC=90°,∴四边形ODFC为矩形.34.(2022·四川省内江市)如图,在▱ABCD中,点E、F在对角线BD上,且BE=DF.求证:(1)△ABE≌△CDF;(2)四边形AECF是平行四边形.【答案】证明:(1)∵四边形ABCD为平行四边形,∴AB=CD,AB//CD,∴∠ABD=∠CDB,在△ABE和△CDF中,AB=CD∠ABE=∠CDFBE=DF,∴△ABE≌△CDF(SAS);(2)由(1)可知,△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∴180°−∠AEB=180°−∠CFD,即∠AEF=∠CFE,∴AE//CF,∵AE=CF,AE//CF,∴四边形AECF是平行四边形.35.(2022·湖南省长沙市)如图,在▱ABCD中,对角线AC,BD相交于点O,AB=AD.(1)求证:AC⊥BD;(2)若点E,F分别为AD,AO的中点,连接EF,EF=32,AO=2,求BD的长及四边形ABCD 的周长.【答案】(1)证明:∵四边形ABCD是平行四边形,AB=AD,∴▱ABCD是菱形,∴AC⊥BD;(2)解:∵点E,F分别为AD,AO的中点,∴EF是△AOD的中位线,∴OD=2EF=3,由(1)可知,四边形ABCD是菱形,∴AB=BC=CD=AD,AC⊥BD,BD=2OD=6,在Rt△AOD中,由勾股定理得:AD=AO2+OD2=22+32=13,∴菱形ABCD的周长=4AD=41336.(2021·四川广安市·中考真题)如图,四边形ABCD是菱形,点E、F分别在边AB、AD=.连接CE、CF.的延长线上,且BE DF求证:CE CF=.【答案】见解析【分析】根据菱形的性质得到BC=CD,∠ADC=∠ABC,根据SAS证明△BEC≌△DFC,可得CE=CF.【详解】解:∵四边形ABCD 是菱形,∴BC=CD ,∠ADC=∠ABC ,∴∠CDF=∠CBE ,在△BEC 和△DFC 中,BE DF CBE CDF BC CD =⎧⎪∠=∠⎨⎪=⎩,∴△BEC ≌△DFC (SAS ),∴CE=CF .【点睛】本题考查了菱形的性质,全等三角形的判定和性质,解题的关键是根据菱形得到判定全等的条件.37.(2021·江苏扬州市·中考真题)如图,在ABC 中,BAC ∠的角平分线交BC 于点D ,//,//DE AB DF AC.(1)试判断四边形AFDE 的形状,并说明理由;(2)若90BAC ∠=︒,且AD =,求四边形AFDE 的面积.【答案】(1)菱形,理由见解析;(2)4【分析】(1)根据DE ∥AB ,DF ∥AC 判定四边形AFDE 是平行四边形,再根据平行线的性质和角平分线的定义得到∠EDA=∠EAD ,可得AE=DE ,即可证明;(2)根据∠BAC=90°得到菱形AFDE是正方形,根据对角线AD求出边长,再根据面积公式计算即可.【详解】解:(1)四边形AFDE是菱形,理由是:∵DE∥AB,DF∥AC,∴四边形AFDE是平行四边形,∵AD平分∠BAC,∴∠FAD=∠EAD,∵DE∥AB,∴∠EDA=∠FAD,∴∠EDA=∠EAD,∴AE=DE,∴平行四边形AFDE是菱形;(2)∵∠BAC=90°,∴四边形AFDE是正方形,∵AD=,=2,∴∴四边形AFDE的面积为2×2=4.【点睛】本题考查了菱形的判定,正方形的判定和性质,平行线的性质,角平分线的定义,解题的关键是掌握特殊四边形的判定方法.38.(2021·江苏连云港市·中考真题)如图,点C是BE的中点,四边形ABCD是平行四边形.(1)求证:四边形ACED是平行四边形;,求证:四边形ACED是矩形.(2)如果AB AE【答案】(1)见解析;(2)见解析【分析】(1)由平行四边形的性质以及点C是BE的中点,得到AD∥CE,AD=CE,从而证明四边形ACED是平行四边形;(2)由平行四边形的性质证得DC=AE,从而证明平行四边形ACED是矩形.【详解】证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC.∵点C是BE的中点,∴BC=CE,∴AD=CE,∵AD∥CE,∴四边形ACED是平行四边形;(2)∵四边形ABCD是平行四边形,∴AB=DC,∵AB=AE,∴DC=AE,∵四边形ACED是平行四边形,∴四边形ACED是矩形.【点睛】本题考查了平行四边形和矩形的判定和性质,正确的识别图形是解题的关键.39.(2021·四川遂宁市·中考真题)如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,过点O 的直线EF 与BA 、DC 的延长线分别交于点E 、F .(1)求证:AE =CF ;(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.【答案】(1)见解析;(2)EF ⊥BD 或EB =ED ,见解析【分析】(1)根据平行四边形的性质和全等三角形的证明方法证明AOE COF V V ≌,则可得到AE =CF ;(2)连接BF ,DE ,由AOE COF V V ≌,得到OE=OF ,又AO=CO ,所以四边形AECF 是平行四边形,则根据EF ⊥BD 可得四边形BFDE 是菱形.【详解】证明:(1)∵四边形ABCD 是平行四边形∴OA =OC ,BE ∥DF∴∠E =∠F在△AOE 和△COF 中E F AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴AOE COF V V ≌()AAS ∴AE =CF(2)当EF ⊥BD 时,四边形BFDE 是菱形,理由如下:如图:连结BF ,DE∵四边形ABCD 是平行四边形∴OB =OD∵AOE COFV V ≌∴OE OF=∴四边形BFDE 是平行四边形∵EF ⊥BD ,∴四边形BFDE 是菱形【点睛】本题主要考查了全等三角形的性质与判定、平行四边形的性质,菱形的判定等知识点,熟悉相关性质,能全等三角形的性质解决问题是解题的关键.40(2020•黄冈)已知:如图,在▱ABCD 中,点O 是CD 的中点,连接AO 并延长,交BC 的延长线于点E ,求证:AD =CE .【分析】只要证明△AOD≌△EOC(ASA)即可解决问题;【解答】证明:∵O是CD的中点,∴OD=CO,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠OCE,在△ADO和△ECO中,∠D=∠OCEOD=OC∠AOD=∠EOC,∴△AOD≌△EOC(ASA),∴AD=CE.41.(2020•扬州)如图,▱ABCD的对角线AC、BD相交于点O,过点O作EF⊥AC,分别交AB、DC于点E、F,连接AF、CE.(1)若OE=32,求EF的长;(2)判断四边形AECF的形状,并说明理由.【分析】(1)判定△AOE≌△COF(ASA),即可得OE=OF=32,进而得出EF的长;(2)先判定四边形AECF是平行四边形,再根据EF⊥AC,即可得到四边形AECF是菱形.【解析】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AO=CO,∴∠FCO=∠EAO,又∵∠AOE=∠COF,∴△AOE≌△COF(ASA),∴OE=OF=32,∴EF=2OE=3;(2)四边形AECF是菱形,理由:∵△AOE≌△COF,∴AE=CF,又∵AE∥CF,∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形.42.(2020•青岛)如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.(1)求证:△ADE≌△CBF;(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.【分析】(1)根据四边形ABCD是平行四边形,可以得到AD=CB,∠ADC=∠CBA,从而可以得到∠ADE=∠CBF,然后根据SAS即可证明结论成立;(2)根据BD平分∠ABC和平行四边形的性质,可以证明▱ABCD是菱形,从而可以得到AC ⊥BD,然后即可得到AC⊥EF,再根据题目中的条件,可以证明四边形AFCE是平行四边形,然后根据AC⊥EF,即可得到四边形AFCE是菱形.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=CB,∠ADC=∠CBA,∴∠ADE=∠CBF,在△ADE和△CBF中,AD=CB∠ADE=∠CBFDE=BF,∴△ADE≌△CBF(SAS);(2)当BD平分∠ABC时,四边形AFCE是菱形,理由:∵BD平分∠ABC,∴∠ABD=∠CBD,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AD∥BC,∴∠ADB=∠CBD,∴∠ABD=∠ADB,∴AB=AD,∴平行四边形ABCD是菱形,∴AC⊥BD,∴AC⊥EF,∵DE=BF,∴OE=OF,又∵OA=OC,∴四边形AFCE是平行四边形,∵AC⊥EF,∴四边形AFCE是菱形.43.(2020•新疆)如图,四边形ABCD是平行四边形,DE∥BF,且分别交对角线AC于点E,F,连接BE,DF.(1)求证:AE=CF;(2)若BE=DE,求证:四边形EBFD为菱形.【分析】(1)根据平行四边形的性质,可以得到AD=CB,AD∥CB,从而可以得到∠DAE=∠BCF,再根据DE∥BF和等角的补角相等,从而可以得到∠AED=∠CFB,然后即可证明△ADE和△CBF全等,从而可以得到AE=CF;(2)根据(1)中的△ADE和△CBF全等,可以得到DE=BF,再根据DE∥BF,即可得到四边形EBFD是平行四边形,再根据BE=DE,即可得到四边形EBFD为菱形.【解答】(1)证明:∵四边形ABCD 是平行四边形,∴AD =CB ,AD ∥CB ,∴∠DAE =∠BCF ,∵DE ∥BF ,∴∠DEF =∠BFE ,∴∠AED =∠CFB ,在△ADE 和△CBF 中,∠DAE =∠BCF ∠AED =∠CFB AD =CB ,∴△ADE ≌△CBF (AAS ),∴AE =CF ;(2)证明:由(1)知△ADE ≌△CBF ,则DE =BF ,又∵DE ∥BF ,∴四边形EBFD 是平行四边形,∵BE =DE ,∴四边形EBFD 为菱形.类型三与相似有关的证明44.(2021·广东中考真题)如图,边长为1的正方形ABCD 中,点E 为AD 的中点.连接BE ,将ABE △沿BE 折叠得到,FBE BF 交AC 于点G ,求CG 的长.【答案】CG =【分析】根据题意,延长BF 交CD 于H 连EH ,通过证明()Rt EDH Rt EFH HL ≌、DHE AEB ∽得到34CH =,再由HGC BGA ∽得到()34CG AC CG =-,进而即可求得CG 的长.【详解】解:延长BF 交CD 于H 连EH ,∵FBE 由ABE △沿BE 折叠得到,∴EA EF =,90EFB EAB ∠=∠=︒,∵E 为AD 中点,正方形ABCD 边长为1,∴12EA ED ==,∴12ED EF ==,∵四边形ABCD 是正方形,∴90D EFB EFH ∠=∠=∠=︒,在Rt EDH △和Rt EFH 中,ED EF EH EH=⎧⎨=⎩,∴()Rt EDH Rt EFH HL ≌,又∵AEB FEB ∠=∠,∴90DEH AEB ∠+∠=︒,∵90ABE AEB ∠+∠=︒,∴ABE DEH ∠=∠,∴DHE AEB ∽,∴12DH AE DE AB ==,∴14DH =,∴13144CH CD DH =-=-=,∵CH AB ∥,∴HGC BGA ∽,∴34CG CH AG AB ==,∴()3344CG AG AC CG ==-,∵1AB =,1CB =,90CBA ∠=︒,∴AC =,∴)34CG CG =,∴CG =.【点睛】本题主要考查了三角形全等的判定及性质、三角形相似的判定及性质以及正方形的性质,熟练掌握相关几何知识是解决本题的关键.45.(2021·湖北鄂州市·中考真题)如图,在ABCD 中,点E 、F 分别在边AD 、BC 上,(1)探究四边形BEDF的形状,并说明理由;(2)连接AC,分别交BE、DF于点G、H,连接BD交AC于点O.若23AGOG=,4AE=,求BC的长.【答案】(1)平行四边形,见解析;(2)16【分析】(1)利用平行四边形的判定定理,两组对边分别平行是平行四边形即可证明;(2)根据23AGOG=,找到边与边的等量关系,再利用三角形相似,建立等式进行求解即可.【详解】(1)四边形BEDF为平行四边形.理由如下:∵四边形ABCD为平行四边形∴ABC ADC∠=∠∵ABE CDF∠=∠∴EBF EDF∠=∠∵四边形ABCD为平行四边形∴//AD BC∴EDF DFC EBF∠=∠=∠∴//BE DF∵//AD BC∴四边形BEDF 为平行四边形(2)设2AG a =,∵23AG OG =∴3OG a =,5AO a=∵四边形ABCD 为平行四边形∴5AO CO a ==,10AC a =,8CG a=∵//AD BC,,AGE CGB AEG CBG EAG BCG ∠=∠∠=∠∠=∠,∴AGE CGB∆∆∽∴14AE AG BC GC ==∵4AE =∴16BC =.【点睛】本题考查了平行四边形的判定定理、相似三角形的判定定理,解题的关键是:熟练掌握相关定理,能进行相关的证明.46.(2021·北京中考真题)如图,在ABC 中,,,AB AC BAC M α=∠=为BC 的中点,点D 在MC 上,以点A 为中心,将线段AD 顺时针旋转α得到线段AE ,连接,BE DE .(1)比较BAE ∠与CAD ∠的大小;用等式表示线段,,BE BM MD 之间的数量关系,并证明;(2)过点M 作AB 的垂线,交DE 于点N ,用等式表示线段NE 与ND 的数量关系,并证明.【答案】(1)BAE CAD ∠=∠,BM BE MD =+,理由见详解;(2)DN EN =,理由见详解.【分析】(1)由题意及旋转的性质易得BAC EAD α∠=∠=,AE AD =,然后可证ABE ACD △≌△,进而问题可求解;(2)过点E 作EH ⊥AB ,垂足为点Q ,交AB 于点H ,由(1)可得ABE ACD ∠=∠,BE CD =,易证BH BE CD ==,进而可得HM DM =,然后可得DMN DHE ∽,最后根据相似三角形的性质可求证.【详解】(1)证明:∵BAC EAD α∠=∠=,∴BAE BAD BAD CAD α∠+∠=∠+∠=,∴BAE CAD ∠=∠,由旋转的性质可得AE AD =,∵AB AC =,∴()ABE ACD SAS ≌,∴BE CD =,∵点M 为BC 的中点,∴BM CM =,∵CM MD CD MD BE =+=+,∴BM BE MD =+;(2)证明:DN EN =,理由如下:过点E 作EH ⊥AB ,垂足为点Q ,交AB 于点H ,如图所示:∴90EQB HQB ∠=∠=︒,由(1)可得ABE ACD △≌△,∴ABE ACD ∠=∠,BE CD =,∵AB AC =,∴ABC C ABE ∠=∠=∠,∵BQ BQ =,∴()BQE BQH ASA ≌,∴BH BE CD ==,∵MB MC =,∴HM DM =,∵MN AB ⊥,∴//MN EH ,∴DMN DHE ∽,∴12DM DN DH DE ==,∴DN EN =.【点睛】本题主要考查全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的性质,熟练掌握全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的性质是解题的关键.47.(2020•长沙)在矩形ABCD 中,E 为DC 边上一点,把△ADE 沿AE 翻折,使点D 恰好落在BC边上的点F.(1)求证:△ABF∽△FCE;(2)若AB=23,AD=4,求EC的长;(3)若AE﹣DE=2EC,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.【分析】(1)根据两角对应相等的两个三角形相似证明即可.(2)设EC=x,证明△ABF∽△FCE,可得AB CF=BF EC,由此即可解决问题.(3)首先证明tanα+tanβ=BF AB+EF AF=BF AB+CF AB=BF+CF AB=BC AB,设AB=CD=a,BC=AD=b,DE=x,解直角三角形求出a,b之间的关系即可解决问题.【解答】(1)证明:∵四边形ABCD是矩形,∴∠B=∠C=∠D=90°,由翻折可知,∠D=∠AFE=90°,∴∠AFB+∠EFC=90°,∠EFC+∠CEF=90°,∴∠AFB=∠FEC,∴△ABF∽△FCE.(2)设EC=x,由翻折可知,AD=AF=4,∴BF=AF2−AB2=16−12=2,∴CF=BC﹣BF=2,∵△ABF∽△FCE,∴AB CF=BF EC,∴2322,∴x=∴EC=(3)∵△ABF∽△FCE,∴AF EF=AB CF,∴tanα+tanβ=BF AB+EF AF=BF AB+CF AB=BF+CF AB=BC AB,设AB=CD=a,BC=AD=b,DE=x,∴AE=DE+2CE=x+2(a﹣x)=2a﹣x,∵AD=AF=b,DE=EF=x,∠B=∠C=∠D=90°,∴BF=b2−a2,CF=x2−(a−x)2=2ax−a2,∵AD2+DE2=AE2,∴b2+x2=(2a﹣x)2,∴a2﹣ax=14b2,∵△ABF∽△FCE,∴AB CF=BF EC,−(a−x)=b2−a2a−x,∴a2﹣ax=b2−a2•2ax−a2,∴14b2=b2−a2•整理得,16a4﹣24a2b2+9b4=0,∴(4a2﹣3b2)2=0,∴b a=233,∴tanα+tanβ=BC AB=48.(2020•怀化)如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD =CA,且∠D=30°.(1)求证:CD是⊙O的切线.(2)分别过A、B两点作直线CD的垂线,垂足分别为E、F两点,过C点作AB的垂线,垂足为点G.求证:CG2=AE•BF.【分析】(1)连接OC,∠CAD=∠D=30°,由OC=OA,进而得到∠OCA=∠CAD=30°,由三角形外角定理得到∠COD=∠A+∠OCA=60°,在△OCD中由内角和定理可知∠OCD=90°即可证明;(2)证明AC是∠EAG的角平分线,CB是∠FCG的角平分线,得到CE=CG,CF=CG,再证明△AEC∽△CFB,对应线段成比例即可求解.【解答】(1)证明:连接OC,如右图所示,∵CA=CD,且∠D=30°,∴∠CAD=∠D=30°,∵OA=OC,∴∠CAD=∠ACO=30°,∴∠COD=∠CAD+∠ACO=30°+30°=60°,∴∠OCD=180°﹣∠D﹣∠COD=180°﹣30°﹣60°=90°,∴OC⊥CD,∴CD是⊙O的切线;(2)∵∠COB=60°,且OC=OB,∴△OCB为等边三角形,∴∠CBG=60°,又∵CG⊥AD,∴∠CGB=90°,∴∠GCB=∠CGB﹣∠CBG=30°,又∵∠GCD=60°,∴CB是∠GCD的角平分线,∵BF⊥CD,BG⊥CG,∴BF=BG,又∵BC=BC,∴Rt△BCG≌Rt△BCF(HL),∴CF=CG.∵∠D=30°,AE⊥ED,∠E=90°,∴∠EAD=60°,又∵∠CAD=30°,∴AC是∠EAG的角平分线,∵CE⊥AE,CG⊥AB,∴CE=CG,∵∠E=∠BFC=90°,∠EAC=30°=∠BCF,∴△AEC∽△CFB,。
中考数学证明题

中考数学证明题第一篇:中考数学证明题中考数学证明题o是已知线段ab上的一点,以ob为半径的圆o交ab于点c,以线段ao为直径的半圆圆o于点d,过点b作ab的垂线与ad的延长线交于点e(1)说明ae切圆o于点d(2)当点o位于线段ab何处时,△odc恰好是等边三角形〉说明理由答案:一题:显然三角形doe是等边三角形:理由:首先能确定o为圆心然后在三角形obd中:bo=od,再因角b为60度,所以三角形obd为等边三角形;同理证明三角形oce为等边三角形从而得到:角bod=角eoc=60度,推出角doe=60度再因为od=oe,三角形doe为等腰三角形,结合上面角doe=60度,得出结论:三角形doe为等边三角形第三题没作思考,有事了,改天再解二题:要证明三角形ode为等边三角形,其实还是要证明角doe=60度,因为我们知道三角形ode是等腰三角形。
此时,不妨设角abc=x度,角acb=y度,不难发现,x+y=120度。
此时我们要明确三个等腰三角形:ode;bod;oce此时在我们在三角形bod中,由于角obd=角odb=x度从而得出角bod=180-2x同理在三角形oce中得出角eoc=180-2y则角bod+角eoc=180-2x+180-2y,整理得:360-2(x+y)把x+y=120代入,得120度。
由于角eoc+角bod=120度,所以角doe就为60度。
外加三角形doe本身为等腰三角形,所以三角形doe为等边三角形!图片发不上来,看参考资料里的1如图,ab⊥bc于b,ef⊥ac于g,df⊥ac于d,bc=df。
求证:ac=ef。
2已知ac平分角bad,ce垂直ab于e,cf垂直ad于f,且bc=cd(1)求证:△bce全等△dcf3.如图所示,过三角形abc的顶点a分别作两底角角b和角c的平分线的垂线,ad垂直于bd于d,ae垂直于ce于e,求证:ed||bc.4.已知,如图,pb、pc分别是△abc的外角平分线,且相交于点p。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、证明题
1. 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
(1)求证:四边形BFDE为平行四边形;
AB ,求BC的长.
(2)若四边形BFDE为菱形,且2
2. 如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM AD,PN CD,垂足分别为M、N.
(1) 求证:ADB=CDB;
(2) 若ADC=90,求证:四边形MPND是正方形.
∠交AB于点E,BF平分3. 如图,四边形ABCD是平行四边形,DE平分ADC
∠交CD于点F.
ABC
=;
(1)求证:DE BF
(2)连接EF,写出图中所有的全等三角形.(不要求证明)
4. 如图,在平行四边形ABCD 中,E 为BC 边上的一点.连结AE 、BD ,且AE=AB . (1)求证:ABE EAD ∠=∠;
(2)若2AEB ADB ∠=∠,求证:四边形ABCD 是菱形.
5. 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
6.四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
7.已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.
8. 如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= °时,四边形BECD是矩形.
9. 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
10. 如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE;
(2)连接DE,求证:四边形CBED是平行四边形.
11. 如图,AB 与
O 相切于点B ,C B 为O 的弦,C O ⊥OA ,OA 与C B 相交于点P ;
(1)求证:AP =AB ;
(2)若4OB =,3AB =,求线段BP 的长.
12.如图,正方形ABCD 中,G 为BC 边上一点,BE AG 于E ,DF AG 于F ,连接DE .
(1)求证:ABE DAF △≌△; (2)若1AF
,四边形ABED 的面积为
6,求EF 的长.
13.如图,∠A=∠B,AE=BE,点D在C
A边上,12
B相交于点O.
∠=∠,AE和D
(1)求证:C
∆AE≌D
∆BE;
(2)若142
∠=,求D
∠B E的度数.
14. 如图,在四边形ABCD中,BD为一条对角线,0
=∠=,
//,2,90
AD BC AD BC ABD
E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分,1
∠=,求AC的长.
BAD BC
15、如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处。
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积。
16、如图,在ABC ∆中, 90=∠ABC , 60=∠BAC 。
ACD ∆是等边三角形,E 是AC 的中点。
连接BE 并延长,交DC 与点F ,求证: ⑴ABE ∆≌CFE ∆
⑵四边形ABFD 是平行四边形。
17、如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF
A
E D
B C
18.如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
(1)求证:AD∥BC;
(2)过点C作CG⊥AD于点F,交AE于点G,若AF=4,求BC的长.
19.(本小题满分8分)已知,如图,在菱形ABCD中,点E、F分别为边AC、AD 的中点,连接AE、CF,求证:ΔADE≌ΔCDF
20.(本小题6分)如图,点D是AB上一点,DF交AC于E,DE=FE,FC∥AB.求证:AE=CE.
B
C F
E A
21.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
22.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.。
