中考复习 第二十七章 相似(含答案)
九年级数学第二十七章相似综合复习测试习题(含答案) (171)

九年级数学第二十七章相似综合复习测试习题(含答案) 若△ABC △△DMN ,3BC MN=,AC =6,则DN =____. 【答案】2【分析】根据三角形的相似,得BC MN =AC DN =3,代入求值即可解题. 【详解】解:∵∵ABC ∵∵DMN ,BC 3MN =, ∵BC MN =AC DN =3, ∵AC=6,∵DN=2.【点睛】本题考查了三角形相似的性质,属于简单题,熟悉三角形相似的性质是解题关键.72.如图所示,在Rt ABC ∆中,90BAC ∠=︒,点G 是重心,联结AG ,过点G 作DG BC ,DG 交AB 于点D ,若6AB =,9BC =,则ADG ∆的周长等于______.【答案】10【分析】延长AG 交BC 于点H, 由G 是重心,推出:2:3AG GH = ,再由//DG BC 得出23AD DG AG AB BH AH ===,从而可求AD,DG,AG 的长度,进而答案可得. 【详解】延长AG 交BC 于点H∵G 是重心,∵:2:3AG GH =∵//DG BC ∵23AD DG AG AB BH AH === ∵90BAC ∠=︒,AH 是斜边中线, 9BC = ∵119 4.522AH BH BC ===⨯= ∵26 4.5 4.53AD DG AG === ∵4,3,3AD DG AG ===∵ADG ∆的周长等于43310++=故答案为:10【点睛】本题主要考查三角形重心的性质及平行线分线段成比例,掌握三角形重心的性质是解题的关键.73.如图,在△ABC 中,M 是AC 边中点,E 是AB 上一点,且AE =14AB ,连接EM 并延长,交BC 的延长线于D ,此时BC △CD 为__________.【答案】2∵1【解析】【分析】过C点作CP∵AB,交DE于P,由PC∵AE知PC CMAE AM=,由AM=CM,得PC=AE,根据AE=14AB得CP=14AB,CP=13BE,由CP∵BE得13CP CDBE BD==,可得BD=3CD,继而得到答案.【详解】过C点作CP∵AB,交DE于P,如图,∵PC∵AE,∵PC CM AE AM=,而AM=CM,∵PC=AE,∵AE=14 AB,∵CP=14 AB,∵CP=13 BE,∵CP∵BE,∵13 CP CDBE BD==,∵BD=3CD,∵BC=2CD,即BC:CD为2:1,故答案为:2:1.【点睛】本题考查平行线分线段成比例.三、解答题74.如图,E为□ABCD的边CD延长线上的一点,连结BE交AC于点O,交AD于点F,求证:BO EOFO BO=.【答案】见解析【解析】【分析】由AB∵CD得∵AOB∵∵COE,有OE:OB=OC:OA;由AD∵BC得∵AOF∵∵COB,有OB:OF=OC:OA,进而解答.【详解】∵AB∵CD,∵∵AOB∵∵COE.∵OE:OB=OC:OA;∵AD∵BC,∵∵AOF∵∵COB.∵OB:OF=OC:OA.∵OB:OF=OE:OB,即:BO EOFO BO【点睛】本题考查了平行四边形的性质与相似三角形的判定与性质,解题的关键是熟练的掌握行四边形的性质与相似三角形的判定与性质.75.如图,l1△l2△l3,AB=3,AD=2,DE=4,EF=7.5.求BC、BE的长?【答案】BC=6,BE=5【分析】根据平行线分线段成比例定理得BFBE =3BC=24,则可计算出BC=6,BF=12BE,然后利用12BE+BE=7.5求出BE的长.【详解】∵l1∵l2∵l3,∵FBBE=ABBC=ADDE,即BFBE=3BC=24,∵BC=6,BF=12BE,∵12BE+BE=7.5,∵BE=5.【点睛】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.。
九年级数学第二十七章相似综合复习测试习题(含答案) (150)
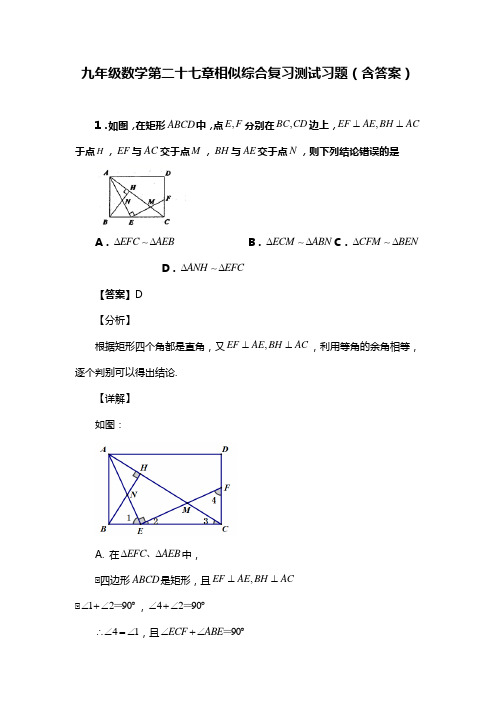
九年级数学第二十七章相似综合复习测试习题(含答案)1.如图,在矩形ABCD 中,点,E F 分别在,BC CD 边上,,EF AE BH AC ⊥⊥于点H ,EF 与AC 交于点M ,BH 与AE 交于点N ,则下列结论错误的是A .EFCAEB ∆∆ B .ECM ABN ∆∆ C .CFM BEN ∆∆D .ANH EFC ∆∆【答案】D【分析】 根据矩形四个角都是直角,又,EF AE BH AC ⊥⊥,利用等角的余角相等,逐个判别可以得出结论.【详解】如图:A. 在EFC AEB ∆∆、中,∵四边形ABCD 是矩形,且,EF AE BH AC ⊥⊥∵1290∠+∠︒=,4290∠+∠︒=41∴∠=∠,且90ECF ABE ∠+∠︒=EFC AEB ∆∆,A 正确;B. 在ECM ABN ∆∆、中,∵四边形ABCD 是矩形,且,EF AE BH AC ⊥⊥∵1290∠+∠︒=,190BAN ∠+∠=︒,则2BAN ∠=∠∵390BAH ∠+∠︒=,90ABH ABH ∠+∠=︒,则3ABN ∠=∠ECM ABN ∆∆,B 正确;C. 在CFM BEN ∆∆、中由前面知:3ABN ∠=∠,又390MCF ∠+∠︒=,90ABN NBE ∠+∠=︒, 则MCF NBE ∠=∠,又∵14∠∠=, CFM BEN ∆∆,C 正确;D.在ANH EFC ∆∆、中已经知道:2BAN ∠=∠,而AE 并不是BAC ∠的角平分线,∵2NAH ∠≠∠,ANH EFC ∆∆,错误.故选:D .【点睛】本题考查了矩形的性质,同角或等角的余角相等,相似三角形的证明,熟练掌握相似三角形的证明方法是解题的关键.2.如图,正方形ABCD 中,M 为BC 上一点,ME AM ⊥,ME 交AD 的延长线于点E .若12AB =,5BM =,则DE 的长为( )A .18B .253C .965D .1095【答案】D【解析】【分析】 先根据题意得出∵ABM ∵∵MCG ,故可得出CG 的长,再求出DG 的长,根据∵MCG ∵∵EDG 即可得出结论.【详解】四边形ABCD 是正方形,AB=12,BM=5,1257MC ∴=-=.ME AM ⊥,90AME ∴∠=︒,90AMB CMG ∴∠+∠=︒,90AMB BAM ∠+∠=︒,BAM CMG ∴∠=∠,90B C ∠=∠=︒,ABMMCG ∴∆∆, AB BM MC CG ∴=,即1257CG=, 解得3512CG =,35109121212DG ∴=-=, AE BC ∥,,E CMG EDG C ∴∠=∠∠=∠,MCG EDG ∴∆∆,MC CG DE DG ∴=,即3571210912DE =, 解得1095DE =. 故选D.【点睛】 本题主要考查相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.3.如图,点F 是ABCD 的边AD 上的三等分点,BF 交AC 于点E ,如果△AEF 的面积为2,那么四边形CDFE 的面积等于( )A .18B .22C .24D .46【答案】B【分析】 连接FC ,先证明∵AEF ∵∵BEC ,得出AE ∵EC=1∵3,所以S ∵EFC =3S ∵AEF ,在根据点F 是□ABCD 的边AD 上的三等分点得出S ∵FCD =2S ∵AFC ,四边形CDFE 的面积=S ∵FCD + S ∵EFC ,再代入∵AEF 的面积为2即可求出四边形CDFE 的面积.【详解】解:∵AD∵BC,∵∵EAF=∵ACB,∵AFE=∵FBC;∵∵AEF=∵BEC,∵∵AEF∵∵BEC,∵AFBC=AEEC=13,∵∵AEF与∵EFC高相等,∵S∵EFC=3S∵AEF,∵点F是□ABCD的边AD上的三等分点,∵S∵FCD=2S∵AFC,∵∵AEF的面积为2,∵四边形CDFE的面积=S∵FCD+ S∵EFC=16+6=22.故选B.【点睛】本题考查了相似三角形的应用与三角形的面积,解题的关键是熟练的掌握相似三角形的应用与三角形的面积的相关知识点.4.如图所示的四边形,与选项中的一个四边形相似,这个四边形是()A.B.C.D.【答案】D【分析】根据勾股定理求出四边形第四条边的长度,进而求出四边形四条边之比,根据相似多边形的性质判断即可.【详解】解:作AE∵BC于E,则四边形AECD为矩形,∵EC=AD=1,AE=CD=3,∵BE=4,=5,由勾股定理得,ABD选项中,四条边之比为1:3:5:5,且对应角相等,故选D.【点睛】本题考查的是相似多边形的判定和性质,掌握相似多边形的对应边的比相等是解题的关键.5.如果把Rt△ABC的各边长都扩大到原来的n倍,那么锐角A的四个三角比值( )A.都缩小到原来的n倍B.都扩大到原来的n倍;C.都没有变化D.不同三角比的变化不一致.【答案】C【分析】根据题意易得边长扩大后的三角形与原三角形相似,那么对应角相等,相应的三角比值不变.【详解】∵各边都扩大n倍,∵新三角形与原三角形的对应边的比为n:1,∵两三角形相似,∵∵A的三角比值不变,故答案为C.【点睛】本题考查锐角三角函数的定义,用到的知识点有:三边对应成比例,两三角形相似;相似三角形的对应角相等.三角函数值只与角的大小有关,与角的边的长短无关.。
九年级数学第二十七章相似综合复习测试习题(含答案) (209)

九年级数学第二十七章相似综合复习测试习题(含答案) 如图,在ABC 中,5cm AB AC ==,6cm BC ,点P 从点A 出发,沿AB 边以1cm/s 的速度向点B 匀速运动;点Q 从点B 出发,沿BC 边以2cm /s 的速度向点C 匀速运动,如果P 、Q 同时出发,当Q 点到达C 点时,P 点随之停止运动.当PBQ △中有一个内角等于12BAC ∠时,求运动时间()t s 的值.【答案】1513s 或2511s 【分析】作AD ⊥BC 交BC 于点D ,由等腰三角形的性质可得出AD 、CD 的长度,∠BAD =∠CAD = 12∠BAC ,根据勾股定理可计算出AD 的长度,要使PBQ △中有一个角等于12BAC ∠即要使PBQ △中有一个角等于∠BAD ,分类讨论,根据相似三角形的判定与性质分别求出∠BPQ =∠BAD 以及∠BQP =∠BAD 时t 的值即可.【详解】作AD ⊥BC 交BC 于点D ,AB =AC ,∴AD =CD =3cm ,∠BAD =∠CAD =12∠BAC ,∴AD, 要使PBQ △中有一个角等于12BAC ∠即要使PBQ △中有一个角等于∠BAD , 分类讨论:(1)当∠BPQ =∠BAD 时,在BPQ 与BAD 中,B B BPQ BAD ∠=∠⎧⎨∠=∠⎩, ∴BPQ ∽BAD , ∴=BQ BP BD BA, AP =t ,BQ =2t ,∴BP =5-t , ∴2t 5t =35-, 解得:t =1513s .(2)当∠BQP =∠BAD 时,在BQP 与BAD 中,B B BQP BAD ∠=∠⎧⎨∠=∠⎩, ∴BQP ∽BAD , ∴=BQ BP AB BD, AP =t ,BQ =2t ,∴BP=5-t,∴2t5t=53-,解得:t=2511s.综上:t=1513s或2511s.【点睛】本题主要考查相似三角形的判定与性质以及勾股定理,熟记相关定理,利用等腰三角形的性质将角进行转化是解题关键,此类问题还需要注意分类讨论.97.已知如图,四边形ABCD和四边形CEFG都是正方形,且AB CE>连接BG、DE.求证:BG DE=.【答案】见解析【分析】先证∽BCG=∽DCE,再证明∽BCG∽∽DCE,即可得出结论.【详解】证明:四边形ABCD 和四边形CEFG 都是为正方形,CD BC ∴=,GC EC =,90BCD GCE ∠=∠=︒,BCG DCE ∴∠=∠在BCG ∆和DCE ∆中DC BC BCG DCE GC EC =⎧⎪∠=∠⎨⎪=⎩BCG DCE ∴∆≅∆BG DE ∴=【点睛】此题考查全等三角形的判定与性质,正方形的性质,解题关键在于掌握判定定理.98.()1已知4a =,9c =,若b 是a ,c 的比例中项,求b 的值.()2已知线段MN 是AB ,CD 的比例中项,4AB cm =,5CD cm =,求MN 的长.并思考两题有何区别.【答案】(1)6b =±;(2)MN =【解析】【分析】(1)根据比例中项的定义可得::a b b c =,由此即可求得b 的值;(2)根据比例中项的概念,AB :MN=MN :CD ,由此即可求得线段MN 的值.【详解】()1∽b 是a ,c 的比例中项,∽::a b b c =,∽2b ac =;b =∽4a =,9c =,∽6b ==±,即6b =±;()2∽MN 是线段,∽0MN >;∽线段MN 是AB ,CD 的比例中项,∽::AB MN MN CD =,∽2MN AB CD =⋅,∽MN =∽4AB cm =,5CD cm =,∽MN ==±;MN 不可能为负值,则MN =通过解答()1、()2发现,c 、MN 同时作为比例中项出现,c 可以取负值,而MN 不可以取负值.【点睛】本题考查了比例中项的定义,根据两条线段的比例中项的平方是两条线段的乘积求线段的长,是解决此类问题的基本思路.99.四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.(1)如图1,在四边形ABCD中,∠ABC=100°,∠ADC=130°,BD≠BC,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;(2)如图2,已知格点∠ABC,请你在正方形网格中画出所有的格点四边形ABCD,使四边形ABCD是以AC为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)(3)如图3,四边形AOBC中,点A在射线OP:y=(x≥0)上,点B在x轴正半轴上,对角线OC平分∠AOB,连接AB.若OC是四边形AOBC 的“相似对角线”,S∠AOB=C的坐标.【答案】(1)证明见解析;(2)见解析;(3)( .【解析】【分析】(1)由BD平分∽ABC可得∽ABD=∽DBC=50,则∽BDC+∽A=130°,根据∽ADC=130°可得∽ADB=∽C,即可求解;(2)如图所示,根据两个三角形夹角相等,夹边成比例,则三角形相似,即可求解;(3)利用∽AOC∽∽COB,则OA•OB=OC2,而S∽AOB=12×OB×y A=12×OB ×OAsin60°【详解】解:(1)∽对角线BD 平分ABC ∠,∽50ABD DBC ∠=∠=︒,∽130BDC C ∠+∠=︒,∽130ADC ∠=︒,∽130ADB BDC ∠+∠=︒,∽ADB C ∠=∠,∽BAD BDC ∆~∆,∽BD 是四边形ABCD 的“相似对角线”;(2)如下图所示:∽∽ABC=∽ACD 1=90°,1AB BC AC CD = , ∽∽ABC ∽∽ACD 1,故:以AC 为“相似对角线”的四边形有:ABCD 1,同理可得:以AC 为“相似对角线”的四边形还有:ABCD 2、ABCD 3、ABCD 4;(3)如图,作AM OB ⊥于M ,CN OB ⊥于N ,∽点A 在射线OP :()0y x =≥上,∽tan AOB ∠=,即60AOB ∠=︒,∽对角线OC 平分AOB ∠,∽30AOC COB ∠=∠=︒,∽OC 是四边形AOBC 的“相似对角线”,∽AOC ∆与COB ∆相似且不全等,∽OAC OCB ∠=∠,∽AOC COB ∆~∆, ∽OA OC OC OB=,即2OA OB OC ⋅=,∽11sin6022AOB S OB AM OB OA ∆=⋅=⋅︒=,∽OC =∽12CN OC ==ON =∽点C 的坐标为(.故答案为(1)证明见解析;(2)见解析;(3)( .【点睛】本题是阅读理解型一次函数综合题,考查相似三角形的判定和性质,理解新定义,锐角三角函数,此类题目通常要弄清楚题意,逐次求解.。
九年级数学第二十七章相似综合复习试题(含答案) (226)

九年级数学第二十七章相似综合复习试题(含答案)在ABC中,90∠=,C(1)如图1,P是AC上的点,过点P作直线截ABC,使截得的三角形与PD BC交AB于D,则截得的ADP与ABC相ABC相似.例如:过点P作//似.请你在图中画出所有满足条件的直线.(2)如图2,Q是BC上异于点B,C的动点,过点Q作直线截ABC,使截得的三角形与ABC相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)【答案】见解析【分析】(1)利用平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理过点P作两条,再利用两组对应角相等的两个三角形相似的判定定理,过点P作两条.(2)把Q点看成从C点出发到B点的动点,发现当Q点在某一个位置时,所作截的三角形与原三角形相似的数量减少了一个,通过此时的临界条件把QC 的长度计算出来,进行分类说明.【详解】(1)如图所示:第一种:利用平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理,过点P分别做AB与BC的平行线PD与PE.分别得到△ADP△△ABC. △PCE△△ACB.第二种:利用两组对应角相等的两个三角形相似的判定定理,过P分别做PG垂直AB于点G,做PF交BC于点F,使△PFC=△A.分别得到△AGP△△ACB, △FPC△△ACB.(2)如图所示,假设点Q从点C开始往点B移动,由(1)可知,作QD△AB,得△BQD△△BAC.作QF交AC于点F,使△QFC=△B,得△QCF△△ACB.作QE△AC,得△BQE△△BCA.作QG△AB,得△QCG△△BCA.当移动到2Q位置时,此时出现点F于点A重合,此时是一个临界点,利用△QCF△△ACB得到QC CFCA CB=,则CF CAQCCB⋅=又此时CA=CF,所以QC=83该点往左移动,不能在三角形ABC内做出作QF交AC于点F,该点往右移动,可以在三角形ABC内做出作QF交AC于点F,使△QCF△△ACB.故当0<QC≤83时,满足条件的直线有4条;当83<QC<6时,满足条件的直线有3条.【点睛】本题通过画图综合性的考察了三角形相似的判定,作图时运用到了平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理,两组对应角相等的两个三角形相似的判定定理.在做此类试题时考虑必须全面,不能漏掉解.97.在一次数学活动课上,李老师带领学生去测量教学楼的高度.在阳光下,测得身高1.65m的黄丽同学BC的影子BA长1.1m,与此同时,测得教学楼DE的影子DF长12.1m.(1)请你在图中画出此时教学楼DE在阳光下的影子DF;(2)请你根据已测得的数据,求出教学楼DE的高度(精确到0.1m).【答案】(1)作图见解析;(2)教学楼DE的高度约是18.2m.【解析】【详解】(1)如图所示,注意AC与EF平行.(2)由AC EF,得△CAB=△EFD.又△ABC=△D=90°,△△ABC △FDE , △CB EF AB FD=, 即1.65=1.112.1DE , 解得DE=18.15≈18.2(米).答:教学楼DE 的高度约为18.2米.98.如图,在等边ABC ∆中,点D 是边AC 上一动点(不与点,A C 重合),连接BD ,作AH BD ⊥于点H ,将线段AH 绕点A 逆时针旋转60︒至线段AE ,连接CE(1)①补全图形;②判断线段BH 与线段CE 的数量关系,并证明;(2)已知4AB =,点M 在边AB 上,且1BM =,作直线HE .①是否存在一个定点P ,使得对于任意的点D ,点P 总在直线HE 上,若存在,请指出点P 的位置,若不存在,请说明理由;②直接写出点M 到直线HE 的距离的最大值.【答案】(1)①见解析;②BH CE =,证明见解析;(2)①存在,点P 是边BC 的中点;【分析】(1)①按要求画出图形即可;②根据全等三角形对应边相等来回答;(2)①点P 为直线HE 与BC 的交点;②通过△BPM △△BAP 问题可解;【详解】(1)①如图;②BH CE =证明ABH ACE ∆≅∆即可(2)①存在点P 是边BC 的中点,理由:设直线HE 与边BC 交于点P可由60ACB AEP ︒∠=∠=得点,,,A E C P 共圆,因为90AEC ︒∠=,所以90APC ︒∠=,即P 是BC 的中点.②如图, 当MP △HE 时,MP 最大,理由:4,2,1AB BP BM ===,BM BP BP AB∴=, B B ∠∠=,△△BPM △△BAP ,△△BMP=△BPA=90︒ ,BP ∴==【点睛】本题考查等腰三角形的性质,全等三角形的判定和性质,点到直线的距离,旋转,相似三角形的判定和性质,勾股定理和圆的有关知识知识,综合性较强.99.如图,D 为反比例函数()0k y k x=<的图象上一点,过D 作DE ⊥x 轴于点E ,DC ⊥y 轴于点C ,一次函数y =-x +2的图象经过C 点,与x 轴相交于A 点,四边形DCAE 的面积为4,求k 的值.【答案】-2【分析】此题先由一次函数y=-x+2求得A 、C 两点坐标,得出△AOC 的面积,则矩形DCOE 的面积即可求出,再由反比例函数系数k 的几何意义及函数图象位于第二象限求得k 的值.【详解】解:由于一次函数y=-x+2的图象经过C 点,与x 轴相交于A 点, 则可求得A (2,0)、C (0,2),即OA=OC=2.△S △AOC =12×2×2=2,|k|=S 矩形DCOE =4-2=2. 又函数图象位于第二象限,k <0,则k=-2.【点睛】本题考查反比例系数k 的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|.100.两个相似三角形一组对应边的长分别是24cm 和12cm ,若他们周长的和是240cm ,求这两个三角形的周长.【答案】80cm 和160cm .【解析】【分析】设两个三角形的周长分别为x 、y ,根据相似三角形周长的比等于对应边的比列出方程,然后求解即可.【详解】解:设两个三角形的周长分别为x 、y . 根据题意得,24212x y ==,△2x y =.△他们周长的和是240cm , △2240x y y y +=+=,解得y =80,x =2×80=160, △这两个三角形的周长分别为80cm 和160cm .。
九年级数学第二十七章相似综合复习试题(含答案) (175)

九年级数学第二十七章相似综合复习试题(含答案) 如图,已知AC ⊥AB ,BD ⊥AB ,AO =78cm ,BO =42cm ,CD =159cm ,求CO 和DO .【答案】103.35,55.65CO cm DO cm ==【解析】试题分析:根据题意,易证AOC BDO ∽,根据相似三角形的判定与性质,列出比例式即可解得CO 和DO 的长.试题解析:设cm,DO x = 则()159cm.CO x =-,,90,.AC AB BD AB A B AOC BOD ⊥⊥∠=∠=∠=∠.AOC BOD ∽∴.AO CO BO DO∴= 即78159.42x x-= 55.65.x ∴=103.35cm 55.65cm.CO DO ∴==,点睛:两组角对应相等,两三角形相似.92.如图,在正方形网格上有111A B C ∆⊥222A B C ∆,这两个三角形相似吗?如果相似,求出111A B C ∆和222A B C ∆的面积比.【答案】相似,相似比为4:1【解析】试题分析:通过观察发现111222135,B AC B A C ∠=∠=︒ 若能计算这两角的夹边对应成比例,则两三角形相似,面积比也可求.试题解析:相似,相似比为2:1,111222:4:1.A B C A B C S S =通过观察图形发现111222135B AC B A C ∠=∠=︒,设每个小方格的边长为1,利用勾股定理可计算112211224, 2.A B A B AC A C ===11221122::2:1.A B A B AC A C ∴==111222.B AC B A C ∴∽111222:4:1.A B C A B C S S =点睛:相似三角形的判定:两边对应成比例及其夹角相等,两三角形相似. 相似三角形的面积比等于相似比的平方.93.已知:如图,在⊥ABC 中,点D 、E 、F 分别在AC 、AB 、BC 边上,且四边形CDEF 是正方形,AC =3,BC =2,求⊥ADE 、⊥EFB 、⊥ACB 的周长之比和面积之比.【答案】周长之比:222A B C ∆的周长:EFB ∆的周长:ACB ∆的周长3:2:5=;::9:4:25ADE EFB ACB S S S ∆∆∆=.【解析】试题分析:要求三个三角形的面积比,可通过证明三个三角形相似,从而得到其相似比,进而求得其面积比.试题解析:∵四边形CDEF 是正方形,,DE BC EF AC ∴,.DE CF EF DC ===.ADE EFB ACB ∴∽∽3.2AD AC DE BC == 设3,2,AD x ED x ==5.AC x ∴=::3:2:5.AD EF AC ∴=∵周长之比:ADE 的周长:EFB △的周长:ACB △的周长3:2:5.= ::9:4:25.ADE EFB ACB S S S ∴=94.如图,在8×8的正方形网格中,⊥CAB 和⊥DEF 的顶点都在边长为1的小正方形的顶点上.(1)填空:AC =________,AB =________;(2)判断⊥CAB 和⊥DEF 是否相似,并说明理由.【答案】;(2)相似,理由见解析【解析】试题分析: (1)根据勾股定理来求AC 、AB 的长度;(2)由“三边法”法来证它们相似.试题解析:(1)如图,由勾股定理,得AC=AB故答案是:;(2)∵CAB 和∵DEF 相似.理由如下:如图,DE =DF =EF . 则2AC BC AB ED FD EF===, 所以∵CAB ∵∵DEF .点睛: 本题考查了相似三角形的判定,勾股定理,勾股定理的逆定理以及锐角三角函数的定义.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.95.如图,⊥O的半径为5,点P在⊥O外,PB交⊥O于A、B两点,PC 交⊥O于D、C两点.(1)求证:PA•PB=PD•PC;(2)若PA=454,AB=194,PD=DC+2,求点O到PC的距离.【答案】(1)证明见试题解析;(2)3.【分析】(1)先连接AD,BC,由圆内接四边形的性质可知∵PAD=∵PCB,∵PDA=∵PBC,故可得出∵PAD∵∵PCB,再由相似三角形的对应边成比例即可得出结论;(2)由PA•PB=PD•PC,求出CD,根据垂径定理可得点O到PC的距离.【详解】(1)连接AD,BC,∵四边形ABDC内接于∵O,∵∵PAD=∵PCB,∵PDA=∵PBC,∵∵PAD∵∵PCB,∵PA PDPC PB,∵PA•PB=PC•PD;(2)连接OD,作OE∵DC,垂足为E,∵PA=454,AB=194,PD=DC+2,∵PB=16,PC=2DC+2,∵PA•PB=PD•PC,∵454×16=(DC+2)(2DC+2),解得:DC=8或DC=﹣11(舍去),∵DE=4,∵OD=5,∵OE=3,即点O到PC的距离为3.【点睛】本题主要考查了相似三角形的判定与性质,牢记其性质与判定是解答本题的关键.。
九年级数学第二十七章相似综合复习测试习题(含答案) (133)

九年级数学第二十七章相似综合复习测试习题(含答案)如图,l1∥l2∥l3,AB=25AC,DF=10,那么DE=_________________.【答案】4【解析】试题解析::∵l1∵l2∵l3,∵AB DE AC DF=.∵AB=25 AC,∵25 ABAC=,∵25 DEDF=.∵DF=10,∵2 105 DE=,∵DE=4.72.如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF EC⊥,交AB于点F,则tan ECF∠=____.【答案】12【解析】试题解析:∵四边形ABCD是正方形,∵AD=DC,∵A=∠D=90°,∵AE=ED,∵CD=AD=2AE,∵∵FEC=90°,∵∵AEF+∵DEC=90°,∵∵DEC+∵DCE=90°,∵∵AEF=∵DCE,∵∵A=∵D,∵∵AEF∵∵DCE,∵1=2 AE EFDC EC=,∵tan∵ECF=12 EFEC=.【点睛】本题考查正方形的性质、相似三角形的判定和性质、三角函数的定义等知识,解题的关键是灵活应用相似三角形的性质解决问题,属于中考常考题型.三、解答题73.如图,在梯形ABCD中,//AB CD,AD=BC,E是CD的中点,BE 交AC于F,过点F作//FG AB,交AE于点G.(1)求证:AG=BF;(2)当2AD CA CF=⋅时,求证:AB AD AG AC⋅=⋅.【答案】(1)见解析;(2)见解析【分析】(1)根据等腰梯形的性质求得∵ADE =∵BCE ,进而证得∵ADE ∵∵BCE ,得出AE =BE ,根据平行线分线段成比例定理即可证得结论;(2)先根据已知条件证得∵CAB ∵∵CBF ,证得AB AC BF BC=,因为BF =AG ,BC =AD ,所以AB AC AG AD=,从而证得AB •AD =AG •AC . 【详解】证明:(1)∵在梯形ABCD 中,AB ∵CD ,AD =BC ,∵∵ADE =∵BCE ,在∵ADE 和∵BCE 中AD BC ADE BCE DE CE =⎧⎪∠=∠⎨⎪=⎩∵∵ADE ∵∵BCE .∵AE =BE ,∵FG ∵AB , ∵AG BF AE BE=, ∵AG =BF .(2)∵AD 2=CA •CF , ∵AD CF CA AD=,∵AD =BC , ∵BC CF CA BC=. ∵∵BCF =∵ACB ,∵∵CAB ∵∵CBF . ∵AB AC BF BC=. ∵BF =AG ,BC =AD , ∵AB AC AG AD=. ∵AB •AD =AG •AC .【点睛】主要考查了三角形相似的判断和性质,平行线分线段成比例定理的应用,解题关键是熟练掌握性质定理,并灵活运用.74.如图,抛物线243y ax ax a =-+(0a >),与y 轴交于点A ,在x 轴的正半轴上取一点B ,使2OB OA =,抛物线的对称轴与抛物线交于点C ,与x 轴交于点D ,与直线AB 交于点E ,连接BC .(1)求点B ,C 的坐标(用含a 的代数式表示);(2)若BCD △与BDE 相似,求a 的值;(3)连接OE ,记OBE △的外心为M ,点M 到直线AB 的距离记为h ,请探究h的值是否会随着a的值变化而变化?如果变化,请写出h的取值范围:如果不变,请求出h的值.【答案】(1)B(6a,0),C(2,a-),(2)1441,,,;(3211134【分析】(1)将抛物线配方为2=--,得出顶点C(2,a-),当x=0时,y a x a(2)y=3a,OA=3a,OB=2OA=6a,即可得出点B坐标;(2)由点B位置不确定分三种情况讨论,若点B在点D的右侧时,若点B在点D的左侧时,若点B与点D重合时,得出1a=此情况不存在,另外∵BCD3与∵BDE相似时有两种情况∵DBC=∵EBD,与∵DCB=∵EBD时利用相似三角形的性质求a的值;(3)由点B位置不确定分三种情况讨论,若点B在点D的右侧时,若点B在点D的左侧时,若点B与点D重合时,利用相似三角形的性质求出MF的长度即可;【详解】(1)22=-+--,y ax ax a a x a43=(2)顶点C坐标为(2,a-),当x=0时,y=3a,A(0,3a),OA=3a,OB=2OA=6a,点B坐标为(6a,0),(2)由(1)知OD=2,OB=6a,BD=6a-2,若点B在点D的右侧时,如图1则6a -20>, ∵13a >, 当∵DBC=∵EBD 时∵tan ∵DBC=tan ∵EBD=OA 1=OB 2, ∵CD 1=BD 2, ∵1=622a a -, 1=2a ∴,当∵DCB=∵EBD 时,tan ∵DCB=tan ∵EBD=OA 1=OB 2, BD 1=CD 2, 6-21=2a a , 411a =, 若点B 在点D 的左侧时,如图2,则1062,03a a <<<<,DB=2-6a ,当∵DBC=∵EBD 时,∵tan ∵DBC=tan ∵EBD=OA 1=OB 2, ∵CD 1=BD 2, ∵1=262a a -, 1=4a ∴, 当∵DCB=∵EBD 时,tan ∵DCB=tan ∵EBD=OA 1=OB 2, BD 1=CD 2, 2-61=2a a , 413a =,若点B 与点D 重合时,则62a =,13a ∴=此情况不存在, 综上所述a 的值为1441211134a =,,,; (3)由题意知点M 在OB 和BE 的垂直平分线上,设OB 和BE 的垂直平分线交于点M ,其中OB 的垂直平分线与OB 交于点G ,BE 的垂直平分线交OB 于点H 交BE 于点F ,当点B 在点D 的右侧时,如图362a ∴>,12a ∴>, BD=6-2a ∴,1tan 2EBD ∠=, 1312ED BD a ∴==-, 由勾股定理可求的BE =1BF=2∴1HF=BF=24-∴, 由勾股定理可求:1554a BH -=, 534a HG BG BH -∴=-=, GMH=EBD ∠∠,sin sin GMH EBD ∴∠=∠=,MF MH HF ∴=+= 当点B 在点D 的左侧时如图4,103a ∴<<, BD=OD-OB=2-6a ∴,1tan tan 2ABO DBE ∴∠=∠=, 1132DE BE a ∴==-, 由勾股定理可求的BE =,122BF BE ∴==,12DE BD ∴==, 由勾股定理可求得5154a BH -∴=, 132GB OB a ==, 534a GH GB BH -∴=+=, 90HBF BHF ∠+∠=︒,+=90GMH BHF ∠∠︒,=HBF GMH ∴∠∠,sin sin HBF GMH ∴∠=∠=,MH ∴==,∴=-=MF MH HF当点B与点D重合时,此时1a=,3此情况不符合题意,舍去,综上所述,点M到直线AB【点睛】本题考查抛物线与坐标轴的交点,抛物线的顶点坐标,分类讨论思想,相似三角形的性质,三角形的外心,锐角三角函数,掌握抛物线与坐标轴交点坐标的求法,配方为抛物线的顶点式,求顶点坐标,会用分类思想研究三角形相似的情况,利用相似的性质求a的值,以及外心到AB的距离.本题难度较大,综合较强,是压轴题.75.如图1,E是等边三角形ABC的边AB所在直线上一点,D是边BC 所在直线上一点,且D与C不重合,若EC=ED.则称D为点C关于等边三角形ABC的反称点,点E称为反称中心.在平面直角坐标系xOy中,(1)已知等边三角形AOC的顶点C的坐标为(2,0),点A在第一象限内,反称中心E在直线AO上,反称点D在直线OC上.①如图2,若E为边AO的中点,在图中作出点C关于等边三角形AOC的反称点D,并直接写出点D的坐标:___.②若AE=2,求点C关于等边三角形AOC的反称点D的坐标;(2)若等边三角形ABC的顶点为B(n,0),C(n+1,0),反称中心E在直线AB上,反称点D在直线BC上,且2≤AE<3.请直接写出点C关于等边三角形ABC的反称点D的横坐标t的取值范围:P_____(用含n的代数式表示).【答案】(1)①(-1,0)②D(-2,0);(2)n-3<t≤n-2或n+2≤t<n+3.【分析】(1)①过点E作EF∵OC,垂足为F,根据等边三角形的性质可得DF=FC=3 2,OF=12,即可求OD=1,即可求点D坐标;②分点E与坐标原点O重合或点E在边OA的延长线上两种情况讨论,根据反称点定义可求点D的坐标;(2)分点E在点E在AB的延长线上或在BA的延长线上,根据平行线分线段成比例的性质,可求CF=DF的值,即可求点D的横坐标t的取值范围.【详解】(1)①如图,过点E作EF∵OC,垂足为F,∵EC=ED,EF∵OC∵DF=FC,∵点C的坐标为(2,0),∵AO=CO=2,∵点E是AO的中点,∵OE=1,∵∵AOC=60°,EF∵OC,∵∵OEF=30°,∵OE=2OF=1∵OF=12,∵OC=2,∵CF=32=DF,∵DO=1∵点D坐标(-1,0)故答案为(-1,0)②∵等边三角形AOC的两个顶点为O(0,0),C(2,0),∵OC=2.∵AO=OC=2.∵E是等边三角形AOC的边AO所在直线上一点,且AE=2,∵点E与坐标原点O重合或点E在边OA的延长线上,如图,若点E与坐标原点O重合,∵EC=ED,EC=2,∵ED=2.∵D是边OC所在直线上一点,且D与C不重合,∵D点坐标为(-2,0)如图,若点E在边OA的延长线上,且AE=2,∵AC=AE=2,∵∵E=∵ACE.∵∵AOC为等边三角形,∵∵OAC=∵ACO=60°.∵∵E=∵ACE=30°.∵∵OCE=90°.∵EC=ED,∵点D与点C重合.这与题目条件中的D与C不重合矛盾,故这种情况不合题意,舍去,综上所述:D(-2,0)(2)∵B(n,0),C(n+1,0),∵BC=1,∵AB=AC=1∵2≤AE<3,∵点E在AB的延长线上或在BA的延长线上,如图点E在AB的延长线上,过点A作AH∵BC,过点E作EF∵BD∵AB=AC,AH∵BC,∵BH=CH=12,∵AH∵BC,EF∵BD ∵AH∵EF∵AB BHBE BF=,若AE=2,AB=1∵BE=1,∵AB BHBE BF==1∵BH=BF=1 2∵CF=32=DF∵D的横坐标为:n-12-32=n-2,若AE=3,AB=1∵BE=2,∵AB BHBE BF==12∵BF=2BH=1∵CF=DF=2∵D的横坐标为:n-1-2=n-3,∵点D的横坐标t的取值范围:n-3<t≤n-2,如图点E在BA的延长线上,过点A作AH∵BC,过点E作EF∵BD,同理可求:点D的横坐标t的取值范围:n+2≤t<n+3,综上所述:点D的横坐标t的取值范围:n-3<t≤n-2或n+2≤t<n+3.故答案为n-3<t≤n-2或n+2≤t<n+3.【点睛】此题考查三角形综合题,等边三角形的性质,平行线分线段成比例,解题关键在于理解题意作辅助线,是中考压轴题.。
九年级数学下册第二十七章相似知识点归纳总结(精华版)(带答案)

九年级数学下册第二十七章相似知识点归纳总结(精华版)单选题1、如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,且将四边形ABDC分成甲、乙、丙、丁四个三角形.若OA:OB=OC:OD=2:3,则此四个三角形的关系,下列叙述正确的是()A.甲与丙相似,乙与丁相似B.甲与丙相似,乙与丁不相似C.甲与丙不相似,乙与丁相似D.甲与丙不相似,乙与丁不相似答案:A分析:利用已知条件得到即OAOC =OBOD,加上对顶角相等,则可判断△AOB∽△COD;再利用比例性质得到AOOB=OCOD,而∠AOC=∠BOD,所以△AOC∽△BOD.解:∵OA:OB=OC:OD=2:3,即OAOC =OBOD,而∠AOB=∠COD,∴△AOB∽△COD,∵OAOC =OBOD,∴AOOB =OCOD,∵∠AOC=∠BOD,∴△AOC∽△BOD.故选:A.小提示:本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.2、两个相似六边形,若对应边之比为3:2,则这两个六边形的周长比为()A.9:4B.9:2C.3:1D.3:2答案:D分析:根据相似图形的性质求解即可.解:因为这两个六边形相似,所以这两个六边形的周长比=对应边之比=3:2,故选:D.小提示:本题考查相似多边形的性质,熟练掌握相似多边形的周长比等于相似比,即相似多边形的周长比等于对应边的比是解题的关键.3、若ab =cd=−2,则a−cb−d=()A.−2B.2C.−12D.12答案:A分析:根据ab =cd=−2,可知a=﹣2b,c=﹣2d,将a和c的值代入求值的代数式化简即可.解:∵ab =cd=−2,∴a=﹣2b,c=﹣2d,∴a−cb−d =−2b+2db−d=−2(b−d)(b−d)=−2.故选:A.小提示:本题考查了比例的性质,解题的关键是根据已知将a和c用b和d正确表示.4、在比例尺为1:50的图纸上,长度为10cm的线段实际长为()A.50cmB.500cmC.150cm D.1500cm答案:B分析:根据成比例线段的性质求解即可.解:∵1:50=10:500,∴长度为10cm 的线段实际长为500cm , 故选B .小提示:本题考查了成比例线段,掌握比例的性质是解题的关键.5、线段AB 的长为2,点C 是线段AB 的黄金分割点,则线段AC 的长可能是( ) A .√5+1B .2﹣√5C .3﹣√5D .√5﹣2 答案:C分析:根据黄金分割点的定义,知AC 可能是较长线段,也可能是较短线段,分别求出即可. 解:分两种情况讨论 (1)如图,∵点C 是线段AB 的黄金分割点,AB =2, ∴AC =√5−12AB =√5−12×2=√5﹣1, 或如图,AC =2﹣(√5﹣1)=3﹣√5,故选:C .小提示:本题主要考查了黄金分割的定义,熟记黄金分割的比值是解题的关键.6、如图,在△ABC 中,∠ABC =90°,以点A 为圆心,以AB 的长为半径作弧交AC 于点D ,连接BD ,再分别以点B ,D 为圆心,大于12BD 的长为半径作弧,两弧交于点P ,作射线AP 交BC 于点E ,连接DE ,则下列结论正确的是( )A.DE垂直平分AC B.△ABE∽△CBAC.BD2=BC⋅BE D.CE⋅AB=BE⋅CA答案:D分析:根据作图可知AP是∠BAC的角平分线,AB=AD,根据SAS证明△ABE≌△ADE,可得EB=ED,∠ADE=∠ABE=90°,根据面积法可得S△ABES△AEC =12AB⋅BE12AC⋅DE=12AB⋅BE12AB⋅EC,可得ABAC=BEEC即可判断D选项正确,其他选项无法证明.解:根据作图可知AP是∠BAC的角平分线,AB=AD,∴∠EAB=∠EAD,在△ABE与△ADE中,{AE=AE∠EAB=∠EADAB=AD,∴△ABE≌△ADE,∴EB=ED,∵∠ABC=90°,∴∠ADE=∠ABE=90°,∴BE⊥AB,ED⊥C,∵S△ABES△AEC =12AB⋅BE12AC⋅DE=12AB⋅BE12AB⋅EC,∴ABAC =BEEC,即CE⋅AB=BE⋅CA.A,B,C选项无法证明.故选:D.小提示:本题考查了作角平分线,全等三角形的性质与判定,三角形面积公式,证明两三角形相似,垂直平分线的性质,理解基本作图是解题的关键.7、如图,AG:GD=3:1,BD:DC=2:3,则AE:EC的值是()A.8:7B.6:5C.3:2D.8:5答案:B分析:过点作DF∥BE交AC于点F,根据平行线分线段成比例定理分别求出CFFE =CDDB=32,AEFE=AGGD=3,进而得到答案.解:如图,过点作DF∥BE交AC于点F,由平行线分线段成比例定理得,则CFEF =CDDB=32,AEEF=AGGD=3,∴CF=32EF,AE=3EF∴EC=CF+EF=52EF∴AE∶EC=3EF∶52EF=6:5,故选:B小提示:本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.8、如图,l1∥l2∥l3,若ABBC =23,DF=15,则EF=()A.5B.6C.7D.9答案:D分析:根据平行线分线段成比例定理可得ABBC =DEEF,根据题意,DE=DF−EF,进而求解.∵l1∥l2∥l3,∴ABBC =DEEF.∵ABBC =23,∴DEEF =23,∵DE=DF−EF,DF=15,∴15−EFEF =23,∴EF=9.故选:D.小提示:本题考查的是平行线分线段成比例定理的应用,灵活运用平行线分线段成比例定理是解本题的关键.9、如图,C为线段AB的黄金分割点(AC<BC),且BC=2,则AB的长为()A.2√5+2B.2√5﹣2C.√5+1D.√5﹣3答案:C分析:黄金分割比定理:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值为√5−12,叫黄金分割比,由此进行求解即可.解:C为线段AB的黄金分割点,BC=2 ,AC<BC∴ACBC =BCAB=√5−12∴AC=2×√5−12=√5−1∴AB=AC+BC=√5−1+2=√5+1故选:C小提示:本题考查黄金分割定理,理解黄金分割定理的概念,熟悉比值是解题的关键.10、如图,点D、E分别在△ABC的边AB、BC上,下列条件中一定能判定DE∥AC的是()A.ADDB =BECEB.BDAD=BEECC.ADAB=CEBED.BDBA=DEAC答案:B分析:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.根据平行线分线段成比例定理对各个选项进行判断即可.A.由ADDB =BECE,不能得到DE∥BC,故本选项不合题意;B.由BDAD =BEEC,能得到DE∥BC,故本选项符合题意;C.由ADAB =CEBE,不能得到DE∥BC,故本选项不合题意;D.由BDBA =DEAC,不能得到DE∥BC,故本选项不符合题意;故选B.小提示:本题考查了平行线分线段成比例定理的应用,如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.填空题11、如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则AFEF的值为______.答案:43分析:过E点作EH∥AC交BD于点H,根据平行线分线段成比例定理,由EH∥CD得到EHCD =34,由于AD=CD,则EH AD =34,然后利用平行线分线段成比例定理得到AFEF的值.过E点作EH∥AC交BD于点H,如图:∵EH∥AC,∴EHCD =BEBC,∵BE=3EC,∴EHCD =3CE4CE=34,∵D为AC的中点,∴AD=CD,∴EHCD =EHAD=34,∵EH∥AD,∴AFEF =ADEH=43.故答案为43.小提示:本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.12、如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB=______m.答案:100分析:由两角对应相等可得△BAD∽△CED,利用对应边成比例即可得两岸间的大致距离AB的长.解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,∴△ABD∽△ECD,∴ABEC =BDCD,即AB=BD×ECCD,解得:AB=120×5060=100(米).故答案为100.小提示:本题主要考查了相似三角形的应用,用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.13、如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD于点E、交BC于点F,则线段EF的长为 __.答案:152##7.5分析:根据矩形的性质和勾股定理求出BD,证明△BOF∽△BCD,根据相似三角形的性质得到比例式,求出EF即可.解:如图:∵四边形ABCD是矩形,∴∠A=90°,又AB=6,AD=BC=8,∴BD=√AB2+AD2=10,∵EF是BD的垂直平分线,∴OB=OD=5,∠BOF=90°,又∠C=90°,∴ΔBOF∽ΔBCD,∴OFCD =BOBC,∴OF6=58,解得,OF=154,∵四边形ABCD是矩形,∴AD//BC,∠A=90°,∴∠EDO=∠FBO,∵EF是BD的垂直平分线,∴BO=DO,EF⊥BD,在ΔDEO和ΔBFO中,{∠EDO=∠FBOBO=DO∠EOD=∠FOB,∴ΔDEO≅ΔBFO(ASA),∴OE=OF,∴EF=2OF=15.2.所以答案是:152小提示:本题考查的是矩形的性质、线段垂直平分线的性质以及勾股定理的应用,掌握矩形的四个角是直角、对边相等以及线段垂直平分线的定义是解题的关键.14、如图,在▱ABCD中,点E在AB上,CE,BD交于点F,若AE:BE=4:3,且BF=2,则DF=_________.答案:143分析:由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,继而可判定△BEF∽△DCF,根据相似三角形的对应边成比例,即可得BF:DF=BE:CD问题得解.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵AE:BE=4:3,∴BE:AB=3:7,∴BE:CD=3:7.∵AB∥CD,∴△BEF∽△DCF,∴BF:DF=BE:CD=3:7,即2:DF=3:7,∴DF=14.3故答案为14.3小提示:此题考查了相似三角形的判定与性质与平行四边形的性质.此题比较简单,解题的关键是根据题意判定△BEF∽△DCF,再利用相似三角形的对应边成比例的性质求解.15、如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,则EF的长为_______.答案:34分析:易证△DEF∽△DAB,△BEF∽△BCD,根据相似三角形的性质可得EFAB =DFDB,EFCD=BFBD,从而可得EFAB+EFCD=BF BD +DFBD=1,然后把AB=1,CD=3代入即可求出EF的值.解:∵AB、CD、EF都与BD垂直,∴AB∥CD∥EF,∴△DEF∽△DAB,△BEF∽△BCD,∴EFAB =DFDB,EFCD=BFBD,∴EFAB +EFCD=BFBD+DFBD=1,∵AB=1,CD=3,∴EF1+EF3=1,∴EF=34,所以答案是:34.小提示:本题考查相似三角形的判定与性质,解决本题的关键是掌握相似三角形对应边成比例.解答题16、如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上、已知纸板的两条边DF=0.5m,EF=0.3m,测得边DF离地面的高度AC =1.5m,CD=10m,求树高AB.答案:树高AB是9米分析:先证得△DEF∽△DCB,可得BCEF =DCDE,再由勾股定理可得DE=0.4m,可得BC=7.5m,即可求解.解:∵∠DEF=∠BCD=90°,∠D=∠D,∴△DEF∽△DCB,∴BCEF =DCDE,∵DF=0.5 m,EF=0.3 m,AC=1.5m,CD=10 m,由勾股定理得DE=√DF2−EF2=0.4 m,∴BC0.3=100.4,∴BC=7.5m,∴AB=AC+BC=1.5+7.5=9(m),答:树高AB是9m.小提示:本题主要考查了相似三角形的应用,熟练掌握相似三角形的判定和性质是解题的关键.17、如图,ΔABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.(1)求证:PG与⊙O相切:(2)若EFAC =58,求BEOC的值;(3)在(2)的条件下,若⊙O的半径为4,PD=OD,求EC的长.答案:(1)见解析;(2)54;(3)6−√13.分析:(1)要证PG与⊙O相切只需证明∠OBG=90°,由∠BAC与∠BDC是同弧所对圆周角且∠BDC=∠DBO可得∠CBG=∠DBC,结合∠DBC+∠OBC=90°即可得证;(2)求BEOC需将BE与OC或OC相等线段放入两三角形中,通过相似求解可得,作OM⊥AC、连接OA,证△BEF∽△OAM得EFAM =BEOA,由AM=12AC、OA=OC知EF12AC=BEOC,结合EFAC=58即可得;(3)Rt△DBC中求得BC=4√3、∠DCB=30°,在Rt△EFC中设EF=x,知EC=2x、FC=√3x、BF=4√3﹣√3x,继而在Rt△BEF中利用勾股定理求出x的,从而得出答案.(1)证明:如图,连接OB,∵OB=OD,∴∠BDC=∠DBO,∵∠BAC=∠GBC、∠BDC=∠BAC,∴∠GBC=∠BDC,∵CD是⊙O的直径,∴∠DBC=90°,∴∠DBO+∠OBC=90°,∴∠GBC+∠OBC=90°,∴∠GBO=90°,∴PG与⊙O相切;(2)解:过点O 作OM ⊥AC 于点M ,连接OA ,∵OC =OA ,OM ⊥AC ,∴∠AOM =∠COM =12∠AOC ,∵ AC ⌢=AC ⌢,∴∠ABC =12∠AOC ,∴∠EBF =∠AOM ,又∵∠EFB =∠OMA =90°,∴ΔBEF ∽ΔOAM ,∴ EF AM =BE OA ,∵AM =12AC ,OA =OC ,∴ EF 12AC =BE OC ,又∵ EF AC =58,∴ BE OC =2×EF AC =2×58=54;(3)解:∵PD =OD ,∠PBO =90°,∴BD =OD =4,在RtΔDBC中,BC=√CD2−BD2=√82−42=4√3,又∵OD=OB,∴ΔDOB是等边三角形,∴∠DOB=60°,∵∠DOB=∠OBC+∠OCB,OB=OC,∴∠OCB=12∠DOB=30°,∴EC=2EF,由勾股定理FC=√EC2−EF2=√4EF2−EF2=√3EF ∴设EF=x,则EC=2x、FC=√3x,∴BF=4√3−√3x,∵BEOC =54,且OC=4,∴BE=5,在RtΔBEF中,BE2=EF2+BF2,∴25=x2+(4√3−√3x)2,整理得4x2−24x+23=0△=242-16×23=208>0解得:x=24±4√132×4=6±√132,∵6+√132>4,舍去,∴x=6−√132,∴EC=6−√13.小提示:本题主要考查圆的综合问题,涉及圆周角定理、圆心角定理、相似三角形的判定与性质、直角三角形的性质,一元二次方程的解法等知识,熟练掌握和运用相关的性质与定理进行解题是关键.18、如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O.BE与AC相交于点F.(1)若BE平分∠CBD,求证:BF⊥AC;(2)找出图中与△OBF相似的三角形,并说明理由;(3)若OF=3,EF=2,求DE的长度.答案:(1)证明见解析(2)△ECF,△BAF与△OBF相似,理由见解析(3)3+√19分析:(1)根据矩形的性质和角平分线的定义即可得出结论;(2)根据判定两个三角形相似的判定定理,找到相应的角度相等即可得出;(3)根据△OBF∽△ECF得出3OA=2BF+9,根据△OBF∽△BAF得出BF2=3(OA+3),联立方程组求解即可.(1)证明:如图所示:∵四边形ABCD为矩形,∴∠2=∠3=∠4,∵DE=BE,∴∠1=∠2,∴∠1=∠3,又∵BE平分∠DBC,∴∠1=∠6,∴∠3=∠6,又∵∠3与∠5互余,∴∠6与∠5互余,∴BF⊥AC;(2)解:△ECF,△BAF与△OBF相似.理由如下:∵∠1=∠2,∠2=∠4,∴∠1=∠4,又∵∠OFB=∠BFO,∴△OBF∽△BAF,∵∠1=∠3,∠OFB=∠EFC,∴△OBF∽△ECF;(3)解:∵△OBF∽△ECF,∴EFOF =CFBF,∴23=CFBF,∴3CF=2BF,∵在矩形ABCD中对角线相互平分,图中OA=OC=OF+FC=3+FC,∴3OA=2BF+9①,∵△OBF∽△BAF,∴OFBF =BFAF,∴BF2=OF⋅AF,∵在矩形ABCD中AF=OA+OF=OA+3,∴BF2=3(OA+3)②,由①②,得BF=1±√19(负值舍去),∴DE=BE=2+1+√19=3+√19.小提示:本题考查矩形综合问题,涉及到矩形的性质、角平分线的性质、角度的互余关系、两个三角形相似的判定与性质等知识点,熟练掌握两个三角形相似的判定与性质是解决问题的关键.。
中考数学一轮复习九下第27章相似图形含答案

相似图形1.平行于三角形一边的直线截其他两边(或两边的延长线)所得对应线段 .2.相似三角形的对应边、对应高、对应周长比都等于 ,而面积的比等于相似比的 .3.相似三角形的判定方法有:(1)两角对应 ,两三角形相似;(2)两边对应成比例,且 相等,两三角形相似;(3)三边对应 ,两三角形相似;(4)平行于三角形一边的直线和其他的两边(或延长线)相交,所构成的三角形与原三角形 .(5)斜边的比等于一组 的比的两个直角三角形相似.4.位似图形上任意一对对应点到位似中心的距离之比等于 ,位似图形的对应边分别 或 .如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比为 或 .1.如图,在△ABC 中,点D ,E 分别在边AB ,AC 上,DE ∥BC.已知AE=6,AD DB =34,则EC 的长是( ) A.4.5 B.8 C.10.5 D.142.如图,已知在△ABC 中,点D 、E 、F 分别是边AB 、AC 、BC 上的点,DE ∥BC ,EF ∥AB ,且AD ∶DB=3∶5,那么CF ∶CB 等于( )A.5∶8B.3∶8C.3∶5D.2∶53.已知△ABC ∽△DEF ,若△ABC 与△DEF 的相似比为3∶4,则△ABC 与△DEF 的面积之比为( )A.4∶3B.3∶4C.16∶9D.9∶164.如图,正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为1,点A 的坐标为(1,0),则E 点的坐标为( ),0) B.(32,32) D.(2,2)5.如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB ⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB等于( )A.60 mB.40 mC.30 mD.20 m6.如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )A.1∶2B.1∶3C.1∶4D.1∶57.如图,P为平行四边形ABCD边AD上一点,E,F分别是PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2,若S=2,则S1+S2= .8.在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,这样的直线最多有条.9.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长米.10.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为 .11.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10 cm,OA′=20 cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是 .12.网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC ∽△DEF.13.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.(1)求证:DC为⊙O的切线;(2)若⊙O的半径为3,AD=4,求AC的长.14.如图,已知AB⊥BD,CD⊥BD.若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在,请说明理由.参考答案知识回顾1.成比例2.相似比平方3.(1)相等(2)夹角(3)成比例(4)相似(5)直角边4.相似比平行在同一条直线上 k -k 达标练习1.B2.A3.D4.C5.B6.A7.88.49.5 10.7 11.1 212.∵,AB=4,,DE=8,∴ACDF=BCEF=ABDE=12,∴△ABC∽△DEF.13.(1)证明:连接OC.∵OC=OA,∴∠OAC=∠OCA.又∠OAC=∠DAC,∴∠DAC=∠OCA.∴OC∥AD.∴OC⊥CD,即OC为⊙O的切线.(2)连接BC.由(1)知△ADC∽△ACB,∴ADAC=ACAB,即AC2=AD·AB.又⊙O的半径为3,∴AB=6,AD=4.∴.14.存在.设BP=x,则DP=10-x.①如果是△ABP∽△CDP,则ABCD=BPDP,即9x=410x-,解得x=9013;②如果是△ABP∽△PDC,则ABPD=BPCD,即910x-=4x,方程无解. 综上,BP的长为9013.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十七章相似
【课标要求】
【能力训练】
1.小明的爷爷退休生活可丰富了!下表是他某日的活动安排.和平广场位于爷爷家东400米,老年大学位于爷爷家西600米.从爷爷家到和平路小学需先向南走300米,再向西走400米.
(1)请依据图示中给定的单位长度,在图中标出和平广场A、老年大学B与和平路小学的位置.
(2)求爷爷家到和平路小学的直线距离.
2.如图,在平行四边形ABCD 中,E 是AD 上一点,连结CE 并延长交BA 的延长线于点F ,则下列结论中错误的是( )
A. ∠AEF =∠DEC
B. FA:CD =AE:BC
C. FA:AB =FE:EC
D. AB =DC
3.在△ABC 中,∠B =25°,AD 是BC 边上的高,并且AD BD DC 2=·,则∠BCA 的度数
为_________。
4.下面是一天中四个不同时刻两个建筑物的影子:
将它们按时间先后顺序进行排列,正确的是( )
A 、③④②①
B 、②④③①
C 、③④①②
D 、③①②④
5.如图,在ABC ∆中,1=BC ,2=AC ,0
90=∠C .
(1)在方格纸①中,画'''C B A ∆,使'''C B A ∆∽ABC ∆,且相似比为2︰1; (2)若将(1)中'''C B A ∆称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点O 为对称中心,并且以直线l 为对称轴的图案.
6.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点个数共有_______个.
7.如图,△ABC 中,AB=BC=AC=3,O 是它的内心,以O 为中心,将△ABC 旋转180°得到△A /
B /
C /
,,则△ABC 与△A /
B /
C '重叠部分的面积为( )
A .
233 B .
33 C .2
3
D . 36 8.某山路的路面坡度i=1:沿此 山路向上前进200m, 升高了____m.
9.某落地钟钟摆的摆长为0.5m,来回摆动的最大夹角为20°. 已知在钟摆的摆动过程中,摆锤离地面的最低高度为am,最大高度为bm,则b-a= ____m(不取近似值). 10.△ABC 中,∠C=90°,点D 在BC 上,BD=6,AD=BC,cos ∠ADC=
3
5
,则DC 的长为______. 11.如图,拦水坝的横断面为梯形ABCD,坡角α=28°,斜坡AB= 9m,
求拦水坝的高BE.(
精确
到0.1m,供选用的数据:sin28°=0.469,cos28°=0.8829, tan28°=0.5317,cos28°=1.880 7)
E
D
C
B
A
12.如图,在△ABC 中,AD 是BC 边上的高,tanB=cos ∠DAC.
(1)求证:AC=BD;(2)若sinC=
12
13
,BC=12,求AD 的长.
13.已知,如图,A 、B 、C 三个村庄在一条东南走向的公路沿线上,AB=2km.在B 村的正北方向
有一个D 村,测得∠DAB=45°,∠DCB=28°, 今将△ACD 区域进行规划,除其中面积为0.5km 2的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.(结果精确到0.1km 2,sin28°=0.469 5,cos28°=0.882 9, tan28°=0.531 7,cos28°=1.880 7)
14.在课本的阅读材料中, 介绍了一个第七届国际数学教育大会的会徽,它的主体图案是由
一连串如图1-15-7所示的直角三角形演化而成的. 设其中的第一个直角三角形OA 1A 2是等腰直角三角形,且OA 1=A 1A 2=A 2A 3=A 3A 4=…=A 8A 9=1, 请你先把图中其他8条线段的长计算出来,填在下面的表格中,然后再计算这8 条线段的长的乘积.
D C
B
A
图(1) 图(2)
15. 如图。
两种规格的钢板原料,图(1)的规格为1m ×5m.图(2)是由5个1m ×1m 的小正方形组成。
电焊工王师傅
准备用其中的一种钢板原料裁剪后焊接成一个无重叠无缝隙的正方形形状的工件(不计加工中的损耗)。
(1)焊接后的正方形工件的边长是
(2)分别在图(1)和图(2)中标出裁剪线,并画出所要求的正方形形状的工件示意图(保留要焊接的痕迹);
(3)从节约焊接材料的角度,试比较选用哪种原料较好?
A 9
A 2
1
答案:
1.略;2.A;3.45度;4.C;5.绘图略;6.40;7.A;8.20;9.0.5-cos20°;10.9;11.4.2;12.证明略,AD=8;13.3.3;14.7270;15.5,第二种。
