7阶椭圆型低通滤波器的设计及仿真
七阶LC滤波器设计报告
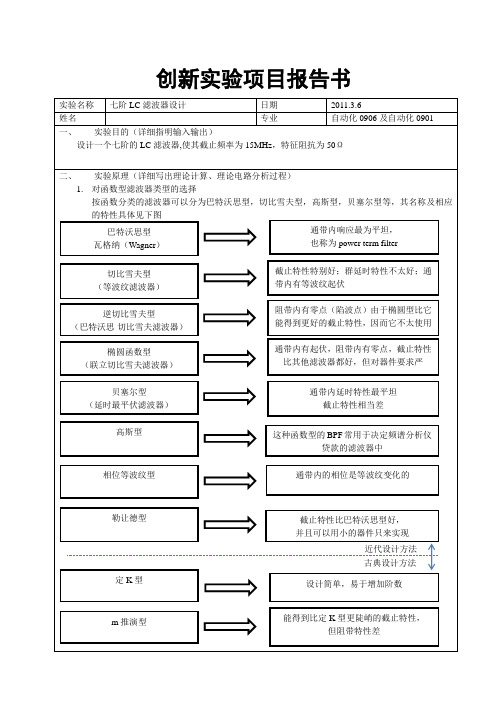
创新实验项目报告书实验名称七阶LC滤波器设计日期2011.3.6姓名专业自动化0906及自动化0901 一、实验目的(详细指明输入输出)设计一个七阶的LC滤波器,使其截止频率为15MHz,特征阻抗为50Ω二、实验原理(详细写出理论计算、理论电路分析过程)1.对函数型滤波器类型的选择按函数分类的滤波器可以分为巴特沃思型,切比雪夫型,高斯型,贝塞尔型等,其名称及相应的特性具体见下图巴特沃思型瓦格纳(Wagner)通带内响应最为平坦,也称为power term filter切比雪夫型(等波纹滤波器)截止特性特别好;群延时特性不太好;通带内有等波纹起伏逆切比雪夫型(巴特沃思-切比雪夫滤波器)阻带内有零点(陷波点)由于椭圆型比它能得到更好的截止特性,因而它不太使用椭圆函数型(联立切比雪夫滤波器)通带内有起伏,阻带内有零点,截止特性比其他滤波器都好,但对器件要求严贝塞尔型(延时最平伏滤波器)通带内延时特性最平坦截止特性相当差能得到比定K型更陡峭的截止特性,但阻带特性差m推演型设计简单,易于增加阶数截止特性比巴特沃思型好,并且可以用小的器件只来实现勒让德型定K型通带内的相位是等波纹变化的相位等波纹型这种函数型的BPF常用于决定频谱分析仪贷款的滤波器中高斯型近代设计方法古典设计方法结合各种设计类型的特性及实现的难易程度决定选用巴特沃思型2.分析与计算首先,根据实验要求可以得到一个7阶归一化的巴特沃思型LPF 电路图。
以下列出的是相对应的T 形和π形电路由于电感比较难绕,而且其数值不好控制,所以我选择电感比较少的π形电路作为基础进行变换。
该实验中要求截止频率达到15MHz ,特征阻抗为50Ω。
在归一化条件下,截止频率为1/(2π)Hz (即约等于0.15915Hz )且特征阻抗为1Ω。
各元件参数值的计算公式为nk L k k 2)12(sin 2C π-=或,式中k=1,2,……,n此实验要求是7阶,因此⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯≈⨯-⨯=≈⨯-⨯==⨯-⨯=≈⨯-⨯=≈⨯-⨯=≈⨯-⨯=24698.172)162(sin2)(80194.172)152(sin 2)(0.272)142(sin 2)(80194.172)132(sin 2)(24698.172)122(sin 2)(44504.072)112(sin 2)(665544332211ππππππL C L C L C L C L C L C 或或或或或或这几个值便是截止频率为1/(2π)Hz (即约等于0.15915Hz )且特征阻抗值为1Ω的7阶巴特沃思型LPF 的元件值。
LC椭圆函数带通滤波器的设计及仿真

LC椭圆函数带通滤波器的设计及仿真第13卷第5期2008年10月哈尔滨理工大学J0URNALHARBINUNIV.SCI.&TECH.V01.13No.5Oct.,2008LC椭圆函数带通滤波器的设计及仿真常会敏,张礼勇,蒋辉雄(哈尔滨理工大学测控技术与通信工程学院,黑龙江哈尔滨150040)摘要:椭圆滤波器在各种滤波器中具有其自身独特的优点,但设计过程往往比较复杂.本文给出了一种简易的计算方法.这种方法需要的初始值数据较少,设计步骤简练,计算量小.并用PSPICE仿真软件分别对椭圆函数低通,高通,带通滤波器进行设计和仿真分析,仿真结果证明了这种滤波器设计方法的有效性.关键词:椭圆函数滤波器;PSPICE仿真;传输特性;耦合器中图分类号:TN713文献标识码:A文章编号:1007—2683(2008)05—0021—04 TheDesignandSimulationofLCEllipticBand——passFilterCHANGHui—min,ZHANGLi—yong,JIANGHui—xiong(SchoolofMe~ure—controlTechnologyandCommunicationEngineering,HarbinUniversityofScienceandTec hnology,Harbin150040,China)Abstract:Throughallkindsoffilters,theellipticoneshaveparticularadvantages,buttheirdes ignprocessesaremorecomplicated.Thisthesismakesuseofaneasycalculationmethodwithsampledesigningsteps,lowcom—putationalcomplexityandneedinglessoriginalvaluedata.PSPICEsimulationsoftwareisus edtodesignandsimu—lateellipticlow—pass,high—passandband—passfilters,andthesimulationresultsshowtheeffectivenessofthescheme.Keywords:ellipticfilter;PSPICESimulation;transmissioncharacteristic;coupler带通滤波器的应用非常广泛,涉及到各个领域.带通滤波器性能的优劣,对提高接收机信噪比,防止邻近信道干扰,提高设备的技术指标,具有十分重要的意义.滤波器的设计技术已比较成熟,根据设计要求,首先确定滤波器的曲线和类型,以及滤波器的阶数,根据设计参数确定具体曲线和归一化元件值,再根据实际去归一化得到实际的元件值.1一种模拟带通滤波器本文通过设计一个1M到30M的【C模拟带通滤波器来表述一种设计方法,如图1所示.设计指标收稿日期:2007—04—29基金项目:国家自然科学基金(60372104)作者简介:常会敏(1980一),女,哈尔滨理工大学硕士研究生确定如下:1)3dB截止频率分别为950k和30.5M;2)30dB截止频率分别为500k和40M;3)lM到30M之间的通带波纹小于0.2dB./\图1带通滤波器曲线由以上截止频率可知,这是一个宽带带通滤波22哈尔滨理工大学第l3卷器,故可以通过设计一个截止频率为30M的低通滤波器和一个截止频率为1M的高通滤波器级联而成.2椭圆函数低通滤波器的设计第一步:计算没计波彤参数,陡度系数为:_1.33(1)出现A…的最低阻带频率,即'=_1_3模角为sin-I1:sin南50.(3)第二步:选择归一化低通滤波器.在阻带端点以内的最小衰减至少为30dB,选择反射系数P:20%,由文[1]可知,它对应的通带波纹为0.18d13;由罔2可知,与P=20%对应的反射损耗分贝数A=13.9dB.故有/l.+A.=30dB+13.9dB=43.9dB(4)图2所示为估算椭圆函数滤波器阶数用的曲线表明,在:1.3时,n=5的滤波器可满足设计要求,具体编号为CO520,0=50..满足设计要求的归一化低通滤波器有两种形式,如图2a,和图2b所示.但考虑到在实际电路的调试过程中,一般用手工制作的电感和从市面上购买的电容相比,手制电感本身的衰减往往比电容衰减大,冈此,使用电感的总数应尽量少.在这里,低通滤波器的设计选择使用图2a形式. .工工L3£一'~;(b)另一种形图2两种归~化低通滤波器形式第三步:查表得到归一化的元件值.即:Ci=0.12031,C2=0.23421,Lz=1.12513,C3=1.61339,C4=0.71418,L4=0.76973,C5=0.81771第四步:对归一化低通滤波器进行频率和阻抗标度.将所有的电抗元件都除上一个频率标度系数(FSF),就可把一个已知滤波器响应标度到不同频率范围,即=㈤只进行频率标度后的滤波器的元件值很不实际,电容值太大,而1n的电阻值也不适宜,这种情况可以刚阻抗标度来解决.任何线性有源或无源网络,如果所有电阻和电感值乘阻抗标度系数z,而所有电容除以同样的系数z,其传递函数维持不变. 在这里,用FSF=2,rrf~=2'rr×30×10.和Z=50,对归一化低通滤波器进行频率和阻抗标度.去归一化数值的计算式为R=RZ(6)L=而L~Z(7)C=—FSF一~Z一(8)得到去归一化元件值,如图3的滤波电路所示.n图330M低通滤波电路采用PSPICE仿真软件,对30M低通滤波器电路仿真,仿真后可得到滤波器的传输特性如图4所示.3椭圆函数高通滤波器的设计弟一步:计算设计波彤参数.陡度系数为争==2(9)Ⅲ现Ai的最低阻带频率,即=丽950k=1.9(10)模角为6f=sin~1=sl~n-11=31.(11)第二步:洗择归一化高诵滤波器.第5期常会敏等:LC椭圆函数带通滤波器的设计及其仿真23 O—lo0ll.十一-'.一'.+1.O1030loo频率/MHz(a)幅频特性曲线,\,;,,.1频率/MHz(b)相频特性曲线图430M低通滤波器幅频,相频特性曲线如果1/s代替归一化低通传递函数中的,可以获得高通滤波器,低通衰减值将在等于低通频率倒数的高通频率上出现.简单地用电容替换每个电感或用电感替换每个电容,且利用元件值的倒数可以将归一化LC低通滤波器变换为相应的高通滤波器,表示为C高通=1/低通,£高通=1/C低通(12)信号源内阻和端接电阻不变.首先选择归一化低通滤波器,在阻带端点以内的最小衰减Ai至少为30dB,依然选择反射系数P=20%,由文[1]中图2—86所示的估算椭圆函数滤波器阶数用的曲线表明,在=1.9时,/I=5的滤波器可满足设计要求,具体编号为C05200:31..为使高通滤波器中电感总数最少,通常选择图2b的归一化低通滤波电路进行变换.查表得归一化低通元件值为L】=0.5773,L2=0.0834,C2=1.2413,L=1.4579,L:0.1788,C4=1.3610,L5=1.2945根据变换规则:C高通=1/L低通和L高通=1/Cf~通, 将归一化低通滤波器变换为归一化高通滤波器,变换结果如图5所示.第三步:计算得到归一化高通滤波器的元件值.C1=1.7322,C2=11.9904,L2=0.8056,图5低通到高通归一化滤波电路的变换C3=0.6859,C4=5.5928,L4=0.7348,第四步:对归一化高通滤波器进行频率和阻抗标度.低通到高通变换之后,把归一化的高通滤波器根据要求的截止频率和阻抗进行标度.这里,FSF= 2=21T×1×10,Z=50.然后同样根据计算公式(1),(2),(3)对归一化高通滤波器进行频率和阻抗标度,标度后的去归一化元件值如图6所示.1V2n图61M高通滤波电路采用PSPICE仿真软件对1M高通滤波器电路仿真,仿真后可得到滤波器的传输特性,如图7所示. O—loo||L』,一f,,VfI.1IrlrO.1lOl0o频率/MHz(a)幅频特性曲线I|lI………一,\\\-~1.01030频率/MHz(h)相频特性曲线图71M高通滤波器幅频特性和相频特性曲线删一一24哈尔滨理工大学第13卷4椭圆函数带通滤波器的设计宽带带通滤波器可通过级联一个低通滤波器和一个高通滤波器得到.这种方法的有效性是基于这样的假设:即这些滤波器即使级联,仍然保持它们自己的响应不变.如果低通和高通滤波器级联,且两个滤波器设计成具有相等的信号源阻抗和端接阻抗,它们的截止频率至少相距一个或两个倍频程,那么,每个滤波器在其通带内将有合适的端接阻抗.如果通带间隔不够, 由于阻抗变化,滤波器将相互影响,这时候常用一衰减器将两个滤波器隔离,使这种影响减至最小.1M到30M的宽带带通滤波器可通过级联一个截止频率为1M的低通滤波器和一个截止频率为30M的高通滤波器得到.两个滤波器通带间隔比较大,故不需要使用衰减器,而直接级联即可.级联成的带通滤波器电路如图8所示.5结语一l00f,|l,:—rI川I●●●●●图81M到30M带通滤波电路同样,采用PSPICE仿真软件对1M到30M的带通滤波器电路进行仿真,可得到滤波器的传输特性, 如图9所示.由文[1]知,设计滤波器时要综合考虑截止特性和相位失真的要求.截止特性好的,相位失真就严重,两者不可兼得.由图4,图7,图9的仿真特性曲线可以看出,在滤波器阻带内有零点出现(毛刺现象),这是由椭圆函数滤波器的特性决定的.根据对滤波器衰减特性的要求,此椭圆函数带通滤波器设计折中了截止特性和相位失真度,符合设计要求.同时这种方法同文[5]的方法相比较,不但克服了其繁杂性,且极大地节省计算量,设计过程非常简练. ,'\\,\,\.0.31.010301001.01030频率/MHz频率/MHz(a)幅频特性曲线(b)相频特性曲线图9IM到30M带通滤波器幅频特性和相频特性曲线电力线为非理想的随机参数通信信道,本身具有高噪声,高衰减,高畸变等特性.利用低压配电线进行高速数据通信,所使用的频段一般在1—30MHz之间.本文设计的1M到3oM带通滤波器通常用于低压电力线通信系统研究中,通常与耦合器联用,在发送端使高频信号经过滤波后耦合到低压电力线上进行传输,同时将电力线上的50Hz工频信号隔离;在接收端也同样起耦合,强电隔离,滤波作用.本文采用一种新的计算方法,用PSPICE仿真软件分别对1M到30M低通,高通,带通滤波器进行了设计和仿真分析,仿真结果与滤波器性能吻合,证明这种滤波器的设计方法是有效的.上述方法也适用于其他频段的椭圆函数低通,高通,带通滤波器的设计及仿真过程,具有一定的灵活性.为设计人员提供了一种参考,也可缩短滤波器设计时间和减少设计人员的劳动强度.参考文献:[1](美)阿瑟.B.威廉斯.电子滤波器设计手册[M].喻春轩,译.北京:电子工业出版社,1986.[2]熊俊俏,卢容德.模拟椭圆低通滤波器的设计与仿真[J].华jE航天工业学院.2001(11):66—67.[3]李秀人.用PSPICE实现电子电路的设计与分折[J].微电子与基础产品.2001(3):51—53.[4]王田,CELESTINOA.Corral,杨士中.椭圆滤波器边带优化设计方法研究[J].仪器仪表.2005(6):562—586.【5JANSARIR.EllipticFilterDesignforaClassofGeneralizedHalf- bandFilters[J].IEEETrans.1985,33(44):1146—1150.,(编辑:付长缨)。
微带低通滤波器的仿真设计

微带低通滤波器的仿真设计陕西理工学院毕业设计微带低通滤波器的仿真设计王艳磊(陕西理工学院电信工程系电子信息工程专业 2007级5班陕西汉中723000)指导教师:贾建科[摘要] 在实际的应用中~射频信号的频率范围非常广~通常所用的有用信号只是在很小的频段内~因此需要通过滤波器来实现。
滤波器是用来选择性地通过或抑制某一频段信号的装置。
在高频是滤波器通常由分布参数元件构成~因为其成本低且有较高的可重复性~而绝大部分分布参数滤波器都是用微带线设计的~通过在电路板上构成电路回路来实现滤波特性。
本文简要介绍了采用高低阻抗微带线实现分布参数低通滤波器的方法~并且着重通过一个具体设计实例给出微带滤波器的整个设计过程和AWR 仿真结果。
[关键词] 微带低通滤波器 AWR 仿真Design and Simulation of Microstrip Low-pass FilterWang Yan lei(Grade 07,Class 5,Major electronics and information engineering ,Electronics and informationengineering Dept.,Shaanxi University of Technology,Hanzhong 723000,Shaanxi)Tutor: Jia Jian Ke[Abstract]: In practical projects, the range of frequency is very wide. Useful signal is usually used only in a narrow band, so it needs filters. Filter is a device which is used to select frequency required. At high frequency, the filter is normallycomposed of distributed parameter components because of low cost and high repeatability. Most distributed parameter filters are designed by the microstrip line and achieve performance by constituting loop on the circuit board. This article briefly describes the method of achieving low-pass filter of distribution parameters with Stepped-Impedance, L-C Ladder Type Low-pass Filters and mainly gives the entire design process and the AWR simulation results based on a specific example.[Key words]: Microstrip Low-pass Filter AWR simulation陕西理工学院毕业设计目录第一章引言 (1)1.1研究的意义 (1)1.2滤波器的发展史 (1)国内外的研究动态 ........................................... 2 1.31.4 本设计主要完成的任务 (4)第二章微波滤波器及微带电路的基本理论 ......................... 5 2.1 微波网络 ................................................... 5 2.1.1 二端口网络 ............................................... 5 2.2 滤波器的传输函数 ........................................... 6 2.2.1 Butterworth响应 (7)Chebyshev2.2.2 响应 (7)Elliptical2.2.3 Function响应 ......................................8 2.3微波滤波器的参数 (9)2.4微带线的基本理论 ............................................ 9 第三章归一化原型滤波器设计 ................................. 12 3.1归一化低通原型滤波器 ....................................... 12 3.2切比雪夫低通原型 ........................................... 13 第四章微带低通滤波器的设计与仿真............................ 15 4.1 理论计算各元件的真实值 .................................... 15 4.2 理论计算微带低通滤波器的实际尺寸 .......................... 15 4.3 AWR软件的介绍 ............................................. 16 4.4仿真与实验结果 ............................................. 16 小结 ........................................................ 21 致谢 ........................................................ 22 [参考文献] (REFERENCES) . (23)陕西理工学院毕业设计附录(A)英文文献 (24)附录(B)英文文献的中文翻译 (30)陕西理工学院毕业设计第一章引言1.1研究的意义无线通信业务的迅猛发展,在给人们的沟通和生活带来方便的同时,无线通信系统也对无线电频谱资源的需求不断增加,使得目前适宜于无线通信的频谱资源变得越来越紧张。
七阶元件级仿真椭圆滤波器设计方法

2021年5月第40卷第5期洛阳师范学院学报Journal of Luoyang Normal UniversityMay,2021Vol.40No.5七阶元件级仿真椭圆滤波器设计方法降雪辉,孙滨(郑州工业应用技术学院信息工程学院,河南新郑451150)摘要:在通信系统中,连续时间滤波器是不可或缺的部分,如何灵活简洁地设计出易于集成、高频特性好、传输特性误差小的滤波器是电路与系统学界研究的重要方向.本文给出一种基于积分器模块的通用设计方法.该方法实现的电路结构中电阻与电容的元件数值合适,易于集成电路的工艺实现,并具有低的元件参数分散度.仿真结果表明所提出的电路方案正确有效,适于全集成.关键词:积分器;连续时间滤波器;信号流图;有限传输零点中图分类号:TN713文献标识码:A文章编号:1009-4970(2021)05-0019-030前言在通信系统中,连续时间滤波器是不可或缺的组成部分如何简洁地设计出易于集成、高频特性好和传输误差小的滤波器是电路系统学研究的重要方向.近年来,采用MOS IC技术设计的基于积分器的滤波器3切得到了广泛关注,这主要是因为基于积分器的滤波器技术十分适合超声频(>100kHz)的应用,且片内电阻与电容的元件数值合适,易于集成电路的工艺实现,并具有低的元件参数分散度,其既可以单片集成,也可以用于片上系统[1°-121.在设计基于积分器的滤波器时,以无源LC梯形网络为原型,采用有源技术模拟该结构的间接设计方法得到了广泛的应用.信号流图(SFG)技术是实现间接设计方法的一种十分有效的技术.参考文献[13]和参考文献[14]采用信号流图技术实现了基于电流传送器的全集成高阶椭圆滤波器,参考文献[15]介绍了基于积分器模块互联的信号流图技术,并给出了全极点滤波器的设计方法.本文采用基于积分器模块互联的信号流图技术,对于有限传输零点的高阶低通滤波器,推导得出了其电路形式和元件参数,并给出一种基于积分器模块的通用设计方法.本结构中的积分器模块既可以用经典的负反馈全差分运算放大器实现,又可以用基于OTA (operational transconductance amplifier)的电路实现.1基于信号流图的高阶椭圆滤波器设计方法对有源梯形滤波器进行设计,首先需设计无源网络,其设计原型为双端接载的LC梯形滤波器,由此得到的有源滤波器保持了LC原型滤波器低灵敏度和低元件参数分散度的特性.采用信号流图方法设计且不含有限传输零点的低通滤波器的方法在多篇文献中已有介绍山切,本文在此基础上,以五阶椭圆低通滤波器为例讨论含有限传输零点的梯形滤波器的信号流图设计方法,并给出其电路结构.全极点五阶低通滤波器的电路结构如图1所示, 其信号流图的设计方法在本文中不进行讨论,只给出其积分器模块互联结构(见图2),采用全差分运算放大器实现的电路结构如图3所示.五阶椭圆低通无源LC滤波器梯形原形电路如图4所示.通过分析推导其信号流图,即可得到设计所有高阶椭圆滤波器的通用方法.首先,对其列出三个节点电压方程:A-/3-(v.-vjs^-v.sC.=o,厶+(%-匕)sC”-i5-v4sC3-(r4-v6)sC b=o +(V4-V6)sC b-I7-V6sC5=0(1)收稿日期:2020-06-08基金项目:河南省高等学校重点科研项目计划(16A510022);河南省高等学校重点科研项目资助项目(20A520039);河南省高等学校青年骨干教师培养计划资助项目(2019GGJS279)作者简介:降雪辉(1979—),女,河南汝州人,博士,副教授;孙滨(1983—),男,河南遂平人,副教授.洛阳师范学院学报2021年第5期图1全极点五阶低通滤波器原形电路再次,采用全差分运算放大器实现了一种五阶椭圆低通滤波器电路,其结构图如图7所示.图中标出了用于实现有限传输零点的耦合电容.图3全差分运算放大器实现全极点五阶滤波器o n --_图4五阶椭圆低通无源LC 梯形滤波器原形电路经整理,可得到三个节点的电压分别表示为公式(2)、公式(3)和公式(4):—售―令 ⑵T/3 -15 Z C aT岭=M +C 。
低通滤波器的设计
低通滤波器的设计一、设计目的1、了解滤波器设计理论基础。
2、掌握滤波器设计软件Filter Solutions使用方法。
3、掌握无源滤波器设计及测试方法。
二、设计要求1、采用Filter Solutions设计低通滤波器。
2、低通滤波器的参数如下:(1)通带截止频率fc=20MHz(2)阻带截止频率fs=22MHz(3)通带最大衰减L1=-1.01db(4)阻带最小衰减L2=-60db三、设计工具Filter solutions2011四、设计原理1、椭圆滤波器(Elliptic filter):这是在通带和阻带等波纹的一种滤波器。
椭圆滤波器相比其他类型的滤波器,在阶数相同的条件下有着最小的通带和阻带波动。
它在通带和阻带的波动相同,这一点区别于在通带和阻带都平坦的巴特沃斯滤波器,以及通带平坦、阻带等波纹或是阻带平坦、通带等波纹的切比雪夫滤波器。
(1)首先看看巴特沃斯滤波器的频响特性:巴植沃思滤源器不同所数的比技0------------------------------------------------------------------------------------------------------- 0 02 口/ Q.E J □£ 1 1.2 /4 1.G 1,9可以看出巴特沃斯的通带和阻带都十分平缓。
(2)接下来是切比雪夫滤波器频响曲线:切比雪夫旗波器不同防地的匕技0 02 0.4 3.6 D,8 1.2 1.4 ',5 1 8看得出来,切比雪夫是阻带平稳,通带等波纹。
(3)接下来是椭圆滤波器:椭圆海谀器不同的效茏比较0 口 2 口4 口.E1 0日1 12 14 1.6 10 22、椭圆函数滤波器特点: 三种滤波器中,椭圆滤波器的过渡带最窄,但通带和阻带都是等波纹的,也就是说过渡带的特性是由牺牲阻带和通带的稳定性换来的。
而对于相同的性能要求,它所需要的阶数最低。
椭圆低通滤波器的设计与仿真

中图 分 类 号 :T 7 3 N 1 文 献 标 识 码 :A 文章 编 号 : 10 0 9—99 2 1) 1 0 0—0 4 2( 2 0 —0 1 0 3
的应用中 ,信号经过 D C A 转换后 ,输 出的信号并
不能真正地连续可变 ,只能输出阶梯模拟信号并
伴 有 杂 散 干 扰 ,这 是 由 于 D C分 辨 率 有 限造 成 A
的 。 为 了得 到特 性 好 的信 号 ,设 计 了一个 椭 圆低 通滤 波器 ,并确 定 了阶数 及相关 参数 。
度 特 性 和 瞬态 特性 ,但 是 它 的过 渡带 过 于平 缓 一 1 ; 切 比雪 夫滤 波 器 的通 带 是 等波 纹 抖 动 的 ,阻带 是 平 坦 的 ,过 渡 带 比 巴特 沃 思 稍 陡 ,但 瞬 态 特 性
1 现 方 案 的 比较 实
滤 波 器可 以分 为有 源 滤 波器 和 无 源滤 波 器 。 1
限 大 阻带 处衰 减 为 无 限大 。而椭 圆 函数滤 波 器 在
率相应特性 ,并能减小体积 。但 由于受到运放带
宽 的限制 ,有源滤 波器 的滤波频带 一般 不是很
高 。无源滤波器采用分立元件进行设计 ,其频率
范 围 比较 宽 ,一般 用 于 高频 设 计 。本 设 计 的输 人
有源滤波器的设计引入了有源元件 一集成运算放 大器 ,由于运算放大器具有近似理想 的特性 ,且 可以省去 电感 ,因此可以得到接近理论预测 的频
差 ;椭圆滤波器的幅值响应在通带和阻带 内都是 等 波纹 的 ,对 于给定 的阶数 和给定 的波纹要 求 , 椭 圆滤波器 的过渡带很窄 ,并且其过渡带下降迅 速。讨论的滤波器都是全极点网络 ,它们仅在无
椭圆形的低通滤波器仿真计算
椭圆形的低通滤波器推导、AR7400低通滤波器原理图AR7400中5-阶的椭圆形的低通滤波器, C71, L15,和C77 组成。
B注鑿cw----- )1---- ------ n------ 畠k J.*FF-lU5CAR7400 IC~.-rCEv*£.■如ALOS站ZfEDiGftTAL"M.S 'KAC.''-LA N-IA"MW■•」.*DO NOT CONNECTEIOQTFRIMTI由元件C75, C70, L14, C79, L16, C76, C80, L17,二、单端线上的椭圆低通滤波器1. 归一化椭圆低通滤波器模型特性:通带内有起伏,阻带内也有起伏:Iff画腑故型LPF的嚣减特性I通带由和駅带山懈有起伏》2. 5-阶椭圆低通滤波器的归一化模型:Ur归一化低通滤波器截止频率为(1/2n)Hz,特征阻抗1 Q;帯内起伏■为6 lidH时的阻帯内J1自斜牛陪诜点的扁■薫徽空LPF的设计裁抿3. 利用归一化模型设计低通滤波器步骤:利用归一化LPF 的设廿 数擔来设计潼波器时的步骤4. 频率和阻抗变换计算公式:… 待设计滤波器的截止频率U == ------------------ : ------------------------基淮滤波器的截止频率[“ L(old)r(new) —M厂C^Ld)mlK待设计滤波器的阻抗 基准滤波當的阻抗I * <nr<) = L(u i (i) * K厂丿、—C (直<oQ (new] .5. 设计一个截止频率为68MHz 阻抗为50Q 的低通滤波器:6. 对归一化低通滤波器滤波器进行频率变换:L2 1.16391H1 --II -i… C2・ L C4-0.21867F '" 0.08130F"~L C 3Lil. 04770H42, 31423 FC51. S3695FC1 1. 51534F5阶归一化低通滤波器截止频率为(1/2n) Hz,特征阻抗1 Q;基准滤波器的截止频率68MHz(l/2n )Hz(l/2n )Hz515243548PFC515240477HLc163S1H725nH 2636953833. 247pF53548pFv5阶低通滤波器截止频率为68M Hz, C2512p F&C3541^pF427. 04 x 100. 08130 F2.3142427. 041 10190诃 511.SS6PFC3c 2427. 04 x 10 '特征阻抗1Q7.对以上滤波器进行阻抗变换L2 2. 725nH〒C53833. 247pF63 X 10—H£二 4乩 04 x 10 6427. 04 x 10 6 —待设计滤波器的截止频率427. 04 x 10 &427. 04 x 10 6— 427. 04 x 10 £0. 2186x10"pF427, 0*2 x10 61. 0477x10 ,F427. 04 x 10 £2. 3142KIO ]2P F427. 04 x 10 60.08130x 101?pF427- 04 x 心1”16391xio Y F427. 04 x 10 &1.63695x 1O 1?PF5152仇1012P F_____L_1朴tC4190pF特设计滤波器阻抗750C1 二3548 诃K6 —511. 896 PFKL ]二2. 45nH * K = C3 =5419 pFK_c 4 二190 PFK _3548 P F---------------- =47. 3pF75511. 396 PF =良 827pF751S3. 975nH5419 P F---------------- ---- 12. 25pF75ISO pF---------- 二 2. 533pF75L 2 = 2. 725rH * K 二 204. 375nH3833. 247pF6 二—3B33. 247pF— ------------------ =51pF75$C372- 25pF〒砧51pF5阶低通滤波器截止频率为 68M Hz,特征阻抗50 Q;8.对5阶低通滤波器截止频率为68MHz ,特征阻抗50Q 仿真;基准澹波需阻抗1Q二75L1133.975nHC26. S27pF204- 375nHC4 2. 533pF5阶低通滤波器截止频率为68MHz,特征阻抗50Q仿真图形仿真结果:通带内有两个起伏点,阻带内有两个陷波点,通带截止频率68MHz插损小于1.2dB,阻带内带外抑制》23 dB (at87 〜125MHz ), > 60 dB(at125 〜860MHz );9.对AR7400单端线滤波器的仿真;当滤波器中的容值和电感值变化时,如下图,并对其进行仿真,AR7400滤波器的一部分仿真结果:通带内有两个起伏点,阻带内有两个陷波点,通带截止频率80MHz 插损小于1.35dB,阻 带内带外抑制》17dB (at90〜〜860MHz );说明:电容变小截止频率变大,带外抑制变小;三、差分线上的椭圆低通滤波器与单端走线的比较差分信号与传统的一根信号线一根地线(即单端信号)相比,其优点是:a 、 抗干扰能力强。
7阶LC滤波器报告
武汉理工大学
开放性实验报告
项目名称:7阶LC滤波器
实验室名称:608-19 创新实验室学生姓名:张天亮王冠赵海峰
创新实验项目报告书
实验名称7阶LC滤波器日期2011-3-1
姓名张天亮王冠赵海峰专业信息学院
一、实验目的(详细指明输入输出)
1、设计一个七阶LC滤波器,要求截止频率15MHz,50欧姆阻抗匹配。
二、实验原理(详细写出理论计算、理论电路分析过程)
1、LC滤波器的介绍
LC滤波器也称为无源滤波器,是传统的谐波补偿装置。
LC滤波器之所以称为无源滤波器,顾名思义,就是该装置不需要额外提供电源。
LC滤波器一般是由滤波电容器、电抗器和电阻器适当组合而成,与谐波源并联,除起滤波作用外,还兼顾无功补偿的需要。
2、LC滤波器的优势
LC滤波器具有结构简单、设备投资少、运行可靠性较高、运行费用较低等优点,应用很广泛。
3、LC滤波器的分类
LC滤波器又分为单调谐滤波器、高通滤波器、双调谐滤波器及三调谐滤波器等几种。
本实验采用filter solutions滤波器设计软件,设置好相应的参数,进行电路图的设计。
然后有Tina软件进行仿真调试。
图1-1 7阶LC滤波器电路图
计算公式如下:
图2 计算公式
图3 filter solutions的仿真曲线
三、实验步骤(记录实验流程,提炼关键步骤)
a)确定元件型号,查找相关资料,设计最初的设计原理图。
b)在仿真软件上进行仿真。
c)进行硬件仿真。
d)按照电路原理图焊接电路板。
e)对电路板进行调试,并进行改进。
基于DDS椭圆型低通滤波器的设计
中国科技核心期刊研究与开发2009年1月第28卷 第1期基于DDS 椭圆型低通滤波器的设计李春剑 吉望西 刘达伦(中国计量科学研究院 北京 100013)摘 要:低通滤波器是直接数字频率合成器的重要组成部分,其性能的优劣直接影响整个直接数字合成器的特性。
本文使用一种全新的归一法,为直接数字频率合成器设计了一个截止频率为100M Hz 的7阶椭圆型低通滤波器,同时通过Multisim9对其进行仿真,仿真结果表明该滤波器幅频特性良好,可以达到预期的指标,在实际应用时元件值应进行必要的调整。
该方法可适用于不同频段不同阶数不同类型滤波器的设计。
关键词:椭圆型低通滤波器;Multisim9仿真;直接数字频率合成器;归一化方法中图分类号:TN713 文献标识码:ADesign of low 2pass elliptic f ilter based on direct digital synthesizerLi Chunjian Ji Wangxi Liu Dalun(National Institute of metrology ,Beijing 100013)Abstract :Low 2pass filter is an important part of t he direct digital synt hesizer ,whose performance directly affect s t he characteristics of the whole synt hesizer.This paper introduces a 7t horder low 2pass elliptic filter wit h t he cut 2off frequency of 100M Hz for t he direct digital synt hesizer wit h a new normalization met hod.Multisim9simulation shows that it has a good p hase frequency characteristic and it can achieve t he desired target s.However ,t he component values should necessa 2rily be adjusted in t he practical application.This met hod can be applied to filters of different frequency segment s ,different orders and different styles.K eyw ords :low 2pass elliptic filter ;simulation ;direct digital synt hesizer ;normalization met hod 作者简介:李春剑,中国计量科学研究院在读硕士研究生,研究方向为原子干涉绝对重力测量。
基于Multisim的有源低通滤波器的设计与仿真分析
作者简介
1/H(w)
闫姝(1984-),女,汉,山西和顺人,助教, 硕士,研究方向:信号与信息处理。
图 5:合点前移的等效变换 可解得该系统的传递函数为
作者单位
兰州石化职业技术学院 730060
甘肃省兰州市
136 • 电子技术与软件工程
Electronic Technology & Software Engineering
基于multisim的有源低通滤波器的设计与仿真分析基于multisim的有源低通滤波器的设计与仿真分析文闫姝关键词有源滤波器传递函数multisim幅频特性本文总结了由低阶系统构建高阶信号系统的基本过程和方法通过子系统函数的级联法结合系统的反馈设计了一类新的有源高阶滤波器最后通过节点法对该电路来进行验证
参考文献
图 4:高阶滤波系统电路图 根据自动控制理论,在电路中可以通过 改变综合点或分支点的位置就能消除回路之间 的交错关系,因此可以对于综合点的前移并进 行如下的等效变换,如图 5 所示。
H(w) H(w)
[1] 徐发强等 .RC 高阶有源滤波器的新型实验 方法 [J]. 现代电子技术 ,2008,2(265):6568. [2] 郑君里等 . 信号与系统 [M]. 北京 : 高等 教育出版社 ,1981. [3] 姚佩阳等 . 自动控制原理 [M]. 北京 : 清 华大学出版社 . 北京 : 北京交通大学出版 社 ,2005.
3 结语
总结了由低阶系统构建高阶信号系统的 基本过程和方法,运用子系统函数的级联、反 馈构建高阶系统的思想来设计有源高阶滤波 器,然后用节点法对设计的电路来进行分析验 证,并用仿真软件 Multisim 进行电路仿真。 本文的研究对于有源低通滤波器的设计具有指 导意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 滤波器 的分 类
滤波器可分 为 :有源滤波器 和无源滤波器 ; 按其 特性又可分为 :巴特沃思 ( 逼近 )滤波器 、
切 比雪 夫 ( 逼 近 )滤 波 器 、逆切 比雪 夫 型 、椭 圆 型滤波器和贝塞尔 ( 逼 近 )滤波 器 等 。其 中 巴特
a c hi e v e t h e d e s i r e d t a r g e t s . Ke y wo r ds : DDS s i g n l a g e n e r a t o r ;n o r ma l i z a t i o n me t h o d; l o w- p a s s e l l i p t i c il f t e r ; Mu l t i s i m1 0; s i mu l a t i o n ’
D OI : 1 0 . 3 9 6 9/ j . i s s n . 1 0 0 9 - 9 4 9 2 . 2 0 1 3 . 1 1 . 0 0 5
7 阶椭圆型低通滤波器的设计及仿真木
王 涛 ,刘 洋 ,左 月明
( 1 . 乌 兰察布职 业学院 机 电技术 系, 内蒙古集宁 0 1 2 0 0 0 ;2 . 山西农业 大学 工学院 , 山西太谷 0 3 0 8 0 1 )
0引言 在D D S 信号发生器实现过程 中,由于 D D S自
身的结构特点 ,实际存在着 固有 的误差 :相位截 断误差 、幅度量化误差 、D A C 转换误差等导致其
兆 赫兹 ,所 以在 这 里选 用 L C无 源 滤 波 器 。在 本
信 号发生器 中,低通滤波器采用具有较窄过渡带
( 1 . E l e c t r o me c h a n i c a ቤተ መጻሕፍቲ ባይዱ T e c h n o l o g y D e p a r t me n t o f Wu l a n c h a b u V o c a t i o n a l C o l l e g e ,J i n i n g 0 1 2 0 0 0 ,C h i n a ;2 .
De s i g n a n d S i mu l a t i o n o f 7 Or d e r Lo w- Pa s s El l i p t i c Fi l t e r
W ANG T a o ,L I U Ya n g 。 ,Z UO Yu e — mi n g
输 出信号 中必然含有 大量 的噪声和干扰n ;又因 为信 号发生器所 用 的D D S 芯片 A D 9 8 5 4 内部没有
滤 波器且输 出端 带有 内部 时钟 干扰成分 ,因此 , 低通 滤波器 ( L P F )的使用是非常必要 的 ,在每 个输 出端都要设 置一个 L P F ,通过选择合适 的截 止 频 率 ,可 较 好 地 滤 除 干扰 和 杂 散 ,其 性 能 的优
摘要 : 低通 滤波器是 D D S 信 号发生器的重要组成部分 , 其性 能的优劣直接影响整个信号 发生器的技 术指标 。使用一种全新的归
一
法 ,为 D D S 信号 发生器 设计 了一个截 止频率 为 1 2 0 M H z 的7 阶椭 圆型低 通滤波 器 ,并 使用 M u l t i s i m l 0 仿 真软件 对其进 行仿
真 ,仿真结果表明该滤波器 幅频特性 良好 ,可 以达到预期的指标 。
关键词 : D D S 信号发生器 ;归一 法 ; 椭 圆型低通滤波器 ;M u l t i s i m 1 0 ;仿 真
中图分类号 : T N 7 1 3 文献标 识码 : A 文章编号 :1 0 0 9 — 9 4 9 2 ( 2 0 1 3 ) 1 1 — 0 0 1 7 — 0 2
En g i n e e r i n g C o l l e g e o f S h a n x i Ag r i c u l t u r a l Un i v e r s i t y ,T a i g u 0 3 0 8 0 1 ,Ch i n a )
Abs t r a c t :L o w— pa s s il f t e r i s a n i mp o r t a n t p a r t o f t h e DDS s i g n a l g e n e r a t o r , wh o s e p e r f o r ma n c e d i r e c t l y a f f e c t s t h e t e c h n i c a l i n d i c a t o r s o f t h e wh o l e s i g n a l g e n e r a t o r . Th i s p a p e r i n t r o d u c e s a 7 o r d e r l o w- p a s s e l l i p t i c f i l t e r wi t h t h e c u t —o f f r e q u e n c y o f 1 2 0 MHz f o r t h e DDS
s i g n a l g e ne r a t o r wi t h a n e w n o r ma li z a t i o n me t h o d . Mu l t i s i m1 0 s i mu l a t i o n s h o ws t h a t i t h a s a g o o d p h a s e f r e q ue n c y c h a r a c t e r i s t i c a n d i t c a n
