二次函数双图像问题
二次函数y=ax2的图像和性质

教案教学内容二次函数y=ax²的图象和性质一、学习目标:1.会用描点法画出二次函数y=ax2的图象;2.根据对特殊函数图象的观察,归纳得出二次函数y=ax2的性质;3.进一步理解二次函数和抛物线的有关知识,并能解决一些简单的应用问题;4.领悟数形结合的数学思想方法,培养观察能力、分析能力和归纳能力.二、知识回顾:1.画函数图象的一般步骤:(1)列表;(2)描点;(3)连线.2.什么是一次函数?怎么画一次函数y=-x+2的图象?形如y=kx+b(k≠0)的函数叫做一次函数.(1)列表:(2)描点;(3)连线.3.什么叫二次函数?一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数,其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.想一想:怎么画二次函数的图象?二次函数有哪些性质?三、知识梳理:1.二次函数y=ax2的图象的画法画二次函数y=ax2的图象,一般用描点法,具体步骤如下:(1)列表:以坐标原点(0,0)为中心,在其左右两边均匀地选取一些便于计算的x值,并计算出对应的y的值,列出表格;(2)描点:把每对x与y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点;(3)连线:按自变量的取值由小到大(或由大到小)的顺序,用平滑的曲线连接各点,即可得到二次函数的大致图像。
【例1】在同一平面直角坐标系中,画出函数y= -2x2,y=x2,y=2x2的图象。
2.二次函数y=ax²的图象和性质:二次函数y=ax²的图象是一条关于y轴对称的抛物线.其图象与性质如下图所示:a的符号a>0 a<0 图象开口方向开口向上开口向下a 的绝对值越大,开口越小顶点坐标(0,0)顶点是最低点顶点是最高点对称轴y轴增减性x>0时,y随x的增大而增大;x<0时,y随x的增大而减小x>0时,y随x的增大而减小;x<0时,y随x的增大而增大最值x =0时,y有最小值0 x =0时,y有最大值0【例2】函数y=(k+1)x2(k+1≠0)的图象的顶点是,对称轴是,当k 时,图象的开口向上,这时函数有最值;当k ,时,图象的开口向下,这时函数有最值。
二次函数的图像和性质(共82张PPT)

y=ax2
向上
y轴 (0,0)
向下
y轴 (0,0)
4、二次函数y=2x2+1的图象与二次函数y=
2x2的图象开口方向、对称轴和顶点坐标是否相
同?它们有什么关系?我们应该采取什么方法
来研究这个问题?
画出函数y=2x2和函数y= 2x2+1的图象, 并加以比较
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y 1 x2 ··· 2
8
4.5
2 0.5 0 0.5 2 4.5
8
···
x
·· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
y 2x2 · 8 4.5 2 0.5 0 0.5 2 4.5 8
·· ·
y y x2 8
y 2x2
···
6
y 1 x2
4
2
2
-4
-2 O
24
在对称轴左侧,y都随x的增大而增大,
在对称轴右侧,y都随 x的增大而减小 .
联系: y=a(x-h)²+k(a≠0) 的图象可以看成y=ax²的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),
再沿对称轴整体上(下)平移|
|个单位 (当
>0时向上平移;当 <0时,向下平移)得到的.
y 1 x2
y1
1 3
x2
2
3
y2
1 3
x2
2
的图像
在同一直角坐标系中
画出函数 y 1 x2 5 y
y1
1 3
x2
2
3
y2
的图像
二次函数y=ax2+bx+c的图像与性质

◆本节课内容一、二次函数y=ax2+bx+c1、二次函数y=ax2+bx+c可以用配方法转化为y=a(x-h)2+k的形式:2、二次函数y=ax2+bx+c的图像的作法:二次函数y=ax2+bx+c的图像是一条对称轴平行于y轴的抛物线。
它的图像常见作法有两种:五点法和平移法。
方法一:五点法先用配方法将y=ax2+bx+c(a≠0)化为y=a(x-h)2+k(a≠0)的形式,确定抛物线的顶点、开口方向、再以顶点为中心,在对称轴的两侧对称地各取两对值进行列表,最后描点画图。
方法二:平移法利用平移法作二次函数y=ax2+bx+c的图像的一般步骤如下:(1)利用配方法将二次函数y=ax2+bx+c化为y=a(x-h)2+k的形式,确定其顶点为(h,k);(2)作出二次函数y=ax2的图像;(3)将函数y=ax2的图像平移,使其顶点(0,0)平移到(h,k),平移后的图像即是二次函数y=ax2+bx+c的图像。
3、二次函数y=ax2+bx+c的图像及性质如下表:二、二次函数y=ax2+bx+c(a≠0)的图像特征与系数a,b,c的符号关系注意:(1)b的符号由a的符号和对称轴的位置来决定(2)a+b+c(或a-b+c)可以看成是x=1(或x=-1)时的函数值。
三、二次函数解析式的求法求二次函数的解析式y=ax2+bx+c,需求出a,b,c的值。
由已知条件(如二次函数图像上三点的坐标)列出关于a,b,c的方程组,求出a,b,c的值,就可以写出二次函数的解析式。
◆课堂练习题型一利用公式法直接求抛物线的顶点、对称轴及最值1、求二次函数y=(x+5)(x-1)的对称轴、顶点及最值。
题型二、由抛物线的顶点、对称轴及最值求字母或代数式的取值范围2、二次函数y=ax2+bx+1(a≠0)的图像的顶点在第一象限,且过点(-1,0)。
设t=a+b+1,则t 的取值范围是()A、0<t<1B、0<t<2C、1<t<2D、-1<t<1题型三、二次函数图像平移规律的直接应用3、抛物线y=-2x2-4x-5经过平移得到抛物线y=-2x2,平移的方法是()A、向左平移1个单位,再向下平移3个单位B、向左平移1个单位,再向上平移3个单位C、向右平移1个单位,再向下平移3个单位D、向右平移1个单位,再向上平移3个单位题型四、根据抛物线的平移求字母的值4、已知抛物线y=x2+4x+1向上平移m(m>0)个单位得到的新抛物线过点(1,8),求m的值1题型五、利用二次函数y=ax2+bx+c的图像判断各项系数的符号5、二次函数y=ax2+bx+c的图像如图,那么abc,2a+b,a+b+c这3个代数式中,值为正数的有( c )A、3个B、2个C、1个D、0个题型六、利用二次函数的性质比较函数值得大小6、若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图像上的三点,则y1,y 2,y3的大小关系是()题型七、利用二次函数的增减性求字母的取值范围7、已知二次函数y=x2-(m+1)x+1,当x≥1时,y随x的增大而增大,求m的取值范围。
二次函数图像中的几何问题

以抛物线上的三个点为顶点的三角形称为抛物线的内接三角形。已知内接三角形的三个顶点的坐标可以求出抛物线的表达式。
例2、已知抛物线与x轴交于点A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3),抛物线顶点为D,联结AD、AC、CD。
(1)求该抛物线的表达式;
(2)△ACD与△COB是否相似?如果相似,请给予证明;如果不相似,请说明理由。
(1)求A、B两点的坐标;(用m的代数式表示)
(2)如果平行四边行ABCD的顶点D在上述二次函数的图像上,求m的值。
四、综合问题
函数图像中的几何问题已成为历年中考的热门考题,而二次函数的图像与几何图形的结合更是考查的重点,因此,熟悉这类问题的解题思路是必须具备的能力。
下面的例题是抛物线与平行四边、相似三角形的综合。
为。
7、抛物线的顶点为M(2,3),且经过点A(0,-1),若该抛物线上另有点B(m,-1),则m的值为。
8、若抛物线 与x轴交于点A、B,与y轴交于点C,且△ABC是等腰直角三角形,则a、c之间的数量关系是。
9、若抛物线的顶点A在x轴上,且抛物线经过B(0,2),△AOB为等腰三角形,则该抛物线的表达式
(3)若直线AB交y轴于点E,在直线AB上找点F,使△CEF∽△AOM,求点F的坐标。
小结:本题涉及的几何图形是:内接于抛物线与直线之间的平行四边形和相似三角形。解题的关键是:(1)函数 图像上的点的坐标可以表示为P(x,f(x)),即用解析式来代替纵坐标;(2)用垂直于x轴的直线去截函数 和 图像,则截得的线段长PQ=∣f(x)-g(x)∣(其中x为点P或点Q的横坐标)。
精练12+1:
1、若抛物线 与x轴相交于点A、B,顶点为P,则△PAB是()
培思数学-------“二次函数图像形状相同” 问题

培思数学-------“二次函数图像形状相同” 问题
1、如果把一个二次函数的图像向上平移a 49个单位(a>0),再向左平移2
5个单位,就得到第二个二次函数2y ax =的图像。
(1)、写出第二个二次函数定点的坐标(可用a 表示);
(2)若第一个二次函数图像经过A(x 1, 0), B(x 2, 0), C (0, y 3)三点,其中x 1<x 2, 且y 3是x 1与x 2的比例中项,求函数解析式。
2,将抛物线 542y 2+-=x x 作下列移动后,求得到新的抛物线方程。
(1)向左平移2个单位,再向下平移3个单位;
(2)顶点不动,将原抛物线开口反向;
(3)以x 轴为对称轴,将原抛物线开口反向。
2、已知抛物线 c bx x a ++=2y 的形状与抛物线 32
1y 2+=x 相同,它的对称轴是x=-2, 它与x 轴两个交点距离为2,求:(1)图像与x 轴两交点坐标; (2)确定二次函数的解析式。
初中数学课件 2二次函数y=ax2的图象

当x ≠ 0时,y<0.
活动三、应用迁移
例1.
(1)若抛物线y=(2-m)xm2-3有最低点,则m=---------------
(2)点A(-3,y1),B(-2,y2),C(-1,y3)在抛物线
y=ax (a<0)上,则y ,y ,y 的大小关系是 2
x>0时,y随x增大而增大 x>0时,y随x增大而减小
做一做
(1)抛物线y=5x 的顶点坐标是(0,0) ,开口 向上 2 -------------------------对称轴是 y轴 ,在对称轴 右 侧,y随着x的增大而增 大;在对称轴左 侧,y随着x的增大而减小,当x= 0 时,函数y的值最小,最小值是 0 ,抛物线y=5x2在x轴 的_上___方(除顶点外). (2)抛物线 y 2 x2 当x<0时,y随着x的 增大而增大 ; 3 当x >0 ,y随着x的增大而减小; ------------------
作业:金榜行动 P4第1-10题,选做P5第6、8题
活动三、应用迁移
例3.已知正方形周长为Ccm,面积为Scm2; (1)求S和C之间的函数关系式,并画出图像; (2)根据图像,求出S=1cm2时,正方形的周长; (3)根据图像,求出C取何值时,S≥4cm2 .
结束寄语
下课了!
只有不断的思考,才会 有新的发现;只有量的 变化,才会有质的进步.
∴x的值可取负数、零、正数
(2)为了计算和描点方便,x取整数.且以1为 间距取值,取有代表性的7对值
画函数y=x2的图象.
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
二次函数图像问题
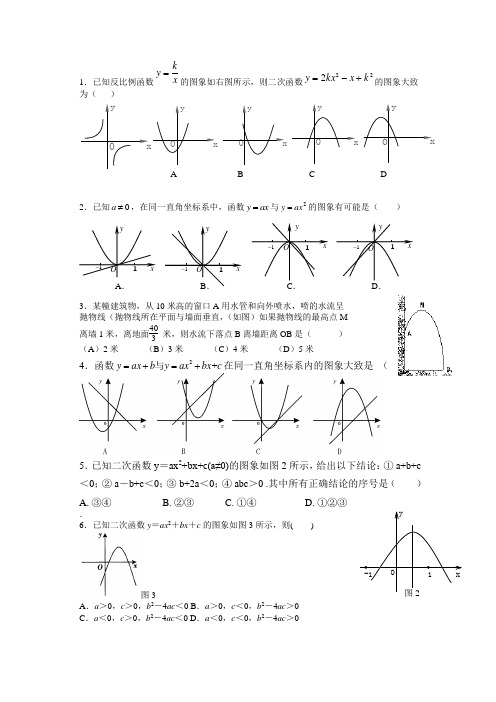
1.已知反比例函数x k
y =
的图象如右图所示,则二次函数2
2
2k x kx y +-=的图象大致为( )
2.已知0≠a ,在同一直角坐标系中,函数ax y =与2ax y =的图象有可能是( )
3.某幢建筑物,从10米高的窗口A 用水管和向外喷水,喷的水流呈 抛物线(抛物线所在平面与墙面垂直,
(如图)如果抛物线的最高点M
离墙1米,离地面40
3
米,则水流下落点B 离墙距离OB 是(
)
(A )2米 (B
)3米 (C )4米
(D )5米
4.函数2
+y ax b y ax bx c =
+=+与在同一直角坐标系内的图象大致是 (
)
5
.已知二次函数y =ax 2+bx+c(a≠0)的图象如图2所示,给出以下结论:① a+b+c
<0;② a -b+c <0;③ b+2a <0;④ abc >0 .其中所有正确结论的序号是( )
A. ③④
B. ②③
C. ①④
D. ①②③
.
6.已知二次函数y =ax 2
+bx +c 的图象如图3所示,则(
)
图3
A .a >0,c >0,b 2-4ac <0
B .a >0,c <0,b 2-4ac >0
C .a <0,c >0,b 2-4ac <0
D .a <0,c <0,b 2
-4ac >0
A . A
B
C D。
图像法解二次函数问题例析
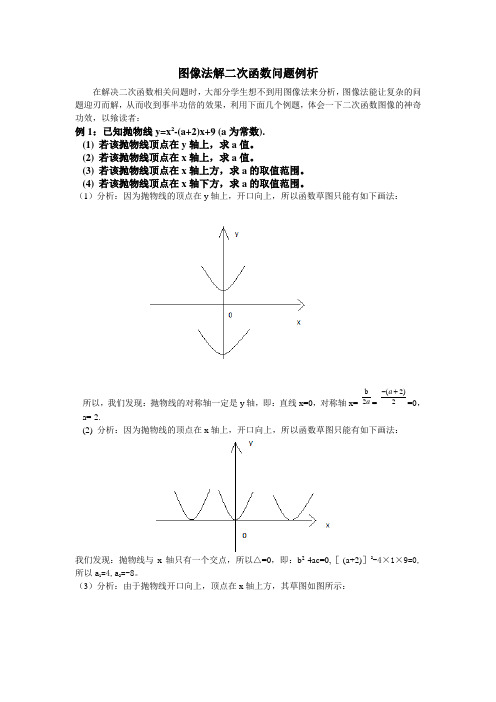
图像法解二次函数问题例析在解决二次函数相关问题时,大部分学生想不到用图像法来分析,图像法能让复杂的问题迎刃而解,从而收到事半功倍的效果,利用下面几个例题,体会一下二次函数图像的神奇功效,以飨读者:例1:已知抛物线y=x2-(a+2)x+9 (a为常数).(1)若该抛物线顶点在y轴上,求a值。
(2)若该抛物线顶点在x轴上,求a值。
(3)若该抛物线顶点在x轴上方,求a的取值范围。
(4)若该抛物线顶点在x轴下方,求a的取值范围。
(1)分析:因为抛物线的顶点在y轴上,开口向上,所以函数草图只能有如下画法:所以,我们发现:抛物线的对称轴一定是y轴,即:直线x=0,对称轴x=-b2a=-(2)2a-+=0,a=-2.(2) 分析:因为抛物线的顶点在x轴上,开口向上,所以函数草图只能有如下画法:我们发现:抛物线与x轴只有一个交点,所以△=0,即:b2-4ac=0,[-(a+2)]2-4×1×9=0,所以a1=4,a2=-8。
(3)分析:由于抛物线开口向上,顶点在x轴上方,其草图如图所示:于是有:抛物线与x轴没有交点,△<0,△=b2-4ac=〔-(a+2)〕2-4×1×9<0,∴a的取值范围是-8<a<4.(4) 分析:由于抛物线开口向上,顶点在x轴下方,其草图如图所示:于是有:抛物线与x轴有两个交点,△>0,△=b2-4ac=〔-(a+2)〕2-4×1×9>0,∴a的取值范围是a<-8或a>4.例2:某二次函数图像经过点A(2,a)和点B(-4,a),则这个二次函数图像对称轴是直线。
分析:抛物线草图如图所示:因为:抛物线是轴对称图形,观察图像得:对称轴是直线x=422-+=-1,即x= -1.例3:已知抛物线y=x2-2x+c经过点A(-1,y1)和点B(2,y2),比较y1与y2的大小。
分析:根据解析式可得:对称轴为直线x=1,且开口向上,抛物线草图如图所示:观察图像得:y1 >y2.例4:若二次函数y=ax2+bx+c (a≠0)图像如图所示,当x=2时,y的值是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数双图像问题 猿题库
单选题
1. 已知抛物线(
)的顶点为,点
,
,
在该抛
物线上,当
恒成立时,
的最小值为()。
A. B. C. D.
2. 如图,抛物线与轴交于点,,把抛物线在轴及其上方的部分记作
,将
向右平移
得
,
与轴交于点,,若与
共有个不同的交点,则的取值范围是()。
A. B. C.
D.
3. 二次函数,当
且
时,的最小值为
,最大值为
,则
的值为
()。
A.
B.
D.
C.
4.
5. 如图,垂直于轴的直线分别与抛物线
和抛物线
交于,两点,
过点作轴分别于轴和抛物线交于点,,过点作
轴分别与轴和抛物线
交于点
, ,则的值为()。
A. B.
C.
D.
6. 已知抛物线与轴交于、两点,将这条抛物线的顶点记为,连接、,则
的值为()。
A. B.
D.
C.
6. 如图,反比例函数
的图象经过二次函数
图象的顶点
(
),则有()。
1
A.
B.
C.
D.
7. 一次函数()、二次函数和反比例函数()在同一直角坐标系中
的图象如图所示,点的坐标为,则下列结论中,正确的是()。
A.
B.
C.
D.
8. 抛物线的图象如图所示,则反比例函数与一次函数在同
一坐标系内的图象大致是()。
9. 已知直线与坐标轴分别交于点,,点在抛物线上,能使
为等腰三角形的点的个数有()。
A. 个
B. 个
C. 个
D. 个
10. 如图,抛物线与交于点,过点作轴的平行线,分别交两条
抛物线于点,。
则以下结论:①无论取何值,的值总是正数;②;③当时,
;④;其中正确结论是()。
2
A. ①②
B. ②③
C. ③④
D. ①④
11. 已知二次函数与轴只有一个交点,且图象过,两点,则、的关
系为()。
A. B. C. D.
12. 给出下列命题及函数,和的图象:①如果,那么;②如果,
那么;③如果,那么;④如果时,那么。
则()。
A. 正确的命题是①④
B. 错误的命题是②③④
C. 正确的命题是①②
D. 错误的命题只有③
13. 如图,已知点,为坐标原点,是线段上任意一点(不含端点,),过、两点的二次
函数和过、两点的二次函数的图象开口均向下,它们的顶点分别为、,射线与相交于点。
当时,这两个二次函数的最大值之和等于()。
A.
B.
C.
D.
14. 如图,直线与轴交于点,与直线交于点,以为边向右作菱形,点恰
与原点重合,抛物线的顶点在直线上移动。
若抛物线与菱形的边、都
有公共点,则的取值范围是()。
3
A.
B.
C.
D.
15. 如图,抛物线与双曲线的交点的横坐标是,则关于的不等式的解集是
()。
A.
B.
C.
D.
16. 如图所示,抛物线()与轴交于点、。
直线与此抛物线
交于点,与轴交于点,在直线上取点,使。
连接、、、。
某同学根据
图象写出下列结论:①;②当时,;③四边形是菱形;
④。
你认为其中正确的是()。
A. ②③④
B. ①②④
C. ①③④
D. ①②③
17. 如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,则下列关系不正确的是
()。
A.
B.
C.
D. ,
4
二次函数双图像问题猿题库
18. 如图,抛物线与交于点,过点作轴的平行线,分别交两条
抛物线于两点,且分别为顶点.则下列结论:
①;②;③是等腰直角三角形;④当时,。
其中正确结论的个数是()。
A. 个
B. 个
C. 个
D. 个
19. 如图,把抛物线沿直线平移个单位后,其顶点在直线上的处,则平移后的抛物线解析
式是()。
A.
B.
C.
D.
20. 如图,在平面直角坐标系中,抛物线经过平移得到抛物线,其对称轴与两段抛物线
所围成的阴影部分的面积为()。
A.
B.
C.
D.
21. 如图,二次函数的图象过点。
它与反比例函数的图象交于点则这
个二次函数的解析式为()。
5。
