期权平价公式
从平价公式的角度看期权常见策略
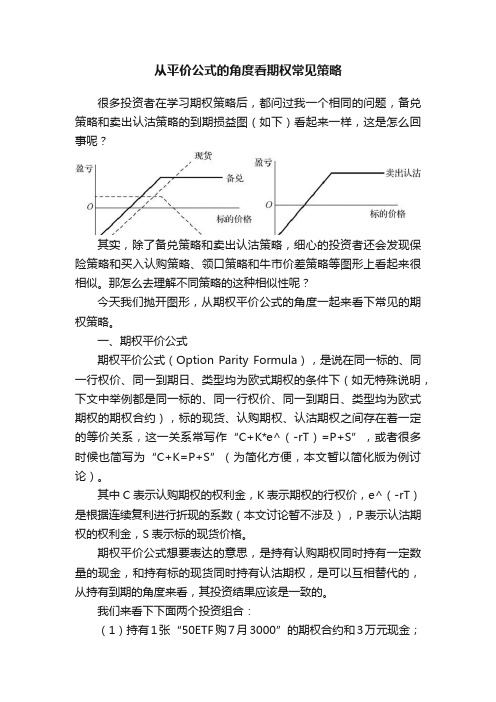
从平价公式的角度看期权常见策略很多投资者在学习期权策略后,都问过我一个相同的问题,备兑策略和卖出认沽策略的到期损益图(如下)看起来一样,这是怎么回事呢?其实,除了备兑策略和卖出认沽策略,细心的投资者还会发现保险策略和买入认购策略、领口策略和牛市价差策略等图形上看起来很相似。
那怎么去理解不同策略的这种相似性呢?今天我们抛开图形,从期权平价公式的角度一起来看下常见的期权策略。
一、期权平价公式期权平价公式(Option Parity Formula),是说在同一标的、同一行权价、同一到期日、类型均为欧式期权的条件下(如无特殊说明,下文中举例都是同一标的、同一行权价、同一到期日、类型均为欧式期权的期权合约),标的现货、认购期权、认沽期权之间存在着一定的等价关系,这一关系常写作“C+K*e^(-rT)=P+S”,或者很多时候也简写为“C+K=P+S”(为简化方便,本文暂以简化版为例讨论)。
其中C表示认购期权的权利金,K表示期权的行权价,e^(-rT)是根据连续复利进行折现的系数(本文讨论暂不涉及),P表示认沽期权的权利金,S表示标的现货价格。
期权平价公式想要表达的意思,是持有认购期权同时持有一定数量的现金,和持有标的现货同时持有认沽期权,是可以互相替代的,从持有到期的角度来看,其投资结果应该是一致的。
我们来看下下面两个投资组合:(1)持有1张“50ETF购7月3000”的期权合约和3万元现金;(2)持有1张“50ETF沽7月3000”的期权合约和10000份50ETF。
假设现在到了7月期权合约到期日,根据50ETF到期价格的不同,我们分情况来讨论:(1)到期50ETF价格高于3元,则组合1中认购合约是实值合约,此时会选择行权,交付3万元现金,然后收到10000份50ETF;组合2中认沽合约是虚值合约,到期失效即可,此时剩余10000份50ETF。
比较组合1、2,都是10000份50ETF,结果是一样的。
(2)到期50ETF价格低于3元,则组合1中认购期权是虚值合约,到期失效即可,此时剩余3万元现金;组合2中认沽合约是实值合约,此时会选择行权,交付10000份50ETF,然后收到3万元现金。
pcp远期平价公式

pcp远期平价公式一、什么是PCP平价公式?Put-CallParity(简称PCP)平价公式是经典的期权定价模型之一。
因其限制条件较少和公式简洁等因素,该模型在场内外期权市场得以广泛运用。
PCP平价公式表述的是相同行权价格、相同到期日的欧式无分红期权的认购期权(C)、认沽期权(P)、标的证券价格(S)和行权价格(K)之间的关系。
其具体公式如下:C+Ke-r(T-t)=P+S公式中K为认购和认沽期权合约的行权价格,Ke-r(T-t)表示对金额K折现,r为无风险利率,T-t为期权合约剩余期限二、公式如何推导?对于公式的推导,我们通常使用资产复制的形式。
我们看以下两种资产组合到期后,标的证券S会出现两种情况。
第一种情况,如果到期标的证券S的价格大于K元,我们观察两种组合的状态:组合一中的认购期权C,由于标的价格大于行权价格,所以投资者选择行权,即用K元购买标的证券S;而持有的Ke-r(T-t)元投资于无风险产品,到期正好获得K元的回报,用于行权,所以最终投资者只持有标的证券S。
组合二中的认沽期权P,由于标的价格大于行权价格,所以投资者放弃权利,即不行权,合约价值归零;而持有的标的证券S没有任何变化,所以最终投资者只持有标的证券S。
因此,当到期标的证券价格S大于K元时,组合一等于组合二,都是持有标的证券S。
第二种情况,如果到期标的证券S的价格小于K元,我们观察两种组合的状态:组合一中的认购期权C,由于标的价格小于行权价格,所以投资者放弃权利,即不行权,合约价值归零;而持有的Ke-r(T-t)元投资于无风险产品,到期正好获得K元的回报,所以投资者最终持有K 元现金。
组合二中的认沽期权P,由于标的价格小于行权价格,所以投资者选择行权,即按照K元的价格将手中的标的证券S卖出,获得K元现金;而持有的标的证券S,正好用于行权交割,卖出标的证券,所以投资者最终仍然持有现金K元。
因此,当到期标的证券价格S小于K元时,组合一等于组合二,都是持有现金K元。
数理金融复习题(含答案)

V
t 1
P m t 1 r 1 r m m
c
mT
代入数据得:
2 20
V
(1
t 1
90 2 0.12 t 2
)
1000 774.30 12 2 20 (1 0.2 )
11.企业 1 在时期 t 1 将发行 100 股股票,该种股票在时期 t 2 的价 值为随机变量 V1 (2) 。企业的资金都是通过发行这种股票而筹集的,以 至于股票持有者有资格获得完全的收益流。最后给出的有关数据是
各股票之间的相关系数为 甲乙 =0.8,乙丙 =0.75,丙甲 =0.85, 银行在 0 时刻
-4-
注:此答案仅供参考,若有错漏敬请见谅!
发行债券,价格为 10 元,1 时刻赎回价为 12.5 元。求 (1)各股票的期望收益率; (2)各股票收益率的方差; (3)若某投资者对甲乙丙三种股票及债券的投资组合为 求 的期望收益率和方差。
(2)?
(3)?
bx 14.若某投资者的效用函数为V ( x ) e , b 0 ,
(1)判断该投资者的风险类型; (2)计算阿罗—伯瑞特(Arrow-Pratt)绝对风险厌恶函数。
解:(1) V ( x) be
bx
0, V ( x) b 2 e bx 0, 所以该投资者为风险厌恶型。
T T 16.已知两种股票 A,B 的期望回报率向量为 r (r1 , r2 ) (0.1, 0.2) ,协
0.1 0.12 V 0.12 0.2 方差矩阵为
计算(1)最小方差证券组合中两种股票 A,B 投资比例; (2) 最小方差证券组合的回报率。
期权平价公式

期权平价公式:
C+ Ke^(-rT)=P+S
认购期权价格C与行权价K的现值之和等于认沽期权的价格P加上标的证券现价S
Ke^(-rT):K乘以e的-rT次方,也就是K的现值。
e 的-rT次方是连续复利的折现系数。
也可用exp(-rT)表示贴现因子。
根据无套利原则推导:
构造两个投资组合。
1.看涨期权C,行权价K,距离到期时间T。
现金账户Ke^(-rT),利率r,期权到期时恰好变成行权价K。
2.看跌期权P,行权价K,距离到期时间T。
标的物股票,现价S。
看到期时这两个投资组合的情况。
1.股价St大于K:投资组合1,行使看涨期权C,花掉现金账户K,买入标的物股票,股价为St。
投资组合2,放弃行使看跌期权,持有股票,股价为St。
2.股价St小于K:投资组合1,放弃行使看涨期权,持有现金K。
投资组合2,行使看跌期权,卖出标的物股票,得到现金K
3.股价等于K:两个期权都不行权,投资组合1现金K,
买
卖出买入
S K C P 买
出
买入
S K C
P 行权价K 低于现
行权价K 高于现投资组合2股票价格等于K 。
从上面的讨论我们可以看到,无论股价如何变化,到期时两个投资组合的价值一定相等,所以他们的现值也一定相等。
根据无套利原则,两个价值相等的投资组合价格一定相等。
所以我们可以得到C+Ke^(-rT)=P+S 。
换一种思路理解:C- P = S- Ke^(-rT)
认购期权价格C 与认沽期权的价格P 的差等于证券现价与行权价K 现值的差。
期权价格计算公式

期权价格计算公式股票的价格变化遵循一维维纳过程,其微分方程如下 dz t s b dt t s a ds ),(),(+=式中:dz 的差分∆Z 满足如下条件的正态分布t z ∆=∈∆在一般情况下,ds 可用下式表示:sdz sdt ds σμ+=----------- (1)或表示为:dz dt sds σμ+= 式中:s μ股票价格的期望漂移率,μ 为一个恒定参数;2)(s σ为股票价格波动的方差, σ 为股票价格的波动率,可以通过观察股票价格的动态系列数据获得。
如果存在一个变量 G ,它是股票S 的一种衍生证卷,它的价格是S 和 t 的函数,G(s,t),那么,S 和G 都受到同一个基本的不确定性因素的影响。
根据ITO 定理,函数G 的行为遵循如下微分方程描述的过程:Sdz S G dt S S G t G S S G dG σσμ∂∂+∂∂+∂∂+∂∂=)21(2222 -------------(2)函数G 的漂移率为222221S SG t G S S G σμ∂∂+∂∂+∂∂ 方差为222)(S SG σ∂∂如果G 代表股票S 的一种期权,我们想用S 和G 构造一组风险中性的证卷组合。
为此,首先将公式(1)、(2)改写成对应的差分形式:z S t S S ∆+∆=∆σμ ---------------(3)z S SG t S G t G S S G G ∆∂∂+∆∂∂+∂∂+∂∂=∆σμ)21(22 ----------(4) 由于公式(3)、(4)中的z ∆t ∆=∈()是相同的维纳过程,只要证卷数量的搭配合理,整卷组合就可以消除z ∆。
恰当的证卷组合是:-1; 卖空一个期权S G∂∂+;买入期权价值变化对股票价格的敏感度,也就是他的偏微分那样多的股票。
定义这个证卷组合的价值为∏,表达式为 S S G G ∏∂∂+-= ---------(5)t ∆时间后,这个证卷组合的价值变化为:S S G G ∆∂∂+∆-=∆∏ -----------(6)将(3)、(4)带入(6),消去z ∆,得:t S S G t G ∆∂∂-∂∂-=∆∏)21(2222σ ---------(7)由于这个证卷组合是风险中性的,所以,它的收益一定与任何一个无风险证卷的收益相同,就是∏∏∆=∆t r ---------(8)将(5)、(7)带入(8),得:t S SG G r t S S G t G ∆∂∂-=∆∂∂+∂∂)()21(2222σ 将上式进一步化简,得:rG S G S S G rS t G =∂∂+∂∂+∂∂222221σ --------(9)这就是获得诺贝尔奖的Black-Scholes 微分方程。
期权平价公式范文

期权平价公式范文
期权是金融衍生品市场上的一种合约,给予期权持有人在未来特定时间内以事先约定的价格买入或卖出标的资产的权利。
购买期权的投资者可以选择是否行使该权利,而出售期权的投资者则必须根据合约的条款执行买卖行为。
平价关系是指具有相同到期日的看涨期权和看跌期权,在特定条件下具有相同的合理价格。
期权平价公式则是用于计算这种平价关系的数学公式。
1.计算看涨期权的平价公式:
C + Ke^{-rt} = P + S
其中C表示看涨期权的价格,K表示行权价格,e表示自然对数的底数,r表示无风险利率,t表示到期日的时间间隔,P表示看跌期权的价格,S表示标的资产的现货价格。
这个公式表明,看涨期权的价格加上购买期权的成本,等于看跌期权的价格加上标的资产的现货价格。
2.计算看跌期权的平价公式:
C + S = P + Ke^{-rt}
其中C表示看涨期权的价格,S表示标的资产的现货价格,P表示看跌期权的价格,K表示行权价格,e表示自然对数的底数,r表示无风险利率,t表示到期日的时间间隔。
这个公式表示,看涨期权的价格加上标的资产的现货价格,等于看跌期权的价格加上购买期权的成本。
3.计算标的资产价格的平价公式:
C - P = S - Ke^{-rt}
其中C表示看涨期权的价格,P表示看跌期权的价格,S表示标的资产的现货价格,K表示行权价格,e表示自然对数的底数,r表示无风险利率,t表示到期日的时间间隔。
这个公式表示,看涨期权的价格减去看跌期权的价格,等于标的资产的现货价格减去购买期权的成本。
期权入门基础知识单选题100道及答案解析

期权入门基础知识单选题100道及答案解析1. 期权是一种赋予期权买方在规定期限内按双方约定的价格()一定数量某种金融资产的权利的合约。
A. 买入B. 卖出C. 买入或卖出D. 以上都不对答案:C解析:期权买方有权在规定期限内按约定价格买入或卖出一定数量的某种金融资产。
2. 以下关于期权的说法,错误的是()A. 期权买方的风险有限B. 期权卖方的收益有限C. 期权买方需要支付权利金D. 期权卖方不需要支付保证金答案:D解析:期权卖方需要支付保证金。
3. 期权按照行权时间的不同,可以分为()A. 欧式期权和美式期权B. 看涨期权和看跌期权C. 实值期权、虚值期权和平值期权D. 场内期权和场外期权答案:A解析:按行权时间分,期权分为欧式期权和美式期权。
4. 欧式期权只能在()行权。
A. 期权到期日B. 期权到期日前的任何一天C. 期权到期日前一周D. 以上都不对答案:A解析:欧式期权只能在到期日行权。
5. 美式期权可以在()行权。
A. 期权到期日B. 期权到期日前的任何一天C. 只能在到期日前一周D. 以上都不对答案:B解析:美式期权在到期日前的任何一天都可行权。
6. 看涨期权的买方预期标的资产价格会()A. 上涨B. 下跌C. 不变D. 以上都有可能答案:A解析:看涨期权买方预期标的资产价格上涨。
7. 看跌期权的买方预期标的资产价格会()A. 上涨B. 下跌C. 不变D. 以上都有可能答案:B解析:看跌期权买方预期标的资产价格下跌。
8. 对于看涨期权,当标的资产价格()执行价格时,期权处于实值状态。
A. 高于B. 低于C. 等于D. 以上都不对答案:A解析:看涨期权,标的资产价格高于执行价格为实值。
9. 对于看跌期权,当标的资产价格()执行价格时,期权处于实值状态。
A. 高于B. 低于C. 等于D. 以上都不对答案:B解析:看跌期权,标的资产价格低于执行价格为实值。
10. 当标的资产价格等于执行价格时,期权处于()状态。
期权定价公式

期权定价公式期权定价公式是:期权价格=内在价值+时间价值。
期权定价模型,由布莱克与斯科尔斯在20世纪70年代提出。
该模型认为,只有股价的当前值与未来的预测有关;变量过去的历史与演变方式与未来的预测不相关。
模型表明,期权价格的决定非常复杂,合约期限、股票现价、无风险资产的利率水平以及交割价格等都会影响期权价格。
期权是购买方支付一定的期权费后所获得的在将来允许的时间买或卖一定数量的基础商品的选择权。
期权价格是期权合约中唯一随市场供求变化而改变的变量,其高低直接影响到买卖双方的盈亏状况,是期权交易的核心问题。
在国际衍生金融市场的形成发展过程中,期权的合理定价是困扰投资者的一大难题。
随着计算机、先进通讯技术的应用,复杂期权定价公式的运用成为可能。
简单期权定价模型。
我们把股价随机末态简化为两个等效的等概率量子态,要么50%的概率上涨到+1X的右边一个标准差处,要么50%的概率下跌到-1X的左边一个标准差处。
显然,对于认购期权,在-1X末态的行权收益是0;在+1X末态的行权收益是S*(1+σ)-K。
其中S是当前(初态)股价,K是到期日的行权价。
根据初态=末态期望值的原理,认购期权价格C=0.5*0+0.5*[S*(1+σ)-K]= 0.5*[S*(1+σ)-K]。
这对于平值和浅度虚值期权是适用的。
对于平值期权K=S,C=0.5*S*σ。
比如,当前股价S=3.3元,月波动率为σ=6%,那么行权价K=3.3元,剩余T=30天期限的平值认购期权价格就是,C=0.5*3.3*6%=0.0990元。
对于深度实值期权,当股价末态为-1X处,仍然会有行权收益。
所以,认购期权价格C=0.5*[S*(1-σ)-K]+0.5*[S*(1+σ)-K]=S-K。
比方说,对于深度实值期权实三K=3.0元,当股价从当前价S=3.3元下跌至末态(-1X处)ST=3.1元,仍然会有3.1-3.0=0.1元的行权收益。
所以,实三期权价格C=S-K=3.3-3.0=0.3元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
买入put 卖出call
买入标的物 S
K C
P 买入put 卖出call 买入标的物
S K
C
P
行权价K 低于现货价格S
行权价K 高于现货价格S 期权平价公式:
C+ Ke^(-rT)=P+S
认购期权价格C 与行权价K 的现值之和等于认沽期权的价格P 加上标的证券现价S Ke^(-rT):K 乘以e 的-rT 次方,也就是K 的现值。
e 的-rT 次方是连续复利的折现系数。
也可用exp (-rT )表示贴现因子。
根据无套利原则推导:
构造两个投资组合。
1.看涨期权C ,行权价K ,距离到期时间T 。
现金账户Ke^(-rT),利率r ,期权到期时恰好变成行权价K 。
2.看跌期权P ,行权价K ,距离到期时间T 。
标的物股票,现价S 。
看到期时这两个投资组合的情况。
1.股价St 大于K :投资组合1,行使看涨期权C ,花掉现金账户K ,买入标的物股票,股价为St 。
投资组合2,放弃行使看跌期权,持有股票,股价为St 。
2.股价St 小于K :投资组合1,放弃行使看涨期权,持有现金K 。
投资组合2,行使看跌期权,卖出标的物股票,得到现金K
3.股价等于K :两个期权都不行权,投资组合1现金K ,投资组合2股票价格等于K 。
从上面的讨论我们可以看到,无论股价如何变化,到期时两个投资组合的价值一定相等,所以他们的现值也一定相等。
根据无套利原则,两个价值相等的投资组合价格一定相等。
所以我们可以得到C+Ke^(-rT)=P+S 。
换一种思路理解:C- P = S- Ke^(-rT)
认购期权价格C 与认沽期权的价格P 的差等于证券现价与行权价K 现值的差。
