平面直角坐标系培优习题
平面直角坐标系经典培优好题

平面直角坐标系第一节平面直角坐标系的基本概念一、基本概念有序数对:把有顺序的两个数a与b组成的数对叫做__________,通常记作__________。
在平面内画两条互相__________、__________重合的数轴,组成平面直角坐标系。
水平的数轴称为__________,竖直的数轴称为__________,两坐标轴的交点为__________,__________数对做点的坐标。
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限、第四象限,坐标轴上的点不属于任何象限。
确定坐标的方法:由点M向__________轴引垂线,垂足在__________轴上的坐标为__________,由点M向__________轴引垂线,垂足在__________轴上的坐标为__________。
基础训练1、写出图中点D,E,F,G的坐标。
在图中找出点比A(1,3),B(-2,-2)2、如图所示,人头左边的嘴角的坐标是()。
A、(1,-1)B、(-4,0)C、(-1,1)D、(-1,-3)二、点的特征1、第一象限上的点的特征:______________________________。
2、第二象限上的点的特征:______________________________。
3、第三象限上的点的特征:______________________________。
4、第四象限上的点的特征:______________________________。
5、原点O 的坐标:_________x 轴上的点的坐标:__________。
y 轴上的点的坐标:__________平行于x 轴直线上的点的________ _坐标相同。
平行于y 轴直线上的点的_________坐标相同。
请分别写出第一象限、第二象限、第三象限、第四象限、X 轴、Y 轴。
基本用法(1)确定点的位置。
培优练习(附答案) -平面直角坐标系

平面直角坐标系一、平面直角坐标系中的点的特征 1、对于点p(x,y),(1)在第一象限时,0>x ,0>y ; (2)在第二象限时,0<x ,0>y ; (3)在第三象限时,0<x ,0<y ; (4)在第四象限时,0>x ,0<y ; 2、对于点p(x,y), (1)在x 轴上时,0=y ,x 可取任意数;(2)在y 轴上时,0=x ,y 可取任意数;3、对于点p(x,y),(1)若在第一、三象限的角平分线上时,y x =;(2)若在第二、四象限的角平分线上时,横、纵坐标互为相反数,即0=+y x . 5、平行于x 轴的直线上的点纵坐标相同,横坐标不同;平行于y 轴的直线上的点的横坐标相同,纵坐标不同.例1:(1)已知在平面直角坐标系中,点2(+m P ,)1+m 是x 轴上的一点,则点P 的坐标为 .(2)若点b a M +(,)ab 在第二象限,则点a N (,)b 在第 象限. (3)已知线段AB ∥x 轴,若点A 的坐标为(1,2),线段AB 的长为3,则点B 的坐标为 .分析:(1)x 轴上的点纵坐标为0;(2)第二象限上的点横坐标为负数,纵坐标为正数;(3)平行于x 轴上的点纵坐标相同.练:1、已知1(M ,)2-,a N (,)b .若MN ∥x 轴,则=a ,=b ;若MN ∥y 轴,则=a ,=b ;MN ⊥x 轴,且MN =2,则N .二、探索点的坐标规律解决点的规律探索型问题应从最简单的情形入手,进而找出规律、解决问题.例2:在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x 轴的正方形.边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为( ) A 、64 B 、49 C 、36 D 、25分析:求出边长1,2,3,4,5,6,7的正方形的整点的个数, 得到边长为1和2的正方形内部有1个整点,边长为3和4的 正方形内部有9个整点,边长为5和6的正方形内部有25个 整点,推出边长为7和8的正方形内部有49个整点, 即可得出答案.-1-111O y x1、在平面直角坐标系中,点1A (1,1),2A (2,4),3A (3,9),4A (4,16),…,用你发现的规律确定点9A 的坐标为 .2、如图,将长方形ABCD 放置在平面直角坐标系中,A B ∥x 轴,且AB =4,AD =2,且A (2,1). (1)求B ,C ,D 的坐标,并说明将长方形ABCD 进行怎样的平移使点C 移到点A 处; (2)y 轴上是否存在点P ,使△PAB 的面积等于长方形ABCD 面积的43,若存在,求出P 点坐标;若不存在,说明理由.DCBA yx4321654321O参考答案例1:(1)P(1,0) (2)第三象限 (3)B (4,2)或(-2,2) 练1:1≠a , 2-=b ;1=a ,2-≠b ; (1,0)或(1,-4) 例2:B练2:(1)4A (2,0);8A (4,0);12A (6,0);(2)n A 4(n 2,0); (3)向上. 例3:18.5 四、巩固练习1、(9,81). 提示:n A n (,2n )2、(1)B (6,1),C (6,3),D (2,3),将长方形ABCD 先向左平移4个单位,再向下平移2个单位,可使点C 移到点A.(2)存在,理由如下:设0(P ,a ),则121-⋅=∆a AB S ABP ∴43241421⨯⨯=-⨯⨯a∴31=-a ,∴4=a 或-2故P (0,4)或(0,-2)。
4平面直角坐标系-点的坐标的确定基础题和培优题

平面直角坐标系【点的坐标的确定】【基础练习】1.已知点P的坐标为(﹣2,a2+1),则点P一定在()A.第一或第三象限B.第二或第四象限C.第二象限D.第三象限2.点P(m+3,m+1)在直角坐标系x轴上,则点P坐标为()A.(0,﹣2)B.(0,2)C.(﹣2,0)D.(2,0)3.点B(﹣3,4)关于y轴的对称点为A,则点A的坐标是()A.(3,4)B.(﹣4,﹣3)C.(4,﹣3)D.(﹣3,﹣4)4.已知A(2,﹣5),AB平行于y轴,则点B的坐标可能是()A.(﹣2,5)B.(2,6)C.(5,﹣5)D.(﹣5,5)5.点M(﹣4,3)关于y轴对称的坐标为()A.(4,3)B.(﹣4,﹣3)C.(4,﹣3)D.(﹣4,3)6.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为()A.(3,2)B.(3,1)C.(2,2)D.(﹣2,2)7.点M(3,﹣4)关于x轴的对称点M′的坐标是()A.(3,4)B.(﹣3,﹣4)C.(﹣3,4)D.(﹣4,3)8.已知y轴上的点P到原点的距离为5,则点P的坐标为()A.(5,0) B.(0,5)或(0,﹣5) C.(0,5) D.(5,0)或(﹣5,0)9.若|m|=2,|n|=3,则点A(m,n)()A.四个象限均有可能B.在第一象限或第三象限或第四象限C.在第一象限或第二象限D.在第二象限或第三象限或第四象限10. 点M (1,2)关于x 轴对称点的坐标为( )A 、(-1,2)B 、(-1,-2)C 、(1,-2)D 、(2,-1)11. 在直角坐标系中,如果a 为正数,那么点(0,a )在( )A .x 轴正半轴上B .x 轴负半轴上C .y 轴正半轴上D .y 轴负半轴上12. 在y 轴上且到点A (0,4)的线段长度为5的点B 的坐标是( )A .(0,9)B .(0,-1)C .(9,0)或(-1,0)D .(0,9)或(0,-1)13. 点P 的横坐标是-3,且到x 轴的距离为5,则P 点的坐标是( )A .(5,-3)或(-5,-3)B .(-3,5)或(-3,-5)C .(-3,5)D .(-3,-5)14. 若4,5==b a ,且点M (a ,b )在第二象限,则点M 的坐标是( )A .(5,4)B .(-5,4)C .(-5,-4)D .(5,-4)15. 如果点P (x ,y )满足xy=0,那么点P 必定在( )A .原点上B .x 轴上C .y 轴上D .坐标轴上16. 在平面直角坐标系中,点P (2,﹣3)关于原点对称点P′的坐标是 .17. 在平面直角坐标系上,若点M (a+5,a ﹣3)在y 轴上,则点M 的坐标为 .18. 已知A (x+5,2x+2)在x 轴上,那么点A 的坐标是 .19. 一只蚂蚁由(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是 .20. 有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为 .21. 已知AB 在y 轴上,A 点的坐标为(0,﹣3),并且AB=7,则B 的坐标为 .22. 点A (3,﹣2)关于y 轴对称的点的坐标是 ;点A 关于原点对称的点的坐标是 .点A 关于x 轴对称的点的坐标为 .23. 若点A 在第二象限,且到x 轴的距离为3,到y 轴的距离为2,则点A 的坐标为_______.24. 点P (3,5)关于y 轴对称的点的坐标是 .25. 点M (-3,-8)到x 轴的距离为_____,到y 轴的距离为______.26. 已知点A (1,1),B (2,2),C (3,3),D (4,4),这些点的横坐标x 和纵坐标y 的关系是______.27. 如果点P (a ,2)在第二象限,那么点Q (-3,a )在_______.28. 点A 在x 轴上,位于原点的右侧,距离坐标原点5个单位长度,则此点的坐标为 ;点B 在y 轴上,位于原点的下方,距离坐标原点5个单位长度,则此点的坐标为 ;点C 在y 轴左侧,在x 轴下方,距离每个坐标轴都是5个单位长度,则此点的坐标为 .29. 通过平移把点A (2,-1)移到点A'(2,2),按同样的平移方式,点B (-3,1)移动到点B',则点B’的坐标是 .30. 已知点M 在轴上,则点M 的坐标为_____.【培优练习】31. 已知△ABC 在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC 关于y 轴对称,那么点A 的对应点A′的坐标为( )A . (﹣4,2)B . (﹣4,﹣2)C . (4,﹣2)D . (4,2)32. 已知点P (x ,y )在第二象限|x+1|=2,|y ﹣2|=3,则点P 的坐标为( )A . (﹣3,5)B . (1,﹣1)C . (﹣3,﹣1)D . (1,5)33. 如图的象棋盘上,若○帅位于点(1,-2)上,○相位于点(3,-2)上,则○炮位于点( ) A .(-1,1) B .(-1,2) C .(-2,1) D .(-2,2)()a a -+4,3y 图3相帅炮34. 已知点P 坐标为(2-a ,3a+6),且P 点到两坐标轴的距离相等,则点P 的坐标是( )A .(3,3)B .(3,-3)C .(6,-6)D .(3,3)或(6,-6)35. 点A (-2,-3)与点B (-3,-2)在直角坐标系中( )A .关于x 轴对称B .关于y 轴对称C .关于原点对称D .不关于坐标轴和原点对称36. 已知点A ,如果点A 关于轴的对称点是B ,点B 关于原点的对称点是C ,那么C 点的坐标是( )A .B .C .D .37. 一只小虫子在一个小方格的线路上爬行,它起始的位置是A (2,2),先爬到B (2,4),再爬到C (5,4),最后爬到D (5,5),则小虫一共爬行了( )个单位.A .7B . 6C . 5D . 438. 已知直角坐标系中的点A ,点B 的坐标分别为A (2,4),B (4,0),且P 为AB 的中点,若将线段AB 向右平移3个单位后,与点P 对应的点为Q ,则点Q 的坐标为( )A .(3,2)B .(6,2)C .(6,4)D .(3,5)39. 已知点M 1(-1,0)、M 2(0,-1)、M 3(-2,-1)、M 4(5,0)、 M 5(0,5)、M 6(-3,2),其中在x 轴上的点的个数是( )A .1 个B .2 个C .3个D .4个40. 如果点P (,)与点P 1(,)关于轴对称,则,的值分别为( )A .B .C .D .41. 小明家的坐标为(1,2),小丽家的坐标为(-2,-1),则小明家在小丽家的( )A .东南方向B .东北方向C .西南方向D .西北方向42. 点A (1,0),B (0,2),点P 在x 轴上,且三角形PAB 的面积为5,则P 点坐标为( )A .(-4,0)B .(6,0)C .(-4,0)或(6,0)D .无法确定43. 一个长方形在平面直角坐标系中三个顶点的坐标为(–1,–1)、(–1,2)、(3,–1),则第四个顶点的坐标为( )A .(2,2)B .(3,2)C .(3,3)D .(2,3)()2,2-x ()2,2()2,2-()1,1--()2,2--m -35-n y m n 3,5=-=n m 3,5==n m 3,5-=-=n m 5,3=-=n m44.在直角坐标中有两点M(a,b),N(a,-b),则这两点()A.关于x轴对称 B.关于y轴对称C.关于原点对称 D.上述结论都不正确45.由坐标平面内的三点A(1,1),B(3,-1),C(1,-3)构成的△ABC是()A.钝角三角形 B.直角三角形; C.锐角三角形 D.等腰直角三角形46.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(-4,-1)、N(0,1),将线段MN平移后得到线段M ′N ′(点M、N分别平移到点M ′、N ′的位置),若点M ′的坐标为(-2,2),则点N ′的坐标为.47.已知点A(-2,2),B(-1,1),C(0,0),D(1,-1),E(2,-2),这些点的横坐标x和纵坐标y的关系是_______.48.ABC中,A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,则对应点A′,B′,C′的坐标分别为_____,_____,_______.49.已知AB∥x轴,A的坐标为(3,2),并且AB=4,则B的坐标为________.50.已知点A(-2,6),B(-1,5),C(0,4),D(1,3),E(2,2),这些点的横坐标x 和纵坐标y的关系是_________.【课后练习】1.到x轴的距离等于2的点组成的图形是()A.过点(0,2)且与x轴平行的直线B.过点(2,0)且与y轴平行的直线C.过点(0,-2)且与x轴平行的直线D.分别过(0,2)和(0,-2)且与x轴平行的两条直线2.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为()A.(-2,-5) B.(-2,5) C.(2,-5) D.(2,5)3.已知三角形的三个顶点坐标分别是(-1,4),(1,1),(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是()A.(-2,2),(3,4),(1,7) B.(-2,2),(4,3),(1,7)C.(2,2),(3,4),(1,7) D.(2,-2),(3,3),(1,7)4.线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,– 1)的对应点D的坐标为()A.(2,9) B.(5,3)C.(1,2) D.(– 9,– 4)5.在平面直角坐标系中,点A(-1,0)与点B(0,2)的距离是.6.由坐标平面内的三点A(-2,-1),B(-1,-4),C(5,-2)构成的三角形是_____三角形.7.如图的围棋盘,放在某个平面直角坐标系内,白棋②的坐标是(-7,-4),白棋④的坐标是(-6,-8),那么黑棋①的坐标是.。
平面直角坐标系培优训练

平面直角坐标系一、选择题1、如图,若在象棋盘上成立直角坐标系,使“帅”位于点(-1, -2).“馬”位于点( 2,-2),则“兵”位于点()A 、( -1,1)B、(-2 ,-1)C、(-3,1)D、(1,-2)(第1题)(第3题)(第8题)2、在平面直角坐标系中,点P 的坐标为( -2,a2+1),则点 P 所在的象限是()A 、第一象限B、第二象限C、第三象限D、第四象限3、如图,在平面直角坐标系中,以O(0,0),A ( 1, 1),B( 3,0)为极点,结构平行四边形,以下各点中不可以作为平行四边形极点坐标的是()A 、( -3,1)B、(4,1)C、( -2,1)D、( 2, -1)4、若点 A (2, n)在 x 轴上,则点 B(n-2,n+1)在()A 、第一象限B、第二象限C、第三象限D、第四象限5、已知点 P(x,|x|),则点 P 必定()A 、在第一象限 B、在第一或第四象限 C、在 x 轴上方 D、不在 x 轴下方6、在直角坐标系中,点( x, y)知足 x+y<0,xy> 0,则点( x,y)在()A 、第一象限B、第二象限C、第三象限D、第四象限7、点 M 在 y 轴的左边,到 x 轴, y 轴的距离分别是 3 和 5,则点 M 的坐标是()A 、( -5,3) B、(-5, -3)C、(5,3)或( -5,3)D、(-5, 3)或( -5, -3)8、如图,一个质点在第一象限及x 轴、 y 轴上运动,一秒钟后,它从原点运动到(0,1),而后接着按图中箭头所示方向运动[ 即( 0, 0)→( 0,1)→( 1,1)→( 1, 0)→ ] ,且每秒运动一个单位长度,那么第2011 秒后质点所在地点的坐标是()A 、( 13,44)B、( 44,13)C、( 45,14)D、(13,45)二、填空题9、察看以下有序数对:(3,-1)(-5,3)(7,-5)(-9,7)依据你发现的规律,第2012 个有序数对是 ____________10、假如点 P( m+3,m+1)在直角坐标系的 x 轴上, P 点坐标为 ____________。
人教版七年级数学下册 第七章 平面直角坐标系 培优专题测试训练(含答案)

人教版七年级数学下册第七章平面直角坐标系培优专题测试训练一、选择题1. 点(-2,1)在平面直角坐标系中所在的象限是( )A.第一象限 B.第二象限 C.第三象限 D.第四象限2. 已知点A的坐标为(2,1),将点A向下平移4个单位长度,得到的点A'的坐标是 ( )A.(6,1)B.(-2,1)C.(2,5)D.(2,-3)3.图是某动物园的平面示意图,若以猴山为原点,向右的水平方向为x轴正方向,向上的竖直方向为y轴正方向建立平面直角坐标系,则熊猫馆所在的象限是 ( )A.第一象限B.第二象限C.第三象限D.第四象限4.在平面直角坐标系中,将点P(x,y)先向左平移4个单位长度,再向上平移3个单位长度后得到点P'(1,2),则点P的坐标为( )A.(2,6)B.(-3,5)C.(-3,1)D.(5,-1)5.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1 mm,则图中转折点P的坐标表示正确的是( )A.(5,30)B.(8,10)C.(9,10)D.(10,10)6. 平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为( )A. (-2,-3)B. (2,-3)C. (-3,2)D. (3,-2)7.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第21秒时,点P的坐标为( )A.(21,-1)B.(21,0)C.(21,1)D.(22,0)8.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点O运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2021次运动后,动点P的坐标是( )A.(2021,1)B.(2021,0)C.(2021,2)D.(2022,0)二、填空题9. 点P(-6,-7)到x轴的距离为 ,到y轴的距离为 .10. 已知点P(3-m,m)在第二象限,则m的取值范围是________.11.如图,线段AB经过平移得到线段A'B',其中点A,B的对应点分别为点A',B',这四个点都在格点上.若线段AB上有一点P(a,b),则点P在A'B'上的对应点P'的坐标为 .12.五子棋是一种两人对弈的棋类游戏,起源于中国古代的传统黑白棋种,规则是在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个同学的对弈图.若白子A的坐标为(0,-2),白子B的坐标为(-2,0),为了不让白方马上获胜,此时黑方应该下在坐标为 的位置.(写出一处即可)13.如图,在三角形ABC中,已知点A(0,4),C(3,0),且三角形ABC的面积为10,则点B的坐标为 .14. 将自然数按以下规律排列:第一列第二列第三列第四列第五列…第一行1451617第二行23615…第三行98714…第四行10111213…第五行………………表中数2在第二行、第一列,与有序数对(2,1)对应,数5与有序数对(1,3)对应,数14与有序数对(3,4)对应.根据这一规律,数2021对应的有序数对为 .15.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P60的坐标是 .16.在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移两个单位称为一次变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(-1,-1),(-3,-1),把△ABC经过连续九次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是__________.三、解答题17. 在如图所示的平面直角坐标系中,描出下列各点:(0,4),(-1,1),(-4,1),(-2,-1),(-3,-4),(0,-2),(3,-4),(2,-1),(4,1),(1,1),(0,4).依次连接各点,观察得到的图形,你觉得它像什么?18.常用的确定物体位置的方法有两种.如图,在4×4的边长为1的小正方形组成的网格中,标有A ,B两点(点A,B之间的距离为m).请你用两种不同的方法表述点B相对于点A的位置.19. 如图所示,已知单位长度为1的方格中有一个三角形ABC.(1)请画出三角形ABC先向上平移3格,再向右平移2格所得的三角形A'B'C'(点A,B,C的对应点分别为点A',B',C');(2)请以点A为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向建立平面直角坐标系(在图中画出),然后写出点B,B'的坐标.20. 如图,在平面直角坐标系中,A(3,4),B(4,1),求三角形AOB的面积.21.如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(4,0),点C的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-A-B-C-O的路线移动(即沿着长方形的边移动一周).(1)点B的坐标为 ;(2)当点P移动了4秒时,求出点P的坐标,并在图中描出此时点P的位置;(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.22.如图,在平面直角坐标系中,已知A(2,3),B(0,2),C(3,0).将三角形ABC的一个顶点平移到坐标原点O处,写出平移方法和另两个对应顶点的坐标.23. 如图,若三角形A 1B 1C 1是由三角形ABC 平移后得到的,且三角形ABC 中任意一点P (x ,y )经过平移后的对应点为P 1(x-5,y+2).(1)求点A 1,B 1,C 1的坐标;(2)求三角形A 1B 1C 1的面积.24. 【阅读】在平面直角坐标系中,以任意两点P (x 1,y 1)、Q (x 2,y 2)为端点的线段中点坐标为1212,22x x y y ++⎛⎫ ⎪⎝⎭.【运用】(1)如图,矩形ONEF 的对角线交于点M ,ON 、OF 分别在x 轴和y 轴上,O 为坐标原点,点E 的坐标为(4,3),求点M 的坐标;(2)在直角坐标系中,有A (-1,2),B (3,1),C (1,4)三点,另有一点D 与点A ,B ,C 构成平行四边形的顶点,求点D 的坐标.答案一、选择题1.B 2.D 3.B 4.D5.C [解析] 如图,过点C作CD⊥y轴于点D,∴CD=50÷2-16=9,OA=OD-AD=40-30=10,∴P(9,10).故选C.6.A 【解析】本题考查了直角坐标平面内的点关于x轴的对称点,点如果关于x轴对称,则它的横坐标不变,纵坐标互为相反数,于是点(-2,3)关于x轴对称的点的坐标为(-2,-3),故选A .7.C [解析] 半径为1的半圆的弧长是×2π×1=π,由此可列下表:故选C.8.A [解析]点P坐标的变化规律可以看作每运动四次一个循环,且横坐标与运动次数相同,纵坐标规律是:第1次纵坐标为1,第3次纵坐标为2,第2次和第4次纵坐标都是0.∵2021=505×4+1,∴经过第2021次运动后,动点P 的坐标是(2021,1).故选A .二、填空题9.7 6 10.m >3 【解析】∵点P 在第二象限,∴其横坐标是负数,纵坐标是正数,则根据题意得出不等式组,解得m >3. {3-m <0m >0)11.(a-2,b+3) [解析]由图可知线段AB 向左平移了2个单位长度,向上平移了3个单位长度,所以P'(a-2,b+3).12.(2,0)或(-2,4)13.(-2,0) [解析] S 三角形ABC =BC ·4=10,解得BC=5,∴OB=5-3=2,∴点B 的坐标为(-2,0).14.(45,5) [解析] 观察表格发现:偶数列的第一行数是“列数”的平方数,奇数行的第一列数是“行数”的平方数.下面从奇数行着手:(1,1)表示1,即12;(3,1)表示9,即32;(5,1)表示25,即52;依此类推可知(45,1)表示452,即2025,于是(45,2)表示2024,(45,3)表示2023,…,(45,5)表示2021.故填(45,5).15.(20,0) [解析] 因为P 3(1,0),P 6(2,0),P 9(3,0),…,所以P 3n (n ,0).当n=20时,P 60(20,0).16.(16,1+) 3解析:可以求得点A (-2,-1-),则第一次变换后点A 的坐标为A 1(0,1+),第二次变换33后点A 的坐标为A 2(2,-1-),可以看出每经过两次变换后点A 的y 坐标就还原,每经过一次3变换x 坐标增加2.因而第九次变换后得到点A 9的坐标为(16,1+).3三、解答题17.解:描点连线如图所示,它像五角星.18.解:方法一:用有序数对(a ,b )表示.比如:以点A为原点,水平向右为x轴正方向,竖直向上为y轴正方向建立平面直角坐标系,则点B相对于点A的位置是(3,3).方法二:用方向和距离表示.比如:点B位于点A的东北方向(或北偏东45°方向),距离点A m处.19.解:(1)如图.(2)如图,以点A为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向建立平面直角坐标系,则B(1,2),B'(3,5).20.[解析]三角形AOB的三边均不与坐标轴平行,不能直接利用三角形的面积公式求面积,需通过作辅助线,用“添补”法间接计算.解:如图,过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,延长EA,FB交于点C,则四边形OECF为长方形.由点A,B的坐标可知AE=3,OE=4,OF=4,BF=1,CE=4,CF=4,所以AC=1,BC=3,所以S三角形AOB=S长方形OECF-S三角形OAE-S三角形ABC-S三角形BOF=4×4-×4×3-×3×1-×4×1=6.5.21.解:(1)(4,6)(2)因为点P的移动速度为每秒2个单位长度,所以当点P移动了4秒时,它移动了8个单位长度,此时点P的坐标为(4,4),图略.(3)当点P到x轴的距离为5个单位长度时,有两种情况:①若点P在AB上,则点P移动了4+5=9(个)单位长度,此时点P移动了9÷2=4.5(秒);②若点P在OC上,则点P移动了4+6+4+1=15(个)单位长度,此时点P移动了15÷2=7.5(秒).综上所述,当点P到x轴的距离为5个单位长度时,点P移动了4.5秒或7.5秒.22.解:(1)若将点A平移到原点O处,则平移方法(不唯一)是向左平移2个单位长度,再向下平移3个单位长度.另两个顶点B,C的对应点的坐标分别是(-2,-1),(1,-3).(2)若将点B平移到原点O处,则平移方法是向下平移2个单位长度.另两个顶点A,C的对应点的坐标分别是(2,1),(3,-2).(3)若将点C平移到原点O处,则平移方法是向左平移3个单位长度.另两个顶点A,B的对应点的坐标分别是(-1,3),(-3,2).23.解:(1)∵三角形ABC中任意一点P(x,y)经过平移后的对应点为P1(x-5,y+2),∴三角形ABC 向左平移5个单位长度,再向上平移2个单位长度(平移方法不唯一)得到三角形A 1B 1C 1.∵A (4,3),B (3,1),C (1,2),∴点A 1的坐标为(-1,5),点B 1的坐标为(-2,3),点C 1的坐标为(-4,4).(2)三角形A 1B 1C 1的面积=三角形ABC 的面积=3×2-×1×3-×1×2-×1×2=.24.解:(1)∵四边形ONEF 是矩形,∴点M 是OE 的中点.∵O (0,0),E (4,3),∴点M 的坐标为.(2,32)(2)设点D 的坐标为(x ,y ).若以AB 为对角线,AC ,BC 为邻边构成平行四边形,则AB ,CD 的中点重合∴Error!,解得,Error!.若以BC 为对角线,AB ,AC 为邻边构成平行四边形,则AD ,BC 的中点重合∴Error!,解得,Error!.若以AC 为对角线,AB ,BC 为邻边构成平行四边形,则BD ,AC 的中点重合∴Error!,解得,Error!.综上可知,点D 的坐标为(1,-1)或(5,3)或(-3,5).。
七年级数学竞赛培优平面直角坐标系含解析
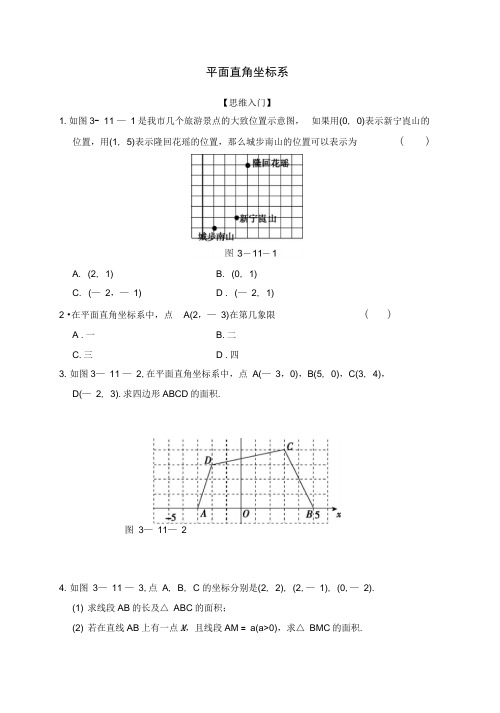
平面直角坐标系【思维入门】1.如图3- 11 —1是我市几个旅游景点的大致位置示意图,如果用(0, 0)表示新宁崀山的位置,用(1, 5)表示隆回花瑶的位置,那么城步南山的位置可以表示为()A. (2, 1)B. (0, 1)C. (—2,—1) D . (—2, 1)2 •在平面直角坐标系中,点A(2,—3)在第几象限()A .一B.二C.三 D .四3. 如图3—11 —2,在平面直角坐标系中,点A(—3,0),B(5, 0),C(3, 4),D(—2, 3).求四边形ABCD的面积.图3—11—24. 如图3—11 —3,点A, B, C 的坐标分别是(2, 2), (2,—1), (0,—2).(1) 求线段AB的长及△ ABC的面积;(2) 若在直线AB上有一点M,且线段AM = a(a>0),求△ BMC的面积.5. 在平面直角坐标系中有两点A( —2, 2), B(3, 2), C是坐标轴上的一点,若△ ABC是直角三角形,则满足条件的点有()A . 1个B . 2个C. 4个 D . 6个6 •在平面直角坐标系中,0为坐标原点,点A的坐标为(1,.3),M为坐标轴上一点,且使得△MOA为等腰三角形,则满足条件的点M的个数为()A . 4B . 5 C. 6 D . 87.如图3—11 —4,在直角坐标系中,0是原点,已知A(4,3),P是坐标轴上的一点,若以0, A,P三点组成的三角形为等腰三角形,则满足条件的点P共有____ 个,写出其中一个点P的坐标是_____ .8.如图3—11 —5,已知坐标平面内的三个点A(1, 3), B(3, 1), 0(0, 0),求厶ABO的面积.【思维升华】9•如图3- 11 —6,弹性小球从点P(0, 3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为P n,贝U点P3的坐标是____ ;点P2 014的坐标是_____ .10.如图3—11 —7,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2, 0),…,那么点A4n+1(n是自然数)的坐标为 .图3—11—711.如图3—11 —8,在平面直角坐标系中,点A, B, C的坐标分别为(1, 0), (0, 1),(—1, 0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称,….照此规律重复下去,则点P2 013的坐标为________________ .—----- 4---------- ——1 -- 1——>C °A耳图3- 11—812•在平面直角坐标系xOy中,对于点P(x, y),我们把点P'—y+ 1, x+ 1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A的伴随点为A4,这样依次得到A1, A2, ______ A3,…,A n,…,若点A1的坐标为(3,1),则点A3的坐标为,点A2014的坐标为____ ;若点A1的坐标为(a, b),对于任意的正整数n,点A n均在x轴上方,则a, b应满足的条件为 _____ .平面直角坐标系【思维入门】1.如图3- 11 —1是我市几个旅游景点的大致位置示意图,如果用(0, 0)表示新宁崀山的位置,用(1, 5)表示隆回花瑶的位置,那么城步南山的位置可以表示为A. (2, 1)B. (0, 1)C. (—2,—1) D . (—2, 1)2 •在平面直角坐标系中,点A(2,—3)在第几象限(D )A .一B.二C.三 D .四3.如图3—11 —2,在平面直角坐标系中,点A(—3,0),B(5, 0),C(3, 4),D(—2, 3).求四边形ABCD的面积.-r - - T -- nt- - - -ir ■-! 1 1 V 1 1 1 I i i i fl&-i - = - -i- - - ii1 l< 1 4 1 Vi ii i ii i i1 1 i i i I1 1 i I 1 11 H 1 1 1 1I b 丨厂i i * 1i 1 h i IP * 1 \ «■1_ _ J_ - JL____________ Y J _ I I1 1 1 * p ■1[I 1 1 f1 ■」K H 1 \ H 1 * i B i \i i iJ 1 \ I _ n1'! 1 P / 1 1i 1 1 i f1 11 1 1 1 f1 1r I \ i ii h 1 i \ 1 11 N 1 «\ ■1r■ r7" -n J i r -i i ■i ■;11 !r 1 1= = i (- A r--1»i> i i \i »、i i i j r i:4-5 :\A\:0 :;;: #5 ;戈图3—11—2解:作DE丄x轴于E, CF丄x轴于F,如答图,1 1 1四边形ABCD 的面积=ADE + S四边形CDEF+BCF = ?X 1 X 3+(3 + 4) X (3 + 2) + 2 X 4 = 23.4•如图3- 11 —3,点A, B, C 的坐标分别是(2, 2), (2,—1), (0,—2).⑴求线段AB的长及△ ABC的面积;(2)若在直线AB上有一点M,且线段AM = a(a>0),求△ BMC的面积.解:(1) •••点A, B的坐标分别是(2, 2), (2,—1),••• AB丄x轴,二AB= 2—(—1)= 3,1S A ABC = 2 X 3X 2 = 3.⑵当M点在BA的延长线上时,MB = a+ 3,1△ BMC 的面积=2X2X (a+ 3)= a+ 3;当M点在线段AB上时,0<a<3, MB = 3 —a,1△ BMC 的面积=2X 2X (3 —a) = 3 —a;当M点在AB的延长线上时,a>3, MB = a —3,1△ BMC 的面积=^X 2X (a—3)= a — 3.【思维拓展】5.在平面直角坐标系中有两点A( —2, 2), B(3, 2), C是坐标轴上的一点,若△ ABC是直角三角形,则满足条件的点有(D )A . 1个B . 2个C. 4个 D . 6个【解析】因为A, B的纵坐标相等,所以AB// x轴•因为C是坐标轴上的一点,所以过点A向x轴引垂线,过点B向x轴引垂线,分别可得一点,以AB为直径作圆,可与坐标轴交于4点,所以满足条件的点共有6个.6 •在平面直角坐标系中,0为坐标原点,点A的坐标为(1,3),M为坐标轴上一点,且使得△MOA为等腰三角形,则满足条件的点M的个数为(C )A . 4B . 5 C. 6 D . 8【解析】如答图,满足条件的点M的个数为6,分别为(—2, 0),(2, 0),(0,2 3),(0,2), (0, —2), 0,斗3.故选 C.r r 4 :'甌! 1* 1 3-----T -------------- -- 1 ----- i1 n ■* 1 t ! U…上II 1 J( 11 11 11 |L _ _ L1 1 H ■1 七\ \帆1 1; --- 「[-■「1/M L42 0 11II 1;1 2M2_________ J__________ ::;-1i 1Il i1;::■;:::* 1 p 1 ____ L - 1- ■------------------- ----------- ---------------- ----------第6题答图7•如图3—11 —4,在直角坐标系中,O是原点,已知A(4, 3), P是坐标轴上的一点,若以O, A, P三点组成的三角形为等腰三角形,则满足条件的点P共有一8—个,写出其中一个点P的坐标是(0, 6),答案不唯一.8.如图3- 11 —5,已知坐标平面内的三个点A(1, 3), B(3, 1), 0(0, 0),求厶ABO的面积.3= 4+ 3- 3= 4.-gxix解:如答图,S A ABO=第8题答图【思维升华】9•如图3- 11 — 6,弹性小球从点P(0, 3)出发,沿所示方向运动,每当小球碰到矩形OABC 的边时反弹,反弹时反射角等于入射角,当小球第 1次碰到矩形的边时的点为 P 1,第2次碰到矩形的边时的点为 P 2,…,第n 次碰到矩形的边时的点为 P n ,贝U 点 P 3的坐标是 —(8, 3)__;点P2 014的坐标是__(5,0)__,当点P 第3次碰到矩形的边时,点P 3的坐标为(8, 3);••• 2 014 £= 335……4 ,•••当点P 第2 014次碰到矩形的边时为第336个循环组的第4次反弹,点P 2 014的坐 标为(5, 0).10. 如图3— 11 — 7,在平面直角坐标系中,一动点从原点O 出发,按向上、向右、向下、 向右的方向依次不断地移动,每次移动一个单位,得到点 A 1(0, 1), A 2(1, 1), A 3(1, 0), A 4(2, 0),…,那么点A 4n +1(n 是自然数)的坐标为__(2n , 1)__.J h y A 2 A .沖 4 凡 ^10 /h1 j t 1 鼻 1 J (. 1 * 1 t 一 t A 0 〒 k 尸 k Aj J 44 A lx A ]2 【解图 3- 11— 7【解析】 由图可知,n = 1时,4X 1+ 1 = 5•点A 5(2, 1),n = 2 时,4X 2+ 1 = 9,点 A 9(4, 1),n = 3 时,4X 3+ 1 = 13,点 A 13(6, 1),所以,点 A 4n + 1(2n , 1).11. 如图3— 11 — 8,在平面直角坐标系中,点A , B , C 的坐标分别为(1, 0), (0, 1),(— 1, 0). —个电动玩具从坐标原点 O 出发,第一次跳跃到点 P 1,使得点P 1与点O 关 于点A 成中心对称;第二次跳跃到点P 2,使得点P 2与点P 1关于点B 成中心对称;第 三次跳跃到点P 3,使得点P 3与点P 2关于点C 成中心对称;第四次跳跃到点 P 4,使 得点P 4与点P 3关于点A 成中心对称;第五次跳跃到点 P 5,使得点P 5与点P 4关于点 B 成中心对称,….照此规律重复下去,则点P2 013的坐标为_(0,— 2)_ .7 +-4 ------------- b ——' -- 1——>C 0 A 兀图 3— 11— 8【解析】 点 P 1(2, 0), P 2( — 2, 2), P 3(0,— 2), P 4(2, 2), P 5( — 2, 0), P 6(0, 0),P 7(2, 0),从而可得出6次一个循环,•••点P 2 013的坐标为(0,— 2). 12. 在平面直角坐标系xOy 中,对于点P(x , y),我们把点P '—y + 1, x + 1)叫做点P 的 伴随点,已知点A 1的伴随点为A 2,点A 2的伴随点为A 3,点A 3的伴随点为A 4,这样 依次得到A 1, A 2, A 3,…,A n ,…,若点A 1的坐标为(3, 1),则点A 3的坐标为 (— 3, 1)__,点A2 014的坐标为_(0, 4)_;若点A 1的坐标为(a , b),对于任意的正整 数n ,点A n 均在x 轴上方,则a , b 应满足的条件为1v a v 1且0v b v 2 .【解析】:A 1的坐标为(3, 1),•-A 2(0, 4), A 3( — 3, 1), A 4(0,— 2), A 5(3, 1),…, 2 013= 6 =335 3,以此类推,每4个点为一个循环组依次循环,2 014-4 = 503……2,•••点A 014的坐标与A2的坐标相同,为(0, 4);•••点A i的坐标为(a,b),• - A2(—b + 1,a+ 1),A3(—a,—b+ 2),A4(b—1,—a + 1),A5(a,b),…,以此类推,每4个点为一个循环组依次循环,•••对于任意的正整数n,点A n均在X轴上方,a+ 1>0,•丿…a+ 1>0,b+ 2>0,4>0,解得—1<a<1,0<b<2.。
平面直角坐标系培优辅导(精心整理)
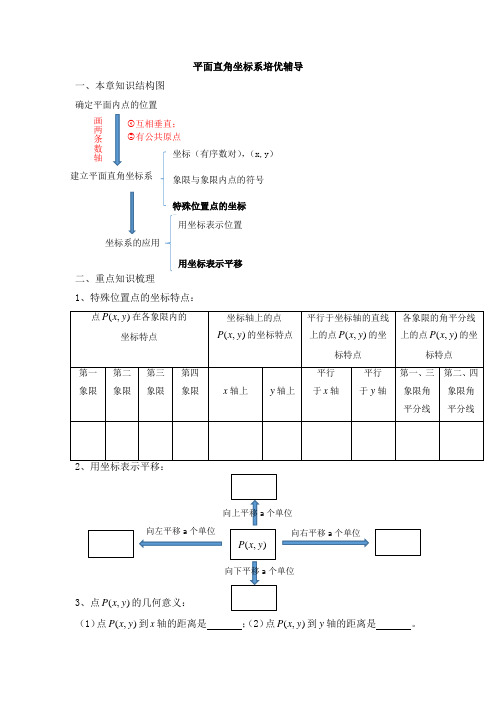
平面直角坐标系培优辅导一、本章知识结构图确定平面内点的位置1、特殊位置点的坐标特点:3、点),(y x P 的几何意义:(1)点),(y x P 到x 轴的距离是;(2)点),(y x P 到y 轴的距离是。
向左平移a 个单位知识应用1、若点P(a,b)在第四象限,则点M(b-a,a-b)在()A. 第一象限B.第二象限C. 第三象限D.第四象限2、在平面直角坐标系中,点()1-m一定在(),12+A.第一象限B.第二象限C.第三象限 D.第四象限3、已知点P(x,y)的坐标满足方程|x+1|+y-2 =0,则点P在()A. 第一象限B.第二象限C. 第三象限D.第四象限4、若点P在x轴的下方, y轴的左方, 到每条件坐标轴的距离都是3,则点P的坐标为( )A. (3,3)B. (-3,3)C. (-3,-3)D. (3,-3).5、已知点P(x,-1)和点Q(2,y)不重合,则对于x,y(1)若PQ∥x轴,则可求得 ;(2)若PQ⊥x轴, 则可求得 .6、在图中所示的平面直角坐标系中表示出下列各点:A(0 , 3),B(1 , -3),C(3 , -5),D(-3 , -5),E(3 , 5),F(5 , 6),G(5 , 0)(1)A点到原点O的距离是;(2)D点到x轴的距离是,到y轴的距离是。
(3)将点C向x轴的负方向平移6个单位,得到新点的坐标为,(4)连接CE,则直线CE与y轴有什么位置关系?(5)依次连接E、F、G三点,求三角形EFG的面积。
7、如图所示的平面直角坐标系中, (1)求三角形ABC 的面积:(2)如果将三角形ABC 向上平移1个单位长度,再向左平移2个单位长度,得到三角形111C B A ,且点A 、B 、C 的对应点分别为点111C B A 、、,请在图中画出三角形111C B A 的位置,并写出点111C B A 、、的坐标;(3)若三角形ABC 内部有一点M , 平移后对应点N 的坐标为(0,3),请直接写出点M 的坐标。
平面直角坐标系培优题(学生)

平面直角坐标系培优训练知识点一:利用象限来确定1.若y=√x−2+√2−x−3,则P(x,y)在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.若点P(a,b)在第三象限,则点M(b−1,−a+1)在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.已知点P(a,b)是平面直角坐标系中第四象限的点,则化简√b2+|b−a|的结果是()A. a−2bB. aC. −a+2bD. −a4.已知点M(1−2m,m−1)在第四象限,则m的取值范围是()A.m<12B. m>1 C. 1>m>12D. −1<m<−125.已知点P(a,b)在第四象限,且|a|=2,|b|=3,则点P的坐标是______.6.已知点P、Q的坐标分别为(2m−5,m−1)、(n+2,2n−1),若点P在第二、四象限的角平分线上,点Q在第一、三象限的角平分线上,则m n的值为________.知识点二:利用距离来确定点的坐标7.点P在第四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为()A. (−3,−2)B. (3,−2)C. (2,3)D. (2,−3)8.已知在平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为()A.−3B. −5C. 1或−3D. 1或−59.已知点P的坐标为(3a+6,2−a),且点P到两坐标轴的距离相等,则点P的坐标是______.10.已知点A(1,2),AC//x轴,AC=5,则点C的坐标是______.11.点P(m−1,m+3)在直角坐标系的y轴上,则P点坐标为()A. (−4,0)B. (0,−4)C. (4,0)D. (0,4)12.点A(m−3,m+1)在第二、四象限的平分线上,则A的坐标为()A. (−1,1)B. (−2,−2)C. (−2,2)D. (2,2)13.已知点M(3a−9,1−a),将M点向左平移3个单位长度后落在y轴上,则a=______.14.在平面直角坐标系中,点A的坐标是(3a−5,a+1).(1)若点A在y轴上,求a的值及点A的坐标.(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.15.已知:点P(2m+4,m−1).试分别根据下列条件,求出P点的坐标.(1)点P在y轴上;(2)点P在x轴上;(3)点P的纵坐标比横坐标大3;(4)点P在过A(2,−3)点,且与x轴平行的直线上.16.已知点A(a−1,−2),B(−3,b+1),根据以下要求确定a、b的值.(1)直线AB//y轴;(2)直线AB//x轴;(3)点A到y轴的距离等于点B到y轴的距离,同时点A到x轴的距离等于点B到x轴的距离.17.在平面直角坐标系中,有点A(−2,a+3),B(b,b−3).(1)当点A在第二象限的角平分线上时,求a的值;(2)当点B到x轴的距离是它到y轴的距离2倍时,求点B坐标及所在的象限位置.18.在平面直角坐标系中,有点A(1,2a+1),B(−a,a−3).(1)当点A在第一象限的角平分线上时,a的值为__________.(2)若线段AB//x轴.①求点A、B的坐标.②若将线段AB平移,点A、B分别平移至A′(x1,3x1+1),B′(x2,2x2−3),求A′,B′坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面直角坐标系练习题(巩固提高篇)一、选择题:1、下列各点中,在第二象限的点是( )A.(2,3)B.(2,-3) C.(-2,3)D.(-2,-3)2、已知点M(-2,b)在第三象限,那么点N(b, 2 )在()A.第一象限 B.第二象限C.第三象限D.第四象限3、若点P(a,b)在第四象限,则点M(b-a,a-b)在()A.第一象限 B. 第二象限C. 第三象限 D. 第四象限4、已知点P(a,b),且ab>0,a+b<0,则点P在( )A.第一象限B.第二象限C.第三象限 D.第四象限5、如果点P(a,b)在第二象限内,那么点P(ab,a-b)在( )A、第一象限B、第二象限C、第三象限D、第四象限6、若点P(x ,y)的坐标满足xy=0(x≠y),则点P在( )A.原点上B.x轴上C.y轴上 D.x轴上或y轴上7、平面直角坐标中,和有序实数对一一对应的是 ( )A.x轴上的所有点 B.y轴上的所有点C.平面直角坐标系内的所有点 D.x轴和y轴上的所有点8、将点A(-4,2)向上平移3个单位长度得到的点B的坐标是( )A. (-1,2)B. (-1,5)C.(-4,-1) D.(-4,5)9、线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(-4,–1)的对应点D的坐标为()A.(2,9)B.(5,3) C.(1,2)D.(– 9,–4)10、点P(m+3,m+1)在x轴上,则P点坐标为()A.(0,-2)B.(2,0)C.(4,0)D.(0,-4)11、点P的横坐标是-3,且到x轴的距离为5,则P点的坐标是( )A.(5,-3)或(-5,-3)B.(-3,5)或(-3,-5)C.(-3,5)D.(-3,-5)12、已知点P(x,y)在第四象限,且│x│=3,│y│=5,则点P的坐标是()A.(-3,5) B.(5,-3) C.(3,-5) D.(-5,3)13、点P(x,y)位于x轴下方,y轴左侧,且x=2 ,y=4,点P的坐标是()A.(4,2) B.(-2,-4) C.(-4,-2)D.(2,4)14、点P(0,-3),以P为圆心,5为半径画圆交y轴负半轴的坐标是( )A.(8,0) B.( 0,-8)C.(0,8) D.(-8,0)15、点E(a,b)到x轴的距离是4,到y轴距离是3,则有()A.a=3,b=4 B.a=±3,b=±4 C.a=4, b=3 D.a=±4,b=±316、将某图形的横坐标都减去2,纵坐标保持不变,则该图形 ( )A .向右平移2个单位 B.向左平移2 个单位 C.向上平移2 个单位 D.向下平移2 个单位 17、如果点M 到x 轴和y 轴的距离相等,则点M横、纵坐标的关系是( )A .相等 B.互为相反数 C.互为倒数 D.相等或互为相反数18、已知正方形ABCD 的三个顶点坐标为A(2,1),B(5,1),D(2,4),现将该正方形向下平移3个单位长度,再向左平移4个单位长度,得到正方形A'B'C'D',则C '点的坐标为( ) A. (5,4) B. (5,1) C. (1,1) D. (-1,-1)19、若点M 在第一、三象限的角平分线上,且点M 到x轴的距离为2,则点M的坐标是( ) A .(2,2) B.(-2,-2) C .(2,2)或(-2,-2) D.(2,-2)或(-2,2) 20、已知P(0,a)在y轴的负半轴上,则Q(21,1a a ---+)在( )A 、y 轴的左边,x 轴的上方B 、y 轴的右边,x 轴的上方C 、y轴的左边,x 轴的下方D 、y 轴的右边,x 轴的下方21、三角形A BC三个顶点的坐标分别是A(-4,-1),B(1,1),C(-1,4),将三角形ABC 向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( ) A.(2,2),(3,4),(1,7) B .(-2,2),(4,3),(1,7) C.(-2,2),(3,4),(1,7) D .(2,-2),(3,3),(1,7)22、已知△AB C的面积为3,边BC 长为2,以B 原点,B C所在的直线为x轴,则点A 的纵坐标为( )A、3 B 、-3 C、6 D、±3 23、点M (a,a-1)不可能在( )A. 第一象限B. 第二象限C. 第三象限 D . 第四象限 二、填空题:1、在电影票上,如果将“8排4号”记作(8,4),那么(10,15)表示____________。
2、点A (-3,5)在第_____象限,到x轴的距离为______,到y 轴的距离为_______;关于原点的对称点坐标为_________,关于x 轴的对称点坐标为_________,关于y 轴的对称点坐标为_________。
3、已知x 轴上点P 到y 轴的距离是3,则点P坐标是_____________。
4、一只蚂蚁由(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是_________。
5、点P(m+3, m+1)在x 轴上,则m = ,点P坐标为 。
6、已知点P (m ,2m-1)在y 轴上,则P 点的坐标是 。
7、一个长方形在平面直角坐标系中三个顶点的坐标为(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标为 8、已知点A (2,-3),线段AB 与坐标轴没有交点,点B的坐标可以是 (写出一个即可) 9、点E 与点F 的纵坐标相同,横坐标不同,则直线E F与y 轴的关系是 10、直线a 平行于x轴,且过点(-2,3)和(5,y),则y =11、若P (x,y)是第四象限内的点,且2,3x y ==,则点P的坐标是12、已知点P 在第二象限,它的横坐标与纵坐标的和为1,点P 的坐标是______(写出一个点即可). 13、已知:A (3,1),B(5,0),E(3,4),则△ABE 的面积为________. 14、点A(1-a,5),B(3,b)关于y 轴对称,则a +b=_______.15、已知点P (m,n)到x 轴的距离为3,到y 轴的距离等于5,则点P 的坐标是 。
16、已知点P 的坐标(2-a,3a +6),且点P 到两坐标轴的距离相等,则点P 的坐标是 . 17、已知点A(3a+5,a-3)在二、四象限的角平分线上,则a =_____.18、在平面直角坐标系内,已知点(1-2a,a-2)在第三象限的角平分线上,则a = ,点的坐标为 。
19、已知点P(0,a)在y 轴的负半轴上,则点Q(-2a -1,-a +1)在第 象限.20、将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy =___________。
三、解答题:1、如图所示的直角坐标系中,三角形ABC 的顶点坐标分别是A(0,0)、B(6,0)、C (5,5)。
求: (1)求三角形ABC 的面积;(2)如果将三角形A BC 向上平移3个单位长度,得三角形A1B 1C1,再向右平移2个单位长度,得到三角形A 2B2C 2。
分别画出三角形A 1B 1C1和三角形A2B 2C2。
并试求出A 2、B 2、C 2的坐标?2、已知点P (a+1,2a-1)关于x 轴的对称点在第一象限,求a 的取值范围.3、在如图所示的平面直角坐标系中表示下面各点: A(0,3);B(1,-3);C (3,-5);D(-3,-5); E (3,5);F(5,7);G (5,0)(1)A点到原点O 的距离是 。
(2)将点C 向x 轴的负方向平移6个单位,它与点 重合。
(3)连接CE ,则直线C E与y 轴是什么关系? (4)点F分别到x 、y 轴的距离是多少?ACAxyB A4、在直角坐标系中,已知点A (-5,0),点B(3,0),C 点在y 轴上,且△ABC 的面积为12, 试确定点C 的坐标。
5、写出如图中△ABC 各顶点的坐标且求出此三角形的面积。
6、如图,△A OB 中,A、B 两点的坐标分别为(-4,-6),(-6,-3),求△AOB 的面积。
7、如图,在直角坐标系中,第一次将三角形OAB 变换成三角形O A1B 1,第二次将三角形OA 1B 1变成三角形OA 2B 2,第三次将三角形OA 2B 2变成三角形O A3B3,已知123(1,3),(2,3),(4,3),(8,3)A A A A ,123(2,0),(4,0),(8,0),(16,0)B B B B 。
(1)、观察每次变换前后的三角形有何变化,找出规律,按此规律再将三角形OA 3B3变换成三角形44OA B ,则3B 的坐标是 ,4B 的坐标是 。
ﻩ(2)若按第(1)题找到的规律将三角形OAB 进行了n次变换,得到三角形OA n Bn ,比较每次变换中三角形顶点坐标有何变化,找出规律,推测n A 的坐标是 ,n B 的坐标是 。
OAB C1xy8、如图,在△A BC中,三个顶点的坐标分别为A (-5,0),B(4,0),C(2,5),将△ABC 沿x 轴正方向平移2个单位长度,再沿y 轴沿负方向平移1个单位长度得到△EFG 。
(1)求△EF G的三个顶点坐标。
(2)求△EFG 的面积。
9、如图,在平面直角坐标系中,点A,B 的坐标分别为(-1,0), (3,0),现同时将点A ,B分别向上平移2个单位,再向右平移 1个单位,分别得到点A,B的对应点C,D ,连接AC,BD,C D. (1)、求点C ,D 的坐标及平行四边形ABDC 的面积ABDC S 四边形(2)、在y 轴上是否存在一点P,连接PA ,PB ,使PAB S ∆=2ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)、点P 是线段BD上的一个动点,连接PC ,PO ,当点P在B D上移动时(不与B ,D 重合)给出下列结论:①DCP BOP CPO∠+∠∠的值不变,②DCP CPOBOP ∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.10、如图:三角形ABC三个顶点A、B、C的坐标分别为A(1,2)、B(4,3)、C(3,1).(1)把三角形A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标;(2)求出三角形A1B1C1的面积11、在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P作向上或向右运动(如图1所示).运动时间(s)与整点个数的关系如下表:整点P从原点出发的时间(s) 可以得到整点P的坐标可以得到整点P的个数1 (0,1)(1,0) 22 (0,2)(1,1),(2,0)33 (0,3)(1,2)(2,1)(3,0) 4………根据上表中的规律,回答下列问题:(1)、当整点P从点O出发4s时,可以得到的整点的个数为________个.(2)、当整点P从点O出发8s时,在直角坐标系(图2)中描出可以得到的所有整点,并顺次连结这些整点.(3)、当整点P从点O出发________s时,可以得到整点(16,4)的位置.图1(试验图)图2。
