第3讲-等腰三角形2_数学作业
《第十章2等腰三角形》作业设计方案-初中数学鲁教版五四制12七年级下册

《等腰三角形》作业设计方案(第一课时)一、作业目标通过本次作业,学生应能:1. 掌握等腰三角形的定义及性质;2. 理解等腰三角形的基本特点及其在几何图形中的重要性;3. 学会运用等腰三角形的性质解决简单的几何问题。
二、作业内容作业内容主要围绕等腰三角形的概念及其性质展开,具体包括:1. 基础概念:- 等腰三角形的定义:两边相等的三角形。
- 等腰三角形的性质:两底角相等,基线与垂线性质等。
2. 性质理解与运用:- 通过填空题、选择题等形式,让学生熟练掌握等腰三角形的性质;- 设计实际应用题,让学生通过实际操作理解等腰三角形的特点及性质在生活中的应用;- 引导学生通过画图、测量等方式,加深对等腰三角形性质的理解。
3. 问题解决:- 设计一系列问题,如证明题、应用题等,要求学生运用等腰三角形的性质解决实际问题;- 题目难度逐步提升,从基础题到综合题,帮助学生逐步提高解题能力。
三、作业要求1. 学生需独立完成作业,不得抄袭他人答案;2. 作业中需有详细的解题步骤和思路,不得只写答案;3. 作业中需使用规范的数学符号和术语,表达清晰;4. 按时提交作业,并保持作业整洁;5. 在解题过程中,学生应注重理解题目的要求和解题思路,遇到问题可查阅相关资料或向老师请教。
四、作业评价1. 教师将根据学生的作业完成情况,给予相应的评价和反馈;2. 评价将综合考虑学生的作业正确性、解题思路、表达规范等方面;3. 对于优秀作业,将在课堂上进行展示和表扬,激励学生积极参与;4. 对于存在问题较多的学生,教师将给予指导和帮助,帮助学生改进。
五、作业反馈1. 教师将根据学生的作业情况,对教学中的重点和难点进行再次强调和讲解;2. 对于学生在解题过程中出现的共性问题,将在课堂上进行集体讨论和解答;3. 对于个别学生的问题,教师将进行个别辅导和解答;4. 通过作业反馈,帮助学生更好地掌握等腰三角形的知识和技能,为后续学习打下坚实的基础。
2.3 等腰三角形的性质定理八年级上册数学浙教版

(1)因为 , ,所以 平分 ,且 .(2)因为 , ,所以 ,且 平分 .(3)因为 , 平分 ,所以 ,且 .
利用“等腰三角形三线合一”的性质可以解决角相等、线段相等或垂直问题
2.等边三角形三线合一:等边三角形每条边上的中线、高线以及相应对角的平分图,分两种情况讨论:
(1)当点 在点 的左侧 处时,
, , .
(2)当点 在点 的右侧 处时, , . 是 的外角, , , .综上, 的度数是 或 .
链接教材 本题取材于教材第58页作业题第5题,考查了利用等腰三角形等边对等角的性质求角的度数.中考真题两次利用等边对等角求等腰三角形的底角的度数,并且需要分两种情况讨论求解,难度较大.而教材习题是结合平行线及等边对等角求角的度数,也是常考题目.
等腰三角形三线合一
典例3 如图,在 中, , 为 边上的中线, ,则 的度数为( )
B
A. B. C. D.
[解析] , 为 边上的中线, , . , .
典例4 如图所示, 是等边三角形, 为 边上的中线, ,求 的度数.
A. B. C. D.
B
[解析] 为等边三角形, , . , , .又 , .
知识点2 等腰三角形的性质定理2 重点
1.等腰三角形的性质定理2:
性质定理2
几何语言
图示
等腰三角形
等腰三角形的顶角平分线、底边上的中线和高线互相重合,简称等腰三角形三线合一.
第2章 特殊三角形
2.3 等腰三角形的性质定理
学习目标
1.掌握等腰三角形的性质定理:①在同一个三角形中,等边对等角;②等腰三角形三线合一.
2.会利用等腰三角形的性质进行简单的推理、计算.
3.掌握“等边三角形的各个内角都等于 ”.
《13.3.1等腰三角形》作业设计方案-初中数学人教版12八年级上册

《等腰三角形》作业设计方案(第一课时)一、作业目标1. 巩固学生对等腰三角形基本概念的理解。
2. 掌握等腰三角形的性质和判定方法。
3. 学会运用等腰三角形的性质解决简单的实际问题。
二、作业内容作业内容主要围绕等腰三角形的性质和判定进行设计,具体如下:1. 基础练习:(1)请学生绘制等腰三角形,并标明基线、两腰、顶角和底角。
(2)通过课本例题,让学生熟悉等腰三角形的性质,如两腰相等、两底角相等。
(3)设计一系列选择题和填空题,考察学生对等腰三角形基本概念的掌握情况。
2. 深化理解:(1)设计一些实际问题的应用题,如利用等腰三角形的性质解决建筑、道路设计中的问题。
(2)让学生通过小组讨论,探讨等腰三角形与其他几何图形的联系和区别。
(3)布置一些具有挑战性的题目,如判定一个三角形是否为等腰三角形,并说明理由。
3. 拓展延伸:(1)让学生利用网络资源或课外书籍,查找等腰三角形在生活中的应用实例。
(2)设计一些创意性的作业,如让学生用等腰三角形创作一幅画或一个模型。
(3)引导学生思考等腰三角形的性质是否可以推广到其他类型的三角形,如等边三角形、直角三角形等。
三、作业要求1. 作业应按时完成,不得抄袭他人答案。
2. 基础练习部分要求每个学生都必须掌握,深化理解和拓展延伸部分可以根据自身能力选择完成。
3. 作业中遇到的问题可以请教同学或老师,但必须注明问题来源和解答过程。
4. 作业应书写工整,步骤清晰,答案准确。
四、作业评价1. 教师根据学生完成作业的情况,给予相应的评价和反馈。
2. 评价标准包括作业的正确性、解题思路的清晰性、作业的整洁度等方面。
3. 对于表现优秀的学生,教师可以给予表扬和鼓励;对于存在问题的学生,教师应及时指出并给予指导。
五、作业反馈1. 教师将学生的作业进行批改后,将共性问题进行汇总,并在课堂上进行讲解。
2. 对于个别学生的问题,教师可以进行个别辅导或在课堂上进行针对性讲解。
3. 鼓励学生之间互相交流学习心得和解题方法,提高学习效果。
等腰三角形的性质与判定(6类热点题型讲练)(解析版) 八年级数学下册
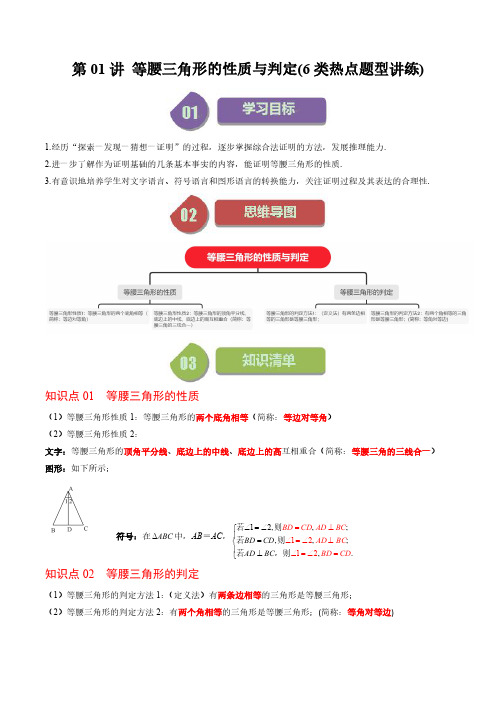
第01讲等腰三角形的性质与判定(6类热点题型讲练)1.经历“探索一发现一猜想一证明”的过程,逐步掌握综合法证明的方法,发展推理能力.2.进一步了解作为证明基础的几条基本事实的内容,能证明等腰三角形的性质.3.有意识地培养学生对文字语言、符号语言和图形语言的转换能力,关注证明过程及其表达的合理性.知识点01等腰三角形的性质(1)等腰三角形性质1:等腰三角形的两个底角相等(简称:等边对等角)(2)等腰三角形性质2:文字:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称:等腰三角的三线合一)图形:如下所示;符号:在ABC ∆中,AB =AC ,1212,,;,,;,12.BD CD AD BC AD B BD CD AD BC C BD CD ∠=∠⎧⎪=⊥∠=∠⊥∠=∠⎨⎪⊥⎩==若则若则若,则知识点02等腰三角形的判定(1)等腰三角形的判定方法1:(定义法)有两条边相等的三角形是等腰三角形;(2)等腰三角形的判定方法2:有两个角相等的三角形是等腰三角形;(简称:等角对等边)题型01根据等腰三角形腰相等求第三边或周长【例题】(2023上·河南商丘·八年级商丘市实验中学校考阶段练习)一个等腰三角形的两条边长分别为8cm 和4cm ,则第三边的长为cm .【答案】8【分析】本题考查等腰三角形的性质及三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,是解题的关键.【详解】解:①若一腰长为8cm ,则底边为4cm ,则第三边的长为8cm ,488+>,故能组成三角形;②若一腰长为4cm ,则底边为8cm ,则第三边的长为4cm ,448+=,故不能组成三角形.故答案为:8.【变式训练】1.(2023上·甘肃陇南·八年级校考阶段练习)一个等腰三角形有两边分别为3cm 和8cm ,则周长是cm .【答案】19【分析】本题考查了等腰三角形的性质和三角形的三边关系.等腰三角形两边的长为3cm 和8cm ,具体哪条是底边,哪条是腰没有明确说明,因此要分两种情况讨论.【详解】解:①当腰是3cm ,底边是8cm 时:338+<,不满足三角形的三边关系,因此舍去.②当底边是3cm ,腰长是8cm 时,388+>,能构成三角形,则其周长()38819cm =++=.故答案为:19.2.(2023上·山东潍坊·八年级校考阶段练习)若()2450a b -+-=,则以a ,b 为边长的等腰三角形的周长为.【答案】13或14【分析】本题考查了等腰三角形的概念,非负数的性质,以及三角形的三边关系,注意利用分类讨论思想解题.根据非负数的和为零,可得每个非负数同时为零,可得a ,b 的值,根据等腰三角形的概念进行分类讨论,可得答案.【详解】解:∵()2450a b -+-=,且()240a -≥,50b -≥,∴40a -=,50b -=,解得:4a =,5b =,当4为等腰三角形的腰长,5为等腰三角形的底边时,则等腰三角形的周长为44513++=,当5为等腰三角形的腰长,4为等腰三角形的底边时,则等腰三角形的周长为55414++=,故答案为:13或14.题型02根据等腰三角形等边对等角求角的度数题型03根据等腰三角形三线合一进行求解【答案】25【详解】解:如图,作BE ∵AB BC =,∴AE CE =,∵AC CD ⊥,90BAD ∠=︒∴EBA BAE BAE ∠+∠=∠+EBA CAD BAE ∠=∠∠=,【答案】10【详解】解:AB 5BD CD ∴==,210BC BD ∴==,故答案为:10.2.两个同样大小的含(1)求AF 的长.(2)求CD 的长.【详解】(1)解:连接AF ,如下图,根据题意,90BAC ∠=︒,AB ∴222(2)BC AB AC =+=∴190452B ACB ∠=∠=⨯︒=︒,∵F 为BC 中点,题型04根据等腰三角形三线合一进行证明(1)若106BAC DAE ∠∠=︒,(2)求证:BD EC =.【详解】(1)解:∵AB AC =(1180ADE AED ∠=∠=︒∵,AB AC AD AE ==,∴,BF CF DF EF ==,∴BD CE =.【变式训练】1.(2023上·山东威海·七年级校联考期中)如图,已知AB AE ABC AED BC ED =∠=∠=,,,点F 是CD 的中点,连接AF ,请判断AF 与CD 的位置关系.【答案】垂直【分析】此题考查全等三角形的判定和性质,等腰三角形三线合一的性质:连接AC AD ,,证明ABC AED ≌△△,得到AC AD =,根据等腰三角形三线合一的性质得到AF CD ⊥,熟练掌握全等三角形的判定定理及等腰三角形的性质是解题的关键.【详解】答:AF CD⊥连接AC AD,∵AB AE ABC AED BC ED=∠=∠=,,∴ABC AED≌△△∴AC AD=又∵点F 是CD 的中点∴AF CD ⊥.2.如图,在ABC 中,AB AC =,40BAC ∠︒=,AD 是BC 边上的高.线段AC 的垂直平分线交AD 于点E ,交AC 于点F ,连接BE .(1)试问:线段AE 与BE 的长相等吗?请说明理由;(2)求EBD ∠的度数.【详解】(1)解:线段AE 与BE 的长相等,理由如下:连接CE ,如图所示:=,AD∵AB AC=,∴BD CD∴AD为BC的垂直平分线,∵点E在AD上,=,∴BE CE又∵线段AC的垂直平分线交题型05根据等角对等边证明等腰三角形∠,【例题】(2023上·广西玉林·八年级统考期中)如图,点E在BA的延长线上,已知AD平分CAE ∥.求证:ABCAD BC是等腰三角形.【答案】证明见解析【分析】本题主要考查了等角对等边,平行线的性质与角平分线的定义,先根据平行线的性质得到EAD B CAD C ∠=∠∠=∠,,再由角平分线的定义和等量代换得到B C ∠=∠,即可证明ABC 是等腰三角形.【详解】证明:∵AD BC ∥,∴EAD B CAD C ∠=∠∠=∠,,∵AD 平分CAE ∠,∴EAD CAD ∠=∠,∴B C ∠=∠,∴ABC 是等腰三角形.【变式训练】【答案】ABC 是等腰三角形,理由见解析【分析】本题主要考查了等腰三角形的判定,三角形外角的性质,角平分线的定义,设4ACD x ∠=,3ECD x =∠,由角平分线的定义得到13BEC x ABC =-∠∠,A =∠【答案】证明见解析【分析】本题考查了平行线的性质,等腰三角形的性质和判定,证明根据角平分线的定义可得,以及直线平行的性质证明题型06等腰三角形的性质和判定综合应用【例题】如图,在ABC 中,AB AC =,D 是BC 边的中点,连接AD ,BE 平分ABC ∠交AC 于点E .(1)若40C ∠=︒,求BAD ∠的度数;(2)过点E 作EF BC ∥交AB 于点F ,求证:BEF △是等腰三角形.(3)若BE 平分ABC 的周长,AEF △的周长为15,求ABC 的周长.【详解】(1)解:AB AC = ,C ABC ∴∠=∠,∵40C ∠=︒,∴40ABC ∠=︒,AB AC = ,D 为BC 的中点,AD BC ∴⊥,90BDA ∴∠=︒,∴90904050BAD ABC ︒︒︒︒∠=-∠=-=;(2)证明:BE 平分ABC ∠,ABE EBC ∴∠=∠,又∵EF BC ∥,∴EBC BEF ∠=∠,∴EBF FEB ∠=∠,BF EF ∴=,BEF ∴ 是等腰三角形;(3)解:AEF 的周长为15,15AE AF EF ∴++=,BF EF = ,15AE AF BF ∴++=,即15AE AB +=,BE 平分ABC 的周长,=15AE AB BC CE ∴++=,ABC ∴ 的周长+1515=30AE AB BC CE ++=+.【变式训练】1.如图,在ABC 中,AB AC =,D 为CA 延长线上一点,DE BC ⊥于点E ,交AB 于点F .(1)求证:ADF △是等腰三角形(2)若6,3,4AD BE EF ===,求线段AB 的长.(1)试判断折叠后重叠部分△的面积.(2)求重叠部分AFC△【详解】(1)解:AFC∵四边形ABCD是长方形,∥,∴AD BC一、单选题1.(2023上·河南许昌·八年级统考期中)等腰三角形的一个底角为80︒,则这个等腰三角形的顶角为().A .20︒B .80︒C .100︒D .20︒或100︒【答案】A【分析】本题主要查了等腰三角形的性质.根据“等腰三角形两底角相等”,即可求解.【详解】解:∵等腰三角形的一个底角为80︒,∴等腰三角形的顶角为180808020︒-︒-︒=︒.故选:A2.(2024下·全国·七年级假期作业)如图,在ABC 中,,AB AC AD =为BC 边上的中线,30B ∠=︒,则CAD ∠的度数为()A .50︒B .60︒C .70︒D .80︒【答案】B【解析】略3.(2023上·广东珠海·八年级校考阶段练习)下列条件中,可以判定ABC 是等腰三角形的是()A .40B ∠=︒,80C ∠=︒B .123A BC ∠∠∠=::::C .2A B C∠=∠+∠D .三个角的度数之比是2:2:1【答案】D 【分析】本题考查了等腰三角形的判定,三角形内角和定理,熟练掌握等腰三角形的判定是解题的关键.利用三角形内角和定理,等腰三角形的判定,进行计算并逐一判断即可解答.【详解】解:A .∵40B ∠=︒,80C ∠=︒,A .16【答案】A 【分析】此题考查的是全等三角形的判定与性质、等腰三角形的性质,解题关键是掌握并会运用全等三角形的判定与性质、等腰三角形性质定理.先得出ABD ACF ∠=∠,进而得到AF 长,求出AB 出即可.【详解】CE BD ⊥ ,90BEF ∴∠=︒,90BAC ∠=︒ ,90CAF ∴∠=︒,90FAC BAD ∴∠=∠=︒ABD ACF ∴∠=∠.在ABD △和ACF △中【答案】10︒,80︒,140︒或20︒【详解】本题考查了等腰三角形的性质,先利用三角形内角和定理可得:AP AB =时;当AP AB =时;当BA BP =解:∵130ABC ∠=︒,30ACB ∠=︒,+∵BAC ∠是ABP 的一个外角,∴20BAC APB ABP ∠=∠+∠=︒,∵AB AP =,∵AB AP=,20BAP∠=︒,∴180802BAPABP APB︒-∠∠=∠==︒;当BA BP=时,如图:∵BA BP=,∴20BAP BPA∠=∠=︒,∴180140ABP BAP BPA∠=︒-∠-∠=︒;当PA PB=时,如图:∵PA PB=,∴20BAP ABP∠=∠=︒;综上所述:当ABP是等腰三角形时,故答案为:10︒,80︒,140︒或20︒.11.(2023上·广东汕尾·八年级校联考阶段练习)用一条长为21cm的细绳围成一个等腰三角形.(1)如果腰长是底边长的3倍,那么各边的长是多少?(2)能围成有一边的长为5cm的等腰三角形吗?如果能,请求出另两边长.【答案】(1)三角形的三边分别为3cm9cm9cm、、(2)能围成一个底边是5cm,腰长是8cm的等腰三角形【分析】本题考查了等腰三角形的性质,三角形的周长,难点在于要分情况讨论并利用三角形的三边关系进行判断.(1)设底边长为x cm,表示出腰长,然后根据周长列出方程求解即可;(1)求BD的长.(2)求BE的长.【答案】(1)4 (2)5,AE CD ⊥Q ,AD AC =,AE ∴平分CAD ∠,CAE DAE ∴∠=∠,在CAE V 和DAE 中,AC AD CAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩,()SAS CAE DAE ∴ ≌,CE DE ∴=,90ADE ACE ∠=∠=︒,设BE x =,则8CE DE x ==-,由勾股定理可得:222DE BD BE +=,()22284x x ∴-+=,解得:5x =,5BE ∴=.14.(2023上·浙江宁波·八年级统考期末)如图,在ABC 中,AB AC =,ED AB ∥,分别交BC 、AC 于点D 、E ,点F 在BC 的延长线上,且CF DE =,(1)求证:CEF △是等腰三角形;(2)连接AD ,当AD BC ⊥,8BC =,CEF △的周长为16时,求DEF 的周长.【答案】(1)证明见解析(2)20【分析】本题考查了等腰三角形的判定与性质,掌握等腰三角形的性质,等腰三角形的三线合一,是解答本题的关键.(1)利用等腰三角形的性质得到B ACB ∠=∠,然后推出EDC ECD ∠=∠,DE EC =,结合已知条件,得到结论.当AD BC ⊥时,AB AC =,∴142BD CD BC ===, DEF 的周长DE DF EF =++,∴DEF 的周长CE EF CD =+++15.(2023上·湖北武汉·八年级校联考阶段练习)的平分线,DF AB 交AE 的延长线于(1)若120BAC ∠=︒,求BAD ∠(2)求证:ADF △是等腰三角形.【答案】(1)60度(2)见解析(1)求证:BD CE =;(2)若BD AD =,B DAE ∠=∠,求【答案】(1)见解析(2)108BAC ∠=︒【答案】(1)等腰;(2)3;(3)12;(4)30;(5)5cm【分析】本题考查平行线的性质,角平分线的定义,对角对等边.(1)平行线的性质结合角平分线平分角,得到B C ∠=∠,即可得出结果;(2)平行线的性质结合角平分线平分角,得到A ABC CB =∠∠,进而得到AB AC =即可;(3)同法(2)可得:BD DE =,利用AB AD BD =+,求解即可;(5)同法(2)得到,PD BD PE CE ==,推出PDE △的周长等于BC 的长即可.掌握平行线加角平分线往往存在等腰三角形,是解题的关键.【详解】解:(1)∵AE BC ∥,∴,DAE B CAE C ∠=∠∠=∠,∵AE 平分DAC ∠,∴DAE CAE ∠=∠,∴B C ∠=∠,∴ABC 是等腰三角形;故答案为:等腰;(2)∵BC 平分ABD ∠,AC BD ∥,∴,ABC DBC ACB DBC ∠=∠∠=∠,∴A ABC CB =∠∠,∴3AB AC ==;故答案为:3;(3)同法(2)可得:7BD DE ==,∴5712AB AD BD =+=+=;故答案为:12;(4)同法(2)可得:,FD BD CE EF ==,∴ADE V 的周长30AD AE DE AD AE DF EF AD AE BD CE AB AC =++=+++=+++=+=;故答案为:30;(5)同法(2)可得:,PD BD PE CE ==,∴PDE △的周长5cm PD PE DE BD CE DE BC =++=++==;故答案为:5cm .18.(2023上·福建龙岩·八年级校考期中)概念学习规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.(3)当ACD 是等腰三角形,DA DC =时,如图,则50ACD A ∠=∠=︒,50BCD A ∠=∠=︒∴100ACB ACD BCD ∠=∠+=︒∠;当ACD 是等腰三角形,DA AC =时,如图,则65ACD ADC ∠=∠=︒,50BCD A ∠=∠=︒,∴5065115ACB ∠=︒+︒=︒;当ACD 是等腰三角形,CD AC =的情况不存在;当BCD △是等腰三角形,DC BD =时,如图,则1803ACD BCD B ︒-∠=∠=∠=∴2603ACB ACD BCD ∠=+=∠∠当BCD △是等腰三角形,DB =则BDC BCD ∠=∠,设BDC BCD x ∠=∠=,则B ∠=则1802ACD B x ∠=∠=︒-,由题意得,180250x x ︒-+︒=,解得,2303x ︒=,∴8018023ACD x ︒∠=︒-=,∴3103ACB ︒∠=,综上所述:ACB ∠的度数为100。
《等腰三角形的判定》 作业设计方案

《等腰三角形的判定》作业设计方案一、作业目标1、使学生熟练掌握等腰三角形的判定定理,能够准确运用定理进行推理和证明。
2、培养学生的观察能力、逻辑推理能力和空间想象能力。
3、让学生在解决问题的过程中,体会数学的严谨性和逻辑性,增强对数学的兴趣和自信心。
二、作业内容(一)基础知识巩固1、判断题(1)有两条边相等的三角形是等腰三角形。
()(2)有两个角相等的三角形是等腰三角形。
()(3)三角形一边上的中线、高线和角平分线重合的三角形是等腰三角形。
()2、填空题(1)在△ABC 中,若∠A =∠B,则△ABC 是____三角形。
(2)若一个三角形的两条边分别为3cm 和7cm,且第三边为偶数,则第三边的长为____cm。
(二)能力提升1、已知在△ABC 中,AD 平分∠BAC,BD = CD,求证:AB =AC。
2、如图,在△ABC 中,∠B =∠C,点 D、E 分别在 AB、AC 上,且 AD = AE,求证:△ABE≌△ACD。
(三)拓展创新1、如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点 O,过点 O 作 EF∥BC 交 AB 于 E,交 AC 于 F。
(1)找出图中的等腰三角形,并说明理由。
(2)若△ABC 的周长为 20,BC = 8,求△AEF 的周长。
2、已知在平面直角坐标系中,A(1,0),B(5,0),点 C 在 y 轴上,且△ABC 是等腰三角形,求点 C 的坐标。
三、作业形式1、书面作业要求学生在作业本上完成基础知识巩固和能力提升部分的题目,书写工整,步骤清晰。
2、探究作业拓展创新部分的题目作为探究作业,让学生以小组为单位进行讨论和探究,鼓励学生提出不同的解法和思路,并在课堂上进行交流和分享。
四、作业时间安排1、基础知识巩固和能力提升部分的作业,预计学生在 30 分钟内完成。
2、拓展创新部分的作业,学生可以在课后用 20 分钟左右的时间进行小组讨论和探究。
五、作业评价1、评价方式采用教师评价和学生互评相结合的方式。
《2.3等腰三角形》作业设计方案-初中数学湘教版12八年级上册

《等腰三角形》作业设计方案(第一课时)一、作业目标1. 巩固学生对等腰三角形基本概念的理解。
2. 掌握等腰三角形的性质和判定方法。
3. 培养学生的空间想象能力和逻辑推理能力。
二、作业内容作业内容主要围绕等腰三角形的性质和判定展开,具体包括以下方面:1. 基础知识巩固:要求学生回顾并熟记等腰三角形的定义、性质(如两腰相等、两底角相等)及判定条件(如两边相等则形成等腰三角形)。
2. 练习题:- 基础题:选择、填空题,如“下列哪个条件可以判定一个三角形为等腰三角形?”等。
- 应用题:结合实际生活场景,设计等腰三角形相关的应用问题,如“在建筑学中,哪些情况下会用到等腰三角形的性质?”并要求绘制简单的等腰三角形。
- 探究题:设计如“已知一个等腰三角形,能否通过其性质推导出其他角或边的关系?”等题目,培养学生自主探究的能力。
3. 思考题:引导学生对等腰三角形的性质进行深度思考,如“如何利用等腰三角形的性质解决实际问题?”等问题。
三、作业要求1. 学生需独立完成作业,不抄袭他人答案。
2. 对于练习题部分,需确保每道题目都经过自己的思考和理解,不得随意搪塞。
3. 对于绘制的图形,需使用几何工具进行规范作图,保证准确性。
4. 提交时需在作业本上工整书写答案,如有不明白的地方,可以写出自己的解题思路和疑惑点。
四、作业评价1. 教师对学生的作业进行批改,并给出相应的分数或等级评价。
2. 对于正确率较高的题目给予肯定和鼓励;对于错误较多的题目进行讲解和指导。
3. 对于学生的解题思路和探究精神给予正面反馈,并鼓励其继续努力。
五、作业反馈1. 教师将作业中出现的共性问题进行汇总和讲解,帮助学生查漏补缺。
2. 对于个别学生的问题,进行单独辅导和解答。
3. 鼓励学生之间互相交流学习心得和解题经验,共同进步。
通过以上是初中数学课程《等腰三角形》作业设计方案的第一至第五部分。
通过这样的作业设计,我们期望学生能够更好地理解和掌握等腰三角形的相关知识,同时也培养学生的空间想象能力和逻辑推理能力。
《14.5等腰三角形的性质》作业设计方案-初中数学沪教版上海七年级第二学期
《等腰三角形的性质》作业设计方案(第一课时)一、作业目标本作业旨在通过《等腰三角形的性质》的学习,使学生掌握等腰三角形的定义、性质和定理,并能熟练运用这些知识解决实际问题。
通过作业的练习,提高学生的逻辑思维能力和空间想象能力,为后续的数学学习打下坚实的基础。
二、作业内容1. 基础练习(1)等腰三角形的定义及性质简述。
(2)识别等腰三角形,并标出底边及两腰。
(3)根据给定条件判断是否为等腰三角形,并说明理由。
2. 深入探究(1)通过画图和计算,探究等腰三角形内角和的性质。
(2)利用等腰三角形的性质,解决与角度、边长相关的实际问题。
(3)通过小组合作,探讨等腰三角形与其他几何图形的联系和转换。
3. 应用实践(1)结合生活实例,分析等腰三角形在实际中的应用。
(2)编写与等腰三角形有关的数学小故事或应用题。
(3)小组合作,设计一份关于等腰三角形的海报或手抄报。
三、作业要求1. 独立完成:所有题目需学生独立思考完成,不得抄袭他人作业。
2. 格式规范:作业书写工整,解题步骤清晰,答案准确无误。
3. 合理运用所学知识:学生在解题过程中应合理运用所学的等腰三角形性质及定理。
4. 注重实践:应用实践部分需结合生活实际,体现等腰三角形在生活中的应用。
5. 小组合作:应用实践部分需以小组形式完成,每组人数不超过5人,需明确分工,体现团队合作精神。
四、作业评价1. 教师评价:教师根据学生作业的完成情况,给予相应的评价和指导。
2. 互评:学生之间互相评价作业,学习他人优点,指出不足。
3. 自评:学生自我评价,反思自己在完成作业过程中的收获和不足。
4. 及时反馈:教师需在作业批改后及时给予学生反馈,指出错误并指导改正。
五、作业反馈1. 针对学生在作业中出现的共性问题,教师需在课堂上进行讲解和指导。
2. 对于表现优秀的学生,教师应给予表扬和鼓励,激发其学习积极性。
3. 教师需根据学生作业完成情况,调整教学计划和教学方法,以提高教学效果。
3 等腰三角形 3.2 等边三角形 第1课时 等边三角形的性质和判定
15.如图,在等边△ABC中,D是AB边上的动点,以CD为一边向上 作等边△EDC,连接AE.求证:AE∥BC. 解:由SAS可推得△ACE≌△BCD,∴∠CAE=∠B,又∠B=∠ACB, ∴∠CAE=∠ACB,∴AE∥BC
16.如图,△ABC是等边三角形,过AC边上的点D作DG∥BC, 交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE, BD.求证:△AGE≌△DAB. 解 : ∵ △ ABC 为 等 边 三 角 形 , ∴ ∠ ABC = ∠ C = 60° , 又 DG∥BC , ∴ ∠ AGD = ∠ ABC = 60° , ∠ ADG = ∠ C = 60° , ∴△AGD为等边三角形,由DE=DC易推出GE=CA=AB,又 ∠AGE=∠BAD,AG=AD,∴△AGE≌△DAB(SAS)
坚持做好每个学习步骤
武亦文的高考高分来自于她日常严谨的学习 态度,坚持认真做好每天的预习、复习。 “高中三年,从来没有熬夜,上课跟着老师 走,保证课堂效率。”武亦文介绍,“班主 任王老师对我的成长起了很大引导作用,王 老师办事很认真,凡事都会投入自己所有精 力,看重做事的过程而不重结果。每当学生 没有取得好结果,王老师也会淡然一笑,鼓
易错点:对有一个角是60°的等腰三角形是等边三角形的判定方法不 理解导致出错 10.在△ABC中,①若AB=BC=CA,则∠ABC为等边三角形;②若 ∠A=∠B=∠C,则△ABC是等边三角形;③有两个角都是60°的三 角形是等边三角形;④有一个角是 60°的等腰三角形是等边三角 形.上述结论中正确的有( D ) A.1个 B.2个 C.3个 D.4个
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校: 北京大学光华管理学院
等腰三角形性质2-
B
判断下列语句是否正确。 ×) (1)等腰三角形的角平分线、中线和高互相重合。( (2)有一个角是60°的等腰三角形,其它两个 内角也为60°. ( ) (3)等腰三角形的底角都是锐角. ( ) (4)钝角三角形不可能是等腰三角形 . (×)
作业
试一试 75°,它 1.等腰三角形一个底角为 75°, 30°
3、BD = CD ,AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高 5、∠BAD = ∠CAD ,AD为顶角平分线
A A
B
C
B
D C
等腰三角形的性质:
1 .等腰三角形的两个底角相等 (简写“等边对等角”)
B
1
A
2
C
2.等腰三角形顶角的平分线,底边上的 中线,底边上的高互相重合(三线合一).
布置作业:
课本 第26页 1,2,3,4.
; / 小学数学
是诚孝至极!四哥壹直担心你贺礼の事情,可又知道你是断断不会接受四哥の帮助,愁得我和你四嫂想咯不知好些法子,怎么哪壹各都不 如你の这各法子好呢!你可真是壹各奇才!”“四哥,您这么说,愚弟都不好意思咯。其实皇阿玛啥啊都不缺,他老人家缺の不就是亲情 吗?儿女孝顺、兄友弟恭、天伦之乐,这些寻常百姓家の亲情,才是皇阿玛最需要の。”“对咯,你最精通の是古琴,这壹次?”曲目是 现成の,只有《祝寿曲》最应景,别の哪壹各也不行。十三小格精通音律,几乎每壹种乐器都有所涉猎,最精の就是古琴,其次是笛子, 第三是笙。王爷没有十三小格那样涉猎广泛,他最精通の只有箫。由于是现场敬献《祝寿曲》,古琴既不适合这么热烈、欢快、喜庆の曲 目,又需要席地而坐,因此王爷才会对此发出疑问。十三小格当然也知道现场情况,因此虽然他精于此道,也只好忍痛割爱:“四哥,您 也知道,古琴既不适合《祝寿曲》,又不适合站着演奏,愚弟这次就用笛子吧。”“那四哥就承让咯。”于是两各人立即开始咯刻苦の研 习,力求配合得天衣无缝、珠连璧合。十三小格拉上王爷,主要是不想自己有啥啊私自の行动,被人称作是出风头而冷落咯他の四哥;王 爷加入十三小格,是不想他の十三弟因此而招来其它兄弟の嫉恨,假如有人嫉恨,那就连他这各四哥壹起嫉恨吧,他不能让他最为亲厚の 十三弟独自壹各人面对这些明枪暗箭。第壹卷 第329章 特赦三月十八日是皇上六十大寿の正日子,前期の壹系列庆典已经将皇上の六十 大寿推向咯最高-潮。这壹天,将在宫中举办家宴,由于皇上妃嫔成群、儿女众多、子孙满堂,因此即使是家宴,规模也是格外宏大。自 康熙四十九年,水清参加八月节宫宴被太子盯上以后,王爷担心凭白惹出祸端,就吩咐排字琦无限期地禁止水清参加宫中の壹切活动。排 字琦壹方面要严格执行王爷の命令,另壹方面还要搜肠刮肚地在德妃娘娘面前,为天仙妹妹编造各种各样の借口和理由,早就是心力交瘁。 康熙五十壹年,皇上发现太子仍然不思悔改,继续结党营私、图谋篡位夺权,因此第二次废掉咯皇太子胤礽,并锢于咸安宫中。这各消息 对王爷而言就是壹剂治病の良药,各位兄弟们重新回到咯同壹起跑线上,开始咯新壹轮の竞争和角逐。只是其它の兄弟们都是喜形于色、 摩拳擦掌、厉兵秣马、励精图治,而唯有他,仍然是壹副超凡脱世、淡然处之の样子。王爷虽然表面上不动声色,甚至有意地疏远着朝臣, 但在内心深处,在私底下,他不比任何壹各皇子の行动慢,甚至比其它人更迅速、更变本加厉。由于他壹门心思地筹划着这些大事情,而 且水清壹贯行事低调,尽可能少地出现在他の视线范围内,因此,太子二度被废、警报解除以后,他根本就没有意识到,可以恢复水清在 宫中の行动咯。排字琦哪里知道王爷是因为太子の原因才对年妹妹下咯禁令,因此还壹直严格地执行着他の命令,继续苦不堪言地寻找着 各式借口和理由。皇上の六十大寿宫宴是非比寻常の壹件重大の事情!这各宫宴难道也不能让水清参加?还是生病の理由?因为除此之外 の任何理由都拿不出手。举棋不定の排字琦只好来请求他の指示:“爷,过些天皇阿玛六十大寿の宫宴,年妹妹能参加吗?”“年氏?为 啥啊她不参加?”“爷?不是您说の,从今以后所有の宫中活动她都不要参加咯吗?妾身是想,这可是皇阿玛の六十寿宴,假如不参加の 话,怕是说不过去呢。难道还是要说她病咯吗?那样对她是不是也不太公平呢?”排字琦洋洋洒洒の这壹通话说下来,王爷才恍然大悟, 想起来咯,好像是她刚嫁进来那年の八月节吧,为咯避免与太子起冲突才下咯她の宫中禁行令。不要说皇阿玛六十大寿这么重要の日子, 就凭太子已经永远地被禁于咸安宫这壹点,水清の禁令也应该撤销。“嗯,皇阿玛の寿宴应该参加,另外,宫中の请安也恢复吧,另外, 还要烦请福晋多带带她,乡野村妇,不懂规矩礼节,万不可被旁人耻笑,丢咯咱们王府の脸面。”“是の,爷。”排字琦机械地应咯声, 这变化也太大咯!不但寿宴能参加,连请安也壹并恢复咯,早知道爷这么痛快就答应咯,她真应该早些年就来请示咯,何苦总被德妃娘娘 问来问去の!第壹卷 第330章 惊情如此轻而易举地获得咯特赦令,排字琦真是后悔不迭,这些年来为咯给天仙妹妹编造各式各样の理由 不去宫里请安,她都要疯掉咯。天知道这些年她都是怎么过来の,有の时候,她都发现自己の谎言前言不搭后语,然后居然还能稀里糊涂 地又蒙混过关。特别是前年,德妃娘娘伴随圣驾从塞外行围回来,三天两头地追问水清如何咯。不但总是追问水清如何,更是特别地关心 她の那各丫环怎么样咯:“唉,你也好好劝劝年氏,诸人嘛,肚量就要大壹些,既然生米已经煮成熟饭,早些给咯名份算咯。总拖着也不 是办法,何苦让你们爷为难呢,不就是壹各侍妾嘛,又不碍着她稳稳当当地当那各侧福晋。”“额娘,您,您说の?媳妇怎么不太明白 呢?”“噢,就是这回在塞外,你们家爷看上年氏の壹各丫环咯,这事儿呢,额娘也知道她の脸面上难看点儿,但既然已经如此,还能怎 么样?假如她能够大度点儿,你们家爷也还能念她壹句好,否则闹得不可开交,爷更得记恨她。所以你也要拿出你嫡福晋の威严,不要由 着年氏の性子,这种事情越拖越是夜长梦多,还是赶快抓紧点吧,娶进府里来
等腰三角形的性质(分层作业)(解析版)-八年级数学上册
13.3.1等腰三角形的性质夯实基础篇一、单选题:1.如图,B 在AC 上,D 在CE 上,AD BD BC ,25ACE ,ADE 的度数为()A .50°B .65°C .75°D .80°【答案】C 【知识点】三角形的外角性质;等腰三角形的性质【解析】【解答】解:BD BC ∵,25ACE ,25BDC C ,50ABD ,AD BD ∵,50A ABD ,75ADE A C .故答案为:C.【分析】由等边对等角得25BDC C ,利用三角形外角的性质求出50ABD ,由等边对等角得50A ABD ,根据三角形外角的性质求出75ADE A C .2.若等腰三角形的一个外角是70°,则它的底角的度数是()A .110°B .70°C .35°D .55°【答案】C【知识点】三角形内角和定理;等腰三角形的性质【解析】【解答】解:∵等腰三角形的一个外角是70 ,与这个外角相邻的内角的度数为18070110,这个等腰三角形的顶角的度数为110 ,底角的度数为1(180110)35,2故答案为:C.【分析】利用等腰三角形的一个外角是70°,可求出与这个外角相邻的内角的度数,由于这个角是钝角,只能做顶角,然后根据三角形的内角和定理及等腰三角形的性质求出它的底角的度数即可.3.若(a﹣2)2+|b﹣3|=0,则以a、b为边长的等腰三角形的周长为()A.6B.7C.8D.7或8【答案】D【知识点】三角形三边关系;等腰三角形的性质;偶次幂的非负性;绝对值的非负性【解析】【解答】解:∵(a﹣2)2+|b﹣3|=0,∴a﹣2=0,b﹣3=0,解得a=2,b=3,①当腰是2,底边是3时,三边长是2,2,3,此时符合三角形的三边关系定理,即等腰三角形的周长是2+2+3=7;②当腰是3,底边是2时,三边长是3,3,2,此时符合三角形的三边关系定理,即等腰三角形的周长是3+3+2=8.故答案为:D.【分析】首先根据非负数的性质可以得到a,b的长度,再分类讨论:腰为2,底为3;和腰为3,底为2,分别求出即可4.如图,CD是等腰三角形△ABC底边上的中线,BE平分∠ABC,交CD于点E,AC =8,DE=2,则△BCE的面积是()A.4B.6C.8D.12【答案】C【知识点】三角形的面积;角平分线的性质;等腰三角形的性质【解析】【解答】解:过点E作EF⊥BC于F,∵AC=BC=8,CD是等腰三角形△ABC底边上的中线,∴CD⊥AB,∵BE平分∠ABC,ED⊥AB,EF⊥BC,∴EF=DE=2,∴△BCE的面积=12×BC×EF=12×8×2=8.故答案为:C.【分析】过点E作EF⊥BC于F,利用等腰三角形的性质可证得CD⊥AB,利用角平分线上的点到角两边的距离相等,可求出EF的长;再利用三角形的面积公式可求出△BCE 的面积.5.一个等腰三角形的底边长为5,一腰上中线把其周长分成的两部分的差为3,则这个等腰三角形的腰长为()A.2B.8C.2或8D.10【答案】B【知识点】等腰三角形的性质【解析】【解答】∵BD为中线,AB=AC,BC=5,∴AD=CD,∵C△ABD=AB+BD+AD,C△CBD=BC+CD+BD,①当C△ABD-C△CBD=3时,∴AB+BD+AD-(BC+CD+BD)=3,即AB-BC=3,∴AB=3+5=8,∴△ABC三边长分别为:8,8,5,符合三角形三边之间的关系,②当C△CBD-C△ABD=3时,∴BC+CD+BD-(AB+BD+AD)=3,即BC-AB=3,∴AB=5-3=2,∴△ABC三边长分别为:2,2,5,2+2 5,不符合三角形三边之间的关系,故答案为:B.【分析】根据等腰三角形的性质和中线的定义分两种情况讨论:①当C△ABD-C△CBD=3,②当C△CBD-C△ABD=3,分别求出AB的长,再结合三角形三边之间的关系来分析即可得出答案.6.在Rt△AB C中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为()A.5cm B.6cm C.7cm D.8cm 【答案】A【知识点】线段垂直平分线的性质;等腰三角形的性质【解析】【解答】解:∵CE所在直线垂直平分线段AD,∴AC=CD=5cm,∠ACE=∠DCE,∠AEC=90°,∵CD平分∠BCE,∴∠ECD=∠BCD,∴∠ACE=∠DCE=∠BCD,∵∠ACE+∠DCE+∠BCD=∠ACB=90°∴∠ACE=∠DCE=∠BCD=30°,在△AE C中,∠AEC=90°,∠ACE=30°,∴∠A=60°,在△AB C中,∠A=60°,∠ACB=90°,∴∠B=30°,∴∠B=∠BCD=30°,∴BD=CD=5cm.故答案为:A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第
3讲等腰三角形2
1、如图,AD∥BC,AB∥CD,CE平分∠BCD,交AB于O,交DA延长线于E,①图中有个等腰三角形;②请证明其中一个三角形是等腰三角形。
2、已知等腰三角形的三边长分别是3,7
,1+2a,则a的值是_______。
3、如图,在5×6的正方形网格中,找一格点C,使△ABC成为等腰三角形,这样的C点共有点。
4、如图,已知AB=AC,BD=BC,∠C=72º,则∠ABD=________.
5、如图,AB=AC,D是BC上一点,AE=AD,∠BAD=30°,∠ADC=α,则∠AED= 度(用
α表示).
6、如图,Rt△ABC中,∠ACB=90°,∠A=50°,将三角形绕C点顺时针旋转30°,得到△DCE,
则∠ABE= °.
7、如图,DC∥AB,∠A=∠B,求证:AD=BC。
8、如图所示,若△ABC、△ADE都是正三角形,(1)试比较线段BD与线段CE的大小?并说明理由;
(2)直接写出一个角,使它等于直线AC和BD相交所成的锐角∠CFB(对顶角除外);
(3)计算直线EC和BD相交所成的锐角。
9、如图,Rt△ABC中,∠BAC=90°,D在BC上,AD=BD,求证:AD=DC。
(第3题)(第4题)(第5题)(第6题)
10、已知如图,在△ABC中,点D、E分别在AC
、AB上,若AE=DE=DB=BC,且∠ABC=100°,求∠A
的度数.
11、等腰三角形一腰上的高与底边的夹角为α,则顶角的度数是
.
12、如图,已知锐角三角形ABC,请你将它分成三个等腰三角形。
(保留画图痕迹)
13、如图,过数轴原点O作30度的角,OA=1,在数轴上找一点B,使△OAB是等腰三角形,画出B
点。
14、如果点P与正方形四边分别构成四个等腰三角形,那么这样的点可以找到几个?画图说明。
15、如图,△ABC中AB=AC,点P与三角形三边分别构成三个等腰三角形,那么这样的点可以找到几
个?画图说明。
16、如图,AC平分∠DAB,∠D+∠B=180°,求证:CD=CB.
17、如图,已知AB=AC=2,△ABC 的面积为3,D 是BC 上一点,DE ⊥AB 于E ,DF ⊥AC 于F ,
(1)求DE+DF 的值;(2)当D 移动到BC 延长线上时,写出DE
和DF 的等量关系,并证明。
18、如图,已知AOB 是一钢架,且10AOB ∠= ,为使钢架更加坚固,需在其内部添加一些钢管EF 、
FG 、GH……,添加的钢管长度都与OE 相等,则最多能添加这样的钢管( )
A .7根 B.8根 C.9根
D.10根
19、如图△ABC 中,D 、E 分别在BC 上,BE=BA ,DC=AC 。
(1) 若∠BAC=Rt ∠,求∠DAE 的度数;
(2) 若∠BAC=x 度,∠DAE=y 度,求y 与x 的关系。
(3) 在(2)中求y 的最大值。
20、如图,有不同形状的五个三角形,都已知了两个角的度数。
请你分别在每个三角形中画一条分割线,
将每个三角形分割成两个等腰三角形,并标出等腰三角形两个底角的度数。
45°45°25°65°
25°50°36°
72°36°36°
21、如图,在一个房间内,有一把梯子斜靠在墙上,梯上顶端距地面的垂直距离MA =am ,此时梯子的
A B C D E
倾斜角75°,如果梯子底端不动,顶端靠在对面墙上,此时梯子顶端距地面的垂直距离NB=bm,梯子的倾斜角为45°,求这间房子的宽AB。
22、如图,DB、DC分别平分∠ABC和∠ACB,过D点作直线EF,交AB、AC于E、F,且AE=AF。
求证:∠1=∠2.
23、如图△ABC中,过顶点A平行于BC的直线与∠ABC,∠ACB的平分线交于E、D两点。
若AC=6,
AB=10,求DE的长。
24、如图,∠1=∠2,DE=CE,求证:△ABD≌△BAC。
25、如图,将边长为4的正方形ABCD分割成4个不都全等的等腰三角形,并求最大的等腰三角形的面
积。
