网格线中的三角函数问题
网格线中的三角函数问题

・ . .
’ . .
由勾股 定理 得 B E =
AB=
・ . ・
, A E = 2
设B D为 , C D为 2 一 , 由勾 股 定理 得
AB - BD = AD , AC 一C D = AD。 ,
・
例 2 如图3 , 在 边 长相 同的小 正方 形 网 格 中, 点 A、 B、 C 、 D都 在 这 些 小 正 方 形 的 顶
点上, A B 、 C D相 交 于 点 P, 则t a n Z AP D的 值 为
( ) .
A. 1 B. 2 C_ 3 D.
故选 : B .
,
A D: T 9 . 3
.
二、 运用方 程 。 以数 解形
.
9
几何 图形 中 的问题转 化 为用代 数 的知识
.
・ .
求解 , 这 就 是数形 结合 思想 中的“ 以数解 形” ,
s i n 肚 A D 去
数 学语言与直观 的图像结合起来 , 关键是代数 问题 与图形之间的相 互转化 , 它可以使代数 问题 几 何化 , 几何问题 代数化. 数学 中的知识 , 有的本身就可以看作是数形 的结合 . 女 口 : 锐角三角函数 的定 义是借助 于直 角三 角形 来定 义的. 下面 我们就 网格线 中锐 角三 角函数 的 问题来 体会这 种数学思
、
-"
'--4 \Fra bibliotek"- - -
.
3
aB D P, 然后 由相似 三 角形 的对 应边 成 比例 . 易得 D P : C P = 1 : 3 , 即 可得 P F : C F = P F : B F = 1 : 2 ,
网格中的三角函数

1网格中的锐角三角函数网格是同学们从小就熟悉的图形,在网格中隐含的条件有:1.直角;2.单位长度。
所以在网格中可以求一个锐角的三角函数,是近几年中考的热点,下面举例说明。
一、在网格中与勾股定理现结合求一个锐角的三角函数。
【例1】 三角形在正方形网格纸中的位如图1,则sin α的值是( ).[解析] 本题在网格中考查锐角的正弦的意义,首先要用勾股定理计算直角三角形斜边的长.一般情况下,为了减小计算量,把小正方形的边长设为1.选C .练习1(广州市2014)如图2,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则( ).(A ) (B ) (C ) (D )练习2 (2014年福州)如图3,在边长为1个单位长度的小正方形所组成的网格中,△ABC 的顶点均在格点上,344543B .; C .35;D .A. 35图3图22sinB 的值是 .3.(2011四川)如图4,在4×4的正方形网格中, tanα= .A .1B .2C .12D4.(2011甘肃兰州)如图5,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC’B’,则tanB’的值为 .A .12B .13C .14 D3. (2011江苏连云港)如图6,△ABC 的顶点都在方格纸的格点上,则sin A =_______.在网格中求一个锐角的三角函数时,根据图中角的位置。
充分利用网格中的直角和边,然后根据勾股定理求出相应的边长,最后利用三角函数公式进行计算,达到解决问题的目的。
二、在网格中与辅助线相结合求一个锐角的三角函数。
【例2】 (2014•贺州)如图7-1网格中的每个小正方形的边长都是1,△ABC 每个顶点都在网格的交点处,则sinA= .[解析] 虽然网格中隐含直角,但是∠A 是△ABC中图7-1图7-2图4图6图5的一个锐角,而△ABC不是直角三角形,不能直接运用三角函数公式进行计算,必须先做辅助线构造直角三角形,使∠A在一个直角三角形中,然后求出所对应的斜边和对边,而后解决问题。
例谈网格中求锐角三角函数值问题

例谈网格中求锐角三角函数值问题●胡永强 (阳山实验初级中学校,江苏苏州 215151) 摘 要:文章研究了在网格中求锐角三角函数值的问题,分别给出两类问题的解决策略,从“化斜为直、转化、方程”等数学思想方法角度对多种解法进行了总结.关键词:网格;锐角三角函数;化斜为直思想;转化思想;方程思想中图分类号:O124.1 文献标识码:A 文章编号:1003 6407(2020)03 0016 03 网格是一种研究数学问题的常用工具,如在图形的各种变换(如平移、翻折、旋转、位似)、函数图像、相似三角形的判定、确定圆弧的圆心、图案设计与面积计算、求锐角三角函数值等问题中有着广泛的应用.据说笛卡尔也曾受到蜘蛛结网的启发,在网格中发明了坐标系,发展出解析几何这门新的数学分支,说明网格与数学问题关系密切.本文主要探讨在网格中求锐角三角函数值问题.1 正方形网格正方形网格中主要有两大类题型:一是角的顶点在格点上;二是角的顶点不在格点上.顶点在格点上的又包括残缺三角形类型和非直角三角形类型两种.对于残缺型需补全三角形,再利用勾股定理求出相关边长即可解决;对于顶点在格点上的非直角三角形类型,常在三角形内部作高线构造直角三角形,利用勾股定理和等面积公式等知识计算出相关线段的长度即可解决;对于角的顶点不在格点上的类型通常作所求角某一条边的平行线,构造所求角的顶点在格点上的同位角,再依托其同位角构造一个直角三角形来解决.下面选取几道例题加以说明.1.1 残缺的格点三角形———补全 例1 如图1,点A,B,C是小正方形的顶点,(上接第15页)体对应关系不容易看出来,但是有了这样的观念,才会在“数形结合”思想的引领下,引入参数,顺藤摸瓜,最后让潜在的事实浮出水面.又比如几何直观的意识在问题探索中的作用.文中在一般化和特殊化原则的互动下,用动态的眼光分析问题,从图3、图4联想到图5、图6,使得一些属性呈现出高度的统一.3.2 教师要成为解题方面学生学习的典范在解题中学会解题,在解题过程的回顾中捕捉看似“浪费”的信息,学会思维环节的取舍.比如文中提及的“两条直线的斜率是互为相反数,即kAC+kBC=0,”这一特殊的数量关系,一旦察觉,就能捕捉到两个等腰三角形,从而开阔了视野.教师在解题教学时引用的例题,正是自己在问题解决过程中经历了“是什么,怎么做,为什么”这样的层层逼近,逐渐“从明确走向深刻”,甚至是领悟到“众里寻他千百度,蓦然回首,那人却在灯火阑珊处”的妙处,因此迫不及待地想把这份体验带给学生.教师应该就自己解题时所经历的“千转百回”和“顿悟”转化为教学形态,从而成为解题方面学生学习的典范.参 考 文 献[1] 波利亚.怎样解题[M].上海:上海科技教育出版社,2007:序言.[2] 裴光亚.教学的底线[J].中学数学教学参考:中旬,2018(4):1.[3] 罗增儒.中学数学解题的理论与实践[M].南宁:广西教育出版社,2008:182.·61·中学教研(数学)2020年第3期收文日期:2019 09 23;修订日期:2019 10 25基金项目:江苏省苏州市教育规划课题(192010343)作者简介:胡永强(1981—),男,江苏新沂人,中学高级教师.研究方向:数学教育.且每个小正方形的边长为1,则tan∠BAC的值为( )A.12 B.1 C.槡33槡 D.3图1图2分析 要计算tan∠BAC的值,需要将∠BAC放到一个直角三角形中.联结BC,如图2,可通过证明△ABE≌△BCD推导出∠ABC是直角,再运用勾股定理求出∠BAC的对边BC和邻边AB的长,进而求出tan∠BAC的值.另外也可由△ABE≌△BCD得出AB=BC,再结合∠ABC是直角,可以根据正切的定义得出tan∠BAC的值为1.1.2 非直角三角形的格点三角形———作高例2 如图3,网格中的每一个正方形的边长都是1,△ABC的每一个顶点都在网格的格点处,则sinA的值为.图3图4分析 要求出sinA的值,需要把∠BAC放到一个直角三角形中,可以过点B或点C作△ABC的高线.受网格所限,如图4,可作BD⊥AC,垂足为点D,运用勾股定理求出边AB的长,运用等面积法求出高BD的长,从而计算出sinA的值.1.3 角的顶点不在格点上类型———平移图5例3 如图5,网格中的每一个正方形的边长都是1,点A,B,C,D都在格点处,AB与CD相交于点O,则tan∠BOD的值为.分析 ∠BOD的顶点O不在格点上,添加高线构造出直角三角形后,边长的计算比较困难.可以考虑平移∠BOD的某一条边,将∠BOD的顶点O平移到某一格点上,进而依托此格点在给定的网格中构造出一个格点直角三角形,这样就可以求出相关锐角的三角函数值,再根据同位角相等进行等量代换,从而解决问题.本题可以平移边OB,也可平移边OD,下面各举一例:1)如图6,平移∠BOD的边OB,使点O平移到点C处,作CE∥AB,过点D作CE的垂线,交CE于点E,得到Rt△CDE.在Rt△CDE中,求出tan∠ECD的值,由CE∥AB可得∠BOD=∠ECD,从而得到tan∠BOD的值.图6图72)如图7,平移∠BOD的边OD至AF处,过点F作AF的垂线交AB于点G,构造Rt△AGF,在Rt△AGF中完成计算.2 非正方形网格除了正方形网格之外,非正方形网格问题近来也频频出现,如矩形网格、菱形网格、等边三角形网格等.这些非正方形网格中问题的解决思路和方法与正方形网格类似,可以将正方形网格中的解题思路和方法迁移过来.2.1 矩形网格———添线例4 图8是一个长方形网格,组成网格的小长方形的长是宽的2倍,△ABC的顶点都是网格中的格点处,则sin∠BAC的值是.图8图9分析 根据网格小长方形的长为宽的2倍,可以添加两条垂线将其转化为正方形网格,如图9所示,将其转化为1.2中的问题,然后通过作高法解决.·71·2020年第3期中学教研(数学)2.2 菱形网格———求角例5 如图10,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角∠O=60°,点A,B,C都在格点上,则tan∠ABC的值是.图10图11分析 此图属于残缺型问题,如图11所示,可以通过延长BC到点D,联结AD构造△ABD,结合∠O=60°这一条件及菱形每条对角线平分一组对角的性质可证明∠ADB是直角,再结合等腰三角形和勾股定理等知识求出线段AD和线段BD的长,从而求出tan∠ABC的值.2.3 等边三角形网格———组合例6 在由10个完全相同的等边三角形构成的网格图中,∠α,∠β如图12所示,则cos(α+β)=.图12图13分析 如图13,将各个点标上字母,联结DE,利用等边三角形的性质及三角形内角和定理可得出∠α=30°.同理可得∠CDE=∠CED=30°=∠α,由∠AEC=60°结合∠AED=∠AEC+∠CED可得出∠AED=90°,设每个小等边三角形的边长为a,则AE=2a,DE=槡3a.在Rt△ADE中,利用勾股定理可得出AD的长,再结合余弦的定义即可求出cos(α+β)的值.3 此类问题中蕴含的几种思想方法3.1 化斜为直思想在初中阶段,求锐角三角函数值常常需要将锐角放在直角三角形中求解,因此构造直角三角形是解决这类问题的首要条件.常用的构造方法是作高线,可以在三角形内部作高,也可以在外部作高,具体作哪条边的高线要结合题目特点作出选择,通常选取较为方便计算的一种情形.在菱形及等边三角形网格中,也需要添加适当的辅助线构造直角三角形以解决问题.3.2 转化思想转化思想是解决数学问题中一种十分常用的数学思想,它是将数学问题由难变易、由陌生变熟悉的过程.转化思想在解决此类问题中比比皆是,如将非直角三角形转化为直角三角形;将顶点不在格点上的角通过作平行线构造同位角转化为顶点在格点上的角;将非格点三角形的情形转化为格点三角形的情形;将长方形网格转化为正方形网格等都体现了转化的思想.3.3 方程思想在求锐角三角函数值的过程中,通常需要先构造直角三角形,再计算出所求三角函数值所需要的边.格点三角形的边长常常借助其形外的直角三角形使用勾股定理作为等量关系列出方程,完成计算;在格点三角形内部构造高线后,常需要用同一图形面积相等作为等量关系列出方程,完成计算;有时候还需要借助网格线的平行关系寻找相似三角形,将相似三角形对应边成比例这条定理作为等量关系列出方程,完成计算.由此可见,方程思想在解决此类问题中意义重大.4 结束语网格中可供研究的数学问题是非常丰富的,本文只是笔者在网格长河中采撷的一朵浪花,列举出在网格中求锐角三角函数值的几种类型及相应的解题策略,结合思考和分析问题的过程归纳出解决此类问题的几种常用数学思想方法.由于水平和经验有限,文中必定存在诸多瑕疵,望读者多批评指正.同时,文中所阐述的解题策略还不够完善,必然还存在其他更多优秀的解法,待广大师生在解题实践过程中不断探索和完善[1].参 考 文 献[1] 姜晓翔.初中数学命题方法之延续策略[J].中国数学教育,2019(6):39 43.·81·中学教研(数学)2020年第3期。
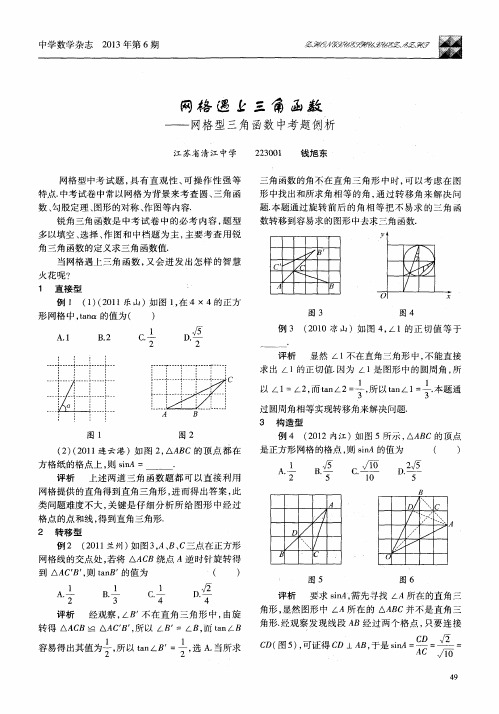
网格遇上三角函数——网格型三角函数中考题例析
.
、
、 、 、 \ 、
、
’
D
、 、 、
由 勾 股 定 理 知 O D : 掣, 所 以 c 。 s 厶 4 0 曰 : .
形 网格 中 , t a n c  ̄ 的值 为 (
A. 1 B. 2 c.
)
D.
, '
图3
图4
例3 ( 2 0 1 0凉 山)如 图 4 , -1的正 切 值 等 于 /
评析 显 然 1 不在 直角 三角 形 中 , 不能 直接
求 出 1的正 切值 . 因为 1 是 图形 中的圆周 角 , 所
( 2 ) ( 2 0 1 1 连 云 港 )如 图 2 , AA BC的顶 点 都 在
方格 纸 的格 点上 , 则s i n A:
.
评析 上述两道三角函数题都 可以直接利用 网格 提供 的直 角得 到直 角三 角形 , 进 而得 出答案 , 此 类问题难度不大 , 关键是仔细分析所给图形 中经过
所 在 的 AA BC并不 是 直 角三
角形 . 经 观察 发 现 线段 A B经 过 两 个 格点 , 只要 连接 5 证得 c D L A B, i = = =
蝴 容易得出其值为÷, 所以t a n / _ B = ÷, 选A . 当所求 c
4 9
C
以 1 : 2 , 而t a n / _ 2: 1 所以t a n 1 :l _ 1
,
.
本 题通
图 1
图 2
过圆周角相等实现转移角来解决 问题. 3 构造 型 例4 ( 2 0 1 2内江 )如 图 5所示 , AA B C的顶点
三角函数专题之网格中的三角函数

三角函数专题训练--网格中的三角函数第一节:网格中的正弦和余弦1.在边长为1的正方形网格中,点A 、B 、C 、D 都在格点上,AB 与CD 相交于点O ,则∠AOD 的正弦值为()A .12B .2C D 2.如图,在2×2正方形网格中,以格点为顶点的△ABC 的面积等于32,则sin ∠CAB =()A .2B .35C .5D .3103.如图,在边长为1的小正方形网格中,点A 、B 、C 、C 都在这些小正方形的顶点上,AB 、CD 相交于点O ,则cos AOD ∠=()A .2B .2C .3D 4.如图,点A ,B ,C 在正方形网格的格点上,则sin ∠BAC 等于()A B C .5D .105.如图,在边长1正网格中,A 、B 、C 都在网格线上,AB 与CD 相交于点D ,则sin ADC ∠是()A B C D 6.如图,点A ,B ,C 在正方形网格的格点上,则sin ∠BAC=()A .6B .26C .13D .137.如图,在45⨯的正方形网格中,每个小正方形的边长都是1,ABC 的顶点都在这些小正方形的顶点上,那么sin ACB ∠的值为().A B C .35D .458.如图,在正方形网格中,△ABC 的位置如图,其中点A 、B 、C 分别在格点上,则sinA 的值是()A B .13C D9.如图,在5×4的正方形网格中,每个小正方形的边长都是l ,△ABC 的顶点都在这些小正方形的顶点上,则cos ∠BAC 的值为()A .43B .34C .35D .4510.在正方形网格中,△ABC 的位置如图所示,则cos ∠B 的值为()A .12B .2C D .311.三角形在方格纸中的位置如图所示,则cos 的值是()A .35B C .45D 12.如图,△ABC 的顶点都是正方形网格中的格点,则cos ∠ABC 等于()AB C D .2313.如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC 的顶点都是网格中的格点,则cos ∠ABC 的值是()A .23B .25C .35D .4514.如图,△ABC 的顶点都在正方形网格的格点上,则cos ∠BAC 的值为()A .34B .25C .35D .4515.如图,在下列网格中,小正方形的边长均为1,点A 、B 、O 都在格点上,则AOB ∠的正弦值是()A .10B .12C .13D .1016.如图,在正方形网格中,小正方形的边长为1,点A 、B 、C 、D 都在格点上,AB 与CD 相交于点O ,则∠AOC 的正弦值是__.17.如图,已知△ABC 的三个顶点均在格点上,则cosA 的值为_______.18.如图所示,AOB ∠是放置在正方形网格中的一个角,则sin AOB ∠的值是________.19.如图所示方格纸中每个小正方形的边长为1,其中有三个格点A 、B 、C ,则sin ∠ABC=_____.20.如图是4×4的正方形网格,点C在∠BAD的一边AD上,且A、B、C为格点,sin∠BAD的值是___________.∠=______.21.如图在边长相同的小正方形组成的网格中,点A、B、O在小正方形的顶点上,则cos OAB22.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC 的余弦值是____.23.如图,在6x6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则cos∠BAC的值是_____.24.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD=___.25.如图,在4×4的正方形网格图中有△ABC,则∠ABC的余弦值为_____.26.如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是_____.27.如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上,则cos∠BAC 的值为_____.的顶点都在小正方形的格点上,28.如图,在44⨯的正方形网格(每个小正方形的边长都是1)中,ABC∠=_______.则sin ACB29.如图,每个小正方形的边长都是1,点A,B,C都在小正方形的顶点上,则∠ABC的正弦值为____.第二节:网格中的正切1.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为()A .2BC .3D2.如图,将△ABC 放在每个小正方形的边长为1的网格中,点A ,B ,C 均在格点上,则tan C 的值是()A .2B .43C .1D .343.如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为()A .12B .1C .3D 4.如图是由边长相同的小正方形组成的网格,A ,B ,P ,Q 四点均在正方形网格的格点上,线段AB ,PQ 相交于点M ,则图中∠QMB 的正切值是()A .12B .1CD .25.如图,ABC 的顶点在正方形网格的格点处,则tan C 的值为()A .12B .13C .2D .16.如图,将 ABC 放在每个小正方形的边长为1的网格中,点A ,B ,C 均在格点上,则∠A 的正切值是()A B C .2D .127.如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC 的顶点都在这些小正方形的顶点上,则tan BAC ∠的值为()A .43B .34C .35D .458.如图,A ,B ,C ,三点在正方形网格线的交点处,若将ABC 绕着点A 逆时针旋转得到AC B ''△,则tan B '的值为()A .12B .13C .14D .49.如图所示,ABC ∆的顶点在正方形网格的格点上,则tan A 的值为()A .12B .2C .2D .10.在图网格中,小正方形的边长为1,点A 、B 、C 、D 都在格点上,AB 与CD 相交于点O ,则∠AOC 的正切值是()A .23B .32C .35D .5311.如图,在方格纸中,点A ,B ,C 都在格点上,则tan ∠ABC 的值是()A .2B .12C D 12.如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,则tan ∠ABC 的值为()A .35B .34C .5D .113.如图,∠AOB 是放置在正方形网格中的一个角,则tan ∠AOB ()A .3B C .1D .2514.∠BAC 放在正方形网格纸的位置如图,则tan ∠BAC 的值为()A .16B .15C .13D .1215.如图,在55 的正方形网格中,每个小正方形的边长均为1,ABC 的顶点均在格点(网格线的交点)上,则tan B 的值为______.16.如图,点A ,B ,C ,D 在正方形网格的格点上,连接AB 、CD 交于点P ,则tan ∠APC =________________.17.如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为_____.18.如图,在5×4的正方形网格中,每个小正方形的边长都是1,ABC 的顶点都在这些小正方形的顶点上,则tan ABC ∠的值为_______.19.如图,在边长为1的正方形网格中,连接格点A ,B 和C ,D ,AB 与CD 相交于点E ,则tan AEC ∠=___.20.如图,在4×5的正方形网格中点A ,B ,C 都在格点上,则tan ∠ABC =_____.21.如图,把n 个边长为1的正方形拼接成一排,求得tan 1BA C ∠=1,tan 2BA C ∠=13,31tan 7BA C ∠=,计算4tan BA C ∠=_________________.22.如图,将BAC ∠放置在55⨯的正方形网格中,如果顶点A 、B 、C 均在格点上,那么BAC ∠的正切值为______.23.如图,在边长相同的小正方形组成的网格中,点A 、B 、C 都在这些小正方形的顶点上,则tan ∠ABC 的值为_____.24.如图,在Rt △ABC 纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点,已知BC =24cm ,则这个展开图可折成的正方体的体积为_____cm 3.25.如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,则tan C =__.26.如图,在正方形网格中,三角形ABC 的三个顶点都在网格中的格点上,则tan ∠B 的值为_____.27.如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,线段AB 、CD ,相交于点P ,则tan APD ∠的值是__________.28.如图,在边长都为1的小正方形组成的网格中,点A ,B ,C ,D 都在这些小正方形的顶点上,AB ,CD 相交于点P ,则tan ∠APD 的值是____________.29.如图,把n 个边长为1的正方形拼接成一排,求得1tan 1BA C ∠=,21tan 3BA C ∠=,31tan 7BA C ∠=,计算4tan BA C ∠=__________,……按此规律,写出tan n BA C ∠=__________(用含n 的代数式表示).。
网格线中的三角函数问题

住R l AA B E r T 1 , l a I 1 厶I B E = 2 . - . . t a n - / 4 P D = 2 .
赣 蠡 法 F a
, f 0 4 ( 2 0 1 6 ・ 山 东淄博 ) 图7 是 由边长相
同的 小 正 方 形 组 成 的 网格 , A、 B、 P 、 Q四 点 均
=
8
A . 2 B .
j
C . 三 D .
二 )
相 同的 小正 方形 戍 的 网格 中 . 点 l 、 B、 C、 D D组 — 一 D
【 方法 探究 】 如 何把 曰 c 住 某 个 翰
三 角形中是解决 本题 的关键 , 仃 m 察可 以发 现: A B在小 正 疗形 的对 角线 『 . 能联想 到 4 5 。
.
. 、 \
\
\ 、
、
\
、 、
\
\
D
例2 ( 2 0 1 6 ・ 福建福 州) 如 图3 , 6 个形状 、
、 \ D
~
大小完全相 同的 菱形组成 网格 , 菱形的顸点称 为格点. 已知 菱形的一个角( /0) 为6 0 。 , - 4 、 、 c 都在格点上 , 则t a n Z A B C的值是 .
转化 . 找 出它的“ 替 身” , 然后进行求解 . 以达到
化难 为易的目的.
C
C
、 \
【 过程展 示 】 如图 2 , 连接 4 C , 则 ̄ C A B =
9 0 。 ,  ̄. .R t %A B Cd A , t a n % 4 B C , 4 C 1 故选 D .
都在 这 些 小正方 = 形 . 4 、 C D相 交于 的顶点 上 ,
网格助解三角函数问题

网格助解三角函数问题作者:***来源:《初中生世界·九年级》2020年第06期初中数学中锐角三角函数是建立在直角三角形的基础上定义的。
但近年来的中考三角函数试题常常脱离直角三角形,需要我们利用网格的特征去构造直角三角形,对转化能力有更高的要求。
下面以2018年扬州市中考第27题为例剖析,希望能给同学们一点启示。
问题呈现如图1,在边长为1的正方形网格中,连接格点D、N和E、C,DN和EC相交于点P,求tan∠CPN的值。
方法归纳求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形。
观察发现问题中的∠CPN不在直角三角形中。
对此,我们常常利用网格画平行线等方法解决,比如连接格点M、N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中。
问题解决(1)直接写出图1中tan∠CPN的值为;(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值。
思维拓展(3)如图3,AB⊥BC,AB=4BC,点M在AB上,且AM=BC,延长CB到N,使BN=2BC,连接AN交CM的延长线于点P。
用上述方法构造网格求∠CPN的度数。
【分析】第(1)问中点P为非网格点,∠CPN也不在直角三角形中,如果直接作垂线构造直角三角形,求线段的长度有难度。
方法归纳提示我们将CE平移,使得它与DN的交点恰好是格点,再利用平行线的性质“两直线平行,内错角相等”解决问题。
第(2)问中,点P也是非网格点,∠CPN也不在直角三角形中,根据方法归纳,我们需要将CM(AN)进行适当的平移,使得它与AN(CM)的交点恰好是格点,再利用平行线的性质“两直线平行,同位角相等(内错角相等)”解决问题。
顺承问题的思路,第(3)问要求我们构造网格圖去解决问题。
我们可以利用网格,构造等腰直角三角形即可。
解:(1)如图1,由勾股定理,得DM=22,MN=2,DN=10,∴DM2+MN2=DN2,∴△DMN为直角三角形,(2)方法一:如图4中,平移AN到CD,连接DM。
在网格中巧求三角函数值

巩固练习
求tanC的值
求tanAOB的值
求tanAOB的值
求sin。
求sin∠BAC的值。
课后作业
1号,2号《同步训练》P49-53 3号—5号《同步训练》P49-52
面积法
D
例2 如图,在边长为1的小正方形组成的网格中 ,点A、B、C、D都在这些小正方形的顶点上,AB、 CD相交于点P,求tan∠APD的值。
E
O
例2 如图,在边长为1的小正方形组成的网格中 ,点A、B、C、D都在这些小正方形的顶点上,AB、 CD相交于点P,求tan∠APD的值。
O
巩固练习
在网格中求锐角三角函数值
例1(2015•山西)如图,在网格中,小正方形的 边长均为1,点A,B,C都在格点上,求∠ABC的正切 值。
利用互相垂直的相似矩形 的对角线构造直角三角形
例1(2015•山西)如图,在网格中,小正方形的 边长均为1,点A,B,C都在格点上,求∠ABC的正切 值。
例3(2015•南京二模)如图,方格纸中有三个格点A 、B、C,求sin∠ABC的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网格线中的三角函数问题
作者:周宏伟
来源:《初中生世界·九年级》2016年第12期
在我们常见的网格线中,有很多三角函数求值问题,题中蕴含着很多思想方法,为便于大家复习,现归纳如下,供大家在学习过程中参考.
一、补形的策略
例1 (2015·山西)如图1,在网格中,小正方形的边长均为1,点A、B、C都在格点上,则∠ABC的正切值是().
A.2
B.[255]
C.[55]
D.[12]
【方法探究】如何把∠ABC放在某个直角三角形中是解决本题的关键,仔细观察可以发现:AB在小正方形的对角线上,能联想到45°角,只要连接AC即可构造出直角,然后在直角三角形中运用三角函数的定义求解.
【过程展示】如图2,连接AC,则∠CAB=90°,在Rt△ABC中,
tan∠ABC=[ACAB]=[12].故选D.
例2 (2016·福建福州)如图3,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A、B、C都在格点上,则tan∠ABC的值是 .
【方法探究】观察网格的特点,首先考虑如何将∠ABC放到一个直角三角形中,这是解决问题的关键.
【过程展示】如图4,连接DA,DC,则点B、C、D在同一直线上,设菱形的边长为a,由题意得∠ADF=30°,∠BDF=60°,∴∠ADB=90°,
AD=[3a],DB=2a,tan∠ABC=[ADBD]=[3a2a]=[32],故答案为[32].
二、转化的思想
例3 (2012·江苏泰州)如图5,在由边长相同的小正方形组成的网格中,点A、B、C、D 都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值为 .
【方法探究】直接求∠APD的正切值比较困难,可以考虑利用线段的平移对∠APD进行转化,找出它的“替身”,然后进行求解,以达到化难为易的目的.
【过程展示】如图6,取小正方形的顶点E,连接AE、BE,由图可知CD∥BE,
∴∠APD=∠ABE,在Rt△ABE中,tan∠ABE=2,∴tan∠APD=2.
例4 (2016·山东淄博)图7是由边长相同的小正方形组成的网格,A、B、P、Q四点均在正方形网格的格点上,线段AB、PQ相交于点M,则图中∠QMB的正切值是().
A.[12]
B.1
C.[3]
D.2
【方法探究】如果直接求tan∠QMB可考虑连接AP、BQ,运用△APM∽△BQM求出AM或BM,然后在Rt△APM或Rt△BQM中求解;如果间接求解,应考虑对∠QMB进行转化,最好的思路是考虑线段的平移.①如图8,平移AB至A′Q,在Rt△A′PQ中求tan∠Q;②如图9,平移AB至PB′,在Rt△B′PQ中求tan∠P;③如图10,平移PQ使其经过线段AB中点D,然后在Rt△ACD中求tan∠ADC.
【过程展示】以第①种平移为例,如图8,平移AB至A′Q后,∠Q=∠QMB,在
Rt△A′PQ中,tan∠Q=[A′PA′Q]=2,所以tan∠QMB=2.故选D.
三、等积法
例5 (2015·四川乐山)如图11,已知△ABC的三个顶点均在格点上,则cosA的值为().
A.[33]
B.[55]
C.[233]
D.[255]
【方法探究】通过作三角形的高构造直角三角形,先利用等积法(或勾股定理)求出高,然后运用余弦的定义解答.
【过程展示】如图11,设小正方形的边长为1,过点B作AC边上的高BD.
由勾股定理得:AC=[32],AB=[10],
由等积法可得:[12]BC∙h=[12]∙AC∙BD,
即[12]×2×3=[12]×[32]∙BD,解得BD=[2],由勾股定理,得AD=[AB2-BD2]=[22],
∴cosA=[ADAB]=[2210]=[255].故选D.
例6 (2014·广西贺州)如图12,网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA= .
【方法探究】在替换与∠A相等的角比较困难的情况下,可以考虑通过作高进行构造,把∠A放在某个直角三角形中进行求解.
【过程展示】如图12,过点C作CE⊥AB,垂足为E,连接AD,则AD⊥BC,从不同的角度把△ABC的面积计算两次得:
S△ABC=[12]AB∙CE=[12]BC∙AD,
所以[12]×[25]×CE=[12]×[22]×[32],
所以CE=[655],在Rt△ACE中,
sin∠CAE=[CEAC]=[65525]=[35].
由此可见,遇到网格中的锐角三角函数求值问题,我们通常有两种思路:一是原地不动,想办法构造直角三角形求解;二是转移该角,如利用平行线进行转化.一般情况下,遇到求三角函数问题优先考虑转化,在没有好的转化思路的情况下再考虑如何构造.
(作者单位:江苏省东台市新街镇中学)。
