高数辅导讲义(4)
武忠祥《2016高等数学辅导讲义》第四章解答

其特征方程为 (r 1)2 (r 1) r3 r2 r 1 0 ,故应选(B).
4.【解】应选(A). 特征方程为 r 2 1 0, 则 r1,2 i, 则特解形式为 y ax2 bx c x( Asin x B cos x).
5.【解】应选(D).由 y C1ex C2e2x xex 为方程的解知, r1 1, r2 2 为两个特征根, 特 征方程为 (r 1)(r 2) r 2 r 2 0 ,正确选项只可能是(C)或(D),将 y xex 代入(D)中的
(5)
联立(5)式和(4)式消去 C1 得
(2x x2) y (x2 2) y 2(1 x) y 6(1 x)
20.【解】将 y 与 x 对调, y
1 x
,
y
(
x x ) 2
1 x
(
x x)
3
代入原方程得 x x e2 y ,则其通解为
又已知有公共切线,得 y 1, y 1,
x0
x0
即 C1 C2 1, C1 2C2 1. 解得 C1 1, C2 0 . 所以 y (1 2x)ex .
19.【解】 y2 y1 x2, y3 y1 ex 为齐次方程的两个线性无关的特解,则所求方程通解为
y C1x2 C2ex 3 。
y C1x2 C2ex 3
(1)
(1)式求导得 y 2C1x C2ex
(2)
再求导得
y 2C1 C2ex
(3)
(3) (2) 得 y y 2C1(1 x)
(4)
(1) (2) 得 y y C1(x2 2x) 3
高等数学辅导讲义
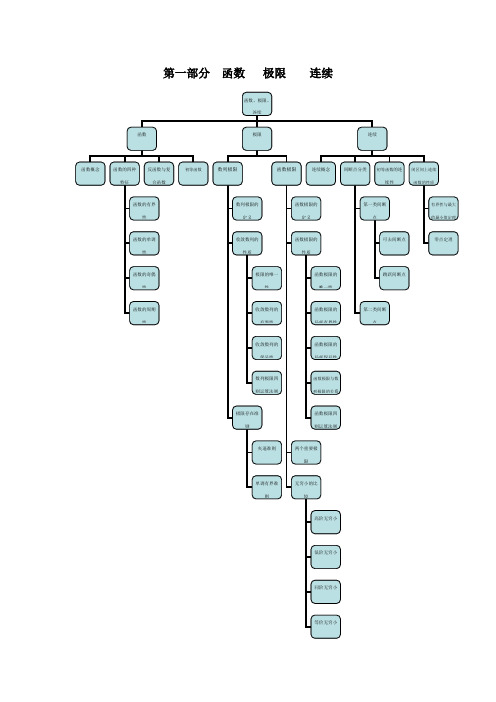
第一部分函数极限连续历年试题分类统计及考点分布本部分常见的题型1.求分段函数的复合函数。
2.求数列极限和函数极限。
3.讨论函数连续性,并判断间断点类型。
4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数 例1 (1988, 5分) 设2(),[()]1x f x e f x xϕ==-且()0x ϕ≥,求()x ϕ及其定义域。
解: 由2()x f x e =知2()[()]1x f x e xϕϕ==-,又()0x ϕ≥,则()0x x ϕ=≤.例2 (1990, 3分) 设函数1,1()0,1x f x x ⎧≤⎪=⎨>⎪⎩,则[()]f f x =1.练习题: (1)设1,1,()0,1,(),1,1,xx f x x g x e x ⎧<⎪===⎨⎪->⎩求[()]f g x 和[()]g f x ,并作出这两个函数的图形。
(2)设20,0,0,0,()(),,0,,0,x x f x g x x x x x ≤≤⎧⎧==⎨⎨>->⎩⎩求[()],[()],[()],[()]f f x g g x f g x g f x .二、 求数列的极限方法一 利用收敛数列的常用性质一般而言,收敛数列有以下四种常用的性质。
性质1(极限的唯一性) 如果数列{}n x 收敛,那么它的极限唯一。
性质2(收敛数列的有界性)如果数列{}n x 收敛,那么数列{}n x 一定有界。
性质3(收敛数列的保号性) 如果lim nn xa→∞=,且0a >(或0a <),那么存在0n N+∈,使得当0n n >时,都有0n x >(或0n x <).性质4(数列极限的四则运算法则) 如果,,lim lim nn n n xa yb →∞→∞==那么(1)()lim nn n xy a b →∞±=±;(2)lim nn n xy a b→∞∙=∙;(3)当0()nyn N +≠∈且0b ≠时,limn n nx a y b→∞=.例3 若 lim nn xa→∞=,则 limn n x a→∞=.注: 例3的逆命题是不对的, 例如我们取(1)nnx =-, 显然1limn n x →∞=,但数列(1)nnx=-没有极限。
09考研高等数学强化讲义(第四章)全

新东方考研高等数学电子教材主讲:汪诚义欢迎使用新东方在线电子教材教材说明:本教案是针对新东方在线使用的内部讲义,本讲义按章节提供。
根据老师的意见,例题的解题步骤不给提供,在课件的板书上有显示,学员自己可以先做题目再听 老师的讲解效果会更好。
严禁翻印、在网上任意传播!第四章 常微分方程§4.1 基本概念和一阶微分方程(甲)内容要点一、基本概念1.常微分方程和阶 2.解、通解和特解 3.初始条件4.齐次线性方程和非齐次线性方程例1.x y e xy y xsin '3''=++为二阶、线性、非齐次方程,如果要求0)0(',1)0(==y y ,这就是初始条件,从而得到特解。
例2.xe y y yy =++sin )'(''2为二阶非线性方程二、变量可分离方程及其推广 1.()()()()0≠=y Q y Q x p dxdyC dx x p y Q dy+=⎰⎰)()(2.齐次方程:⎪⎭⎫ ⎝⎛=x y f dx dy 令,u x y =则,,dx du x u dx dy xu y +==代入后得 )(u f dxdu x u =+,则C x C xdxu u f du +=+=-⎰⎰ln )(三、一阶线性方程及其推广 1.()()x Q y x P dxdy=+ 通解])([)()(C dx e x Q e y dxx p dx x p +⎰⎰=⎰- 2.()()()1,0≠=+ααy x Q y x P dx dy(数学三不考,数一、二要考) )()(1x Q y x P dxdy y =+--αα )()(1111x Q y x P dxdy =+---ααα令z y=-α1 则为一阶线性方程四、全微分方程及其推广(数学一) 1.()()0,,=+dy y x Q dx y x P ,满足yPx Q ∂∂=∂∂ 2.()()0,,=+dy y x Q dx y x P ,y P x Q ∂∂≠∂∂但存在()y x R ,,使()()yRP x RQ ∂∂=∂∂五、差分方程(数学三)(乙)典型例题例1.求dxdyxy dx dy xy =+22的通解。
(完整word版)高等数学辅导讲义

第一部分函数极限连续历年试题分类统计及考点分布本部分常见的题型1.求分段函数的复合函数。
2.求数列极限和函数极限。
3.讨论函数连续性,并判断间断点类型。
4.确定方程在给定区间上有无实根。
一、 求分段函数的复合函数例1 (1988, 5分) 设2(),[()]1x f x e f x x ϕ==-且()0x ϕ≥,求()x ϕ及其定义域。
解: 由2()x f x e =知2()[()]1x f x e x ϕϕ==-,又()0x ϕ≥,则()0x x ϕ=≤.例2 (1990, 3分) 设函数1,1()0,1x f x x ⎧≤⎪=⎨>⎪⎩,则[()]f f x =1.练习题: (1)设 1,1,()0,1,(),1,1,x x f x x g x e x ⎧<⎪===⎨⎪->⎩求[()]f g x 和[()]g f x , 并作出这两个函数的图形。
(2)设20,0,0,0,()(),,0,,0,x x f x g x x x x x ≤≤⎧⎧==⎨⎨>->⎩⎩求[()],[()],[()],[()]f f x g g x f g x g f x .二、 求数列的极限方法一 利用收敛数列的常用性质一般而言,收敛数列有以下四种常用的性质。
性质1(极限的唯一性) 如果数列{}n x 收敛,那么它的极限唯一。
性质2(收敛数列的有界性)如果数列{}n x 收敛,那么数列{}n x 一定有界。
性质3(收敛数列的保号性) 如果lim n n x a →∞=,且0a >(或0a <),那么存在0n N +∈,使得当0n n >时,都有0n x >(或0n x <).性质4(数列极限的四则运算法则) 如果,,lim lim n n n n x a y b →∞→∞==那么(1)()lim n n n x y a b →∞±=±;(2)lim n n n x y a b →∞•=•;(3)当0()n y n N +≠∈且0b ≠时,limn n n x a y b→∞=.例3 若lim nn xa →∞=,则lim nn xa →∞=.注: 例3的逆命题是不对的, 例如我们取(1)n n x =-, 显然1lim n n x →∞=,但数列(1)n n x =-没有极限。
(完整版)考研高数讲义高数第四章不定积分上课资料

12 四、基本积分表 (1)kdx (2)dxx (3)xdx (4)dxax ;dxex (5)21xdx (6)21xdx
持之以恒,厚积薄发
13 (7)xdxcos (8)xdxsin (9)xdxdxx22seccos1 (10)xdxdxx22cscsin1 (11)xdxxtansec (12)xdxxcotcsc
持之以恒,厚积薄发
23 (5)dxxx21; (6)xdxtan; 【答案】(5)()322113xC; (6)ln|cos|xC
第四章 不定积分
24 (7))ln21(xxdx; (8)xdxx52cossin; 【答案】(7)ln||1122xC; (8)sinsinsin357121357xxxC
第四章 不定积分
44 2211=()dxdxaxbxcaxhk公式求解 =2222(2)221ln||22mmbaxbnmxnaadxdxaxbxcaxbxcmmbaxbxcndxaaaxbxc
持之以恒,厚积薄发
45 【例1】求下列不定积分 (1)2239dxxx ; 【答案】(1)21ln|23|ln|3|99xxC
第四章 不定积分
46 (2)322xxdx Caxaxadxarctan122; 【答案】(2)11arctan22xC
持之以恒,厚积薄发
47 (3)2(31)23xdxxx; 【答案】(3)231ln|23|2arctan22xxxC
第四章 不定积分
48 (4)321xdxxx 【答案】(4)212321arctan233xxxC
持之以恒,厚积薄发
3 原函数存在定理:连续函数必有原函数——即若)(xf在I上连续,则必存在)(xF,使得当xI时,)()(xfxF。 【例1】设)(xF是)(xf在(,)ab上的一个原函数,则()()fxFx在(,)ab上( ) (A)可导 (B)连续 (C)存在原函数 (D)是初等函数 【答案】(C)
高等数学ch04第4讲

1
x
a
dx a
a
ln
x
a
c
2
x
a a
n
dx
1
a
n
x
a 1n
c
3
mx x2 px
n
dxp
q
2
4q
0
4
x2
mx n px q
n
dxp
2
4q
0
第三种情形举例说明
例4:求
x
2
x1 x
2
dx
解:原式
1 2
2x x2
1 x
dx 2
3 2
x2
1 x
dx 2
1 ln x2 2 1 ln x
x
dz a2
然后用递推公式求结果
n
例5:求
x
x1
1x
2dx
解:令
x
x1
1x
2
x
a
1
x
b
2
即x 1 ax 2 bx 1
令x 1得a 2,令x 2得b 3
原式
2 x1
x
3
2
dx
2ln x 1 3ln x 2 c
例6:求
1
1 x
3
dx
解:令 1 a bx c 1 x3 1 x x2 x 1
1 t2
t2t 2
dt
1 t2 1 t2
1 2
1
t
tdt
1 2
1 t
1dt
1 ln t
2
t
c
1 2
ln
tg
x 2
tg
高数讲义第四节有理函数的积分全

例9
求积分
1
x
1 xdx x
解 令 1 x t 1 x t2,
x
x
x
t
1 2
, 1
dx
2tdt t2 1
2,
例9
求积分
1
x
1 xdx x
解
令 1 x t x
x
xt2211a12,dxdx
1
2a
ln
x2tdat tx2 a1
2
C,
1 x
1
x
xdx
t
2
1t
t
2
2t
12
dt
2
x
2)
1
A 2x
Bx 1
C x2
解:令:
x
1 (1
x)
2
A x
B 1 x
C (1 x)
2
1 A(1 x)2 B x(1 x) C x
取 x1, 得 C 1; 取 x0, 得 A1;
再取 x 2 , 得 1 (1 2)2 B2(1 2) 2 , B 1 ;
1 x (1 x) 2
t
3
1 t 1
1dt
6
(t
2
t
1
t
1
)dt 1
2t 3 3t 2 6t 6 ln | t 1 | C
2 x 1 33 x 1 36 x 1 6 ln(6 x 1 1) C.
说明 无理函数去根号时, 取根指数的最小公倍数.
例11 求积分
x 3x 1
dx. 2x 1
解 先对分母进行有理化
f (x) 为真分式 , 当 m n 时
f (x) 为假分式
大学数学(高数微积分)第四章矩阵第四节(课堂讲义)

引例 逆矩阵的定义 矩阵可逆的条件 可逆矩阵的性质 克拉默法则的另一证法 矩阵乘积的秩的性质
一、引例
二、逆矩阵的定义
1. 可逆的定义
定义 10 n 级方阵 A 称为可逆的,如果 级方阵有Bn,使得
AB = BA = E ,
(1)
这里 E 是 n 级单位矩阵.
定义 11 如果矩阵 B 适合 (1),那么就称 的逆矩为阵A,记为 A-1 .
|A*| = |A|n-1.
2),
证 由于 AA* = A*A = |A|E , 所以
|A| |A*|) |A| 0, 即 A 可逆, (4) 式两端除以 |A| 即
得
|A*| = |A|n-1.
(2) |A| = 0, 且 A = O, 则 A* = O, 结论显然成 立.
的? 如果 A 可逆,怎样求 A-1 ?
为此先引入伴随
矩阵的概念.
1. 伴随矩阵
定义 12 设 Aij 是矩 阵
a11 a12 a1n
A
a21
a22
a2n
an1 an2 ann
中元素 aij 的代数余子式,矩阵
A11 A21 An1
| AA-1 | = | A | | A-1 | = | E | = 1 ,
因而 | A | 0,即 A 非退化 .
定理 3 不但给出了一矩阵可逆的条件,同时 也给出了求逆矩阵的公式 (4) ,用公式 (4) 求逆矩
阵的方法叫伴随矩阵法.
下面利用伴随矩阵法求逆阵.
证毕
例 1 用伴随矩阵法求下列矩阵的逆阵
而
2 2 3 A2E 1 1 0,
1 2 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 一元函数积分学§3.1 不定积分甲 内容要点一.基本概念与性质1.原函数与不定积分的概念设函数()x f 和()x F 在区间I 上有定义,若()()x f x F ='在区间I 上成立,则称()x F 为()x f 在区间I 上的原函数,()x f 在区间I 中的全体原函数称为()x f 在区间I 的不定积分,记以()⎰dx x f 。
其中⎰称为积分号,x 称为积分变量,()x f 称为被积函数,()dx x f 称为被积表达式。
2.不定积分的性质 设()()C x F dx x f +=⎰,其中()x F 为()x f 的一个原函数,C 为任意常数。
则(1)()()C x F dx x F +='⎰或 ()()⎰+=C x F x dF (2)()[]()x f dx x f ='⎰ 或 ()[]()dx x f dx x f d =⎰(3)()()⎰⎰=dx x f k dx x kf (4)()()[]()()⎰⎰⎰±=±dx x g dx x f dx x g x f3.原函数的存在性设()x f 在区间I 上连续,则()x f 在区间I 上原函数一定存在,但初等函数的原函数不一定是初等函数。
例如()⎰dx x 2sin ,()⎰dx x 2cos ,⎰dx x x sin ,⎰dx x x cos ,⎰x dx ln ,dx e x ⎰-2等。
被积函数有原函数,但不能用初等函数表示,故这些不定积分均称为积不出来。
二.基本积分公式1.C x dx x ++=⎰+11ααα(),实常数1-≠α 2.⎰+=C x dx x ln 13.⎰+=C a adx a x xln 1 ()1,0≠>a aC e dx e x x +=⎰4.⎰+=C x xdx sin cos 5.⎰+-=C x xdx cos sin6.C x dx x xdx +==⎰⎰tan cos 1sec 227.C x dx xxdx +-==⎰⎰cot sin 1csc 228.C x xdx x +=⎰sec sec tan 9.C x xdx x +-=⎰csc csc cot 10.C x xdx +-=⎰cos ln tan 11.C x xdx +=⎰sin ln cot 12.C x x xdx ++=⎰tan sec ln sec 13.C x x xdx +-=⎰cot csc ln csc 14.⎰+=-C axx a dx arcsin22 ()0>a 15.C axa x a dx +=+⎰arctan 122 ()0>a 16.C x a x a a x a dx +-+=-⎰ln 2122 ()0>a17.C a x x a x dx +±+=±⎰2222ln ()0>a三.换元积分法和分部积分法1.第一换元积分法(凑微分法) 设()()C u F du u f +=⎰,又()x ϕ可导,则()[]()()[]()()()du u f x u x d x f dx x x f ⎰⎰⎰=='ϕϕϕϕϕ令()()[]C x F C u F +=+=ϕ这里要求读者对常用的微分公式要“倒背如流”,也就是非常熟练地凑出微分。
常用的几种凑微分形式:(1)()()()⎰⎰++=+b ax d b ax f adx b ax f 1()0≠a (2)()()()⎰⎰++=+-b ax d b ax f na dx x b ax f nn n n 11 ()0,0≠≠n a(3)()()()x d x f x dxx f ln ln ln ⎰⎰=(4)⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛⎰⎰x d x f x dx x f 1112 (5)()()()⎰⎰=x d x f x dx x f2 (6)()()()⎰⎰=xx x x a d a f adx a a f ln 1 ()1,0≠>a a ()()()⎰⎰=xx xxe d ef dx e e f(7)()()()⎰⎰=x d x f xdx x f sin sin cos sin (8)()()()⎰⎰-=x d x f xdx x f cos cos sin cos (9)()()()⎰⎰=x d x f xdx x f tan tan sec tan 2(10)()()()⎰⎰-=x d x f xdx x f cot cot csccot 2(11)()()()⎰⎰=x d x f xdx x x f sec sec tan sec sec (12)()()()⎰⎰-=x d x f xdx x x f csc csc cot csc csc(13)()()()⎰⎰=-x d x f dx xx f arcsin arcsin 1arcsin 2(14)()()()⎰⎰-=-x d x f dx xx f arccos arccos 1arccos 2(15)()()()⎰⎰=+x d x f dx x x f arctan arctan 1arctan 2 (16)()()()⎰⎰-=+x arc d x arc f dx xx arc f cot cot 1cot 2(17)⎰⎰⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=+⎪⎭⎫ ⎝⎛x d x f dx x x f 1arctan 1arctan 11arctan 2 (18)()[]()[]()()⎰⎰++++=+++22222222ln ln ln a x x d a x x f dx ax a x x f ()0>a(19)()[]()[]()()⎰⎰-+-+=--+22222222ln ln ln a x x d a x x f dx ax a x x f ()0>a(20)()()()C x f dx x f x f +='⎰ln ()()0≠x f2.第二换元积分法设()t x ϕ=可导,且()0≠'t ϕ,若()[]()()C t G dt t t f +='⎰ϕϕ,则()()()[]()()()[]C x G C t G dt t t f t x dx x f +=+='=⎰⎰-1ϕϕϕϕ令其中()x t 1-=ϕ为()t x ϕ=的反函数。
第二换元积分法绝大多数用于根式的被积函数,通过换元把根式去掉,其常见的变量替换分为两大类: 第一类:被积函数是x 与n b ax +或x 与ndcx b ax ++或由xe 构成的代数式的根式,例如b ae x +等。
只要令根式()t x g n =,解出()t x ϕ=已经不再有根式,那么就作这种变量替换()t x ϕ=即可。
第二类:被积函数含有()0 2≠++A C Bx Ax ,如果仍令t C Bx Ax =++2解出()t x ϕ=仍是根号,那么这样变量替换不行,要作特殊处理,将0>A 时先化为()[]220l x x A ±-,0<A 时,先化为()()[]202x x l A ---然后再作下列三种三角替换之一:根式的形式所作替换三角形示意图(求反函数用)22x a -t a x sin =22x a +t a x tan =22a x -t a x sec =比较简单。
例1.()22222221a x d a x dx a x x --=-⎰⎰()C a xC u du u u a x +-=+==-⎰3222322313121令例2.()⎰⎰⎰-=+++=+2222222222222121dt a t t t a x a x d xa x dx x a x 令 ⎰⎰⎥⎦⎤⎢⎣⎡-+=-=dt a t a dt a t t 2222221 C xa a x a a a a x C t a t a a t ++++-++=++-+=222222ln 2ln2 例3.()⎰⎰⎰⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛+=>+22221111101x x d x x dx x x xdx()C x x C tt tdt t x+⎪⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛++-=+++-=+-=⎰222111ln 1ln 11令3.分部积分法设()x u ,()x v 均有连续的导数,则()()()()()()⎰⎰-=x du x v x v x u x dv x u或()()()()()()⎰⎰'-='dx x v x u x v x u dx x v x u使用分部积分法时被积函数中谁看作()x u 谁看作()x v '有一定规律。
(1)()axn e x P ,()ax x P n sin ,()ax x P n cos 情形,()x P n 为n 次多项式,a 为常数,要进行n 次分部积分法,每次均取axe ,ax sin ,ax cos 为()x v ';多项式部分为()x u 。
(2)()x x P n ln ,()x x P n arcsin ,()x x P n arctan 情形,()x P n 为n 次多项式取()x P n 为()x v ',而x ln ,x arcsin ,x arctan 为()x u ,用分部积分法一次,被积函数的形式发生变化,再考虑其它方法。
(3)bx e axsin ,bx e axcos 情形,进行二次分部积分法后要移项,合并。
(4)比较复杂的被积函数使用分部积分法,要用凑微分法,使尽量多的因子和dx 凑成()x dv 。
乙 典型例题 一.直接积分法所谓直接积分法就是用代数或三角恒等式,并用积分的性质和基本积分公式能直接求出不定积分,它要求初等数学有关公式很熟练。
例1.求()dx xx ⎰-21解:原式⎰⎰⎪⎪⎭⎫ ⎝⎛+-=+-=-dx x x x dx xx x 2321212221 C x x x ++-=25232152342例2.求下列不定积分(1)⎰++dx x x 1124 (2)()⎰+1x x dx(3)⎰+-232x x dx(4)()⎰+122x x dx 例3.求dx xxx ⎰⋅-⋅32532 例4.求下列不定积分(1)⎰xdx 2tan (2)⎰⋅x x dx22cos sin例5.求下列不定积分 (1)⎰dx x 2sin2(2)⎰-dx xx x sin cos 2cos (3)⎰dx xx x22cos sin 2cos (4)⎰++dx x x 2cos 1cos 12 分析:三角函数中的倍角公式1cos 2sin 21sin cos 2cos 2222-=-=-=x x x x x ,在不定积分的计算中常可起到简化计算的作用。
