normal distribution 正态分布表
正态分布 t分布

未知时,以样本标准差 S 代替 σ 所得到的统 计量
xμ S/ n
态分布,而是服从 t 分布(t-distribution)。 它的概率分布密度函数如下:
t 分布概率密度曲线特点: 1、t 分布受自由度的制约,每一个自由度都有一条 t 分布概率密度曲线。 2、t 分布概率密度曲线以纵轴为对称轴,左右对称, 且在t=0时,取得最大值。 3、与标准正态分布曲线相比,t 分布曲线顶部略低, 两尾部稍高而平。df 越小这种趋势越明显。df 越大,t 分布越趋近于标准正态分布。当n >50时,t 分布与标 准正态分布的区别很小;n >100时,t 分布基本与标准 正态分布相同;n→+∞时,t 分布与标准正态分布完全 一致。
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
x=
1 2
x
-3 -2 -1 0
x=
1 2 3 x
x=
不同均数 均值 反映随机变量的平均水平(位置参数),向 右平移表示逐渐增大,向左平移表示逐渐减小。
(1)曲线在x 轴的上方,与x 轴永不相交 (2)曲线是单峰的,它关于直线 x=μ对称 1 (3)曲线在 x=μ 处达到峰值(最高点) σ 2π (4)曲线与横轴 x所夹面积为1
例3 某地1986年120名8岁男孩身高均数为 X =123.02cm ,标准差为S=4.79cm,试估 计: (1)该地8岁男孩身高在130cm以上者占该地8 岁男孩总数的百分比; (2)身高在120cm~128cm者占该地8岁男孩总 数的百分比; (3)该地80%的男孩身高集中在哪个范围?
t 分布
利用公式,查附表得: (1) P(x<1.64) =Φ(1.64) =0.9495 (2) P (x≥2.58) =1-Φ(2.58) =1-0.9951 =0.0049 (3) P (│x│≥2.56) =2-2Φ(2.56) =2-2×0.9948 =0.0104 (4) P (0.34<x≤1.53) =Φ(1.53)-Φ(0.34) = 0.9370-0.6331=0.3039 (5) P(x<-1.82) =1-Φ(1.82) =1-0.9656 =0.0344
利用Excel的NORMSDIST计算正态分布函数表

利用Excel的NORMSDIST函数建立正态分布表董大钧,乔莉理工大学应用技术学院、信息与控制分院,113122摘要:利用Excel办公软件特有的NORMSDIST函数可以很准确方便的建立正态分布表、查找某分位数点的正态分布概率值,极大的提高了数理统计的效率。
该函数可返回指定平均值和标准偏差的正态分布函数,将其引入到统计及数据分析处理过程中,代替原有的手工查找正态分布表,除具有直观、形象、易用等特点外,更增加了动态功能,极大提高了工作效率及准确性。
关键词:Excel;正态分布;函数;统计引言正态分布是应用最广泛的连续概率分布,生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。
例如,在生产条件不变的情况下,某种产品的力、抗压强度、口径、长度等指标;同一种生物体的身长、体重等指标;同一种种子的重量;测量同一物体的误差;弹着点沿某一方向的偏差;某个地区的年降水量;以及理想气体分子的速度分量等等。
一般来说,如果一个量是由许多微小的独立随机因素影响的结果,那么就可以认为这个量具有正态分布。
从理论上看,正态分布具有很多良好的性质,许多概率分布可以用它来近似;还有一些常用的概率分布是由它直接导出的,例如对数正态分布、t分布、F分布等。
在科学研究及数理统计计算过程中,人们往往要通过某本概率统计教材附录中的正态分布表去查找,非常麻烦。
若手头有计算机,并安装有Excel软件,就可以利用Excel的NORMSDIST( x )函数进行计算某分位数点的正态分布概率值,或建立一个正态分布表,准确又方便。
1 正态分布及其应用正态分布(normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为N(μ,σ2 )。
则其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
正态分布

三. 特征
1. 是单峰曲线,x=μ 2. 以均数μ为中心左右对称 3. 有2个参数,μ:位置参数, σ:变异度参数 σ越大,数据越分散,曲线越平坦。 特别地 N(0,1)称为标准正态分布 (z分布、u分布)
四.正态曲线下面积的分布规律
通过对密度函数积分我们可以知道正态曲线下, 横轴上所夹的面积为1,标准正态分布下1.96~1.96部分的面积为0.95 (可以通过积分 求得)。也就是说|u|>1.96的面积为0.05,对 任意的x,-x~x区间面积为多少呢?统计学家 已将此编制成了正态分布界值表,不过表中 的面积是指p(u<x), 也记作φ(x)。
3. 正态分布是许多统计方法的理论 基础,如后面要讲的t检验、方差分析、 相关回归等,t分布、二项分布、 Poisson分布的极限分布也是正态分布。
4.估计频数分布
例 出生体重低于2500克为低体重儿。若 由某项研究得某地婴儿出生体重均数为 3200克,标准差为350克,估计该地当 年低体重儿所占的比例。2. 源自计医学正常值范围x u s
例 120名健康成年男性农民舒张压的均数 为10.1kPa,标准差为0.93kPa,求舒张 压的95%双侧正常值范围。 ±1.96s =10.1±1.96×0.93 即 8.28~11.92 kPa 95%参考范围(reference range)或正常 范围(normal range)仅仅告知95%健 康者的测定值在此范围之内,并非告知 凡在此范围之内皆健康,也非告知凡在 此范围之外皆不健康,所以不可将之作 为诊断标准。
以上讨论的是标准正态分布,对一般的正 态分布,某指标x~N(μ,σ2),则 u=(x-μ)/σ~N(0,1) 即-1.96<u<1.96的面积为0.95 μ-1.96σ<x<μ+1.96σ的面积为0.95
第六章 正态分布及其应用

一.正态分布
♦
正态分布( 正态分布(normal distribution)也称
为常态分布, 为常态分布,是连续型随机变量概率分布的一 种,是在数理统计的理论与实际应用中占有最 重要地位的一种理论分布。 重要地位的一种理论分布。
♦
正态分布由棣.莫弗于1733年发现的。 正态分布由棣.莫弗于1733年发现的。拉 1733年发现的
无限延伸,但永不与基线相交。 无限延伸,但永不与基线相交。 差为1。从Z=-3至Z=+3之间几乎分布着全 Z=-3 Z=+3 部数据。 部数据。
♦
拐点为正负一个标准差处 ⑸.曲线的拐点为正负一个标准差处。 曲线的拐点为正负一个标准差处。
二.标准正态分布表及使用
1.标准正态分布表
♦
利用积分公式可求出正态曲线下任何
2σ 2
公式所描述的正态曲线, 两个参数决定。 公式所描述的正态曲线,由σ和μ两个参数决定。
2.标准正态分布曲线
将标准分数代入正态曲线函数 并且, 并且,令σ=1 则公式变换为标准正态分布函数: 则公式变换为标准正态分布函数:
1 Y= ⋅e 2π
Z2 − 2
♦
以Z为横坐标,以Y 为横坐标,
为纵坐标,可绘制标准正 为纵坐标, 态分布曲线。 态分布曲线。
♦
标准正态分布曲线的
纵线高度Y为概率密度, 纵线高度Y为概率密度, 曲线下的面积为概率。 曲线下的面积为概率。
3.标准正态分布曲线的特点
♦ ♦ ♦ ♦
⑴.曲线在Z=0处达到最高点 曲线在Z=0 Z= ⑵.曲线以Z=0处为中心,双侧对称 曲线以Z=0处为中心, Z= ⑶.曲线从最高点向左右缓慢下降,向两侧 曲线从最高点向左右缓慢下降, 平均数为 ⑷.标准正态分布曲线的平均数为0,标准 标准正态分布曲线的平均数
正态分布(Normaldistribution)也称“常态分布”,又名高斯分布

正态分布(Normaldistribution)也称“常态分布”,⼜名⾼斯分布常⽤希腊字母符号:
正态分布公式
曲线可以表⽰为:称x服从正态分布,记为 X~N(m,s2),其中µ为均值,s为标zhuan准差,X∈(-∞,+ ∞ )。
其中根号2侧部分可以看成密度函数的积分为1,你就可以看成为了凑出来1特意设置的⼀个框架⽆实际意义。
标准正态分布另正态分布的µ为0,s为1。
判断⼀组数是否符合正态分布主要看 P值是否⼤于0.05。
1、∫
不定积分
不定积分的定义为:若函数f(x)在某区间 I 上存在⼀个原函数F(x),则称F(x)+C(C为任意常数)为f(x)在该区间上的不定积分,记为
2、∮
闭合曲⾯积分
3、∝
⽆穷⼩
4、∞
⽆穷⼤
5、∨
集合符号,并
6、∧
集合符号,交
7、∑
求和符号,连加
8、∏
求积符号,连乘
9、∪
逻辑符号,并
10、≌
全等
11、∈
集合符号,属于
12、∵
因为
13、∴
所以
14、∽
相似
15、√
开⽅。
正态分布图作图指导-Normal distribution curve
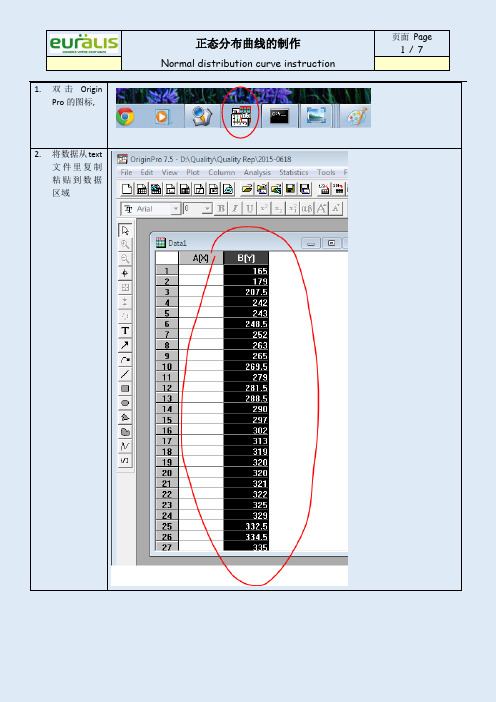
1.双击Origin
Pro的图标,
2.将数据从text
文件里复制
粘贴到数据
区域
3.按照如下路
径,选择频率
分
析.Frequency
Count
4.设置起点终
点和步进,一
般步进50,单
击ok
5.选择生成的
X,Y列数据,点
击plot,按如
下路径画图,
--------------------
6.对得到的柱
形图进行颜
色调整,默认
是红色。
7.单击菜单栏
的Analysis选
项,按照图中
路径,选择高
级拟合
(Advanced
Fitting Tool)
8.在Advanced
Fitting Tool
菜单界面选
择Action-Fit
9.弹出的对话
框,选择
Active
Dateset。
10.选择100Iter,
单击Done。
11.对模型的解
释框内容进
行删除,只保
留Model,
Equation,and
R2的信息。
12.右击边框,在
属性
Properties窗
口中去掉边
框。
13.对坐标轴进
行命名
14.右击空白区
域,弹出菜单
中单击添加
Text选项,添
加本图表的
制作日期。
15.右击图标空
白区域,探出
菜单中选择
Export Page
导出图片,图
片DPI选择
200,格式选
择png or jpg
16.最后,保存数
据。
标准正态分布示意图

lgG = lg(12571032040)=lg(571032040)1/12=1/1 2(7lg5+3lg10+lg20+lg40)=0.89966
为简化计算, 可两边取对数
G = lg-1(lgG)= lg-10.89966 = 7.94
加权法: G=lg-1( lgx/ ), 当变量值个数 较多或变量值为频数表资料时
(3) (4)=(2)(3) (5)=(2)(4)
1 127
16129
• 129 131
4 524
68644
• 133 135
9 1215
164025
• 137 139
28 3829
540988
• 141 143
35 5005
715715
• 145 147
27 3969
583443
• 149 151
11 1661
250811
• 153 155
4 620
96100
• 157161 159 • 合计 •
1 159
120 17172
(ƒ)( ƒx)
25181
2461136
( ƒx2)
•
2461136 - (17172)2/120
• s=
•
120 - 1
•
• 三、变异系数: 又称离散系数。代号为CV。
甲的变异程度>乙组
一、极差和四分位间距
• (一)全距: R(range), 亦称极差。即一组变量 值中最大值与最小值之差。
• R甲=4.0 - 2.8 = 1.2 • R乙=3.8 - 3.0 = 0.8 • 优点: 简单明了 • 缺点: 仅考虑了资料的最大值与最小值, 不能反
正态分布(高斯分布)

正态分布(⾼斯分布)正态分布(Normal distribution)⼜名⾼斯分布(Gaussian distribution),是⼀个在数学、物理及⼯程等领域都⾮常重要的概率分布,在统计学的许多⽅⾯有着重⼤的影响⼒。
正态分布是⾃然科学与⾏为科学中的定量现象的⼀个⽅便模型。
各种各样的⼼理学测试分数和物理现象⽐如光⼦计数都被发现近似地服从正态分布。
尽管这些现象的根本原因经常是未知的,理论上可以证明如果把许多⼩作⽤加起来看做⼀个变量,那么这个变量服从正态分布(在R.N.Bracewell的Fourier transform and its application中可以找到⼀种简单的证明)。
正态分布出现在许多区域统计:例如, 采样分布均值是近似地正态的,既使被采样的样本总体并不服从正态分布。
另外,常态分布信息熵在所有的已知均值及⽅差的分布中最⼤,这使得它作为⼀种均值以及⽅差已知的分布的⾃然选择。
正态分布是在统计以及许多统计测试中最⼴泛应⽤的⼀类分布。
在概率论,正态分布是⼏种连续以及离散分布的极限分布。
正态态分布最早是亚伯拉罕·棣莫弗在1734年发表的⼀篇关于⼆项分布⽂章中提出的。
拉普拉斯在1812年发表的《分析概率论》拉普拉斯定理。
(Theorie Analytique des Probabilites)中对棣莫佛的结论作了扩展。
现在这⼀结论通常被称为棣莫佛-拉普拉斯定理。
拉普拉斯在误差分析试验中使⽤了正态分布。
勒让德于1805年引⼊最⼩⼆乘法这⼀重要⽅法;⽽⾼斯则宣称他早在1794年就使⽤了该⽅法,并通过假设误差服从正态分布给出了严格的证明。
“钟形曲线”这个名字可以追溯到Jouffret他在1872年⾸次提出这个术语"钟形曲⾯",⽤来指代⼆元正态分布(bivariate normal)。
正态分布这个名字还被Charles S. Peirce、Francis Galton、Wilhelm Lexis在1875分布独⽴的使⽤。
