三角形的角及倒角模型
三角形角度计算模型

三角形角度计算模型1. 三角形的角三角形的内角与外角:三角形的相邻两条边所组成的角叫做三角形的内角.三角形的任意一边与另一边的反向延长线所组成的角叫做三角形的外角.2. 三角形内角和定理三角形内角和定理:三角形三个内角和等于180°,即在△ABC 中,180A B C ∠+∠+∠=°. 三角形内角和定理的推论:推论:三角形的一个外角等于和它不相邻的两个内角的和.利用三角形内角和定理及其推论的关键是:根据图形特点,将若干个分散的角集中到一个三角形中.3. 三角形常见角度计算模型(1)“A ”字型:如图1,D 、E 分别为AB 、AC 上的点,则B C ADE AED ∠+∠=∠+∠.如图2,180BDE CED A ∠+∠=°+∠.(2)“8”字型:如图3,AD 、BC 相交于点O ,则A B C D ∠+∠=∠+∠.(3)燕尾型:如图4,BOC A B C ∠=∠+∠+∠.如图5,A O BDO CEO ∠+∠=∠+∠.(4)两个内角平分线所成的角与第三个角之间的关系:如图6,∠ABC 、∠ACB 的内角平分线相交于点P ,则1902P A ∠=°+∠.DCABO图3 BOA图4 图7图8ABC FPEBCDE A 图1C PBA 图6B 图5CDE A O BCDE A图2(5)一个内角平分线与一个外角平分线所成的角与第三个角之间的关系: 如图7,∠ACE 与∠ABC 的平分线相交于点P ,则12P A ∠=∠.(6)两个外角平分线所成的角与第三个角之间的关系:如图8,∠CBF 与∠BCE 的平分线相交于点P ,则1902P A ∠=°−∠.(7)同角或等角的余角相等在两个直角三角形中,如果题中隐含着一个直角三角形的一个锐角与另一个直角三角形的锐角相等(同角或对顶角),则剩下的另一组锐角也相等.如图9,在Rt △ABC 和Rt △CDE 中,B 、C 、D 在一条直线上,则A DCE ∠=∠,ACB E ∠=∠. 如图10,在Rt △ABC 中,90C ∠=°,DE ⊥AB ,由于C C ∠=∠(公共角),则B AED ∠=∠. 如图11,在Rt △ABC 和Rt △ACD 中,由于C C ∠=∠(公共角),所以DAC B ∠=∠. 如图12,在Rt △ABC 和Rt △CDE 中,由于C C ∠=∠(公共角),所以B E ∠=∠. 如图12,在Rt △AEF 和Rt △BDF 中,由于AFE BFD ∠=∠(对顶角),所以B E ∠=∠.图11EDCBA 图12FAB C D E 图9AB C D 图10E。
三角形的四大模型

三角形的四大模型三角形是几何学中最基本的形状之一,它具有许多重要的性质和特点。
在研究三角形时,我们可以采用不同的模型来帮助我们理解和解决问题。
下面将介绍三角形的四大模型:欧拉模型、特里希亚特中心模型、边-角模型和向量模型。
一、欧拉模型欧拉模型通过研究三角形的顶点、边和面之间的关系来理解三角形的性质。
欧拉公式是欧拉模型中的重要定理之一,它表达了三角形的顶点数、边数和面数之间的关系。
根据欧拉公式,三角形的顶点数加上面数减去边数等于2。
这个定理可以用来验证三角形是否构成一个封闭的几何图形。
欧拉模型还可以帮助我们研究三角形的垂心、重心、外心和内心等特殊点的性质。
这些特殊点有助于我们理解三角形的对称性、平衡性和内切性质。
二、特里希亚特中心模型特里希亚特中心模型是通过研究三角形的三个特殊点来理解三角形的性质。
特里希亚特中心包括三角形的重心、外心和内心。
重心是三角形三条中线的交点,外心是三角形三条外接圆的交点,内心是三角形三条内切圆的交点。
特里希亚特中心模型可以帮助我们研究三角形的平衡性、外接性和内切性质。
例如,通过研究重心,我们可以了解三角形的平衡点和质心的性质;通过研究外心,我们可以了解三角形的外接圆和外心角的性质;通过研究内心,我们可以了解三角形的内切圆和内心角的性质。
三、边-角模型边-角模型是通过研究三角形的边和角之间的关系来理解三角形的性质。
边-角模型可以帮助我们研究三角形的角度关系、边长关系和面积关系。
在边-角模型中,我们可以利用三角函数来计算三角形的角度、边长和面积。
例如,正弦定理可以用来计算三角形的边长,余弦定理可以用来计算三角形的角度,海伦公式可以用来计算三角形的面积。
四、向量模型向量模型是通过利用向量的特性来理解三角形的性质。
向量模型可以帮助我们研究三角形的平行性、共线性和向量运算等。
在向量模型中,我们可以用向量的减法来计算两个向量之间的夹角,用向量的叉乘来计算两个向量构成的平行四边形的面积。
三角形倒角8个基本型

三角形倒角8个基本型
三角形倒角8个基本型
一、直角三角形型
指三角形的三条边均为直线,作工时采ユ直角三角形的两个外角倒角。
该型可分为正直角三角形和倒直角三角形两种型型。
二、锐角三角形型
指三角形的三条边均为直线,作工时采ユ锐角三角形的两个外角倒角。
该型可分为正锐角三角形和倒锐角三角形两种型型。
三、圆角三角形型
指三角形的三条边均为弧线,作工时采ユ圆角三角形的两个外角倒角。
该型可分为正圆角三角形和倒圆角三角形两种型型。
四、菱形型
指四条边均为直线的多边形,作工时采ユ菱形的两个外角倒角。
该型可分为正菱形和倒菱形两种型型。
五、六边形型
指六条边均为直线的多边形,作工时采ユ六边形的四个外角倒角。
该型可分为正六边形和倒六边形两种型型。
六、椭圆型
指四条边均为椭圆的多边形,作工时采ユ椭圆的两个外角倒角。
该型可分为正椭圆和倒椭圆两种型型。
七、不规则四边形型
指由不同正方形、长方形或多边形组成的不规则四边形,作工时
采ユ不规则四边形的四个外角倒角。
该型可分为正不规则四边形和倒不规则四边形两种型型。
八、五角形型
指五条边均为直线的多边形,作工时采ユ五角形的五个外角倒角。
该型可分为正五角形和倒五角形两种型型。
2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型近年来各地考试中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题高分线模型、双垂直模型、子母型双垂直模型(射影定理模型)进行梳理及对应试题分析,方便掌握。
模型1:高分线模型条件:AD 是高,AE 是角平分线结论:∠DAE=2B C∠∠-例1.(2023秋·浙江·八年级专题练习)如图,在ABC 中,30A ∠=︒,50B ∠=︒,CD 为ACB ∠的平分线,CE AB ⊥于点E ,则ECD ∠度数为()A .5︒B .8︒C .10︒D .12︒【答案】C 【分析】依据直角三角形,即可得到40BCE ∠=︒,再根据30A ∠=︒,CD 平分ACB ∠,即可得到BCD ∠的度数,再根据DCE BCD BCE ∠=∠-∠进行计算即可.【详解】解:50,B CE AB ∠=︒⊥ ,40BCE ∴∠=︒,又30A ∠=︒ ,CD 平分ACB ∠,1118050305022()BCD BCA ∴∠=∠=⨯︒-︒-︒=︒,504010DCE BCD BCE ∴∠=∠-∠=︒-︒=︒,故选:C .【点睛】本题考查的是三角形内角和定理,熟知三角形内角和是180︒是解答此题的关键.例2.(2023春·河南南阳·七年级统考期末)如图,在△ABC 中,∠1=∠2,G 为AD 的中点,BG 的延长线交AC 于点E ,F 为AB 上的一点,CF 与AD 垂直,交AD 于点H ,则下面判断正确的有()①AD 是△ABE 的角平分线;②BE 是△ABD 的边AD 上的中线;③CH 是△ACD 的边AD 上的高;④AH 是△ACF 的角平分线和高A .1个B .2个C .3个D .4个【答案】B【详解】解:①根据三角形的角平分线的概念,知AG 是△ABE 的角平分线,故此说法错误;②根据三角形的中线的概念,知BG 是△ABD 的边AD 上的中线,故此说法错误;③根据三角形的高的概念,知CH 为△ACD 的边AD 上的高,故此说法正确;④根据三角形的角平分线和高的概念,知AH 是△ACF 的角平分线和高线,故此说法正确.故选:B .【点睛】本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.例3.(2023·安徽合肥·七年级统考期末)如图,已知AD 、AE 分别是Rt △ABC 的高和中线,AB =9cm ,AC =12cm ,BC =15cm ,试求:(1)AD 的长度;(2)△ACE 和△ABE 的周长的差.【答案】(1)AD 的长度为365cm ;(2)△ACE 和△ABE 的周长的差是3cm .【分析】(1)利用直角三角形的面积法来求线段AD 的长度;(2)由于AE 是中线,那么BE =CE ,再表示△ACE 的周长和△ABE 的周长,化简可得△ACE 的周长﹣△ABE 的周长=AC ﹣AB 即可.【详解】解:(1)∵∠BAC =90°,AD 是边BC 上的高,∴S △ACB =12AB•AC =12BC•AD ,∵AB =9cm ,AC =12cm ,BC =15cm ,∴AD =AB AC CB ⋅=91215⨯=365(cm ),即AD 的长度为365cm ;(2)∵AE 为BC 边上的中线,∴BE =CE ,∴△ACE 的周长﹣△ABE 的周长=AC+AE+CE ﹣(AB+BE+AE )=AC ﹣AB =12﹣9=3(cm ),即△ACE 和△ABE 的周长的差是3cm .【点睛】此题主要考查了三角形的面积,关键是掌握直角三角形的面积求法.例4.(2023·广东东莞·八年级校考阶段练习)如图,在ABC 中,AD ,AE 分别是ABC 的高和角平分线,若30B ∠=︒,50C ∠=︒.(1)求DAE ∠的度数.(2)试写出DAE ∠与C B ∠-∠关系式,并证明.(3)如图,F 为AE 的延长线上的一点,FD BC ⊥于D ,这时AFD ∠与C B ∠-∠的关系式是否变化,说明理由.【答案】(1)10︒(2)()12DAE C B ∠=∠-∠(3)不变,理由见解析【分析】(1)根据三角形内角和求出BAC ∠,根据角平分线的定义得到50BAE ∠=︒,根据高线的性质得到90ADE ∠=︒,从而求出60BAD ∠=︒,继而根据角的和差得到结果;(2)根据角平分线的定义得到12BAE BAC ∠=∠,根据三角形内角和求出119022EAC B C ∠=︒-∠-∠,根据角的和差得到结果;(3)过A 作AG BC ⊥于G ,结合(2)知1()2EAG C B ∠=∠-∠,证明FD AG ∥,得到AFD EAG ∠=∠,即可证明.【详解】(1)解:∵30B ∠=︒,50C ∠=︒,∴1805030100BAC ∠=︒-︒-︒=︒,∵AE 平分BAC ∠,∴1502BAE CAE BAC ∠=∠=∠=︒,∵AD 是高,∴90ADE ∠=︒,∵30B ∠=︒,∴60BAD ∠=︒,∴10DAE BAD BAE ∠=∠-∠=︒;(2)()12DAE C B ∠=∠-∠,证明如下:∵AE 平分BAC ∠,∴12EAC BAC ∠=∠,∵180BAC B C ∠=︒-∠-∠,∴()11101902822B C B C EAC ︒-∠-∠-∠︒-==∠∠,∴EAD EAC DAC ∠=∠-∠()11090922B C C =︒∠---∠︒-∠()12C B =∠-∠;(3)不变,理由是:如图,过A 作AG BC ⊥于G ,由(2)可知:1()2EAG C B ∠=∠-∠,AG BC ⊥ ,90AGB ∠=︒,FD BC ⊥ ,90FDC ∴∠=︒,AGD FDC ∴∠=∠,FD AG ∴∥,AFD EAG ∴∠=∠,1()2AFD C B ∴∠=∠-∠.【点睛】本题主要考查三角形的内角和定理、角平分线的性质、直角三角形的性质和平行线的判定与性质,熟练掌握三角形的内角和定理和角平分线的性质是解题的关键.模型2:双垂直模型结论:①∠A =∠C ;②∠B =∠AFD =∠CFE ;③AB CD AE BC ⋅=⋅。
三角形的角及倒角模型

第二讲三角形的角及倒角模型(总7页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第二讲 三角形的角及倒角模型1、 如图1,求证:AB +AE >BC +CD +DE2、 如图2,AC 、BD 是四边形ABCD 的对角线,且AC 、BD 相交于点O ,求证:AC +BD >21(AB +BC +CD +AD )。
3、 如图3,⊿ADE 和⊿ABC 中,∠EAD =∠AED =∠BAC =∠BCA =45°又有∠BAD =∠BCF ,(1) 求∠ECF +∠DAC +∠ECA 的度数;(2) 判断ED 与FC 的位置关系,并对你的结论加以证明。
4、 求∠a 的度数。
5、如图5,∠A =30°,求∠B +∠C +∠D +∠E 的度数。
6、将图6-1中线段AD上一点E(点A、D除外)向下拖动,依次可得图6-2、图6-3、图6-4,分别探究图6-2、图6-3、图6-4中∠A、∠B、∠C、∠D、∠E(∠AED)之间有什么关系7、如图7,在⊿ABC中D是BC上任意一点,E是AD上任意一点,试说明:AB+AC>BE+EC。
8、如图8,已知DM平分∠ADC,BM平分∠ABC,且∠A=27°,∠M=33°,则∠C=。
9、如图9所示,点E和点D分别在⊿ABC的边BA和CA的延长线上,CF、EF 分别平分∠ACB和∠AED,试探索∠F与∠B,∠D的关系:。
10、如图10,⊿ABC的一条外角平分线是CE,F是CA延长线上一点,FG∥EC 交AB于点G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数。
11、如图11,在⊿ABC中,∠B=∠C,FD⊥BC,ED⊥AB,∠AFD=158°,则∠EDF=。
12、如图12-1,BP、CP是任意⊿ABC的∠B、∠C的角平分线。
(1)探求∠BPC与∠A的数量关系。
三角形的倒角

三角形的倒角题型一:三角形的倒角模型“飞镖模型”“8字模型”注意:飞镖和8字模型不可以直接使用,需要证明后再用.【例1】(1)如下左图,∠B=45°,∠A=30°,∠C=25°,试求∠ADC的角度.(2)如下右图,∠A=30°,∠B=45°,∠D=50°,试求∠C的角度.【例2】如图:在∠M的两边上分别取点P、点Q,在∠M内部取一点N,连接PN、QN,探索∠PNQ、∠M、∠MPN与∠MQN之间的数量关系,并证明你的结论.【例3】(1)如图1,∠A+∠B+∠C+∠D+∠E=__________.(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F=__________.图1 图2题型二:三角形中常见倒角构图图1I为∠A、∠B平分线的交点图2E为△ABC两外角平分线的交点图3P为∠B的平分线和△ABC外角平分线的交点图4AD为∠BAC的平分线,AE为BC上的高图5E为∠ABC,∠ADC平分线的交点图6BE,DE为∠AB C和∠ADC的平分线【例4】已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:图1 图2 图3(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;(2)仔细观察,在图2中“8字形”的个数:______个;(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)(5)如图3所示,求∠A+∠B+∠C+∠D+∠E+∠F=_________.【例5】如图1,∠MON=90°,点A、B分别在射线OM、ON上,(1)∠MAB和∠NBA的平分线相交于点P,点A和点B在运动过程中,∠P的大小是否发生变化?(2)如图2,若延长BA至E,在∠ABO的内部作射线BF交OM于点C,若∠ABC、∠CAE和∠ACF的角平分线交于点G,过点G作GH⊥BE于H,判断∠AGH与∠BGC的大小关系,并说明理由.图1 图2【例6】如图,在△ABC 中,1BO 、2BO 是∠ABC 的三等分线,1CO 、2CO 是∠ACB 的三等分线,(1)当∠A =60°时,∠C BO 2=______°;(2)请你探究∠C BO 1与∠C BO 2之间的数量关系.【演练1】(1)如图∠A =30°,求∠B +∠C +∠D +∠E 的度数.(2)如图1,求∠A +∠B +∠C +∠D +∠E +∠F =____________. (3)如图2,求∠A +∠B +∠C +∠D =____________.图1 图2【演练2】将图1中线段AD 上一点E (点A 、D 除外)向下拖动,依次可得图2、图3、图4.分别探究图2、图3、图4中∠A 、∠B 、∠C 、∠D 、∠E (∠AED )之间有什么关系?图1 图2 图3 图4【演练3】(1)如图①,分别在△ABC 的两个外角内部作射线BM 、CM ,相交于点P , 则∠A +∠ABM +∠ACN +∠BPC(2)如图②,分别在△C B A ''的两个外角作射线''M B 、''N C ,相交于点'P ,探索∠'A 、∠'''M B A 、'''N C A 与∠'''C P B 之间的数量关系,并证明你的结论.(3)如图③,分别在△C B A ''的一个内角和一个外角作射线''M B 、''N C ,相交于点'P ,探索∠'A 、∠'''M B A 、'''N C A 与∠'''C P B 之间的数量关系,并证明你的结论.图① 图② 图③【演练4】(1)如图①,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ADC=40°,∠ABC=30°,求∠AEC的大小;(2)如图②,∠BAD的平分线AE与∠BCD的平分线CE交于点E,∠ADC=m°,∠ABC=n°,求∠AEC的大小;(3)如图③,∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间是否仍存在某种等量关系?若存在,请写出你得结论,并给出证明;若不存在,请说明理由.图①图②图③【演练5】同学们都知道,平面内两条直线的位置关系只有相交和平行两种.已知AB∥CD.如图1,点P在AB、CD外部时,由AB∥CD,有∠B=∠BOD,B∠D.又因为∠BOD 是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠(1)已知AB∥CD.如图2,点P在AB、CD内部时,上述结论是否成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请你说明你的结论;(2)在图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?说明理由;(3)利用第(2)小题的结论求图4中∠A+∠B+∠C+∠D+∠E+∠F的度数.图1 图2 图3 图4。
第4讲 倒角模型(学生版)
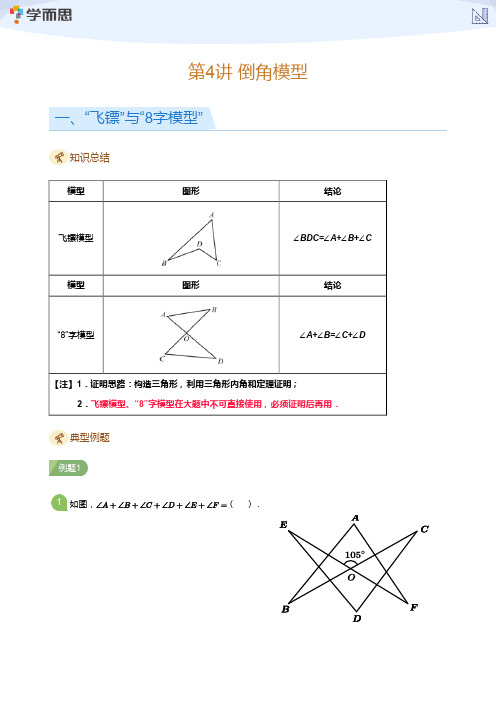
巩固1
如图,
,
,
,则
.
巩固2
如下图,
,
,
,则 的度数为
度.
巩固3 如图,
度.
巩固4
如图,点 和点 分在
的边 和 的延长线上, , 分别平分
和
,若
,
,则 的大小是
.
巩固5
如图,点 是
两个内角平分线的交点,点 是
,则
的度数为( )
两个外角平分线的交点,如果
A.
B.
C.
D.
巩固6
如图,在
中,
交于点 ,依次类推,
,
与
的角平分线交于 ,
与
的角平分线交于点 ,则
与
的角平分线
的度数是
度.
巩固7
如图⑴, 、 是任意
的 、 的角平分线.
(1) 探求
与 的数量关系.
(2)
能等于 吗?说明理由.
(3) 当 为多少度时,
?
(4) 把图⑴中的
变成图⑵中的四边形
, 、 仍然是 , 的平分线,猜想
与 、 有何数量关系?(只写出猜想结果,不写过程)
首先得到:当 时,如图 ,
,
当 时,如图 ,
,
如图 ,猜想
.
A
B
C
图
图
图
三、数学万花筒
帕斯卡12岁证明任意三角形内角和180度 帕斯卡12岁证明任意三角形内角和180度。 任意两个相同直角三角形一定能拼成长方形,每一个长方形的内角和是360(四个直角)恰好包含了直 角三角形的6个内角,所以一个直角三角形的内角和是360÷2=180。
;
的平
三角形中的倒角模型——飞镖模型、风筝模型以及翻角模型 学生版
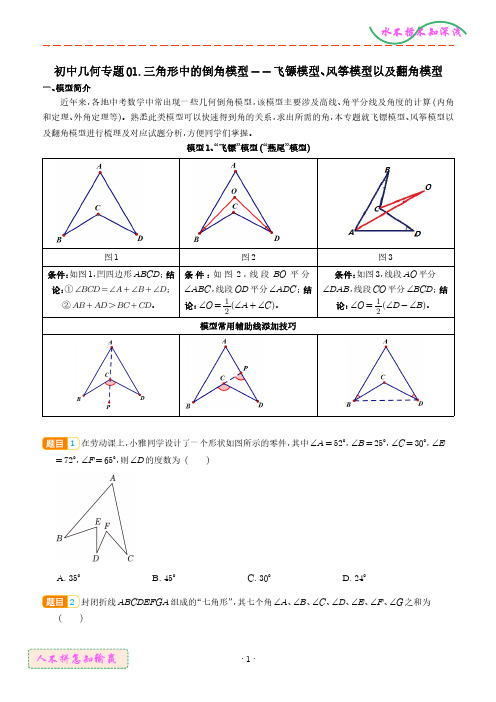
初中几何专题01.三角形中的倒角模型--飞镖模型、风筝模型以及翻角模型一、模型简介近年来,各地中考数学中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉此类模型可以快速得到角的关系,求出所需的角,本专题就飞镖模型、风筝模型以及翻角模型进行梳理及对应试题分析,方便同学们掌握。
模型1、“飞镖”模型(“燕尾”模型)图1图2图3条件:如图1,凹四边形ABCD;结论:①∠BCD=∠A+∠B+∠D;②AB+AD>BC+CD。
条件:如图2,线段BO平分∠ABC,线段OD平分∠ADC;结论:∠O=12(∠A+∠C)。
条件:如图3,线段AO平分∠DAB,线段CO平分∠BCD;结论:∠O=12(∠D-∠B)。
模型常用辅助线添加技巧1在劳动课上,小雅同学设计了一个形状如图所示的零件,其中∠A=52°,∠B=25°,∠C=30°,∠E =72°,∠F=65°,则∠D的度数为()A.35°B.45°C.30°D.24°2封闭折线ABCDEFGA组成的“七角形”,其七个角∠A、∠B、∠C、∠D、∠E、∠F、∠G之和为()A.180°B.270°C.360°D.720°3请阅读下列材料,并完成相应的任务:有趣的“飞镖图”如图,这种形似飞镖的四边形,可以形象地称它为“飞镖图”.当我们仔细观察后发现,它实际上就是凹四边形.那么它具有哪些性质呢?又将怎样应用呢?下面我们进行认识与探究:凹四边形通俗地说,就是一个角“凹”进去的四边形,其性质有:凹四边形中最大内角外面的角等于其余三个内角之和.(即如图1.∠ADB=∠A+∠B+∠C)理由如下:方法一:如图2,连结AB,则在△ABC中,∠C+∠CAB+∠CBA=180°,即∠1+∠2+∠3+∠4+∠C=180°,又∵在△ABD中,∠1+∠2+∠ADB=180°,∴∠ADB=∠3+∠4+∠C,即∠ADB=∠CAD+∠CBD+∠C.方法二:如图3,连结CD并延长至F,∵∠1和∠3分别是△ACD和△BCD的一个外角,⋯大家在探究的过程中,还发现有很多方法可以证明这一结论.任务:(1)填空:“方法一”主要依据的一个数学定理是;(2)探索及应用:根据“方法二”中辅助线的添加方式,写出该证明过程的剩余部分.2、风筝模型(鹰爪模型)或角内翻模型图1图21)风筝(鹰爪)模型:结论:∠A+∠O=∠1+∠2;2)风筝(鹰爪)模型(变形):结论:∠A+∠O=∠2-∠1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲 三角形的角及倒角模型
1、 如图1,求证:AB +AE >BC +CD +DE
2、 如图2,AC 、BD 是四边形ABCD 的对角线,且AC 、BD 相交于点O ,求证:AC +BD >2
1(AB +BC +CD +AD )。
3、 如图3,⊿ADE 和⊿ABC 中,∠EAD =∠AED =∠BAC =∠BCA =45°又有∠BAD =∠BCF ,
(1) 求∠ECF +∠DAC +∠ECA 的度数;
(2) 判断ED 与FC 的位置关系,并对你的结论加以证明。
4、 求∠a 的度数。
5、如图5,∠A =30°,求∠B +∠C +∠D +∠E 的度数。
6、将图6-1中线段AD 上一点E (点A 、D 除外)向下拖动,依次可得图6-2、图6-3、图6-4,分别探究图6-2、图6-3、图6-4中∠A 、∠B 、∠C 、∠D 、∠E (∠AED )之间有什么关系?
7、如图7,在⊿ABC 中D 是BC 上任意一点,E 是AD 上任意一点,试说明:AB +AC >BE +EC 。
8、如图8,已知DM 平分∠ADC ,BM 平分∠ABC ,且∠A =27°,∠M =33°,则∠C = 。
9、如图9所示,点E 和点D 分别在⊿ABC 的边BA 和CA 的延长线上,CF 、EF 分别平分∠ACB 和∠AED ,试探索∠F 与∠B ,∠D 的关系: 。
10、如图10,⊿ABC 的一条外角平分线是CE ,F 是CA 延长线上一点,FG ∥EC 交AB 于点G ,已知∠DCE =50°,∠ABC =40°,求∠FGA 的度数。
11、如图11,在⊿ABC 中,∠B =∠C ,FD ⊥BC ,ED ⊥AB ,∠AFD =158°,则∠EDF
=。
12、如图12-1,BP、CP是任意⊿ABC的∠B、∠C的角平分线。
(1)探求∠BPC与∠A的数量关系。
(2)∠BPC能等于90度吗?说明理由。
(3)当∠A为多少度时,∠BPC=2∠A?
(4)把图12-1中的⊿ABC变成图12-2中的四边形ABCD,BP、CP仍然是∠B、∠C 的角平分线,猜想∠BPC与∠A,∠D有何数量关系?(只写出猜想结果,不写说理过程)。
13、如图13,在⊿ABC中,∠ABC的两个外角平分线交于点F,探索∠F和∠A的关系。
14、如图14,在⊿ABC中,∠ABC的平分线与∠ABC的外角平分线交于点A
1
,若∠A
=40°,则∠A
1为度;同样的方法作出∠A
2
,则∠A
2
的度数是度;
依次下去,当作出∠A
n
时,它的度数是度。
15、如图15,由图15-1的⊿ABC沿DE折叠得到图15-2;图3;图4。
(1)如图2,猜想∠BDA+CEA与∠A的关系,并说明理由;
(2)如图3,猜想∠BDA+CEA与∠A的关系,并说明理由;
(3)如图4,猜想∠BDA+CEA与∠A的关系,并说明理由;
16、如图16,已知⊿ABC,将点A向下拖动,依次可得到图1、图2、图3。
分别探究图中
∠A、∠B、∠C、∠D、∠E有什么关系?
17、(1)小明有两根5㎝、8㎝的木棒,他想以这两根木棒为边做一个等腰三角形,还需再选用一根()长的木棒。
A、5㎝
B、8㎝
C、5㎝或8㎝
D、大于3㎝且小于13㎝的任意长
(2)⊿ABC中,有两边长分别为6和7,则周长l的取值范围是()
A、1<l<13
B、13<l<25
C、14<l<26
D、无法确定(3)已知⊿ABC的边长分别为2x+1,3x,5,则⊿ABC的周长L的取值范围是()A、6<L<36 B、10<L≤11 C、11≤L<36 D、10<L <36
(4)设a,b,c是⊿ABC的三边长,则:|a+b+c|+|a-b-c|+|b-c-a|+|c -b-a|=。
18、(1)已知四根长度分别为3、6、8、10的木棒,任意选取三根木棒组成一个三角形,那么可以组成三角形的个数为()
A、1个
B、2个
C、3个
D、4个
(2)长为9、6、5、3的四根木条,选其中三根组成三角形,共有()种选法。
A、4
B、3
C、2
D、1
19、⑴盒中装有四根长度分别为1、3、4、5的细木棒,小明手中有一根长度为3的细木棒,现从盒中取出两根细木棒与小明手中的细木棒放在一起组成三角形,则不同的取法有()
A、3种
B、4种
C、5种
D、6种
⑵设a,b,c均为自然数,且a≤b≤c,a+b+c=11,试问以a,b,c不边长的三角形有多少个?
20、如图,⊿ABC中,∠C=90°,∠BAC的平分线交BC于点在,点E是AB上的一个动点,若CD=4,则DE的最小值为。
21、如图,在⊿ABC中,点D、E、F分别为边BC、AD、CE的中点,且S⊿ABC=6平方厘米,则S阴影=。
22、给出下列命题:
①三角形的一个外角大于它的任何一个内角;
②若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形;
③三角形的最小内角不能大于60°;
④三角形的一个外角等于和它不相邻的两个内角的和。
其中真命题有()个
23、在⊿ABC中,2∠A=3∠B,且∠C-30°=∠A+∠B,则⊿ABC是()
A、锐角三角形
B、钝角三角形
C、有一个角是30度的直角三角形
D、等腰直角三角形
24、如图,在⊿ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=。
25、如图,⊿ABC的三条角平分线交于I点(∠ACB>∠ABC),AI交BC于D,作IE ⊥BC于E,下列结论:①∠CID+∠ABI=90°;②∠BID=∠CIE;③∠IBD=∠DIE;
④∠DIE=∠ACI-∠ABI。
其中正确的结论是()(填序号)
26、⑴如图,∠ACD是⊿ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,……,∠An-1BC的平分线与∠An-1CD 的平分线交于点An,同样操作,作⊿ABC的两个外角的平分线BP1,CP1交于点P1,⊿A1BC中两个外角的平分线BP2,CP2交于点P2,……,⊿An-1BC两个外角的平分线BPn,CPn,交于点Pn,设∠A=a,则∠BPnC=。
⑵如图,在⊿ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2,…,∠A2012BC和∠A2012CD的平分线
交于点A2013,则∠A2013=度。
⑶已知∠ACE是⊿ABC的外角,BD平分∠ABC,CD平分∠ACE,∠BAC=50°,则∠BDC的度数为,∠CAD的度数为。
⑷如右图所示,在⊿ABC中,CD、BE是外角平分线,BD、CE是内角平分线,BE、CE 交于E,BD、CD交于D,试探索∠D与∠E的关系:。
27、阅读下面的材料,并解决问题:已知在⊿ABC中,∠A=60°,
如图1∠ABC、∠ACB的角平分线交于点O,则可求得∠BOC=120°;
如图2,∠ABC、∠ACB的三等分点交于点O1、O2,则∠BO1C=。
如图3,∠ABC、∠ACB的n等分线交于点O1、O2、……On,则∠BO1C =。
∠BOn-1C=。
(用含n的代数式表示)。
