经典开放性问题全解析
2023年中考语文复习开放性试题汇编之句子(含答案)

2023年中考语文复习开放性试题汇编之句子一.试题(共20小题)1.(2023 昌乐县模拟)下列句子的标点符号使用正确无误的一项是()A.他很想弄明白《黄鹤楼》一诗是怎样将神话传说与眼前录物融为一体的?B.据王粲的《英雄记钞》说,诸葛亮与徐庶、石广元、孟公威等人一道游学读书,“三人务于精熟,而亮独观其大略”。
C.全班同学再也忍不住了,大家弯腰、摇头、挤眉、弄眼,一齐哄堂大笑!:D.“我跟你玩儿呀”!这一天,忽然有谁在他耳边轻轻地这样说。
2.(2023 昌乐县模拟)下列句子没有使用修辞手法的一项是()A.仰着头,才望见峰顶,中间是一线蔚蓝的天空。
B.荒山变绿产业兴,青砖蓝瓦新居起。
C.像柳絮一般的雪,像芦花一般的雪,像蒲公英的带绒毛的种子一般的雪,在风中飞舞。
D.许多到中国来旅游的外宾,看到詹天佑留下的伟大工程,怎能不赞叹不已呢?3.(2023 阜新模拟)选出对下列病句修改有误的一项是()A.由于这所大学忽视理论的应用,使该大学输出的有用的科学技术人才逐年减少。
(修改:删掉“由于”或“使”)B.一个人工作能力的高低,不在于他掌握了多少知识,关键是看他做出了突出的成绩。
(修改:“看他”后面加“是否”)C.董卿在主持《朗读者》节目时,旁征博引,妙语连珠,令广大观众目不暇接。
(修改:“旁征博引”和“妙语连珠”互换)D.许多超市将个头大的西瓜切成小块出售,一块西瓜不超过5块钱左右,非常划算。
(修改:“不超过”和“左右”去掉一个)4.(2023 铁东区一模)下列句子没有语病的一项是()A.千山风景区提前全面启动春季防火,坚决打赢春季防火灭火攻坚战。
B.工程师向大家介绍说,现场采样是一个环境监测中十分重要的环节。
C.中国园林南北风格不一,南方多为清秀婉约,北方多为宏伟壮丽。
D.中学生校园足球赛决赛将于下周五进行,九一队和九二队争夺冠亚军。
5.(2023 零陵区一模)下列句子中,有语病的一项是()A.家庭,是我们每个人踏入人生的第一个课堂,也是家国情怀的根基所在。
初中数学开放性问题

初中数学开放性问题1. 8×86=688,这个算式,把乘数的个位数6放在被乘数之首,十位数8放在被乘数之尾, 得688即乘积,还有没有这样的算式?若有,请写出它们。
2.有一些合数分解成质数的积,等式两边的数码的和相等,如:6036=2×2×3×503,6+ 0+3+6=2+2+3+5+0+3。
数学爱好者史密斯发现493 777 5=3×5×5×65 837,4+9+3+7+7+7+5=3+5+5+6+5+8+3+7,493 777 5恰为史密斯家的电话号码,这个数又是已知的具有上述性质的最大的数。
在10000以内的合数有360个具有这样的性质,请你尽可能多地写出它们。
3.现有四个有理数3,4,-6,10。
将这四个数(每个数用且只用一次)进行加、减、乘、 除四则运算,使其结果等于24,其三种本质不同的运算式如下:(1)__________(2)___________(3)_________ 另有四个数3,-5,7,-13,可通过运算式(4)_____________使其结果等于24。
4.某位老师在讲“实数”时,画了一个图(如图),即“以数轴上的单位长线段作一个正方 形,然后以原点O 为圆心,正方形的对角线长为半径画弧交x 轴于点A ”,作这样的图是用来说明_______。
5.用实际例子说明绝对值的几何意义。
6.定义一种运算“∧”,对任何两个正数a 和b 有ba ab b a +=∧。
验证运算“∧”是否具有 交换律、结合律、对加法的分配律?即 )()()(),()(,c a b a c b a c b a c b a a b b a ∧+∧=+∧∧∧=∧∧∧=∧是否成立?请你给出另一种新的运算定义,使其具有交换律、结合律或者对他运算的分配律。
7.已知1,2,2三个数,请你添上一个数,写出一个比例式:__________。
8.写出一个只含有字母X 的代数式(要求:(1)要使此代数式有意义,字母X 必须取全体 正数;(2)此代数式的值恒为负数):______________________。
开放性问题

开放性问题一个数学问题的构成含有四个要素:题目的条件、解题的依据、解题的方法、题目的结论,如果题目所含的四个要素是解题者已经知道,或者结论虽未指明,但它是完全确定的,这样的问题就是封闭性的数学问题.开放性问题是相对于封闭性问题而言,从所呈现问题的方式看,有下列几种基本形式: 1.条件开放题称条件不充分或没有确定已知条件的开放性问题为条件开放题,解题时需执果寻因,根据结论和已有的已知条件,寻找使得结论成立的其他条件. 2.结论开放题称结论不确定或没有确定结论的开放性问题为结论开放题,解题时需由因导果,由已知条件导出相应结论. 3.判断性开放题称判定几何图形的形状大小、图形的位置关系、方程(组)的解的情况或判定具有某种性质的数学对象是否存在的开放题问题称为判断性开放题,解题的基本思路是:由已知条件及知识作出判断,然后加以证明. 【例题求解】【例1】 如图,⊙O 与⊙O 1外切于点T ,PT 为其内公切线,AB 为其外公切线,且A 、B 为切点,AB 与PT 相交于点P ,根据图中所给出的已知条件及线段,请写出一个正确结论,并加以证明. (杭州市中考题)思路点拨 为了能写出更多的正确结论,我们可以从以下几分角度作探索,线段关系,角的关系、三角形的关系及由此推出的相应结论.注:明确要求将数学开放性题作为中考试题,还是近一二年的事情.开放性问题没有明确的目标和解题方向,留有极大的探索空间.解开放性问题,不具有定向的解题思路,解题时总要有合情合理、实事求是的分析,要把归纳与演绎协调配合起来,把直觉发现与逻辑推理相互结合起来,把一般能力和数学能力 同时发挥出来.杭州市对本例评分标准是以正确结论的难易程度为标准灵活打分,分值直接反映考生的能力及创新性.【例2】 如图,四边形ABCD 是⊙O 的内接四边形,A 是BD 的中点,过A 点的切线与CB 的延长线交于点E .(1)求证:AB ·DA=CO ·BE ;(2)若点E 在CB 延长线上运动,点A 在BD 上运动,使切线EA 变为割线EFA ,其他条件不变,问具备什么条件使原结论成立? (要求画出示意图,注明条件,不要求证明) (北京市海淀区中考题)思路点拨 对于(2),能画出图形尽可能画出图形,要使结论AB ·DA=CD ·BE 成立,即要证△ABE ∽△CDA ,已有条件∠ABE=∠CDA ,还需增加等角条件,这可由多种途径得到.⌒⌒注:许多开放性问题解题思路也是开放的(多角度、多维度思考),探索的条件或结论并不惟一.故解开放性问题,应尽可能深入探究,发散思维,提高思维的品质,切忌入宝山而空返.【例3】(1)如图1,若⊙O1与⊙O2外切于A,BC是⊙O1与⊙O2外公切线,B、C为切点,求证:AB⊥AC.(2)如图2,若⊙O1与⊙O2外离,BC是⊙O1与⊙O2的外公切线,B、C为切点,连心线O1 O2分别交⊙O1、⊙O2于M、N,BM、CN的延长线交于P,则BP与CP是否垂直?证明你的结论.(3)如图3,若⊙O1与⊙O2相交,BC是⊙O1与⊙O2的公切线,B、C为切点,连心线O1 O2分别交⊙O1、⊙O2于M、N,Q是线段MN上一点,连结BQ、CQ,则BQ与CQ是否垂直?证明你的结论.思路点拨本例是在基本条件不变的情况下,通过运动改变两圆的位置而设计的,在运动变化中,结论可能改变或不变,关键是把(1)的证法类比运用到(2)、(3)问题中.注:开放性问题还有以下呈现方式:(1)先提出特殊情况进行研究,再要求归纳猜测和确定一般结论;(2)先对某一给定条件和结论的问题进行研究,再探讨改变条件时其结论应发生的变化,或改变结论时其条件相应发生的变化.【例4】已知直线4y(k>0)与x轴、y轴分别交于A、C两点,开口向上的抛物线=kx-=2过A、C两点,且与x轴交于另一点B.y++axcbx(1)如果A、B两点到原点O的距离AO、BO满足AO=3BO,点B到直线AC的距离16,求这条直线和抛物线的解析式;等于5(2)是否存在这样的抛物线,使得tan∠ACB=2,且△ABC外接圆截得y轴所得的弦长等于5?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.(无锡市中考题)16”,利用等积变换求出A、B两点的距思路点拨(1)通过“点B到直线AC的距离等于5离;(2)先假设存在这样的抛物线,再由条件推理计算求得,最后加以验证即可.注:解存在性开放问题的基本方法是假设求解法,即假设存在→演绎推理→得出结论(合理或矛盾).【例5】如图,这些等腰三角形与正三角形的形状有差异,我们把它与正三角形的接近程度称为“正度”.在研究“正度”时,应保证相似三角形的“正度”相等.设等腰三角形的底和腰分别为a、b,底角和顶角分别为α、β.要求“正度”的值是非负数.同学甲认为:可用式子ba-的值越小,表示等腰三角形越接近a-来表示“正度”,b正三角形;同学乙认为:可用式子βα-的值越小,表示等腰三角形越接α-来表示“正度”,β近正三角形.探究:(1)他们的方案哪个较为合理,为什么?(2)对你认为不够合理的方案,请加以改进(给出式子即可);(3)请再给出一种衡量“正度”的表达式. (安徽省中考题)思路点拨通过阅读,正确理解“正度”这个新概念,同时也要抓住“在研究‘正度’时,应保证相似三角形的‘正度’相等”这句话的实质,可先采取举实例加深对“正度”的理解,再判断方案的合理性并改进方法.注:(1)解结论开放题往往要充分利用条件进行大胆而合理的猜想,通过观察、比较、联想、猜测、推理和截判断等探索活动,发现规律,得出结论.(2)阅读是学习的重要途径,在这种阅读型研究性问题中,涌现了许多介绍新的知识和新的研究方法的问题,能极大地开阔我们的视野.(3)研究性学习是课程改革的一个亮点,研究性学习是美国芝加哥大学教授施瓦布在《作为探究的科学教学》的演讲时提出的.他主张引导学生直接用科学研究的方式进行教学,即设定情境、提出问题、分析问题、设计实验、验证假设、分析结果、得出结论.研究性问题是近年中考中出现的一种新题型,它要求我们适应新情况,通过实践,增强探究和创新意识,学习科学研究方法.学力训练1.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD,②AB=BC;③AB⊥BC;④AO=OC.其中正确的是.(把你认为正确的结论的序号都填上) (安徽省中考题)2.如图,是一个边长为a的小正方形与两个长、宽分别为a、b的小矩形ABCD,则整个图形可表达出一些有关多项式分解因式的等式,请你写出其中任意三个等式:①;②;③.(泉州市中考题)3.有一个二次函数的图象,三位学生分别说出了它的一些特点:甲:对称轴是直线4x;=乙:与x轴两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式:.(北京市东城区中考题)4.如图,已知AB为⊙O的直径,直线l与⊙O相切于点D,AC⊥l于C,AC交⊙O于点E,DF⊥AB于F.(1)图中哪条线段与BF相等?试证明你的结论;(2)若AE=3,CD=2,求⊙O的直径.(威海市中考题)5.在一个服装厂里有大量形状为等腰直角三角形的边角布料(如图).现找出其中的一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其他边相切,请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径).(黄冈市中考题)6.如图,抛物线c=2与x轴交于点A(x1,0),B(x2,0)( x1<0<x2),与y轴交于点+bxy+axC(0,-2),若OB=4OA,且以AB为直径的圆过C点.(1)求此抛物线的解析式;(2)若点D 在此抛物线上,且AD ∥CB . ①求D 点的坐标;②在x 轴下方的抛物线上,是否存在点P 使得△APD 的面积与四边形ACBD 的面积相等?若存在,求出点P 坐标;若不存在,请说明理由.(连云港市中考题)7.给定四个命题:①sinl5°与sin75°的平方和为1;②函数682+-=x xy的最小值为-10;③4341aaa -=-;④xx xx --=--510510,则x=10”,其中错误的命题的个数是 .(“我爱数学”初中生夏令营试题) 8.①在实数范围内,一元二次方程02=++c bx ax的根为aacbb x242-±-=;②在△ABC中,若AC 2+BC 2>AB 2,则△ABC 是锐角三角形;③在△ABC 和△AB 1C 1中,a 、b 、c 分别为△ABC 的三边,1a 、1b 、1c 分别为△AB 1C 1的三边,若a >1a ,b >1b ,c >1c ,则△ABC 的面积大S 于△AB 1C 1的面积S 1.以上三个命题中,真命题的个数是( )(全国初中数学联赛试题)A .0B .1C .2D .39.已知:AB 是⊙O 的直径,AP 、AQ 是⊙O 的两条弦,如图1,经过B 做⊙O 的切线l ,分别交直线AP 、AQ 于点M 、N .可以得出结论AP ·AM =AQ ·AN 成立.(1)若将直线l 向上平行移动,使直线l 与⊙O 相交,如图2所示,其他条件不变,上述结论是否成立?若成立,写出证明,若不成立,说明理由;(2)若将直线l 继续向上平行移动,使直线l 与⊙O 相离,其他条件不变,请在图3上画出符合条件的图形,上述结论成立吗?若成立,写出证明;若不成立,说明理由.10.如图,已知圆心A(0,3), A 与x 轴相切,⊙B 的圆心在x 轴的正半轴上,且⊙B 与⊙A 外切于点P ,两圆的公切线MP 交y 轴于点M ,交x 轴于点N . (1)若sin ∠OAB=54,求直线MP 的解析式及经过M 、N 、B 三点的抛物线的解析式;(2)若A 的位置大小不变,⊙B 的圆心在x 轴的正半轴上移动,并使⊙B 与⊙A 始终外切,过M 作⊙B 的切线MC ,切点为C 在此变化过程中探究: ①四边形OMCB 是什么四边形,对你的结论加以证明;②经过M 、N 、B 点的抛物线内是否存在以BN 为腰的等腰三角形?若存在,表示出来;若不存在,说明理由. (山西省中考题)11.有一张矩形纸片ABCD,E、F、分别是BC、AD上的点(但不与顶点重合),若EF将矩形ABCD分成面积相等的两部分,设AB=a,AD=b,BE=x.(1)求证:AF=EC;(2)用剪刀将该纸片沿直线EF剪开后,再将梯形纸片ABEF沿AB对称翻折,平移拼接在梯形ECDF的下方,使一底边重合,一腰落在DC的延长线上,拼接后,下方梯形记作EE'B'C.①当bx:为何值时,直线E'E经过原矩形的一个顶点?②在直线E'E经过原矩形的一个顶点的情形下,连结BE',直线BE'与EF是否平行?你若认为平行,请给予证明;你若认为不平行,试探究当a与b有何种数量关系时,它们就垂直?(江西省中考题) 12.(1)证明:若x取任意整数时,二次函数ca-、+=2总取整数值,那么,a2、bbxaxy+c都是整数.(2)写出上述命题的逆命题,且证明你的结论.(全国初中数学竞赛题)13.已知四边形ABCD的面积为32,AB、CD、AC的长都是整数,且它们的和为16.(1)这样的四边形有几个?(2)求这样的四边形边长的平方和的最小值. (全国初中数学联赛题)参考答案。
中考数学复习第二讲《开放探究型问题》经典题型含答案

中考数学复习专题第二讲开放探究型问题【要点梳理】开放探究型问题的内涵:所谓开放探究型问题是指已知条件、解题依据、解题方法、问题结论这四项要素中,缺少解题要素两个或两个以上,需要通过观察、分析、比较、概括、推理、判断等探索活动来确定所需求的条件或结论或方法.(1)常规题的结论往往是唯一确定的,而多数开放探究题的结论是不确定或不是唯一的,它是给学生有自由思考的余地和充分展示思想的广阔空间;(2)解决此类问题的方法,可以不拘形式,有时需要发现问题的结论,有时需要尽可能多地找出解决问题的方法,有时则需要指出解题的思路等.对于开放探究型问题,需要通过观察、比较、分析、综合及猜想,展开发散性思维,充分运用已学过的数学知识和数学方法,经过归纳、类比、联想等推理的手段,得出正确的结论.在解开放探究题时,常通过确定结论或补全条件,将开放性问题转化为封闭性问题.【学法指导】三个解题方法(1)条件开放型问题:由已知的结论反思题目应具备怎样的条件,即从题目的结论出发,结合图形挖掘条件,逆向追索,逐步探寻,是一种分析型思维方式.它要求解题者善于从问题的结论出发,逆向追索,多途寻因;(2)结论开放型问题:从剖析题意入手,充分捕捉题设信息,通过由因导果,顺向推理或联想、类比、猜测等,从而获得所求的结论;(3)条件和结论都开放型:此类问题没有明确的条件和结论,并且符合条件的结论具有多样性,需将已知的信息集中进行分析,探索问题成立所必须具备的条件或特定的条件应该有什么结论,通过这一思维活动得出事物内在联系,从而把握事物的整体性和一般性.【考点解析】条件开放型问题(2017贵州安顺)如图,DB∥AC,且DB=AC,E是AC的中点,(1)求证:BC=DE;(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?【考点】LC:矩形的判定;L7:平行四边形的判定与性质.【分析】(1)要证明BC=DE,只要证四边形BCED是平行四边形.通过给出的已知条件便可.(2)矩形的判定方法有多种,可选择利用“对角线相等的平行四边形为矩形”来解决.【解答】(1)证明:∵E是AC中点,∴EC=AC.∵DB=AC,∴DB∥EC.又∵DB∥EC,∴四边形DBCE是平行四边形.∴BC=DE.(2)添加AB=BC.( 5分)理由:∵DB AE,∴四边形DBEA是平行四边形.∵BC=DE,AB=BC,∴AB=DE.∴▭ADBE是矩形.结论开放型问题(2017广西河池)(1)如图1,在正方形ABCD中,点E,F分别在BC,CD 上,AE⊥BF于点M,求证:AE=BF;(2)如图2,将(1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE ⊥BF于点M,探究AE与BF的数量关系,并证明你的结论.【考点】S9:相似三角形的判定与性质;KD:全等三角形的判定与性质;LE:正方形的性质.【分析】(1)根据正方形的性质,可得∠ABC与∠C的关系,AB与BC的关系,根据两直线垂直,可得∠AMB的度数,根据直角三角形锐角的关系,可得∠ABM与∠BAM的关系,根据同角的余角相等,可得∠BAM与∠CBF的关系,根据ASA,可得△ABE≌△BCF,根据全等三角形的性质,可得答案;(2)根据矩形的性质得到∠ABC=∠C,由余角的性质得到∠BAM=∠CBF,根据相似三角形的性质即可得到结论.【解答】(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠C,AB=BC.∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF.在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴AE=BF;(2)解:AB=BC,理由:∵四边形ABCD是矩形,∴∠ABC=∠C,∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF,∴△ABE∽△BCF,∴=,∴AB=BC.存在开放型问题(2017广东)如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:点B的坐标为(2,2);(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD 的长度;若不存在,请说明理由;(3)①求证: =;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.【考点】SO:相似形综合题.【分析】(1)求出AB、BC的长即可解决问题;(2)存在.连接BE,取BE的中点K,连接DK、KC.首先证明B、D、E、C 四点共圆,可得∠DBC=∠DCE,∠EDC=∠EBC,由tan∠ACO==,推出∠ACO=30°,∠ACD=60°由△DEC是等腰三角形,观察图象可知,只有ED=EC,推出∠DBC=∠DCE=∠EDC=∠EBC=30°,推出∠DBC=∠BCD=60°,可得△DBC是等边三角形,推出DC=BC=2,由此即可解决问题;(3)①由(2)可知,B、D、E、C四点共圆,推出∠DBC=∠DCE=30°,由此即可解决问题;②作DH⊥AB于H.想办法用x表示BD、DE的长,构建二次函数即可解决问题;【解答】解:(1)∵四边形AOCB是矩形,∴BC=OA=2,OC=AB=2,∠BCO=∠BAO=90°,∴B(2,2).故答案为(2,2).(2)存在.理由如下:连接BE,取BE的中点K,连接DK、KC.∵∠BDE=∠BCE=90°,∴KD=KB=KE=KC,∴B、D、E、C四点共圆,∴∠DBC=∠DCE,∠EDC=∠EBC,∵tan∠ACO==,∴∠ACO=30°,∠ACB=60°①如图1中,△DEC是等腰三角形,观察图象可知,只有ED=EC,∴∠DBC=∠DCE=∠EDC=∠EBC=30°,∴∠DBC=∠BCD=60°,∴△DBC是等边三角形,∴DC=BC=2,在Rt△AOC中,∵∠ACO=30°,OA=2,∴AC=2AO=4,∴AD=AC﹣CD=4﹣2=2.∴当AD=2时,△DEC是等腰三角形.②如图2中,∵△DCE是等腰三角形,易知CD=CE,∠DBC=∠DEC=∠CDE=15°,∴∠ABD=∠ADB=75°,∴AB=AD=2,综上所述,满足条件的AD的值为2或2.(3)①由(2)可知,B、D、E、C四点共圆,∴∠DBC=∠DCE=30°,∴tan∠DBE=,∴=.②如图2中,作DH⊥AB于H.在Rt△ADH中,∵AD=x,∠DAH=∠ACO=30°,∴DH=AD=x,AH==x,∴BH=2﹣x,在Rt△BDH中,BD==,∴DE=BD=•,∴矩形BDEF的面积为y= []2=(x2﹣6x+12),即y=x2﹣2x+4,∴y=(x﹣3)2+,∵>0,∴x=3时,y有最小值.综合开放型问题(2017山东泰安)如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E 是AB的中点,F是AC延长线上一点.(1)若ED⊥EF,求证:ED=EF;(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE 是否为平行四边形?并证明你的结论(请先补全图形,再解答);(3)若ED=EF,ED与EF垂直吗?若垂直给出证明.【考点】LO:四边形综合题.【分析】(1)根据平行四边形的想知道的AD=AC,AD⊥AC,连接CE,根据全等三角形的判定和性质即可得到结论;(2)根据全等三角形的性质得到CF=AD,等量代换得到AC=CF,于是得到CP=AB=AE,根据平行四边形的判定定理即可得到四边形ACPE为平行四边形;(3)过E作EM⊥DA交DA的延长线于M,过E作EN⊥FC交FC的延长线于N,证得△AME≌△CNE,△ADE≌△CFE,根据全等三角形的性质即可得到结论.【解答】(1)证明:在▱ABCD中,∵AD=AC,AD⊥AC,∴AC=BC,AC⊥BC,连接CE,∵E是AB的中点,∴AE=EC,CE⊥AB,∴∠ACE=∠BCE=45°,∴∠ECF=∠EAD=135°,∵ED⊥EF,∴∠CEF=∠AED=90°﹣∠CED,在△CEF和△AED中,,∴△CEF≌△AED,∴ED=EF;(2)解:由(1)知△CEF≌△AED,CF=AD,∵AD=AC,∴AC=CF,∵DP∥AB,∴FP=PB,∴CP=AB=AE,∴四边形ACPE为平行四边形;(3)解:垂直,理由:过E作EM⊥DA交DA的延长线于M,过E作EN⊥FC交FC的延长线于N,在△AME与△CNE中,,∴△AME≌△CNE,∴∠ADE=∠CFE,在△ADE与△CFE中,,∴△ADE≌△CFE,∴∠DEA=∠FEC,∵∠DEA+∠DEC=90°,∴∠CEF+∠DEC=90°,∴∠DEF=90°,∴ED⊥EF.【真题训练】训练一:(2017日照)如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.(1)求证:△DCA≌△EAC;(2)只需添加一个条件,即AD=BC(答案不唯一),可使四边形ABCD 为矩形.请加以证明.训练二:(2017湖北荆州)如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.(1)求证:△ACD≌△EDC;(2)请探究△BDE的形状,并说明理由.训练三:如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.训练四:(2017广东)如图,在平面直角坐标系中,O为原点,四边形ABCO 是矩形,点A,C的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB 为邻边作矩形BDEF.(1)填空:点B的坐标为(2,2);(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD 的长度;若不存在,请说明理由;(3)①求证: =;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.训练五:(2017•黑龙江)在四边形ABCD中,对角线AC、BD交于点O.若四边形ABCD是正方形如图1:则有AC=BD,AC⊥BD.旋转图1中的Rt△COD到图2所示的位置,AC′与BD′有什么关系?(直接写出)若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC′与BD′又有什么关系?写出结论并证明.参考答案:训练一:(2017日照)如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.(1)求证:△DCA≌△EAC;(2)只需添加一个条件,即AD=BC(答案不唯一),可使四边形ABCD 为矩形.请加以证明.【考点】LC:矩形的判定;KD:全等三角形的判定与性质.【分析】(1)由SSS证明△DCA≌△EAC即可;(2)先证明四边形ABCD是平行四边形,再由全等三角形的性质得出∠D=90°,即可得出结论.【解答】(1)证明:在△DCA和△EAC中,,∴△DCA≌△EAC(SSS);(2)解:添加AD=BC,可使四边形ABCD为矩形;理由如下:∵AB=DC,AD=BC,∴四边形ABCD是平行四边形,∵CE⊥AE,∴∠E=90°,由(1)得:△DCA≌△EAC,∴∠D=∠E=90°,∴四边形ABCD为矩形;故答案为:AD=BC(答案不唯一).训练二:(2017湖北荆州)如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.(1)求证:△ACD≌△EDC;(2)请探究△BDE的形状,并说明理由.【考点】LB:矩形的性质;KD:全等三角形的判定与性质;Q2:平移的性质.【分析】(1)由矩形的性质得出AB=DC,AC=BD,AD=BC,∠ADC=∠ABC=90°,由平移的性质得:DE=AC,CE=BC,∠DCE=∠ABC=90°,DC=AB,得出AD=EC,由SAS即可得出结论;(2)由AC=BD,DE=AC,得出BD=DE即可.【解答】(1)证明:∵四边形ABCD是矩形,∴AB=DC,AC=BD,AD=BC,∠ADC=∠ABC=90°,由平移的性质得:DE=AC,CE=BC,∠DCE=∠ABC=90°,DC=AB,∴AD=EC,在△ACD和△EDC中,,∴△ACD≌△EDC(SAS);(2)解:△BDE是等腰三角形;理由如下:∵AC=BD,DE=AC,∴BD=DE,∴△BDE是等腰三角形.训练三:如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.【考点】L9:菱形的判定;KX:三角形中位线定理;L7:平行四边形的判定与性质.【分析】(1)由三角形中位线定理得出DE∥AC,AC=2DE,求出EF∥AC,EF=AC,得出四边形ACEF是平行四边形,即可得出AF=CE;(2)由直角三角形的性质得出∠BAC=60°,AC=AB=AE,证出△AEC是等边三角形,得出AC=CE,即可得出结论.【解答】(1)证明:∵点D,E分别是边BC,AB上的中点,∴DE∥AC,AC=2DE,∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE;(2)解:当∠B=30°时,四边形ACEF是菱形;理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°,AC=AB=AE,∴△AEC是等边三角形,∴AC=CE,又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形.训练四:(2017广东)如图,在平面直角坐标系中,O为原点,四边形ABCO 是矩形,点A,C的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB 为邻边作矩形BDEF.(1)填空:点B的坐标为(2,2);(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD 的长度;若不存在,请说明理由;(3)①求证: =;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.【考点】SO:相似形综合题.【分析】(1)求出AB、BC的长即可解决问题;(2)存在.连接BE,取BE的中点K,连接DK、KC.首先证明B、D、E、C 四点共圆,可得∠DBC=∠DCE,∠EDC=∠EBC,由tan∠ACO==,推出∠ACO=30°,∠ACD=60°由△DEC是等腰三角形,观察图象可知,只有ED=EC,推出∠DBC=∠DCE=∠EDC=∠EBC=30°,推出∠DBC=∠BCD=60°,可得△DBC是等边三角形,推出DC=BC=2,由此即可解决问题;(3)①由(2)可知,B、D、E、C四点共圆,推出∠DBC=∠DCE=30°,由此即可解决问题;②作DH⊥AB于H.想办法用x表示BD、DE的长,构建二次函数即可解决问题;【解答】解:(1)∵四边形AOCB是矩形,∴BC=OA=2,OC=AB=2,∠BCO=∠BAO=90°,∴B(2,2).故答案为(2,2).(2)存在.理由如下:连接BE,取BE的中点K,连接DK、KC.∵∠BDE=∠BCE=90°,∴KD=KB=KE=KC,∴B、D、E、C四点共圆,∴∠DBC=∠DCE,∠EDC=∠EBC,∵tan∠ACO==,∴∠ACO=30°,∠ACB=60°①如图1中,△DEC是等腰三角形,观察图象可知,只有ED=EC,∴∠DBC=∠DCE=∠EDC=∠EBC=30°,∴∠DBC=∠BCD=60°,∴△DBC是等边三角形,∴DC=BC=2,在Rt△AOC中,∵∠ACO=30°,OA=2,∴AC=2AO=4,∴AD=AC﹣CD=4﹣2=2.∴当AD=2时,△DEC是等腰三角形.②如图2中,∵△DCE是等腰三角形,易知CD=CE,∠DBC=∠DEC=∠CDE=15°,∴∠ABD=∠ADB=75°,∴AB=AD=2,综上所述,满足条件的AD的值为2或2.(3)①由(2)可知,B、D、E、C四点共圆,∴∠DBC=∠DCE=30°,∴tan∠DBE=,∴=.②如图2中,作DH⊥AB于H.在Rt△ADH中,∵AD=x,∠DAH=∠ACO=30°,∴DH=AD=x,AH==x,∴BH=2﹣x,在Rt△BDH中,BD==,∴DE=BD=•,∴矩形BDEF的面积为y= []2=(x2﹣6x+12),即y=x2﹣2x+4,∴y=(x﹣3)2+,∵>0,∴x=3时,y有最小值.训练五:(2017•黑龙江)在四边形ABCD中,对角线AC、BD交于点O.若四边形ABCD是正方形如图1:则有AC=BD,AC⊥BD.旋转图1中的Rt△COD到图2所示的位置,AC′与BD′有什么关系?(直接写出)若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC′与BD′又有什么关系?写出结论并证明.【考点】LE:正方形的性质;KD:全等三角形的判定与性质;L8:菱形的性质;R2:旋转的性质.【分析】图2:根据四边形ABCD是正方形,得到AO=OC,BO=OD,AC⊥BD,根据旋转的性质得到OD′=OD,OC′=OC,∠D′OD=∠C′OC,等量代换得到AO=BO,OC′=OD′,∠AOC′=∠BOD′,根据全等三角形的性质得到AC′=BD′,∠OAC′=∠OBD′,于是得到结论;图3:根据四边形ABCD是菱形,得到AC⊥BD,AO=CO,BO=DO,求得OB=√3OA,OD=√3OC,根据旋转的性质得到OD′=OD,OC′=OC,∠D′OD=∠C′OC,求得OD′=√3OC′,∠AOC′=∠BOD′,根据相似三角形的性质得到BD′=√3AC′,于是得到结论.【解答】解:图2结论:AC′=BD′,AC′⊥BD′,理由:∵四边形ABCD是正方形,∴AO=OC,BO=OD,AC⊥BD,∵将Rt△COD旋转得到Rt△C′OD′,∴OD′=OD,OC′=OC,∠D′OD=∠C′OC,∴AO=BO,OC′=OD′,∠AOC′=∠BOD′,在△AOC′与△BOD′中,{AO=BO∠AOC′=∠BOD′OC′=OD′,∴△AOC′≌△BOD′,∴AC′=BD′,∠OAC′=∠OBD′,∵∠AO′D′=∠BO′O,∠O′BO+∠BO′O=90°,∴∠O′AC′+∠AO′D′=90°,∴AC′⊥BD′;图3结论:BD′=√3AC′,AC′⊥BD’理由:∵四边形ABCD是菱形,∴AC⊥BD,AO=CO,BO=DO,∵∠ABC=60°,∴∠ABO=30°,∴OB=√3OA,OD=√3OC,∵将Rt△COD旋转得到Rt△C′OD′,∴OD′=OD,OC′=OC,∠D′OD=∠C′OC,∴OD′=√3OC′,∠AOC′=∠BOD′,∴OBOA =OD′OC′=√3,∴△AOC′∽△BOD′,∴BD′AC′=OBOA=√3,∠OAC′=∠OBD′,∴BD′=√3AC′,∵∠AO′D′=∠BO′O,∠O′BO+∠BO′O=90°,∴∠O′AC′+∠AO′D′=90°,∴AC′⊥BD′.【点评】本题考查了正方形的性质,菱形的性质,全等三角形的判定和性质,相似三角形的判定和性质,旋转的性质,正确的识别图形是解题的关键.。
第42题开放性试题即论证观点题深度解析汇总(3)

第42题开放性试题即论证观点题深度解析汇总(3)敬告广大读者:从近期开始,本公众号系统地推出第42题经典试题的深度解析系列,既有高考真题,也有我原创的试题,也有优质模拟题,主要是通过分析解读题干和材料和提供多种答案示例,给大家提供解答的方法思路,并最终掌握应对开放性试题即论证观点题的解答策略,从而能够从容应对这种试题。
特别说明,本系列文章是史老师原创作品,欢迎广大师生批评指正。
3.(2020年全国Ⅲ卷·42)阅读材料,完成下列要求。
(12分)材料表1摘自1995年7~8月对江苏昆山,浙江乐清的部分农民进行的调查统计,调查对象中近60%为18~35岁的青壮年。
表1 1995年7~8月江苏昆山、浙江乐清部分农民调查统计单位:%——据周晓虹《传统与变迁》根据材料并结合所学知识,就材料整体或其中任意一点拟定一个论题,并予以阐述。
(要求:论题明确,持论有据,论证充分,表达清晰。
)【解析】本题通过提供了一段一手史料——调查统计表,创设了一个与现实生活密切相关的学习情景,以此来考查发现和论证历史问题,独立提出观点的能力。
是十年来开放性试题即论证观点题的最新尝试,也可以说是旧高考向新高考过度的尝试,还可以说是全国卷中主观试题中新高考形式的第一题,这要引起使用全国卷试题省份广大师生的高度重视,不妨在2021年的复习备考中多加训练。
怎样训练呢?最便捷的办法就是多研究山东省的新高考试题及其各地市命制的模拟题。
从近年来试题考查方向来看,突出了对“四史”(党史、国史、改革开放史和社会主义发展史)的考查。
解答本题关键是将调查统计情况置于熟悉的时空背景下进行分析说明,即用史实说明解释民众对思想观念发生的变化,这里边包含着逻辑因果关系,只要考生能把所学史实与农民思想观念变化之间的因果关系解释清楚就OK啦。
【解读题干】(1)“根据材料并结合所学知识”→是为作答依据。
依据题干材料给时间“1995年”,将题干材料“农民思想观念变化”和所学知识“改革开放史”精准定位,用到的关键能力是“准确掌握历史时序,将历史事物置于特定历史环境下进行分析的能力。
(初中物理讲练)专题23 物理学史与开放性问题
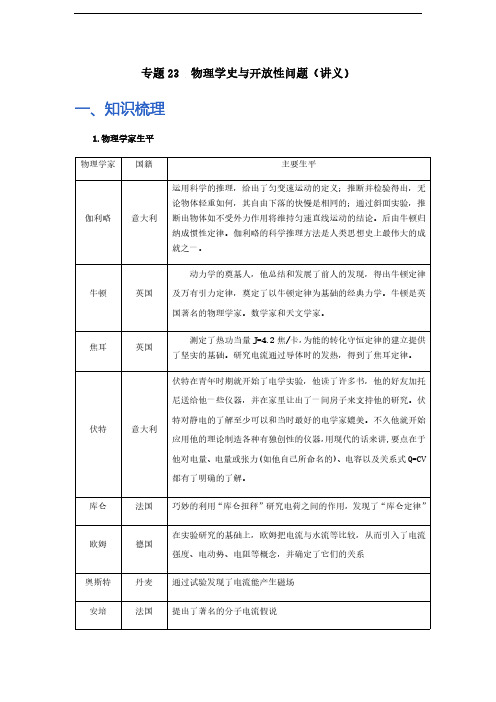
专题23 物理学史与开放性问题(讲义)一、知识梳理1.物理学家生平2.历史上物理学家的主要贡献历史上物理学家主要贡献国别伽利略运动物体不受外力恒速前进意大利笛卡尔运动物体不受外力不仅速度大小不变,而且运动方向也不变法国牛顿牛顿第一定律(又叫惯性定律)、万有引力定律、光的色散英国奥托·格里克马德堡半球实验,有力证明了大气压的存在德国托里拆利托里拆利实验,首先测出大气压的值意大利欧姆首先通过实验得到电流跟电压、电阻定量关系(即欧姆定律);德国焦耳最先确定电流的热量跟电流、电阻和通电时间的关系(即焦耳定律)英国奥斯特发现电流的磁场(即电流的磁效应)丹麦法拉第电磁感应现象的发现(根据这一发现,后来发明了电动机,是人类大规模用电成为可能,开辟了电气化时代)英国阿基米德阿基米德原理(F浮=G排)、杠杆平衡条件(又叫杠杆原理)希腊安培判定通电螺线管的极性跟电流方向关系的法则(即安培定则)法国汤姆生电子的发现英国爱迪生白炽灯泡的发明美国墨翟小孔成像中国瑞利氩气的发现,1894年(与化学家拉姆塞合作)英国昂尼斯超导现象(零电阻效应)的发现荷兰贝尔早期电话的发明美国莫尔斯电报机的发明美国麦克斯韦预言了电磁波的存在,建立了电磁场理论英国赫兹用实验证实了电磁波的存在德国爱因斯坦提出了真空中的光速是物体运动的极限速度理论德国沈括磁偏角的发现中国3.用科学家名字命名的物理量单位物理量单位物理量单位电量库仑电流安培电压伏特电阻欧姆电功率瓦特电能焦耳力牛顿压强帕斯卡功焦耳功率瓦特能焦耳摄氏温度摄氏度频率赫兹热力学温度开尔文4.物理规律物理规律名称物理规律内容物理学家牛顿第一定律任何物体都要保持匀速直线运动或静止状态,直到外力迫使它改变运动状态为止牛顿欧姆定律一段导体中的电流与这段导体两端的电压成正比,与这段导体的电阻成反比;公式是:RUI=欧姆阿基米德原理浸在液体里的物体受到液体竖直向上的浮力,浮力的大小等于物体排开液体受到的重力;公式是:F浮=G排阿基米德焦耳定律通电导体放出的热量与通过导体的电流的平方、导体电阻、通电时间成正比;公式是:RtIQ2=焦耳二、重点与难点★重点一:开放性问题近年来,中考物理试题中开放性试题越来越多出现在中考试卷中。
工作范文中的开放性问题与答案解析

工作范文中的开放性问题与答案解析在工作范文中,我们常常会遇到一些开放性问题,这些问题需要我们仔细思考和探讨,并提供合理的答案解析。
本文将就工作范文中的开放性问题与答案解析进行探讨,希望能够给读者一些参考和启发。
一、问题一:在面临困难或挑战时,您是如何应对的?这是一个经常在工作场景中出现的问题。
在回答这个问题时,应该从真实的例子中出发,具体描述你面临困难或挑战的情况,并阐述你是如何应对的。
例如,你可以回答说:我曾经在一个项目中遇到了严重的时间压力,我所在的团队需要在短时间内完成大量的工作。
我采取的应对策略是先确立优先级,然后组织团队成员合理分工,最后加班加点完成任务。
最终,我们成功地按时完成了项目,并获得了客户的高度赞扬。
从这个例子可以看出,面对困难或挑战时,你展现出了积极的态度和解决问题的能力,这对于工作范文中的评估非常重要。
二、问题二:您是如何管理时间的?时间管理是工作中非常重要的一项能力。
在回答这个问题时,可以具体描述你在工作中如何安排时间,如何有效地完成任务。
例如,你可以回答说:为了更好地管理时间,我通常会在每天工作开始之前制定当天的任务清单,并根据任务的紧急程度和重要性进行排序。
我会设定时间段集中进行工作,避免分散注意力。
另外,我还会设置适当的休息时间,以保持精力充沛。
通过这个回答,可以展示出你对时间的合理利用和组织能力,能够高效地处理工作任务。
三、问题三:请描述一个你与同事或团队成员存在分歧的情况,你是如何处理的?在工作中,人与人之间难免会产生分歧。
回答这个问题时,可以选择一个真实的例子来说明你在团队合作中如何处理分歧,并达到和谐的解决方案。
例如,你可以回答说:我们曾经在一个项目中发生了分歧,团队成员对于项目的具体实施方案存在不同意见。
在这种情况下,我主动组织了一次团队会议,邀请大家畅所欲言,充分表达各自的观点。
通过开放的讨论和充分沟通,我们最终达成了共识,并找到了一个既能满足项目需求又能兼顾团队成员意见的解决方案。
中考数学专题复习 开放性问题-人教版初中九年级全册数学试题

开放性问题【专题点拨】开放探索问题是指已知条件、解题依据、解题方法、问题结论这四项要素中,缺少解题要素两个或两个以上,或者条件、结论有待探求、补充等.【解题策略】在解决开放探索问题的时候,需解题者经过探索确定结论或补全条件,将开放性问题转化为封闭性问题,然后选择合适的解题途径完成最后的解答.【典例解析】类型一:条件开放型问题例题1:(2016·某某省滨州市·14分)如图,已知抛物线y=﹣x2﹣x+2与x轴交于A、B两点,与y轴交于点C(1)求点A,B,C的坐标;(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题;函数及其图象.【分析】(1)分别令y=0,x=0,即可解决问题.(2)由图象可知AB只能为平行四边形的边,易知点E坐标(﹣7,﹣)或(5,﹣),由此不难解决问题.(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.【解答】解:(1)令y=0得﹣x2﹣x+2=0,∴x2+2x﹣8=0,x=﹣4或2,∴点A坐标(2,0),点B坐标(﹣4,0),令x=0,得y=2,∴点C坐标(0,2).(2)由图象可知AB只能为平行四边形的边,∵AB=EF=6,对称轴x=﹣1,∴点E的横坐标为﹣7或5,∴点E坐标(﹣7,﹣)或(5,﹣),此时点F(﹣1,﹣),∴以A,B,E,F为顶点的平行四边形的面积=6×=.(3)如图所示,①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,在RT△CM1N中,==,∴点M1坐标(﹣1,2+),点M2坐标(﹣1,2﹣).②当M3为顶点时,∵直线AC解析式为y=﹣x+1,线段AC的垂直平分线为y=x,∴点M3坐标为(﹣1,﹣1).③当点A为顶点的等腰三角形不存在.综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+)或(﹣1.2﹣).【点评】本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识,解题的关键是熟练掌握抛物线与坐标轴交点的求法,学会分类讨论的思想,属于中考压轴题.变式训练1:(2016·某某某某)如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)(1)求抛物线的解析式;(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P 的坐标和四边形ABPC的最大面积.(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.类型二:结论开放型问题例题2:(2016·某某随州·3分)二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c >0;(4)若点A(﹣3,y1)、点B(﹣,y2)、点C(,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有()A.2个 B.3个 C.4个 D.5个【解析】二次函数图象与系数的关系.(1)正确.根据对称轴公式计算即可.(2)错误,利用x=﹣3时,y<0,即可判断.(3)正确.由图象可知抛物线经过(﹣1,0)和(5,0),列出方程组求出a、b即可判断.(4)错误.利用函数图象即可判断.(5)正确.利用二次函数与二次不等式关系即可解决问题.【解答】解:(1)正确.∵﹣ =2,∴4a+b=0.故正确.(2)错误.∵x=﹣3时,y<0,∴9a﹣3b+c<0,∴9a+c<3b,故(2)错误.(3)正确.由图象可知抛物线经过(﹣1,0)和(5,0),∴解得,∴8a+7b+2c=8a﹣28a﹣10a=﹣30a,∵a<0,∴8a+7b=2c>0,故(3)正确.(4)错误,∵点A(﹣3,y1)、点B(﹣,y2)、点C(,y3),∵﹣2=,2﹣(﹣)=,∴<∴点C离对称轴的距离近,∴y3>y2,∵a<0,﹣3<﹣<2,∴y1<y2∴y1<y2<y3,故(4)错误.(5)正确.∵a<0,∴(x+1)(x﹣5)=﹣3/a>0,即(x+1)(x﹣5)>0,故x<﹣1或x>5,故(5)正确.∴正确的有三个,故选B.变式训练2:(2016·某某某某·3分)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x 轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c>0④当y>0时,x的取值X围是﹣1≤x<3⑤当x<0时,y随x增大而增大其中结论正确的个数是()A.4个B.3个C.2个D.1个类型三:解题策略开放型例题3:(2014 年某某襄阳)如图 Z3-1,在△ABC 中,点D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)(2)选择其中的成立条件进行证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典开放性问题全解析
经典开放性问题全解析
经典问题1:请简单介绍一下你通常的娱乐和消遣方式,包括运动和兴趣。
常见回答
本人兴趣爱好广泛,尤其喜好足球、篮球等体育活动,阅读、写作也是兴趣所在,在业余时间还喜欢上网、旅游等……
回答点评
果然是爱好广泛,回答简练。
但细读下来,好像每一个大学男生的兴趣爱好都是这些吧。
这样的回答无疑是告诉HR:
我很普通!
问题剖析
对于介绍自己兴趣爱好的问题,在网申中出现率在80%以上。
因为HR想要了解一个“有血有肉”的你,喜好是最简单而直
观的途径,而你对自己的描述也要比个人资料形象生动一些。
介绍自己的兴趣爱好,要突出重点,并说明为何有这些喜好。
主要介绍那些与申请职位相关的兴趣以及需要团队协作的
爱好,也可突出有个性的特色爱好,以给HR留下深刻印象。
语言应尽量生动、流畅,毕竟HR选人时会有主观因素。
经典问题2:请描述自己大学中最突出的非学业成就。
常见回答
大学4年中我个人最大的非学业成就是坚持写日记,虽然多数只是记录每日发生的琐事,但能坚持4年非常不容易。
日记主要记录了我大学4年的生活、见闻以及一些感悟和体会,可以说是自己成长的轨迹,也是未来的一笔巨大财富。
回答点评
一说到非学业成就,很多人就要抓耳挠腮了,更何况是“最突出”的。
但即便是“小事”,申请者也可以通过突出事件的意义和自己的感触使其变成一种成就。
4年如一日的记日记就是很了不起的成就。
答题者坚持不懈、认真生活的人生态度跃然纸上。
对于这样的“有心人”,HR怎能视而不见呢?
问题剖析
对于这类问题,HR目的是从你的回答中判断出你的价值观,即在你眼里什么最重要;对你而言,什么才是成就,因此突出成功经历的经过才是最重要的。
虽然问题是在问成就是什么,但既然是非学业成就,HR真正希望你能告诉他的是你是怎样获得成就的,过程是什么,至于你具体获得的是什么HR并不关心。
另外,尽量不要谈论在学校所学习的东西,而要突出从生活实践中获得的成就。
经典问题3:关于职业生涯的规划,请谈谈你未来3~5 年的打算。
我希望用1年时间适应公司文化,融入团队并了解业务流程,2~3年时间掌握工作技巧,提升工作能力,成为主管,5年之内成为经理……
回答点评
你的雄心壮志还是说给父母听比较好。
对于一个尚未踏进职场的学生而言,有非常明晰的职业规划并不太现实。
如果简单回答出一个未来工作的“流水账”,很可能让用人单位觉得
你缺乏思考。
问题剖析
HR所以这样问是希望挖掘你应聘的深层次动机,看你是否
具有稳定性。
建议回答不要过于具体,在不清楚对方职级和晋升条件的情况下,过于具体的回答都不明智。
而是要突出你的职业规划以及成长方向。
对于这种问题,要根据每个公司的实际情况作答,并尽量从公司的理念里找企业的人才培养方向。
经典问题4:谈一谈你大学期间最成功∕遗憾的一件事是什么?为什么?
常见回答
大学期间最成功的经历是组织了XX大型活动,在活动中起到了举足轻重的作用。
这次成功的经验让我学到了N多宝贵道理,并树立信心……
领导式发言永远不会提起HR的兴趣,自然也不会对你有深刻的印象。
这是向HR展示你个人能力的好机会,怎么能草草回答呢?
问题剖析
对于“记事”类问题,要强调你在事件中起到了什么作用,以
及学到了什么道理。
不论是成功还是失败的经历,你都要告诉HR出现的问题和你怎样用能力去解决问题;你完成某事或者做出某决定是在怎样的背景下;当时你具有怎样的资源;面临怎样的困难,最终的目标是什么;你是如何行动的(利用资源、克服困难、处理突发情况等等);最后的结果是什么。
对于这类题目的回答,有一个基本思路,即“STAR”原则。
S=Situation,T=Target,A=Action,R=Result。
如果是失败的事例,你还需要分析失败的原因,并总结你得到的经验教训。
经典问题5:你认为自己最大的缺点是什么?
常见回答
我最大的缺点是做事比较偏激,喜欢钻牛角尖。
对于许多问题的看法经常与周围人不同,常因此产生分歧和争论……
回答点评
此回答的潜台词是:我是一个作风严谨的人,对待工作一丝不苟,并有自己独到的见解。
这样回答将“欲扬先抑”这种战
术诠释的淋漓尽致,变着法的夸自己。
但要注意不可以太明显。
问题剖析
关于“自我评价”类的问题,HR是希望更深层次的了解你,但很可能不是通过你的答案,而是通过你评价自己的方式。
经典问题6:你为什么选择我们公司?
常见回答
贵公司作为世界500强企业,在行业内的领导地位令人景仰,我希望能加入这个伟大的集体,促使自己成长并取得成功。
我十分看好贵公司所在的行业,我认为贵公司十分重视人才,而且这项工作很适合我,相信自己一定能做好……
回答点评
大段的描述很难让HR有耐心读下去,没有给招聘方任何“有价值的”的产品反馈。
一味地照搬企业简介上的“好话”,就差对着企业商标庄严宣誓了吧。
问题剖析
这一类问题对看清自己,给自己一个清晰的定位很有帮助。
另外作为招聘单位,既希望看到你对公司产品的热爱,也希望看到你中肯的评价,这些“有价值”的评价,不应只是从网上下载的官话和套话。
回答这类问题要注意体现:a、你求
职的动机、愿望以及对此项工作的态度。
b、从行业、企业
和岗位这3个角度来回答。
经典问题7:你认为本公司职员应该具备哪几样品质?
常见回答
贵公司作为一家世界知名企业,其员工首先要拥有很强的集体荣誉感及团队协作能力。
对待工作认真负责,并有很强的自我学习能力和创新能力。
同时为了与企业追求进步的文化相融合,员工本人的乐观上进、积极进取也是必不可少的。
回答点评
抛开有针对性的具体公司,这个回答可以作为一个较好的范本。
原因是其三句话不离企业。
说到企业雇员的品质时,不仅所使用的积极词语都是正确的,更为关键的是体现出企业的“品质”。
问题剖析
HR当然知道最适合他们公司的人应该具备什么品质,那你呢?如果你想求职成功的话,当然得说你就是这种适合他们公司的人。
你要告诉他们为什么你最适合这份工作。
在回答时,一定要用事例、数据具体描述,不能只是大概描述哪几点,这些品质应该从企业简介中去发掘。
但更重要的是结合前面问题展现出自己的能力特点。
最后还要暗示,你是符合企业要求的,你将来能为企业在哪些方面作出何种贡献。
总之,开放型问题是网申中重要的环节,也是最花时间的地方。
一次用时两个小时的网申,回答开放型问题一般会占用一半以上的时间,这也从一个侧面反映出了开放型问题的重
要性。
回答开放式问题的关键是展现出你的能力特点,即为什么企业需要你。
比较各个公司的开放型题目,会发现问题差别不大,所以我们可以提早准备。
另外,由于回答开放型问题没有限制,应聘者容易自由发挥。
但所谓言多必失,这种“自由”往往会使你犯下很多不易察觉的错误,需要细心应对。
