机器学习算法隐马尔可夫模型算法理论知识及算法实现代码实现最全整理汇总
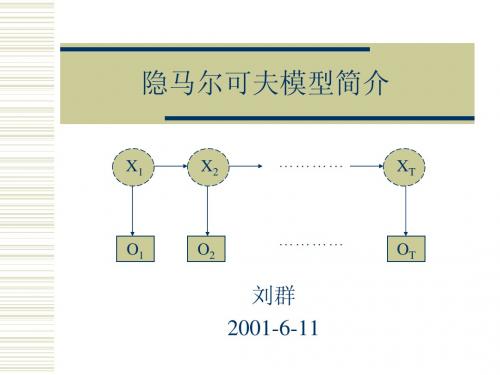
5隐马尔可夫模型简介
算法
评估问题:向前算法
定义向前变量 采用动态规划算法,复杂度O(N2T)
解码问题:韦特比(Viterbi)算法
采用动态规划算法,复杂度O(N2T)
学习问题:向前向后算法
EM算法的一个特例,带隐变量的最大似然估计
算法:向前算法(一)
P (O | λ ) = ∑ P (O, X | λ ) = ∑ P ( X | λ ) P (O | X , λ )
隐马尔可夫模型简介
X1 X2 ………… XT
O1
O2
…………
OT
刘群 2001-6-11
假设
对于一个随机事件,有一个观察值序列:O1,...,OT 该事件隐含着一个状态序列:X1,...,XT 假设1:马尔可夫假设(状态构成一阶马尔可夫链) p(Xi|Xi-1…X1) = p(Xi|Xi-1) 假设2:不动性假设(状态与具体时间无关) p(Xi+1|Xi) = p(Xj+1|Xj),对任意i,j成立 假设3:输出独立性假设(输出仅与当前状态有关) p(O1,...,OT | X1,...,XT) = Π p(Ot | Xt)
资源
Rabiner, L. R., A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition, Proceedings of the IEEE, vol. 77, no. 2, Feb. 1989, pgs 257 - 285. There is a lot of notation but verbose explanations accompany. 翁富良,王野翊,计算语言学导论,中国社会科学出版 社,1998 HTK:HMM Toolkit Hidden Markov Model (HMM) White Paper (GeneMatcher) ……
详细讲解隐马尔可夫模型配有实际例题

05
隐马尔可夫模型的优缺点
优点分析
能够处理序列数据,适用于 语音识别、自然语言处理等 领域
模型简单,易于理解和实现
具有较强的鲁棒性,能够适 应各种类型的数据
可以通过训练数据学习模型 的参数,提高模型的准确性
和泛化能力
缺点分析
计算复杂度高:隐马尔可夫模型的训练和预测需要大量的计算资源。
模型参数多:隐马尔可夫模型需要估计的状态转移概率和发射概率数量庞大,容易导致过拟合。
模型评估与调整
评估指标:准确率、召回率、F1值等 调整方法:调整模型参数、增加训练数据、调整模型结构等 评估工具:Python库(如sklern、pyrch等)、自定义评估函数等 调整策略:根据评估结果,选择合适的调整方法,以提高模型性能。
模型选择与决策
隐马尔可夫模型的定义和特点 隐马尔可夫模型的建立方法 隐马尔可夫模型的参数估计 隐马尔可夫模型的决策过程 隐马尔可夫模型的实际应用案例分析
04
隐马尔可夫模型的应用实例
语音识别
语音识别技术简介
隐马尔可夫模型在语音识 别中的应用
语音识别系统的组成和原 理
隐马尔可夫模型在语音识 别中的具体应用案例
自然语言处理
语音识别:将语音信号转化为文字 机器翻译:将一种语言的文本翻译成另一种语言 文本生成:根据输入生成连贯的文本 情感分析:分析文本中的情感倾向,如积极、消极、中性等
生物信息学
DN序列分析: 使用隐马尔可 夫模型预测DN 序列的进化关
系
RN结构预测: 利用隐马尔可 夫模型预测RN 的二级结构和
三级结构
蛋白质结构预 测:通过隐马 尔可夫模型预 测蛋白质的三 维结构和功能
基因调控网络 分析:使用隐 马尔可夫模型 分析基因调控 网络的动态变
隐马尔可夫模型算法及其在语音识别中的应用

隐马尔可夫模型算法及其在语音识别中的应用隐马尔可夫模型(Hidden Markov Model,HMM)算法是一种经典的统计模型,常被用于对序列数据的建模与分析。
目前,在语音识别、生物信息学、自然语言处理等领域中,HMM算法已经得到广泛的应用。
本文将阐述HMM算法的基本原理及其在语音识别中的应用。
一、HMM算法的基本原理1.概率有限状态自动机HMM算法是一种概率有限状态自动机(Probabilistic Finite State Automata,PFSA)。
PFSA是一种用于描述随机序列的有限状态自动机,在描述序列数据的时候可以考虑序列的概率分布。
PFSA主要包括以下几个部分:(1)一个有限状态的集合S={s_1,s_2,…,s_N},其中s_i表示第i个状态。
(2)一个有限的输出字母表A={a_1,a_2,…,a_K},其中a_i表示第i个输出字母。
(3)一个大小为N×N的转移概率矩阵Ψ={ψ_ij},其中ψ_ij表示在状态s_i的前提下,转移到状态s_j的概率。
(4)一个大小为N×K的输出概率矩阵Φ={φ_ik},其中φ_ik 表示在状态s_i的前提下,输出字母a_k的概率。
2. 隐藏状态在HMM中,序列的具体生成过程是由一个隐藏状态序列和一个观测序列组成的。
隐藏状态是指对于每个观测值而言,在每个时刻都存在一个对应的隐藏状态,但这个隐藏状态对于观测者来说是不可见的。
这就是所谓的“隐藏”状态。
隐藏状态和观测序列中的每个观测值都有一定的概率联系。
3. HMM模型在HMM模型中,隐藏状态和可观察到的输出状态是联合的,且它们都服从马尔可夫过程。
根据不同的模型,HMM模型可以划分为左-右模型、符合模型、环模型等。
其中最常见的是左-右模型。
在这种模型中,隐藏状态之间存在着马尔可夫链的转移。
在任何隐藏状态上,当前状态接下来可以转移到最多两个状态:向右移动一格或不变。
4. HMM的三个问题在HMM模型中,有三个基本问题:概率计算问题、状态路径问题和参数训练问题。
隐马尔可夫模型.pptx

第28页/共85页
学习问题
• Baum-Welch重估计公式
• 已知X和 的情况下,t时刻为状态i,t+1时刻为状态j的后验概率
θ
ij
(t
)
i
(t
1)aij P(XT
b |
jk
θ)
j
(t
)
向前
向后
T
jl (t)
t 1 l
bˆ v(t )vk
jk
T
jl (t)
t 1 l
第29页/共85页
例如:ML估计
第10页/共85页
估值问题
• 直接计算HMM模型产生可见长度为T的符号序列X的概率
其中,
表示状态 的初始概率
假设HMM中有c个隐状态,则计算复杂度为
!
例如:c=10,T=20,基本运算1021次!
(1)
第11页/共85页
O(cTT )
估值问题
• 解决方案
• 递归计算
t时刻的计算仅涉及上一步的结果,以及
x1和x3统计独立,而 其他特征对不独立
第32页/共85页
相关性例子
• 汽车的状态 • 发动机温度 • 油温 • 油压 • 轮胎内气压
• 相关性 • 油压与轮胎内气压相互独立 • 油温与发动机温度相关
第33页/共85页
贝叶斯置信网
• 用图的形式来表示特征之间的因果依赖性 • 贝叶斯置信网(Bayesian belief net) • 因果网(causal network) • 置信网(belief net)
P(θi )
P(θi | X)
θi P(X | θi )
第20页/共85页
解码问题
隐马尔科夫(HMM)模型详解及代码实现

机器学习之隐马尔科夫模型(HMM)机器学习之隐马尔科夫模型(HMM)1、隐马尔科夫模型介绍2、隐马尔科夫数学原理3、Python代码实现隐马尔科夫模型4、总结隐马尔可夫模型介绍马尔科夫模型(hidden Markov model,HMM)是关于时序的概率模型,描述由一个隐藏的马尔科夫随机生成不可观测的状态随机序列,再由各个状态生成一个观测从而产生观测随机序列的过程,属于一个生成模型。
下面我们来从概率学角度定义马尔科夫模型,从一个典型例子开始:假设有4个盒子,每个盒子里面有不同数量的红、白两种颜色的球,具体如下表:盒子编号1234红球数5368白球数5742现在从这些盒子中取出T个球,取样规则为每次选择一个盒子取出一个球,记录其颜色,放回。
在这个过程中,我们只能观测到球的颜色的序列,观测不到球是从哪个盒子中取出来的,即观测不到盒子的序列,这里有两个随机序列,一个是盒子的序列(状态序列),一个是球的颜色的观测序列(观测序列),前者是隐藏的,只有后者是可观测的。
这里就构成了一个马尔科夫的例子。
定义是所有的可能的状态集合,V是所有的可能的观测的集合:其中,N是可能的状态数,M是可能的观测数,例如上例中N=4,M=2。
是长度为T的状态序列,是对应的观测序列:A是状态转移概率矩阵:其中, 是指在时刻处于状态的条件下在时刻转移到状态的概率。
B是观测概率矩阵:其中, 是指在时刻处于状态的条件下生成观测的概率。
是初始状态概率向量:其中, 是指在时刻=1处于状态的概率。
由此可得到,隐马尔可夫模型的三元符号表示,即称为隐马尔可夫模型的三要素。
由定义可知隐马尔可夫模型做了两个基本假设:(1)齐次马尔科夫性假设,即假设隐藏的马尔科夫链在任意时刻的状态只和-1状态有关;(2)观测独立性假设,观测只和当前时刻状态有关;仍以上面的盒子取球为例,假设我们定义盒子和球模型:状态集合: = {盒子1,盒子2,盒子3,盒子4}, N=4观测集合: = {红球,白球} M=2初始化概率分布:状态转移矩阵:观测矩阵:(1)转移概率的估计:假设样本中时刻t处于状态i,时刻t+1转移到状态j 的频数为那么转台转移概率的估计是:(2)观测概率的估计:设样本中状态为j并观测为k的频数是那么状态j观测为k的概率, (3)初始状态概率的估计为S个样本中初始状态为的频率。
《隐马尔可夫模型》课件

隐马尔可夫模型在许多领域都有应用,如语音识 别、自然语言处理、生物信息学和金融预测等。
隐马尔可夫模型的应用领域
01
语音识别
用于将语音转换为文本,或识别说 话人的意图。
生物信息学
用于分析基因序列、蛋白质序列和 代谢物序列等。
03 隐马尔可夫模型的建立
观察概率矩阵的确定
总结词
观察概率矩阵描述了在给定状态下,观察到不同状态的概率 分布。
详细描述
观察概率矩阵是隐马尔可夫模型中的重要组成部分,它表示 了在给定状态下,观察到不同状态的概率分布。例如,在语 音识别中,观察概率矩阵可以表示在特定语音状态下发出不 同音素的概率。
状态转移概率矩阵的确定
VS
原理
通过动态规划找到最大概率的路径,该路 径对应于最可能的隐藏状态序列。
05 隐马尔可夫模型的优化与 改进
特征选择与模型参数优化
要点一
特征选择
选择与目标状态和观测结果相关的特征,提高模型预测准 确率。
要点二
模型参数优化
通过调整模型参数,如状态转移概率和观测概率,以改进 模型性能。
高阶隐马尔可夫模型
初始状态概率分布表示了隐马尔可夫模型在初始时刻处于各个状态的概率。这个概率分布是隐马尔可 夫模型的重要参数之一,它决定了模型在初始时刻所处的状态。在某些应用中,初始状态概率分布可 以根据具体问题来确定,也可以通过实验数据来估计。
04 隐马尔可夫模型的训练与 预测
前向-后向算法
前向算法
用于计算给定观察序列和模型参 数下,从初始状态到某个终止状 态的所有可能路径的概率。
《隐马尔可夫模型》 ppt课件
大数据分析中基于隐马尔可夫模型的聚类算法研究

大数据分析中基于隐马尔可夫模型的聚类算法研究一、引言近年来,人类社会逐渐向着信息化、智能化的方向发展,各种信息技术不断涌现。
在这其中,大数据技术是一项重要的技术,它的出现,极大地改变了数据处理的方式,大数据分析技术也因此得到了大力推广。
大数据分析涉及许多领域,而在聚类算法上,基于隐马尔可夫模型的算法在大数据分析中具有重要的应用价值。
二、基于隐马尔可夫模型的聚类算法隐马尔可夫模型是一种广泛应用于大数据分析中的概率模型。
隐马尔可夫模型是一种特殊的图模型,它由一个隐藏的马尔可夫链和一个观察序列组成。
这个模型假定在一定条件下,某个状态只与它之前的有限状态有关,即它有一个马尔可夫性。
假如我们已知在每个时刻系统处在哪个状态下观测到某些值,反过来就可以推理出系统的状态。
隐马尔可夫模型利用了不同状态下的特征,对大数据进行聚类处理,故隐马尔可夫模型也被称为混合模型。
在聚类算法中使用隐马尔可夫模型,主要分以下几个步骤:1. 设定初始值,将每一个样本通过随机数分到不同的簇中。
2. 通过条件概率密度函数,计算每一组数据是属于某一簇的概率,并根据概率将数据分配至对应的簇中。
3. 计算每个簇的类中心。
4. 计算每个簇各个成员与该簇中心点的距离,如果超过了预设的一定距离,视为离群点,将其从该簇中移除。
5. 重复进行第二步至第四步,直到满足一定的停止条件为止。
基于隐马尔可夫模型的聚类算法相较于其他聚类算法有一定的优势,其主要表现在:1. 当样本分布不是特别明显时,基于隐马尔可夫模型的聚类算法能够有效地识别出数据实现聚类分析。
2. 基于隐马尔可夫模型的聚类算法不依赖于样本数量,无选样偏差。
3. 隐马尔可夫模型很好地描述了样本数据的分布特点,可以有效地归纳数据的本质特征。
三、基于隐马尔可夫模型的聚类算法在实际应用中的应用隐马尔可夫模型聚类算法可以应用在许多的实际应用场景中,如新闻文本分类、足迹轨迹相似性分析、社交网络聚类、股票价格预测等。
自然语言处理技术中常用的机器学习算法介绍

自然语言处理技术中常用的机器学习算法介绍自然语言处理(Natural Language Processing,NLP)是人工智能领域中研究人类语言与计算机之间交互的一门学科。
在NLP领域中,机器学习算法被广泛应用于语言模型、文本分类、命名实体识别、情感分析等任务中。
本文将介绍NLP中常用的机器学习算法,包括支持向量机(Support Vector Machine,SVM)、朴素贝叶斯(Naive Bayes)、隐马尔可夫模型(Hidden Markov Model,HMM)和递归神经网络(Recurrent Neural Network,RNN)。
支持向量机(SVM)是一种常用的监督学习算法,广泛用于文本分类、情感分析等NLP任务中。
其核心思想是将数据映射到高维空间,通过构建一个最优的超平面,来实现数据的分类。
SVM在处理小样本、非线性和高维特征等问题上具有较好的性能。
朴素贝叶斯(Naive Bayes)是一种基于概率的分类算法,常用于文本分类任务。
它基于贝叶斯定理和特征间的条件独立性假设,可以在给定训练数据的条件下,通过计算后验概率来进行分类。
朴素贝叶斯算法简单、计算效率高,并且对输入数据的特征空间进行了较弱的假设,适用于处理大规模的文本分类问题。
隐马尔可夫模型(HMM)是一种统计模型,常用于语音识别、机器翻译等NLP任务中。
HMM假设系统是一个由不可观察的隐含状态和观测到的可见状态组成的过程,通过观察到的状态序列来估计最可能的隐含状态序列。
HMM广泛应用于词性标注、命名实体识别等任务中,具有较好的效果。
递归神经网络(RNN)是一种具有记忆能力的神经网络,适用于处理序列数据,如语言模型、机器翻译等NLP任务。
RNN通过引入循环结构,可以对序列中的上下文信息进行建模。
长短期记忆网络(Long Short-Term Memory,LSTM)是RNN的一种改进,通过引入门控机制解决了传统RNN存在的长期依赖问题,更适合处理长文本和复杂语义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机器学习算法隐马尔可夫模型算法理论知识及算法实现
代码实现最全整理汇总
HMM算法有三个核心问题:
1.评估问题:给定观测序列和模型参数,计算观测序列出现的概率。
2.解码问题:给定观测序列和模型参数,推测最可能的隐藏状态序列。
3.学习问题:给定观测序列,估计模型参数的最大似然估计。
下面是隐马尔可夫模型算法实现的代码示例(基于Python):
1.基本定义
```python
import numpy as np
#定义隐马尔可夫模型
class HMM(object):
def __init__(self, A, B, pi):
self.A = A # 状态转移概率矩阵
self.B = B # 观测概率矩阵
self.pi = pi # 初始状态概率向量
self.N = self.A.shape[0] # 状态数
self.M = self.B.shape[1] # 观测数
```
2.评估问题
```python
#前向算法
def forward(self, O):
T = len(O)
alpha = np.zeros((T, self.N))
alpha[0] = self.pi * self.B[:, O[0]]
for t in range(1, T):
for i in range(self.N):
alpha[t, i] = np.sum(alpha[t-1] * self.A[:, i]) * self.B[i, O[t]]
return alpha
#后向算法
def backward(self, O):
T = len(O)
beta = np.zeros((T, self.N))
beta[T-1] = 1
for t in range(T-2, -1, -1):
for i in range(self.N):
beta[t, i] = np.sum(beta[t+1] * self.A[i] * self.B[:, O[t+1]])
return beta
#前向后向算法,计算观测序列的概率
def evaluate(self, O):
alpha = self.forward(O)
return np.sum(alpha[-1])
```
3.解码问题
```python
#维特比算法
def viterbi(self, O):
T = len(O)
delta = np.zeros((T, self.N))
psi = np.zeros((T, self.N), dtype=int)
delta[0] = self.pi * self.B[:, O[0]]
for t in range(1, T):
for i in range(self.N):
delta[t, i] = np.max(delta[t-1] * self.A[:, i]) * self.B[i, O[t]]
psi[t, i] = np.argmax(delta[t-1] * self.A[:, i])
z = np.zeros(T, dtype=int)
z[-1] = np.argmax(delta[-1])
for t in range(T-2, -1, -1):
z[t] = psi[t+1, z[t+1]]
return z
```
4. 学习问题(Baum-Welch算法)
```python
def learn(self, O_list, max_iter=100):
P_O_list = [self.evaluate(O) for O in O_list]
for n in range(max_iter):
gamma_sum = np.zeros((self.N, self.N))
epsilon_sum = np.zeros((self.N, self.M))
pi_new = self.pi * 0
for O, P_O in zip(O_list, P_O_list):
alpha = self.forward(O)
beta = self.backward(O)
gamma = alpha * beta / P_O
T = len(O)
epsilon = np.zeros((self.N, self.N, T))
for t in range(T-1):
for i in range(self.N):
for j in range(self.N):
epsilon[i, j, t] = alpha[t, i] * self.A[i, j] * self.B[j, O[t+1]] * beta[t+1, j] / P_O
gamma_sum += np.sum(gamma[:T-1], axis=0)
epsilon_sum += np.sum(epsilon[:, :, :T-1], axis=2)
pi_new += gamma[0]
self.A = epsilon_sum / gamma_sum[:, np.newaxis]
self.B = np.zeros((self.N, self.M))
for k in range(self.M):
mask = np.array([o == k for O in O_list for o in O])
self.B[:, k] = np.sum(np.stack([gamma[mask, i] for i in range(self.N)]), axis=1) / np.sum(gamma, axis=0)
self.pi = pi_new / len(O_list)
P_O_list_new = [self.evaluate(O) for O in O_list]
if np.linalg.norm(np.array(P_O_list) -
np.array(P_O_list_new)) < 1e-6:
break
P_O_list = P_O_list_new
```
这些代码实现了隐马尔可夫模型的基本功能,包括评估问题、解码问题和学习问题。
根据具体需求,可以进一步进行优化和扩展。
