第4章 SPSS基本统计分析
SPSS第四章基本统计分析

中 0 500 0
高 0 0 600
一致
1 - 29
青 中 老
低 0 0 400
中 0 600 0
高 500 0 0
应用举例
受教育程度越高通信支出越高吗? 受教育程度越高通信支出比例越高吗?
1 - 30
多选项分析
什么是多选项问题?
(1)即:在回答某些问题时,答案在两个以上 例如:请问您平时主要的休闲娱乐方式是: a.看电视、听广播 b.玩游戏 c.体育运动 d.逛街购物e.经常去港澳游玩 f.看书学习 g.喝酒聊天 h.工作太忙,没时间休闲娱乐 又如:您经常浏览的网站?在下列品牌中您信任哪些 品牌? (2)多选项问题不能直接处理。因为SPSS中的一个变 量对每一个答案只能取一个值。
2 2
2
C
2
1 - 27
分析列联表中变量间的关系
Ordinal(定序变量)
反映定序变量一致性指标 行变量等级越高,列变量等级也越高或越低 ——一致性高 行变量等级越高,列变量等级不定——不一 致 指标绝对值越大越相关,越接近0越无关
1 - 28
定序变量一致性检验
年龄与工资收入交叉列联表 低 青 400 一致 中 0 老 0
n 3
3
计算描述统计量
描述陡峭程度的统计量
峰度(kurtosis):描述某变量所有变量值 分布形态陡缓程度的统计量。
峭度为0表示与正态分布峭度相同。 大于0表示比正态分布陡,尖峰。 小于0表示比正态分布缓;平峰。
Kurtosis
1 - 12
1 n -1
i 1 ( xi x) / SD 3
n 4 4
计算描述统计量
第4章-SPSS基本统计分析

2016/12/25
21
基本描述统计量
描述离散程度的统计量
离散程度:指一组数据远离“中心值”的程度。 即考查所有数据相对于“中心值”分布的疏密程度。 如果数据都紧密地集中在“中心值”的周围,数 据的离散程度较小,则说明“中心值”对数据的 代表性就好; 如果数据比较松散地分布在“中心值”的周围, 数据的离散程度较大,则 “中心值”说明数据特 征是不具有代表性的。
案例
利用“大学生职业生涯规划数据”进行 以下分析:
1. 计算专业和职业认知得分的基本描述统计
量,并比较男女生的得分差异; 2. 分析是否存在专业和职业认知得分的异常 值。
应用举例
基本描述统计
以“居民储蓄调查数据”为例,对一次存(取)款金 额。有两个分析目标: 目标一:计算存(取)款金额的基本描述统计量,并对 城镇储户和农村储户进行比较 (数据拆分)
SK 0
左(负)偏态
x
M M
152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 e 169o170 171 172 173 174 175
基本描述统计量
描述陡峭程度的统计量
– 峰度(kurtosis): 描述某变量取值分布形态陡缓程
龄
合 计
频数分析表
频数分析的任务: 编制频数分布表
用宽度相同的条形的高度或长短来表示频数分布变化的图 如果有缺省值,那 – 各组的名称 形。使用于定序和定类变量的分析 么有效百分比能更 – 频数(Frequency) 加准确地反映取值 用圆形及圆内扇形的面积来表示频数百分比变化的图形。 – 百分比(Percent) 分布状况
《统计分析与SPSS的应用(第五版)》课后练习答案解析(第4章)
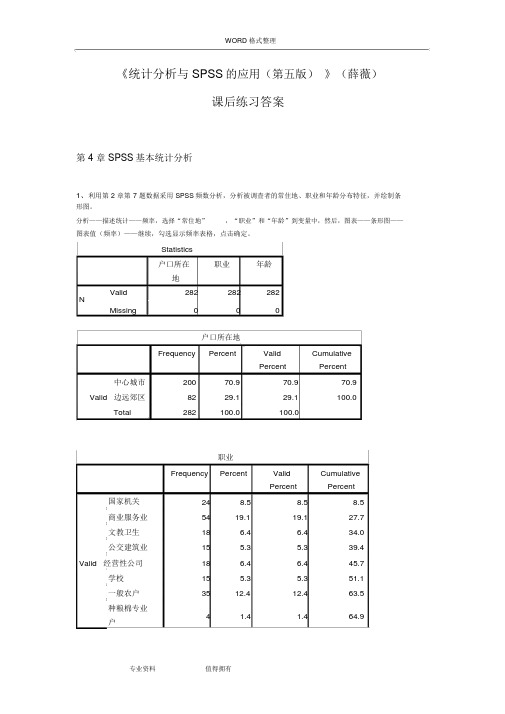
WORD 格式整理《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第 4 章 SPSS基本统计分析1、利用第2章第7题数据采用SPSS频数分析,分析被调查者的常住地、职业和年龄分布特征,并绘制条形图。
分析——描述统计——频率,选择“常住地”,“职业”和“年龄”到变量中,然后,图表——条形图——图表值(频率)——继续,勾选显示频率表格,点击确定。
Statistics户口所在职业年龄地Valid282282282NMissing000户口所在地Frequency Percent Valid CumulativePercent Percent中心城市20070.970.970.9 Valid 边远郊区8229.129.1100.0Total282100.0100.0职业Frequency Percent Valid CumulativePercent Percent 国家机关248.58.58.5商业服务业5419.119.127.7文教卫生18 6.4 6.434.0公交建筑业15 5.3 5.339.4Valid 经营性公司18 6.4 6.445.7学校15 5.3 5.351.1一般农户3512.412.463.5种粮棉专业4 1.4 1.464.9户WORD 格式整理种果菜专业10 3.5 3.568.4户工商运专业3412.112.180.5户退役人员17 6.0 6.086.5金融机构3512.412.498.9现役军人3 1.1 1.1100.0Total282100.0100.0年龄Frequency Percent Valid CumulativePercent Percent20 岁以下4 1.4 1.4 1.420~35 岁14651.851.853.2 Valid 35~50 岁9132.332.385.550 岁以上4114.514.5100.0Total282100.0100.0分析:本次调查的有效样本为282 份。
spss第四章描述统计简介PPT课件

当n 为奇数时:正中间位置号码=(n+1)/2 样本中位数=X(n+1)/2
当n为偶数时:正中间位置号码=(n+1)/2是小数,处于n/2与(n/2)+1之间。 样本中位数=(Xn/2+X(n/2)+1)/2 如5位同学的学习成绩:3,3,3,4,5。中间位置是第三位,中位数:3。 如果六位同学: 3,3,4,5,5,5。中间位置是3与4位中间的位置,中位数为: (4+5)/2=4.5
第四章 描述统计量简介
2024/10/23
第三章 样本数据特征的初步分析
1
调查杭州市居民收入情况,得到
调查顾客对产品的满意第度情四况章, 获得100个样本数据,能分
样本100统个计样本量数描据,述根据这些数据,
析出哪些信息?
你最想得到哪些信息?
调查大学生群体中对手机品牌的偏 好程度,你如何描述调查结果?
• 选择Percentile Values 栏中的 选项,输出所选变量的百分值
• Dispersion(离差)栏,用于
指定输出反映变量离散程度的 统计量
• Central Tendency (集中趋势)
栏,用于指定输出反映变量集 中趋势的统计量
• Distribution (分布特征)栏,
用于指定输出描述分布形状和
如果样本容量为n,那么,某个样本值出现 的频率=该样本值出现的频次/n
2024/10/23
第三章 样本数据特征的初步分析
9
分类数据或顺序数据描述频次与 频率的图形方法
统计分析与SPSS的应用(第五版)课后练习答案(第4章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第4章SPSS基本统计分析1、利用第2章第7题数据采用SPSS频数分析,分析被调查者的常住地、职业和年龄分布特征,并绘制条形图。
分析一一描述统计一一频率,选择“常住地” ,“职业”和“年龄”到变量中,然后,图表一一条形图一一图表值(频率)一一继续,勾选显示频率表格,点击确定。
种果菜专业户工商运专业户退役人员金融机构现役军人Total103417353282年龄|Freque ncy Perce nt ValidPerce ntCumulativePerce nt 20岁以下420~35 岁146Valid 35~50 岁9150岁以上41Total282■■-■I T d ItlSi祷分析:本次调查的有效样本为282份。
常住地的分布状况是:在中心城市的人最多,有200人,而在边远郊区只有82人;职业的分布状况是:在商业服务业的人最多,其次是一般农户和金融机构;年龄方面:在35-50岁的人最多。
由于变量中无缺失数据,因此频数分布表中的百分比相同。
2、利用第2章第7题数据,从数据的集中趋势、离散程度以及分布形状等角度,分析被调查者本次存款金额的基本特征,并与标准正态分布曲线进行对比。
进一步,对不同常住地储户存款金额的基本特征进行对比分析。
分析一一描述统计一一描述,选择存款金额到变量中。
点击选项,勾选均值、标准差、方差、最小值、最大值、范围、偏度、峰度、按变量列表,点击继续一一确定。
分析:由表中可以看出,有效样本为282份,存(取)款金额的均值是,标准差为,峰度系数为,偏度系数为。
与标准正态分布曲线进行对比,由峰度系数可以看出,此表的存款金额的数据分布比标准正态分布更陡峭;由偏度系数可以看出,此表的存款金额的数据为右偏分布,表明此表的存款金额均值对平均水平的测度偏大。
分析:由表中可以看出,中心城市有200人,边远郊区为82人。
两部分样本存取款金额均呈右偏尖峰分布,且边远郊区更明显。
第4章 SPSS基本统计分析(课后练习参考)

第4章 SPSS基本统计分析(课后练习参考)1、利用习题二第6题数据,采用SPSS数据筛选功能将数据分成两份文件。
其中,第一份数据文件存储常住地是“沿海或中心繁华城市”且本次存款金额在1000至5000之间的调查数据;第二份数据文件是按照简单随机抽样所选取的70%的样本数据。
第一份文件:选取数据数据——选择个案——如果条件满足——存款>=1000&存款<5000&常住地=沿海或中心繁华城市。
第二份文件:选取数据数据——选择个案——随机个案样本——输入70。
2、利用习题二第6题数据,将其按常住地(升序)、收入水平(升序)、存款金额(降序)进行多重排序。
排序数据——排序个案——把常住地、收入水平、存款金额作为排序依据分别设置排列顺序。
3、利用习题二第4题的完整数据,对每个学生计算得优课程数和得良课程数,并按得优课程数的降序排序。
计算转换——对个案内的值计数输入目标变量及目标标签,把所有课程选取到数字变量,定义值——设分数的区间,之后再排序。
4、利用习题二第4题的完整数据,计算每个学生课程的平均分以及标准差。
同时,计算男生和女生各科成绩的平均分。
方法一:利用描述性统计,数据——转置学号放在名称变量,全部课程放在变量框中,确定后,完成转置。
分析——描述统计——描述,将所有学生变量全选到变量框中,点击选项——勾选均值、标准差。
先拆分数据——拆分文件按性别拆分,分析——描述统计——描述,全部课程放在变量框中,选项——均值。
方法二:利用变量计算,转换——计算变量分别输入目标变量名称及标签——均值用函数mean完成平均分的计算,标准差用函数SD完成标准差的计算。
数据——分类汇总——性别作为分组变量、全部课程作为变量摘要、(创建只包含汇总变量的新数据集并命名)——确定5、利用习题二第6题数据,大致浏览存款金额的数据分布状况,并选择恰当的组限和组距进行组距分组。
根据存款金额排序,观察其最大值与最小值,算出组数和组距。
spss4-2(基本统计分析)

频数分析表
Central tendency: 用于定义描述 集中趋势的一组指标: 均数(Mean)、中位数(Median)、 众数(Mode)、总和(Sum)。
频数分析表
Dispersion:定义描述 离散趋势的一组指标: Std.deviation:标准差 Variance:方差 Range :全距 Minimum:最小值 Maximum:最大值 S.E.mean:标准误
众数
(不唯一性)
无众数 原始数据: 8 10 5 9 12 6
一个众数 原始数据:
6
5
9
8
5
5
多于一个众数 原始数据: 25 28 28 36 42 42
中位数
(median)
1. 排序后处于中间位置上的值
50%
2. 不受极端值的影响
Me
50%
3. 主要用于顺序数据,也可用数值型数据,但不能 用于分类数据 4. 各变量值与中位数的离差绝对值之和最小,即
8
9
1
2
3
4
5
6
7
n 1 9 1 位置 5 2 2 中位数 1080
数值型数据的中位数
(10个数据的算例)
【例】:10个家庭的人均月收入数据
排 序: 660 750 780 850 1630 2000 位 置: 960 1080 1250 1500
9
10
n 1 10 1 位置 5.5 2 2
2 众数(Mode):出现频率最高的数 3 中位数(Median):将数据排序后位于正中间 的数值。适合于所有分布类型的数据 4 总和(Sum)
众数
(mode) 1. 出现次数最多的变量值
SPSS统计分析第四章均值比较与T检验

N 258 216
Mean $41441.8 $26031.9
Std. Dev iation $19,499.214 $7,558.021
Std. Error Mean $1213.97
$514.258
左第一栏为分析变量标签和分类变量标签 N观测量数目 Mean均值 Std. Deviation标准差 Std. Error Mean标准误
三、配对样本T检验
配对样本T检验(Paired Sample T test)用 于检验两个相关的样本是否来自具有相同均 值的总体。这种相关的或配对的样本常常来 自这样的实验结果,在实验中被观测对象在 实验前后均被观测。两个变量可以是before after,配对分析的测度也不是必须来自同一 个观测对象。一对可以两者组合而成。
练习题
已知某水样中含CaCO3的真值为20.7mg/L, 现用某方法重复测定该水样11次CaCO3的含 量(mg/L)为:20.99,20.41,20.10, 20.00,20.91,22.60,20.99,20.41, 20.00,23.00,22.00。问该方法测得的均值 是否偏高?
2、Independent Sample T test(独立样本T检验)
例题一
现有银行雇员工资为例,检验男女雇员现工 资是否有显著差异。一个是要比较salary变量 的均值,另一个是gender变量作为分水平变 量。 (data09--03) 。
分析变量的简单描述性统计量
Gender Current Salary Male
F emale
Group Statistics
如果你试图比较的变量明显不是正态分布的,则应该 考虑使用一种非参数检验过程(Nonparametric test)。 如果想比较的变量是分类变量,应该使用Crosstabs 功能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集 中 趋 势 栏
离散趋势
分布形态栏
输出统计量对话框
案例:分析人均住房面积的分布情况,并对本 市户口和外地户口家庭进行比较
展示所有样本的四分位数:在变量【variable(s)】中
选择“人均面积”,在【statistics】中选择四分位数 【quartiles】即可。
按“户口状况”对数据进行拆分,然后分类比较人均住
⑷按【format】,可以调整频数分布表中数据的输出顺 序,这里选择频数的降序【descending counts】。 累计
变 量值
频 数
百分 比
此外,在SPSS输出窗口中用鼠标双击待编辑的图形,会 出出现【chart editor】图形编辑窗口。例如在 【elements】选择【show data lables】,可以在图中显示 频数数据。
SPSS提供了计算任意分位数的功能,用户可以指定将 数据等分为n份(Cut points for n equal groups)。 还可以直接指定分位点(Percentile)。
四分位差(也称内距或四分位距)
它是上四分位数(QU,即位于75%)与下四分位数(
QL,即位于25%)。计算公式为:Qd =QU-QL 四分位差反映了中间50%数据的离散程度,其数值越 小,说明中间的数据越集中;其数值越大,说明中间 的数据越分散。
结果一:人均住房面积频数分布表
结果二:分组后人均住房面积直方图
扩展二
计算分位数
分位数是变量在不同分位点上的取值。分位点在0- 100之间。
一般使用较多的是四分位点(Quartiles),即将所有数 据按升序排序后平均等分成四份,各分位点依次是25 %,50%,75%。于是四分位数便分别是25%,50% ,75%点所对应的变量值。此外,还有八分位数、十 六分位数等。
房面积的分位数。 操作:先使用【data】中【 split file】按“户口状况” 进行拆分,再选择【analyze】→【descriptive statistics】→ 【frequercies】,选择“人均面积”,并仅在【statistics】 中选择四分位数【quartiles】即可。
4.2计算基本描述统计量 ——对定距数据分布的精确认识
4.1 4.2 4.3 4.4 4.5
频数分析 计算基本描述统计量 交叉分组下的频数分析 多选项分析 比率分析
学习目标及内容:
掌握SPSS频数分析的基本方法及其操作 明确基本描述统计量的含义,并掌握其操作
掌握交叉列联分析的基本方法,了解卡方检验的基本 思想,并熟练操作 掌握对多选项问题的不同拆分方法和应用场合,并能 用于数据分析
1 n 3 3 Skewness ( xi x) / S n 1 i 1
当分布为对称分布时,正负总偏差相等,偏 度值等于0; 当分布为不对称分布时,正负总偏差不相等,偏度 值大于0或小于0。 偏度值大于0表示正偏差值大,称为正偏或右偏; 偏度值小于0表示负偏差值大,称为负偏或左偏. 偏度绝对值越大,表示数据分布形态的偏斜程度越 偏大。
(2) 任务二是绘制统计图 ①柱形图或条形图(bar chart) 条形图用横坐标的长短表示频数(百分比)的变化, 柱形图用纵坐标的高度表示频数(百分比),如下图 。 适合于定序和定类变量;
②饼图(pie chart):用圆形或扇形的面积表示频数、 百分比的变化。
③直方图(histograms):用矩形的面积表示频数分布变 化的图形,适用于定距性变量的分析。可以附加正态 分布曲线。
常见的刻画离散程度的描述统计量如下: (1)全距(Range):也称极差,是数据的最大值 (Maximum)与最小值(Minimum)之间的绝对 离差。 (2)样本方差(Variance):也是表示变量取值离 散程度的统计量,是各变量值与算术平均数离差平 方的算术平均数。其计算公式为:
1 2 S ( xi x) n 1 i 1
案例二:利用住房状况数据,分析人均住房面积 是否存在不均衡的现象
人均住房面积是否均衡,可以从人均住房面积是否 有大量的异常值入手。假设人均住房面积的总体分布 为正态分布,根据统计学中的3σ准则,异常值指在3 个标准差之外的变量值。
xi x P{ zi 3} 99.7%
3 原则认为正态分布中大概有0.3%的异常值,超 过这个标准就认为数据分布不均衡。
目的:精确把握变量的总体分布状况,了解数据的集 中趋势、离散趋势、对称程度、陡峭程度。 常见的基本描述统计量有三大类:
刻画集中趋势的统计量 刻画离散程度的统计量 刻画分布形态的统计量
4.2.1 基本描述统计量
一、刻画集中趋势的描述统计量 集中趋势是指一组数据向某一中心值靠拢的倾 向。 (1)均值(Mean):即算术平均数,是反映某变量 所有取值的集中趋势或平均水平的指标。如某企业 职工的平均月收入。其计算公式为:
操作:运用前面介绍的分组操作按“人均面积”将住房 分成1、2、3、4组,并赋给变量值,如1为人均住房 “小于10平方米”„ 【transform】→【recode into different variables】 然后选择频数分析【analyze】→【descriptive statistics】 → 【frequercies】,采用“分组后的人均面积”作 为计算频数的变量。在【charts】中使用直方图 histograms,带正态曲线with normal curve;
zi
xi x
~ N (0,1)
计算人均住房面积标准化值的操作:
【analyze】→【descriptive statistics】→ 【descriptives】→【save standardized values as variables】 SPSS会自动生成一个变量名存放人均住房面积的标准 化值“Z人均面积” 然后分别使用排序【sort by】(可以观察到异常值)、 分组【recode into different variables】、频数分析 功能
1 n x xi n i 1
(2)中位数(Median):即一组数据按升序排序后,处于中间 位置上的数据值。如评价社会的老龄化程度时,可用中位数 。 (3)众数(Mode):即一组数据中出现次数最多的数据值。如 生产鞋的厂商在制定各种型号鞋的生产计划时应该运用众数 。 (4)均值标准误差(Standard Error of Mean):描述样本均值 与总体均值之间的平均差异程度的统计量。其计算公式为:
数据分布特征和描述统计量
4.2.2计算基本描述统计量的应用举例 案例一:按户口状况对“人均住房面积”计 算基本描述统计量,并分别对本市户口和外 地户口家庭进行比较。 【analyze】→【descriptive statistics】→ 【descriptives】,在【variables】框中选“人 均面积”,再按【options】,从中选择需要 的特征描述。
(2)峰度(Kurtosis):描述变量取值分布形态陡峭程 度的统计量。其计算公式为:
1 n 4 4 Kurtosis ( xi x) / S 3 n 1 i 1
当数据分布与标准正态分布的陡峭程度相同时,峰 度值等于0; 峰度大于0表示数据的分布比标准正态分布更陡峭,为 尖峰分布; 峰度小于0表示数据的分布比标准正态分布平缓,为平 峰分布。
4.1频数分析
4.1.1频数分析的目的和基本任务
1、目的:基本统计分析往往从频数分析开始。通过频数分 析能够了解变量取值的状况,对把握数据的分布特征是非 常有用的。 2、基本任务 (1)频数分析的第一个基本任务是编制频数分布表。 频数(Frequency):即变量值落在某个区间(或某个 类别)中的次数 百分比(Percent):即各频数占总样本数的百分比 有效百分比(Valid Percent):即各频数占有效样本数 的百分比,这里有效样本数=总样本-缺失样本数 累计百分比(Cumulative Percent):即各百分比逐级 累加起来的结果。最终取值为1。
4.1.3 SPSS频数分析的扩展功能
按【statistics】还可以计算其他重要的统计量,如计 算分位数percentile values、以及反映集中趋势和 离散程度的统计量。这些扩展分析较适合于定距型变 量。 扩展一
定距型变量的频数分析 例如:分析 “人均住房面积”的分布情况
由于“人均面积”属于定距型变量,需要进行分组后, 才能进行频数分析。
问题:分析户主的从业状况和房屋产权情况 操作: ⑴选择【analyze】→【descriptive statistics】→ 【frequercies】
4.1.2频数分析的应用举例(住房状况调 查)
⑵再选择频数分析变量,即“从业状况”、“房屋产权” 到【varable(s)】框中 ⑶按【charts】选统计图形,在【chart values】中选择坐标 的含义(柱形、饼图),其中【frequencies】表示频数, 【percentages】表示百分比。
职 称* 文 化 程 度Crosstabulation 文 化 程 度 本 科 职 称 高 级 工 程 师 Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total 1 33.3% 25.0% 6.3% 1 25.0% 25.0% 6.3% 2 33.3% 50.0% 12.5% 0 .0% .0% .0% 4 25.0% 100.0% 25.0% 专 科 1 33.3% 25.0% 6.3% 3 75.0% 75.0% 18.8% 0 .0% .0% .0% 0 .0% .0% .0% 4 25.0% 100.0% 25.0% 高 中 1 33.3% 20.0% 6.3% 0 .0% .0% .0% 1 16.7% 20.0% 6.3% 3 100.0% 60.0% 18.8% 5 31.3% 100.0% 31.3% 初 中 0 .0% .0% .0% 0 .0% .0% .0% 3 50.0% 100.0% 18.8% 0 .0% .0% .0% 3 18.8% 100.0% 18.8% Total 3 100.0% 18.8% 18.8% 4 100.0% 25.0% 25.0% 6 100.0% 37.5% 37.5% 3 100.0% 18.8% 18.8% 16 100.0% 100.0% 100.0%
