华师大版九年级上册数学全章课后复习
华师大版数学九年级上册全册复习课件精选全文

④解这两个一元一次方程,它们的解就是原方程的解.
第22章┃ 复习
3.一元二次方程根的判别式 由于一元二次方程的根的个数由代数式_b_2_-__4_a_c_____的符 号决定,因此把_b_2_-__4_a_c____叫做一元二次方程根的判别式. (1)当_b_2_-__4_a_c_>__0___时,一元二次方程 ax2+bx+c=0(a≠0) 有 x2=两_个__不_-_相_b_-等__的2_ba_实2_-_数_4_a根_c_,__即__x_1_=_____.-__b_+___2_ab_2-__4_a_c________,
•第二十一章 二次根式 •21.1《二次根式》 •21.2二次根式的乘除法 •21.3二次根式的加减法
第21章┃ 复习
1.二次根式的概念 一般地,我们把形如__a__(a≥0)的式子叫做二次根式.
第21章┃ 复习
2.二次根式的性质
(1) a≥___0___(a≥0);(2)( a)2=___a___(a≥0);
解:移项,得 x2-4x=1,两边都加上 4,得 x2-4x+4=1 +4,即(x-2)2=5,两边开平方,得 x-2=± 5,即 x= 2± 5,所以 x1=2- 5,x2=2+ 5.
Байду номын сангаас
第22章┃ 复习
方法技巧 如果方程具备(x+a)2=b(b≥0)型,用直接开平方法解较简 单,如果不具备,应考虑因式分解法.用因式分解法解方程时, 应先把右边化为 0,再把左边因式分解,因式分解法简单,但 有局限性.因式分解法不能用时,观察如果二次项系数是 1, 一次项系数是偶数,用配方法解较简单.如果都不行,就用公 式法,公式法是解一元二次方程的万能方法,但要先化成一般 式确定 a,b,c,计算 b2-4ac.
【新华东师大版】九年级数学上册:21《二次根式》章末复习学案(含答案)
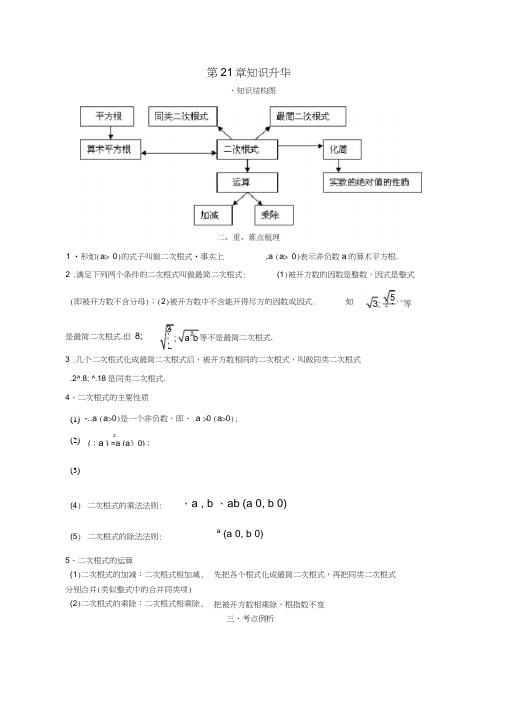
第21章知识升华3 .几个二次根式化成最简二次根式后,被开方数相同的二次根式,叫做同类二次根式 .2^.8; ^.18是同类二次根式. 4、二次根式的主要性质-..a (a >0)是一个非负数,即、.a >0 (a >0);5、二次根式的运算分别合并(类似整式中的合并同类项)三、考点例析2 .满足下列两个条件的二次根式叫做最简二次根式:(1)被开方数的因数是整数,因式是整式(即被开方数不含分母);(2)被开方数中不含能开得尽方的因数或因式.如2・a b等(2) 2(;a ) =a (a 》0); (3)(4) 二次根式的乘法法则:、a , b 、ab (a 0, b 0)(5) 二次根式的除法法则:a(a 0, b 0)(1) (1)二次根式的加减:二次根式相加减, 先把各个根式化成最简二次根式,再把同类二次根式(2)二次根式的乘除:二次根式相乘除, 把被开方数相乘除,根指数不变、知识结构图1 •形如(a > 0)的式子叫做二次根式•事实上 ,a (a > 0)表示非负数a 的算术平方根.等不是最简二次根式.3是最简二次根式.但 8;考点1:最简二次根式例1、(2010年哈尔滨市)在下列根式4.5a; - 2a [、b; , 8x 中,最简二次根式的个数为(),2a 3中有因式a 2可以开出,.8x 中有因数22可以开出,所以、:2a 3; 8X 不是最简二次根式.故选C.考点2:同类二次根式 例2、(2010年北京市)下列根式中,能与合并的是() A .24B..12C. , 3D. 18分析:能与.3合并的应是.3的同类二次根式, 这几个二次根式都不是最简二次根式,应先化为最简二次根式,刀=厶6;忑23;于;•吊3巨所以与4是同类二次根C.考点3:二次根式的运算A . 4个 B. 3个 C. 2 个 D.1分析:4.5a; _ b 是最简二次根式, 例3、(2010年青海省)若最简二次根式/1 人3 4 A. aB. a —43C. a 1D.a 1a 与2a 的被开方数相同,则a 的值为() 的被开方数相同;即1a 4 2a ,解得a 1 ,故选4、(2010年山东省东营市F 列计算正确的是()A . B.「43C.D.分析:由二次根式的性质和运算法则的 2 2,2 .2、2.而B 选项中明显用被开方数除以非被开方数,错用二次根式除法法则 ;C 选项用平方差公式即可得 4— 5 = — 1;D 选项丢了才1这”故选A.例5、(2010年江西省)化简2 2 2得( )式的是,12,故选B.分析:最简二次根式四、热点、易混点追踪1、概念理解模糊、审题不清例1、有下列命题:(1)二次根式的被开方数是相负数,最简二次根式;(3)若, 是二次根式,则a 0,b 0.其中正确的个数有(A .— 2 B. C. 2D.4.2 2分析:由二次根式的性质和运算法则得, 、,8 J ,22 2,2 2 2“ 2.故选 A.考点4:化简2例6、 (2010年北京市)计算近1分析:原式=2(2 1)2 .2 1 1.考点5:运用二次根式的性质化简 例7、( 2010年江西省) 已知 a 2,贝,,(a 2)2分析:a 2, a0,2 a.例8、 (2010年绍兴) 化简 \ 4x 24x 1 2x2得( A . 2B.4x 4C.D.4x 4.分析:由2x 3 0,得2x 10 ,所以,4x 2 4x 1. 2x 3 22x (2x 3) = 2x 2x 3 2,故应选A.考点6:二次根式成立的条件例9、(2010年山西省课该实验区)代数式1厂有意义时,字母x 的取值范围(A . x 1 B.x 1 C.D.x 0 且 x 1.分析:由分母不为零和二次根式的被开方数为非负数,所以 x 10,即x 1.故选A考点7:估算二次根式例10、(2010年沈阳课改) 估算 ,24 3的值为()A . 在 5和6之间 B. 在6和7之间C. 在7和8之间D.在8和9之间.分析:因为\ 16、;24、、25 即 4^.24 5,所以 7 .243 8.故选 C.则其值是非负数;(2)... x 2 y 2是)个.A 、0B 、1C 、2错解:选D.剖析:本例中,(1)错在对二次根式概念的狭隘理解,认为形如,.a a 0的式子就是二次.事实上,—2 .. a a 0等也是二次根式,但它是非正数.(2) (3)错在将二次根式的概念与其性质.a aa 0,b\ b Jb例2、已知,2x 3与,5是同类二次根式,则 x 的值为( )选项A 错在是解2x 3 5而得,这考虑仅仅是最简二次根式的情况 .当2x52x 5也是同类二次根式,故选C.2、对性质成立的条件理解不透定成立的有( )个.A 、0B 、1 错解:选D.必须满足a 0,b 0 .故选A.3、忽视几何图形中的条件限制2 例4、已知a,b,c ABC 的三边长,求• a b c错解:原式=abcbac 2b 2c .剖析:本例错在忽视了“三角形两边之和大于第三边”条件的限制,而导致错误 原式=a b c b a c 2a .4、计算不依据法则,随意而为 例5、下列计算:(1).2a . 3a . 5a ; (2)3. 2 2、、2 1 ; (3) 2 . 2 2. 2; (4).132 122132 ,122 1 ; (5)亦2 <4 2.正确的个数有()A 、3B 、4C 、5D 、非上述答案 错解:选C.根式,而二次根式的值是非负数的 错在忽视了 X 2y 2 0的条件. 为一谈了,事实上只要满足 -b0即可•故选A.A 、 4B 、5C 、无数个D、非上述答案错解: 选A.剖析: 例3、有下列各式:(1) . ab 2b ;(2) . a 211 ;(3)1ab b剖析:(1)错在a b 不一定是非负数,(2)错在忽视了a 1的条件, (3)错在等式要成立,的值.剖析: (1 )错在臆造 2 .、3 ,5 ; (2)错在合并冋类二次根式是只考虑了“系数”;(3)错在套用了整数与分数相加的法则; (4 )、(5)错在想巧算、快算反而弄巧成拙.故5个都错,选D.5、求解顾后不瞻前f ---------例6、若'4—X 有意义,则x 的取值范围是V x 14x0错解:由题意,得,解得0 x 4.x 0剖析:本例虽然考虑到被开方数的取值情况,但忽视了分母不能为零这个条件,正确结果为0 x 4 且 x 1.例7、先化简 X —1.. x 2 x ,然后再选择合适的数求值•J x 1----- 2错解:原式="X 1 _ J'x x 1 X 1 j x .当x =0时,原式=0. y/x 16、忽视隐含条件,使结论多解、漏解 例9、化简a错解:原式=•• xy xy 2 _ xy 2 3剖析:虽然xy 3,但我们并不知道 x, y 的取值符号,因此要进行讨论.(1 )当x 0, y 0 时,原式=xy xy 2 xy 2 3; ( 2 ) 当 x 0, y 0时,原式=、xy xy 2 xy 2 3.故填 2 3.剖析: 由题意,知x1 ,当x =0时,原式无意义, 因此只可取x1的数求值.如取x =4时,原式=6.例8、2解方程:x2 x 24错解: 原方程变为:2x 4x 4x 4x 4,解得:X 1 2,X 2 2.剖析: 只顾一直做下去, 以为求得解了就大功告成,是犯这类错误的特点.如果解题后,回过头来验证一下,就可以避免这类错误了,本题中, x =— 2时,x 无意义,所以x =2.错解:原式=a3 2a2a 5(a 1(a 3)3)剖析:本例隐含着.2 a0,则a 2,化简得原式=1.7、已知xy 3, y i —的值是;y8米的正方形大厅,它是由大小完全相同的黑白方砖密铺而成,则每一块方砖的边长为( ) A 、8B、2 + 1C 、2 D五、本章达标测试、选择题(每小题 3分,共30分):1、已知、、2卩 与、一5是同类二次根式,则 x 的值为( A 、 4、无数个D 、非上述答案2、有下列各式: a 1a 1 ; ( 2) : a b $ a b ;( 3)定成立的有( A 、如果实数x, y 满足x 0,则的值为A 、若.14.02 x10,y 的值为(A 、 14.02、0.1402、1.402A 、 A 、 C 、A 、 8、 A 、如果」一x 2yx 2y F 列运算正确的是(1.52 0.521.5 如果代数式 第一象限F 列各组二次根式中, 4xy 4y 22y1,贝U x,2 y 的关系为、x 2yx 2y0.5、2.0?2x、第二象限那么直角坐标系中点C 、第三象限x 的取值范围相同的是(m, n 的位置在(、第四象限9、如图所示,有一边长为 D二、填空题(每小题2分,共20分):10、请写出一个无理数使它与「3 1的积是有理数:___________ . __________11若常a a 0,贝U a的取值范围是 ___________________________ .若=7a & ,贝卩a的取值范围是12、已知二次根式J2a 1与J7是同类二次根式,试写出三个a的可能取值13、一个密码系统的原理如下所示:输入x T x21 T输出,如果输出结果为13时,则输入的x =15、已知0.2 a , 「03 b,则.0.24用含a,b的代数式表示为.16、已知A n】,B 3. n 2 (n为正整数),当n 5时,有A B.请用计算器计算当n 62时,A、B的若干值,并由此归纳出当n 6时,A B间的大小关系为17、数a、b在数轴上的位置如图所示,化简.(a 1)2(b 1)2. (a b)2= _____ .18、已知长方形相邻两边之比为 2 : 3,对角线长为.39,则长方形的面积为 _.19、规定两种新运算:a b a b,c d .c - d,如3 2 329,2 3 .2 .3 .6 ,1那么12 - 3 = .2三、解答题(70 分):20、(8分)不使用计算器,计算,113.14 0- 4554* 54' 521、(10分)已知x y 2 .3, y x2、、3,求x2y2 2 z xy xz yz 的值.22、(10分)图1是-种两种口味的火锅,为了制造这种火锅,我们把这个实际问题转化为一个26、数学问题就是在一圆筒里放入两种不同的物体, 并用一个长方形的金属薄片(金属厚度忽略不计) 分隔开来(如图2),已知圆筒高为20cm ,容积为25120cm 3,问这个长方形玻璃薄片的面积为 多少?( 取3.14,玻璃薄片的上边与圆筒的上底面持平)25、(7分)阅读理解:.12 .48r(10分)同学们都知道对于 -a 的式子,可以将分子、分母同乘以.b 来化去分母中的根号,Vb23、( 10分)边长为a 的正方形桌面,正中间有一个边长为 a的正方形方孔.3若沿图中虚线锯开,可以拼成一个新的正方形桌面.你会拼吗?试求出新的正方形边长.24、( 7分)已知: ,a^=| a2ab b 2 a b 2,一个同学在化简.7 4.3时是这样化简的:7 4-3 ,44.3 3 ,22 才水3 (奇.(2 G)2=2+ G .请仿照这个同学的做法化简:J4 6 5阶行列式,规定它的运算法则为ad be ,如2 6 5 48,现在请你计算2、2图1如1_ -_22,那么如果分母中是形如、a b的形式,该怎么办呢?办法有的是,我们可以利用平方差公式,将分子、分母同乘以Ja b ,从而化去分母中的根号,如参考答案一、 1 〜9、C A D C B D B C C 二、 10、、、3 1 11、 a 0, O v a w 1 12、 3, 31, 87 13、 土 2.3 14、 土 22 15、 2ab 16、 A B 17、 一 2 18、18 19、~7、20、 x51221、1522、解: 设圆柱形圆筒的底面半径为X ,则:x =25120 V 3.1420 20cm ,故长方形玻璃薄片的面积应为:20 40 800 cm 2 .23、解: 设新正方形的边长为x , 根据题意有: 2 2x a1 a 2,解得X 2 &a .3324、3 —:』5cu 47 L25、6626、 (1) 10 4、. 543 11 1 .3 1-L J .根据以上介绍,请你解答下面的问题:2(1) 4已知------- 的整数部分为.5 1a ,小数部分为b ,求a 2 b 2的值. (2) 1 试着化简:1 .22<3(2)原式=—L1—吕迈9康i忑近i 近运忑丘''、品屆4^晶。
华师大版数学九年级上册章末复习课件

sin2 A cos2 A 1
4.特殊角的三角函数
α sinα cosα
30° 1
3
2
2
45° 2
2
2
2
60° 3
1
2
2
tanα
3 3 1
3
5.解直角三角形的基本类型及其解法
(1)已知两直角边a、b或一直角边a,锐角A
c a2 b2 tan A a
b
b c2 a2 sin A a
2.如图,一段河坝的断面为梯形ABCD,试 根据图中数据,求出坡角α和坝底宽AD.(结果 保留根号)
B 5m
A
4.5m C
i 1: 3
4m α
D
E
B 4.5m C
5m AF
i 1: 3
4m α
D
E
解:∵ i 1 : =3tanα
∴α=30°,ED= 4 3
过点B作BF∥CE,则Rt△AFB中,
章末复习
华东师大版九年级上册
• 复习目标: 1.通过复习,使学生系统地掌握本章知识, 熟练应用三角函数进行计算. 2.了解仰角、俯角、坡度等相关概念,掌握 直角三角形的边与边、角与角、边与角的关 系,能应用这些关系解决相关问题.
知识结构
两个锐角互余
直 角 三 角 形
斜边上的中线等于斜边的一半
解
直
E
F
解:如图
tan 42 AF tan 61 AF
CF
EF
∵EF=CF-120
E
F
∴tan42°CF=tan61°(CF-120)
解得CF=240 ∴AF=216,则AB=AF+FB=216+1.2≈217(米)
2020华师大版九年级数学上册第24章 解直角三角形专题复习

【文库独家】华师大版九年级上册第24章 解直角三角形专题复习一. 本周教学内容:直角三角形边角关系专题复习 一. 知识体系:1. 三种三角函数与直角三角形中边与角的关系,在Rt △中 ①的对边的斜边tan ααα=∠∠②的对边的斜边sin ααα=∠∠③的邻边的斜边cos ααα=∠∠在此应注意的问题是无论是求哪一个角的三角函数,一定要先把这个角放在直角三角形中 2. 特殊角的三角函数值,可用表格来说明注:此表可借助特殊直角三角形三边的关系来记忆3. 三角函数的有关计算(对于一般角的三角函数值可利用计算器)41234.三角函数的应用()测山的高度()测楼的高度()测塔的高度()其它⎧⎨⎪⎪⎩⎪⎪二. 例题分析例1. 如图在等腰直角三角形ABC 中,∠C=90°,AC=6,D 是AC 上一点,若tan ∠=DBA AD 15,求的长。
A E B分析:解三角函数题目最关键的是要构造合适的直角三角形,把已知角放在所构造的直角三角形中。
本题已知所以可以过作于把放于tan ,,∠=⊥∠DBA D DE AB E DBA Rt DBE 15∆中,然后根据正切函数的定义,即可弄清DE 与BE 的长度关系,再结合等腰Rt △的性质,此题就不难解答了。
解:过D 作DE ⊥AB 于E ∴△DBE 和△DEA 为Rt △tan ∠==∴==DBE DE BE DE x BE x 155设则∴=+=AB DE BE x 6又为等腰为等腰∆∆∆∆ACB Rt A Rt DEA Rt ∴∠=∴45∴==∴=AE DE xAD x 2又, AC AB AC x x =∴==∴=∴=62626622∴==⋅==AD x AD 22222即例2. 如图湖泊的中央有一个建筑物AB ,某人在地面C 处测得其顶部A 的仰角为60°,然后,自C 处沿BC 方向行100m 到D 点,又测得其顶部A 的仰角为30°,求建筑物的高(结果保留根号)A分析:本题的关键在于(1)DB-CB=100(2)Rt △ABC 与Rt △ADB 有一条共同的线段AB ,因此只要利用Rt △ABC 和Rt △ADB 分别用AB 表示出DB 和CB 即可列出方程DB-CB=100,问题便可迎刃而解。
第22章 一元二次方程复习和小结-九年级数学上册(华东师大版)

3.使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元 二次方程的解也叫做一元二次方程的根.
第22章 一元二次方程
二、一元二次方程的解法 解法一:直接开平方法 ➢ 变形:将方程化为含未知数的完全平方式=非负常 数的形式; ➢ 开方:利用平方根的定义,将方程转化为两个一元一次方程; ➢ 求解:解一元一次方程,得出方程的根.
, x1x2=
2a 2 a
,
因为
x1
-
x1x2
+
x2
=
1
-
a,所以
3a 1 a
2a a
2
1
a,即 a 1 a
1
a,
解得 a1 = 1,a2 = - 1.当 a = 1 时,原方程有两个相等的
实数根,不合题意,舍去.所以 a = -1.
第22章 一元二次方程
5
∵5k + 20<0,∴Δ<0,∴没有实数根.
第22章 一元二次方程
5.已知一元二次方程:①x2 + 2x + 3 =0,②x2 - 2x - 3 = 0,下列说法正确
的是( B ) A.①②都有实数解
B.①无实数解,②有实数解
C.①②都无实数解 D.①有实数解,②无实数解
【解析】选 B.一元二次方程①的判别式的值为 Δ = b2 - 4ac = 4 - 12= - 8 <0,所以方程无实数根;一元二次方程②的判别式的值为 Δ = b2 - 4ac = 4 + 12 = 16>0,所以方程有两个不相等的实数根.
15 ,x2
3 3
15
(5)3x
最新华师大版九年级上册数学全册知识点总结

最新华师大版九年级上册数学全册知识点总结或减去一个数使得方程左边成为一个完全平方,最后使用完全平方公式解方程.3)公式法:利用求根公式解一元二次方程的方法.求根公式:对于一元二次方程ax2bx c0,它的两个根分别为:x1,2b b24ac2a其中,b24ac叫做判别式.当b24ac0时,方程有两个不等实数根;当b24ac0时,方程有两个相等实数根;当b24ac0时,方程没有实数根.4)因式分解法:将一元二次方程变形,使其成为两个一次因式的乘积,然后利用积零原理”解方程.5)图像法:利用二次函数的图像解一元二次方程的方法.将一元二次方程化为二次函数的标准式y ax2bx c,然后根据二次函数的图像,求出方程的实数根.3.一元二次方程的应用:1)利用一元二次方程解决实际问题.2)利用一元二次方程的图像分析实际问题.1.一次项系数的一半的平方可以配成完全平方公式。
2.公式法是一种用求根公式解一元二次方程的方法,其中一元二次方程ax+bx+c=(a≠)的求根公式为x=(-b±√(b²-4ac))/2a。
3.因式分解法是一种利用因式分解求解方程的方法,其步骤为将方程右边化为0,然后利用提取公因式、公式法或十字相乘等方法将其化为乘积的形式。
4.一元二次方程的根的判别式为△=b²-4ac,其中当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相同的实数根;当△<0时,方程没有实数根。
5.XXX定理指出,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数,两根之积等于常数项除以二次项系数所得的商。
6.一元二次方程可以用二次函数来表示,当y=0时就构成了一元二次方程,而在平面直角坐标系中,一元二次方程的解就是二次函数与X轴的交点。
7.比例式中,a、d为外项,b、c为内项,b=c时,b为a、d的比例中项。
8.比例具有基本性质、更比性质、合比性质和等比性质。
华东师大初中数学九年级上册《一元二次方程》全章复习与巩固—知识讲解(提高)(精选)

《一元二次方程》全章复习与巩固—知识讲解(提高)【学习目标】1.了解一元二次方程及有关概念;2.掌握通过配方法、公式法、因式分解法降次──解一元二次方程;3.掌握依据实际问题建立一元二次方程的数学模型的方法.【知识网络】【要点梳理】要点一、一元二次方程的有关概念1.一元二次方程的概念:通过化简后,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程,叫做一元二次方程.2.一元二次方程的一般式:3.一元二次方程的解:使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解,也叫做一元二次方程的根. 要点诠释:判断一个方程是否为一元二次方程时,首先观察其是否是整式方程,否则一定不是一元二次方程;其次再将整式方程整理化简使方程的右边为0,看是否具备另两个条件:①一个未知数;②未知数的最高次数为2.对有关一元二次方程定义的题目,要充分考虑定义的三个特点,不要忽视二次项系数不为0. 要点二、一元二次方程的解法 1.基本思想一元二次方程−−−→降次一元一次方程 2.基本解法直接开平方法、配方法、公式法、因式分解法. 要点诠释:解一元二次方程时,根据方程特点,灵活选择解题方法,先考虑能否用直接开平方法和因式分解 法,再考虑用公式法.要点三、一元二次方程根的判别式及根与系数的关系 1.一元二次方程根的判别式一元二次方程)0(02≠=++a c bx ax 中,ac b 42-叫做一元二次方程)0(02≠=++a c bx ax 的根的判别式,通常用“∆”来表示,即ac b 42-=∆.(1)当△>0时,一元二次方程有2个不相等的实数根; (2)当△=0时,一元二次方程有2个相等的实数根; (3)当△<0时,一元二次方程没有实数根.【高清ID 号:388528 关联的位置名称(播放点名称):根系关系】 2.一元二次方程的根与系数的关系如果一元二次方程)0(02≠=++a c bx ax 的两个实数根是21x x ,, 那么a b x x -=+21,ac x x =21. 注意它的使用条件为a ≠0, Δ≥0.要点诠释:1.一元二次方程的根的判别式正反都成立.利用其可以解决以下问题:(1)不解方程判定方程根的情况; (2)根据参系数的性质确定根的范围; (3)解与根有关的证明题.2. 一元二次方程根与系数的应用很多:(1)已知方程的一根,不解方程求另一根及参数系数;(2)已知方程,求含有两根对称式的代数式的值及有关未知数系数; (3)已知方程两根,求作以方程两根或其代数式为根的一元二次方程. 要点四、列一元二次方程解应用题 1.列方程解实际问题的三个重要环节: 一是整体地、系统地审题; 二是把握问题中的等量关系;三是正确求解方程并检验解的合理性.2.利用方程解决实际问题的关键是寻找等量关系.3.解决应用题的一般步骤:审 (审题目,分清已知量、未知量、等量关系等); 设 (设未知数,有时会用未知数表示相关的量); 列 (根据题目中的等量关系,列出方程);解 (解方程,注意分式方程需检验,将所求量表示清晰); 验 (检验方程的解能否保证实际问题有意义); 答 (写出答案,切忌答非所问). 4.常见应用题型数字问题、平均变化率问题、利息问题、利润(销售)问题、形积问题等.要点诠释:列方程解应用题就是先把实际问题抽象为数学问题(列方程),然后由数学问题的解决而获得对实际问题的解决.【典型例题】类型一、一元二次方程的有关概念1.已知(m -1)x |m|+1+3x -2=0是关于x 的一元二次方程,求m 的值. 【答案与解析】依题意得|m|+1=2,即|m|=1, 解得m =±1,又∵m -1≠0,∴m ≠1, 故m =-1.【总结升华】依题意可知m -1≠0与|m|+1=2必须同时成立,因此求出满足上述两个条件的m 的值即可.特别是二次项系数应为非零数这一隐含条件要注意.举一反三:【变式】若方程2(310m m x mx --=是关于x 的一元二次方程,求m 的值.【答案】根据题意得22,0,m m ⎧=⎪⎨-≠⎪⎩ 解得所以当方程2(310m m x mx --=是关于x的一元二次方程时,m =.类型二、一元二次方程的解法2.解下列一元二次方程.(1)224(3)25(2)0x x ---=; (2)225(3)9x x -=-; (3)2(21)4(21)40x x ++++=. 【答案与解析】(1)原方程可化为:22[2(3)][5(2)]0x x ---=, 即(2x-6)2-(5x-10)2=0,∴ (2x-6+5x-10)(2x-6-5x+10)=0,即(7x-16)(-3x+4)=0,∴ 7x-16=0或-3x+4=0,∴ 1167x =,243x =. (2)25(3)(3)(3)x x x -=+-, 25(3)(3)(3)0x x x --+-=,∴ (x-3)[5(x-3)-(x+3)]=0,即(x-3)(4x-18)=0,∴ x-3=0或4x-18=0,∴ 13x =,292x =. (3)2(21)4(21)40x x ++++=,∴ 2(212)0x ++=.即2(23)0x +=,∴ 1232x x ==-. 【总结升华】 (1)方程左边可变形为22[2(3)][5(2)]x x ---,因此可用平方差公式分解因式; (2)中方程右边分解后为(x-3)(x+3),与左边中的(x-3)2有公共的因式, 可移项后提取公因式(x-3)后解题;(3)的左边具有完全平方公式的特点,可用公式变为(2x+1+2)2=0再求解.举一反三:【变式】解方程: (1)3x+15=-2x 2-10x ; (2)x 2-3x =(2-x)(x-3). 【答案】(1)移项,得3x+15+(2x 2+10x)=0,∴ 3(x+5)+2x(x+5)=0, 即(x+5)(3+2x)=0,∴ x+5=0或3+2x =0,∴ 15x =-,232x =-. (2)原方程可化为x(x-3)=(2-x)(x-3),移项,x(x-3)-(2-x)(x-3)=0, ∴ (x-3)(2x-2)=0,∴ x-3=0或2x-2=0,∴ 13x =,21x =.类型三、一元二次方程根的判别式的应用3.关于x 的方程2(5)410a x x ---=有实数根.则a 满足( ) A .a ≥1 B .a >1且a ≠5 C .a ≥1且a ≠5 D .a ≠5【答案】A ;【解析】①当50a -=,即5a =时,有410x --=,14x =-,有实数根; ②当50a -≠时,由△≥0得2(4)4(5)(1)0a --⨯-⨯-≥,解得1a ≥且5a ≠.综上所述,使关于x 的方程2(5)410a x x ---=有实数根的a 的取值范围是1a ≥.答案:A【总结升华】注意“关于x 的方程”与“关于x 的一元二次方程”的区别,前者既可以是一元一次方程,也可以是一元二次方程,所以必须分类讨论,而后者隐含着二次项系数不能为0.【高清ID 号:388528 关联的位置名称(播放点名称):一元二次方程的根的判别式】4. k 为何值时,关于x 的二次方程2690kx x -+= (1)k 满足 时,方程有两个不等的实数根; (2)k 满足 时,方程有两个相等的实数根; (3)k 满足 时,方程无实数根.【答案】(1)10k k ≠<,且;(2)1k =;(3)1k >. 【解析】求判别式,注意二次项系数的取值范围. 【总结升华】根据判别式ac b 42-=∆及k ≠0求解.类型四、一元二次方程的根与系数的关系5.(2016•凉山州)已知x 1、x 2是一元二次方程3x 2=6﹣2x 的两根,则x 1﹣x 1x 2+x 2的值是( ) A .B .C .D .【思路点拨】由x 1、x 2是一元二次方程3x 2=6﹣2x 的两根,结合根与系数的关系可得出x 1+x 2=﹣,x 1•x 2=﹣2,将其代入x 1﹣x 1x 2+x 2中即可算出结果.【答案】D . 【解析】解:∵x 1、x 2是一元二次方程3x 2=6﹣2x 的两根, ∴x 1+x 2=﹣=﹣,x 1•x 2==﹣2, ∴x 1﹣x 1x 2+x 2=﹣﹣(﹣2)=. 故选D .【总结升华】本题考查了根与系数的关系,解题的关键是得出x 1+x 2=﹣,x 1•x 2=﹣2.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系得出两根之和与两根之积是关键. 举一反三:【变式】已知关于x 的方程2(1)(23)10k x k x k -+-++=有两个不相等的实数根1x 、2x . (1)求k 的取值范围;(2)是否存在实数k ,使方程的两实数根互为相反数?如果存在,求出k 的值;如果不存在, 请说明理由. 【答案】(1)根据题意,得△=(2k-3)2-4(k-1)(k+1)=224129412130k k k k -+-=-+>,所以1312k<.由k-1≠0,得k≠1.当1312k<且k≠1时,方程有两个不相等的实数根;(2) 不存在.如果方程的两个实数根互为相反数,则12231kx xk -+=-=-,解得32k=.当32k=时,判别式△=-5<0,方程没有实数根.所以不存在实数k,使方程的两个实数根互为相反数.类型五、一元二次方程的应用6.(2015•青岛模拟)随着青奥会的临近,青奥特许商品销售逐渐火爆.甲、乙两家青奥商品专卖店一月份销售额分别为10万元和15万元,三月份销售额甲店比乙店多10万元.已知甲店二、三月份销售额的月平均增长率是乙店二、三月份月平均增长率的2倍,求甲店、乙店这两个月的月平均增长率各是多少?【答案与解析】解:设乙店销售额月平均增长率为x,由题意得:10(1+2x)2﹣15(1+x)2=10,解得x1=60%,x2=﹣1(舍去).2x=120%.答:甲、乙两店这两个月的月平均增长率分别是120%、60%.【总结升华】此题考查了一元二次方程的应用,为运用方程解决实际问题的应用题型.举一反三:【变式】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程。
华东师大版数学九年级上册22章一元二次方程复习课件(第一课时共30张)

及时反馈
1、下列方程是不是一元二次方程,若不是 一元二次方程,请说明理由:
(1) (x-1)2=4 (2) x2-2x=8 (3) x2=y+1
(4) x3-2x2=1 (5) ax2+bx+c=0 (6) 32x+x=1 (7) x2-3x+4=x2-7 (8) 3x2 1 2 0
华东师大版九年级上册
第22章 一元二次方程 章末复习 第一课时
学而不疑则怠,疑而不探则空
全章知识结构
一元二次方程 方程两边都是整式
的定义
只含有一个未知数
一 ax²+bx+c=0(a0) 未知数的最高次数是2
元
直接开平方法 (x a)2 b b 0
二
次 一元二次方程
方
的解法
程
因式分解法 (x a)(x b) 0
⑤(x-3)2=2(3-x) ⑥5(m+2)2=8 ⑦3y2-y-1=0
⑧2x2+4x-1=0 ⑨(x-2)2-16=0 ⑩x2-6x-9991=0
合适运用直接开平方法的
;
合适运用因式分解法的
;
合适运用公式法的
;
合适运用配方法的
.
3、将4个数a、b、c、d排成2行2列,两边各加
一条竖线记成 a
c
b ,定义 a
一元二次方程,则( C )
A、m=±2
B、m=2
C、m=-2
D、m≠ ±2
4、若 m 2x2 m 2x 2 0是关于x的一元
二次方程,则m 。
5、若方程 (m 2)xm2 2 (m 1)x 2 0 是 关于x的一元二次方程,则m的值为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专项训练(5)九年级上册全章训练及答案1.(2010.南京)=⋅a a 82_____________.2.(2009.太原)用配方法解方程x 2-2x-5=0时,原方程应该变形为______ _____________________.3.(2010.无锡)方程x 2-3x+1=0的解是____________________.4.(2010.兰州)上海世博会的某纪念品原价168元,连续两次降价a ﹪后,售价为128元,则可列方程为__________________________.5.(2010.河南)如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,则下列结论:①BC=2DE;②△ADE ∽△ABC;③,ACABAE AD =其中正确的个数为__________个.ED ABChBA ED CA'B'C'D'E'O第5题图 第6题 第7题6.(2011.浙江宁波)如图,某游乐场一山顶滑梯的高为h ,滑梯的坡角为a ,那么滑梯的长l 为____________.7.(2008.湖北荆州)如图所示,五边形ABCDE 和五边形A′B′C′D′E′是位似图形,O 为位似中心,OD=21OD′,则ABB A ''为__________.8.(2012.鹤壁)一元二次方程3x 2-kx+k=0有两个相等的实数根,则k 的值为____________.9.(2010.上海)一元二次方程x 2+6x+a =0有两个不相等的实数根,则a 的取值范围是________________.10.(2010.焦作)若21,x x 是一元二次方程0572=+-x x 的两个根,则2111x x +=___________. 11.(2011.新乡)关于x 的一元二次方程-x 2+(2k+1)x+2-k 2=0有实数根,则k 的取值范围是_________________.12.(2011.安阳)如图,在正方形ABCD 中,M 是BC 边上的动点,N 在CD上,且CN=41CD,若AB=1,设BM=x,当x=_______时,以A 、B 、M 为顶点的三角形和以N 、C 、M 为顶点的三角形相似.CADBMNC'A'ABC第12题 第13题 第14题13.(2012.江苏)如图,在正方形网格中,=∠ABC sin ___________. 14.(2010湖南益阳)如图,将以A 为顶点的等腰直角三角形ABC 沿直线BC 平移到△A′B′C′,使B′与C 重合,连结A′B ,则=∠''tan BC A ___ _____________.15.(2012.商丘)如图所示,某河堤的横断面是梯形ABCD,BC ∥AD,迎水坡AB 长13米,且,512tan =∠BAE 在河堤的高BE=_________米. 16.(2012.安阳)如图所示,在□ABCD 中,点E 为CD 的中点,连结BE,若∠ABE=∠ACB,AB=,2则AC=__________.OE DACB第15题 第16题 第17题17.(2010湖北武汉)如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子边缘A 处看到旗杆的顶端E 的影子,已知AB=2m,CD=1.5 m,BF=20m,BD=2m,则EF=___________m. 18.(2011.郑州)如图所示,△ABC 和△ABD 是相似三角形,点D 在AC 上,∠ABD=∠C,若AD=3,CD=6,则AB=__________.ABCD第18题 第20题 第21题19.(2009.安徽)已知锐角A 满足关系式,03sin 7sin 22=+-A A 则=A sin __________.20.(2008.郑州)如图所示,在△ABC 中,AD ⊥BC,CE ⊥AB,且BE=2AE, AD=33,∠tan BCE=,33则CE=___________. 21.(2008.山东)如图所示,在△ABC 中,∠ACB=90°,CD ⊥AB,若AC=32,AB=,23则∠tan BCD=____________.22.(2010.安徽模拟)如图,∠A=30°,∠tan B=32,23=AC ,则AB=_____________.AB C第22题 第23题 第24题23.(2010.山东日照)如图,在等腰直角△ABC 中,∠C=90°,AC=6,D 是AC 上一点,若∠tan DBA=,51则AD 的长为___________.24.(2011.漯河)如图,∠1=∠2,添加一个条件:__________,使△ADE ∽ △ACB.25.(2007.新乡)如图所示,△ABC 中,∠C=90°,∠B=30°,AD 是∠BAC 的平分线.已知AB=,34那么AD=_____________.第25题 第26题 第27题26.(2007.安阳)如图所示,在矩形ABCD 中, CE ⊥BD,BE=2,DE=8,设 ∠ACE=a ,则=a tan __________.27.(2008.南阳)如图所示,为了测量某建筑物AB 的高度,在平地上C 处测得建筑物顶端A 的仰角为30°,沿CB 方向前进12m 到达D 处,在D 处测得建筑物顶端A 的仰角为45°,则建筑物AB 的高度为______________米.28.(2009.郑州)如图,△ABC 中,∠B=30°,点P 是AB 上一点,AP=2BP, PQ ⊥BC,连结AQ,则∠cos AQC=____________.QABCP FEOCADBC'A'CAB第28题 第29题 第30题29.(2008福建厦门)如图,正方形ABCD 的对角线交于点O,E 是BC 的中点,DE 交AC 于F,若DE=12,则EF=__________.30.(2007.广东)如图,把△ABC 沿着AB 边平移到△A′B′C′的位置,它们重叠部分(即图中阴影部分)的面积是△ABC 面积的一半,若AB=2,则该三角形移动的距离AA′=_____________.31.(2010.杭州)一元二次方程x 2+x+41=0的根的情况是_____________ _________________.32.(2012.内蒙古)若关于x 的一元二次方程x 2-mx+5(m-5)=0的两个正实数根分别为x 1、x 2,且2x 1+x 2=7,则m 的值为____________. 33.(2009.山东)若()0≠n n 是关于x 的方程022=++n mx x 的根,则n m +=___________.34.(青岛中考).________1362=-⨯35.(2011.山西)“五一”节期间,某电器按成本价提高30﹪后标价,再打8折(标价的80﹪)销售,售价为2080元,设该电器的成本价为x 元,可列方程为________________________.36.(2012.信阳)如图,在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADE=60°,BD=4,CE=,34则△ABC 的面积为____________.EABCaE CO AD BNM FED ABC第36题 第37题 第38题37.(2006.新疆)如图所示,是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=a ,彩电后背AD 平行于前沿BC,且与BC 的距离为60cm,若AO=100cm,则墙角O 到前沿BC 的距离OE 为_________cm. 38.(2007.天津)如图所示,在梯形ABCD 中, AB ∥CD,EF 为梯形的中位线,若EF=18cm,MN=8cm,则AB 的长等于____________cm.39.(2011.甘肃)如图所示,A 、B 、C 三点在正方形网格线的交点处,若将 △ACB 绕着点A 逆时针旋转得到△A C′B′,则='tan B____________.y xlCABODCAB第39题 第40题 第41题40.(2011.平顶山)如图,直线33+-=x y 与横、纵数轴的交点分别为A 、B,△AOB 与△ACB 关于直线l 对称,则点C 的坐标为________.41.(2010.内蒙古)如图,已知等腰△ABC 中,AB=AC,顶角∠A=36°,BD为∠ABC 的平分线,下列结论中:①BC=BD=AD;②;DCAD S S BCD ABD =∆∆③BC 2=CD·AC;④若AB=2,则BC=.15-其中正确的结论是_______. 42.(2007.重庆)如图,△ABC 中,∠C=90°,∠A <∠B,以AB 边上的中线CM 为折痕将△ACM 折叠,使点A 落在点D 处,如果CD 恰好与AB 垂直,则tan A=____________.FDB CA E第42题 第43题 第44题43.(2011.新乡)如图,两建筑物间的水平距离为a 米,从A 处测得D 点的俯角为a ,测得C 点的俯角为b ,则较低建筑物CD 的高为 ( ) (A )a 米(B )a tan a 米(C )btan a米(D )()a b tan tan -a 米 44.(2011.濮阳)如图,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD,使点B 落在AD 边上的点F 处,若AB=4,BC=5,则∠tan AFE 的值为______________.45.(2011.洛阳)计算:=+-︒︒3845cos 260sin 3____________.46.(2009.海南)如图,在△ABC 中,∠A=90°,AC=6,cm AB=8,cm 把AB 边翻折,使AB 边落在BC 边上,点A 落在点E 处,折痕为BD,则∠sin DBE=_____________.D'DAC第46题 第47题47.(2009.新乡)如图,已知正方形ABCD,如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上的D′处,那么tan ∠BA D′=__________.48.已知521,521+=-=b a ,则ab b a ++=_____________.49.如图,已知梯形ABCD 中,AD ∥BC,AE=EB,EF ∥DC,EF=1.2 cm,则DC 的长为__________ cm.DFE A BCBAD OFEC第49题 第50题50.如图所示, △ABC 与△DEF 是位似图形,位似比为2︰3,已知AB=4,则DE 的长为_____________. 51.(2011.漯河)解方程: x 2+3x-1=0.52.(2012.信阳)先化简,再求值:,211212+-÷⎪⎭⎫ ⎝⎛-+a a a 其中.13+=a53.(2010.重庆)先化简,再求值:,12212122++-÷⎪⎭⎫⎝⎛+---x x x x x x xx 其中x 满足方程.012=--x x54.(2010.新乡)如图,学校准备建一个矩形花圃ABCD,已知花圃的一边靠墙(墙的最大可用长度为10m ),其余用总长为30m 的篱笆围成,且中间隔有一道篱笆(平行于AB ).如果要围成面积为63 m 2花圃,应该怎样围?CA D B55.(2011.新乡期末)某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°.若CD=10米,请求出雕塑AB的高度(结果保留根号).第55题第56题56.(2011.新乡期末)如图,在边长为1的正方形网格中有一个△ABC.在建立平面直角坐标系后,O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).(1)把△ABC沿x轴向左平移3个单位得到△A1B1C1,请你画出△A1B1C1;(2)请你以C为位似中心,在网格中画出将△ABC放大到原来2倍的△A2B2C2;(3)请你写出△A2B2C2三个顶点的坐标.57.(2011.新乡期末)已知:如图①,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连结PQ.设运动时间为t(s)(0<t<2),解决下列问题:(1)当t为何值时,PQ∥BC;(2)如图②,连结PC,并把△PQC沿QC翻折, 得到四边形PQP′C,那么是否存在某一时刻t,使得四边形PQP′C为菱形?若存在,求出此时t的值;若不存在,说明理由.图①图②2012.11.24.星期六.凌晨03点36分专项训练(5)九年级上册全章训练参考答案.51.解:132=+x x2132321323213234132349149322-=+=+±=+=⎪⎭⎫ ⎝⎛++=++x x x x x x 或∴2133,213321--=+-=x x . 52.解:211212+-÷⎪⎭⎫ ⎝⎛-+a a a ()()()()11112211122221--=-++⨯++-=-++⨯⎪⎭⎫ ⎝⎛++-+=a a a a a a a a a a a a当13+=a 时原式33311131-=-=-+-=. 53.解:12212122++-÷⎪⎭⎫⎝⎛+---x x x x x x xx ()()()()()()()()()()()()22222211211121211211211211x x x x x x x x x x x x x x x x x x x x x x x x x +=-+⨯+-=-+⨯++--=-+⨯+---+=∵012=--x x∴12+=x x 原式111=++=x x . 注意:本题在代入求值时采用的是整体思想,不必解方程.54.解:设围成的花圃的长为x m,则花圃的宽为330x-m.可列方程为: 63330=-⋅xx 整理得:0189302=+-x x 即:()()0921=--x x解得:),(211舍去不合题意=x ,92=x73930=-m 答:应使花圃的长为9 m,宽为7 m.注意:因为题目已经告知墙的最大可用长度为10 m,所以21=x ,即AB=21 m 不合题意,要舍去.要认真读题、审题,充分理解题目的意思.55.解: 作CE ⊥AB 于点E.由题意可知,△ACD 为直角三角形,且∠ADC=30° ∴5102121=⨯==CD AC 米 在Rt △ACE 中,∵∠ACE=30°.∴2521==AC AE 米523cos CEAC CE ACE ===∠ ∴235=CE 米 ∵BE=CE ∴235=BE 米 ∴2355+=+=BE AE AB 米 即雕塑AB 的高度为2355+米. 第55题图56.解:(1)略;(2)略;(3)()7,62A 、()502,B 、()1,22C . 57.解:(1)由题意可知,t BP =cm,t AQ 2=cm在Rt △ABC 中,由勾股定理得:522=+=BC AC AB cm ∴()t BP AB AP -=-=5cm ∵BC PQ // ∴4255,tt AC AQ AB AP =-= 解之得:710=t ∴当710=t s 时,BC PQ //; (2)存在,910=t s,理由如下: 过点P 作PK ⊥AC 于点K ∴BC PK //∵四边形PQP′C 为菱形 ∴()t tQC KC KQ -=-===22242cm ∴()()222+=-+=t t t AK cm()KQ AQ AK +=∵BC PK // ∴4255,+=-=t t AC AK AB AP 解之得:910=t ∴存在910=t s,使得四边形PQP′C 为菱形..第57题图部分填空题答案提示CADBMN第12题图●12.解:本题为易错题,容易忽略另外一种情况. 分为两种情况:①当△ABM ∽ △MCN 时,有4111,xx CN BM MC AB =-= 解之得:2121==x x ; ②当△ABM ∽ △NCM 时,有x xCM BM NC AB -==1411,解之得:54=x . ∴应填5421或.第14题图●14.解:作A′H ⊥CC′于点H.设=AB m ,则m BC 2=m CH H A 22'== ∴m CH BC BH 223=+= 在Rt △A′BH 中3122322tan '''===∠m mBH H A BC A . OE D ACB第16题图●16.解: ∵四边形ABCD 为平行四边形∴AB=CD=2,AB ∥CD ∴AB ∥CE∴△AOB ∽ △COE ∴2==COAOCE AB (E 为CD 的中点).∴AO=2CO,AC AO 32=∵∠ABE=∠ACB ∴∠ABO=∠ACB 又∵∠BAO=∠CAB ∴△AOB ∽ △ABC ∴2,AB AC AO AC ABAB AO =⋅= ∴()2232=⋅AC AC∴3=AC .●19.解:设m A =sin ,则有()()()()03120123120362037222=--=---=+--=+-m m m m m m m m m m解之得:3,2121==m m ∵A 为锐角 ∴1sin 0<<A ∴21sin 1==m A . 第23题图●23.解:作DE ⊥AB由题意知△ADE 为等腰直角三角形 ∴AE=DE在Rt △ABC 中,∵AC=BC=6 ∴26=AB在Rt △BDE 中,∵51tan =∠DBA ∴AE DE BE BE DE 55,51=== ∴2,266===AE AE AB 在Rt △ADE 中,由勾股定理得:()2222==AD.第27题图●27.解:设x BD x AB ==则, ∵∠C=30° ∴33tan ==BC AB C ∴3312=+x x 解之得:366+=x即建筑物AB 的高度为()366+米.第28题图●28.解:过点A 作AH ⊥BC 于点H,并设m PQ =.在Rt △BPQ 中,∵∠B=30° ∴33tan ===BQ m BQ PQ B ∴m BQ 3= ∵AP=2BP ∴AB=3BP∵AH ⊥BC, PQ ⊥BC ∴PQ ∥AH ∴APBP QH BQ AB BP AH PQ ==, ∴213,31==QH m AH m ∴m QH m AH 32,3== 在Rt △AQH 中,由勾股定理得:m QH AH AQ 2122=+=∴7722132cos ===∠mm AQ QH AQC . ●29.解:不难证明: △ADF ∽ △CEF∴DFEFAD CE = ∵E 是BC 的中点,BC=AD∴21==DF EF AD CE ∴4123131=⨯==DE EF . FEOCADB第29题图●32.解:由韦达定理知:m x x =+21,()5521-=⋅m x x∴得到方程组:⎩⎨⎧=+=+m x x x x 212172解之得:⎩⎨⎧-=-=72721m x mx∴()()()55727-=--m m m 解之得:6,221==m m由题意知:()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧>->>->-≥---05500720705202m m m m m m解之得:75<<m ∴6=m ()舍去2=m .●36.解:设4,-==x CD x AB 则 可以证明:△ABD ∽ △DCE∴3444,=-=x x CE BD DC AB 解之得:6=x即等边△ABC 的边长为6,从而可以求出其面积为39.注意:这里提出一个问题:怎样证明△ABD ∽ △DCE?EABC第36题图证明:●38.解:为帮助本题的解决,这里补充一道证明题,过程与结论很重要! 题目:如图所示,在梯形ABCD 中,E 、F 分别是AD 、BC 的中点,连结EF,分别交两条对角线AC 、BD 于M 、N 两点.求证:()CD AB MN -=21.NM FE D ABC证明:∵E 、F 分别为AD 、BC 的中点 ∴EF 是梯形ABCD 的中位线 ∴EF ∥AB ∥CD ∴NF ∥CD, MF ∥AB∴N 、M 分别为BD 、AC 的中点 ∴NF 、MF 分别为△BCD 和△ABC 的中位线 ∴AB MF CD NF 21,21==∵NF MF MN -= ∴()CD AB CD AB MN -=-=212121. 回到本题: 由题意知:362==+EF CD AB (1) 由上面的结论有:162==-MN CD AB (2) 联立(1)(2)得:16362+=AB AB=26 cm.DAB C第41题图解:根据在同一个三角形中等角对等边不能得出BC=BD=AD,即结论①正确; 分别过点A 、C 作BD 的垂线AE 、CF,如下图所示.∴AE BD S ABD⋅=∆21CF BD S BCD ⋅=∆21∴CFAES S BCD ABD =∆∆ 容易证明:△ADE ∽ △CDF∴CD ADCF AE = ∴CDAD S S BCD ABD =∆∆ ∴结论②正确;∵△BCD ∽ △ABC∴BCCDAB BC = ∴AB CD BC ⋅=2 ∵AB=AC ∴AC CD BC ⋅=2∴结论③正确;设x AD AC CD x BC -=-==2,则 由结论③,∵AC CD BC ⋅=2∴()222⨯-=x x整理得:0422=-+x x解之得:15-=x (15--=x 舍去)∴15-=BC ∴结论④正确.综上所述,正确的结论是:①②③④.F DBCA E第44题图●44.解: ∵四边形ABCD 是矩形 ∴AB=CD=4,BC=AD=5 设x AE =,则x FE BE -==4 在Rt △DCF 中,∵CF=BC=5,CD=4 ∴DF=3,AF=AD -DF=2 在Rt △AEF 中,由勾股定理得:()22222242x x EF AF AE -=+=+解之得:23=x ,即23=AE ∴43223tan ===∠AF AE AFE ..第46题图●46.解: 在Rt △ABC 中,∵AC=6 cm, AB=8 cm ∴BC=10 cm∵AB=EB=8 cm(根据翻折) ∴CE=BC -EB=2 cm设x CD x AD x DE -===6,,则 在Rt △ABC 中,由勾股定理得:()22222262x x CD DE CE -=+=+解之得:38=x ,即38=DE cm 在Rt △BDE 中,由勾股定理得:310883822=+⎪⎭⎫⎝⎛=BD cm∴1010310838sin ===∠BD DE DBE . DFE A BC第49题图●49.解:作AG ∥CD,交BC 于点G .∴四边形AGCD 为平行四边形 ∴AG=CD ∵EF ∥CD ∴EF ∥AG ∵AE=BE ∴21==AB BE AG EF ∴AG=2EF=2.4 cm∴CD=2.4 cm.注意:本题中,EF 是△ABG 的中位线.2015. 9. 29 星期二 22 : 06。
