圆与圆的位置关系测试题
与圆有关的位置关系同步训练及测试题

1 与圆有关的位置关系同步训练点与圆的位置关系同步训练 一.选择题1.若⊙O 的半径为4cm ,点A 到圆心O 的距离为3cm ,那么点A 与⊙O 的位置关系是( ) A .点A 在圆内 B .点A 在圆上 c .点A 在圆外 D .不能确定2. 有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.正确的有A .4个B .3个C . 2个D . 1个 3. 下列说法正确的是( )A. 经过三点一定可以作一个圆B. 任一个圆一定有内接三角形并且只有一个内接三角形C. 任意一个三角形一定有一个外接圆并且只有一个外接圆D. 三角形的外心到三角形三边的点距离相等 二. 填空题1.经过一点P 可以作_______个圆;经过两点P 、Q 可以作________•个圆,•圆心在_________上;经过不在同一直线上的三个点可以作________个圆,•圆心是________的交点.2.边长为a 的等边三角形外接圆半径为_______,圆心到边的距离为________.3.直角三角形的外心是______的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________.第一题图 第二题图 三.解答题1.在Rt △ABC 中,∠C=90°,BC=3m ,AC=4m ,以B 为圆心,以BC 为半径作⊙B ,D 、E 是AB 、AC 中点,D 、E 分别与⊙O 有怎样的位置关系?2.△ABC 中,AB=1,AC 、BC 是关于x 的一元二次方程(m+5)x 2-(2m-5)x+12=0两个根,外接圆O 的面积为4,求m 的值.直线与圆的位置关系同步训练 一.选择题线l 的距离为7cm ,则直线l 与⊙O 的位置关系是 1.⊙O 的直径为12cm ,圆心O 到直( )A.相交 B.相切 C.相离 D.不能确定22.⊙O 的半径为3cm ,点P 是直线l 上一点,OP 长为5cm ,则直线l 与⊙O 的位置关系为( )A. 相交B. 相切C. 相离D. 相交、相切、相离都有可能3.OA 平分∠BOC ,P 是OA 上任一点,C 不与点O 重合,且以P 为圆心的圆与OC 相离,那么圆P 与OB 的位置关系是( )(A )相离 (B )相切 (C )相交 (D )不确定二、填空题1.如图,AB 为⊙O 直径,BD 切⊙O 于B 点,•若AB=10,AC=8,则DC 长为___2.如图,P 为⊙O 外一点,PA 、PB 为⊙O 的切线,A 、B 为切点,弦AB 与PO 交于C ,⊙O 半径为1,PO=2,则AC=__∠AOB=___3.设I 是△ABC 的内心,O 是△ABC 的外心,∠A=80°,则∠BIC=•__ •∠BOC=___三. 解答题1.Rt △ABC 的斜边AB=8cm ,AC=4cm .(1)以点C 为圆心作圆,当半径为多长时,直线AB 与⊙C 相切?为什么?(2)以点C 为圆心,分别以2cm 和4cm 为半径作两个圆,这两个圆与直线AB 分别有怎样的位置关系?2、AB 是⊙O 的直径,D 在AB 的延长线上,BD=OB ,C 在圆上,∠CAB=30°.求证:DC 是⊙O 的切线. 3.⊙O 是△ABC 的内切圆,切点为D 、E 、F ,如果AE=1,CD=2,BF=3,且△ABC 的面积为6.求内切圆的半径r .圆与圆的位置关系同步训练3选择题1 两圆半径是R 和r(R >r),圆心距是d,且R 2+d 2 - r 2=2dR,则两圆的位置关系为 ( ) A.相交 B.内切 C.外切 D.内切或外切2 在平面直角坐标系中,两圆的圆心坐标分别为(0,1)和(1,0),半径分别是1和2,这两个圆的位置关系是 ( ) A.外离 B.相切 C.相交 D.内含3. 两个同心圆的半径分别为3cm 和5cm ,弦AB 与小圆相切于点C ,AB 的长为( ) A .4cm B .5cm C .6cm D .8cm 4.△ABC 的三边分别切⊙O 于D ,E ,F ,若∠A=50°,则∠DEF=( ) A .65° B .50° C .130° D .80°一.填空题1.、已知⊙A 、⊙B 相切,圆心距为10 cm ,⊙A 的半径为4 cm ,则⊙B 的半径为 2.两圆相交,半径分别为3 cm 和4 cm ,圆心距为5 cm , 两圆的公共弦长为3.两圆的圆心距为3,两圆的半径分别是方程x 2-4x+3=0的两根,•这两个圆 的位置关系是4.⊙O 的半径为3cm ,点M 是⊙O 外一点,OM=4cm ,则以M 为圆心且与⊙O•相切的圆的半径一定是 二.解答题1.⊙O 1和⊙O 2外切于P 点,过P 的直线交⊙O 1于A,交⊙O 2于B ,求证:O 1A ∥O 2B2.⊙O 1和⊙O 2外切于A ,AB 是⊙O 1的直径,BD 切⊙O 2于D ,交⊙O 1于C , 求证:AB ·CD =AC ·BD43.两个同样大小的肥皂泡黏在一起,其剖面如图1所示(点O ,O ′是圆心),分隔两个肥皂泡的肥皂膜PQ 成一条直线,TP 、NP 分别为两圆的切线,求∠TPN 的大小.点与圆的位置关系同步训练一.选择题1.A2.B3.C 二.填空题. 1.无数,无数,线段PQ 的垂直平分线,一个,三边中垂线 2. 接圆半径a 33,圆心到边的距离为a 63 3,斜边中点, 内部, 外部三.解答题1 解: 点D 在⊙B 内 E 在⊙B 外2.m=20.直线与圆的位置关系同步训练 选择题1..C.2.D.3. A . 二、填空题 1.412 2. 2120° 3.130° 160° 三.解答题1. (1)当半径为时,AB 与⊙C 相切.(2) 当r=2时,d>r ,⊙C 与直线AB 相离; 当r=4时,d<r ,⊙C 与直线AB 相交.2.证明:连结OC 、BC .说明△BDC 为等腰三角形,∠OCD=90°, 最后得到DC 是⊙O 的切线.3.所求的内切圆的半径为1.圆与圆的位置关系同步训练 一.选择题5. 1. D. 2. C. 3. D 4. A 二.填空题1. 6 或142. 4.8cm3. 相交4. R=1或7三.解答题1.提示:连接O 1 O 2,则O 1 O 2必过切点P2. 连结O 2D ,可知O 2D ∥AC 则所以,只需证即可 3.∠TPN=360°-2×90°-60°=120°直线与圆、圆与圆的位置关系单元测试一、选择题(每题5分,共30分)1. ⊙O 的直径是3,直线l 与⊙0相交,圆心O 到直线l 的距离是d ,则d 应满足 ( ) A. d>3 B. 1.5<d<3 C. O ≤d<1.5 D.d<O2. 在平面直角坐标系中,以点(2 , l )为圆心、1为半径的圆必与( )A. x 轴相交B.y 轴相交C. x 轴相切D. y 轴相切3. 两圆的圆心距是3,两圆的半径是方程x 2-3x+2=0的两个根,这两个圆的位置关系是( ) A .外离 B .外切 C .相交 D .内切4.⊙O 1与⊙O 2内切,它们的半径分别为2和3,这两圆的圆心距d 满足( ) (A )d=5 (B )d=1 (C )1<d <5 (D )d >5 5.如图,PA 为⊙O 的切线,A 为切点,PO 交⊙O 于点B ,PA =3,OA =4,则cos ∠APO 的值为( )(A )34 (B )35 (C )45 (D ) 436.如图,AB 是⊙O 的直径,P 是AB 延长线上的一点, PC 切⊙O 于点C ,PC=3、PB :AB=1:3,则⊙O 的半 径等于( )A . 25 B. 3 C. 49 D. 296二、填空题(每小题5分,共40分)1、已知直线AB 是⊙O 的切线,A 为切点,点D 在⊙O 上,且∠OBA=40°,则∠ADC=2.如图,在△ABC 中,∠A=90°,AB =AC =2cm ,⊙A 与BC 相切于点D ,则⊙A 的半径为 cm . 3.两圆内切,其中一个圆的半径为5,两圆的圆心 距为2,则另一个圆的半径是 4.如图,已知∠AOB =30°,M 为OB 边上一点,以M 为圆心、2 cm 为半径作⊙M .若点M 在OB 边上运 动,则当OM = cm 时,⊙M 与OA 相切.5.P 为⊙O 外一点,PA 、PB 分别切⊙O 于点A 、B ,∠APB=50°,点C 为⊙O 上一点(不与A 、B )重合,则∠ACB 的度数为6、△ABC 是半径为2 cm 的圆内接三角形,若BC=23 cm ,则∠A 的度数为 7.已知正三角形的内切圆半径为 33 cm ,则它的边长是( )cm8.已知半径均为1厘米的两圆外切,半径为2厘米,且和这两圆都相切的 圆共有( )个三、解答题(共50分)1(本题8分)一个主题雕塑是由置放于地面l 上两个半径均为2米的半圆与半径为4米的⊙A 构成.点B 、C 分别是两个半圆的圆心,⊙A 分别与两个半圆相切于点E 、F ,BC 长为8米.求EF 的长2.(14分AB 是⊙O 的直径,BC 是⊙O 的切线, D 是⊙O 上一点,且AD ∥OC (1)求证:△ADB ∽△OBC(2)若AB=2,AD 的长(保留根号)3.(本题14分)正方形网格中,每个小正方形的边长为1个单位,以O 为原点建立平面直角坐标系。
六年级数学第一单元圆测试题

六年级数学第一单元圆测试题一、填空题(每题2分,共10分)1. 圆中心的一点叫做(圆心),一般用字母(O)表示。
- 解析:这是圆的基本概念,圆心是圆的中心位置的点,是圆的重要组成部分,用字母O表示是数学中的规定。
2. 在同一个圆里,所有的半径都(相等),所有的直径都(相等)。
- 解析:根据圆的定义和性质,圆是到定点(圆心)的距离等于定长(半径)的点的集合,所以同一个圆中半径长度都一样;直径是半径的两倍,所以直径也都相等。
3. 一个圆的半径是3厘米,直径是(6)厘米。
- 解析:因为在圆中直径d = 2r(r为半径),已知半径r = 3厘米,所以直径d=2×3 = 6厘米。
4. 圆的周长总是直径的(π倍),这个倍数是一个(固定不变)的数,叫做(圆周率),用字母(π)表示。
- 解析:通过大量的测量和数学研究发现,圆的周长C与直径d之间存在着C = πd的关系,π是一个无限不循环小数,是一个固定不变的值,它是圆周率的表示符号。
5. 把一个圆平均分成若干份,可以拼成一个近似的(长方形),这个长方形的长相当于圆的(周长的一半),宽相当于圆的(半径)。
- 解析:这是圆面积公式推导过程中的重要内容。
将圆平均分成若干个小扇形,然后拼成近似长方形,从图形的变化可以看出长方形的长近似于圆周长的一半(C÷2 = πr),宽近似于圆的半径r。
二、判断题(每题2分,共10分)1. 直径都是半径的2倍。
(×)- 解析:必须是在同一个圆或等圆中直径才是半径的2倍,如果没有这个前提条件,这句话是错误的。
2. 圆的半径扩大3倍,直径也扩大3倍。
(√)- 解析:因为d = 2r,当r扩大3倍变为3r时,直径d = 2×3r = 6r,6r是原来直径2r的3倍,所以这句话正确。
3. 圆的周长是直径的3.14倍。
(×)- 解析:圆的周长是直径的π倍,π是一个无限不循环小数,3.14只是它的近似值,所以不能说圆的周长就是直径的3.14倍。
初中九年级数学圆测试题及答案

初中九年级数学圆测试题及答案与圆有关的位置关系圆与点的位置关系有三种:点在圆外、点在圆上、点在圆内。
对应的点到圆心的距离d和半径r之间的数量关系分别为:d。
r、d = r、d < r。
直线与圆的位置关系有三种:相交、相切、相离。
对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为:d。
r。
圆与圆的位置关系有五种:内含、相内切、相交、相外切、外离。
两圆的圆心距d和两圆的半径R、r(R≥r)之间的数量关系分别为:d。
R+r。
圆的切线垂直于过切点的半径;经过直径的一端,并且垂直于这条直径的直线是圆的切线。
从圆外一点可以向圆引两条切线,切线长相等,这点与圆心之间的连线平分这两条切线的夹角。
与圆有关的计算圆的周长为2πr,1°的圆心角所对的弧长为πr/180,n°的圆心角所对的弧长为nπr/180,弧长公式为l=nπr。
圆的面积为πr^2,1°的圆心角所在的扇形面积为πr^2/360,n°的圆心角所在的扇形面积为S=nπr^2/360(n为圆心角的度数,R为圆的半径)。
圆锥的侧面积公式:S=πrl(其中r为底面的半径,l为母线的长)。
圆锥的侧面积与底面积之和称为圆锥的全面积。
圆柱的侧面积公式:S=2πrl(其中r为底面圆的半径,l为圆柱的高)。
4.已知∠BOC为130°,O是△XXX的内心,求∠A的度数。
解析:由内心的性质可知,∠BOC=2∠A,所以∠A=65°,选项B。
5.已知∠A=100°,∠C=30°,求∠DFE的度数。
解析:由内切圆的性质可知,∠DFE=90°-1/2(∠A+∠C)=55°,选项A。
6.将羊拴在使草地上活动区域面积最大的位置,即正方形的对角线中点处,选项B。
7.两圆心距离等于半径之差的情况为内含,等于半径之和的情况为外切,大于半径之和小于半径之差的情况为相交,两圆心距离为3,所以为相交,选项C。
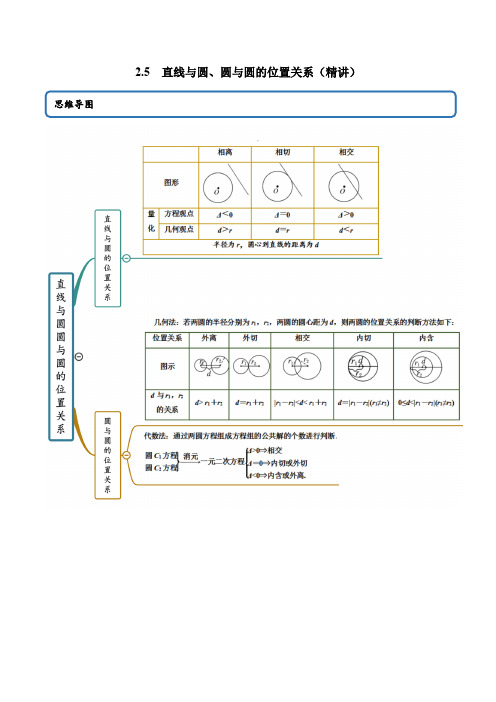
2-5 直线与圆、圆与圆的位置关系(精讲)(原卷版)
2.5 直线与圆、圆与圆的位置关系(精讲)考点一直线与圆的位置关系【例1】(1)(2021·遵义师范学院附属实验学校)圆22(3)(3)8x y-+-=与直线3460x y++=的位置关系是()A.相交B.相切C.相离D.无法确定(2).(2021·全国高二专题练习)直线():120l kx y k k R-++=∈与圆22:5C x y+=的公共点个数为()A.0个B.1个C.2个D.1个或2个(3)(2021·黑龙江哈尔滨市)若过点()4,3A的直线l与曲线22231x y有公共点,则直线l的斜率的取值范围为()A.⎡⎣B.(C.33⎡-⎢⎣⎦D.,33⎛-⎝⎭(4)(2021·浙江高二期末)已知曲线y=与直线10kx y k-+-=有两个不同的交点,则实数k的取值范围是()A.13,24⎡⎫⎪⎢⎣⎭B.30,4⎛⎫⎪⎝⎭C.12,23⎡⎫⎪⎢⎣⎭D.12,43⎡⎫⎪⎢⎣⎭【一隅三反】1.(2021·江苏南京市·高二期末)直线10x +=与圆()2211x y -+=的位置关系是( ) A .直线过圆心B .相切C .相离D .相交2.(2021·四川成都市)若圆22()1(0)x a y a -+=>与直线3y x =只有一个公共点,则 a 的值为( )A .1BC .2D .3.(2021·浙江高二期末)直线:1l y ax a =-+与圆224x y +=的位置关系是( )A .相交B .相切C .相离D .与a 的大小有关4.(2021·全国高二专题练习)若直线0x y b +-=0y +=有公共点,则b 的取值范围是( )A .[-B .[C .[1,1]-D .[5.(2021·河北保定市·高二期末)(多选)已知圆22:(1)(1)169C x y -+-=,直线:450,l kx y k k R --+=∈.则下列选项正确的是( )A .直线l 恒过定点B .直线l 与圆C 的位置可能相交、相切和相离 C .直线l 被圆C 截得的最短弦长为12D .直线l 被圆C 截得的最短弦长对应的k 值为34- 考点二 直线与圆的弦长【例2】(1)(2021·四川成都市)直线1y x =-被圆22220x y y ++-=截得的弦长为( )A .1B .2C D .(2).(2021·浙江高二期末)已知直线:0l kx y k -+-=被圆224x y +=截得的弦长为点(),m n 是直线l 上的任意一点,则22m n +的最小值为( ) A .1 B .2 C .3 D .4【一隅三反】1.(2021·安徽省泗县第一中学)直线40x y -+=被圆22(2)(2)2x y ++-=截得的弦长为( )AB .C .D .2.(2021·浙江高二期末)已知过点()1,3P 的直线l 被圆()2224x y -+=截得的弦长为l 的方程是( ) A .43130x y +-= B .34150x y +-=C .34150x y +-=或1x =D .43130x y +-=或1x =3.(2021·贵溪市实验中学高二期末)直线y kx =被圆222x y +=截得的弦长为( )A .B .2C D .与k 的取值有关4.(2021·天水市第一中学高二期中)已知直线0x ay a +-=和圆220x y x +-=的交点为A ,B ,且1AB =,则实数a 的值为( ) A .2B .1C .12D .1-5.(2021·全国高二课时练习)若P (2,-1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程是( ) A .x -y -3=0 B .2x +y -3=0 C .x +y -1=0D .2x -y -5=06.(2021·辽宁辽阳市·高二期末)已知圆22:4850C x y x y +-+-=,直线:20l mx y m --=. (1)证明:直线l 与圆C 相交.(2)设l 与圆C 交于,M N 两点,若MN =,求直线l 的倾斜角及其方程.考点三 圆上的点到直线距离【例3】(1)(2021·福建三明市·高二期末)圆()2222x y -+=上动点到直线20x y ++=的距离的最小值为( )A B .C .D .(2)(2021·四川巴中市·(文))圆22(1)(1)4x y ++-=上到直线:0l x y ++=的距离为1的点共有( ) A .1个 B .2个 C .3个 D .4个【一隅三反】1.(2021·六安市裕安区新安中学)已知半径为2的圆经过点(1,0),其圆心到直线34120x y -+=的距离的最小值为( ) A .0B .1C .2D .32.(2021·全国高二课时练习)已知点M 是直线3420x y +-=上的动点,点N 为圆22(1)(1)1x y +++=上的动点,则||MN 的最小值为 A .45B .1C .95D .1353.(2021·全国高二专题练习)在圆()2224x y -+=上有且仅有两个点到直线340x y a ++=的距离为1,则a 的取值范围为__________.考点四 圆与圆的位置关系【例4】(1)(2021·浙江高二期末)圆221:(1)1C x y -+=与圆222:(4)(4)17C x y -+-=的位置关系为( ) A .内切B .相切C .相交D .外离(2)(2021·北京高二期末)已知圆1O 的方程为22()()4x a y b -+-=,圆2O 的方程为22(1)1x y b +-+=,其中,a b ∈R .那么这两个圆的位置关系不可能为( ) A .外离 B .外切 C .内含 D .内切【一隅三反】1.(2021·全国高二专题练习)圆2220x y x +-=与圆22(1)(2)9x y -++=的位置关系为( ) A .内切B .相交C .外切D .相离2.(2021·江西上高二中高二其他模拟(文))已知圆()221:210C x y x my m R +-++=∈关于直线210x y ++=对称,圆2C 的标准方程是()()222316x y ++-=,则圆1C 与圆2C 的位置关系是( )A .相离B .相切C .相交D .内含3.(2021·全国高二(文))已知圆1C 的标准方程是()()224425x y -+-=,圆2C :22430x y x my +-++=关于直线10x ++=对称,则圆1C 与圆2C 的位置关系为( )A .相离B .相切C .相交D .内含4.(2021·四川凉山彝族自治州·高二期末(文))已知圆221:1C x y +=和圆()()2222:20C x y r r +-=>,若圆1C 和2C 有公共点,则r 的取值范围是( ) A .(]0,1B .(]0,3C .[]1,3D .[)1,+∞5.(2021·山东聊城市·高二期末)已知圆()()()221:80C x a y a a -+-=>与圆222:220C x y x y +--=没有公共点,则实数a 的取值范围为( ) A .()0,2 B .()4,+∞C .()()0,24,+∞ D .()()()0,10,24,⋃⋃+∞ 考点五 圆与圆相交弦【例5】(1)(2021·湖南湘潭市)已知圆221:40C x y +-=与圆222:44120C x y x y +-+-=相交于,A B两点,则两圆的公共弦AB =A .B .CD .2(2)(2021·天津市南仓中学高二期末)已知圆221:4C x y +=和圆()222:2600C x y ay a ++-=>的公共弦长为2,则实数a 的值为( )A .3BC .2D【一隅三反】1.(2021·辽宁高三其他模拟)圆O :229x y +=与圆1O :()()222316x y -+-=交于A 、B 两点,则AB =( )A .6B .5C .13D .132.(2021·山东济南市·高二期末)(多选)已知圆221:1C x y +=和圆222:40C x y x +-=的公共点为A ,B ,则( )A .12||2C C =B .直线AB 的方程是14x =C .12AC AC ⊥D .||2AB =3.(2021·全国高二课时练习)(多选)圆221:20x y x O +-=和圆222:240O x y x y ++-=的交点为A ,B ,则有( )A .公共弦AB 所在直线方程为0x y -= B .线段AB 中垂线方程为10x y +-=C .公共弦AB 的长为2D .P 为圆1O 上一动点,则P 到直线AB 1+考点六 切线及切线长【例6-1】(2021·浙江高二单元测试)由直线1y x =+上的点向圆()2231x y -+=作切线,则切线长的最小值为( )A .1BC .D .3【例6-2】(1)(2021·全国)经过点M 的圆2210x y +=的切线方程是( )A .100x -=B 2100y -+=C .100x -+=D .2100x +-=(2)(2021·重庆字水中学高二期末)(多选)过点(2,0)作圆222690x y x y +--+=的切线l ,则直线l 的方程为( )A .3460x y +-=B .4380x y +-=C .20x -=D .20x +=(3)(2021·全国)过点(2,2)-作圆224x y +=的切线,若切点为A 、B ,则直线AB 的方程是( ) A .20x y ++=B .20x y -+=C .20x y +-=D .20x y --=【例6-3】(2021·四川眉山市·高二期末(文))圆221:1C x y +=与圆222:870C x y y +-+=公切线的条数为( )A .0B .1C .2D .3【例6-4】(2021·全国高二课时练习)已知P (x ,y )是直线kx +y +3=0(k >0)上一动点,PA ,PB 是圆C :2x +2y -2y =0的两条切线,.A 、B 是切点,若四边形PACB k 的值为( )A BC .D .【一隅三反】1.(2021·全国高二课时练习)P 是直线x +y -2=0上的一动点,过点P 向圆22:(2)(8)4C x y ++-=引切线,则切线长的最小值为( )A .B .C .2D .22.(2021·西安市铁一中学高二期末(理))由直线2y x =+上的点向圆22(4)(2)1x y -++=引切线,则切线长的最小值为A B C .D 3.(2021·安徽马鞍山市·马鞍山二中高二期末(文))若从坐标原点O 向圆22:12270C x y x +-+=作两条切线,切点分别为A ,B ,则线段AB 的长为( )A .32B .3C .2D .4.(2021·重庆市南坪中学校高二月考)过坐标原点O 作圆(x ﹣2)2+(y ﹣3)2=4的两条切线,切点为A ,B .直线AB 被圆截得弦AB 的长度为( )A B C D5.(2021·浙江高二期末)过点()2,1作圆224x y +=的切线,切线的方程为( )A .34100x y +-=B .3420x y --=C .2x =或3420x y --=D .2x =或34100x y +-=6.(2021·全国高二课时练习)经过点()2,1M -作圆225x y +=的切线,则切线的方程为A .250x y --=B 50y ++=C 5y +=D .250x y ++=7.(2021·安徽池州市·高二期末(理))若圆221:2440C x y x y +---=,圆222:61020C x y x y +---=,则1C ,2C 的公切线条数为( )A .1B .2C .3D .48.(2021·六安市裕安区新安中学高二开学考试(理))若圆22(1)(3)4x y -+-=与圆22(2)(1)5x y a +++=+有且仅有三条公切线,则a =( )A .-4B .-1C .4D .119.(2021·四川眉山市·仁寿一中高二开学考试(文))已知点(,)P x y 是直线240x y -+=上一动点,直线,PA PB 是圆22:20C x y y ++=的两条切线,,A B 为切点,C 为圆心,则四边形PACB 面积的最小值是( )A .2BC .D .4 考点七 实际生活运用【例7】(2021·上海高二专题练习)如图,某海面上有O 、A 、B 三个小岛(面积大小忽略不计),A 岛在O 岛的北偏东45︒方向距O 岛B 岛在O 岛的正东方向距O 岛20千米处.以O 为坐标原点,O 的正东方向为x 轴的正方向,1千米为单位长度,建立平面直角坐标系.圆C 经过O 、A 、B 三点.(1)求圆C 的方程;(2)若圆C 区域内有未知暗礁,现有一船D 在O 岛的南偏西30°方向距O 岛40千米处,正沿着北偏东45︒行驶,若不改变方向,试问该船有没有触礁的危险?【一隅三反】1.(2021·重庆巴蜀中学高一期中)如图,某个圆拱桥的水面跨度是20米,拱顶离水面4米;当水面下降1米后,桥在水面的跨度为()A.B.C.D.2.(2021·上海高二专题练习)有一种大型商品,A、B两地都有出售,且价格相同,某地居民从两地之一购得商品后运回的费用是:每单位距离,A地的运费是B地运费的2倍﹐已知A、B两地相距6千米,顾客购物的唯一标准是总费用较低.建立适当的平面直角坐标系(1)求A、B两地的售货区域的分界线的方程﹔(2)画出分界线的方程表示的曲线的示意图,并指出在方程的曲线上、曲线内、曲线外的居民如何选择购货地.考点八综合运用【例8】(2021·全国高二课时练习)已知圆C的圆心坐标为C(3,0),且该圆经过点A(0,4).(1)求圆C的标准方程;(2)若点B也在圆C上,且弦AB长为8,求直线AB的方程;(3)直线l交圆C于M,N两点,若直线AM,AN的斜率之积为2,求证:直线l过一个定点,并求出该定点坐标.(4)直线l交圆C于M,N两点,若直线AM,AN的斜率之和为0,求证:直线l的斜率是定值,并求出该定值.【一隅三反】1.(2021·全国高二课时练习)已知圆()()22:1225C x y -+-=和直线()():211740l m x m y m +++--=.(1)证明:不论 m 为何实数,直线l 都与圆 C 相交于两点;(2)求直线被圆 C 截得的最短弦长并求此时直线l 的方程;(3)已知点(,)P x y 在圆C 上,求22xy +的最大值.2(2021·浙江高二单元测试)已知圆22(3)(4)16x y -+-=,直线1:0l kx y k --=,且直线1l 与圆交于不同的两点,P Q ,定点A 的坐标为(1,0).(1)求实数k 的取值范围;(2)若,P Q 两点的中点为M ,直线1l 与直线2:240l x y ++=的交点为N ,求证:||||AM AN ⋅为定值.3.(2021·内蒙古包头市·高二期末(文))已知圆O :228x y +=,()1,2M -是圆O 内一点,()4,0P 是圆O 外一点.(1)AB 是圆O 中过点M 最长的弦,CD 是圆O 中过点M 最短的弦,求四边形ACBD 的面积;(2)过点P 作直线l 交圆于E 、F 两点,求OEF 面积的最大值,并求此时直线l 的方程.。
圆的测试题

1、两个同心圆的半径分别为2cm 和4cm ,大圆的弦AB 与小圆相切,那么AB=________2、已知⊙O 与⊙Q 的半径分别为3cm 和7cm ,两圆的圆心距O 1 O 2 =10cm ,则两圆的位置关系是________3、下列命题正确的是( )A .相等的圆心角所对的弦相等B .等弦所对的弧相等C .等弧所对的弦相等D .垂直于弦的直线平分弦4.若∠OAB=30°,OA=10cm ,则以O 为圆心,6cm 为半径的圆与射线AB 的位置关系是( )A .相交B .相切C .相离D .不能确定7.Rt △ABC 中,∠C=90°,AB=10,AC=6,以C 为圆心作⊙C 和AB 相切,则⊙C 的半径长为_______________8.⊙O 内最长弦长为m ,直线l 与⊙O 相离,设点O 到l 的距离为d ,则d 与m 的关系是( )A .d =m B .d >m C .d >2m D .d <2m 9.以三角形的一边长为直径的圆切三角形的另一边,则该三角形为( ) A .锐角三角形 B .直角三角形C .钝角三角形D .等边三角形 10.菱形对角线的交点为O ,以O 为圆心,以O 到菱形一边的距离为半径的圆与其他几边的关系为( )A .相交 B .相切 C .相离 D .不能确定11.⊙O 的半径为6,⊙O 的一条弦AB 为63,以3为半径的同心圆与直线AB 的位置关系是( )A .相离 B .相交 C .相切 D .不能确定12.下列四边形中一定有内切圆的是( )A .直角梯形B 等腰梯形C .矩形D .菱形13.已知△ABC 的内切圆O 与各边相切于D 、E 、F ,那么点O 是△DEF 的( )A .三条中线交点B .三条高的交点C .三条角平分线交点D .三条边的垂直平分线的交点14.给出下列命题:①任一个三角形一定有一个外接圆,并且只有一个外接圆;②任一个圆一定有一个内接三角形,并且只有一个内接三角形;③任一个三角形一定有一个内切圆,并且只有一个内切圆;④任一个圆一定有一个外切三角形,并且只有一个外切三角形.其中真命题共有( )A .1个B .2个C .3个D 4个15下列命题正确的是( )A .相等的圆心角所对的弦相等B .等弦所对的弧相等C .等弧所对的弦相等D .垂直于弦的直线平分弦16下列图形中,既有内切圆又有外接圆的是( )A .菱形B .矩形C .正方形D .等腰梯形17.如果一个正多边形的每个外角都等于36°,那么这个正多边形的中心角等于( )A .36°B .18°C .72°D .54°18.下列命题正确的是( ) A .正三角形的内切圆的半径与外接圆半径之比为2:1;B .正六边形的边长等于其外接圆的半径;C .圆的外切正多边形的边长等于其边心距的2倍;D .各边相等的圆的外切四边形是正方形。
人教版数学九年级上学期《圆》单元测试题(附答案)

10.如图,A B是半圆的直径,点D是弧A C的中点,∠A B C=500,则∠D A B等于( )
A. 55°B. 60°C. 65°D. 70°
二、填空题
11.如图,A C与B D交于P,A D、B C延长交于点E,∠AEC=37°,∠C AE=31°,则∠APB的度数为.
(1)求证:DE∥B C;
(2)若AF=CE,求线段B C的长度.
27.如图,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4.
(1)求点C的坐标;
(2)连接MG、B C,求证:MG∥B C.
[答案]8
12.已知点O到直线l的距离为6,以O为圆心,r为半径作⊙O,若⊙O上只有3个点到直线l的距离为2,则r的值为_____.
13.用一张半径为9Cm、圆心角为120°的扇形纸片,做成一个圆锥形冰淇淋的侧面(不计接缝),那么这个圆锥形冰淇淋的底面半径是_________Cm.
14.如图,⊙C与∠AOB 两边分别相切,其中OA边与⊙C相切于点P.若∠AOB=90°,OP=4,则OC的长为____.
A. ∠APB=30°B. ∠APB>30°C. ∠APB<30°D. 不能确定
[答案]C
[解析]
[分析]
连接B C,已知∠AOB=60°,∠AOB与∠A C B为优弧A B所对的圆心角和圆周角,利用圆周角定理求得∠A C B,再利用三角形外角的性质得出答案即可.
[详解]如图,
∵∠AOB与∠A C B为优弧A B所对的圆心角和圆周角,
人教版数学九年级上册《圆》测试题及答案

圆基础知识+两套题附参考答案与圆有关的位置关系1.点与圆的位置关系共有三种:① 点在圆外 ,② 点在圆上 ,③ 点在圆内 ;对应的点到圆心的距离d 和半径r 之间的数量关系分别为: ①d > r ,②d = r ,③d < r.2.直线与圆的位置关系共有三种:① 相交 ,② 相切 ,③ 相离 ; 对应的圆心到直线的距离d 和圆的半径r 之间的数量关系分别为: ①d < r ,②d = r ,③d > r.3.圆与圆的位置关系共有五种:① 内含 ,② 相内切 ,③ 相交 ,④ 相外切 ,⑤ 外离 ; 两圆的圆心距d 和两圆的半径R 、r (R ≥r )之间的数量关系分别为:①d < R-r ,②d = R-r ,③ R-r < d < R+ r ,④d = R+r ,⑤d > R+r. 4.圆的切线 垂直于 过切点的半径;经过 直径 的一端,并且 垂直于 这条 直径 的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长 相等,这点与圆心之间的连线 平分 这两条切线的夹角。
与圆有关的计算1.圆的周长为 2πr ,1°的圆心角所对的弧长为 180rπ ,n °的圆心角所对的弧长为 180rn π ,弧长公式为180r n lπ=n 为圆心角的度数上为圆半径) .2. 圆的面积为 πr 2,1°的圆心角所在的扇形面积为 3602r π ,n °的圆心角所在的扇形面积为S= 360n 2R π⨯ = rl 21(n 为圆心角的度数,R 为圆的半径). 3.圆柱的侧面积公式:S= 2 πr l (其中r 为 底面圆 的半径 ,l 为 圆柱 的高.)4. 圆锥的侧面积公式:S=πr l (其中r 为 底面 的半径 ,l 为 母线 的长.) 圆锥的侧面积与底面积之和称为圆锥的全面积A 组一、选择题(每小题3分,共45分)1.在△ABC 中,∠C=90°,AB =3cm ,BC =2cm,以点A 为圆心,以2.5cm 为半径作圆,则点C 和⊙A 的位置关系是( )。
人教版九年级上册数学《圆》单元测试卷(含答案)

人教版九年级上册数学《圆》单元测试卷姓名:__________班级:__________考号:__________一 、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.已知与的半径分别为和3,若两圆相交,则两圆的圆心距满足( )A .B .C .D .2.已知圆内一点到圆周上的点的最大距离是7,最小距离是5,则该圆的半径是( )A .2B .6C .12D .73.如图,AB 为O 的直径,CD 为弦, AB CD ⊥,如果70BOC ∠=︒,那么A ∠的大小为( )A . 070B . 035C . 030D .20︒4.在同圆中,CD 的度数小于180︒,且2AB CD =,那么弦AB 和弦CD 的大小关系为( )A .AB CD > B .AB CD =C .AB CD < D .无法确定5.如图,四边形ABCD 是圆内接四边形,E 是BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )A .115︒B .105︒C .100︒D .95︒ 6.Rt ABC ∆中,90C ∠=︒,3cm AC =,4cm BC =,给出下列三个结论: ①以点C 为圆心,3 cm 长为半径的圆与AB 相离;②以点C 为圆心,4cm 长为半径的圆与AB 相切;③以点C 为圆心,5cm 长为半径的圆与AB 相交.上述结论中正确的个数是1O 2O 2m 5m =1m =5m >15m <<EDC BA( )A .0个B .l 个C .2个D .3个7.在中,,,.把绕点顺时针旋转后,得到,如图所示,则点所走过的路径长为( )A .B .cmC .cmD .cm8.如图,已知A 、B 两点的坐标分别为(2,0)、(0,2),⊙C 的圆心坐标为(-1,0),半径为1.若D 是⊙C 上的一个动点,线段DA 与y 轴交于点E ,则ABE 面积的最小值是A .2B .1C .D .9.在圆柱形油槽内装有一些油.截面如图所示,油面宽AB 为6分米,如果再注入一些油后,油面AB 上升1分米,油面宽度为8分米,圆柱形油槽直径MN 为( ) A .6分米 B .8分米 C .10 分米 D .12 分米10.如图,△ABC 是⊙O 的内接三角形,AD ⊥BC 于D 点,且AC=5,CD=3,AB=4,则⊙O 的直径等于( )Rt ABC △90C ∠=︒4BC cm =3AC cm =ABC △A 90︒11AB C △B 54π52π5π△22-2A.B. C. D .7 二 、填空题(本大题共5小题,每小题3分,共15分)11.已知1O ⊙与2O ⊙半径的长是方程27120x x -+=的两根,且1212O O =,则1O ⊙与2O ⊙的位置关系是___________.12.在Rt △ABC 中,∠C=90°,AC=3,BC=4,将△ABC 绕边AC 所在直线旋转一周得到圆锥,则该圆锥的侧面积是 .13.如图,ABC ∆内接于O ⊙,120AB BC ABC =∠=︒,,AD 为O ⊙的直径,6AD =,那么BD =_________.14.如图是一个圆锥形型的纸杯的侧面展开图,已知圆锥底面半径为5cm ,母线长为15cm ,那么纸杯的侧面积为 cm 2.(结果保留π)15.已知正六边形的边心距为,则它的周长是 .三 、解答题(本大题共7小题,共55分)16.如图,以等腰ABC ∆中的腰AB 为直径作O ,交BC 于点D .过点D 作DE AC ⊥,垂足为E .(1)求证:DE 为O 的切线;B(2)若O 的半径为5,60BAC ∠=︒,求DE 的长.17.如图⊙O 半径为2,弦BD =,A 为弧BD 的中点,E 为弦AC 的中点,且在BD上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆与圆的位置关系
课堂训练
1.填空:
2.⊙O1和⊙O2的半径分别为3厘米和4厘米,在下列条件下,求⊙O1和⊙O2位置关系:(1)O1O2=8厘米
(2)O1O2=7厘米
(3)O1O2=5厘米
(4)O1O2=1厘米
(5)O1O2=0.5厘米
(6)O1和O2重合
3 如图, ⊙O的半径为3cm,点P是⊙O外的一点,OP=5cm.
求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?并画图
(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少? 并画图
4.已知⊙A、⊙B相切,圆心距为10 cm,其中⊙A的半径为4 cm,求⊙B的半径
5.如图,AB 既是⊙C 的切线也是⊙D 的切线,⊙C 与⊙D 相外切,⊙C 的半径r=1,⊙D 的半径R=3,求四边形ABCD 的面积。
6.已知⊙1O 、⊙2O 相交于点A 、B ,∠A 1O B = 120°,∠A 2O B = 60°,1O 2O = 6cm 。
求:(1)∠1O A 2O 的度数;2)⊙1O 的半径1r 和⊙2O 的半径2r 。
晚间训练
1. 若两圆没有交点,则这两个圆的位置关系是
; 若两圆有一个交点,则这两个圆的位置关系是 ; 若两圆有两个交点,则这两个圆的位置关系是 ;
2.(06佛山)圆和圆有多种位置关系,与图中不同的圆和圆的位置关系是 .
A B C
3.⊙O 1 和⊙O 2的半径分别为3厘米和5厘米,在下列条件下,求⊙O 1 和⊙O 2位置关系: (1)O 1O 2=0.5厘米 .答 (2)O 1O 2=2厘米 答. (3)O 1O 2=6厘米. 答 (4)O 1O 2=8厘米. 答 (5)O 1O 2=10厘米. 答
4.两圆相切,圆心距为8cm,已知其中一圆半径为5cm, 求另一圆半径.
D C A
B
1
O 2
O B
A
5.三角形三边长为5cm 、12cm 、13cm ,以三角形三个顶点为圆心的三个圆两两外切, 求此三个圆的半径.
6. 已知:半径均为1cm 的两个圆外切,半径均为2cm 且和这两圆都相切的圆有多少个?试画出它们的图形.
7.如图,AB 既是⊙C 的切线也是⊙D 的切线,⊙C 与⊙D 相外切,⊙C 的半径r=2,⊙D 的半径R=6,求四边形ABCD 的面积。
[提高题]如图,抛物线y =-x
2+bx +c 与x 轴交于A (1,0),B (-3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC
的周长最小?若存在,求出点Q 的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限内是否存在一点P ,使△PBC 的面积最大?,若存
在,求出点P 的坐标及△PBC。
