应用光学第四章
合集下载
应用光学 郁道银版的课件 工程光学 第四章)
对于无限远的物体，光学系统的所有光 孔被其前面的光学零件在物空间所成的像 中，直径最小的一个光孔像就是系统的入 瞳。
视场光阑、入射窗、出射窗
光学系统的成像范围是有限的。
照相机中底片框限制了被成像范围 的大小
工具显微镜中分划板的直径决定成 像物体的大小
第三节望远镜系统中成像光束的选择
典型的双目望远镜系统是由一个物镜、一 对转向棱镜、一个分划板和一组目镜构成的， 如图4-7所示。有关光学数据如下：
或加大，从而达到调节光能量以适应外界
不同的照明条件。显然可变光阑不能放在
镜头L上，否A1则A2
的大小就不可变了。
底片框B1B2 的大小确定的。超出底片框的
范围，光线被遮拦，底片就不能感光。
在光学系统中，不论是限制成像光束口径、 或者是限制成像范围的光孔或框，都统称为 “光阑”。
限制进入光学系统的成像光束口径的光阑 称为“孔径光阑” ，例如照像系统中的可 变光阑 A 就是孔径光阑。
渐晕光阑
光阑以减少轴外像差为目的，使物空 间轴外点发出的、原本能通过上述两 种光孔的成像光束只能部分通过，这 种光阑称为渐晕光阑。
入射光瞳通过整个光学系统所成的像就是 出射光瞳
入瞳与出瞳对整个光学系统是共轭的。 如果光阑在整个光学系统的像空间，那
么它本身也就是出射光瞳；
反之，若在物空间，它就是入射光瞳
光学系统中的光束限制
§1 照像系统和光阑 §2 望远镜系统中成像光束的选择 §3 显微镜系统中的光束限制与分析 §4 光学系统的景深 补充: 光学系统的分辨率
实际光学系统与理想光学系统不同， 其参与成像的光束宽度和成像范围都是 有限的。限制来自于光学零件的尺寸大 小和其他金属框。从光学设计的角度看， 如何合理的选择成像光束是必须分析的 问题。光学系统不同，对参与成像的光 束位置和宽度要求也不同。
视场光阑、入射窗、出射窗
光学系统的成像范围是有限的。
照相机中底片框限制了被成像范围 的大小
工具显微镜中分划板的直径决定成 像物体的大小
第三节望远镜系统中成像光束的选择
典型的双目望远镜系统是由一个物镜、一 对转向棱镜、一个分划板和一组目镜构成的， 如图4-7所示。有关光学数据如下：
或加大，从而达到调节光能量以适应外界
不同的照明条件。显然可变光阑不能放在
镜头L上，否A1则A2
的大小就不可变了。
底片框B1B2 的大小确定的。超出底片框的
范围，光线被遮拦，底片就不能感光。
在光学系统中，不论是限制成像光束口径、 或者是限制成像范围的光孔或框，都统称为 “光阑”。
限制进入光学系统的成像光束口径的光阑 称为“孔径光阑” ，例如照像系统中的可 变光阑 A 就是孔径光阑。
渐晕光阑
光阑以减少轴外像差为目的，使物空 间轴外点发出的、原本能通过上述两 种光孔的成像光束只能部分通过，这 种光阑称为渐晕光阑。
入射光瞳通过整个光学系统所成的像就是 出射光瞳
入瞳与出瞳对整个光学系统是共轭的。 如果光阑在整个光学系统的像空间，那
么它本身也就是出射光瞳；
反之，若在物空间，它就是入射光瞳
光学系统中的光束限制
§1 照像系统和光阑 §2 望远镜系统中成像光束的选择 §3 显微镜系统中的光束限制与分析 §4 光学系统的景深 补充: 光学系统的分辨率
实际光学系统与理想光学系统不同， 其参与成像的光束宽度和成像范围都是 有限的。限制来自于光学零件的尺寸大 小和其他金属框。从光学设计的角度看， 如何合理的选择成像光束是必须分析的 问题。光学系统不同，对参与成像的光 束位置和宽度要求也不同。
应用光学第四章
30
光路计算中，棱镜等效平行平板的厚度 L为棱镜光轴长度，设棱镜的通光光束 口径为D，则
LkD
k 取决于棱镜的结构形式，与棱镜的大
小无关，称为棱镜的结构参数。
2019/8/15
31
（二）、几种典型棱镜的展开
2019/8/15
32
1.直角棱镜展开
L=D
D
L
一次反射时
k=1
L—棱镜的光轴长度， D—入射光束口径
2019/8/15
42
y
o
z
x
A1
B1
z 1' o 1'
x 1' y 1' z
y
o x
o1
oy
D1
F2
A2
C1 B2
o2
oy
o 2' D2
C2
x 2' z 2'
y 2' E2
直角棱镜反射 屋脊棱镜反射
2019/8/15
43
y x
z
y′ z′ x′
y
x z
z′ y′
x′
2019/8/15
44
屋脊棱镜的平面表示方法
反射次序，由P1转到P2的方向。
二次反射像与原物坐标系相同，成一致像 。
位于主截面（两平面镜的公共垂直面）内 的光线，不论入射光线方向如何，出射光 线的转角永远等于两平面镜夹角的两倍。
2019/8/15
15
五角棱镜
2019/8/15
16
§4-4 棱镜和棱镜的展开
主要讲述把多个反射面集成在同 一块光学材料上的情况
斯密特棱镜
2019/8/15
其特点是： 光路在棱镜 中的光路很 长，可以折 叠光路，使 仪器紧凑。
(应用光学)第四章平面镜棱镜成像
应用光学（第四版）
4 平面镜棱镜系统
两个互相垂直 的反射面称为
屋脊面
直角棱镜
屋脊棱镜
这种两个互相垂直的反射面称为屋脊面， 而带有屋脊面的棱镜称为屋脊棱镜。
应用光学（第四版）
4 平面镜棱镜系统
y x
z
y′
z′
x′
y
x z
z′ y′
x′
一次镜面反射成镜像，两次镜面反射成一致像。
一次屋脊棱镜成一致像，两次屋脊棱镜成一致像。
当两平面镜一起转动时，出射光线的 转角不变，出射光线位置发生平移。
右手坐标系经两次反射重新还原成为
右手坐标系，成一致像。
应用光学（第四版）
4 平面镜棱镜系统 4.4~4.6 棱镜的展开与棱镜外形尺寸的计算
一、平行平板的成像性质
即入射光与出射光相互平行。
应用光学（第四版）
4 平面镜棱镜系统
• 平行平面板的出射光线BS′ 和入射光线SA是平行的
4 平面镜棱镜系统
二、棱镜转动定理
考虑：像的方向 像的位置
P' P' P
P
符号规则 ；对着转轴向量观察时，逆时针 为正，顺时针为负。
棱镜转动定理
应用光学（第四版）
4 平面镜棱镜系统 1、在平行光路中工作的棱镜，绕垂直于棱镜主界面的z轴转动
y
z
x
应用光学（第四版）
y'
z'
x'
4 平面镜棱镜系统
应用光学（第四版）
∠A’OA”=2∠POP’，转动方向于平面镜转动方向相同
应用光学（第四版）
4 平面镜棱镜系统 • 平面镜的平移
A B
P
Q
h
4 平面镜棱镜系统
两个互相垂直 的反射面称为
屋脊面
直角棱镜
屋脊棱镜
这种两个互相垂直的反射面称为屋脊面， 而带有屋脊面的棱镜称为屋脊棱镜。
应用光学（第四版）
4 平面镜棱镜系统
y x
z
y′
z′
x′
y
x z
z′ y′
x′
一次镜面反射成镜像，两次镜面反射成一致像。
一次屋脊棱镜成一致像，两次屋脊棱镜成一致像。
当两平面镜一起转动时，出射光线的 转角不变，出射光线位置发生平移。
右手坐标系经两次反射重新还原成为
右手坐标系，成一致像。
应用光学（第四版）
4 平面镜棱镜系统 4.4~4.6 棱镜的展开与棱镜外形尺寸的计算
一、平行平板的成像性质
即入射光与出射光相互平行。
应用光学（第四版）
4 平面镜棱镜系统
• 平行平面板的出射光线BS′ 和入射光线SA是平行的
4 平面镜棱镜系统
二、棱镜转动定理
考虑：像的方向 像的位置
P' P' P
P
符号规则 ；对着转轴向量观察时，逆时针 为正，顺时针为负。
棱镜转动定理
应用光学（第四版）
4 平面镜棱镜系统 1、在平行光路中工作的棱镜，绕垂直于棱镜主界面的z轴转动
y
z
x
应用光学（第四版）
y'
z'
x'
4 平面镜棱镜系统
应用光学（第四版）
∠A’OA”=2∠POP’，转动方向于平面镜转动方向相同
应用光学（第四版）
4 平面镜棱镜系统 • 平面镜的平移
A B
P
Q
h
《应用光学》第4章 平面镜棱镜系统1
L ' d (1 tgI2 ) d (1 sin I2 )
• 图4-14所示为一个 三次反射棱镜，称为 斯密特棱镜。它使光 轴折转45°角。由于 棱镜中的光轴折叠， 因此，对缩小仪器的 体积非常有利。
图4-14
15
2）屋脊棱镜
光学系统中，光线经平面镜棱镜系统时的反射次数 可能为奇数，这时物体成镜像，为了获得和物相似 的像，在不宜再增加反射面的情况下，可以用两个 互相垂直的反射面代替其中的一个反射面，这两个 互相垂直的反射面叫作屋脊面。带有屋脊面的棱镜 叫屋脊棱镜。
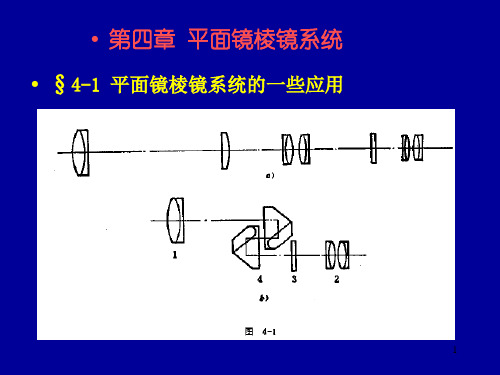
• 第四章 平面镜棱镜系统 • §4-1 平面镜棱镜系统的一些应用
1
平面镜或棱镜、透镜组成的系统，则能满足系统改变 光束方向和物象间方位的要求。如目前使用的军用观 察望远镜，由于在系统中使用了棱镜，如图4-1b所示， 所以它在不加入导向透镜的情况下即可获得正像，同 时又大大地缩小了仪器的体积，减轻了仪器的重量。
下列关系：
由O1O2M得
2i1 2i2 或者 2(i1 i2 )
因二平面镜的法线交于N，
故由O1O2N得
i1 i2或 i1 i2
带入上式得 2
8
从上式可知， 与i角大小无关，只取决于两平面镜 间的夹角，因此，光线方向的改变可以根据设计需 要通过选择适当的角来实现。如果保持两平面镜间
和折射棱镜定义相同，反射棱镜的折射面和反射 面均称为棱镜的工作面，工作面的交线成反射棱镜的 棱，和各棱垂直的截面称为主截面，光学系统的光轴 位在棱镜中的 部分称为反射棱镜的光轴。
10
图4-10
11
图4-11
12
• 一、反射棱镜的分类
•常用的反射棱镜可分为三类：简单棱镜、屋脊 棱镜和复合棱镜。
《应用光学》总结
2 Applied Optics
1 1 1 1 n( - ) = n' ( - ) = Q r l r l'
阿贝不变量,用Q表示.说明一折射球面的物空间 和像空间的Q值是相等的
n' - n n' u' - nu = h r
近轴光经球面折射前,后的u和u′ 角的关系
3
Applied Optics
折射球面物,像位置l和l′ 之间的关系,称为单个☆ 折射球面的物像位置公式.
自备铅笔,作图题一律用铅笔作答! 自备铅笔,作图题一律用铅笔作答! 试卷用黑色钢笔或签字笔作答! 试卷用黑色钢笔或签字笔作答
18
Applied Optics
《应用光学》答疑时间安排
时间:1月14日晚上 日晚上7:00-9:00 时间: 月 日晚上 地点:科研楼313信息光学教研室 地点:科研楼 信息光学教研室
16
Applied Optics
第八章 像差 七种像差的形成原因,表现形式,对成像的影响. 如何减小像差(球差,慧差等) 系统分辨率
17
Applied Optics
考试类型
填空( 填空(约38分) 分 简答题( 简答题(约16分) 分 作图题( 理想光学系统成像,平面镜棱 作图题(约18分,理想光学系统成像 平面镜棱 分 理想光学系统成像 镜系统成像方向,棱镜的选择 棱镜的选择) 镜系统成像方向,棱镜的选择) 折射球面焦距, 证明或计算题 (约28分,折射球面焦距,成像 约 分 折射球面焦距 成像; 双光组组合的焦点位置,焦距 主点位置;望远镜 焦距,主点位置 双光组组合的焦点位置 焦距 主点位置 望远镜 视放大率,显微镜 孔径光阑,视场光阑的确定 显微镜;孔径光阑 视放大率 显微镜 孔径光阑 视场光阑的确定)
1 1 1 1 n( - ) = n' ( - ) = Q r l r l'
阿贝不变量,用Q表示.说明一折射球面的物空间 和像空间的Q值是相等的
n' - n n' u' - nu = h r
近轴光经球面折射前,后的u和u′ 角的关系
3
Applied Optics
折射球面物,像位置l和l′ 之间的关系,称为单个☆ 折射球面的物像位置公式.
自备铅笔,作图题一律用铅笔作答! 自备铅笔,作图题一律用铅笔作答! 试卷用黑色钢笔或签字笔作答! 试卷用黑色钢笔或签字笔作答
18
Applied Optics
《应用光学》答疑时间安排
时间:1月14日晚上 日晚上7:00-9:00 时间: 月 日晚上 地点:科研楼313信息光学教研室 地点:科研楼 信息光学教研室
16
Applied Optics
第八章 像差 七种像差的形成原因,表现形式,对成像的影响. 如何减小像差(球差,慧差等) 系统分辨率
17
Applied Optics
考试类型
填空( 填空(约38分) 分 简答题( 简答题(约16分) 分 作图题( 理想光学系统成像,平面镜棱 作图题(约18分,理想光学系统成像 平面镜棱 分 理想光学系统成像 镜系统成像方向,棱镜的选择 棱镜的选择) 镜系统成像方向,棱镜的选择) 折射球面焦距, 证明或计算题 (约28分,折射球面焦距,成像 约 分 折射球面焦距 成像; 双光组组合的焦点位置,焦距 主点位置;望远镜 焦距,主点位置 双光组组合的焦点位置 焦距 主点位置 望远镜 视放大率,显微镜 孔径光阑,视场光阑的确定 显微镜;孔径光阑 视放大率 显微镜 孔径光阑 视场光阑的确定)
应用光学第四章
反射棱镜(léngjìng)的类型
(2) 屋脊(wūjǐ)棱 当棱镜镜中的一个（或多个）反射面由被称作屋脊的两个互 相垂直的反射面所取代，且屋脊的顶位于主截面内（如图 4-13b），这种棱镜称为屋脊棱镜。屋脊面的作用是增加 一次反射，以改变物像的坐标系关系 。
y
z O x
y Oz
x
y' O'
x' z'
tgI1 ' sin I1 ' 1 代入式（4-7），得 l' d (1 1 ) （4-9）
tgI1 sin I1 n
n
该式表明，在近轴区，平行平板对物点的轴向
位移Δl′只与平板的厚度和折射率有关，而与物
体的位置以及孔径角无关。
精品资料
平行(píngxíng)平板的等效空气层
如图4-21所示 ,等效(děnɡ
任何情况下，维持沿光轴 的坐标轴（如z轴）方向不
变，但透镜成倒像时，将 使物面上的两个垂直于光
轴的坐标轴（如x轴和y轴）同时 反向。
y z
x z'
x' y'
x" y" z"
图4-16 复合棱镜的坐标变换
精品资料
棱镜系统(xìtǒng)成像的物像坐标
变化
例4-1：判断(pànduàn)图4-17中物体经光学 系统后的坐标方向。
前表面的折射角）
精品资料
反射棱镜的等效作用(zuòyòng)与 展开
图4-18多种棱镜的展开(zhǎn kāi) a）二次反射直角棱镜；b）道威棱镜； c）五角棱镜；
d）等边棱镜；e）半五角棱镜；f）斯密特棱镜
精品资料
反射棱镜的等效(děnɡ xiào)作用与 展开
应用光学第四章 平面镜棱镜系统
统 主截面位置任意的平面镜棱镜系统
单一主截面的平面镜棱镜系统
在x’方向（光轴）上，与光轴的出射方向相同； 在y’方向（主截面内）上，
光轴同向，反射次数为偶数， y和y’同向；反射次 数为奇数， y和y’反向。
光轴反向，反射次数为偶数， y和y’反向；反射次 数为奇数， y和y’同向。
在z’方向（垂直于主截面）上，
注意，xyz，x’y’z’只表示物像的方向而不表 示物像的位置。
确定棱镜系统成像方向 x’轴与出射光轴重合
y’和z’的方向确定有两种方法：
反弹折转法 利用法则法
反弹折转法实例
y x
z
x’
y’ z’
y
y’ z’ x’
x z
利用法则法
利用法则的方法，我们将平面镜棱镜系统 分成三类
具有单一主截面的平面镜棱镜系统 具有两个相互垂直的主截面的平面镜棱镜系
y
z
x
z’ x’
y’
y’’
z’’ x’’
y’’’
x’’’ z’’’
分析系统的成像方向实例
分析系统的成像方向练习
如果两平面镜相对转动，则出射光线方向改变了2。
应用举例
测距仪中，入射光线经过两端的平面镜反射以后 改变90o，且要求该角度保持稳定不变。
方法一：单平面镜。 方法二：双平面镜。
方法三：最可靠的方法是将两个反射面做在同一块 玻璃上– 棱镜。
4-4 棱镜和棱镜展开
一、光学系统中常用的两类棱镜 反射棱镜
Δl’是ΔL’在近轴区的近似。 对于理想光学系统（对近轴区）有：
1. 轴向位移只正比于d 2. Δl’与入射角无关 3. d愈大，平板愈厚，轴向位移Δl’愈大
平行平板的等效光学系统
单一主截面的平面镜棱镜系统
在x’方向（光轴）上，与光轴的出射方向相同； 在y’方向（主截面内）上，
光轴同向，反射次数为偶数， y和y’同向；反射次 数为奇数， y和y’反向。
光轴反向，反射次数为偶数， y和y’反向；反射次 数为奇数， y和y’同向。
在z’方向（垂直于主截面）上，
注意，xyz，x’y’z’只表示物像的方向而不表 示物像的位置。
确定棱镜系统成像方向 x’轴与出射光轴重合
y’和z’的方向确定有两种方法：
反弹折转法 利用法则法
反弹折转法实例
y x
z
x’
y’ z’
y
y’ z’ x’
x z
利用法则法
利用法则的方法，我们将平面镜棱镜系统 分成三类
具有单一主截面的平面镜棱镜系统 具有两个相互垂直的主截面的平面镜棱镜系
y
z
x
z’ x’
y’
y’’
z’’ x’’
y’’’
x’’’ z’’’
分析系统的成像方向实例
分析系统的成像方向练习
如果两平面镜相对转动，则出射光线方向改变了2。
应用举例
测距仪中，入射光线经过两端的平面镜反射以后 改变90o，且要求该角度保持稳定不变。
方法一：单平面镜。 方法二：双平面镜。
方法三：最可靠的方法是将两个反射面做在同一块 玻璃上– 棱镜。
4-4 棱镜和棱镜展开
一、光学系统中常用的两类棱镜 反射棱镜
Δl’是ΔL’在近轴区的近似。 对于理想光学系统（对近轴区）有：
1. 轴向位移只正比于d 2. Δl’与入射角无关 3. d愈大，平板愈厚，轴向位移Δl’愈大
平行平板的等效光学系统
应用光学第四章光学系统中成像光束的限制
28
远心光路
孔阑设于焦平面上的光 学系统称远心光学系统。
孔阑设于像方焦面，物 方主光线平行于光轴，称 物方远心光学系统。 孔阑设于物方焦面，像 方主光线平行于光轴， 称像方远心光学系统。
有利于减小或消除调焦误差
29
30
➢典型系统的光束限制
放大镜成一正立、放大的虚像。人眼是孔径光阑（出瞳），限制的是 成像光束，放大镜本身是视场光阑（入射窗），限制的是成像范围。 其最大的视场由入瞳的下边缘与入射窗的上边缘决定。
31
望远镜
32
显微系统
由物镜与目镜构成，在中间也有一实像面，可放置分划板，用于观察近处的 物体。显微系统它的物镜焦距与目镜焦距都比较短，从而出现较大的光学间 隔。当物经显微系统成像时，实现的是二次成像过程，物位于物方焦面附近， 经物镜成一放大的、倒立的实像，实像面一般位于目镜的物方焦面附近，之 后再经目镜成一正立、放大的虚像。最终的结果是：成一倒立、放大的虚像。
结论4：系统中的光阑只是针对某一物体位置而言的，若物体位置发生了变 化，则原光阑会失去限光作用。
12
视场光阑的确定 入窗与出窗
视场光阑位置
13
入窗—视场光阑经前面光学系统的像 ---限制物方视场的大小
出窗—视场光阑经后面光学系统像 ---限制像方视场的大小
物PQ上Q1点以上的主光线都被透镜 边缘挡住而不能通过系统----透镜 边缘的边框限制着通过系统的主光 线—限制着物面上的成像范围
标准镜头 广角镜头 微距镜头 望远镜头 变焦镜头 望远镜头 26
摄影时怎样控制景深?
要拍摄小景深的照片，如特定 镜头，应选择长焦距、大的相 对孔径即小的光圈数，对准距 离近。
要拍摄大景深的照片，如远景 镜头，应选择短焦距、小的相 对孔径即大的光圈数，对准距 离远。
远心光路
孔阑设于焦平面上的光 学系统称远心光学系统。
孔阑设于像方焦面，物 方主光线平行于光轴，称 物方远心光学系统。 孔阑设于物方焦面，像 方主光线平行于光轴， 称像方远心光学系统。
有利于减小或消除调焦误差
29
30
➢典型系统的光束限制
放大镜成一正立、放大的虚像。人眼是孔径光阑（出瞳），限制的是 成像光束，放大镜本身是视场光阑（入射窗），限制的是成像范围。 其最大的视场由入瞳的下边缘与入射窗的上边缘决定。
31
望远镜
32
显微系统
由物镜与目镜构成，在中间也有一实像面，可放置分划板，用于观察近处的 物体。显微系统它的物镜焦距与目镜焦距都比较短，从而出现较大的光学间 隔。当物经显微系统成像时，实现的是二次成像过程，物位于物方焦面附近， 经物镜成一放大的、倒立的实像，实像面一般位于目镜的物方焦面附近，之 后再经目镜成一正立、放大的虚像。最终的结果是：成一倒立、放大的虚像。
结论4：系统中的光阑只是针对某一物体位置而言的，若物体位置发生了变 化，则原光阑会失去限光作用。
12
视场光阑的确定 入窗与出窗
视场光阑位置
13
入窗—视场光阑经前面光学系统的像 ---限制物方视场的大小
出窗—视场光阑经后面光学系统像 ---限制像方视场的大小
物PQ上Q1点以上的主光线都被透镜 边缘挡住而不能通过系统----透镜 边缘的边框限制着通过系统的主光 线—限制着物面上的成像范围
标准镜头 广角镜头 微距镜头 望远镜头 变焦镜头 望远镜头 26
摄影时怎样控制景深?
要拍摄小景深的照片，如特定 镜头，应选择长焦距、大的相 对孔径即小的光圈数，对准距 离近。
要拍摄大景深的照片，如远景 镜头，应选择短焦距、小的相 对孔径即大的光圈数，对准距 离远。
物理光学与应用光学第四章
光阑 M1 M2
A
N1 N2 1
2
合理选择光阑的位臵，在保证成像质量的前提下，可以使 整个光学系统的尺寸减少，系统的结构均称。
2.
视场光阑 它是决定物平面上或物空间中成像范围的光阑。
以上的两种光阑是光学系统系统中最重要的光阑，任何系统 都有这两种光阑的 。
3.
消杂光光阑 (1) 杂光
非成像的光，来自反射面反射的光，仪器内壁反射的光等。
(5)
第一节
光阑
——限制成像光束和成像范围
一、孔径光阑 (Aperture Stops)
1、孔径光阑的定义和作用
★ 含义1：限制轴上物点成像光束孔径角大小的光阑。
★ 含义2：孔径光阑的位臵不同，但都起到了对轴上物点成 像光束宽度的限制作用；只需相应的改变光阑大小，即可保 证轴上物点成像光束的孔径角不变。
-
P1
U
U'
O2
P2 P
孔径光阑
减小孔径光阑并不会对视场产生影响
视场光阑在像方对光线的限制在本质上是在物方对光 线的限制。
例：有一个由三个光学零件组成的光组，透镜O1, 其口径D1＝4mm．f’1=36mm，透镜O2，其 口径 D2＝12mm，f’2=15mm,二透镜间隔 195mm，在离透镜O1右180mm处设有一光孔 D3＝10mm，物点离透镜Ol为-45mm．1）求 孔径光阑和入瞳出瞳的大小和位置?2)求视场光 阑和入窗出窗的大小和位置？
A
45
D1=4mm
D3=10mm D3
D2=12mm
O1 180 195
F2
O2
D2=12mm
D3 D =10mm D =4mm 3 1 F2 180 O1 45
A
N1 N2 1
2
合理选择光阑的位臵，在保证成像质量的前提下，可以使 整个光学系统的尺寸减少，系统的结构均称。
2.
视场光阑 它是决定物平面上或物空间中成像范围的光阑。
以上的两种光阑是光学系统系统中最重要的光阑，任何系统 都有这两种光阑的 。
3.
消杂光光阑 (1) 杂光
非成像的光，来自反射面反射的光，仪器内壁反射的光等。
(5)
第一节
光阑
——限制成像光束和成像范围
一、孔径光阑 (Aperture Stops)
1、孔径光阑的定义和作用
★ 含义1：限制轴上物点成像光束孔径角大小的光阑。
★ 含义2：孔径光阑的位臵不同，但都起到了对轴上物点成 像光束宽度的限制作用；只需相应的改变光阑大小，即可保 证轴上物点成像光束的孔径角不变。
-
P1
U
U'
O2
P2 P
孔径光阑
减小孔径光阑并不会对视场产生影响
视场光阑在像方对光线的限制在本质上是在物方对光 线的限制。
例：有一个由三个光学零件组成的光组，透镜O1, 其口径D1＝4mm．f’1=36mm，透镜O2，其 口径 D2＝12mm，f’2=15mm,二透镜间隔 195mm，在离透镜O1右180mm处设有一光孔 D3＝10mm，物点离透镜Ol为-45mm．1）求 孔径光阑和入瞳出瞳的大小和位置?2)求视场光 阑和入窗出窗的大小和位置？
A
45
D1=4mm
D3=10mm D3
D2=12mm
O1 180 195
F2
O2
D2=12mm
D3 D =10mm D =4mm 3 1 F2 180 O1 45
应用光学第四章复习进程
应⽤光学第四章复习进程应⽤光学第四章本章要点1. 理想光学系统原始定义2. 理想光学系统的焦点、焦平⾯、主点、主平⾯3. 理想光学系统的节点4. 理想光学系统的物像位置关系，⽜顿公式和⾼斯公式5. 理想光学系统物⽅焦距与像⽅焦距的关系6. 理想光学系统的拉⽒不变量7. 理想光学系统的光焦度及其与焦距的关系8. 理想光学系统的垂轴放⼤率、沿轴放⼤率和⾓放⼤率及其关系9. ⼏个特殊位置的三种放⼤率10. 理想光学系统的作图法11. 理想光学系统的组合：作图法和计算法12.远距型和反远距型理想光学系统模型13. 多光组组合，正切计算法，截距计算法14. 各光组对总光焦度得贡献15. 焦距仪基本原理16. 望远镜系统的理想光学系统模型17. 视觉放⼤率概念18. 望远镜与其他光组的组合19. 薄透镜成像原理20. 厚透镜的基点和基⾯及其与光组组合的关系引⾔单个折射球⾯（或反射球⾯）单薄透镜对细⼩平⾯以细光束成完善像实际光学系统对具有⼀定⼤⼩的物（视场）以宽光束（孔径）⼀个光学系统必须由若⼲元件组成，经反复精密计算，使其成像接近完善。
开始时，⾸先将系统看成是理想的§4-1 理想光学系统及其原始定义[返回本章要点]理想光学系统——像与物是完全相似的物空间像空间点——>共轭点直线——>共轭直线直线上的点——>共轭直线上的共轭点理想光学系统理论——⾼斯光学§4-2 理想光学系统的基点和基⾯⼀、焦点F，F’与焦平⾯[返回本章要点]物⽅⽆穷远A F’: 后焦点，像⽅焦点轴上物点 F A’( 处）F：前焦点，物⽅焦点A→ F’:物⽅⽆穷远垂轴平⾯的共轭平⾯为通过 F’的垂轴平⾯（后焦平⾯，像⽅焦⾯）F’→A：像⽅⽆穷远垂轴平⾯的共轭平⾯为物⽅过 F 的垂轴平⾯（前焦平⾯，物⽅焦⾯）注意：这⾥F与F’不为共轭点，A与A’也不为共轭点⼆、主点H，H’和主平⾯[返回本章要点]延长 TE1，FS1交于Q H，H’亦为⼀对共轭点延长 SkR，EkF’交于Q’点H,H'——物（像）⽅主点，前（后）主点，QH,Q'H'——物（像）⽅主⾯，前（后）主⾯，且HQ与H'Q'共轭,β = 1，物、像⽅主⾯是⼀对β=1的物像共轭⾯光学系统总包含⼀对主点（主平⾯），⼀对焦点（焦平⾯），前者是⼀对共轭点（⾯），后者不是像⽅焦距，后焦距物⽅焦距，前焦距只要⼀对主点、⼀对焦点的相对位置⼀定，⼀个光学系统的理想模型就定了。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 2
D
07.02.2021
k 1 2 1.707 2
37
4.等腰棱镜展开
LDctgDctgb
2
k ctg b
2
07.02.2021
38
5.五角棱镜展开
L22D k2 23.414
07.02.2021
39
6.斯密特棱镜展开
A k1 22.41B4'
D'
B
07.02.2021
A' C
L12D
07.02.2021
11
平面镜旋转特性的应用： 光学比较仪中的光学杠杆
M
L1
A
H H'
A'
M a)
P
支点 a 测杆 P
MM为分划板
07.02.2021
PP为反射镜 12
M
A'
A
L1 H H'
M -f
F' b)
P
a
测杆 P
07.02.2021
13
P
AP
I1
I1
O1
O2
I2
I2
q
N
β=2θ
q
即：按入射光线的顺序，以反 射面为镜面，求其对称像，并 依次画出反射棱镜的展开图。
07.02.2021
28
07.02.2021
29
07.02.2021
30
L
平行平板的厚度就是反射棱镜的展开长度 或称光轴长度（L）。
展开后应先找到棱镜限制光束的位置， 再求尺寸，即棱镜通光光束的口径（D）。
07.02.2021
07.02.2021
22
F
F′
平行光经透镜成像时加一平面镜
平行光经透镜成像于焦点F’上
07.02.2021
23
A′
把平面镜换成直角棱镜
07.02.2021
24
A′
A
对于这种光路的等效光路
07.02.2021
25
2. 棱镜的展开
把棱镜的光轴截面沿着它 的反射面展开，取消棱镜的 反射，以平行玻璃板的折射 代替棱镜折射的方法称为
40
§4-5 屋脊面和屋脊棱镜
如果在不改变光轴方向和主截面内成像方向的 条件下需要得到物体的一致像而又不想增加反射棱 镜时，怎么办？
可用交线位于光轴面内的两个相互垂直的 反射面来取代其中的一个反射面，使垂直于主 截面内的坐标被这两个相互垂直的反射面依次 反射而改变方向，从而得到物体的一致像。
31
光路计算中，棱镜等效平行平板的厚度 L为棱镜光轴长度，设棱镜的通光光束 口径为D，则
LkD
k 取决于棱镜的结构形式，与棱镜的大
小无关，称为棱镜的结构参数。
07.02.2021
32
（二）、几种典型棱镜的展开
07.02.2021
33
1.直角棱镜展开
L=D
D
L
一次反射时
k=1
L—棱镜的光轴长度， D—入射光束口径
“棱镜的展开”
07.02.2021
26
(1).为了使棱镜和共轴球面系统组合后， 仍能保持共轴球面系统的特性，必须对棱 镜的结构提出一定的要求：
a．棱镜展开后玻璃板的两个表面必 须平行。
b．如果棱镜位于会聚光束中，则光 轴必须和棱镜的入射及出射表面相垂 直。
07.02.2021
27
(2).展开方法 利用棱镜反射面的性质， 将转折的光路拉直。
A1'(A2)
8
凡一次镜面反射或奇次镜面 反射像被称为镜像；
凡二次镜面反射或偶次 镜面 反射像被称为一致像
07.02.2021
9
§4-3 平面镜的旋转及其应用
平面镜的旋转与平移效应
∠A’OA”=2∠POP’
07.02.2021
10
平面镜的旋转与平移效应
A B
A ′A ″=2h
P
Qh
A”
2h
A’
应用光学第四章
单击此处输入你的副标题，请尽量言 简意赅的阐述观点。
第四章 平面镜棱镜系统
07.02.2021
2
§4-1 平面镜棱镜系统在光学仪器中的应用
平面镜棱镜在光学系统中的作用
改变共轴系统的光轴方向（减少体积和减 轻重量） 改变像的方向 利用平面镜转动作用扩大仪器的放大率 改变观察方向扩大仪器的观测范围 实现分光、合像和微位移
反射次序，由P1转到P2的方向。
二次反射像与原物坐标系相同，成一致像 。
位于主截面（两平面镜的公共垂直面）内 的光线，不论入射光线方向如何，出射光 线的转角永远等于两平面镜夹角的两倍。
07.02.2021
16
五角棱镜
07.02.2021
17
§4-4 棱镜和棱镜的展开
主要讲述把多个反射面集成在同 一块光学材料上的情况
表 轴
轴
6
一、单平面镜的成像特性
平面镜能对整个空间任意物点理想成 像；物点和像点对平面镜而言是对称 的； 物和像大小相等，但形状不同；
凡一次镜面反射或奇次 镜面反射像 被称为镜像；
07.02.2021
7
二
A2'
、
双
平
面
镜
O2
的
q
成
P
像 特 ∠APA2”= 2θ
性07.02.2021
P A
O1 P1
反射棱镜：把多个反射面作在同一块光学 材料（如玻璃）上的光学零件。
注：光线在棱镜反射面上的入射角大于 临界角时，在反射面发生全反射，不镀膜
07.02.2021
18
一、基本定义
ABC---棱镜光轴
A
07.02.2021
光轴：光学系
统的光轴在棱镜 中的部分
光轴长度：
C
棱镜光轴的几
何长度；
B
AB+BC=
棱镜光轴长度
19
一、基本定义
07.02.2021
光轴 工作面
棱 主截面 光轴截面
20
一、基本定义
07.02.2021
光轴 光轴截面
入射光轴截面 出射光轴截面
21
二、棱镜的等效作用与展开
㈠、等效作用与展开方法
1.等效作用 反射棱镜有两个折射 面和若干反射面，若不考虑反射面， 光线在两个折射面之间的行为等效于 一个平行平板
07.02.2021
34
D
L=2D
K=2
L二Leabharlann 反射时，L—棱镜的光轴长度，D —入射光束口径
07.02.2021
35
2.道威棱镜展开
D L
L 2nD 2n2 11 2n
k 2n2 11
必须注意，这类棱镜因为光轴不垂直于棱镜面入射，
故只能用在平行光束中
07.02.2021
36
3.半五角棱镜展开
L 1
M
β≤90
b
07.02.2021
P
14
β角与I角的大小无关，只取决于两平
面镜夹角的大小θ
当双平面镜绕棱线转动时，只要保
持θ角不变，二次反射像是不动的，
即出射光线的方向不变，但光线位置 要产生平行位移。
07.02.2021
15
双平面镜具有以下成像性质：
二次反射像的位置应在物体绕棱线（P点
）转动2θ角处，转动方向应是反射面按
07.02.2021
3
§4-2 平面镜的成像性质
一、单平面镜的成像特性
A B
P
O
Q
A’
07.02.2021
4
一、单平面镜的成像特性
A’
P
A
07.02.2021
Q
5
一、单平面镜的成像特性
采 P
用
右y
手
x
坐
O
标z
法
则
Q
07.02.2021
y'
x'
O’
z'
X Y Z
大
拇
食指
指代
中 指 代 表
代 表 轴