九年级数学等腰梯形的性质和判定
初中数学等腰梯形的性质和定理学习技巧

初中数学等腰梯形的性质和定理学习技巧学习初中数学中关于等腰梯形的性质和定理时,以下是一些有效的学习技巧:1.理解定义:首先确保你清楚等腰梯形的定义:等腰梯形是一组对边平行,另一组对边不平行但相等的四边形。
理解这个定义是掌握等腰梯形性质的基础。
2.掌握基本性质:等腰梯形有一些基本的性质,如两腰相等、两底平行、对角线相等、同一底上的两个角相等。
深入理解和记忆这些性质,它们将是你解题的关键。
3.学习判定定理:等腰梯形的判定定理主要有两条对角线相等的梯形是等腰梯形,以及一组对边平行,另一组对边相等的四边形是等腰梯形等。
理解这些定理的条件和结论,并能够灵活应用它们。
4.大量练习:通过做大量的练习题来巩固对等腰梯形性质和定理的理解。
从简单的题目开始,逐步挑战更复杂的题目,提升解题能力。
5.图形直观:利用图形来辅助学习。
绘制等腰梯形并标记出重要的元素(如腰、底、对角线、角等),这样可以更直观地理解等腰梯形的性质和定理。
6.关联与对比:将等腰梯形的性质与矩形、平行四边形、菱形等其他四边形进行对比和关联,找出它们之间的异同点,加深对等腰梯形知识的理解。
7.总结归纳:将学习到的等腰梯形性质和定理进行归纳整理,形成自己的知识体系。
这样可以帮助你更好地记忆和应用这些知识。
8.参与讨论:与同学或老师讨论等腰梯形相关的问题,通过交流和分享来加深对等腰梯形性质和定理的理解。
9.持续复习:定期复习等腰梯形的性质和定理,确保你能够长期记忆和应用它们。
在复习过程中,可以不断回顾和巩固之前学过的知识,形成更加完整的知识体系。
遵循这些学习技巧,你将能够更好地掌握初中数学中等腰梯形的性质和定理,提高解题能力。
初中数学知识归纳梯形的性质与判定

初中数学知识归纳梯形的性质与判定梯形是初中数学中一个重要的几何图形,它的性质与判定常常出现在数学考试中。
本文将对梯形的性质与判定进行归纳总结,帮助初中生们更好地理解和运用梯形。
梯形的定义:梯形是一个有四边的几何图形,其中两边是平行线段,另外两边则不一定平行。
这两个平行线段被称为梯形的上底和下底,两个非平行的边被称为梯形的斜边。
梯形上底和下底之间的垂直距离被称为梯形的高。
梯形的性质与定理:1. 梯形的对角线相等:梯形的两条对角线分别连接了梯形的非相邻顶点,而这两条对角线相等。
证明:画出梯形的对角线,然后利用平行线和同位角的性质,可以证明两条对角线相等。
2. 梯形的底角和顶角互补:梯形的底角和顶角之和为180度。
证明:利用平行线和同位角的性质,可以证明底角和顶角之和为180度。
3. 等腰梯形的性质:如果一个梯形的两个腰(斜边)相等,那么这个梯形就是等腰梯形。
证明:利用等腰三角形的性质,可以证明一个梯形的两个腰相等。
4. 等腰梯形的底角相等:如果一个梯形是等腰梯形,那么这个梯形的底角相等。
证明:利用等腰三角形的性质,可以证明一个梯形的底角相等。
5. 直角梯形的性质:如果一个梯形的一个内角是直角,那么这个梯形就是直角梯形。
证明:利用直角三角形的性质,可以证明一个梯形的一个内角是直角。
梯形的判定方法:在做题时,我们有时需要通过给定条件来判定一个四边形是否是梯形。
常用的判定方法有以下几种:1. 如果一个四边形的两条对角线相等,并且底角和顶角之和为180度,那么这个四边形是梯形。
2. 如果一个四边形的两条对边都平行,并且有一对对角线相等,那么这个四边形是梯形。
3. 如果一个四边形的两条对边都平行,并且有一条边平分了另一条边,那么这个四边形是梯形。
4. 如果一个四边形的两条对边都平行,并且有一条边垂直于另一条边,那么这个四边形是梯形。
通过以上性质与判定方法,我们可以更加准确地判断和运用梯形。
在解决几何问题时,我们可以根据题目给出的条件,应用相关的性质与判定方法,灵活运用,得出正确的结论。
学案等腰梯形的判定和性质

3.若等腰梯形两底之差等于一腰长,那么这个梯形的一内角是( )
四.积累与总结
1.本节课你认为自己解决的最好问题是什么?
2.本节课学完后你知道等腰梯形有哪些性质和判定?
3.梯形中有哪些重要辅助线?
五.课堂检测.
(4)观察你自己画的梯形,我们在共同探讨一下,梯形还有那些性质?
提示:类比平行四边形的性质,从边、角、对角线方面去考虑。
可得出等腰梯形的两条的对角线相等。
教学反思
第1页
九年级数学学科等腰梯形的判定和性质学案10月10日 主备:陈晓丽
学习内容
等腰梯形的判定和性质
教学导引
2.证明:等腰梯形的两条对角线相等。
学生自己完成,小组讲评。总结等腰梯形有哪些性质。
3.提出问题:(1)等腰梯形在同一底上的两个角相等的逆命题是什么?
他成立吗?如果成立,请证明。
三.巩固应用.
1.在梯形ABCD中,AD∥BC,若AC=BD,求证:AB=CD
1.在梯形ABCD中,AD∥BC,AC=3,BD=4,AC⊥BD,求梯形ABCD的面积。
学习目标
能够运用综合法证明等腰梯形的判定和性质
重点
等腰梯形的判定和性质
难点
探索寻求பைடு நூலகம்理的证明过程
一.巧设现实情景,引入新课
在前面我们已经学习了平行四边形,知道了两边平行的四边形是平行四边形,我们同学回想一下,我们生活有哪些四边形是一边平行,而另一边不平行?这类图形是什么图形呢?什么是等腰梯形呢?这就是我们这节课学习的等腰梯形的判定和性质。
二.探究新知(合作学习)
1.证明:等腰梯形在同一底上的两个角相等。
九年级数学等腰梯形的性质和判定

§1.4等腰梯形的的性质与判定
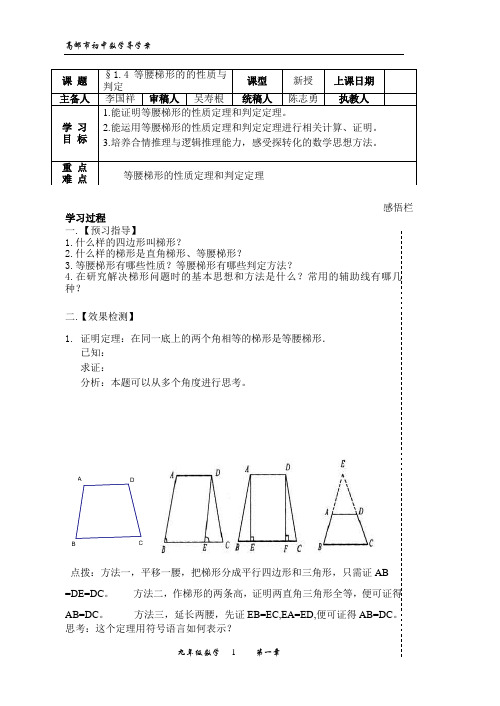
学习过程一.【预习指导】1.什么样的四边形叫梯形?2.什么样的梯形是直角梯形、等腰梯形?3.等腰梯形有哪些性质?等腰梯形有哪些判定方法?4.在研究解决梯形问题时的基本思想和方法是什么?常用的辅助线有哪几种?二.【效果检测】1. 证明定理:在同一底上的两个角相等的梯形是等腰梯形. 已知:求证:分析:本题可以从多个角度进行思考。
点拨:方法一,平移一腰,把梯形分成平行四边形和三角形,只需证AB=DE=DC 。
方法二,作梯形的两条高,证明两直角三角形全等,便可证得AB=DC 。
方法三,延长两腰,先证EB=EC,EA=ED,便可证得AB=DC 。
思考:这个定理用符号语言如何表示?感悟栏DC B A三.【小组检查】感悟栏小组内成员就上述习题进行讨论、修正。
四.【布置任务】师生互动探究问题1. “在同一底上的两个角相等的梯形是等腰梯形”的逆命题是什么?证明:等腰梯形同一底上的两底角相等。
思考:这个定理用符号语言如何表示?问题2. 等腰梯形的两条对角线相等。
思考:这个定理用符号语言如何表示?五.【小组交流】学生展示1.证明:等腰梯形同一底上的两底角相等。
2.证明:两条对角线相等的梯形是等腰梯形六.【课堂训练】拓展延伸问题3.如图等腰梯形ABCD 中,AD ∥BC ,AB=DC ,M 是AD 的中点, 求证:BM=CM思考:你能够用一个命题概括吗?拓展:(1)如图等腰梯形ABCD 中,AD ∥BC ,BM=CM 。
求证: M 是AD 的中点(2)如图梯形ABCD 中,AD ∥BC ,M 是AD 的中点,BM=CM 。
求证:四边形ABFE 是等腰梯形;七.【课堂小结】1.梯形性质和判定定理是什么?2.解决梯形问题的基本思想和方法有哪些?3.解决梯形问题时,常用的辅助线有哪几种?.4.你还有哪些困惑?B C A M D感悟栏八.【课堂反馈】 班级____________ 姓名________ 成绩____________1.四边形的四个内角的度数比是2∶3∶3∶4,则这个四边形是( )A.等腰梯形B.直角梯形C.平行四边形D.不能确定2.在等腰梯形ABCD 中,AD ∥BC ,AE ⊥BC 于E ,且AE=AD ,BC=3AD ,则∠B 等于( )A.30°B.45°C.60°D.135°3.梯形的上底长为6 cm ,将一腰平移到上底的另一端点位置后与另一腰和 下底所构成的三角形的周长为20 cm ,那么梯形的周长为_______.4.梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AD=8,BC=11,则CD=____。
九年级数学等腰梯形的性质和判定(PPT)3-3

等腰梯形的判定定理:
在同一底上的两个角相等的梯形 是等腰梯形.
学习目标:
1、会能证明等腰梯形的性质定理和判定定理。 2、逐步学会分析和综合的思考方法,发展思考能力。 3、经历证明的过程,不断感受证明的必要性、感受合情
推理和演绎推理都是人们正确认识事物的重要途径。 4、感受探索活研究指出:“每餐只吃马铃薯和全脂牛奶就可获得人体所需要的全部营养元素”,可以说:“马铃薯是接近全价的营养食 物。” [] 但是,马铃薯中所含氧化酶和茄素等直接影响了马铃薯的加工和食用。氧化酶主要有过氧化酶、细胞色素氧化酶、酪氨酸酶、葡萄糖氧化酶、抗坏 血酸氧化酶等,这些酶; 炒股配资 ; 主要分布在马铃薯能发芽的部位。马铃薯在空气中的褐变就是其氧化底物绿原酚和酪 氨酸在氧化酶的参与下发生的生化反应。茄素是一种含氮配糖体,很难溶于水,有剧毒。马铃薯的茄素含量以未成熟的块茎为多,占鲜重的.%~.8%。如果 每g鲜块茎中茄素含量达到了mg,食用后人体就会出现中毒症状。因此,在块茎发芽和表皮变绿时一定要把芽和芽眼挖掉,把绿色部分去除干净后才能食用。 [] 经济价值 马铃薯产量高、营养丰富,是粮、菜、饲、工业原料兼用 马铃薯 马铃薯 的农作物。在我国东北的南部、华北和华东地区,马铃薯作为早春蔬菜 成为农村致富的重要作物;在华东的南部和华南大部,马铃薯作为冬种作物与水稻轮作,鲜薯出口可以获得极大的经济效益;在西北地区和西南山区,马铃 薯作为主要的粮食作物发挥着重要的作用。 [] 近几年来,马铃薯食品加工、淀粉加工业迅速发展。在食品加工业中,以马铃薯为原料,可加工成各种速冻方 便食品和休闲食品,如脱水制品、油薯片、速冻薯条、膨化食品等,同时其还可深加工成果葡糖浆、柠檬酸、可生物降解塑料、黏合剂、增强剂及医上的多 种添加剂等。 [] 马铃薯淀粉在世界市场上比玉米淀粉更有竞争力,马铃薯高产国家将大约总产量的%用于淀粉加工,全世界淀粉产量的%来自马铃薯。马铃 薯淀粉与其他作物的淀粉相比,马铃薯淀粉糊化度高、糊化温度低、透明度好、黏结力强、拉伸性大。马铃薯变性淀粉在许多领域都有应用,如衍生物的加 工、生产果葡糖浆、制取柠檬酸、生产可生物降解的塑料等。 [] 据专家测算:马铃薯加工成普通淀粉可增值一倍,特种淀粉可增值十几倍,生产生物胶可增 值多倍,加工成油薯条、薯片、膨化食品可增值~倍。 [] 用及保健价值 马铃薯不但营养价值高,而且还有较广泛的用价值。我国中医学认为,马铃薯有和 胃、健脾、益气的功效,可以预防和治疗多种疾病,还有解毒、消炎之功效。 [] ⒈预防中风 马铃薯中含有丰富的B族维生素和优质纤维素,这在延缓人体衰 葱油洋芋擦擦 葱油洋芋擦擦 老过程中有重要作用。马铃薯富含的膳食纤维、蔗糖有助于防治消化道癌症和控制血液中胆固醇的含量。马铃薯中
九年级数学等腰梯形、三角形中位线、梯形中位线华东师大版知识精讲

九年级数学等腰梯形、三角形中位线、梯形中位线华东师大版【同步教育信息】一. 本周教学内容:等腰梯形、三角形中位线、梯形中位线1. 等腰梯形:性质:等腰梯形的同一底边上的两个内角相等。
等腰梯形的两条对角线相等。
判定:同一条底边上的两个内角相等的梯形是等腰梯形,两条对角线相等的梯形是等腰梯形。
2. 三角形的中位线定义:我们把连结三角形两边中点的线段叫做三角形的中位线。
定理:三角形的中位线平行于第三边,并且等于第三边的一半。
3. 梯形的中位线定义:连结梯形两腰中点的线段叫做梯形的中位线。
定理:梯形的中位线平行于两底边,并且等于两底和的一半。
【典型例题】例1. 已知等腰梯形ABCD 中,AB=CD ,∠===B AD cm BC cm 601549°,,,求它的腰长。
A D分析:要求腰长,也就是求AB 的长,通过作辅助线将已知条件集中到一个三角形中,过A 作AE//CD 交BC 于E ,得到一个平行四边形AECD 和△ABE ,易知△ABE 是等边三角形,由BE=BC -AD ,这样问题就解决了。
解:过A 作AE//DC 交BC 于E∵四边形ABCD 是等腰梯形 ∴∠=∠=B C 60° 又∵AD//BC ,AE//DC ∴四边形AECD 是平行四边形。
∴====∴=AD EC cm AE DC AB CD AB AE15,,∴△ABE 是等边三角形。
又 BC cm =49∴=-=∴==BE cm AB BE cm49153434()A D例2. 已知:如图所示,在等腰梯形ABCD 中,对角线AC=BC+AD ,求∠DBC 的度数。
分析:由等腰梯形的性质得AC=BD ,又题设与对角线有关,考虑平移对角线BD 到AE 的位置,则∠=∠DBC E ,需求∠E ,猜想△ACE 是等边三角形。
解:过A 作AE//BD 交CB 的延长线于E ,则四边形AEBD 是平行四边形。
∴==∴=+=+=AE DB AD BECE BC BE BC AD AC,∵梯形ABCD 是等腰梯形。
中考数学专题二十二:梯形(含详细参考答案)

中考数学专题复习第二十二讲梯形【基础知识回顾】一、 梯形的定义、分类、和面积:1、定义:一组对边平行,而另一组对边的四边形,叫做梯形。
其中,平行的两边叫做两底间的距离叫做梯形的2、分类:梯形3、梯形的面积:梯形= (上底+下底) X 高【赵老师提醒:要判定一个四边形是梯形,除了要注明它有一组对边外,还需注明另一组对边不平行或的这组对边不相等】二、等腰梯形的性质和判定:1、性质:⑴等腰梯形的两腰相等,相等⑵等腰梯形的对角线⑶等腰梯形是对称图形一般梯形特殊梯形等腰梯形:两腰 的梯形叫做等腰梯形直角梯形:一腰与底 的梯形叫做直角梯形2、判定:⑴用定义:先证明四边形是梯形,再证明其两腰相等⑵同一底上两个角的梯形是等腰梯形⑶对角线的梯形是等腰梯形【赵老师提醒:1、梯形的性质和判定中同一底上的两个角相等“不被成”两底角相等2、等腰梯形所有的判定方法都必须先证它是梯形3、解决梯形问题的基本思路是通过做辅助线将梯形转化为形式常见的辅助线作法有要注意根据题目的特点灵活选用辅助线】【重点考点例析】考点一:梯形的基本概念和性质例1 (2012•内江)如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD= 9.思路分析:过点B作BE∥AC交DC的延长线于点E,过点B 作BF⊥DC于点F,判断出△BDE是等腰直角三角形,求出BF,继而利用梯形的面积公式即可求解.解答:解:过点B作BE∥AC交DC的延长线于点E,过点B 作BF⊥DC于点F,则AC=BE,DE=DC+CE=DC+AB=6,又∵BD=AC 且BD⊥AC,∴△BDE是等腰直角三角形,∴BF=DE=3,故可得梯形ABCD的面积为(AB+CD)×BF=9.故答案为:9.点评:此题考查了梯形的知识,平移一条对角线是经常用到的一种辅助线的作法,同学们要注意掌握,解答本题也要熟练等腰直角三角形的性质,难度一般.对应训练1.(2012•无锡)如图,梯形ABCD中,AD∥BC,AD=3,AB=5,BC=9,CD的垂直平分线交BC于E,连接DE,则四边形ABED 的周长等于()A.17B.18C.19D.201.考点:;.分析:由CD的垂直平分线交BC于E,根据线段垂直平分线的性质,即可得DE=CE,即可得四边形ABED的周长为AB+BC+AD,继而求得答案.解答:解:∵CD的垂直平分线交BC于E,∴DE=CE,∵AD=3,AB=5,BC=9,∴四边形ABED的周长为:AB+BE+DE+AD=AB+BE+EC+AD=AB+BC+AD=5+9+3=17.故选A.点评:此题考查了线段垂直平分线的性质.此题比较简单,注意掌握数形结合思想与转化思想的应用是解此题的关键.考点二:等腰梯形的性质例2 (2012•呼和浩特)已知:在等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,则梯形的面积是()A.25B.50C.25 D.思路分析:过点D作DE∥AC交BC的延长线于点E,作DF⊥BC 于F,证平行四边形ADEC,推出AC=DE=BD,∠BDE=90°,根据等腰三角形性质推出BF=DF=EF= BE,求出DF,根据梯形的面积公式求出即可.解答:解:过点D作DE∥AC交BC的延长线于点E,∵AD∥BC (已知),即AD∥CE,∴四边形ACED是平行四边形,∴AD=CE=3,AC=DE,在等腰梯形ABCD中,AC=DB,∴DB=DE (等量代换),∵AC⊥BD,AC∥DE,∴DB⊥DE,∴△BDE是等腰直角三角形,作DF⊥BC于F,则DF=BE=5,S梯形ABCD=(AD+BC)•DF=(3+7)×5=25,故选A.点评:本题主要考查对等腰三角形性质,平行四边形的性质和判定,等腰梯形的性质,等腰直角三角形等知识点的理解和掌握,能求出高DF的长是解此题的关键.对应训练2.(2012•厦门)如图,在等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,若OB=3,则OC= 3.2.3考点:.分析:先根据梯形是等腰梯形可知,AB=CD,∠BCD=∠ABC,再由全等三角形的判定定理得出△ABC≌△DCB,由全等三角形的对应角相等即可得出∠DBC=∠ACB,由等角对等边即可得出OB=OC=3.解答:解:∵梯形ABCD是等腰梯形,∴AB=CD,∠BCD=∠ABC,在△ABC与△DCB中,∵,∴△ABC≌△DCB,∴∠DBC=∠ACB,∴OB=OC=3.故答案为:3.点评:本题考查的是等腰梯形的性质及全等三角形的判定与性质,熟知在三角形中,等角对等边是解答此题的关键.考点三:等腰梯形的判定例3 (2012•襄阳)如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.(1)求证:梯形ABCD是等腰梯形;(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求出此时菱形AECD的面积.考点:;;.分析:(1)由AD∥BC,由平行线的性质,可证得∠DEC=∠EDA,∠BEA=∠EAD,又由EA=ED,由等腰三角形的性质,可得∠EAD=∠EDA,则可得∠DEC=∠AEB,继而证得△DEC≌△AEB,即可得梯形ABCD是等腰梯形;(2)由AD∥BC,BE=EC=AD,可得四边形ABED和四边形AECD均为平行四边形,又由AB⊥AC,AE=BE=EC,易证得四边形AECD是菱形;过A作AG⊥BE 于点G,易得△ABE是等边三角形,即可求得答案AG的长,继而求得菱形AECD的面积.解答:(1)证明:∵AD∥BC,∴∠DEC=∠EDA,∠BEA=∠EAD,又∵EA=ED,∴∠EAD=∠EDA,∴∠DEC=∠AEB,又∵EB=EC,∴△DEC≌△AEB,∴AB=CD,∴梯形ABCD是等腰梯形.(2)当AB⊥AC时,四边形AECD是菱形.证明:∵AD∥BC,BE=EC=AD,∴四边形ABED和四边形AECD均为平行四边形.∴AB=ED,∵AB⊥AC,∴AE=BE=EC,∴四边形AECD是菱形.过A作AG⊥BE于点G,∵AE=BE=AB=2,∴△ABE是等边三角形,∴∠AEB=60°,∴AG=,∴S菱形AECD=EC•AG=2×=2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
女性,65岁,反复咳嗽,咳痰伴喘息30年,加重1周入院。查体:神清,紫绀,颈静脉怒张,双肺散在中小水泡音及干鸣音,心率120次/分,律齐。肝肋下3cm,双下肢指凹性水肿。外周血白细胞12×109/L,中性粒细胞80%。胸片示右下肺动脉干17cm。双肺纹理重。对该患者最重要的治疗措施 项目管理过程组的实施过程包括协调人员和资源,以便实施项目计划并生产出项目或项目阶段的产品或可交付成果。下列不属于项目实施过程的是。A.组建一个项目团队B.制定项目章程C.确保项目质量D.采购必需的资源 《银行业监督管理法》规定的银行业监督管理目标是。 在冬季的东北地区用水温计测水温时,读数应s内完成,避免水温计表面形成薄冰,影响读数的准确性。 连接右心房到左心房的结间束称为。A.Bachmann束B.James束C.传导速度比心房肌慢D.P波增宽切迹E.具有潜在自律性 第一度房室传导阻滞是指PR间期超过A.0.10秒B.0.12秒C.0.20秒D.0.32秒E.0.40秒 支气管与心源性哮喘鉴别如有困难时忌用A.沙丁胺醇B.氨茶碱C.异丙嗪D.泼尼松E.吗啡 下面对CT扫描方法的叙述,错误的是A.高分辨率CT扫描:通过薄层或超薄层、高的输出量、足够大的矩阵、骨算法和小视野图像重建,获得良好的组织细微结构及高的图像空间分辨率的CT扫描方法B.动态扫描:指静脉团注对比剂后,在极短的时间内对某一组织器官进行快速连续扫描,扫描结束后 冯•诺依曼理论的核心是存储程序和。 男患,9岁发病,表现为发作性一侧面肌抽搐,持续1~2分钟,多在夜间发作,2~3个月发作1次。头部MRI检查未见异常,EEG为背景活动正常基础上,中央-颞区高波幅棘-慢波。口服卡马西平有效,16岁以后未再发病。最可能的诊断A.颞叶癫痫B.顶叶癫痫C.额叶癫痫D.青少年肌阵挛癫痫E.伴中央 下列对于四管制空调水系统评述错误的是。A.优点是系统简单、初投资少B.过渡季会出现朝阳房间需要供冷而背阳房间需要供热的情况C.四管制优点是能同时满足供冷、供热的要求D.缺点是初投资高,管路系统复杂,且占有一定的空间 用标准化量表对个体的心理特征进行研究的方法是A.实验法B.观察法C.访谈法D.调查法E.测验法 某轮排水量为15000t,全船垂向重量力矩∑pizi=92763×9.81kN•m,船舶稳心距基线高度KM=7.28m,则其初稳性高度为m。A.0.60B.0.80C.1.10D.1.36 中华人民共和国卫生部颁布的《医务人员医德规范及实施办法》这一文献的基本精神是。A.对患者一视同仁B.文明礼貌服务C.廉洁行医D.为患者保守医密E.实行社会主义人道主义 促进脂肪肝形成的有关因素有A.碳水化合物摄入过多B.肝内形成的甘油三酯增多或氧化减少C.脂蛋白合成增多D.蛋白质摄入过多E.进入肝脏的脂肪酸过少 采用热压灭菌法,用什么蒸气灭菌效果最好A.湿饱和蒸气B.水蒸气C.饱和蒸汽D.过热蒸气E.沸水 营业日工前打印时,“8-批报表管理”下选项“1-批报表打印”,输入日期应是;“9-授权、其他”下选项“批报表查询下载”,输入报表日期应是。A、昨天的日期,昨天的日期B、昨天的日期,当天的日期C、当天的日期,当天的日期D、当天的日期,昨天的日期 下列各项中,不按照“财产转让所得”项目计征个人所得税的是。A.个人销售无偿受赠不动产的所得B.职工将企业改制中取得的量化资产转让ቤተ መጻሕፍቲ ባይዱ.个人转让房屋D.股份制企业为个人股东购买住房而支出的款项 管直流放大器由工作电源、基极分压电路、输入回路、输出回路和组成。A.隔直B.稳压电源C.二极管D.三极管 血液最为重要的缓冲系统是:A.CO2B.PaCO2C.HCO3-D.HCO3-/H2CO3E.H2CO3 经国家劳动和社会保障部批准,在,我国开始启动心理咨询师的职业化工作,由国家颁布《心理咨询师国家职业标准》(试用版)。A.1985年10月B.1995年8月C.2001年8月D.2003年6月 授权是指领导者授予下属一定的A.权力B.责任C.权力和责任D.任务E.职责 签发空头支票或者签发与其预留的签章不符的支票,不以骗取财物为目的的,由中国人民银行处以票面金额但不低于元的罚款;持票人有权要求出票人赔偿支票金额的赔偿金。 下列民事诉讼参与人中,在诉讼中无需回避的是()。A.审判人员B.鉴定人C.证人D.翻译人员 关于记账式债券的论述不正确的是。A.记账式债券是有实物形态的票券,所以可以记名、挂失,安全性较高B.发行时间短,发行效率高,交易手续简便,成本低,交易安全C.投资者进行记账式债券买卖,必须在证券交易所设立账户D.我国1994年开始发行记账式债券 发生下列()情形时,安全生产许可证颁发管理机关应当暂扣或吊销企业的安全生产许可证。A.主管部门发现企业不再具备安全生产条件的B.超越法定职权颁发安全生产许可证的C.违反法定程序颁发安全生产D.工作人员滥用职权、玩忽职守颁发安全生产许可证的 演示紧急外科洗手的过程。 修改项目符号的颜色、大小是通过打开菜单的对话框来实现的。A.格式│字体B.格式│项目符号C.格式│幻灯片颜色方案D.插入│符号 发动机传统点火装置中,能起保护触点、提升点火电压的器件是。A.点火线圈B.电容器C.附加电阻D.铂金火花塞 三凹征是指A.胸骨上凹、肋间隙、锁骨上凹B.胸骨上凹、肋间隙、腋窝C.肋间隙、锁骨上凹、剑突下吸气时凹陷D.胸骨上凹、肋间隙、剑突下吸气时凹陷E.胸骨上凹、锁骨上凹、剑突下吸气时凹陷 灌肠时压力宜低的情况为A.做乙状结肠镜检查前灌肠B.做胆囊切除术前灌肠C.10%水合氯醛灌肠D.高热患者降温灌肠E.行子宫切除术前的灌肠 蒸汽对汽轮机转子和汽缸等金属部件的放热系数并非固定不变,是随着蒸汽的、和的变化而变化的。 城市电网的建设与改造应如何进行? 假设检验一般有两个相互对立的假设,即和。 男性40岁。腹泻1天。排水样便5次,不发热,无腹痛及里急后重。粪便高倍镜视野镜检,脓细胞0~2个,红细胞1~3个,结肠阿米巴滋养体0~1个。涂片染色见革兰阴性弯曲且排列成鱼群样细菌。悬滴法动力(+),最可能的诊断是A.细菌性痢疾B.阿米巴痢疾C.霍乱D.血吸虫病E.急性肠炎
