福建省福州八中高三毕业班第六次质量检查 (2)
2024届福建省福州市第八中学高三第六次质量检查语文试题

福州八中2024—2024学年高三毕业班第六次质量检查语文试题考试时间:150分钟试卷满分:150分一、现代文阅读(一)论述类文本阅读(9分,毎小题 3分)阅读下面的文字,完成1--3题中国史学原本注意图像。
先秦时期的《山海经》记录了很多地理、物产、民俗、宗教、山川鸟兽等内容,原来也有图像,只是在流传的过程中日渐遗失,最终只剩下文字。
中国史学,素有“左图右史”的传统。
宋代的郑樵在《图谱略》中说:“古之学者为学有要,置图于左,置书于右,索象于图,索理于书。
”当然,图像不仅指平面的图画,凡是在平面或是空间构成图形、实体的物体都可以称之为图像。
宋以后,文字气场越来越大,在表现思想方面的特长凸显,与此同时,由于传播相对困难、表意欠缺深度和精确性,图像的重要性日渐式微。
这之后,出现过一个可以重拾图像地位的机会,那就是形成于北宋、发达于清朝后期的金石学。
金石学是以器物上的铭文和石刻碑碣上的碑文为主要探讨对象的一门学科。
但它的缺憾在于,没有将器物本身的造型,位置等作为历史资料或者思想观念的表述来看待。
虽然从某种角度来讲,书法也是一种图像,但远远不够,终归那些古代的铜器、石刻,包含了丰富的图像和历史文化信息。
与传统史学不同,国内现代史学始于20世纪初,可以梁启超《新史学》的问世作为标记。
梁启超强调史学既是一门科学,也是一门艺术,并推崇史料的价值。
王国维、陈寅恪等国学大师呼吁重视甲骨文献、简牍文书等地下史料。
此外还发觉了一批档案文献,包括敦煌莫高窟藏经洞经卷及“八千麻袋”的清宫大内档案等,都将史料利用及史学探讨往前推了一大步。
虽然在迭出的新史料中,文学大家们也对图像流露过深厚的爱好,但图像在史料中的地位并未发生突破性变更。
郑振铎就指责过“轻图像而重文字”的习惯。
即便这样,郑氏所编写的《插图本中国文学史》也免不了只是个“插图本”。
直到上个世纪80年头,历史探讨有了较为宽松的叙述探讨环境,图像和历史的沟通融合渐趋深化。
福建省福州八中高三数学第六次质检考试试题 文 新人教A版

数学(文)试题考试时间:120分钟 试卷满分:150分第Ⅰ卷(选择题 共60分)一、选择题:( 每小题5分,共60分. 在给出的A 、B 、C 、D 四个选项中,只有一项符合题目要求,在答题纸的相应区域内作答)1.已知集合{}sin ,,M y y x x R ∈=={}0,1,2N =,则M N =A . {}1,0,1-B .[]0,1C .{}0,1D .{}0,1,22. 下列结论错误的...是 A .命题“若p ,则q ”与命题“若,q ⌝则p ⌝”互为逆否命题; B .命题:[0,1],1xp x e ∀∈≥,命题2:,10,q x R x x ∃∈++<则p q ∨为真; C .“若22,am bm <则a b <”的逆命题为真命题;D .若q p ∨为假命题,则p 、q 均为假命题.3.已知平面向量b a b k a //),4,2(),3,2(=-=,则实数k 等于A .12B .13C .14D .154.执行右边的程序框图,输出S 的值为 A. 14 B. 20 C. 30 D. 555.设变量x ,y 满足约束条件20424x x y x y -≥⎧⎪+≤⎨⎪-≤⎩,则z x y =-的最大值为A .0B .2C .3D .46.为了了解某校高三400名学生的数学学业水平测试成绩,制成样本频率分布直方图如图,规定不低于60分为及格,不低于80分为优秀,则及格率与优秀人数分别是 A.60%,60B.60%,80C.80%,80D.80%,607.设,x y R ∈,且2y 是1x +和1x -的等比中项,则动点(),x y 的轨迹为除去x 轴上点的 A .一条直线 B .一个圆 C .双曲线的一支 D .一个椭圆 8.在等差数列{}n a 中,若351024a a a ++=,则此数列的前13项的和等于 A .8B .13C .16D .2610. 在花园小区内有一块三边长分别为3米 、4米、5米的三角形绿化地,有一只小狗在其内部玩耍,若不考虑小狗的大小,则在任意指定的某时刻,小狗与三角形三个顶点的距离均超过1米的概率是A .16π-B .112π-C .23π-D .22π-11. 过双曲线22221(0,0)x y a bab 的左焦点(,0)(0)Fc c ,作圆2224a xy的切线,切点为E ,延长FE 交双曲线右支于点P ,若-=2,则双曲线的离心率为A 10B 10C 10D .212. 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为012i a a a a ,{01}∈,(012i =,,),传输信息为00121h a a a h ,其中001102h a a h h a =⊕=⊕,,⊕运算规则为: 000⊕=,011⊕=,101⊕=,110⊕=,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是 A .11010B .01100C .00011D . 10111第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.将答案填在答题卡的相应位置.13.已知124(0)9a a =>,则23log a = .14. 将直线240x y --=绕着其与x 轴的交点逆时针旋 转4π得到直线m ,则m 的方程为 . 15.如图是一个几何体的三视图(单位:cm ). 这个几何体的表面积为 cm 2.16.在平面直角坐标系中, ABC ∆的顶点A 、B 分别是(第15题图)侧视图 2俯视图正视图 13311离心率为e 的圆锥曲线221x y m n+=的焦点,顶点C 在该 曲线上.一同学已正确地推得:当0m n >>时,有(sin sin )sin e A B C ⋅+=.类似地,当0m >、0n <时,有(e ⋅ )sin C =.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)如图,三棱柱ABC -A 1B 1 C 1中,侧棱AA 1⊥平面ABC ,AB=BC=AA 1=2,AC=2,E ,F 分别是A 1B ,BC 的中点. (I )证明:EF ∥平面A A l C l C ; (II )证明:平面A 1ABB 1⊥平面BEC .18.(本小题满分12分) 已知a→=(sin x ,cos x ),b →=(cos x ,cos x ),函数()f x =→a •→b . (I )求函数()f x 的单调递增区间;(II )函数()f x 的图象可以由函数y =sin x 的图象经过怎样的变换得到?19.(本小题满分12分)设关于x 的一元二次方程2220x ax b ++=.(I )若a,b 都是从集合{}1234,,,中任取的数字,求方程有实根的概率;(II )若a 是从区间[0,4]中任取的数字,b 是从区间[1,4]中任取的数字,求方程有实根的概率.20.(本小题满分12分)已知等差数列{}n a 的公差0d ≠,它的前n 项和为n S ,若570S =,且7222a ,a ,a 成等比数列.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设数列{}6(1)n na n S ++的前n 项和为n T ,求证:1<2n T ≤.21.(本小题满分12分) 设函数323()(1)1,32a f x x x a x a -+++=其中为实数。
2021届福建省福州市第八中学高三毕业班第六次质量检查理科数学试卷

2021年福建省福州市第八中学高三毕业班第六次质量检查理科数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.设i 是虚数单位,复数1()1aiz a R i-=∈+为纯虚数,则复数z 的虚部为 A .i - B .2i - C .1- D .2- 2.下列命题中,真命题是 A .0x R ∃∈,使得00x e ≤ B .C .2,2x x R x ∀∈>D .1,1a b >>是1ab >的充分不必要条件3. 对于函数2(),f x x mx n =++若()0,()0f a f b >>,则函数()f x 在区间(,)a b 内 A .一定有零点 B .一定没有零点 C .可能有两个零点D .至多有一个零点4.二项式102x⎛+ ⎝的展开式中的常数项是A .第10项B .第9项C .第8项D .第7项5.某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的表面积为( )A .32π+B C .32π D .32π+6.设x R ∈, 对于使22x x M -+≤成立的所有常数M 中,我们把M 的最小值1叫做22x x -+ 的上确界.若,a b R +∈,且1a b +=,则122a b--的上确界为A .5-B .4-C .92D .92-7.a 为如图所示的程序框图中输出的结果,则化简 cos()a πθ-的结果是A .cos θB .cos θ-C .sin θD .sin θ-8.设1F ,2F 是双曲线12222=-by a x 0(>a ,)0>b 的左、右两个焦点,若双曲线右支上存在一点P ,使0)(22=⋅+F OF (O 为坐标原点),且||3||21PF PF =,则双曲线的离心率为 A.12 B1 C.12+ D1+ 9.设P 是不等式组⎪⎩⎪⎨⎧≤+-≥-≥≥310,0y x y x y x 表示的平面区域内的任意一点,向量)1,1(=→m ,)1,2(=→n ,若→→→+=n m OP μλ(μλ,为实数),则μλ-的最大值为 A .4 B .3 C .-1 D .-210.已知函数f(x)={x +1x ,x >0x 3+3,x ≤0 ,则关于x 的方程f(2x 2+x)=a(a >2)的根的个数不可能为A .3B .4C .5D .6二、填空题 11.计算定积分=+⎰-dx x x 112)sin (____________.12. 设ABC ∆内角C B A ,,的对边分别为c b a ,,,且满足,53cos cos a C b B c =-则=CBtan tan .13.设等差数列}{n a 和等比数列}{n b 首项都是1,公差和公比都是2,则=++432b b b a a a .14.如图所示,记正方体1111-ABCD A B C D 的中心为O ,面11B BCC 的中心为E ,11B C的中点为.F 则空间四边形1D OEF 在该正方体各个面上的投影可能是 .(把你认为正确命题的序号填写在答题纸上)15.已知数列A :123,,,,na a a a *(3)n n N ≥∈,中,令{}*|,1,,A i j T x x a a i j n i j N ==+≤<≤∈,()A card T 表示集合A T 中元素的个数.若1i i a a c +-=(c 为常数,且0c ≠,11i n ≤≤-)则()A card T = .三、解答题16.已知向量m ⃗⃗ =(√3sin x4,1),n ⃗ =(cos x4,cos 2x4),记f(x)=m ⃗⃗ ⋅n ⃗ .(I )若f(a)=32,求cos(2π3−a)的值;(Ⅱ)将函数y =f(x)的图象向右平移2π3个单位得到y =g(x)的图象,若函数y =g(x)−k 在[0,7π3]上有零点,求实数k 的取值范围.17.某工厂生产A ,B 两种元件,其质量按测试指标划分,指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100个进行检测,检测结果统计如下: 测试[70,76)[76,82)[82,88)[88,94)[94,100]ABCD1B 1C 1D 1A EFO指标元件A 8 12 40 32 8元件B 7 18 40 29 6(1)试分别估计元件A,元件B为正品的概率;(2)生产1个元件A,若是正品则盈利40元,若是次品则亏损5元;生产1个元件B,若是正品则盈利50元,若是次品则亏损10元.在(1)的前提下,(ⅰ)X为生产1个元件A和1个元件B所得的总利润,求随机变量X的分布列和数学期望;(ⅱ)求生产5个元件B所得利润不少于140元的概率.18.(本小题满分13分)已知四棱锥P ABCD-中,PA ABCD⊥平面,底面ABCD 是边长为a的菱形,120BAD∠=︒,PA b=.(Ⅰ)求证:PBD PAC⊥平面平面;(Ⅱ)设AC与BD交于点O,M为OC中点,若二面角O PM D--的正切值为26求:a b的值.19.(本小题满分13分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且∆APB面积的最大值为3(1)求椭圆C的方程及离心率;(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD 为直径的圆与直线PF的位置关系,并加以证明.OF EPD BAy x20.(本小题满分14分)已知函数()ln ln ,(),xf x x ag x ae =-=其中a 为常数,函数()y f x =和()y g x =的图象在它们与坐标轴交点的切线互相平行.(Ⅰ)求a 的值;(Ⅱ)求函数()()(1)F x f x g x =--的单调区间;(Ⅲ)若不等式()(1)[(1)]0xf x k x f g x -+-≤在区间[1,)+∞上恒成立,求实数k 的取值范围.21.选修4-2:矩阵与变换已知二阶矩阵M 有特征值λ1=4及属于特征值4的一个特征向量并有特征值及属于特征值-1的一个特征向量,(Ⅰ )求矩阵M ;(Ⅱ )求5M α.22.(本小题满分7分) 选修4—4:极坐标与参数方程已知曲线C 的极坐标方程是θρcos 4=.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是t t y t x (sin cos 1⎩⎨⎧=+=αα是参数).(Ⅰ)写出曲线C 的参数方程;(Ⅱ)若直线l 与曲线C 相交于A 、B 两点,且14=AB ,求直线l 的倾斜角α的值. 23.(本小题满分7分) 选修4—5:不等式选讲 已知关于的不等式:的整数解有且仅有一个值为2.(Ⅰ)求整数的值;(Ⅱ)已知,若,求的最大值.参考答案1.C【解析】i a a i i i ai i ai z 2121)1)(1()1)(1(11+--=-+--=+-= 为纯虚数,则021=-a 且021≠+a .,则1=a ,虚部 为1-.考点:复数的运算. 2.D 【解析】 A .的值域为,所以“0x R ∃∈,使得00x e ≤”是假命题;B .,当且仅当,即成立(而),所以“”为假命题;C .当时,,所以“2,2x x R x ∀∈>”为假命题;D .当,由不等式的性质,得;而满足,不满足,所以“是1ab >的充分不必要条件”是假命题;故选D .考点:命题的判定. 3.C 【解析】试题分析:由二次函数性质及零点存在定理可知C 正确. 考点:二次函数性质、零点存在定理. 4.B【解析】二项式102x ⎛+ ⎝的展开式中的通项为k k k kk k k x C x x C T 2520102110210122)(---+=⎪⎪⎭⎫ ⎝⎛=,令02520=-k ,解得8=k ,即常数项为第9项.考点:二项式定理. 5. A【详解】试题分析:由题意得,根据所给的三视图可得,该几何体为圆锥的一半,那该几何体的表面积为该圆锥表面积的一半与轴截面的面积之和,又该圆锥的侧面展开图为扇形,所以侧面积为1122ππ⨯⨯⨯=,底面积为12π,观察三视图可知,轴截面为边长为2的正三角形,所轴截面面积为12222⨯⨯⨯=32π+ A. 考点:几何体的三视图及几何体的表面积. 【方法点晴】本题主要考查了空间几何体的三视图的应用,着重考查了推理和运算能力及空间想象能力,属于中档试题,解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则,还原出原几何体的形状,属于基础题,本题的解答中,根据所盖的三视图可得,该几何体为圆锥的一半,那该几何体的表面积为该圆锥表面积的一半与轴截面的面积之和是解答问题的关键. 6.D 【解析】求122a b --的上确界,即求122a b--的最大值.1,0,0=+>>b a b a , 29)22225()2225()222(221-=⋅+-≤++-=+++-=--∴b a a b b a a b b b a a b a b a (当且仅当baa b 22=,即a b 2=时取等号). 考点:基本不等式. 7.A【解析】1,2==i a ;2,1211=-=-=i a ;3,21111==+=i a ;4,22111==-=i a ;⋅⋅⋅;即a 值具有周期性,周期为3;而167132014⋅⋅⋅=÷;所以输出a 值为2;则()()θθπθπcos 2cos cos =-=-a .考点:程序框图与诱导公式. 8.D【解析】由题意,得()()022222=-=-⋅+OF OF OF ,即2OF OP =,又213PF PF = ,所以21F PF ∆为直角三角形,且21PF PF ⊥,则22,132=-=c a ,所以椭圆的离心率1313222+=-==a c e . 考点:双曲线的性质. 9.A【解析】由n m OP μλ+=及)1,2(),1,1(==n m ,得),2(μλμλ++=OP ,则⎪⎪⎩⎪⎪⎨⎧≤+-≥≥+≥+3321002μλμμλμλ;画出可行域和目标函数基准线x y =,如图所示.设y x t -=,将y x t -=化为t x y -=,当直线t x y -=向右下方平移时,直线在y 轴的截距t -减小,t 变大;由图像可得当直线t x y -=过点)1,3(-C 时,t 取到最大值4)1(3=--.考点:简单的线性规划. 10.A 【解析】 画出的图像如图所示,由图像可知:当时,;当时,. 设,则当时,直线与的图像有3个交点,即有3个根(两个正根、一个负根);当时,直线与的图像有3个交点,即有3个根(两个正根、一个零根);当时,直线与的图像有2个交点,即有2个正根;当时,直线与的图像有2个交点,即有2个根(一个正根、一个负根);,所以当时,有0个根;当时,有1个根当时,有2个不等根;综上所述,的根的个数可能为3,4,5;不可能为3个..考点:函数的零点. 11.32 【解析】321cos 311cos 31|cos 31)sin (113112=⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=+--⎰x x dx x x . 考点:微积分基本定理. 12.41【解析】由正弦定理,得)sin(53cos sin cos sin C B C B B C +=-, 即)sin cos cos (sin 53cos sin cos sin C B C B C B B C +=-,则B C B C sin cos 58cos sin 52=, 则41cos sin cos sin tan tan ==B C C B C B . 考点:正弦定理与三角恒等变形. 13.25【解析】由题意,得数列{}n a {}n b 的通项公式分别为12,12-=-=n n n b n a ;则1212-=-=n n b b a n ;则=++432b b b a a a ()()()25121212432=-+-+-. 考点:等差数列、等比数列. 14.①②④【解析】空间四边形1D OEF 在该正方体前后面上的投影是①;空间四边形1D OEF 在该正方体左右面上的投影是②;空间四边形1D OEF 在该正方体上下面上的投影是④;故填①②④.考点:图形的投影. 15.32-n【解析】由c a a i i =-+1,c 为常数,可得{}i a 是等差数列,且首项为1a ,公差为c ,通项公式为di a a i )1(1-+=,所以A :c n a c a c a a )1(,,2,,1111-+⋅⋅⋅++,则{}c n a c a c a c a T A )32(2,,32,22,21111-+⋅⋅⋅+++=,且为等差数列,所以共有32-n 项.考点:新定义型题目. 16.(1)1;(2).【解析】试题分析:(Ⅰ)先化简求得的解析式,由已知可求得的值,从而可求cos(2π3−a);(Ⅱ)先求得y =g(x)−k 的解析式,从而可求的值域,由函数y =g(x)的图象与直线在[0,7π3]有交点,即可求出实数的取值范围.试题解析:(I)由已知f(a)=32得sin(α2+π6)+12=32,于是α=4kπ+2π3,k ∈Z ∴cos(2π3−α)=cos(2π3−4kπ−2π3)=1-----------4分(II)f(x)=√3sin x4cos x4+cos 2x4=sin(x2+π6)+12------------6分将函数y =f(x)的图象向右平移2π3个单位得到函数g(x)=sin(12x −π6)+12的图象. -----8分当x ∈[0,7π3]时,−π6≤12x −π6≤π,所以−12≤sin(12x −π6)≤1, 所以0≤sin(12x −π6)+12≤32. 若函数y =g(x)−k 在[0,7π3]上有零点,则k ∈[0,32]------------12分 考点:1.三角函数的图象与性质;2.三角函数的恒等变换应用;3.平面向量及应用. 17.(1);(2)(i )66;(ii ).【解析】试题分析:本题主要考查古典概型、独立事件、二项分布等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,根据已知中的“指标大于或等于82为合格品,小于82为次品”得到大于等于82的合格品的个数为40+32+8件,同理乙的合格品个数为40+29+6件,再利用古典概型计算概率;结合第一问的结论,利用独立事件,对于甲和乙来说:合格合格、合格不合格、不合格合格、不合格不合格,四种情况分别计算概率,最后列出分布列;设出5件中的合格品数n件,则次品5-n件,利用“合格品可盈利50元,若是次品则亏损10元”列出不等式,解出n的取值范围,得到n=4或n=5,再利用二项分布计算概率.试题解析:(Ⅰ)芯片甲为合格品的概率约为,芯片乙为合格品的概率约为.(Ⅱ)(ⅰ)随机变量X的所有取值为90,45,30,﹣15.;;;.所以,随机变量X的分布列为:(ⅱ)设生产的5件芯片乙中合格品n件,则次品有5﹣n件.依题意,得50n﹣10(5﹣n)≥140,解得.所以n=4,或n=5.设“生产5件芯片乙所获得的利润不少于140元”为事件A,则.考点:古典概型、独立事件、二项分布.18.(1)证明见解析;(2)3:4.【解析】试题分析:(1)利用面面垂直的判定定理进行证明;(2)建立空间直角坐标系,利用空间向量进行求解.试题解析:(Ⅰ)因为PA ⊥平面ABCD ,所以PA ⊥BD 又ABCD 为菱形,所以AC ⊥BD,所以BD ⊥平面PAC 从而平面PBD ⊥平面PAC .(Ⅱ)方法1.过O 作OH ⊥PM 交PM 于H ,连HD因为DO ⊥平面PAC,可以推出DH ⊥PM,所以∠OHD 为O-PM-D 的平面角 8分 又3,,44a a OD OM AM ===,且OH APOMPM= 10分 从而·4aOH==12分 tan ODOHD OH ∠===所以22916a b =,即43a b =. 13分 法二:如图,以A 为原点,,AD AP 所在直线为y 轴,z 轴建立空间直角坐标系,则(0,0,),(0,,0)P b D a,3,,0)8M a,1,,0)4O a 8分 从而333(0,,),(,,)88PD a b PM a a b =-=-3(,,0)4OD a =- 9分 因为BD ⊥平面PAC,所以平面PMO 的一个法向量为3(,,0)4OD a =-. 10分 设平面PMD 的法向量为(,,)n x y z =,由,PD n PM n ⊥⊥得3330,088PD nay bz PM n ax ay bz ⋅=-=⋅=+-=取,,x y b z a ===,即,,)n b a = 11分设OD 与n 的夹角为θ,则二面角O PM D --大小与θ相等 从而tan θ=cos 15θ=531cos 5||||ab abOD n OD n a θ-+⋅===⋅从而43b a =,即:4:3a b =.考点:1.面面垂直的判定定理;2.二面角;3.空间向量的应用.19.(1)椭圆C 的方程为22143x y +=,离心率为21;(2)以BD 为直径的圆与直线PF 相切. 【解析】试题分析:(1)利用待定系数法进行求解;(2)设出直线的方程,联立直线与椭圆的方程,整理成关于x 的一元二次方程,利用中点坐标公式求其线段中点,写出圆的方程,利用圆心到直线的距离公式进行证明.试题解析:(1)由题意可设椭圆C 的方程为22221(0)x y a b a b+=>>,(,0)F c .由题意知解得b =1c =. 3分故椭圆C 的方程为22143x y +=,离心率为12. 5分 (Ⅱ)以BD 为直径的圆与直线PF 相切.证明如下:由题意可设直线AP 的方程为(2)y k x =+(0)k ≠. 则点D 坐标为(2, 4)k ,BD 中点E 的坐标为(2, 2)k . 6分由22(2),143y k x x y =+⎧⎪⎨+=⎪⎩得2222(34)1616120k x k x k +++-=. 7分设点P 的坐标为00(,)x y ,则2021612234k x k --=+.所以2026834k x k -=+,00212(2)34ky k x k =+=+. 9分 因为点F 坐标为(1, 0), 当12k =±时,点P 的坐标为3(1, )2±,点D 的坐标为(2, 2)±. 直线PF x ⊥轴,此时以BD 为直径的圆22(2)(1)1x y -+=与直线PF 相切. 10分 当12k ≠±时,则直线PF 的斜率0204114PF y k k x k==--. 所以直线PF 的方程为24(1)14ky x k=--. 点E 到直线PF的距离d =322228142||14|14|k k k k k k +-==+-. ⎧⎪⎨⎪⎩2221222, .a b a a b c ⋅⋅===+又因为||4||BD k = ,所以1||2d BD =. 故以BD 为直径的圆与直线PF 相切.综上得,当直线AP 绕点A 转动时,以BD 为直径的圆与直线PF 相切. 考点:1.椭圆的标准方程;2.直线椭圆的位置关系;3.直线与圆的位置关系. 20.(1)1=a ;(2)单调递增区间为(0,1),单调递减区间为()+∞,1;(3)1[,)2+∞. 【解析】试题分析:(1)利用导数的几何意义进行求解;(2)求导,利用导数的符号求函数的单调区间;(3)构造函数,将不等式恒成立问题转化为求函数的最值问题. 试题解析:(Ⅰ)()f x 与坐标轴交点为(,0)a ,1()f a a'=, 1分 ()g x 与坐标轴交点为(0,)a ,(0)g a '= 2分1a a∴=解得1a =±,又0a >,故1a = 4分 (Ⅱ)由(Ⅰ)知()ln ,()xf x xg x e ==,1()ln ,(0,)x F x x e x -=-∈+∞1111()x x xe F x e x x---'∴=-= 5分令1()1x h x xe-=-,显然函数()h x 在区间(0,)+∞上单调递减,且(1)0h = 6分当(0,1)x ∈时,()0h x >,()0F x '∴>,()F x ∴在(0,1)上单调递增当(1,)x ∈+∞时,()0h x <,()0F x '∴<,()F x ∴在(1,)+∞上单调递减 8分 故()F x 的单调递增区间为(0,1),单调递减区间为(1,)+∞. 9分(2)原不等式等价于:2ln (1)0x x k x --≤在区间[1,)+∞上恒成立.设2()ln (1)(1)x x x k x x ϕ=--≥ 则()ln 12x x kx ϕ'=+- 10分 令()()ln 12(1)u x x x kx x ϕ'==+-≥112()2ku x k x x-'∴=-=11分①0k ≤时,()0,()u x x ϕ''>在区间[1,)+∞上单调递增,()(1)120x k ϕϕ''>=->()x ϕ∴在[1,)+∞上单调递增,()(1)0x ϕϕ≥=不符合题意,舍去. 12分②当102k <<时,若1(1,),()02x u x k '∈> 则()x ϕ'在1(1,)2k上单调递增,()(1)120x k ϕϕ''>=-> ()x ϕ∴在[1,)+∞上单调递增,()(1)0x ϕϕ≥=不符合题意,舍去. 13分 ③当12k ≥时,()0u x '≤在[1,)+∞恒成立, ()x ϕ'∴在[1,)+∞上单调递减()(1)120x k ϕϕ''∴≤=-≤ ()x ϕ∴在[1,)+∞上单调递减()(1)0x ϕϕ≤=即2ln (1)0x x k x --≤对x ∈[1,)+∞恒成立,综上所述,实数k 的取值范围是1[,)2+∞.考点:1.导数的几何意义;2.函数的单调性;3.不等式恒成立问题. 21.(1);(2).【解析】试题分析:(1)利用矩阵的运算法则进行求解;(2)利用矩阵的乘法法则进行求解.试题解析:(Ⅰ)设M =a b c d ⎛⎫⎪⎝⎭, 则a b 228 4c d 3312⎛⎫⎛⎫⎛⎫⎛⎫==⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,∴2a 3b 8{2c 3d 12+=+=① 又a b 111 1c d 111-⎛⎫⎛⎫⎛⎫⎛⎫=-= ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭(),∴a b 1{c d 1-=--=② 由①②可得a=1,b=2,c=3,d=2,∴M =12.32⎛⎫⎪⎝⎭4分(Ⅱ)易知,∴561(1)1M αα-⎛⎫=-= ⎪⎝⎭.考点:矩阵的运算.22.(1)⎩⎨⎧=+=ϕϕsin 2cos 22y x ;(2)4πα=或43π.【解析】试题分析:(1)利用⎩⎨⎧==ϕρϕρsin cos y x 将极坐标方程化成普通方程,再化成参数方程;(2)将圆的参数方程化成普通方程,再利用直线与圆的位置关系和弦长公式进行求解. 试题解析:(Ⅰ)由θρcos 4=得:θρρcos 42=,x y x 422=+∴, 2分 即4)2(22=+-y x ,所以曲线C 的参数方程:⎩⎨⎧=+=ϕϕsin 2cos 22y x (ϕ为参数) 3分(Ⅱ)将⎩⎨⎧=+=ααsin cos 1t y t x 代入圆的方程得4)sin ()1cos 22=+-ααt t (,化简得03cos 22=--αt t .设A 、B 两点对应的参数分别为1t 、2t ,则⎩⎨⎧-==+3cos 22121t t t t α, 5分()1412cos 4422122121=+=-+=-=∴αt t t t t t AB ,∴2cos 42=α,22cos ±=α,4πα=或43π. 考点:1.曲线的普通方程、参数方程、极坐标方程的互化;2.直线与圆的位置关系. 23.(1);(2).【解析】试题分析:( I )由,得因不等式的整数解为2又不等式仅有一个整数解2,;(Ⅱ)由柯西不等式可知:所以即试题解析:(I )由,得不等式的整数解为2,又不等式仅有一个整数解2,3分(Ⅱ)显然由柯西不等式可知:所以即当且仅当时取等号,最大值为7分考点:均值不等式。
福建省福州市第八中学高三英语第六次质量检查试题

福州八中2016—2017学年高三毕业班第六次质量检查英语试题考试时间:120分钟试卷满分:150分第I卷(计分100分)第一部分听力(共两节,满分30分)第一节听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Where does the woman want to go?A. To Oxford.B. To Liverpool.C. To London.2. How many people will go to the tennis game?A. 2.B. 3.C. 4.3. What does the woman ask the boy to do after school?A. Put away his school bag.B. Move the kitchen table.C. Hang up his coat.4. What do we know about Linda Rivera?A. She went traveling.B. She started a company.C. She was fired.5. What does the man mean?A. He prefers cold weather.B. He has had a difficult week.C. The temperature was good last week.第二节听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. How will the man choose the music?A. By letting a person decide on it.B. By asking people for their advice.C. By allowing everyone to bring a piece.7. What is the woman going to do?A. Help prepare for the party.B. Tell the man a phone number.C. Ask Sonia for some information.听第7段材料,回答第8、9题。
福州八中学年高三毕业班第六次质量检查.docx

高中数学学习材料马鸣风萧萧*整理制作福州八中2015—2016学年高三毕业班第六次质量检查数学(理)试题考试时间:120分钟 试卷满分:150分 2016.2.15第Ⅰ卷一、选择题:本大题共12小题,每小题5分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{5,35}M a a =-+,{1,3}N =,若M N ⋂≠∅,则实数a 的值为 A .1 B .2 C .4 D .1或2 2.复数321iz i i =+-(i 为虚数单位)的共轭复数为 A .12i + B .1i - C .1i -D .12i - 3.已知等差数列{a n }的前n 项和为S n ,S 5=﹣20,则﹣6a 4+3a 5= A .﹣20 B .4 C .12 D .204.在平行四边形ABCD 中,AC=5,BD=4,则AB uu u r •BC uu u r =A .414B .﹣414C .94D .﹣945.已知圆O :224x y +=上到直线:l x y a +=的距离等于1的点至少有2个,则a 的取值范围为 A .(32,32)- B .(,32)(32,)-∞-⋃+∞C .(22,22)-D .[32,32]-6.甲、乙等5人在9月3号参加了纪念抗日战争胜利70周年阅兵庆典后,在天安门广场排成一排拍照留念,甲和乙必须相邻且都不站在两端的排法有( )种. A .12 B .24 C .48 D.1207.已知向量1(s i n ,)2m A =与向量(3,s i n 3c o s )n A A =+共线,其中A 是ABC ∆的内角,则角A 的大小为A. 6πB. 4πC.3πD.2π 8.某程序框图如图所示,该程序运行后输出的S 的值是 A .1007 B .2015 C .2016 D .30249.若双曲线22221(0,0)x ya b a b-=>>与直线2y x =无交点,则离心率e 的取值范围是 A .(1,2) B .(1,2] C .(1,5)D . (1,5]10.一个几何体的三视图如图所示,则这个几何体外接球的体积为 A .10002πB .200πC .2003πD .100023π 11.设实数,x y 满足条件203600,0x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩,若目标函数()0,0z ax by a b =+>>的最大值为12,则32a b +的最小值为A .256B .83C .113D .412.已知定义域为R 的函数g (x ),当x ∈(﹣1,1]时,g (x )=211,10132,01x x x x x ⎧--<≤⎪+⎨⎪-+<≤⎩,且g (x+2)=g (x )对∀x ∈R 恒成立,若函数f (x )=g (x )﹣m (x+1)在区间[﹣1,5]内有6个零点,则实数m 的取值范围是 A .(25,23) B .(﹣∞,25]∪(23,+∞)C .[25,23)D .[25,23] 第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.开始1,0i S ==cos 12i i a i π=⋅+iS S a =+2016?i <=1i i +结束S输出是否13.已知02sin a xdx π=-⎰,则二项式52a x x ⎛⎫+ ⎪⎝⎭的展开式中x 的系数为 .14.已知向量()1,3a =,向量()3,b m =.若向量b 在向量a 方向上的投影为3,则实数m = .15.设数列{}n a 的前n 项和为n S ,且121a a ==,{}(2)n n nS n a ++为等差数列,则数列{}n a 的通项公式n a = . 16.设点P 在曲线xe y 21=上,点Q 在曲线)2ln(x y =上,则||PQ 的最小值为 .三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分) 如图所示,在四边形ABCD 中, D ∠=2B ∠,且1AD =,3CD =,3cos 3B =. (Ⅰ)求△ACD 的面积;(Ⅱ)若23BC =,求AB 的长.18.(本小题满分12分)2015年高中学业水平考试之后,为了调查同学们的考试成绩,随机抽查了某高中的高二一班的10名同学的语文、数学、英语成绩,已知其考试等级分为A ,B ,C ,现在对他们的成绩进行量化:A 级记为2分,B 级记为1分,C 级记为0分,用(x ,y ,z )表示每位同学的语文、数学、英语的得分情况,再用综合指标w=x+y+z 的值评定该同学的得分等级.若w≥4,则得分等级为一级;若2≤w≤3.则得分等级为二级;若0≤w≤1,则得分等级为三级.得到如下结果:(Ⅰ)在这10名同学中任取两人,求这两位同学英语得分相同的概率;(Ⅱ)从得分等级是一级的同学中任取一人,其综合指标为a ,从得分等级不是一级的同学中任取一人,其综合指标为b,记随机变量X=a ﹣b ,求X 的分布列及其数学期望.19.(本小题满分12分)如图,在三棱柱ABC ﹣A 1B 1C 1中,∠BAC=90°,AB=AC=2,A 1A=4,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.(1)证明:A 1D ⊥平面A 1BC ;(2)求二面角A 1﹣BD ﹣B 1的平面角的余弦值.20.(本小题满分12分)如图,已知00(,)M x y 是椭圆C :13622=+y x 上的任一点,从原点O 向圆M :()()22002x x y y -+-=作两条切线,分别交椭圆于点P 、Q .(Ⅰ)若直线OP ,OQ 的斜率存在,并记为1k ,2k ,求证:12k k 为定值; (Ⅱ)试问22OP OQ +是否为定值?若是,求出该值;若不是,说明理由.人员编号A 1A 2A 3A 4A 5A 6A 7A 8A 9A 10(x ,y ,z ) (1,1,2) (2,1,1) (2,2,2) (0,0,1) (1,2,1) (1,2,2) (1,1,1) (1,2,2) (1,2,1) (1,1,1)ABCD21.(本小题满分12分)设函数2()ln (32)f x x a x x =+-+,其中a R ∈. (Ⅰ)讨论()f x 极值点的个数;(Ⅱ)设12a =-,函数()2()(3)2g x f x x λ=-++,若1x ,2x (12x x ≠)满足12()()g x g x =且1202x x x +=,证明:0'()0g x ≠.请考生在第22、23、24题中任选一题做答.答题时请写清题号并将相应信息点涂黑. 22.(本小题满分10分)【选修4-1:几何证明选讲】如图,正方形ABCD 边长为2,以D 为圆心、DA 为半径的圆弧与以BC 为直径的半圆O 交于点F ,连结CF 并延长交AB 于点E .(Ⅰ)求证:AE EB =; (Ⅱ)求EF FC ⋅的值.23.(本小题满分10分)【选修4-4:坐标系与参数方程】已知曲线C 的参数方程是⎩⎨⎧+=+=θθsin 2c os1y x (θ为参数),直线l 的极坐标方程为24s in =⎪⎭⎫⎝⎛+πθρ.(其中坐标系满足极坐标原点与直角坐标系原点重合,极轴与直角坐标系x 轴正半轴重合,单位长度相同.)(Ⅰ)将曲线C 的参数方程化为普通方程,将直线l 的极坐标方程化为直角坐标方程;(Ⅱ)设M 是直线l 与x 轴的交点,N 是曲线C 上一动点,求MN 的最大值. 24.(本小题满分10分)【选修4-5:不等式选讲】已知函数122)(--+=x x x f . (Ⅰ)求不等式2)(-≥x f 的解集;(Ⅱ)对任意[)+∞∈,a x ,都有)(x f a x -≤成立,求实数a 的取值范围.EFOB CAD福州八中2015—2016学年高三毕业班第六次质量检查数学(理)试卷参考答案及评分标准一.选择题:本大题共12小题,每小题5分.题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DACCABCDDDDC二.填空题:本大题共4小题,每小题5分. 13.640- 14.3 15.12n n- 16.)2ln 1(2- 三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)解:(Ⅰ)311cos 22cos cos 2-=-==B B D ………………………2分 因为()0,D π∠∈,所以22sin 3D =,…………………………4分 所以△ACD 的面积1sin 22S AD CD D =⋅⋅⋅=.………………6分 (Ⅱ)解法一:在△ACD 中,12cos 2222=⋅⋅-+=D DC AD DC AD AC , 所以23AC =.……………………………………………………8分在△ABC 中,12cos 2222=⋅⋅-+=B BC AB BC AB AC ……………10分 把已知条件代入并化简得:042=-AB AB 因为0AB ≠,所以4AB = ……12分 解法二:在△ACD 中,在△ACD 中,12cos 2222=⋅⋅-+=D DC AD DC AD AC , 所以23AC =.…………………………………………………………8分因为23BC =,sin sin AC ABB ACB=∠,所以 ()23sin sin 2AB B B π=-,………10分 得4AB =.…………………………………………………………………………12分18.(本小题满分12分)试题解析:解:(Ⅰ)在这10名同学中任取两人,基本事件总数n==45,……………1分 ∵A 1,A 3,A 6,A 8等4名学生的英语成绩都是2分,另外6名学生的英语成绩都是1分, ∴任取的两名学生的英语成绩相同的基本事件个数m==21,………3分 ∴这两位同学英语得分相同的概率p=.…………………………4分(Ⅱ)得分等级是一级的同学有A 1,A 2,A 3,A 5,A 6,A 8,A 9,其中A 1,A 2,A 5,A 9的综合指标为4,A 6,A 8的综合指标为5,A 3的综合指标为6,得分等级为二级的同学有A 4,综合指标为1,A 7,A 10,综合指标都是3,∴X 的可能取值为1,2,3,4,5,………………………………5分P (X=1)==,………………………………6分P (X=2)==,………………………………7分P(X=3)==,………………………………8分P(X=4)==,………………………………8分P(X=5)==,………………………………9分∴X的分布列为:X 1 2 3 4 5P……………………………………………………10分所以,X的数学期望EX==.…………12分考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,在历年高考中这部分内容都是必考知识点,是中档题.19.(本小题满分12分)【试题解析】(1)证明:如图,以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系.………………1分则BC=AC=2,A1O==,易知A1(0,0,),B(,0,0),C(﹣,0,0),A(0,,0),D(0,﹣,),B1(,﹣,),……………2分=(0,﹣,0),=(﹣,﹣,),=(﹣,0,0),=(﹣2,0,0),=(0,0,),……………………4分∵•=0,∴A1D⊥OA1,又∵•=0,∴A1D⊥BC,又∵OA1∩BC=O,∴A1D⊥平面A1BC;……………………6分(2)解:设平面A1BD的法向量为=(x,y,z),由,得,取z=1,得=(,0,1),…7分设平面B1BD的法向量为=(x,y,z),由,得,取z=1,得=(0,,1),8分∴cos<,>===,………10分又∵该二面角为钝角,……………………11分∴二面角A1﹣BD﹣B1的平面角的余弦值为﹣.……………………12分考点:二面角的平面角及求法;直线与平面垂直的判定.点评:本题考查空间中线面垂直的判定定理,考查求二面角的三角函数值,注意解题方法的积累,属于中档题. 20.(本小题满分12分) 【试题解析】(1)因为直线OP :1y k x =以及OQ :2y k x =与圆M 相切,所以21||21001=+-ky x k ,化简得:022)2(201002120=-+--y k y x k x ……………………1分 同理:022)2(202002220=-+--y k y x k x ,……………………2分 20122022y k k x -∴⋅=-………………………………3分 因为点00(,)M x y 在椭圆C 上,所以2200163x y +=,即2200132y x =-,……4分 所以201220111222x k k x -==--.………………6分(2)22OP OQ +是定值,定值为9.………………7分理由如下: 法一:(i )当直线OP 、OQ 不落在坐标轴上时,设),(,),(2211y x Q y x P ,联立122,1,63y k x x y =⎧⎪⎨+=⎪⎩解得21212211216,126.12x k k y k ⎧=⎪+⎪⎨⎪=⎪+⎩所以222111216(1)12k x y k ++=+, 同理,得222222226(1)12k x y k ++=+,………………9分由1212k k =-,所以2222221122OP OQ x y x y +=+++221222126(1)6(1)1212k k k k ++=+++ 2211221116(1())6(1)211212()2k k k k +-+=+++-212191812k k +=+9=……………………10分 (ii )当直线OP 、OQ 落在坐标轴上时,显然有22OP OQ +9=,…………11分 综上:22OP OQ +9=……………………9分法二:(i )当直线OP 、OQ 不落在坐标轴上时,设),(,),(2211y x Q y x P , 因为1212k k =-,所以2222121214y y x x =,…………………………7分因为),(,),(2211y x Q y x P 在椭圆C 上,所以22112222163163x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,即22112222132132y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩,…8分所以22221212111(3)(3)224x x x x --=,整理得22126x x +=,所以222212121133322y y x x ⎛⎫⎛⎫+=-+-= ⎪ ⎪⎝⎭⎝⎭,所以22OP OQ +9=.…………10分(ii )当直线OP 、OQ 落在坐标轴上时,显然有22OP OQ +9=,…………11分综上:22OP OQ +9=.…………………………12分考点:1.椭圆的定义与几何性质;2.直线与圆的位置关系;3.直线与椭圆的位置关系. 21.(本小题满分12分)【试题解析】(1)函数()f x 的定义域为(0,)+∞,1(23)1'()(23)ax x f x a x x x-+=+-=.……1分 令()(23)1g x ax x =-+.①当0a =时,()1x ϕ=,()ln f x x =,所以,函数()f x 在(0,)+∞上单调递增,无极值;……2分②当0a <时,()x ϕ在3(0,)4上单调递增,在3(,)4+∞上单调递减,且(0)10ϕ=>,所以,()x ϕ在(0,)+∞上有唯一零点,从而函数()f x 在(0,)+∞上有唯一极值点;…………3分③当0a >时,若39()1048a ϕ=-≥,即809a <≤时,则()0x ϕ≥在(0,)+∞上恒成立,从而'()0f x ≥在(0,)+∞上恒成立,函数()f x 在(0,)+∞上单调递增,无极值;…………4分若39()1048a ϕ=-<,即89a >,由于(0)10ϕ=>,则()x ϕ在(0,)+∞上有两个零点,从而函数()f x 在(0,)+∞上有两个极值点.………………5分综上所述:当0a <时,函数()f x 在(0,)+∞上有唯一极值点; 当809a ≤≤时,函数()f x 在(0,)+∞上无极值点; 当89a >时,函数()f x 在(0,)+∞上有两个极值点.…………………………6分 (2)2()2ln g x x x x λ=--,2()2g x x xλ=--.假设结论不成立,则有22111222120002ln 2ln , 2,220,x x x x x x x x x x x λλλ⎧⎪--=--⎪⎪+=⎨⎪⎪--=⎪⎩①②③…………7分由①,得221121222ln ()()0x x x x x x λ----=,∴12012ln 22x x x x x λ=--,……8分由③,得0022x x λ=-,∴12120ln1x x x x x =-,即121212ln 2xx x x x x =-+,即11212222ln 1x x x x x x -=+.④……9分 令12x t x =,不妨设12x x <,22()ln 1t u t t t -=-+(01t <<),………………10分 则22(1)'()0(1)t u t t t -=>+,………………11分 ∴()u t 在01t <<上增函数,()(1)0u t u <=,∴④式不成立,与假设矛盾. ∴0'()0g x ≠.………………12分考点:1、利用导数研究函数的单调性;2、函数的极值;3、反证法. 在第22、23、24题中任选一题做答. 22(本小题满分10分) 解:(Ⅰ)由以D 为圆心DA 为半径作圆,而ABCD 为正方形,∴EA 为圆D 的切线 ………………………………………………(1分)依据切割线定理得2EA EF EC =⋅ ………………………………(2分) 另外圆O 以BC 为直径,∴EB 是圆O 的切线,………………(3分) 同样依据切割线定理得2EB EF EC =⋅……………………………(4分) 故AE EB =………………………………………(5分) (Ⅱ)连结BF ,∵BC 为圆O 直径,∴BF EC ⊥ ………………………………(6分)由BF CE BE BC S BCE ⋅=⋅=∆2121 得552521=⨯=BF …………………………(8分) 又在Rt BCE∆中,由射影定理得542==⋅BF FC EF ……………………(10分) 23.(本小题满分10分)解:(Ⅰ)曲线C 的参数方程可化为 ()()12122=-+-y x ………………(2分) 直线l 的方程为24sin =⎪⎭⎫⎝⎛+πθρ展开得 2sin cos =+θρθρ…………(4分)直线l 的直角坐标方程为 02=-+y x ………………………………………(5分)(Ⅱ)令0y =,得2x =,即M 点的坐标为(2,0)………………………(6分) 又曲线C 为圆,圆C 的圆心坐标为()2,1,半径1r =,则5MC =………(8分) 所以51MN MC r +=+≤,MN ∴的最大值为51+.…………………(10分) 24(本小题满分10分) 解:(Ⅰ)()f x ≥-2当2-≤x 时,24-≥-x , 即2≥x ,∴φ∈x ;………………………………(1分)当12<<-x 时,23-≥x ,即32-≥x ,∴213x -≤< …………………………(2分) 当1≥x 时,24-≥+-x , 即6≤x , ∴1≤x ≤6 ………………………………(3分)E FOBCAD综上,解集为{x |23-≤x ≤6} …………………………………………………(4分) (Ⅱ)⎪⎩⎪⎨⎧≥+-<<--≤-=1,412,32,4)(x x x x x x x f ,……………………………………(5分)令a x y -=,a -表示直线的纵截距,当直线过()1,3点时,2=-a ; ∴当a-≥2,即a ≤-2时成立;……………………………………………(7分)当2<-a ,即2->a 时,令a x x -=+-4, 得22ax +=, ∴a ≥2+2a,即a ≥4时成立,………………………………………………(9分) 综上a ≤-2或a ≥4 …………………………………………………………(10分)。
福州八中高三毕业班第六次质量检查

第9题图高中化学学习材料(灿若寒星**整理制作)福州八中2015—2016学年高三毕业班第六次质量检查理科综合考试时间:150分钟 试卷满分:300分2016.2.16第Ⅰ卷(选择题共126分)一、选择题:本题共13小题,每题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
7.化学与生活密切相关。
下列说法不正确的是 A .用含增塑剂的聚氯乙烯薄膜作食品包装材料 B .用浸泡过高锰酸钾溶液的硅藻土保鲜水果 C .次氯酸钠溶液可用于环境的消毒杀菌D .中国古代用明矾溶液的酸性清洗铜镜表面的铜锈8.设N A 表示阿伏加德罗常数的值,下列叙述正确的是A .电解精炼铜,当电路中通过的电子数为0.1N A 时,阳极质量减少为3.2gB .0.5L1 mol•L -1NaHS 溶液中,Na +和HS -离子数之和为N AC .Na 2O 2和Na 2S 的固体混合物7.8g ,其中Na +数为0.3N AD .3.0g 甲醛和甲酸甲酯的混合物中含有的原子数为0.4N A9.用如图所示装置进行下列实验:将①中溶液滴入②中,预测的现象与实际相符的是10.分子式为C 10H 20O 2的酯,在一定条件下可发生如下图的转化过程:则符合上述条件的酯的结构可有A .2种B .4种C .6种D .8种11.下列离子方程式书写正确的是 A .Fe(OH)3溶于氢碘酸:Fe(OH)3+3H +=Fe 3++3H 2OB .Ca(HCO 3)2溶液与少量NaOH 溶液反应:HCO 3-+Ca 2++OH -=CaCO 3↓+H 2O选项①中物质②中物质预测②中的现象A 稀H 2SO 4 纯碱溶液 立即产生气泡B 无水乙醇酸性KMnO 4溶液立即褪色 C 偏铝酸钠溶液 稀盐酸 立即产生白色沉淀D 稀盐酸滴有酚酞的水玻璃 产生胶冻状的难溶物图1图2 C.以石墨作电极电解氯化铝溶液:2Cl-+2H2O电解2OH-+H2↑+Cl2↑D.FeBr2与等物质的量的Cl2反应:2Fe2++4Br-+3Cl2=2Fe3++6Cl-+2Br212.人工光合作用能够借助太阳能,用CO2和H2O制备化学原料。
福建省福州八中高三数学第六次质检考试试题 理 新人教A版
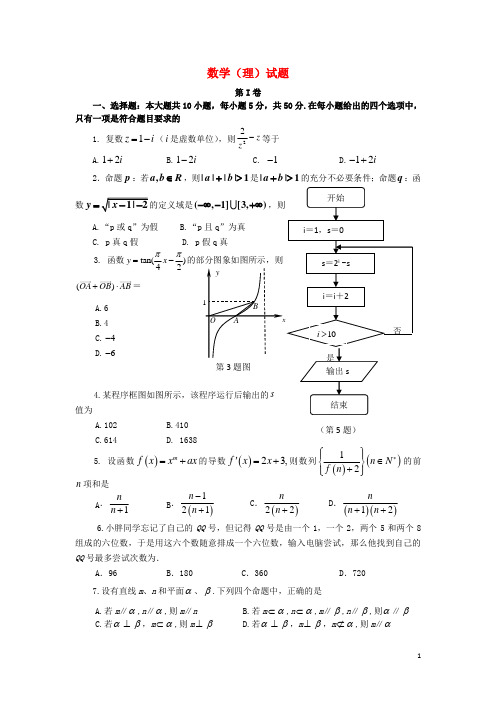
第3题图(第5题)数学(理)试题第I 卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的1. 复数1z i =-(i 是虚数单位),则22zz-等于A.12i +B.12i -C. 1-D.12i -+2.命题p :若,a b R ∈,则||||1a b +>是||1a b +>的充分不必要条件;命题q :函数y =(,1][3,)-∞-+∞,则 A.“p 或q ”为假 B.“p 且q ”为真C. p 真q 假D. p 假q 真3. 函数tan()42y x ππ=-的部分图象如图所示,则()OA OB AB +⋅= A.6B.4C.4-D.6-4.某程序框图如图所示,该程序运行后输出的s 值为 A.102 B.410C.614D. 16385. 设函数()mf x x ax =+的导数()23,f x x '=+则数列()()12n N f n *⎧⎫⎪⎪∈⎨⎬+⎪⎪⎩⎭的前n 项和是A .1nn +B .()121n n -+C .()22n n +D .()()12nn n ++6.小胖同学忘记了自己的QQ 号,但记得QQ 号是由一个1,一个2,两个5和两个8组成的六位数,于是用这六个数随意排成一个六位数,输入电脑尝试,那么他找到自己的QQ 号最多尝试次数为.A .96B .180C .360D .7207.设有直线m 、n 和平面α、β.下列四个命题中,正确的是 A.若m ∥α,n ∥α,则m ∥n B.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β,m ⊂α,则m ⊥βD.若α⊥β,m ⊥β,m ⊄α,则m ∥α8.如果实数,x y 满足等式2y x =,那么1yx +的最大值是A .-1B.1C .-21D .219.已知两点M (0,0),N (126,55--),给出下列曲线方程:①4x+2y-1=0; ②x 2+y 2=3; ③222x y +=1; ④222x y -=1.在曲线上存在点P 满足|MP|=|NP|的所有曲线方程是A.①③B.②④C.①②③D.②③④10.若函数b ax x x f ++=2)(有两个不同的零点21,x x ,且3121<<<x x ,那么在(1),(3)f f 两个函数值中A.只有一个小于1B.至少有一个小于1C.都小于1D.可能都大于1 第Ⅱ卷二、.填空题:本大题5小题,每小题4分,共20分.11.已知数列{}n a 满足,*11212,,2n n n a a a a a n N ++=∈’+2==.令1n n n b a a +=-, 则1n nb b += . 12.已知2log (1),(0)()(3)(1)(2)(0)x x f x f f x f x x -≤⎧=⎨--->⎩,则的值等于 .13.如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量为 ___千克. 14.给出下列四个结论: ①“若22am bm <则a b <”的逆否命题为真; ②若0()f x 为()f x 的极值,则0()0f x '=; ③函数()sin f x x x =-(x R ∈)有3个零点;④对于任意实数x ,有()(),()()f x f x g x g x -=--=且x >0时,()0,()0f x g x ''>>,则x <0时()()f x g x ''>.其中正确结论的序号是 .(填上所有正确结论的序号) 15. 定义:, min{,}, a a b a b b a b ≤⎧=⎨>⎩,在区域0206x y ≤≤⎧⎨≤≤⎩内任取一点(,)P x y ,则x 、y满足22min{2,4}2x x y x y x x y ++++=++的概率为____________.三、解答题:本大题6小题,共80分.解答应写出文字说明,正明过程和演算步骤.16.(本小题满分13分) 甲,乙,丙三位学生独立地解同一道题,甲做对的概率为12,乙、丙做对的概率分别为m 和n (m >n ),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:(Ⅰ)求m ,n 的值;(Ⅱ) 记事件E ={函数2()231f x x x ξ=-++在区间[1,1]-上不单调},求()P E ; (Ⅲ)令12()10E λξ=-,试计算 (12||)x dx λλ--⎰的值.17.(本小题满分13分)如图,在六面体ABCDEFG 中,平面ABC ∥平面DEFG ,AD ⊥平面DEFG ,ED ⊥DG ,EF ∥DG.且AB =AD =DE =DG =2,AC =EF =1.(1)求证:BF ∥平面ACGD ; (2)求二面角D —CG —F 的余弦值. 18.(本小题满分13分)若向量(3cos ,sin ),(sin ,0),a x x b x ωωω==其中0ω>,记函数1()()2f x a b b =+⋅-,若函数()f x 的图像与直线y m =(m 为常数)相切,并且切点的横坐标依次成公差为π的等差数列. (1)求()f x 的表达式及m 的值; (2)将函数()y f x =的图像向左平移12π,得到()y g x =的图像,当7(,)24x ππ∈时,()y g x =与cos y α=图象的交点横坐标成等比数列,求钝角α的值.ξ0 1 23 P 14a b 12420. (本小题满分14分)已知函数3221()(1)ln(1)3f x x ax a x a =-+-++(其中a 为常数).(1)若()f x 在区间(1,1)-上不单调,求a 的取值范围;(2)若存在一条与y 轴垂直的直线和函数2()()(1)ln F x f x a x x =--+的图象相切,且切点的横坐标0x 满足02x >,求实数a 的取值范围;(3)记函数()y f x =的极大值点为m ,极小值点为n ,若3sin 25xm n +≥对于[0,]x π∈恒成立,试求a 的取值范围.21.(本小题满分14分)本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,多作不给分,满分14分.(1)已知,a b R ∈,矩阵⎥⎦⎤⎢⎣⎡-=b a A 21所对应的变换将直线10x y +-=变换为自身. ①求a,b 的值;②求矩阵A 的逆矩阵1-A .(2)已知直线l 的参数方程为⎩⎪⎨⎪⎧x =4-2t ,y =t -2(t 为参数),P 是椭圆x 24+y 2=1上任意一点,求点P 到直线l 的距离的最大值. (3)设函数f (x )=|x -a |+3x ,其中a >0. ①当a =1时,求不等式f (x )≥3x +2的解集; ②若不等式f (x )≤0的解集为{x |x ≤-1},求a 的值.福州八中2013—2014高三毕业班第六次质量检查数学(理)试卷参考答案及评分标准三、解答题:(本大题共6小题,共75分. 解答应写出文字说明、推理过程或演算步骤) 16.(本小题满分13分)解:设事件A ={甲做对},事件B ={乙做对},事件C ={丙做对},由题意知,12P A P B m P C n ===(),(),(). (Ⅰ) 由题意知1101124P P ABC m n ξ===--=()()()(), …………1分 113224P P ABC mn ξ====()(), …………………………2分 整理得:112mn =,712m n +=.由m n >,解得13m =,14n =. …………………………………………4分(Ⅱ)由题意知1a P P ABC P ABC P ABC ξ===++()()()() 11111111122224m n m n m n =--+-+-=()()()(), ……………………5分 函数2()231f x x x ξ=-++在区间[1,1]-上不单调,∴对称轴3(1,1)4x ξ=∈-4433ξ⇒-<<0ξ⇒=,或1ξ=……………………7分()(0)(1)P E P P ξξ∴==+=1111742424=+=………………………………………8分 (Ⅲ)(2)1(0)(1)(3)b P P P P ξξξξ===-=-=-==14,∴13()0(0)1(1)2(2)3(3)12E P P P P ξξξξξ=⨯=+⨯=+⨯=+⨯== …………10分12()103E λξ∴=-= 故33(12||)(12||)x dx x dx λλ---=-⎰⎰33(12)(12)x dx x dx -=++-⎰⎰202330()|()|12x x x x -=++-=- ………13分17.(本小题满分13分)解析:方法一:(1)设DG 的中点为M ,连接AM ,FM .则由已知条件易证四边形DEFM 是平行四边形.∴MF ∥DE ,且MF =DE . ∵平面ABC ∥平面DEFG ,∴AB ∥DE ,……………………………………2分 ∵AB =DE .∴MF ∥AB ,………………………………3分 又MF =AB ,∴四边形ABFM 是平行四边形, ∴BF ∥AM .……………………………………4分 又BF ⊄平面ACGD ,AM ⊂平面ACGD ,故BF ∥平面ACGD .…………………………6分 (2)由已知AD ⊥平面DEFG ,∴DE ⊥AD .又DE ⊥DG , ∴DE ⊥平面ADGC .∵MF ∥DE ,∴MF ⊥平面ADGC .在平面ADGC 中,过M 作MN ⊥GC ,垂足为N ,连接NF ,则∠MNF 为所求二面角的平面角. ………………8分连接CM .∵平面ABC ∥平面DEFG ,.∴cos ∠MNF =MN FN =2552305=66.∴二面角DCGF 的余弦值为66.…………13分方法二:由题意可得,AD ,DE ,DG 两两垂直,故可建立如图所示的空间直角坐标系.则A (0,0,2),B (2,0,2),C (0,1,2),E (2,0,0),G (0,2,0),F (2,1,0).………………2分(1)=(2,1,0)-(2,0,2)=(0,1,-2),=(0,2,0)-(0,1,2)=(0,1,-2),………………4分∴=,所以BF ∥CG . 又BF ⊄平面ACGD ,故BF ∥平面ACGD .……………………6分(2)=(0,2,0)-(2,1,0)=(-2,1,0). 设平面BCGF 的法向量为n 1=(x ,y ,z ), 则…………………………9分令y =2,则n 1=(1,2,1).则平面ADGC 的法向量n 2=(1,0,0).………………11分∴cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=1×112+22+12×12+02+02=66. 由于所求的二面角为锐二面角,∴二面角DCGF 的余弦值为66.………13分18.(本小题满分13分) (1)解:(3cos ,sin ),(sin ,0),a x x b x ωωω==211()()3cos sin sin(2)226f x a b b x x x x πωωωω∴=+⋅-=+-=-……4分由题意可知其周期为π,故1ω=,则()sin(2)6f x x π=-,1m =±.…………7分(2)解:将()sin(2)6f x x π=-的图像向左平移12π,得到()sin 2g x x =,……9分 由其对称性,可设交点横坐标分别为1113,,2x x x ππ-+, 有 2111139()(),216x x x x πππ-=+=则 ………………11分 95cos sin sin cos888πππα==-= 则58πα= ……13分 19.(本小题满分14分)(1)由题意可知直线l 的方程为0)23(=--+c cy bx ,…………2分因为直线与圆1)3(:222=-+y x c 相切,所以123322=++-=cb cc cd ,……4分即,222c a =从而;22=e …………………6分 (2)设),(y x P 、圆2C 的圆心记为2C ,则122222=+cy c x (c ﹥0),又22222222)()(N C PC N C PC M C PC PN PM -=+⋅+=⋅=)(172)3(1)3(2222c y c c y y x ≤≤-+++-=--+ . …………………10分 ①当但解得时,325,49217)3()(3022-==+++--=⋅<<c c c c MAX,3325>-=c 故舍去;……………………………………………12分②当此时椭圆方程为解得时,,4,49217)(32==+=⋅≥c c c MAX 1163222=+y x. 综上所述,椭圆的方程为1163222=+y x . …………………14分 20. (本小题满分14分)解:(Ⅰ)3221()(1)ln(1)3f x x ax a x a =-+-++,22()21f x x ax a '∴=-+- …………………………1分因为函数()f x 在区间(1,1)-不单调,所以函数()f x '在(1,1)-上存在零点. 而()0f x '=的两根为1a -,1a +,区间长为2, ∴()f x '在区间(1,1)-上不可能有2个零点.所以(1)(1)0f f ''-<, ……………………………………2分即2(2)(2)0a a a +-<,又由题意可知:1a >-∴(1,0)(0,2)a ∈-.……………………………………………………4分(Ⅱ)2321()()(1)ln ln ln(1)3F x f x a x x x ax x a =--+=-+++,21()2F x x ax x'=-+,存在一条与y 轴垂直的直线和函数2()()(1)ln F x f x a x x =--+的图象相切,且切点的横坐标0x ,200001()20F x x ax x '∴=-+=02011()2a x x ⇒=+,0(2)x >………………6分 令211()()2h x x x =+(2)x >,则312()(1)2h x x'=-当2x >时,312()(1)02h x x'=->,∴211()()2h x x x =+在(2,)+∞上为增函数,从而0020119()()(2)28h x x h x =+>=,又由题意可知:1a >-98a ∴> ………………………………………………………9分(Ⅲ)22()21f x x ax a '=-+-,,由2()03h x x π'=⇒=, 当2[0,)3x π∈时,()0h x '>,当2(,]3x ππ∈时,()0h x '<, ∴当23x π=时,()h x 取最大值为2()13h π=,……………………………13分 为满足题意,必须max 25()m n h x +≥,所以731a +≥,又由题意可知:1a >-, 27a ∴≥- …………………………………………14分21.(本小题满分14分)(1)①取直线10x y +-=上两点(0,1),(1,0),由⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-20121,11021a b a b b a 在矩阵A 所对应的线性变换作用下的的象是(1,b ),(-a ,2)仍在直线10x y +-=上,代入直线方程,得a=1,b=0……………………………………4分②设⎥⎦⎤⎢⎣⎡=-q p n m A 1,由⎥⎦⎤⎢⎣⎡=-10011AA ,得⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡10010211q p n m∴⎪⎪⎩⎪⎪⎨⎧==+-==+-102012p q p m n m ,解得:⎪⎪⎪⎩⎪⎪⎪⎨⎧====211210q p n m ,即⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-2112101A …………………………7分 另解:∵20211-=-=A ,由公式,得∴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-------=-211210212221201A ………………7分(2)直线l 的参数方程为⎩⎪⎨⎪⎧x =4-2t ,y =t -2(t 为参数),故直线l 的普通方程为x +2y =0.……1分 因为P 为椭圆x 24+y 2=1上任意点,故可设P (2cos θ,sin θ),其中θ∈R .……2分 因此点P 到直线l 的距离是d =|2cos θ+2sin θ|12+22=…5分所以当θ=k π+π4,k ∈Z 时,d 取得最大值2105 (7)分(3)①当a =1时,f (x )≥3x +2可化为|x -1|≥2. 由此可得x ≥3或x ≤-1.故不等式f (x )≥3x +2的解集为{x |x ≥3或x ≤-1}.……………………3分 ②由f (x )≤0得|x -a |+3x ≤0. 此不等式化为不等式组⎩⎪⎨⎪⎧x ≥a x -a +3x ≤0或⎩⎪⎨⎪⎧x ≤aa -x +3x ≤0 即⎩⎪⎨⎪⎧x ≥a ,x ≤a4,或⎩⎪⎨⎪⎧x ≤a ,x ≤-a2 (5)分因为a >0,所以不等式组的解集为{x |x ≤-a2}.由题设可得-a2=-1,故a =2.……7分。
福建省福州市第八中学高三毕业班第六次质量检查语文试卷

【精品】福建省福州市第八中学高三毕业班第六次质量检查语文试卷学校:___________姓名:___________班级:___________考号:___________一、句子默写1.补写出下列名句名篇中的空缺部分。
(6分)(1)兄弟不知,。
(《诗经·氓》)(2),依依墟里烟。
(陶渊明《归园田居》)(3)春江花朝秋月夜,。
(白居易《琵琶行并序》)(4)想当年,气吞万里如虎。
(辛弃疾《永遇乐京口北固亭怀古》)(5)本图宦达,。
(李密《陈情表》)(6)___________________,拄杖无时夜叩门。
(陆游《游山西村》)二、文言文阅读阅读下面文言文,完成后面的题。
焚驴志王若虚岁己未,河朔大旱,远迩焦然无主赖①。
镇阳帅自言忧农,督下祈雨甚急。
厌禳②小数靡不为之,竟无验。
既久,怪诬之说兴。
适民家有产白驴者,或指曰:“此旱之由也。
云方兴,驴辄仰号之,云辄散不留。
是物不死,旱胡得止?”一人臆倡,众万以附。
帅闻之以为然,命亟取,将焚之。
驴见梦于府之属某曰:“冤哉焚也!天祸流行,民自罹之,吾何预焉?吾生不幸为异类,又不幸堕于畜兽。
乘负驾驭,惟人所命;驱叱鞭篓,亦惟人所加;劳辱以终,吾分然也。
若乃水旱之事,岂其所知,而欲置斯酷欤?孰诬我者,而帅从之!祸有存乎天,有因乎人。
人者可以自求,而天者可以委之也。
殷之旱也,有桑林之祷③,言出而雨。
卫之旱也,为伐邢之役④,师兴而雨。
汉旱,卜式请烹弘羊;唐旱,李中敏乞斩郑注。
救旱之术多矣,盍亦求诸是类乎?求之不得,无所归咎,则存乎天也,委焉而已。
不求诸人,不委诸天,以无稽之言,而谓我之愆。
嘻,其不然!暴巫投魃⑤,既已迂矣,今兹无乃复甚?杀我而有利于人,吾何爱一死?如其未也,焉用为是以益恶?滥杀,不仁;轻信,不智;不仁不智,帅胡取焉?吾子,其属也,敢私以诉。
”某谢而觉,请诸帅,而释之。
人情初不怿也。
未几而雨,则弥月不解,潦溢伤禾,岁卒以空。
人无复议驴。
[注]①无主赖:无所依恃。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20XX年中学测试
中
学
试
题
试
卷
科目:
年级:
考点:
监考老师:
日期:
2021-2021福建省福州八中高三毕业班第六次质量检查
理科综合试题化学部分
考试时间:150分钟试卷满分:300分
可能用到的相对原子质量:
H—1 O—16 N—14 Na—23 C—12 Ba—137 S—32 Cu—64 Cl—35.5
第Ⅰ卷(选择题共21,每小题6分,共126分)
一、选择题(在每小题给出的四个选项中,只有一个选项最符合题目要求)
6.据报道,月球上有大量3He存在。
以下关于3He的说法正确的是()
A.是4He的同分异构体B.比4He多一个中子
C.是4He的同位素D.比4He少一个质子
7.下列说法不正确的是()A.NaOH、SO2、CH2=CH2都能使溴水褪色,但原理各不相同
B.活性炭、氯气和二氧化硫都能使品红溶液褪色,且原理相同
C.Al、NaHCO3、CH3COONH4既能跟盐酸反应,又能跟烧碱溶液反应
D.C6H5OH、FeSO4溶液、Na2SO3溶液在空气中都易因氧化而变质
8.在容积不变的密闭容器中,一定条件下进行如下反应:
NO(g)+ CO(g)N2(g)+ CO2(g);△H=-373.2kJ/mol。
下图曲线a表示该反应过程中,NO的转化率与反应时间的关系。
若改变起始条件,使反应过程按照曲线b进行,可采取的措施是()
A.加催化剂B.向密闭容器中通入氩气
C.降低温度D.增大反应物中NO的浓度
9.下列各组比较中,前者比后者大的是()
A.25℃,pH均为2的盐酸和CH3COOH溶液中溶质的物质的量浓度
B.将pH=4的盐酸和醋酸分别稀释成pH=5的溶液,所加水的量
C.同温、同浓度的NaCl溶液和氨水的导电能力
D.25℃时,pH均为3的HCl和FeCl3溶液中水的电离程度
10.某电解池内盛有某电解质溶液,插入两根电极,通电后欲达到下列要求:①阳极质量不变②阴极质量增加③电解液pH变小。
则可选用的电极材料和电解质溶液是()
A.铂做阳极、铜做阴极,电解硫酸铜溶液
B.石墨做阳极和阴极,电解硫酸
C.铜做阳极、铁做阴极,电解氯化铜溶液
D.铜做阳极、铜做阴极,电解硫酸铜溶液
11.设N A为阿伏加德罗常数值,下列说法正确的是()
A.7.8gNa2O2与足量的CO2反应,转移的电子数为0.2N A
B.常温常压时,36g重氧(18O2)气体所含分子数为N A
C.17g羟基中含有的电子数为10N A
D.标准状况下,22.4L苯所含的分子数约为N A
12.下列离子方程式,正确的是()
A.往NaOH溶液中滴加少量AlCl3溶液Al3+ + 3OH— == Al(OH)3↓
B.石灰石和盐酸溶液反应CO32—+ 2H+ === CO2↑+ H2O
C.向氯化亚铁溶液中通入氯气Fe2+ + Cl2 == Fe3+ + 2Cl—
D.向Ba(OH)2溶液中逐滴加入NaHCO3溶液至Ba2+刚好沉淀完全:
Ba2++OH-+HCO3-=BaCO3↓+H2O
13.某有机物A是农药生产中的一种中间体,其结构简式如下,下列叙述正确的是()
A.有机物A属于芳香烃
B.有机物A可以和Br2的CCl4溶液发生加成反应
C.有机物A和浓硫酸混合加热,可以发生消去反应
D.1molA和足量的NaOH溶液反应,最多可以消耗3molNaOH
第Ⅱ卷(非选择题共10小题,共174分)
26.(10分)以海水中常见物质A为原料可以发展很多种工业,下图中包含了中学课本中介绍的几种基本工业生产,请根据各物质之间的转化关系回答下列问题:
(1)C 和D 、C 和G 反应都可以制取消毒剂。
C 和G 反应制取的消毒剂中有效成分的
化学式为______________________。
(2)电解A 溶液反应的离子方程式为_______________________________
(3)将F 和J 通入A 的饱和溶液中,反应的化学方程式为:
_____________________________________________________________________
(4)图中所示工业制法获得的纯碱中常含有NaCl 杂质,用下述方法可以测定样品中
NaCl 的质量分数。
①检验沉淀是否洗涤干净的方法是_________________________________
②样品中NaCl 的质量分数的数学表达式为__________________________
27.(15分)A 、B 、C 是中学化学常见的三种短周期元素,已知①A 元素原子最外层电子数
是次外层电子数的2倍;②B 元素最高正价与负价的代数和为2;③C 元素有多种化合价,且常温下C 元素的单质与某种一元碱溶液反应,可得两种含C 元素的化合物;④B 、C 两种元素质子数之和是A 元素质子数的4倍。
(1)写出A 、B 、C 三种元素的名称ABC
(2)写出B 的最高价氧化物的水化物与A 的单质反应的化学方程式:
(3)由B 、C 两种元素组成的化合物X ,常温下为易挥发的淡黄色液体,X 分子为三角
锥形分子,且分子里B 、C 两种原子最外层均达到8个电子的稳定结构。
X 遇水蒸气可生成一种常见的漂白性物质;则X 的分子式为,分子中B 、C 原子间的化学键类型为(填“极性键”或“非极性键”); X 与水反应的化学方程式为
(4)A 、B 两元素可形成一种硬度比金刚石还大的化合物Y ,化合物Y 中,A 、B 两原
克
固体称量低温烘干、冷却洗涤水沉淀过滤溶液过量溶液样品n BaCl 溶解O H 克m 22−−−−−−−→−−−→−−−−−−−−→−−−→−
子以单键相结合,且每个原子最外层均达到8个电子的稳定结构,则Y的化学式
为,Y的硬度比金刚石硬度大的原因是:
28.(18分)某芳香烃A有如下六步转化:
(1)写出反应类型:②⑤
(2)写出结构简式A,D
(3)写出E所含的官能团
(4)写出反应②和⑥的化学方程式
②
⑥
(5)有机物的同分异构体有多种,写出同时满足:
①遇FeCl3溶液显紫色,②苯环上的一氯取代物中只有两种,③属于酯类三个要求
的同分异构体的结构简式三种
29.(17分)某研究小组用如图所示装置进行铜与浓硫酸反应的实验研究。
(1)写出试管B中的实验现象____________________________________。
(2)写出A中反应的化学方程式:___________________________。
(3)充分反应后,若A试管中有铜片剩余,继续向A中加入H2O2,发现铜片溶解,反应的离子方程式为__________。
(4)充分反应后,若A试管中无铜片剩余,但出现白色混浊,该白色固体是________,
初步确认该白色固体是什么物质的实验操作方法是__________________。
(5)B试管口的棉花应沾有的试剂是____________________________________。
(6)小组成员向(3)反应后的溶液中加入足量的氧化铜。
使剩余的硫酸全部转化为硫酸铜,过滤后,将滤液加热浓缩,冷却后结晶制得硫酸铜晶体(CuSO4·xH2O)。
小组成员采用加热法测定该晶体里结晶水x的值
①在他们的实验操作中,至少称量四次,最后两次称量的目的是
②下面是其中一次实验的数据:
坩埚质量坩埚与晶体的总质量加热后坩埚与固体总质量
11.0g 37.8g 27.0g
根据上表数据计算判断x的实测值比理论值(x=5)____________(填“偏大”、“偏小”),这次实验中产生误差的原因可能是__________(填序号)
A.硫酸铜晶体中含有不挥发的杂质B.实验前晶体表面有湿存水
C.加热时有晶体飞溅出去D.加热失水后露置在空气中冷却。
