数理方程作业
数理方程第二次作业参考答案

第二次作业1.化下列方程为标准形式:0=+yy xx yu u解:根据题意可得y c b a ===,0,1,则有y ac b -=-=∆2。
(1)当0=y 时,0=∆,方程为抛物型方程,标准形式为0=xx u ;(2)当0>y 时,0<∆,方程为椭圆型方程,对应的特征方程为022=+ydx dy解得两条特征线为C ix y =±2 选取变换x y ==ηξ,2,带入原方程可得01=-+ξηηξξξu u u (3)当0<y 时,0>∆,方程为双曲型方程,对应的特征方程为022=+ydx dy解得两条特征线为C x y =±--2 选取变换y x y x -+=--=2,2ηξ,带入原方程可得()()ηξξηηξu u u ---=21 2.确定下列方程的通解:023=+-yy xy xx u u u解:根据题意可得2,23,1=-==c b a ,0412>=-=∆ac b ,方程为双曲型方程,对应的特征方程为 02322=++dx dxdy dy解得两条特征线为212C x y C x y =+=+选取变换x y x y 2,+=+=ηξ,可把原方程化简为0=ξηu此方程的通解是()()ηξg f u +=其中是g f ,关于ηξ,的任意二次可微的连续函数,所以原方程的通解为()()y x g y x f u +++=2作业中出现的问题:第一题:1.有的同学以为特征线就是通解,这也太荒谬了。
2.有的同学没有讨论0=y 时候的情况。
3.作变量代换的时候有的同学设的变量很复杂,不可取。
另外化简的时候没有化到最简,方程中还包含y x ,。
此外有的同学认为书上最简形式的椭圆、双曲方程就是本题的结果,这是完全错误的。
还有计算问题也出现了很多。
第二题:1.到0=ξηu 这一步都没有什么大问题,主要是后面求这个积分出现了问题,一方面有的同学最后结果中后面还带着积分号,另一方面有很多同学都没有讨论g f ,和性质。
数理方程习题全解
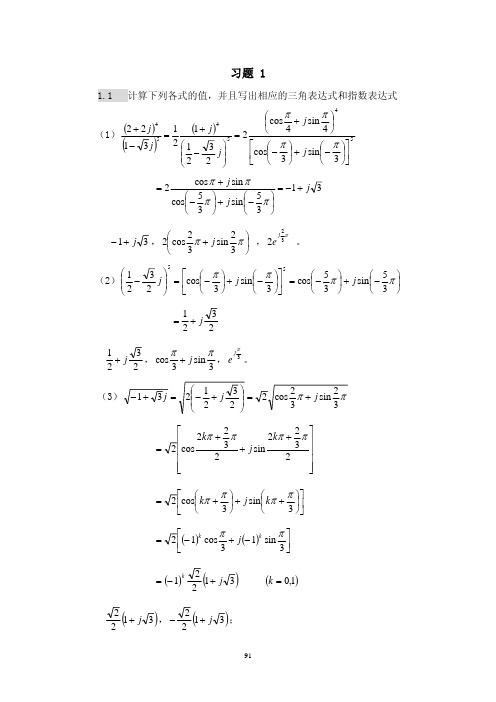
93
2k 1 j sin 2k 1 = 2 cos 4 4
k 0,1,2,3
1 1 k 0 : z1 2 cos j sin 2 j 1 j 4 4 2 2 3 3 1 1 k 1 : z2 2 cos j sin 2 j 1 j 4 4 2 2 5 5 1 1 k 2 : z3 2 cos j sin 2 j 1 j 4 4 2 2 7 7 1 1 k 3 : z4 2 cos j sin 2 j 1 j 4 4 2 2
3 8
k k 2 8 cos j sin 2 16 2 16
3 3 8 3
k 0,1,2,3
7 7 2 cos j sin , 2 8 cos j sin , 16 16 16 16 9 15 15 9 2 cos j sin , 2 8 cos j sin ; 16 16 16 16
1 3 5 5 (2) j sin cos j sin 2 2 j cos 3 3 3 3 1 3 j 2 2
4
cos j sin 4 4
4
2
cos j sin 1 j 3 5 5 cos j sin 3 3
数理方程30题

u(x,t) = cos at sin x
注记:如果用系数计算公式
∫ ∫ Cn
=
2 L
L sin(ξ ) sin(nξ )dξ
0
, Dn
=
2 nπa
L 0 × sin(nξ )dξ ,(n=1,2,……)
0
会得出同样结论。
例 8.用分离变量法求解双曲型方程初边值问题
⎧u ⎪⎪⎨u
[Cn
n=1
cos
nπ L
t
+
Dn
sin
nπ L
t]sin
nπ L
x
利用初值条件,得
∑ ∑ ∞ Cn
n=0
sin
nπ L
x
=
x(L −
x) , π L
∞
nDn
n=0
sin
nπ L
x
=
0
为计算系数,首先令ϕ(x) = x(L − x) ,显然ϕ(0) = 0,ϕ(L) = 0 ,且
ϕ′(x) = L − 2x ,ϕ′′(x) = −2
x x
+ +
C1 C2
⎡ ∂ξ
构造变换:
⎧ξ ⎩⎨η
= =
2 sin 4 sin
x x
+ +
cos cos
y y
,
⎢ ⎢ ⎢
∂x ∂η
⎢⎣ ∂x
∂ξ ⎤
∂y ∂η
⎥ ⎥ ⎥
=
⎡2 ⎢⎣4
cos cos
x x
∂y ⎥⎦
− sin y⎤ − sin y⎥⎦
所以, a12 = 8sin 2 y cos2 x − 18cos2 x sin 2 y + 8cos2 x sin 2 y = −2 cos2 x sin 2 y
数理方程习题解答

d dx
k
(x)
dy dx
q(x)
y
(x)
y
0
在第一类齐次边界条件及自然条件下
特征函数系
Pm (r)
J
n
(
(n m R
)
r)
m 1, 2,...
R 0
rJ
n
(
(n) m R
r
)J
n
(
(n) k R
r)dr
0 mk
R2 2
J
2 n1
(m(n)
)
R2 2
J
2 n1
(
(n m
)
)
mk
设
① ② ①-②
J0 ( x)
贝塞尔函数的图象
J1(x)
J 2 ( x)
J3 ( x)
贝塞尔方程在第一 类边界条件下的 特征值和特征函数
r2P(r) rP(r) (r2 n2 )P(r) 0
P(r) rR 0
P(r) r0
Jn ( R) 0
R
(n) m
(m 1, 2,...)
(n) m
(
(n) m
贝塞尔函数的性质(4)
二维热传导物理问题
u
t
a2
2u x2
2u y 2
u t0 (x, y)
,
x2 y2 R2
u 0 x2 y2 R2
u(x, y,t) V (x, y)T (t)
T (t) a2T (y 2
V
0
V 0 x2 y2 R2
贝塞尔函数的性质(1)
第一类贝赛尔函数:
在整个数轴上收敛,在每个指定的点都
取有限值 第二类贝赛尔函数:
数理方程课程第一次作业讲解

第一题:
设函数u(x,y,z)及矢量
A P(x, y,z)i Q(x, y,z) j R(x, y,z)k
的三个坐标函数都有二阶连续偏导数,求证:
(1)rot( gradu) 0 (2)div(rotA) 0 2u 2u 2u (3)div( gradu) 2 2 2 x y z
u ( x dx ) u ( x) u T x x F ( x) sin t t 2 dx
2
令a2=T/
2 2u u 2 a f ( x) sin t 2 2 t x
u( x, t ) x0 0
u( x, t ) x L 0
深圳大学电子科学与技术学院
u u u u u a t t t
2u u u u u u u 2 u 2 u a a a a t t t 2 2 u 2u 2u a 2 2 2
u u u u u x x x
2u u u u u u u u u 2 x x x 2u 2u 2u 2 2 2
u 2u
深圳大学电子科学与技术学院
第二题:
若F(z)、G(z)是任意两个二次连续可微函数, 验证u=F(x+at)+G(x-at)满足方程
2 2u u 2 a 2 2 t x
电子科大 数理方程(谷超豪)作业4

P746.用分离变量法求解由下述调和方程的第一边界问题所描述的矩形平板)0,0b y a x ≤≤≤≤(上的稳定温度分布:⎪⎪⎪⎩⎪⎪⎪⎨⎧=====∂∂+∂∂.0),(,sin )0,(0),(),0(02222b x u a x x u y a u y u y uxu π 解:令)()(),(y Y x X y x u =代入方程 ,得λ-=''-=''YY x X x X )()(再由一对齐次边界条件0),(),0(==y a u y u 得0)()0(==a X X由此得边值问题 ⎩⎨⎧===+''0)()0(0a X X X X λ由第一章讨论知,当2)(an n πλλ==时,以上问题有零解 .s i n )(x an x X n π= ),2,1( =n又 0)(2=-''n n Y an Y π求出通解,得yan n yan n n eB eA Y ππ-+=所以 ∑∞=-+=1.s i n)()(n ya n n yan n x an eB eA y x u πππ,由另一对边值,得⎪⎪⎭⎪⎪⎬⎫+=+=∑∑∞=-∞=11s i n )(0s i n )(s i n n b a n n b a n n n n n x a n e B e A x a n B A a xπππππ 由此得,⎪⎩⎪⎨⎧==+==+=+-,2,10,3,20111n e B e A n B A B A ba n nb a n nn n ππ,解得 bashe A baππ--=211 bashe B baππ211=,3,20===n B A n n代入),(y x u 的表达式得x ae e bash y x u y b ay b aππππsin)(121),()()(----⋅=x ay b xsh bashπππsin)(1-=P794.证明当u(M)在闭曲面Γ的外部调和,并且在无穷远处成立着 ))(1(),1()(2∞→=∂∂=oM oMoMr r o ru r o M u则公式(2.6)仍成立,但0M 是Γ外的任一点。
数理方程习题

第三章 习题
1 设y = y (x)是一条连接点A(0, a)和点B (l, b)的光滑曲线,即y = y (x) ∈ C 1 [0, l], 且y (0) = a, y (l) = b. 试建立连接A, B 两点的短程线所满足的变分问题以及等价的常微分方程边 值问题,并求出它的解. 2 求解以下变分问题: 设M = {v | v (x) ∈ C 1 [0, 1], v (1) = 0} 求u(x) ∈ M ,使得 J (u) = min J (v )
i=N +1
gi (φi , φ1 )H , · · ·
N +M ∑ i=N +1
)T gi (φi , φN )H .
由此可以看出通过变分原理与分片线性插值函数相结合,有限元方法从根本上 克服了Galerkin方法所带来的不足. 从而使变分方法焕发了新的生命力,得到 了工程与科学的很多领域的广泛认可,成为了当前解决实际问题的重要手段. 当然有关刚度矩阵的构成以及算法上的一些具体实施细节,例如区域的自动剖 分,节点的有序排列等内容已超出本课程的要求,在计算方法课程中有专门介 绍,在这里我们只介绍形成算法的基本原函数只能在Ω的边界∂ Ω上达 11 (强极值原理)一个定义在Ω 到它的最大和最小值. 试比较这个论断与定理4.2的差别. 提示:利用调和函数的平均值公式,通过反证法导出矛盾.
88
第三章 变分方法与近似求解
通过与上面完全相仿的推导,我们得到⃗ c = (c1 , · · · cN )T 适合的代数方程组 ⃗∗ , K⃗ c=f ⃗∗ 为 这里荷载向量f ⃗∗ = f ⃗− f ( N +M ∑
89
0<x<1
b. 取S N = Span{sin nπx, n = 1, · · · , 2N } 证明由Galerkin方法得到的近似解可 表为 uN (x) =
数理方程例题

数学物理方程例题和习题(2009-10-31)一、常微分方程回顾1.一阶常微分方程常数变易法用于解源函数不为零的常微分方程问题⎩⎨⎧=>=+'α)0(0),()()(y x x f x ry x y 先求解对应的齐次方程(源函数为零):0)()(=+'x ry x y用常微分方程分离变量方法:ry dxdy-= → rdx y dy -= → c rx y +-=ln 得齐次方程通解)exp()(rx C x y -=为了求解非齐次方程(源函数不为零),应用常数变易法。
将上式中C 替换为待定函数,设 )exp()()(rx x u x y -=对其求导数,得)exp()()exp()()(rx x u r rx x u x y ---'=')()exp()(x ry rx x u --'=将其代入非齐次方程,得)()exp()(x f rx x u =-' → )()exp()(x f rx x u ='→ C d f r x u x+=⎰)()ex p()(ξξξ代入表达式)exp()()(rx x u x y -=,得)ex p(])()ex p([)(0rx C d f r x y x-+=⎰ξξξ应用初始条件,得解函数⎰--+-=xd f x r rx x y 0)()](ex p[)ex p()(ξξξα从两部分解读解函数的意义。
第一部分利用了初始条件的信息,第二部分利用了微分方程右端项的信息。
它们分别是两个子问题的解⎩⎨⎧==+'α)0(0y ry y ,⎩⎨⎧==+'0)0()(y x f ry y 2.二阶常微分方程常数变易法二阶常微分方程初值问题⎩⎨⎧='=>=+''βαω)0(,)0(0),()()(2y y x x f x y x y 先考虑对应齐次方程:02=+''y y ω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 将函数 f ( x) = a(1 − x / l ), x ∈ (0, l ) 展开为傅立叶级数, 并使 f (0) =
f (l ) = 0
4. 试用分离变量法求解细杆导热问题,杆长为 l,两端保持为零度,
初始温度分布为 u t =0 = bx(l − x) / l 2
5. 长为 l 的均匀杆,两端受压长度变为 l (1 − 2ε ) ,放手后自由振动,
求解杆的振动。
6. 在铀块中,除了中子的扩散运动外,还进行着中子的增殖过程,
每秒钟在单位体积内产生的中子数正比于该处的中子浓度 u, 即可 表为βu,研究厚度为 l 的层状铀块,求其临界厚度(铀块厚度超 过临界厚度时,其中子浓度随时间急剧增长以致爆炸) 。
utt = a 2u xx , 7. 求 解 定 解 问 题 u x = 0 = 0, u x x =l = t , u t =0 = 0, ut t =0 = 0, 0 < x < l, t > 0 t≥0 0≤ x≤l
8. 在均匀静电场 E0 中放置一接地的导体球,球的半径为 R,求球外
电场的电势。
数理方程作业
1. 长为 l 的均匀弦, 两端 (x = 0, l) 固定, 弦中张力 T0, 在点 x = h 处
以横向力 F 拉弦,达到平衡后放手后任其自由振动,写出初始条 件,并表为定解问题。
2. 长为 l 的均匀杆,初始温度为 u0,端点 x = l 处保定解问题。
