2016中考数学复习针对性训练:相似的应用十五(针对陕西中考第21题)
陕西省中考数学总复习 相似图形学案(无答案)

相似图形一:【课前预习】(一):【知识梳理】1.比例基本性质及运用(1)线段比的含义:如果选用同一长度单位得两条线段a、b的长度分别为m、n,那么就说这两条线段的比是a:b=m:n,或写成a m=b n,和数的一样,两条线段的比a、b中,a叫做比的前项 b叫做比的后项.注意:①针对两条线段;②两条线段的长度单位相同,但与所采用的单位无关;③其比值为一个不带单位的正数.(2)线段成比例及有关概念的意义:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段。
2.相似三角形的性质和判定(1)相似三角形定义:对应角相等,对应边成比例的两个三角形叫做相似三角形,相似三角形的对应边的比叫做相似比.相似比为1的两个三角形是全等三角形。
(2)相似三角形的性质:①相似三角形的对应角相等,对应边成比例.②相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比.③相似三角形周长的比等于相似比.④相似三角形面积的比等于相似比的平方.(3)相似三角形的判定:①两角对应相等的两个三角形相似.②两边对应成比例,且夹角相等的两个三角形相似.③三边对应成比例的两个三角形相似.④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.注意:①直角三角形被斜边上的高分成的两个三角形和原三角形相似.②在运用三角形相似的性质和判定时,要找对对应角、对应边,相等的角所对的边是对应边.(二):【课前练习】1.已知xy=3,那么x yy的值是____________2.已知点C是线段AB的黄金分割点,带ACAB≈0.6 18,那么CBAC的近似值是_______3.已知三个数1,2, 3 ,请你再添上一个(只填一个)数,使它们能构成一个比例式,则这个数是。
4.两直角边的长分别为3和4的直角三角形的斜边与斜边上的高的比为()A.5:3 B.5:4 C.5:12 D.25:125. 如图,各组图形中相似的是___________________(只填序号).二:【经典考题剖析】1.雨后初晴,一学生在运动场上玩耍,从他前面2m远一块小积水处,他看到旗杆顶端的倒影,如果旗杆底端到积水处的距离为40m,该生的眼部高度是1.5m,那么旗杆的高度是___________m.2.在比例尺为1:8000的南京市城区地图上,太平南路的长度约为25 cm,它的实际长度约为()A.320cm B.320m C.2000cm D.2000m3.如图,D、E两点分别在△CAB上,且 DE与BC不平行,请填上一个你认为适合的条件_________,使得△ADE∽△ABC.4.如图,AD⊥BC于D,CE⊥AB 于E,交 AD于F,图中相似三角形的对数是()A.3 B.4 C.5 D.65.创新实验学校设计的矩形花坛的平面图,这个花坛的长为10m,宽为6m.⑴在比例尺为1:50的平面图上,这个矩形花坛的长和宽各是多少cm?⑵在平面图上,这个花坛的长和宽的比是多少?⑶花坛的长和宽的比为多少?⑷你发现这两个比有什么关系?三:【课后训练】1.下列各组线段中.能成比例的是()A.3,6,7,9 B.2,5,6,8 C.3,6,9,18 D.1,2,3,42.某校有两块相似的多边形草坪,其面积比为9:4,其中一块草坪的周长是36米,则另一块草坪的周长是()A.24米 B.54米 C.24米或54米 D.36米或54米3.下列说法中正确的是()A.两个直角三角形一定相似; B.两个等腰三角形一定相似C.两个等腰直角三角形一定相似; D.两个等腰梯形一定相似4.如图,D是△ABC的边AB上的点,请你添加一个条件,使△ACD与△ABC相似.你添加的条件是___________5.如果点C为线段 AB的黄金分割点,且AC>BC,则下列各式不正确的是()A.AB:AC=AC:BC B.AC=352-ABC、AC=512+AB D.AC≈0.61 8AB6.△ABC中,D是AB上的一点,再在 AC上取一点 E,使得△ADE与△ABC相似,则满足这样条件的E点共有()A.0个 B.1个 C.2个 D.无数个7.厨房角柜的台面是三角形,如图,如果把各边中点的连线所围成的三角形铺成黑色大理石.(图中阴影部分)其余部分铺成白色大理石,那么黑色大理石的面积与白色大理石面积的比是()A.14B.41C.13D.348.在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使B点与C点重合,如图,则折痕DE 的长是多少?9.如图,在yABCD 中,过点B 作BE ⊥CD ,垂足为E ,连结AE ,F 为AE 上一点,且∠BFE =∠C .⑴ 求证:△ABF ∽△EAD ;⑵ 若AB=4,∠BA=30°,求AE 的长;⑶ 在⑴、⑵的条件下,若AD=3,求BF 的长.10.如图,在△ABC 中,BA=BC=20cm ,AC=30cm ,点P 从A 点出发,沿AB 以每秒4cm 的速度向B 点运动,同时点Q 从C 点出发,沿CA 以每秒3㎝的速度向A 点运动,设运动的时间为x.⑴当x 为何值时,PQ ∥BC ? ⑵当P 13BCQ B QABC ABCS S S S ∆∆∆∆=时,求的值。
陕西省2016中考数学复习针对性训练:全等、相似十四(针对陕西中考第20、24题)

全等、相似十四(针对陕西中考第20、24题)1.(2015·汉中模拟)已知:如图,在△ABC 中,∠BAC =90°,AB =AC ,AD 是斜边BC 上的高,点E 为AB 边上一点,连接ED ,过点D 作DF ⊥DE 交AC 于点F.求证:△BDE ≌△ADF.证明:∵∠BAC =90°,AB =AC ,AD ⊥BC ,∴∠B =∠DAC =45°,BD =AD ,又∵DE ⊥DF ,∴∠BDE +∠EDA =∠ADF +∠EDA =90°,∴∠BDE =∠ADF ,∴△BDE ≌△ADF(ASA )2.如图,在△ABC 和△DCB 中,∠A =∠D =90°,AC =BD ,AC 与BD 相交于点O.(1)求证:△ABC ≌△DCB ;(2)△OBC 是何种三角形?证明你的结论.解:(1)在△ABC 和△DCB 中,∠A =∠D =90°,AC =BD ,BC 为公共边,∴Rt △ABC ≌Rt △DCB(HL ) (2)△OBC 是等腰三角形,∵Rt △ABC ≌Rt △DCB ,∴∠ACB =∠DBC ,∴OB =OC ,∴△OBC 是等腰三角形3.(2015·湖州)如图,在正方形ABCD 中,E ,F 分别是边AD ,CD 上的点,AE =ED ,DF =14DC ,连接EF 并延长交BC 的延长线于点G . (1)求证:△ABE ∽△DEF ;(2)若正方形的边长为4,求BG 的长.解:(1)证明:∵ABCD 为正方形,∴AD =AB =DC =BC ,∠A =∠D =90°,∵AE =ED ,∴AE AB =12,∵DF =14DC ,∴DF DE =12,∴AE AB =DF DE,∴△ABE ∽△DEF (2)∵ABCD 为正方形,∴ED ∥BG ,∴ED CG =DF CF ,又∵DF =14DC ,正方形的边长为4,∴ED =2,CG =6,∴BG =BC +CG =104.如图,在△ABC 中, BD ⊥AC 于D ,CE ⊥AB 于E ,DG ⊥BC 于G 交BA 的延长线于H ,GD 交CE 于F ,求证:GD 2=GF·GH.解:∵DG ⊥BC 于G ,CE ⊥AB 于E, ∴∠FGC =∠FEH =90°,而∠1=∠2,∴∠3=∠4,∴△CGF ∽△HGB, ∴CG GH =GF GB,∴CG ·GB =GF ·GH ①, 又∵BD ⊥AC 于D ,DG ⊥BC 于G, ∴∠BDC =∠BGD =90°, ∴∠BDG +∠GDC =∠BDG +∠DBG =90°,∠GDC =∠DBG ,△DGB ∽△CGD, ∴DG CG =GB DG,DG 2=CG·GB ②,由①②可知:GD 2=GF·GH。
2016年全国中考数学真题分类 相似形及应用(习题解析)

2016年全国中考数学真题分类相似形及应用一、选择题1.(2016安徽,8,4分)如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为()A.4 B.4C.6 D.4【考点】相似三角形的判定与性质.【分析】根据AD是中线,得出CD=4,再根据AA证出△CBA∽△CAD,得出=,求出AC即可.【解答】解:∵BC=8,∴CD=4,在△CBA和△CAD中,∵∠B=∠DAC,∠C=∠C,∴△CBA∽△CAD,∴=,∴AC2=CD•BC=4×8=32,∴AC=4;故选B.2.(2016甘肃定西,7,3分)如果两个相似三角形的面积比是1:4,那么它们的周长比是()A.1:16 B.1:4 C.1:6 D.1:2【分析】根据相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方解答即可.【解答】解:∵两个相似三角形的面积比是1:4,∴两个相似三角形的相似比是1:2,∴两个相似三角形的周长比是1:2, 故选:D .【点评】本题考查的是相似三角形的性质,掌握相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方是解题的关键.3. (2016浙江杭州,2,3分) 如图,已知直线a ∥b ∥c ,直线m 交直线a ,b ,c 于点A ,B ,C ,直线n 交直线a ,b ,c 于点D ,E ,F ,若12AB BC=,则DE EF=( )FE D CB A cb a nmA. 13B.12C. 23D.1 【答案】B4.(2016新疆生产建设兵团,7,5分)如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,下列说法中不正确的是( )A .DE=BCB . =C .△ADE ∽△ABCD .S △ADE :S △ABC =1:2【考点】相似三角形的判定与性质;三角形中位线定理.【分析】根据中位线的性质定理得到DE ∥BC ,DE=BC ,再根据平行线分线段成比例定理和相似三角形的性质即可判定. 【解答】解:∵D 、E 分别是AB 、AC 的中点, ∴DE ∥BC ,DE=BC , ∴=,△ADE ∽△ABC ,∴,∴A,B,C正确,D错误;故选:D.【点评】该题主要考查了平行线分线段成比例定理和相似三角形的性质即可判定;解题的关键是正确找出对应线段,准确列出比例式求解、计算、判断或证明.5.(2016河北,15,2分)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似...的是( C )第15题图答案:C解析:只要三个角相等,或者一角相等,两边成比例即可。
中考数学复习《相似》专题训练--附参考答案
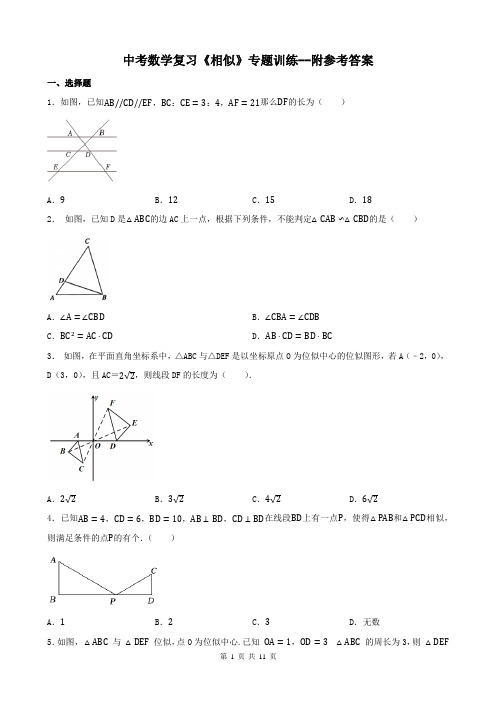
中考数学复习《相似》专题训练--附参考答案一、选择题1.如图,已知AB//CD//EF,BC:CE=3:4,AF=21那么DF的长为()A.9B.12C.15D.182.如图,已知D是△ABC的边AC上一点,根据下列条件,不能判定△CAB∽△CBD的是()A.∠A=∠CBD B.∠CBA=∠CDBC.BC2=AC⋅CD D.AB⋅CD=BD⋅BC3.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且AC=2√2,则线段DF的长度为().A.2√2B.3√2C.4√2D.6√24.已知AB=4,CD=6,BD=10,AB⊥BD,CD⊥BD在线段BD上有一点P,使得△PAB和△PCD相似,则满足条件的点P的有个.()A.1B.2C.3D.无数5.如图,△ABC与△DEF位似,点O为位似中心.已知OA=1,OD=3△ABC的周长为3,则△DEF的周长是()A.4 B.6 C.9 D.276.如图,为了估计某一条河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS 垂直的直线b的交点为R,如果QS = 60m,ST =120m,QR=80m,则这条河的宽度PQ为()A.40m B.120m C.60m D.180m7.如图,在Rt△ABC中∠ACB=90°,AC=BC,CD⊥AB点E为AC边上的中点,连接BE交CD于点F.若AC=4√2,则BF的长为().A.163B.4 C.2√103D.4√1038.如图,在△OAB中∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=9x(x>0)的图象经过点B和点C,那么点C的坐标是()A.(3,3)B.(3,1.5)C.(4.5,2)D.(9,1)二、填空题9.已知两个相似三角形的相似比为4:9,那么这两个三角形的周长之比为.10.如图,在△ABC中,D为AB上一点,且∠ACD=∠B,若AD=2,BD= 5,则AC=211.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .12.如图,P是平行四边形ABCD边BC上的一点,M、N分别是PA、PD的中点,若△PMN的面积为3cm2,则平行四边形ABCD的面积是cm2.13.如图,四边形ABCD是菱形,E为对角线BD的延长线上一点,且BD=8,DE=2∠BAE=45°则AB 的长为.三、解答题14.如图,AD、BE是的高,连接.(1)求证:∽;(2)若点D是的中点,CE=3,BE=4,求的长.15.已知:如图,在菱形中,点,分别在边,上,的延长线交的延长线于点,的延长线交的延长线于点. (1)求证:; (2)如果,求证:.16.如图,在矩形ABCD 中,点G 在边BC 上(不与点B 、C 重合),连接AG ,作DF ⊥AG 于点F ,BE ⊥AG 于点E.(1)若AG =AD ,求证:AB =DF ;(2)设BG BC =k ,连接BF 、DE ,设∠EDF =α,∠EBF =β,求tana tanβ的值.17.如图1,已知点O 在四边形ABCD 的边AB 上,且OA =OB =OC =OD =2,OC 平分∠BOD ,与BD 交于点G ,AC 分别与BD 、OD 交于点E 、F .(1)求证:OC ∥AD ;(2)如图2,若DE =DF ,求AE AF 的值;(3)当四边形ABCD 的周长取最大值时,求DE DF 的值.18.如图1, ABD 内接于,AD 是直径, BAD 的平分线交BD 于H ,交 于点C ,连接O ODC 并延长,交AB 的延长线于点E.(1)求证: AE=AD ;(2)若 32BEAB = ,求 AHHC 的值(3)如图2,连接CB 并延长,交DA 的延长线于点F ,若 ,6AH HC AF == 求 BEC 的面积.参考答案1.B2.D3.B4.B5.C6.B7.D8.D9.4:910.311.2:112.2413.4√1014.(1)证明:∵、是的高∴∵∴∽;(2)解:∵点D是的中点∴在中∵∴∴∵∽∴∴∴∴.15.(1)证明:∵四边形ABCD是菱形∴∵∴∴∵∴∴∵∴;(2)证明:∵∴ .∵∴∠B=∠EAG,∠BCE=∠G∴△AGE∽△BCE∴∴∵∴∴.16.(1)证明:∵四边形ABCD是矩形∴AD//BC∴∠DAG=∠BGA∵DF⊥AG ∴∠DFA=∠BEG=90°∵∠ABC=90°∴∠DFA=∠ABC在△ADF和△GAB中{∠DAG=∠BGA ∠DFA=∠ABC AD=AG∴△ADF≌△GAB∴AB=DF(2)解:由已知得:∵∠DFA=∠BEG=90°∴在Rt△DEF中tanα=EFDF;在Rt△BEF中∴tanαtanβ=EFDFEFBE=BEDF∵∠DAG=∠BGA∴△DFA∽△BEG∴BEDF =BGAD∵四边形ABCD是矩形∴AD=BC∵BGBC=k∴BEDF =BGAD=BGBC=k∴tanαtanβ=BEDF=k17.(1)证明:∵AO=OD ∴∠OAD=∠ADO∵OC平分∠BOD∴∠DOC=∠COB又∵∠DOC+∠COB∠=∠OAD+∠ADO ∴∠ADO=∠DOC∴CO∥AD;(2)解:∵OA=OB=OC∴∠ADB=90°∴△AOD和△ABD是等腰直角三角形∴AD= √2AO∴ADAO=√2∵DE=DF∴∠DFE=∠AED∵∠DFE=∠AFO∴∠AFO=∠AED∵∠AOF=∠ADE=90°∴△ADE∽△AOF∴AEAF =ADAO= √2;(3)解:如图2∵OD=OB,∠BOC=∠DOC,∴△BOC≌△DOC(SAS),∴BC=CD 设BC=CD=x,CG=m,则OG=2﹣m∵OB2﹣OG2=BC2﹣CG2∴4﹣(2﹣m)2=x2﹣m2,解得:m =14x2,∴OG=2 −14x2∵OD=OB,∠DOG=∠BOG,∴G为BD的中点又∵O为AB的中点,∴AD=2OG=4 −12x2∴四边形ABCD的周长为2BC+AD+AB=2x+4 −12x2+ 4 =−12x2+ 2x+8 =−12(x−2)2+ 10∵−12< 0,∴x=2时,四边形ABCD的周长有最大值为10.∴BC=2∴△BCO为等边三角形,∴∠BOC=60°,∵OC∥AD,∴∠DAC=∠COB=60°∴∠ADF =∠DOC =60°,∠DAE =30°,∴∠AFD =90°,∴DE DA =√33 ,DF =12 DA ∴DE DF =2√33 .18.(1)证明:∵AD 是 的直径90ACD ACE ∴∠=∠=︒∵AC 平分DAC EAC ∴∠=∠在△ACD 和△ACE 中∵∠ACD=∠ACE ,AC=AC ,∠DAC=∠EAC∴△ACD ≌△ACE (ASA )AE AD ∴=(2)解:如图,连接OC 交BD 于G 32BE AB = 设 3,2BE x AB x == 则 5AD AE AB BE x ==+= ,OC= AD= 52x DAC EAC ∠=∠BC CD ∴=∴OC 垂直平分BD又∵O 为AD 的中点∴OG 为△ABD 的中位线 ∴OC ∥AB ,OG= 1AB 2x = ,CG= 53OC OG=22x x x --= ABH CGH ∴~24332AH AB x HC CG x ∴===O BAD ∠12第 11 页 共 11 页 (3)解:如图,连接OC 交BD 于G由(2)可知:OC ∥AB ,OG= AB ∴∠BHA=∠GCH在△BHA 和△GHC 中 ∵∠BHA=∠GCH ,AH=CH ,∠BHA=∠GHC ()BHA GHC ASA ∴≅∴CG AB =设 OG m = ,则 2,3CG AB m OA OC m ==== 又 //OC AB∴FAB FOC ~FA AB FO OC∴= 62633m m m∴=+ 1m ∴= 2,6,4AB AD BE ∴=== ∵AD 是 的直径90ABD EBD ∴∠=∠=︒22226242BD AD AB =--=114428222EBD S EB BD ∴=⋅=⨯⨯= 又 ,ACD ACE ≅ EC CD ∴= 11824222BEC EBD S S ∴==⨯=12O。
陕西中考题21题相似中考题实际应用集锦

1.如图,在BE AD ABC ,中,∆是两条中线,则=∆∆ABC EDC S S :( )A .1∶2B .2∶3C .1∶3D .1∶42.(本题满分8分) 在一次数学测验活动中,小明到操场测量旗杆AB 的高度.他手拿一支铅笔MN ,边观察边移动(铅笔MN 始终与地面垂直).如示意图,当小明移动到D 点时,眼睛C 与铅笔、旗杆的顶端M 、A 共线,同时,眼睛C 与它们的底端N 、B 也恰好共线.此时,测得DB=50m ,小明的眼睛C 到铅笔的距离为0.65m ,铅笔MN 的长为0.16m ,请你帮助小明计算出旗杆AB 的高度(结果精确到0.1m ).3.(本题满分8分)某市在一道路拓宽改造过程中,发现原来道路两边的路灯除照亮路面的圆的面积不能满足需要外,亮度效果足以满足拓宽后的设计标准,因此,经设计人员研究,只要将路灯的灯杆增加一定的高度,使其照亮路面圆的面积为原来的2倍即可。
已知原来路灯灯高为7.5米,请你求出原灯杆至少再增加多少米,才能符合拓宽后的设计要求?(结果精确到0.1米)(第21题图)4.(本题满分8分)小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度 1.2CD =m ,0.8CE =m ,30CA =m (点A E C 、、在同一直线上).已知小明的身高EF 是1.7m ,请你帮小明求出楼高AB (结果精确到0.1m ).5(本题满分8分)一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D 的高度.如图,当李明走到点A 处时,张龙测得李明直立时升高AM 与其影子长AE 正好相等;接着李明沿AC 方向继续向前走,走到点B 处时,李明直立时的升高1.75m ,求路灯的高CD 的长。
中考数学复习《相似》专项综合练习含答案

中考数学复习《相似》专项综合练习含答案一、相似1.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣ x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.【答案】(1)解:把A(-2,0),B(4,0)代入抛物线y=ax2+bx-1,得解得∴抛物线解析式为:y= x2−x−1∴抛物线对称轴为直线x=- =1(2)解:存在使四边形ACPO的周长最小,只需PC+PO最小∴取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P 点.设过点C′、O直线解析式为:y=kx∴k=-∴y=- x则P点坐标为(1,- )(3)解:当△AOC∽△MNC时,如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E∵∠ACO=∠NCD,∠AOC=∠CND=90°∴∠CDN=∠CAO由相似,∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称,则N为DM中点设点N坐标为(a,- a-1)由△EDN∽△OAC∴ED=2a∴点D坐标为(0,- a−1)∵N为DM中点∴点M坐标为(2a,a−1)把M代入y= x2−x−1,解得a=4则N点坐标为(4,-3)当△AOC∽△CNM时,∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点N由(2)N(2,-1)∴N点坐标为(4,-3)或(2,-1)【解析】【分析】(1)根据点A、B的坐标,可求出抛物线的解析式,再求出它的对称轴即可解答。
(2)使四边形ACPO的周长最小,只需PC+PO最小,取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P点,利用待定系数法求出直线C′O的解析式,再求出点P的坐标。
陕西省中考数学总复习 相似三角形应用学案(无答案)
相似三角形应用一:【课前预习】(一):【知识梳理】1.相似多边及位似图形(1) 定义:对应角相等,对应边成比例的两个多边形叫做相似多边形.(2) 相似多边形的性质:(1)相似多边形的周长的比等于相似比;(2)相似多边形的对应对角线的比等于相似比;(3)相似多边形的面积的比等于相似比的平方;(4)相似多边形的对应对角线相似,相似比等于相似多边形的相似比.(3) 位似图形的定义:如果两个图形不仅是相似图形.而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又叫做位似比.2.相似的应用: 相似形的性质与识别在日常生活中有非常广泛的应用,如可应用其对应边成比例来求一些线段的长;可运用相似三角形的原理来进行测量等(二):【课前练习】1.下列说法正确的是()A.所有的矩形都是相似形 B.所有的正方形都是相似形C.对应角相等的两个多边形相似 D.对应边成比例的两个多边形相似2.用作位似图形的方法,可以将一个图形放大或缩小,位似中心的位置可选在()A.原图形的外部 B.原图形的内部 C.原图形的边上 D.任意位置3.如图是小明做的一个风筝的支架,AB=40cm,BP=60cm,△ABC∽△APQ的相似比是()A.3:2 B.2:3 C.2:5 D.3:54.如图,正方形的网格中,∠1+∠2+∠3+∠4+∠5等于( )A.175° B.180° C.210 ° D.225°5.如图,Rt△ABC中,有三个内接正方形,DF=9cm,GK=6cm,求第三个正方形的边长PQ.二:【经典考题剖析】1.小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是30cm,幻灯片到屏幕的距离是30㎝,幻灯片上小树的高度是10cm,则屏幕上小树的高度是()A.50cm B.500cm C.60cm D、600cm2.如图是跷跷板的示意图.支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,横板上下可转动的最大角度(即∠A′OA)是()A.80° B.60° C.40° D.20°3.一条河的两岸是平行的,在河的这一岸每隔5m有一棵树,在河的对岸每隔50m有一根电线杆,在这岸离开岸边25m处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有两棵树,求河的宽度.4.(1)请在如图所示的方格纸中,将△ABC向上平移3格,再向右平移6格,得△A1B1C1,再将△A1B1C1绕点B1按顺时针方向旋转90°,得△A2B1C2,最后将△A2B1C2以点C2为位似中心放大到2倍,得△A3B3C2;(2)请在方格纸的适当位置画上坐标轴(一个小正方形的边长为1个单位长度),在你所建立的直角坐标系中,点C、C1、C2的坐标分别为:点C( )、点C1( )、点C2( )、5.我们已经学习了相似三角形,也知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长、对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形,请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由三:【课后训练】1.针孔成像问题:根据图中尺寸(AB∥A′B′),可以知道物像A′B′的长与物AB的长之间的关系是____________.2.如图,上是Rt△ABC的斜边 BC上异于 B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有()条.A.1 B.2 C.3 D.43.位似图形上任意一对对应点到位似中心的距离之比等于________.4.如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC= 6 ,AD=2,那么当AB 的长等于时,使得两个直角三角形相似.5.有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.(1)设CE=x(厘米),EF=a(厘米),求出由x和a算出y的计算公式;(2)现有甲、乙两组同学,每组三人,每人各选择一个适当的位置尽力跳了一次,且均刚好触到斜杆,由所得公式算得两组同学弹跳成绩如下表所示,由于某种原因,甲组Cx 厘米,a=205厘米,请你计算同学的弹跳成绩认不清,但知他弹跳时的位置为150C同学此次的弹跳成绩,并从两组同学弹跳成绩的整齐程度比较甲、乙两组同学的弹跳成绩。
中考数学专题题库∶相似的综合题附详细答案
中考数学专题题库∶相似的综合题附详细答案一、相似1.如图,抛物线与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B 运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.(1)求抛物线的解析式和对称轴;(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)设四边形DECO的面积为s,求s关于t的函数表达式.【答案】(1)解:把A(﹣4,0),B(1,0),点C(0,2)代入得:,解得:,∴抛物线的解析式为:,对称轴为:直线x=﹣;(2)解:存在,∵AD=2t,∴DF=AD=2t,∴OF=4﹣4t,∴D(2t﹣4,0),∵直线AC的解析式为:,∴E(2t﹣4,t),∵△EFC为直角三角形,分三种情况讨论:①当∠EFC=90°,则△DEF∽△OFC,∴,即,解得:t= ;②当∠FEC=90°,∴∠AEF=90°,∴△AEF是等腰直角三角形,∴DE= AF,即t=2t,∴t=0,(舍去),③当∠ACF=90°,则AC2+CF2=AF2,即(42+22)+[22+(4t﹣4)2]=(4t)2,解得:t= ,∴存在某一时刻t,使得△EFC为直角三角形,此时,t= 或;(3)解:∵B(1,0),C(0,2),∴直线BC的解析式为:y=﹣2x+2,当D在y轴的左侧时,S= (DE+OC)•OD= (t+2)•(4﹣2t)=﹣t2+4 (0<t<2);当D在y轴的右侧时,如图2,∵OD=4t﹣4,DE=﹣8t+10,S= (DE+OC)•OD= (﹣8t+10+2)•(4t﹣4),即(2<t<).综上所述:【解析】【分析】(1)(1)利用待定系数法,将点A、B、C的坐标代入函数解析式,建立方程组求解即可。
部编数学九年级下册专题21相似应用(解析版)含答案
专题21 相似应用1.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO OD^,EF FG^.已知小明的身高EF为1.8米,求旗杆的高AB.【解答】解:解法一://AD EGQ,ADO EGF\Ð=Ð,90AOD EFGÐ=Ð=°Q,AOD EFG\D D∽,\AO ODEF FG=,即201.82.4AO=,15AO\=,同理得BOC AODD D∽,\BO OCAO OD=,即161520BO=,12BO\=,15123AB AO BO\=-=-=(米);解法二:如图,过点C作CM OD^于C,交AD于M,EGF MDCD DQ∽,\EF CM FG DC =,即1.82.42016CM =-,3CM \=,即3AB CM ==(米),答:旗杆的高AB 是3米.2.如图,利用标杆DE 测量楼高,点A ,D ,B 在同一直线上,DE AC ^,BC AC ^,垂足分别为E ,C .若测得1AE m =, 1.5DE m =,5CE m =,楼高BC 是多少?【解答】解:DE AC ^Q ,BC AC ^,//DE BC \,ADE ABC \D D ∽,\AE DE AC BC =,\1 1.515BC=+,9()BC m \=,答:楼高BC 是9m .3.如图,一块材料的形状是锐角三角形ABC ,边120BC mm =,高80AD mm =,把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少?【解答】解:Q 四边形EGHF 为正方形,//BC EF \,AEF ABC \D D ∽;设正方形零件的边长为xmm ,则KD EF x ==mm ,(80)AK x mm =-,AD BC ^Q ,\EF AK BC AD =,\8012080x x -=,解得:48x =.答:正方形零件的边长为48mm .4.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A ,在他们所在的岸边选择了点B ,使得AB 与河岸垂直,并在B 点竖起标杆BC ,再在AB 的延长线上选择点D ,竖起标杆DE ,使得点E 与点C 、A 共线.已知:CB AD ^,ED AD ^,测得1BC m =, 1.5DE m =,8.5BD m =.测量示意图如图所示.请根据相关测量信息,求河宽AB .【解答】解://BC DE Q ,ABC ADE \D D ∽,\BC AB DE AD =,\11.58.5AB AB =+,17()AB m \=,经检验:17AB =是分式方程的解,答:河宽AB 的长为17米.5.小颍想利用标杆和皮尺测量自己小区大门口前遮雨玻璃水平宽度AB ,他在楼门前水平地面上选择一条直线CH ,//AB CH ,在CH 上距离C 点8米的D 处竖立标杆DE ,DE CH ^,他沿着DH 方向走了2米到点N 处,发现他的视线从M 处通过标杆的顶端E 正好落在遮雨玻璃的B 点处,继续沿原方向再走2米到点Q 处,发现他的视线从P 处通过标杆的顶端E 正好落在遮雨玻璃的A 点处,求遮雨玻璃的水平宽度AB .【解答】解:连接AE ,过E 作EI AC ^于点I ,延长PM 交AC 于J ,交ED 于K ,则8IE JK CD ===,2KM DM DN NQ ====,//JE PJ \,AEJ EPK Ð=Ð,90AJE EKP Ð=Ð=°Q ,AEJ EPK \D D ∽,\8222AE IE EP KP ===+,//AB MP Q ,\AB AE PM PE =,即22AB =,4AB \=,答:遮雨玻璃的水平宽度AB 为4m .6.5月10日上午,庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行,习近平总书记重要讲话引发各界青年热烈反响.某校为庆祝共青团成立100周年升起了共青团旗帜,李优和贺基旭想用所学知识测量该旗帜的宽度MN ,他们进行了如下操作:如图,首先,李优在C 处竖立一根标杆BC ,地面上的点A 、标杆顶端B 和点N 在一条直线上, 1.5BC =米,1AC =米,8AG =米;然后,贺基旭手持自制直角三角纸板DEF ,使长直角边DF 与水平地面平行,调整位置,恰好在P 点时点D 、E 、M 在一条直线上, 1.5DP =米,23.6PG =米,2DF EF =,已知DP PA ^,MG PA ^,BC PA ^,点P 、G 、C 、A 在同一水平直线上,点N 在MG 上,求旗帜的宽度MN .【解答】解:如图,延长DF 交MG 于Q ,则DQ MG ^,23.6DQ PG ==,BC AP ^Q ,MG AP ^,//BC MG \,ABC ANG \D D ∽,\BC AC NG AG =,即1.518NG =,12NG \=,同理得:DEF DMQ D D ∽,\EF MQ DF DQ=,2DF EF =Q ,1123.611.822MQ DQ \==´=,11.8 1.512 1.3MN MQ QG GN \=+-=+-=(米).答:旗帜的宽度MN 是1.3米.7.小丽和小明想测量河对岸一建筑物AB 的高度.如图,他们先在地面上放一面平面镜E ,小丽在射线AE 上调整自己与镜子的距离,直到刚好能从镜子中看到建筑物的顶端B ,此时她与镜子的距离2CE =米,然后小明在距离建筑物6米处安装了一个测倾器GH ,测得60HGE Ð=°,若小丽的眼睛距离地面高度 1.6CD =米,1GH =米,AB AC ^,GH AC ^,DC AC ^,点A ,H ,E ,C 在同一条直线上.请你利用这些数据,求建筑物的高度AB .(结果精确到0.1米,参考数据1.414» 1.732».)【解答】解:由题意得:6AH =米,AB AC ^Q ,GH AC ^,DC AC ^,90BAE DCE GHE \Ð=Ð=Ð=°,在Rt GHE D 中,60HGE Ð=°,1GH =米,tan tan 60EH HGE GHÐ==°=QEH \==(米),(6AE AH EH \=+=(米),AEB CED Ð=ÐQ ,90BAE DCE Ð=Ð=°,ABE CDE \D D ∽,\AB AE CD CE=,即1.6AB =解得: 4.8 6.2AB =+»(米),答:建筑物的高度AB 约为6.2米.8.毕业季临近,我校为学生搭建了“理想之门”,希望同学们跨越理想之门,走向成功之路.“理想之门”最高处直立于点B 之上,周围有圆柱体底座,不能直接测量到B 点,小明想利用所学的数学知识测量AB 的高度.阳光下,他在点C 处放一镜子(处于“理想之门”的影子中),并作一标记,来回走动,走到点D 时,看到“理想之门”顶点A 在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度 1.5ED =米,2CD =米.然后,小明从点D 沿DH 方向走了1米,到达“理想之门”影子的末端G 处,此时,测得小明身高 1.6FG =米,影长 3.2GH =米,求“理想之门”的高AB .【解答】解:由题意可得:90ABC EDC FGH Ð=Ð=Ð=°,ACB ECD Ð=Ð,AGB GHF Ð=Ð,故ABC EDC D D ∽,ABG FGH D D ∽,则ED CD AB BC =,GF HG AB BG =,即1.52AB BC =,1.6 3.23AB BC =+,解得:92AB =(米),故“理想之门”的高AB 为92米.9.某校数学社团开展“探索生活中的数学”研学活动,准备测量秦始皇雕塑AB 的高度.如图所示,首先,在阳光下,某一时刻,小玉在雕塑影子顶端D 处竖立一根高2米的标杆CD ,此时测得标杆CD 的影子DE 为2米;然后,在H 处竖立一根高2.5米的标杆GH ,小婷从H 处沿BH 后退0.8米到N 处恰好看到点G 、A 在一条直线上,小婷的眼睛到地面的距离 1.5MN =米,24DN =米,已知CD EN ^,AB EN ^,GH EN ^,MN EN ^,点E 、D 、B 、H 、N 在同一水平直线上,请根据以上数据求出秦始皇雕塑AB 的高度.【解答】解:设AB x =米,Q 高2米的标杆CD 的影子DE 为2米,BD AB x \==米,过M 作MF AB ^于F ,交GH 于J ,则四边形BHJF ,MNHJ 是矩形,1.5BF MN HJ \===米,0.8MJ NH ==米,1GJ \=米,(24)FM x\=-米,( 1.5)AF x=-米,//GJ AFQ,MGJ MAF\D D∽,\GJ MJAF MF=,10.81.524x x=--,解得:14x=,14AB\=米,答:秦始皇雕塑AB的高度为14米.10.阳光明媚的一天实践课上,亮亮准备用所学知识测量教学楼前一座假山AB的高度,如图,亮亮在地面上的点F处,眼睛贴地观察,看到假山顶端A、教学楼顶端C在一条直线上.此时他起身在F处站直,发现自己的影子末端和教学楼的影子末端恰好重合于点G处,测得2FG=米,亮亮的身高EF为1.6米.假山的底部B处因有花园围栏,无法到达,但经询问和进行部分测量后得知,9BF=米,点D、B、F、G在一条直线上,CD DG^,AB DG^,EF DG^,已知教学楼CD的高度为16米,请你求出假山的高度AB.【解答】解:CD DG^Q,EF DG^,//EF CD\,GEF GCD\D D∽,\EF GFCD GD=,即1.621692DB=++,解得9BD=.CD DG^Q,AB DG^,//AB CD\,FAB FCD \D D∽,\AB FBCD FD=,即91699AB=+,解得8AB=,\假山的高度AB为8米.11.如图,为了测量平静的河面的宽度,即EP的长,在离河岸D点3.2米远的B点,立一根长为1.6米的标杆AB,在河对岸的岸边有一根长为4.5米的电线杆MF,电线杆的顶端M在河里的倒影为点N,即PM PN=,两岸均高出水平面0.75米,即0.75DE FP==米,经测量此时A、D、N 三点在同一直线上,并且点M、F、P、N共线,点B、D、F共线,若AB、DE、MF均垂直于河面EP,求河宽EP是多少米?【解答】解:延长AB交EP的反向延长线于点H,则四边形BDEH是矩形,0.75BH DE\==,//BD EH,1.60.752.35AH AB BH AB DE\=+=+=+=,//BD OHQ,ABD AHO\D D∽,\BD AB HO AH=,\3.2 1.62.35 HO=,4.7HO\=,PM PN=Q, 4.5MF=米,0.75FP=米,5.25PN MF FP \=+=米,AH EP ^Q ,PN EP ^,//AH PN \,AHO NPO \D D ∽,\AH HO NP PO =,\2.35 4.75.25PO=,10.5PO \=,10.5(4.7 3.2)12PE PO OE \=+=+-=,答:河宽EP 是12米.12.如图,在某次军事演习中,阴影部分为我军地面以下的战壕,前方有两栋高楼AB 、CD ,已知10AB =米,62CD =米,敌军在高楼CD 中与我军对抗我军战士在距离点20B 米的点P 处观测,视线PA 经过点A 落到CD 上的点E 处,30ED =米,点P 、B 、D 在一条直线上.该战士向点B 的方向行走12米到点Q 处观测,请问他此时能否看到高楼CD 的最高点C ?请通过计算说明理由.【解答】解:他此时能否看到高楼CD 的最高点C ,理由:AB PD ^Q ,CD PD ^,//AB CD \,APB EPD \D D ∽,\AB PB DE PD =,\102030PD=,60PD \=米,602040BD PD PB\=-=-=(米),连接QA并延长交DC于F,则ABQ FDQD D∽,\AB QB DF QD=,\1020126012 DF-=-,60DF\=米62<米,\他此时能看到高楼CD的最高点C.13.如图,阳阳要测量一座钟塔的高度CD,他在与钟塔底端处在同水平面上的地面放置一面镜子,并在镜子上做一个标记E,当他站在离镜子E处1.4 m的B处时,看到钟塔的顶端在镜子中的像与标记E重合.已知B,E,D在同直线上,阳阳的眼睛离地面的高度 1.6AB=m,14.7DE=m,求钟塔的高度CD.【解答】解:AB BD^Q,CD BD^,90ABE CDE\Ð=Ð=°,AEB CEDÐ=ÐQ,ABE CDE\D D∽,\AB BE CD DE=,\1.6 1.414.7 CD=,16.8 CD m\=,故钟塔的高度CD为16.8m.14.《九章算术》中记载了一种测量井深的方法.如图,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D点观察井内水岸C点,视线DC与井口的直径AB交于点E.如果测得 1.8AB=米,1BD=米,0.2BE=米.请求出井深AC的长.【解答】解:由题意得://BD AC,D ACD\Ð=Ð,A ABDÐ=Ð,BDE ACE\D D∽,\BD AC BE AE=,\10.2 1.80.2AC=-,解得:8AC=,答:井深AC的长为8米.15.雨过天晴,小李急忙跑到室外呼吸新鲜空气,广场上E处有一处积水,如图,若小李站在D处距积水2米,他正好从水面上看到距他约10米的前方一棵树的顶端A的影子已知点D、E、B在同一直线上,AB BD^,CD BD^,小李的眼睛到地面的距离CD为1.6米,求树AB的高.(CED AEBÐ=,积水水面大小忽略不计)【解答】解:由题意得:CDE ABE D D ∽,\CD DE AB BE=,1.6CD =Q 米,2DE =米,8BE =米,即:1.628AB =,解得: 6.4AB =,答:树高大约是6.4米.16.小丽想利用所学知识测量旗杆AB 的高度,如图,小丽在自家窗边看见旗杆和住宅楼之间有一棵大树DE ,小丽通过调整自己的位置,发现半蹲于窗边,眼睛位于C 处时,恰好看到旗杆顶端A 、大树顶端D 在一条直线上,小丽用测距仪测得眼睛到大树和旗杆的水平距离CH 、CG 分别为7米、28米,眼睛到地面的距离CF 为3.5米,已知大树DE 的高度为7米,//CG BF 交AB 于点G ,AB BF ^于点B ,DE BF ^于点E ,交CG 于点H ,CF BF ^于点F .求旗杆AB 的高度.【解答】解:由题意知 3.5BG HE CF ===米,7 3.5 3.5DH DE CF \=-=-=(米),AB BF ^Q ,DE BF ^,//AG DH \,CDH CAG \D D ∽,\728DH CH AG CG ==,即3.5728AG =,14AG \=米,14 3.517.5AB AG GB \=+=+=(米),\旗杆AB 的高度为17.5米.17.小明想用镜子测量校园内一棵松树的高度,如图所示,他把镜子放在水平地面上的C 点,沿着直线BC 后退到点F ,这时恰好在镜子里看到树梢顶点A 的像,量得10BC =米,2CF =米.已知EF 、AB 均与地面BF 垂直,小明的眼睛距离地面1.5米(即 1.5EF =米),请你求出松树AB 的高.【解答】解:根据题意,得ECF ACB Ð=Ð,90CFE CBA Ð=Ð=°,则CFE CBA D D ∽,则EF CF AB BC =,即1.5210AB =,解得:7.5AB =米.答:松树的高为7.5米.18.某校社会实践小组为了测量古塔的高度,在地面上C 处垂直于地面竖立了高度为2米的标杆CD ,这时地面上的点E ,标杆的顶端点D ,古塔的塔尖点B 正好在同一直线上,测得 1.2EC =米,将标杆向后平移到点G 处,这时地面上的点F ,标杆的顶端点H ,古塔的塔尖点B 正好在同一直线上(点F ,点G ,点E ,点C 与古塔底处的点A 在同一直线上),这时测得 1.8FG =米,20CG =米,请你根据以上数据,计算古塔的高度AB .【解答】解:根据题意得,EDC EBA D D ∽,FHG FBA D D ∽,\DC EC BA EA =,GH FG AB AF=DC HG =Q ,\FG EC AF EA =,\ 1.8 1.21.820 1.2CA AC=+++,40CA\=(米),\2 1.21.240 AB=+,68.7AB\»米,答:古塔的高度AB约为68.7米.19.小明利用数学课所学知识测量学校门口路灯的高度.如图:AB为路灯主杆,AE为路灯的悬臂,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A、标杆顶端D和地面上一点G在同一直线上,此时小明发现路灯E、标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B、标杆底端C和地面上点F、点G在同一水平线上).这时小明测得FG长1.5米,路灯的正下方H距离路灯主杆底端B的距离为3米.请根据以上信息求出路灯主杆AB的高度.【解答】解:过点D作DM AB^于M,交EH于点N,//AE BGQ,AB BG^,AE AB\^,DM AB ^Q ,////AE MD BG \,AM \等于ADE D 的边AE 上的高,AB BG ^Q ,EH BG ^,CD BG ^,////AB EH CD \,3AE BH \==米. 1.8BM CD ==米,//AE BG Q ,ADE GDF \D D ∽,\AE AM GF CD =,即31.5 1.8AM =,3.6AM \=(米),5.4AB AM BM \=+=(米),答:路灯主杆AB 的高度为5.4米.20.小明想通过自己所学的知识测量一段笔直的高架桥MN 上DQ 段的运行距离,设计了如下的测量方案:已知在高架桥的一侧有一排居民楼AB (楼顶AB 与高架桥MN 在同一水平面上,且AB 与点D 正好在同一直线上),测得35AB =米,小明先站在A 处,测得视线与高架桥MN 的垂直距离15AH =米,小明又站在B 处,使得视线与BQ 在一条直线上,此时测得45BQ =米,且90QBA Ð=°,求此高架桥上DQ 段的运行距离.【解答】解:AH DQ ^Q ,90AHD DBQ \Ð=Ð=°,ADH QDB Ð=ÐQ ,ADH QDB \D D ∽,\151453AD AH DQ BQ ===,设AD x =,3DQ x =,35BD x \=+,在Rt BDQ D 中,222DQ BD BQ =+Q ,222(3)(35)45x x \=++,25x\=(负值舍去),\高架桥上DQ段的运行距离为75米.21.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离8.7EC m=,窗口高 1.8AB m=,求窗口底边离地面的高BC.【解答】解://AE BDQ,ECA DCB\D D∽,\BC CD AC EC=.8.7EC m=Q, 2.7ED m=,6CD m\=.1.8AB m=Q,1.8AC BC m\=+,\61.88.7 BCBC=+,解得:4BC=,即窗口底边离地面的高为4m.22.如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知10AB m=,15CD m=,求点M离地面的高度MH.【解答】解://AB CDQ,ABM DCM\D D∽,\102153BH ABHD CD===,(相似三角形对应高的比等于相似比),//MH ABQ,MDH ADB\D D∽,\35 MH DHAB BD==,\3 105 MH=,解得6MH=.答:点M离地面的高度MH为6m.。
陕西省中考数学复习针对性训练:一次函数的应用十七(针对陕西中考第22题)
一次函数的应用十七(针对陕西中考第22题)1.(2015·榆林模拟)甲、乙二人分别从相距21千米的A ,B 两地同时出发相向而行.如图,l 1,l 2分别表示甲、乙两人距A 地的距离y(千米)与时间t(小时)之间的关系.(1)求l 2的函数表达式;(2)甲行AB 段比乙行BA 段少用多少小时?解:(1)l 2的函数表达式为y =-6t +21 (2)甲行AB 段比乙行BA 段少用2.1小时2.某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km )计算,甲汽车租赁公司的月租费是y 1元,乙汽车租赁公司的月租费是y 2元.如果y 1,y 2与x 之间的关系如图所示.(1)求y 1,y 2与x 之间的函数关系;(2)每月用车路程在什么范围内,租用甲汽车租赁公司的车所需费用较少?解:(1)设y 2=kx ,把(2000,2000)代入可得2000=2000k ,解得k =1,所以y 2=x ,设y 1=k ′x +1000,把(2000,2000)代入可得2000=2000k ′+1000,解得k ′=12,所以y 1=12x +1000 (2)由图象可得,每月用车路程大于2000 km 时,租用甲汽车租赁公司的车所需费用较少3.做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A ,B 两种款式的服装合计30件,并且每售出一件A 款式和B 款式服装,甲店铺获利润分别为30元和35元,乙店铺获利润分别为26元和36元.某日,王老板进A 款式服装36件,B 款式服装24件,并将这批服装分配给两个店铺各30件.(1)怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?(2)怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?解:(1)设A 款式服装分配到甲店铺为x 件,则分配到乙店铺为(36-x)件;B 款式分配到甲店铺为(30-x)件,分配到乙店铺为(x -6)件.根据题意得:30x +35×(30-x)=26×(36-x)+36(x -6),解得x =22,所以36-x =14(件),30-x =8(件),x -6=16(件),故A 款式服装分配到甲店铺为22件,则分配到乙店铺为14件;B 款式服装分配到甲店铺为8件,分配到乙店铺为16件,能使两个店铺在销售完这批服装后所获利润相同 (2)设总利润为w 元,根据题意得:30x +35×(30-x)≥950,解得x ≤20,∴6≤x ≤20.w =30x +35×(30-x)+26×(36-x)+36(x -6)=5x +1770,∵k =5>0,∴w 随x 的增大而增大,∴当x =20时,w 有最大值1870,∴A 款式服装分配给甲、乙两店铺分别为20件和16件,B 款式服装分配给甲、乙两店铺分别为10件和14件时,最大的总利润是1870元4.(2015·陕西模拟)花石镇组织10辆汽车装运完A ,B ,C 三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题:(1)设装运A 种湘莲的车辆数为x ,装运B 种湘莲的车辆数为y ,求y 与x 之间的函数关系式;(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.解:(1)设装A ,由题意得:12x +10y +8(10-x -y)=100,∴y =10-2x (2)10-x -y =10-x -(10-2x)=x ,故装C 种车也为x 辆,∴⎩⎨⎧x ≥2,10-2x ≥2,解得2≤x ≤4,x 为整数,∴x =2,3,4,故车辆有3种安排方案,方案如下:方案一:装A 种2辆车,装B 种6辆车,装C 种2辆车;方案二:装A 种3辆车,装B 种4辆车,装C 种3辆车; 方案三:装A 种4辆车,装B 种2辆车,装C 种4辆车(3)设销售利润为W(万元),则W =3×12x +4×10×(10-2x)+2×8x =-28x +400,∴W 是x 的一次函数,且x 增大时,W 减少,∴x =2时,W 最大=400-28×2=344(万元)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似的应用十五(针对陕西中考第21题)
1.小红用下面的方法来测量学校教学大楼AB 的高度:如图,在水平地面点E 处放一面平面镜,镜子与教学大楼的距离AE =20米.当她与镜子的距离CE =2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC =1.6米,请你帮助小红测量出大楼AB 的高度(注:入射角=反射角).
解:根据反射定律知:∠FEB =∠FED ,∴∠BEA =∠DEC ,∠BAE =∠DCE =90°,
∴△BAE ∽△DCE ,∴AB DC =AE EC ,∵CE =2.5米,DC =1.6米,∴AB 1.6=202.5
,∴AB =12.8,∴大楼AB 的高为12.8米
2.(2015·邵阳)如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF 来测量操场旗杆AB 的高度,他们通过调整测量位置,使斜边DF 与地面保持平行,并使边DE 与旗杆顶点A 在同一直线上,已知DE =0.5米,EF =0.25米,目测点D 到地面的距离DG =1.5米,到旗杆的水平距离DC =20米,求旗杆的高度.
解:由题意可得:△DEF ∽△DCA ,则DE DC =EF AC
,∵DE =0.5米,EF =0.25米,DG =1.5 m ,DC =20 m ,∴0.520=0.25AC
,解得:AC =10,故AB =AC +BC =10+1.5=11.5(m ),答:旗杆的高度为11.5 m
3.又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6 m ;
乙:我们相距36 m .
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)
解:如图,
CD =EF =BH =1.6 m ,CE =DF =36 m ,∠ADH =30°,∠AFH =60°,在Rt △AHF 中,∵tan ∠AFH =AH FH ,∴FH =AH tan 60°,在Rt △ADH 中,∵tan ∠ADH =AH DH ,∴DH =AH tan 30°
,而DH -FH =DF ,∴
AH tan 30°-AH tan 60°=36,即AH 33-AH 3
=36,∴AH =183,∴AB =AH +BH =183+1.6≈33(m ).答:纪念塔的高度约为33 m
4.(2015·镇江)某兴趣小组开展课外活动.如图,A ,B 两地相距12米,小明从点A 出发沿AB 方向匀速前进,2秒后到达点D ,此时他(CD)在某一灯光下的影长为AD ,继续按原速行走2秒到达点F ,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H ,此时他(GH)在同一灯光下的影长为BH(点C ,E ,G 在一条直线上).
(1)请在图中画出光源O 点的位置,并画出他位于点F 时在这个灯光下的影长FM(不写画法); (2)求小明原来的速度.
解:(1)如图
(2)设小明原来的速度为x m /s ,则CE =2x m ,AM =AF -MF =(4x -1.2) m ,EG =2×
1.5x =3x m ,BM =AB -AM =12-(4x -1.2)=13.2-4x ,∵点C ,E ,G 在一条直线上,CG
∥AB ,∴△OCE ∽△OAM ,△OEG ∽△OMB ,∴CE AM =OE OM ,EG BM =OE OM ,∴CE AM =EG BM
,即2x 4x -1.2=3x 13.2-4x
,解得x =1.5,经检验x =1.5为方程的解,∴小明原来的速度为1.5 m /s .答:小明原来的速度为1.5 m /s。
