同轴度最大实体尺寸计算例子
孔的直线度最大实体尺寸,例题

孔的直线度是指孔内径与其长度之间的互相垂直度误差。
而孔的最大实体尺寸则是指孔内径与孔的长度之间所能容纳的最大实体尺寸。
以下通过例题来详细讲解孔的直线度最大实体尺寸。
1. 问题描述:假设有一圆柱状零件,其孔的直线度要求为0.02mm,孔的内径为20mm,长度为50mm。
现在需要确定该孔能容纳的最大实体尺寸。
2. 计算过程:根据直线度的要求,我们知道孔的内径与孔的长度之间的垂直度误差不应超过0.02mm。
我们需要确定在这个误差范围内,孔能容纳的最大实体尺寸。
根据公式:最大实体尺寸 = 内径尺寸 - 孔的长径公差其中,内径尺寸为20mm,孔的长径公差可根据实际情况确定。
3. 公差确定:假设孔的长径公差为0.03mm,代入公式计算可得:最大实体尺寸 = 20mm - 0.03mm = 19.97mm根据上述公差和计算得出的结果,该孔能容纳的最大实体尺寸为19.97mm。
4. 结论:根据所给的孔的直线度要求、内径和长度以及长径公差的确定,我们计算出该孔能容纳的最大实体尺寸为19.97mm。
这个结果将有助于在实际生产中正确选择适合孔的实体尺寸,从而确保零件的装配和使用的精度和稳定性。
总结:孔的直线度最大实体尺寸是确定孔在允许的误差情况下所能容纳的最大实体尺寸,通过上述例题的计算分析,我们了解了如何根据直线度要求、孔的尺寸和公差确定孔的最大实体尺寸。
这对于工程和制造实践有着重要的意义。
在实际生产中,合理确定孔的最大实体尺寸能够有效控制零件装配的精度,提高产品的质量和稳定性。
对于工程师和制造人员来说,掌握孔的直线度最大实体尺寸的计算方法是非常重要的,也是提高工作效率和产品品质的关键。
孔的直线度最大实体尺寸在制造工程中起着至关重要的作用。
在实际生产中,孔和轴的配合是常见的装配方式,因此孔的尺寸和公差必须严格控制,以确保零件装配的精度和稳定性。
下面我们将继续探讨孔的直线度最大实体尺寸的计算方法和其在工程中的应用。
1. 孔的直线度最大实体尺寸的计算方法在上文的例题中,我们已经了解了孔的直线度最大实体尺寸的计算方法。
最大实体状态(尺寸、边界)

即:
DMV D fe Dmin t形位 dMV d fe dmax t形位
最大实体实效边界:尺寸为最大实体实效尺寸的 边界。
最大实体实效尺寸(单一要素)
最大实体实效尺寸(关联要素)
最小实体实效状态(尺寸、边界)
最大实体要求应用实例(二)
A
ø0.04 M A
如图所示,被测轴应满足下列要求: 实际尺寸在Ø 11.95mm~ Ø 12mm之内; 实际轮廓不得超出关联最大实体实效边界,即关 联体外作用尺寸不大于关联最大实体实效尺寸 dMMVS=dMMS+t=12+0.04=12.04mm
A
ø0.04 M A
当被测轴处在最小实体状态时,其轴线对A 基准轴线的同轴度误差允许达到最大值,即等于 图样给出的同轴度公差( Ø 0.04 )与轴的尺寸公 差(0.05)之和( Ø 0.09 )。
DM Dmin dM dmax
最小实体状态(尺寸、边界)
最小实体状态(LMC):实际要素在给定长度上具 有最小实体时(材料量最少时)的状态,称为最小 实体状态。 最小实体尺寸(LMS):实际要素在最小实体状 态下的极限尺寸。
(孔的最大极限尺寸Dmax和轴的最小极限dmin)
即:
DL Dmax
最大实体实效边界:
在配合的全长上,孔、轴为最大实体尺寸, 且其轴线的形状和位置误差等于给出公差值时的 体外作用尺寸称为最大实体实效尺寸(MMVS)。
轴的最大实体实效尺寸的代号为 dMV ,孔的最大 实体实效尺寸的代号为 DMV
。
用公式表示为 :
dMV d fe da f dMML t dmax t DMV Dfe Da f DMML t Dmin t
同轴度规计算公式

同轴度规计算公式同轴度(Coaxiality)是一种用于测量物体间轴线的同心度的度量标准。
它常用于工程和制造业中,特别是在需要保持高精度和高质量的产品制造中。
同轴度的计算公式可以根据具体的测量对象和测量方法而有所不同。
下面将介绍几种常见的同轴度计算公式。
1.直线同轴度公式直线同轴度是指两个轴线在其共同延长线上的距离差的最大值。
假设有两条直线轴线AB和CD,它们与一条公共轴线EF相互平行。
直线同轴度的计算公式如下:同轴度 = max(AB' - CD') 公式1其中,AB'和CD'分别是测量轴线AB和CD到共同轴线EF的距离。
2.圆同轴度公式圆同轴度是指一个内圆和一个外圆的同心度。
假设内圆的半径是R1,外圆的半径是R2,它们的中心点分别为A和B。
圆同轴度的计算公式如下:同轴度 = max(,AB, - ,R2 - R1,, ,AB, - ,R2 + R1,)公式2其中,AB,表示A点和B点之间的距离。
3.球同轴度公式球同轴度是指两个球心之间的距离差的最大值。
假设有两个球心A和B,它们之间的距离为d,球同轴度的计算公式如下:同轴度 = max(,d - R1 - R2,, ,d - ,R1 - R2,) 公式3其中,R1和R2分别表示两个球的半径。
以上是几种常见的同轴度计算公式,它们分别适用于直线、圆和球的同轴度测量。
在实际应用中,我们可以根据具体的需求和测量对象选择适合的计算公式。
同时,为了保证测量的准确性,还需要选择恰当的测量方法和仪器,并遵循严格的测量流程和标准。
同轴度公差的最大允许值

同轴度公差的最大允许值1. 什么是同轴度公差?同轴度公差(Coaxiality Tolerance)是指在机械制造中,用于描述两个或多个圆柱体的轴线之间允许的最大偏差。
同轴度公差是一种几何公差,用于确保多个零件的轴线能够保持在一条直线上,从而保证装配的精度和可靠性。
2. 同轴度公差的重要性在机械制造中,很多零件的装配需要保证其轴线的同轴度,以确保整个系统的性能和可靠性。
如果同轴度公差超过了最大允许值,可能会导致以下问题:•零件装配困难:同轴度公差超过最大允许值会导致零件的装配困难,增加了生产成本和时间。
•系统性能下降:如果零件的轴线不能保持在一条直线上,可能会导致系统的性能下降,影响产品的质量和可靠性。
•寿命减少:同轴度公差超过最大允许值可能导致零件的寿命减少,因为不同轴线之间的偏差会增加零件的摩擦和磨损。
因此,合理设置同轴度公差的最大允许值对于保证产品质量、提高生产效率和降低成本具有重要意义。
3. 同轴度公差的计算方法同轴度公差的计算方法通常基于国际标准,如ISO 1101。
根据ISO标准,同轴度公差可以使用两种方法进行计算:•最大材料条件(MMC):在最大材料条件下,零件的轴线之间的最大偏差是最大允许值。
MMC方法适用于要求零件轴线之间的偏差尽可能小的情况。
•最小材料条件(LMC):在最小材料条件下,零件的轴线之间的最小偏差是最大允许值。
LMC方法适用于要求零件轴线之间的偏差尽可能大的情况。
在实际应用中,通常根据具体的设计要求和性能要求选择适当的计算方法和最大允许值。
4. 影响同轴度公差的因素同轴度公差的最大允许值受到多种因素的影响,包括但不限于:•零件的尺寸和形状:零件的尺寸和形状会直接影响同轴度公差的最大允许值。
通常,较大的零件允许的同轴度公差较大,较小的零件允许的同轴度公差较小。
•零件的材料:不同材料的零件对同轴度公差的最大允许值有不同的要求。
例如,金属零件通常允许的同轴度公差较小,而塑料零件允许的同轴度公差较大。
同轴度检测量规设计计算
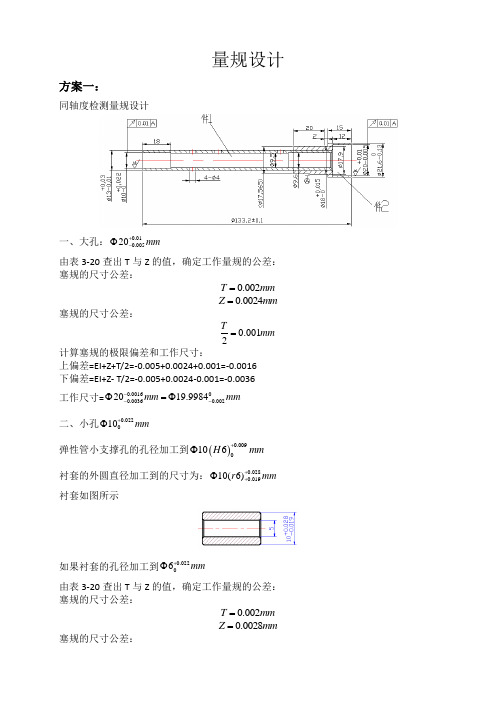
量规设计方案一:同轴度检测量规设计一、大孔:0.010.00520mm +-Φ由表3-20查出T 与Z 的值,确定工作量规的公差:塞规的尺寸公差:0.002T mm =0.0024Z mm =塞规的尺寸公差:0.0012T mm = 计算塞规的极限偏差和工作尺寸:上偏差=EI+Z+T/2=-0.005+0.0024+0.001=-0.0016下偏差=EI+Z- T/2=-0.005+0.0024-0.001=-0.0036工作尺寸=0.001600.00360.0022019.9984mm mm ---Φ=Φ二、小孔0.022010mm +Φ弹性管小支撑孔的孔径加工到()0.0090106H mm +Φ衬套的外圆直径加工到的尺寸为:0.0280.01910(6)r mm ++Φ衬套如图所示如果衬套的孔径加工到0.02206mm +Φ由表3-20查出T 与Z 的值,确定工作量规的公差:塞规的尺寸公差:0.002T mm =0.0028Z mm =塞规的尺寸公差:0.0012T mm = 计算塞规的极限偏差和工作尺寸:上偏差=EI+Z+T/2=0+0.0028+0.001=0.0038下偏差=EI+Z- T/2=0+0.0028-0.001=0.0018工作尺寸=0.00380.0020.001806 6.0018mm mm +++Φ=Φ 然而要检测弹性管的两支撑孔的同轴度,所以衬套的孔径应该加到的尺寸为: ()0.0220.0220060.0150.0050.0020.002 6.024mm mm ++Φ++++=方案二:一、同轴度检测量规设计(1)大孔端的工作部分为()0.0020.00200200.00519.995mm mm ++Φ-=Φ 最大实体实效尺寸(包容原则)(2)小孔端的工作部分:同轴度检查量规穿过小孔工作部分的尺寸为:0.00206mm +Φ衬套的孔径应该加到的尺寸为:()0.0220.0220060.0150.0050.0020.002 6.024mm mm++Φ++++= 弹性管小支撑孔的孔径加工到()0.0090106H mm +Φ衬套的外圆直径加工到的尺寸为:0.0280.01910(6)r mm ++Φ弹性管大支撑孔的孔径加工到工件要求尺寸0.010.00520mm +-Φ注:我认为方案一合适,方案二不合适,原因是:方案二只适用于要求遵守包容要求的轴和孔。
最大实体尺寸计算例子

最大实体尺寸计算例子最大实体尺寸计算是指在给定的空间中,确定最大可能尺寸的过程。
实体可以是物体、结构或系统中的一部分,它可以具有各种形状和材料。
通过计算最大实体尺寸,可以确保所设计的物体或结构在给定的限制条件下能够满足其功能和安全要求。
最大实体尺寸计算通常需要考虑以下几个关键方面:1. 功能需求:首先需要明确实体的功能需求,比如承受特定负载、容纳特定物体、满足特定的尺寸限制等。
这些需求将直接影响实体尺寸的计算结果。
2. 材料属性:实体所使用的材料会影响其最大可行尺寸。
材料的力学性能和属性,如强度、刚度、延展性等,将决定实体能否满足其功能需求。
3. 应力和变形分析:应力和变形分析是确定最大实体尺寸的重要工具。
通过对实体应力和变形进行数值模拟或理论分析,可以确定实体在给定负载下的行为,并确定其尺寸是否足够。
4. 安全因素:在计算最大实体尺寸时,需要考虑安全因素。
这包括确保实体能够承受额外的载荷和不确定性,以及在设计中留有足够的安全余量。
5. 制造和装配要求:最大实体尺寸的计算还需要考虑制造和装配过程中的要求。
例如,需要考虑材料加工的可行性、装配操作的可行性以及相关的成本因素。
最大实体尺寸计算的具体方法因具体情况而异。
以下是一些常用的参考内容:1. 材料力学性能手册:材料力学性能手册提供了各种材料的力学性能数据,如强度、刚度、延展性等。
根据所使用材料的性能要求,可以确定满足功能需求的最大可行尺寸。
2. 工程手册和设计规范:各种工程手册和设计规范提供了用于计算实体尺寸的公式和方法。
这些手册和规范经过广泛验证,可以提供可靠的计算准则。
3. 有限元分析软件:有限元分析软件是一种常用的工具,可以对实体进行数值模拟和应力分析。
通过输入实体的几何形状、材料参数和边界条件,可以获得实体的应力和变形情况,并确定其最大可行尺寸。
4. 成本和制造参数估算:考虑实际的制造和装配要求,进行相关的成本估算和制造参数分析。
这包括材料成本、加工成本、装配成本等。
最大实体尺寸

其中:轴取“+”;孔取“-” 最大实体实效边界:尺寸为最大实体实效 尺寸的边界。
最大实体实效尺寸:
最小实体实效状态(尺寸、边界):
LMVC:在给定长度上,实际尺寸要素处于最 小实体状态,且其几何误差等于给出公差值时 的综合极限状态,称为最小实体实效状态。 LMVS:最小实体实效状态下的体内作用尺寸, 称为最小实体实效尺寸。
LMVS=LMS ± t 其中:轴取“-”;孔取“+” 最小实体实效边界:尺寸为最小实体实效尺寸的 边界。
*几何公差值能够增大多少,取决于被测要 素偏离最大实体状态的程度。
*几何公差值的最大值为图样上给定的形状 公差值+尺寸公差值。
最大实体要求应用举例(一)
φ0.1 M
最大实体实效边界
dMMVS φ20
0 -0.3
φ0.1
Ø2 0
如图所示,该轴应满足下列要求:
实际尺寸在φ19.7mm~φ20mm之内;
2、包容要求
定义:实际要素应遵守最大实体边界,其 局部实际尺寸不得超过最小实体尺寸。 标注:在单一要素尺寸极限偏差或公差带 代号之后加注符号“Ⓔ ”, 应用:适用于单一要素。主要用于需要严 格保证配合性质的场合。 边界:最大实体边界。
包容要求标注
φ30h7 E φ30
包容要求应用举例
最大实体边界
例题
20
0.021 0
பைடு நூலகம்
20
0
0.021
E
40
0.1 0
同轴度计算及测量

坐标测量机同轴度测量问题分析前言坐标测量机是采用坐标测量原理测量同轴度的,这样的方法能够严格按照定义计算评定同轴度的具体结果.然而在机械加工过程中往往采用打表的办法测量同轴度,由于实际所选用基准的差异,就会造成两种方法所得结果的差异,尤其当基准要素的长度相对被测要素离开基准要素的轴向距离较短时两种结果可能大相径庭.许多坐标测量机操作人员经常为此所困扰,本文从实用的角度出发,对坐标测量机测量同轴度的方法进行分析探讨.一、同轴度的公差带与误差值的计算1. 定义:同轴度公差带是直径为公差值且与基准轴线同轴的圆柱面内的区域.2. 误差值的计算根据同轴度及其公差带的定义,同轴度误差的计算是非常简单的,即被测轴线到基准轴线(包含其延长线)的最大距离(空间距离)值的两倍.二、造成问题的原因由于同轴度的定义和计算都非常简单,所以坐标测量软件均不会出现计算评定方法上的错误,之所以在许多实际情况下会与打表测量的结果或人们的直觉出入很大,绝大多数都是由于基准的选择不同造成的.坐标测量软件会严格的依据操作者所选定的基准进行评定,只要基准不出问题,结果也不会出现问题;而打表时实际起基准作用的究竟是那个要素,对许多操作者来说往往是没有清晰概念的.例如在图一中,要求的基准应该是左侧直径为30mm,长度为40mm的一段圆柱轴线即A,打表时应根据这一段圆柱将工件找正(为避免母线直线度误差的影响,最好用在两端打跳动的办法找正),但实际情况是许多操作者会选择在整个工件上左端A和右端B打表的办法进行找正,从而使得实际的基准变成了A-B .图二显示被测轴线的偏离量一定时,选用两种不同基准计算结果的差异.当基准选为A即直径为30mm,长度为40mm的一段圆柱轴线时,右端直径为36m,长度为40mm的一段圆柱轴线的最大偏离量若为5,同轴度为10;当基准选为A-B即左右两端轴的共同轴线时, 右端直径为36m,长度为40mm的一段圆柱轴线的最大偏离量为1.67,同轴度为3.34.在图三所示的情形中,基准选用的差异造成的同轴度评定结果差异更大:左右两端圆柱的轴线不但有偏离,而且不平行.当基准选为A即直径为30mm,长度为40mm的一段圆柱轴线时,右端一段圆柱轴线的最大偏离量若为7,同轴度为14;当基准选为A-B即左右两端轴的共同轴线时, 右端圆柱轴线的最大偏离量为0.33,同轴度为0.66.由以上二例可见基准选择对同轴度计算的影响之大.三、问题的解决既然问题主要是由于基准地选择导致的,那么问题的解决也应由合理选择基准要素着手.机械零件在其形成的过程中一般会有四种性质不同的基准:设计基准、使用基准、加工基准、测量基准.测量师一般会选用设计基准作为测量基准,但是在某些特殊情况下可能需要选用其他的基准,例如设计基准仅存在于设计图纸上,零件上无法找到,或者设计基准要求不合理.就需要选用使用基准或加工基准作为测量基准.为保证零件功能地实现,一般应优先选用使用基准.如图四,当Ф16的轴孔为有一定配合长度的过盈配合而且轴肩处没有约束时, 轴或孔能起到定向及定位作用,充当了实际基准;而当轴孔配合长度短或配合性质为间隙配合时, 轴或孔起不到定向作用,也不能充当实际基准.在此情况下,如果轴肩处有约束(即有配合要求)则轴肩实际起到定向作用;如果轴肩处没有约束,则可能是实际配合的两处轴孔(Ф16和Ф12)共同起到定向及定位作用,成为实际上的基准.(如图五)综上所述,使用基准需要根据零部件的结构特点及相互之间的配合关系综合分析确定,在有些情况下设计图纸上相互关联的尺寸配合及位置公差要求可能会自相矛盾,这时需要与相关人员进行沟通解决.图六是一个实际图纸上出现的不合理的同轴度要求的例子:凭直觉看,右端圆孔的同轴度公差为0.1mm,无论是加工还是测量都不会存在什么难度,但分析的结果却与直觉全然不同.左端作为基准的圆柱长度只有3mm,用坐标测量机测量时若测针球径为1.5mm,球顶到工件侧面留0.1mm的间隙,左端面留0.15mm的缩进量,则有效的可测量长度也只能到2mm.此圆柱测量时若第二截面中心相对于第一截面中心的位置测量误差为1μm,则由这两个测得的截面中心计算出的圆柱轴线延伸到零件最右端时距真实的圆柱轴线就有583/2=291.5μm的偏离(如图七所示),这意味着右端圆柱轴线的同轴度误差为583μm即0.583mm.对大多数坐标测量机而言1μm的位置测量误差并不为过,然而由此造成同轴度测量评定的误差却是不可接受的.即使时当今世界最高精度的坐标测量机其标称的精度也不过是0.5μm,我们假定其测量这样两个圆截面时相对的位置误差为0.3μm,那么仍将造成0.1749mm的误差.显然,不是坐标测量机都出了问题,而只能是设计要求本身出了问题.事实上,无论该零件在装配时怎样与其他零件连接,左端3mm长的外圆柱都不可能起到为整个零件定向的作用.如果是通过左端的靠肩面连接,则应以此面为第一基准(限制基准的方向)以A为第二基准(限制基准的位置),对右端内孔的位置度进行控制; 如果左端的靠肩面不连接,则应以左端外圆和右端内孔的共同轴线为基准对右端内孔的同轴度进行控制.在这样的要求下,一般的坐标测量机对0.01-0.02mm的公差通常能应对有余;而高精度的坐标测量机则能满足0.003-0.005mm公差的测量需求.同轴度同轴度:[tóngzhóudù]properalignment同轴度:是定位公差,理论正确位置即为基准轴线.由于被测轴线对基准轴线的不同点可能在空间各个方向上出现,故其公差带为一以基准轴线为轴线的圆柱体,公差值为该圆柱体的直径,在公差值前总加注符号“φ”.同轴度公差:是用来控制理论上应同轴的被测轴线与基准轴线的不同轴程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同轴度最大实体尺寸计算例子
同轴度最大实体尺寸计算例子
什么是同轴度最大实体尺寸?
同轴度最大实体尺寸是指在三维几何中,通过计算找到物体最宽
处的宽度,用于确定物体的体积或尺寸。
实例1:矩形木板
•长度:180cm
•宽度:60cm
•厚度:2cm
根据矩形木板的尺寸,我们可以计算出其同轴度最大实体尺寸。
只需比较宽度、厚度即可。
由于宽度为60cm,厚度为2cm,所以
最大实体尺寸为60cm。
实例2:圆柱体水桶
•长度:40cm
•直径:30cm
根据圆柱体水桶的尺寸,我们可以计算出其同轴度最大实体尺寸。
只需比较直径即可。
由于直径为30cm,所以最大实体尺寸为30cm。
实例3:立方体盒子
•长度:50cm
•宽度:50cm
•高度:50cm
根据立方体盒子的尺寸,我们可以计算出其同轴度最大实体尺寸。
只需比较长度、宽度、高度中的最大值即可。
由于长度、宽度、
高度均为50cm,所以最大实体尺寸为50cm。
实例4:不规则物体
对于不规则形状的物体,计算同轴度最大实体尺寸可能需要更复
杂的方法。
我们可以使用三维建模软件或测量工具来确定不规则物体的最宽处,并计算得出同轴度最大实体尺寸。
结论
同轴度最大实体尺寸计算可以帮助我们确定物体的最大尺寸,在
设计、制造或运输中都有重要的应用。
通过比较物体尺寸的不同维度,我们可以快速找到物体的最大宽度,从而做出相应的决策。
实例5:长方体箱子
•长度:80cm
•宽度:30cm
•高度:40cm
根据长方体箱子的尺寸,我们可以计算出其同轴度最大实体尺寸。
只需比较长度、宽度、高度中的最大值即可。
由于高度为40cm,
所以最大实体尺寸为40cm。
实例6:球形水果
•直径:20cm
根据球形水果的尺寸,我们可以计算出其同轴度最大实体尺寸。
由于球形物体在任何方向上的直径是相同的,所以最大实体尺寸
为20cm。
实例7:三角形金属板
•边长1:30cm
•边长2:40cm
•边长3:50cm
根据三角形金属板的尺寸,我们可以计算出其同轴度最大实体尺寸。
只需比较三条边中的最大值即可。
由于边长3为50cm,所以最大
实体尺寸为50cm。
实例8:梯形塑料管
•上底:20cm
•下底:30cm
•高度:25cm
根据梯形塑料管的尺寸,我们可以计算出其同轴度最大实体尺寸。
只需比较上底、下底、高度中的最大值即可。
由于高度为25cm,
所以最大实体尺寸为25cm。
结论
同轴度最大实体尺寸计算可以应用于各种形状的物体。
通过比较
不同维度的尺寸,我们可以确定物体的最大宽度,从而更好地进行设计、制造或运输。
这一计算方法在工程领域、建筑设计、物流等方面
具有实际应用的重要性。
无论是规则形状还是不规则形状的物体,我
们都可以通过适当的方法计算出其同轴度最大实体尺寸。
